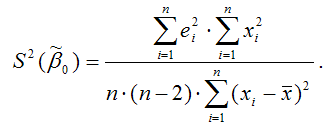
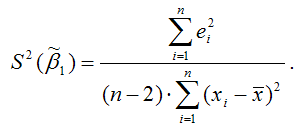
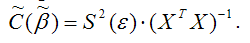
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.
Для оценки качества модели регрессии используются специальные показатели.
Качество линейной модели парной регрессии характеризуется с помощью следующих показателей:
1) парной линейный коэффициент корреляции, который рассчитывается по формуле:
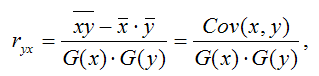где G(x) – среднеквадратическое отклонение независимой переменной;
G(y) – среднеквадратическое отклонение зависимой переменной.
Также парный линейный коэффициент корреляции можно рассчитать через МНК-оценку коэффициента модели регрессии
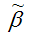по формуле:
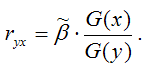Парный линейный коэффициент корреляции характеризует степень тесноты связи между исследуемыми переменными. Он рассчитывается только для количественных переменных. Чем ближе модуль значения коэффициента корреляции к единице, тем более тесной является связь между исследуемыми переменными. Данный коэффициент изменяется в пределах [-1; +1]. Если значение коэффициента корреляции находится в пределах от нуля до единицы, то связь между переменными прямая, т. е. с увеличением независимой переменной увеличивается и зависимая переменная, и наборот. Если коэффициент корреляции находится в пределах от минус еиницы до нуля, то связь между переменными обратная, т. е. с увеличением независимой переменной уменьшается зависимая переменная, и наоборот. Если коэффициент корреляции равен нулю, то связь между переменными отсутствует. Если коэффициент корреляции равен единице или минус единице, то связь между переменными существует функциональная связь, т. е. изменения независимой и зависимой переменных полностью соответствуют друг другу.
2) коэффициент детерминации рассчитывается как вадрат парного линейного коэффициента корреляции и обозначается как ryx2. Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимой переменной, в общем объёме вариации.
Качество линейной модели множественной регрессии характеризуется с помощью показателей, построенных на основе теоремы о разложении дисперсий.
Теорема. Общая дисперсия зависимой переменной может быть разложена на объяснённую и необъяснённую построенной моделью регрессии дисперсии:
G2(y)=σ2(y)+δ2(y),
где G2(y) – это общая дисперсия зависимой переменной;
σ2(y) – это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:
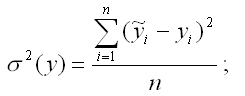δ2(y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:
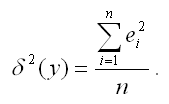С использованием теоремы о разложении дисперсий рассчитываются следующие показатели качества линейной модели множественной регрессии:
1) множественный коэффициент корреляции между зависимой переменной у и несколькими независимыми переменными хi:
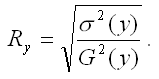Данный коэффициент характеризует степень тесноты связи между зависимой и независимыми переменными. Свойства множественного коэффициента корреляции аналогичны свойствам линейнойго парного коэффициента корреляции.
2) теоретический коэффициент детерминации рассчитывается как квадрат множественного коэффициента корреляции:
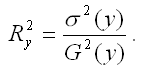Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимых переменных;
3) показатель
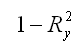характеризует в процентном отношении ту долю вариации зависимой переменной, которая не учитывается а построенной модели регрессии;
4) среднеквадратическая ошибка модели регрессии (Mean square error – MSE):
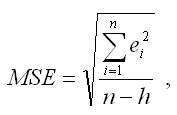где h– это количество параметров, входящих в модель регрессии.
Если показатель среднеквадратической ошибки окажется меньше показателя среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений β(у), то модель регрессии можно считать качественной.
Показатель среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений рассчитывается по формуле:
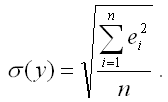5) показатель средней ошибки аппроксимации рассчитывается по формуле:
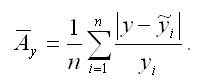Если величина данного показателя составляет менее 6-7%, то качество построенной модели регрессии считается хорошим. Максимально допустимым значением показателя средней ошибки аппроксимации считается 12-15 %.
Для оценки качества модели регрессии используются специальные показатели.
Качество линейной модели парной регрессии характеризуется с помощью следующих показателей:
1) парной линейный коэффициент корреляции, который рассчитывается по формуле:
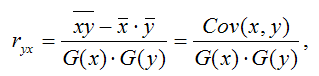
G(y) – среднеквадратическое отклонение зависимой переменной.
Также парный линейный коэффициент корреляции можно рассчитать через МНК-оценку коэффициента модели регрессии
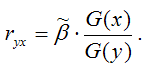
2) коэффициент детерминации рассчитывается как вадрат парного линейного коэффициента корреляции и обозначается как ryx2. Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимой переменной, в общем объёме вариации.
Качество линейной модели множественной регрессии характеризуется с помощью показателей, построенных на основе теоремы о разложении дисперсий.
Теорема. Общая дисперсия зависимой переменной может быть разложена на объяснённую и необъяснённую построенной моделью регрессии дисперсии:
G2(y)=σ2(y)+δ2(y),
где G2(y) – это общая дисперсия зависимой переменной;
σ2(y) – это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:
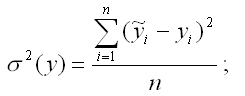
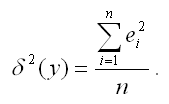
1) множественный коэффициент корреляции между зависимой переменной у и несколькими независимыми переменными хi:
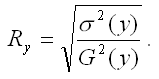
2) теоретический коэффициент детерминации рассчитывается как квадрат множественного коэффициента корреляции:
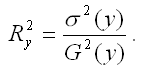
3) показатель
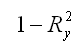
4) среднеквадратическая ошибка модели регрессии (Mean square error – MSE):
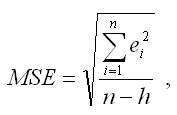
Если показатель среднеквадратической ошибки окажется меньше показателя среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений β(у), то модель регрессии можно считать качественной.
Показатель среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений рассчитывается по формуле:
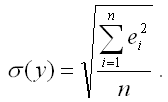
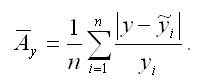
19. Понятие статистической гипотезы. Общая постановка задачи проверки статистической гипотезы
Проверка статистических гипотез – это один из основных методов математической статистики, который используется в эконометрике.
С помощью методов математической статистики можно проверить предположения о законе распределения некоторой случайной величины (генеральной совокупности), о значениях параметров этого закона (например, математического ожидания или дисперсии), о наличии корреляционной зависимости между случайными величинами, определенными на множестве объектов одной и той же генеральной совокупности.
Предположим, что на основании имеющихся данных у исследователя есть основания выдвинуть предположения о законе распределения или о параметре закона распределения случайной величины (или генеральной совокупности, на множестве объектов которой определена эта случайная величина). Задача проверки статистической гипотезы заключается в подтверждении или опровержении этого предположения на основании выборочных (экспериментальных) данных.
Статистической гипотезой называется любое предположение о виде неизвестного закона распределения или о параметрах известных распределений.
Параметрической гипотезой называется гипотеза о значениях параметров распределения или о сравнительной величине параметров двух распределений.
Примером параметрической статистической гипотезы является гипотеза о равенстве математических ожиданий двух нормальных совокупностей.
Непараметрическими гипотезами называются гипотезы о виде распределения случайной величины.
Проверка статистической гипотезы означает проверку соответствия выборочных данных выдвинутой гипотезе.
Параллельно с выдвигаемой основной гипотезой рассматривают и противоречащую ей гипотезу, которая называется конкурирующей или альтернативной. Противоречащая гипотеза считается справедливой, если основная выдвинутая гипотеза отвергается.
Нулевой, основной или проверяемой гипотезой называется первоначально выдвинутая гипотеза, которая обозначается Н0.
Конкурирующей или альтернативной гипотезой называется гипотеза, которая противоречит основной гипотезе Н0 и обозначается Н1.
Например, основная гипотеза Н0 состоит в том, что математическое ожидание μ равно значению μ0. В этом случае конкурирующая гипотеза Н1 может состоять в предположении, что математическое ожидание μ не равно (больше или меньше) значения μ0:
Н0: μ=μ0;
Н1: μ≠μ0,
или
Н1: μ>μ0,
или
Н1: μ<μ0.
Простой гипотезой называется гипотеза, которая содержит только одно предположение. Например, гипотеза о том, что параметр распределения Пуассона λ равен значению λ0, является простой. Основная гипотеза о том, что математическое ожидание нормального распределения равно 5 (при известной дисперсии), т.е.
Н0: а=5,
также является простой.
Сложной гипотезой называется гипотеза, которая состоит из нескольких простых гипотез. Например, сложная гипотеза вида:
Н0: λ>4,
состоит из множества простых гипотез вида:
Н0: λ>m,
где m – это люблое число, большее четырёх.
С помощью методов математической статистики можно проверить предположения о законе распределения некоторой случайной величины (генеральной совокупности), о значениях параметров этого закона (например, математического ожидания или дисперсии), о наличии корреляционной зависимости между случайными величинами, определенными на множестве объектов одной и той же генеральной совокупности.
Предположим, что на основании имеющихся данных у исследователя есть основания выдвинуть предположения о законе распределения или о параметре закона распределения случайной величины (или генеральной совокупности, на множестве объектов которой определена эта случайная величина). Задача проверки статистической гипотезы заключается в подтверждении или опровержении этого предположения на основании выборочных (экспериментальных) данных.
Статистической гипотезой называется любое предположение о виде неизвестного закона распределения или о параметрах известных распределений.
Параметрической гипотезой называется гипотеза о значениях параметров распределения или о сравнительной величине параметров двух распределений.
Примером параметрической статистической гипотезы является гипотеза о равенстве математических ожиданий двух нормальных совокупностей.
Непараметрическими гипотезами называются гипотезы о виде распределения случайной величины.
Проверка статистической гипотезы означает проверку соответствия выборочных данных выдвинутой гипотезе.
Параллельно с выдвигаемой основной гипотезой рассматривают и противоречащую ей гипотезу, которая называется конкурирующей или альтернативной. Противоречащая гипотеза считается справедливой, если основная выдвинутая гипотеза отвергается.
Нулевой, основной или проверяемой гипотезой называется первоначально выдвинутая гипотеза, которая обозначается Н0.
Конкурирующей или альтернативной гипотезой называется гипотеза, которая противоречит основной гипотезе Н0 и обозначается Н1.
Например, основная гипотеза Н0 состоит в том, что математическое ожидание μ равно значению μ0. В этом случае конкурирующая гипотеза Н1 может состоять в предположении, что математическое ожидание μ не равно (больше или меньше) значения μ0:
Н0: μ=μ0;
Н1: μ≠μ0,
или
Н1: μ>μ0,
или
Н1: μ<μ0.
Простой гипотезой называется гипотеза, которая содержит только одно предположение. Например, гипотеза о том, что параметр распределения Пуассона λ равен значению λ0, является простой. Основная гипотеза о том, что математическое ожидание нормального распределения равно 5 (при известной дисперсии), т.е.
Н0: а=5,
также является простой.
Сложной гипотезой называется гипотеза, которая состоит из нескольких простых гипотез. Например, сложная гипотеза вида:
Н0: λ>4,
состоит из множества простых гипотез вида:
Н0: λ>m,
где m – это люблое число, большее четырёх.
20. Ошибки первого и второго рода. Понятие о статистических критериях. Критическая область, критические точки
Проверка статистической гипотезы означает проверку согласования исходных выборочных данных с выдвинутой основной гипотезой. При этом возможно возникновение двух ситуаций – основная гипотеза может подтвердиться, а может и опровергнуться. Следовательно, при проверке статистических гипотез существует вероятность допустить ошибку, приняв или опровергнув верную гипотезу.
При проверке статистических гипотез можно допустить ошибки первого или второго рода
Ошибкой первого рода называется ошибка, состоящая в опровержении верной гипотезы.
Ошибкой второго рода называется ошибка, состоящая в принятии ложной гипотезы.
Уровнем значимостиа называется вероятность совершения ошибки первого рода.
Значение уровеня значимости а обычно задаётся близким к нулю (например, 0,05; 0,01;0,02 и т. д.), потому что чем меньше значение уровеня значимости, тем меньше вероятность совершения ошибки первого рода, состоящую в опровержении верной гипотезы Н0.
Вероятность совершения ошибки второго рода, т. е. принятия ложной гипотезы, обозначается β.
При проверке нулевой гипотезы Н0возможно возникновение следующих ситуаций:
Проверка справедливости сттатистическвх гипотез осуществляется с помощью различных статистических критериев.
Статистическим критерием называется случайная величина, которая используется с целью проверки нулевой гипотезы.
Статистические критерии называются соответственно тому закону распределения, которому они подчиняются, т. е. F-критерий подчиняется распределению Фишера-Снедекора, χ2-критерий подчиняется χ2-распределению, Т-критерий подчиняется распределению Стьюдента, U-критерий подчиняется нормальному распределению.
Наблюдаемым значением статистического критерия называется значение критерия, которое рассчитано по выборочной совокупности, подчиняющейся определённому закону распределения.
Множество всех возможных значений выбранного статистического критерия делится на два непересекающихся подмножества. Первое подмножество включает в себя те значения критерия, при которых основная гипотеза отвергается, а второе подмножество – те значения критерия, при которых основная гипотеза принимается.
Критической областью называется множество возможных значений статистического критерия, при которых основная гипотеза отвергается.
Областью принятия гипотезы или областью допустимых значений называется множество возможных значений статистического критерия, при которых основная гипотеза принимается.
Если наблюдаемое значение статистического критерия, рассчитанное по данным выборочной совокупности, принадлежит критической области, то основная гипотеза отвергается. Если наблюдаемое значение статистического критерия принадлежит области принятия гипотезы, то основная гипотеза принимается.
Критическими точками или квантилями называются точки, разграничивающие критическую область и область принятия гипотезы.
Критические области могут быть как односторонними, так и двусторонними.
При проверке статистических гипотез можно допустить ошибки первого или второго рода
Ошибкой первого рода называется ошибка, состоящая в опровержении верной гипотезы.
Ошибкой второго рода называется ошибка, состоящая в принятии ложной гипотезы.
Уровнем значимостиа называется вероятность совершения ошибки первого рода.
Значение уровеня значимости а обычно задаётся близким к нулю (например, 0,05; 0,01;0,02 и т. д.), потому что чем меньше значение уровеня значимости, тем меньше вероятность совершения ошибки первого рода, состоящую в опровержении верной гипотезы Н0.
Вероятность совершения ошибки второго рода, т. е. принятия ложной гипотезы, обозначается β.
При проверке нулевой гипотезы Н0возможно возникновение следующих ситуаций:
Проверка справедливости сттатистическвх гипотез осуществляется с помощью различных статистических критериев.
Статистическим критерием называется случайная величина, которая используется с целью проверки нулевой гипотезы.
Статистические критерии называются соответственно тому закону распределения, которому они подчиняются, т. е. F-критерий подчиняется распределению Фишера-Снедекора, χ2-критерий подчиняется χ2-распределению, Т-критерий подчиняется распределению Стьюдента, U-критерий подчиняется нормальному распределению.
Наблюдаемым значением статистического критерия называется значение критерия, которое рассчитано по выборочной совокупности, подчиняющейся определённому закону распределения.
Множество всех возможных значений выбранного статистического критерия делится на два непересекающихся подмножества. Первое подмножество включает в себя те значения критерия, при которых основная гипотеза отвергается, а второе подмножество – те значения критерия, при которых основная гипотеза принимается.
Критической областью называется множество возможных значений статистического критерия, при которых основная гипотеза отвергается.
Областью принятия гипотезы или областью допустимых значений называется множество возможных значений статистического критерия, при которых основная гипотеза принимается.
Если наблюдаемое значение статистического критерия, рассчитанное по данным выборочной совокупности, принадлежит критической области, то основная гипотеза отвергается. Если наблюдаемое значение статистического критерия принадлежит области принятия гипотезы, то основная гипотеза принимается.
Критическими точками или квантилями называются точки, разграничивающие критическую область и область принятия гипотезы.
Критические области могут быть как односторонними, так и двусторонними.
21. Правосторонняя критическая область. Левосторонняя и двусторонняя критические области. Мощность критерия
При проверке статистических гипотез используют правосторонние, левосторонние и двусторонние критические области.
Правосторонняя критическая область характеризуется неравенством вида:
L>lкр,
где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;
lкр, – это положительное значение статистического критерия, определяемое по таблице распределения данного критерия.
Следовательно, для определения правосторонней критической области необходимо рассчитать положительное значение статистического критерия lкр.
Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, вероятность того, что значение статистического критерия L будет больше значения lкр, равна заданному уровню значимости, т.е. P(L>lкр)=a.
Для каждого статистического критерия рассчитаны специальные таблицы, с помощью которых определяют критическую точку, удовлетворяющую заданному уровню значимости.
Левосторонняя критическая область характеризуется неравенством вида:
L<lкр,
где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;
lкр, — это отрицательное значение статистического критерия, определяемое по таблице распределения данного критерия.
Следовательно, для определения левосторонней критической области необходимо найти рассчитать отрицательное значение статистического критерия lкр.
Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, вероятность того, что значение статистического критерия L будет меньше значения lкр, равна заданному уровню значимости, т.е. P(L<lкр)=a.
Двусторонняя критическая область характеризуется двумя неравенствами вида:
L>lкр1 и L<lкр2,
где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;
lкр1 – это положительное значение статистического критерия, определяемое по таблице распределения данного критерия;
lкр2 — это отрицательное значение статистического критерия, определяемое по таблице распределения данного критерия;
lкр1> lкр2.
Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, сумма вероятностей того, что значение статистического критерия L будет больше значения lкр1 или меньше значения lкр2, равна заданному уровню значимости, т.е. P(L>lкр1)+(L<lкр2)=a.
Выбор критической области осуществляется исходя из вида конкурирующей гипотезы Н1. При этом применяются следующие правила:
1) правосторонняя критическая область выбирается в том случае, если Н1:>;
2) левосторонняя критическая область выбирается в том случае, если Н1:‹;
3) двусторонняя критическая область выбирается в том случае, если Н1:≠.
Предположим, что заданы следующие параметры:
1) статистический критерий L;
2) критическая область W, где H0 отклоняется;
3) область принятия гипотезы
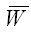где H0 не отклоняется;
4) вероятность совершить ошибку первого рода a;
5) вероятность совершить ошибку второго рода β.
Тогда справедливо утверждение о том, что выражение
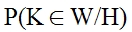является вероятностью того, что статистический критерий L попадёт в критическую область, если верна гипотеза H.
При построении критической области учитываются два требования:
1) вероятность того, что статистический критерий L попадёт в критическую область, если верна Н0, равна а:
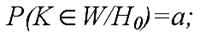данное равенство задаёт вероятность совершения ошибки первого рода;
2) вероятность того, что статистический критерий L попадёт в критическую область (область отклонения гипотезы Н0 в пользу гипотезы Н1), если верна гипотеза Н1:
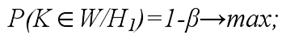данное равенство задаёт вероятность принятия правильной гипотезы.
Мощностью статистического критерия называется вероятность попадания данного критерия в критическую область, при условии, что справедлива конкурирующая гипотеза Н1, т. е.выражение 1-β является мощностью критерия.
Если уровень значимости уже выбран, то критическую область следует строить так, чтобы мощность критерия была максимальной. Выполнение этого требования обеспечивает минимальную ошибку второго рода, состоящую в том, что будет принята неправильная гипотеза.
Правосторонняя критическая область характеризуется неравенством вида:
L>lкр,
где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;
lкр, – это положительное значение статистического критерия, определяемое по таблице распределения данного критерия.
Следовательно, для определения правосторонней критической области необходимо рассчитать положительное значение статистического критерия lкр.
Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, вероятность того, что значение статистического критерия L будет больше значения lкр, равна заданному уровню значимости, т.е. P(L>lкр)=a.
Для каждого статистического критерия рассчитаны специальные таблицы, с помощью которых определяют критическую точку, удовлетворяющую заданному уровню значимости.
Левосторонняя критическая область характеризуется неравенством вида:
L<lкр,
где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;
lкр, — это отрицательное значение статистического критерия, определяемое по таблице распределения данного критерия.
Следовательно, для определения левосторонней критической области необходимо найти рассчитать отрицательное значение статистического критерия lкр.
Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, вероятность того, что значение статистического критерия L будет меньше значения lкр, равна заданному уровню значимости, т.е. P(L<lкр)=a.
Двусторонняя критическая область характеризуется двумя неравенствами вида:
L>lкр1 и L<lкр2,
где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;
lкр1 – это положительное значение статистического критерия, определяемое по таблице распределения данного критерия;
lкр2 — это отрицательное значение статистического критерия, определяемое по таблице распределения данного критерия;
lкр1> lкр2.
Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, сумма вероятностей того, что значение статистического критерия L будет больше значения lкр1 или меньше значения lкр2, равна заданному уровню значимости, т.е. P(L>lкр1)+(L<lкр2)=a.
Выбор критической области осуществляется исходя из вида конкурирующей гипотезы Н1. При этом применяются следующие правила:
1) правосторонняя критическая область выбирается в том случае, если Н1:>;
2) левосторонняя критическая область выбирается в том случае, если Н1:‹;
3) двусторонняя критическая область выбирается в том случае, если Н1:≠.
Предположим, что заданы следующие параметры:
1) статистический критерий L;
2) критическая область W, где H0 отклоняется;
3) область принятия гипотезы
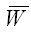
4) вероятность совершить ошибку первого рода a;
5) вероятность совершить ошибку второго рода β.
Тогда справедливо утверждение о том, что выражение
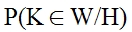
При построении критической области учитываются два требования:
1) вероятность того, что статистический критерий L попадёт в критическую область, если верна Н0, равна а:
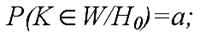
2) вероятность того, что статистический критерий L попадёт в критическую область (область отклонения гипотезы Н0 в пользу гипотезы Н1), если верна гипотеза Н1:
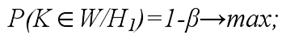
Мощностью статистического критерия называется вероятность попадания данного критерия в критическую область, при условии, что справедлива конкурирующая гипотеза Н1, т. е.выражение 1-β является мощностью критерия.
Если уровень значимости уже выбран, то критическую область следует строить так, чтобы мощность критерия была максимальной. Выполнение этого требования обеспечивает минимальную ошибку второго рода, состоящую в том, что будет принята неправильная гипотеза.
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.
Необходимость проверки гипотез о значимости параметров модели вызвана тем, что в дальнейшем построенную модель будут использовать для дальнейших экономических расчётов.
Предположим, что по данным выборочной совокупности была построена линейная модель парной регрессии. Задача состоит в проверке значимости оценок неизвестных коэффициентов модели, полученных методом наименьших квадратов.
Основная гипотеза состоит в предположении о незначимости коэффициентов регрессии, т. е.
Н0:β0=0, или Н0:β1=0.
Обратная или конкурирующая гипотеза состоит в предположении о значимости коэффициентов регрессии, т.е.
Н1:β0≠0, или Н1:β1≠0.
Данные гипотезы проверяются с помощью t-критерия Стьюдента.
Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают со значением t-критерия, которое определяется по таблице распределения Стьюдента и называется критическим.
Критическое значение t-критерия зависит от уровня значимости и числа степеней свободы.
Уровнем значимостиа называется величина, которая рассчитывается по формуле:
а=1-γ,
где γ – это доверительная вероятность попадания оцениваемого параметра в доверительный интервал. Значение доверительной вероятности должно быть близким к единице, например, 0.95, 0.99. Следовательно, уровень значимости а можно определить как вероятность того, что оцениваемый параметр не попадёт в доверительный интервал.
Числом степеней свободы называется показатель, который рассчитывается как разность между объёмом выборочной совокупности n и числом оцениваемых параметров по данной выборке h. Для линейной модели парной регрессии число степеней свободы рассчитывается как (n-2), потому что по данным выборочной совокупности оцениваются только два параметра – β0 и β1.
Таким образом, критическое значение t-критерия Стьюдента определяется как tкрит(а;n-h).
При проверке основной гипотезы вида Н0:β1=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:
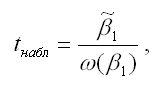
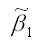где – оценка параметра модели регрессии β1;
ω(β1) – величина стандартной ошибки параметра модели регрессии β1.
Показатель стандартной ошибки параметра модели регрессии β1 для линейной модели парной регрессии рассчитывается по формуле:
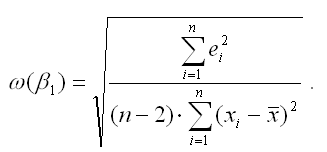Числитель стандартной ошибки может быть рассчитан через парный коэффициент детерминации следующим образом:
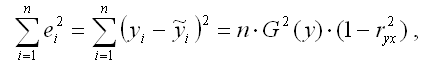где G2(y) – общая дисперсия зависимой переменной;
r2yx – парный коэффициент детерминации между зависимой и независимой переменными.
При проверке основной гипотезы β0=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:
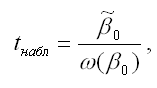где
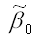– оценка параметра модели регрессии β0;
ω(β0) – величина стандартной ошибки параметра модели регрессии β0.
Показатель стандартной ошибки параметра β0 модели регрессии для линейной модели парной регрессии рассчитывается по формуле:
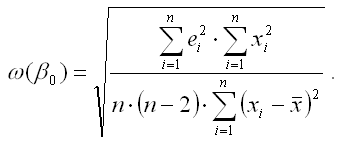При проверке основных гипотез возможны следующие ситуации:
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|›tкрит, то с вероятностью (1-а) или γ основная гипотеза о незначимости параметров модели регрессии отвергается.
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|≤tкрит, то с вероятностью а или (1-γ) основная гипотеза о незначимости параметров модели регрессии принимается.
Необходимость проверки гипотез о значимости параметров модели вызвана тем, что в дальнейшем построенную модель будут использовать для дальнейших экономических расчётов.
Предположим, что по данным выборочной совокупности была построена линейная модель парной регрессии. Задача состоит в проверке значимости оценок неизвестных коэффициентов модели, полученных методом наименьших квадратов.
Основная гипотеза состоит в предположении о незначимости коэффициентов регрессии, т. е.
Н0:β0=0, или Н0:β1=0.
Обратная или конкурирующая гипотеза состоит в предположении о значимости коэффициентов регрессии, т.е.
Н1:β0≠0, или Н1:β1≠0.
Данные гипотезы проверяются с помощью t-критерия Стьюдента.
Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают со значением t-критерия, которое определяется по таблице распределения Стьюдента и называется критическим.
Критическое значение t-критерия зависит от уровня значимости и числа степеней свободы.
Уровнем значимостиа называется величина, которая рассчитывается по формуле:
а=1-γ,
где γ – это доверительная вероятность попадания оцениваемого параметра в доверительный интервал. Значение доверительной вероятности должно быть близким к единице, например, 0.95, 0.99. Следовательно, уровень значимости а можно определить как вероятность того, что оцениваемый параметр не попадёт в доверительный интервал.
Числом степеней свободы называется показатель, который рассчитывается как разность между объёмом выборочной совокупности n и числом оцениваемых параметров по данной выборке h. Для линейной модели парной регрессии число степеней свободы рассчитывается как (n-2), потому что по данным выборочной совокупности оцениваются только два параметра – β0 и β1.
Таким образом, критическое значение t-критерия Стьюдента определяется как tкрит(а;n-h).
При проверке основной гипотезы вида Н0:β1=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:
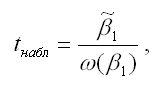
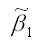
ω(β1) – величина стандартной ошибки параметра модели регрессии β1.
Показатель стандартной ошибки параметра модели регрессии β1 для линейной модели парной регрессии рассчитывается по формуле:
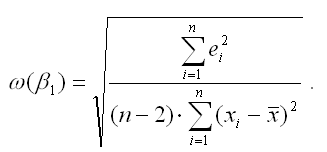
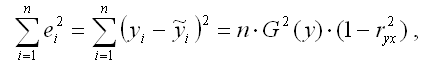
r2yx – парный коэффициент детерминации между зависимой и независимой переменными.
При проверке основной гипотезы β0=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:
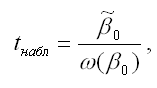
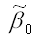
ω(β0) – величина стандартной ошибки параметра модели регрессии β0.
Показатель стандартной ошибки параметра β0 модели регрессии для линейной модели парной регрессии рассчитывается по формуле:
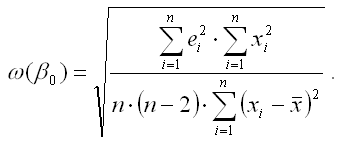
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|›tкрит, то с вероятностью (1-а) или γ основная гипотеза о незначимости параметров модели регрессии отвергается.
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|≤tкрит, то с вероятностью а или (1-γ) основная гипотеза о незначимости параметров модели регрессии принимается.
23. Проверка гипотезы о значимости парного коэффициента корреляции
Предположим, что по данным выборочной совокупности была построена линейная модель парной регрессии. Задача состоит в проверке значимости парного коэффициента корреляции между результативной переменной у и факторной переменной х.
Основная гипотеза состоит в предположении о незначимости парного коэффициента корреляции, т. е.
Н0:rxy=0.
Обратная или конкурирующая гипотеза состоит в предположении о значимости парного коэффициента корреляции, т. е.
Н1:rxy≠0.
Данные гипотезы проверяются с помощью t-критерия Стьюдента.
Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением t-критерия, которое определяется по таблице распределения Стьюдента.
При проверке значимости парного коэффициента корреляции критическое значение t-критерия определяется как tкрит(a;n-h), где а – уровень значимости, (n-h) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента.
При проверке основной гипотезы вида Н0:rxy=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:
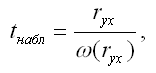где ryx – выборочный парный коэффициент корреляции между результативной переменной у и факторной переменной х, который рассчитывается по формуле:
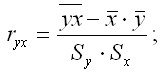ω(ryx) – величина стандартной ошибки парного выборочного коэффициента корреляции.
Показатель стандартной ошибки парного выборочного коэффициента корреляции для линейной модели парной регрессии рассчитывается по формуле:
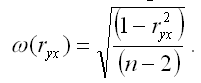Если данное выражение подставить в формулу для расчёта наблюдаемого значения t-критерия для проверки гипотезы вида Н0:rxy=0, то получим:
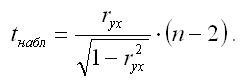При проверке основной гипотезы возможны следующие ситуации:
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е.
tнабл|>tкрит, то с вероятностью (1-а) или γ основная гипотеза о незначимости парного коэффициента корреляции отвергается.
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т.е. |tнабл|≤tкрит, то с вероятностью а или (1-γ) основная гипотеза о незначимости парного коэффициента корреляции принимается. В этом случае корреляционная зависимость между исследуемыми переменными отсутствует, и продолжение регрессионного анализа считается нецелесообразным.
Применение t-статистики Стьюдента для проверки гипотезы вида Н0:rxy=0 основано на выполнении двух условий:
1) если объём выборочной совокупности достаточно велик (n≥30);
2) коэффициент корреляции по модулю значительно меньше единицы:
0,45≤|ryx|≤0.75.
В том случае, если модуль парного выборочного коэффициента корреляции близок к единице, то гипотеза вида Н0:rxy=0 также может быть проверена с помощью z-статистики. Данный метод оценки значимости парного коэффициента корреляции был предложен Р. Фишером.
Основная гипотеза состоит в предположении о незначимости парного коэффициента корреляции, т. е.
Н0:rxy=0.
Обратная или конкурирующая гипотеза состоит в предположении о значимости парного коэффициента корреляции, т. е.
Н1:rxy≠0.
Данные гипотезы проверяются с помощью t-критерия Стьюдента.
Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением t-критерия, которое определяется по таблице распределения Стьюдента.
При проверке значимости парного коэффициента корреляции критическое значение t-критерия определяется как tкрит(a;n-h), где а – уровень значимости, (n-h) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента.
При проверке основной гипотезы вида Н0:rxy=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:
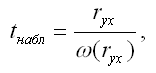
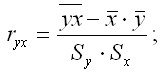
Показатель стандартной ошибки парного выборочного коэффициента корреляции для линейной модели парной регрессии рассчитывается по формуле:
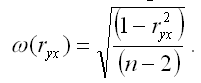
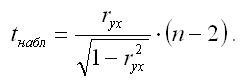
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е.
tнабл|>tкрит, то с вероятностью (1-а) или γ основная гипотеза о незначимости парного коэффициента корреляции отвергается.
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т.е. |tнабл|≤tкрит, то с вероятностью а или (1-γ) основная гипотеза о незначимости парного коэффициента корреляции принимается. В этом случае корреляционная зависимость между исследуемыми переменными отсутствует, и продолжение регрессионного анализа считается нецелесообразным.
Применение t-статистики Стьюдента для проверки гипотезы вида Н0:rxy=0 основано на выполнении двух условий:
1) если объём выборочной совокупности достаточно велик (n≥30);
2) коэффициент корреляции по модулю значительно меньше единицы:
0,45≤|ryx|≤0.75.
В том случае, если модуль парного выборочного коэффициента корреляции близок к единице, то гипотеза вида Н0:rxy=0 также может быть проверена с помощью z-статистики. Данный метод оценки значимости парного коэффициента корреляции был предложен Р. Фишером.
Конец бесплатного ознакомительного фрагмента