Второй вопрос – величина и важность критериев. Как только формула модели определена, разработчикам следует разграничить величину и весовой коэффициент критерия. В предыдущей формуле B, C, D – величины соответствующих факторов конкретного проекта, в то время как b, c, d – весовые коэффициенты, назначенные этим факторам, которые отражают важность, присвоенную им принимающим решение лицом. В случае взаимозаменяемых факторов отношение b/c представляет собой показатель взаимозаменяемости между факторами B и C. Если B уменьшается на единицу, то C должен возрасти как минимум на величину b/c, чтобы сумма данных факторов осталась постоянной или возросла. Иными словами, менеджер, принимающий решение, волен жертвовать одним фактором в пользу другого в соответствии с их весами до тех пор, пока полная сумма остается постоянной или возрастает.
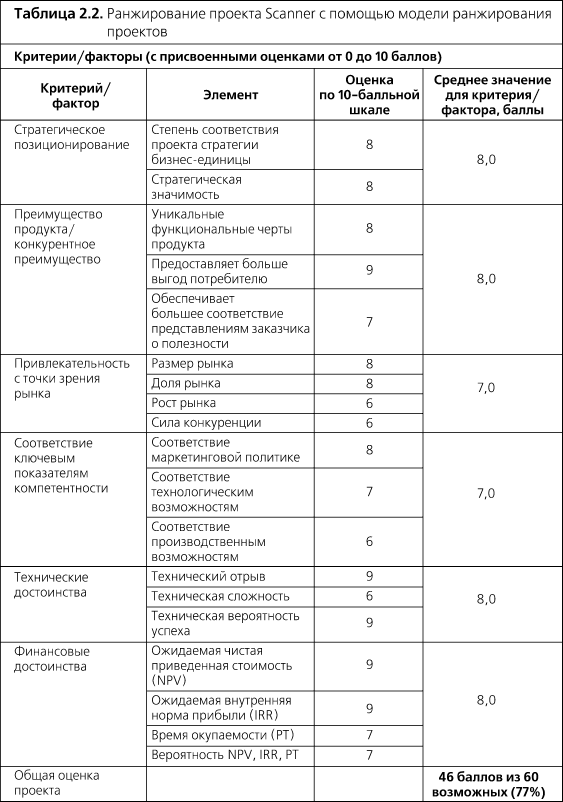
Для определения ранжирования проектов в табл. 2.2 (столбец «Элемент») использована простая модель, описываемая формулой:
Общий балл = B + C + D.Здесь общий балл равен сумме B, C и D, то есть сумме значений таких соответствующих им критериев, как уникальные функциональные характеристики продукта или техническая сложность (см. табл. 2.2).
Наконец, третий вопрос, требующий решения, – это вопрос измерения критериев. Некоторые критерии (такие как расходы и прибыли) поддаются объективному измерению, другие (такие как вероятность успеха и стратегическая важность) не поддаются и потому должны быть получены на основе суждения. Модели ранжирования могут легко включать в себя объективные и субъективные (определяемые на основе суждения) критерии. Хорошо, если субъективные критерии оцениваются по шкале, «проградуированной» в ключевых фразах, – это обеспечит единообразную оценку данного фактора для каждого из проектов. Оценки следует выполнять в пределах какой-либо удобной шкалы, например 10-балльной (см. врезку «Пример шкалы для измерения величины критерия “Доступность носителей навыков”»). Такая шкала должна быть разработана для каждого критерия, требующего субъективной оценки (см. табл. 2.2). Объективные факторы (в частности, стоимость) могут быть измерены непосредственно, что избавляет от необходимости использования подобной шкалы.
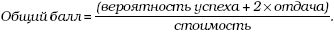
Ранжирование проектов. После того как определены критерии, выбрана формула, описывающая модель, установлены весовые коэффициенты и заданы измерительные шкалы, можно приступать к ранжированию проектов-кандидатов. Следует иметь в виду, что хотя менеджер, принимающий решение, должен получить у руководства информацию о критериях и их относительных весах, действие это выполняется единожды. Специфические и относящиеся к конкретным проектам данные в большинстве случаев предоставляются теми, кто предлагает эти проекты. Такие данные бывают объективными (например, стоимость, количество рабочих часов, использование станков) или представляют собой рейтинги в соответствии со шкалами, установленными ответственным менеджером. В некоторых случаях проектно-специфические данные могут быть получены не от тех, кто предлагает проект, а из альтернативных источников. Например, информацию о вероятности рыночного успеха или финансовой отдаче легче узнать в отделе маркетинга, чем в отделе НИОКР. Таким образом, хотя проектно-специфические данные нужно получать по каждому конкретному проекту, подлежащему ранжированию, сами критерии и их весовые коэффициенты должны оставаться неизменными до тех пор, пока руководство не примет решения об их пересмотре.
В большинстве случаев проектные данные имеют вид чисел, выраженных в некоторых единицах измерения и отличающихся по величине: вероятность в виде десятичной дроби меньше единицы, денежная стоимость в виде положительного числа, оценка по той или иной шкале в виде целого числа и т. д. Все эти значения необходимо привести к общему диапазону. Рассмотрим табл. 2.6, в которой изображен портфель, сформированный из предложенных проектов. Величины критериев по модулю варьируются в диапазоне от трех знаков слева от запятой до двух знаков справа от нее. Проектные данные принято стандартизировать путем вычитания из значения каждого критерия для каждого проекта его значения, усредненного по всем проектам, с последующим делением полученной разности на стандартное отклонение значения по каждому проекту. В терминах табл. 2.6 это означает вычитание из каждого значения столбца некоторого среднего для данного столбца значения, а затем деление полученной разности на стандартное отклонение для этого же столбца. После того как проектные данные загружены в электронную таблицу, процесс стандартизации становится тривиальным. Он выполняется одинаково легко как для десяти проектов, так и для тысячи.
ПРИМЕР ШКАЛЫ ДЛЯ ИЗМЕРЕНИЯ ВЕЛИЧИНЫ КРИТЕРИЯ «ДОСТУПНОСТЬ НОСИТЕЛЕЙ НАВЫКОВ»Предположив, что значения критериев, относящиеся к конкретным проектам, имеют приблизительно нормальное распределение, можно ожидать, что результатом такой операции будет стандартизованная величина, распределенная в диапазоне от – 3 до +3. Этот диапазон следует преобразовать в диапазон положительных величин. Если какое-либо из значений в таблице изначально равно нулю, стандартизованное значение также должно быть равно нулю. Для соблюдения данного требования необходимо ко всем значениям критерия в столбце прибавить абсолютную величину наиболее отрицательного значения данного критерия, получившегося после вышеописанной процедуры вычитания и деления. В результате будут получены стандартизованные величины, находящиеся в диапазоне от 0 приблизительно до +6. Если ни одно из первоначальных значений не равнялось нулю, к каждому значению нужно сначала прибавить 1, а затем – абсолютную величину наиболее отрицательного значения данного критерия. Это даст нам набор стандартизованных величин, укладывающихся в диапазон приблизительно от +1 до +7. Затем данные стандартизованные величины должны быть подставлены в формулу модели. Далее каждый проект получает балльную оценку, основанную на относительных весах, которые установлены руководством, и проектно-специфических данных, которые предоставлены теми, кто предлагает этот проект (и, возможно, другими подразделениями).
10. Все навыки имеются в достаточном объеме (с запасом).
9. Все навыки доступны в необходимом объеме (без запаса).
8. Все технические навыки доступны.
7. Большинство профессиональных навыков доступно.
6. Необходима некоторая переподготовка носителей технических навыков.
5. Необходима некоторая переподготовка носителей профессиональных навыков.
4. Необходима существенная переподготовка носителей технических навыков.
3. Необходима существенная переподготовка носителей профессиональных навыков.
2. Все носители технических навыков должны быть наняты.
1. Все носители технических навыков и некоторые носители профессиональных навыков должны быть наняты.
0. Все носители технических и профессиональных навыков должны быть наняты.
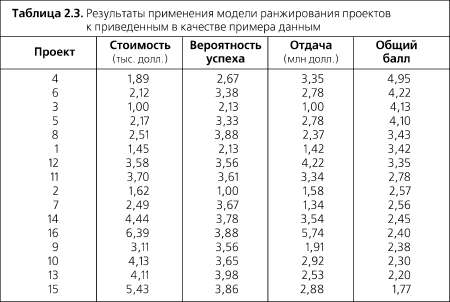
В табл. 2.3 показаны результаты применения вышеописанной модели к стандартизованным оценкам из табл. 2.6. Строки таблицы переупорядочены по убыванию общей оценки. Если стандартизованные значения загружаются в электронную таблицу, процесс вычисления становится тривиальным. Переупорядочивание строк таблицы в соответствии с убыванием общего балла также легко выполняется в электронной таблице. В нашем примере проект 4 имеет наивысшую оценку. Другие проекты ранжируются в соответствии со своими оценками. Следующим шагом могло бы стать утверждение проектов на выполнение – для этого нужно двигаться от начала списка вниз до тех пор, пока не будет исчерпан бюджет. Следует отметить, что различие оценок проектов 8 и 1 проявляется лишь в третьей значащей цифре. Поскольку исходные данные имели точность лишь в одну-две значащие цифры, к подобному различию не стоит относиться серьезно.
Использование моделей ранжирования проектов
Когда использовать модель. Хотя данные методы могут применяться для проектов любого типа, особенно хорошие результаты достигаются на ранних фазах жизненного цикла проекта – когда принимаются основные решения по выбору проектов. Возьмем, например, проекты разработки новых продуктов. Когда проект находится на ранних фазах, его рыночная отдача лежит в отдаленном будущем и может даже не рассматриваться в качестве критерия достоинств. Зато критерием, часто учитываемым в моделях ранжирования, становятся технические достоинства, и этот критерий может оказаться более значимым, чем экономическая отдача. Модели ранжирования проектов равно хорошо работают и с большими, и с малыми проектами других типов. Окончательная оценка обычно используется с двумя целями:
1. Для принятия решения продолжать/прекратить. Моменты принятия решения о продолжении или прекращении работ расположены в конкретных местах процесса управления, часто по завершении фаз проекта. Их предназначение – помочь решить, какие новые проекты инициировать и какие из выполняемых продолжить или прекратить.
2. Для расстановки приоритетов проектов. На данном этапе производятся выделение ресурсов в новые проекты, которые решено выполнять, а также подготовка полного списка новых и уже существующих проектов, куда уже выделены ресурсы, и расстановка приоритетов внутри этого списка.
Сравнение модели ранжирования проектов и аналитического иерархического процесса (AHP) – двух рассматриваемых нами инструментов ранжирования проектов – представлено в разделе «Аналитический иерархический процесс».
Время использования. Хотя принципы, лежащие в основе моделей ранжирования проектов, сравнительно просты, разработка эффективной модели может стать очень времяемким делом. В частности, в нашем примере компании потребовалось несколько лет для того, чтобы тщательно отобрать, описать, дать рабочие определения и протестировать каждый критерий на состоятельность и надежность. Эта детальная модель оценки включила в себя 19 критериев и была предназначена для ранжирования проектов стратегического роста. Применение модели подобного типа для сортировки, оценивания и ранжирования большой группы проектов вполне может занять один-два дня у каждого из тех, кто принимает решения. Иногда при принятии решений используются готовые модели для оценивания меньших, тактических проектов, что, как правило, требует нескольких часов работы (см. врезку «Советы по использованию моделей ранжирования проектов»).
Выгоды. Ценность модели ранжирования проектов состоит в возможности ее адаптации к конкретной ситуации, в которой принимается решение, с учетом многочисленных целей и критериев, имеющих характер как объективных данных, так и суждений, которые считаются важными [2]. Это позволяет избежать чрезмерного акцентирования на финансовых критериях, которые, как правило, не отличаются высокой надежностью на ранних этапах жизни проекта. При таком подходе принятие решений вынужденно базируется на тщательном рассмотрении каждого проекта с точки зрения единой совокупности критериев; особое внимание здесь уделяется критически важным критериям, поскольку одни критерии более важны, чем другие (что устанавливается путем присвоения весов). И наконец, модели ранжирования проектов могут быть подвергнуты анализу чувствительности – определению того, какое изменение весовых коэффициентов требуется для получения значительного изменения приоритетов.
Преимущества и недостатки. Существует множество точек зрения на преимущества и недостатки модели ранжирования проектов. Рассмотрим, в частности, следующие преимущества:
• модель концептуально проста. Она сводит сложную процедуру выбора и принятия решения к удобному в практическом использовании набору конкретных вопросов и выдает на выходе единообразные оценки, что существенно облегчает отбор проектов. Возможно, именно это является главной причиной широкого распространения моделей ранжирования проектов;
• она полностью прозрачна. Любой человек может изучить модель, проверить результат ее применения и понять, почему рейтинг получился именно таким;
• похоже, она работает. Несколько проведенных исследований показали, что модель способствует принятию верных решений. Представители Procter & Gamble утверждают, что их компьютерные модели ранжирования проектов имеют 85%-ную предсказательную способность [1];
• ее легко использовать. Менеджеры, вовлеченные в процесс отбора проектов, охарактеризовали модели ранжирования как инструменты, отличающиеся наибольшей легкостью в использовании и в высшей степени подходящие для отбора проектов.
• мнимая точность. Использование моделей неявно подразумевает, что полученные с их помощью результаты имеют высокую точность. На самом деле это отнюдь не так, и полученные оценки часто случайны. Именно поэтому моделями ранжирования проектов нельзя злоупотреблять, а их результаты не следует воспринимать как данность;
• потенциальная неэффективность распределения недостаточных ресурсов. Дело здесь в том, что модели ранжирования проектов не накладывают ограничений на требуемые ресурсы при максимизации оценки проекта – в отличие от ряда экономических методов, которые это делают;
• расход времени. Этот недостаток должен рассматриваться в свете важности принимаемых решений. В том случае, когда решения действительно являются ключевыми, на них следует потратить дополнительное время.
Вариации. Основные вариации в использовании моделей тесно связаны с такой их особенностью, как затраты времени. В попытках уменьшить время, необходимое на отбор проектов, компании ищут другие пути. Вместо того чтобы оценивать проекты силами высшего руководства и практиковать проведение дискуссий, в некоторых компаниях менеджеры сначала на совещании выполняют предварительную сортировку проектов и деление их на несколько групп по важности, а затем переходят к индивидуальному голосованию внутри групп. Другие опираются на оценки, выставленные отдельными лицами до проведения совещания. И хотя этот подход очень эффективен в смысле уменьшения затрат времени, он лишает людей, принимающих решение, возможности коллегиального изучения и обсуждения каждого фактора и достижения консенсуса. В редких случаях существует практика предварительного оценивания проектов силами самих проектных команд, после чего выставленные оценки выносятся на суд менеджеров, которые их принимают или опровергают.
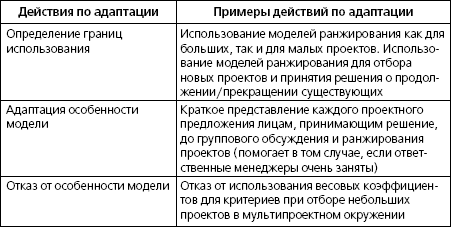
Адаптация моделей ранжирования проектов под нужды пользователя. Хотя модели ранжирования проектов – это очень полезные инструменты, необходимо понимать, что рассмотренные нами варианты носят общий характер и, как следствие, требуют адаптации под конкретные особенности и проекты компании. Ниже мы приведем ряд тезисов, касающихся такой адаптации.
1. Для принятия решения продолжать/прекратить. Моменты принятия решения о продолжении или прекращении работ расположены в конкретных местах процесса управления, часто по завершении фаз проекта. Их предназначение – помочь решить, какие новые проекты инициировать и какие из выполняемых продолжить или прекратить.
2. Для расстановки приоритетов проектов. На данном этапе производятся выделение ресурсов в новые проекты, которые решено выполнять, а также подготовка полного списка новых и уже существующих проектов, куда уже выделены ресурсы, и расстановка приоритетов внутри этого списка.
Сравнение модели ранжирования проектов и аналитического иерархического процесса (AHP) – двух рассматриваемых нами инструментов ранжирования проектов – представлено в разделе «Аналитический иерархический процесс».
Время использования. Хотя принципы, лежащие в основе моделей ранжирования проектов, сравнительно просты, разработка эффективной модели может стать очень времяемким делом. В частности, в нашем примере компании потребовалось несколько лет для того, чтобы тщательно отобрать, описать, дать рабочие определения и протестировать каждый критерий на состоятельность и надежность. Эта детальная модель оценки включила в себя 19 критериев и была предназначена для ранжирования проектов стратегического роста. Применение модели подобного типа для сортировки, оценивания и ранжирования большой группы проектов вполне может занять один-два дня у каждого из тех, кто принимает решения. Иногда при принятии решений используются готовые модели для оценивания меньших, тактических проектов, что, как правило, требует нескольких часов работы (см. врезку «Советы по использованию моделей ранжирования проектов»).
Выгоды. Ценность модели ранжирования проектов состоит в возможности ее адаптации к конкретной ситуации, в которой принимается решение, с учетом многочисленных целей и критериев, имеющих характер как объективных данных, так и суждений, которые считаются важными [2]. Это позволяет избежать чрезмерного акцентирования на финансовых критериях, которые, как правило, не отличаются высокой надежностью на ранних этапах жизни проекта. При таком подходе принятие решений вынужденно базируется на тщательном рассмотрении каждого проекта с точки зрения единой совокупности критериев; особое внимание здесь уделяется критически важным критериям, поскольку одни критерии более важны, чем другие (что устанавливается путем присвоения весов). И наконец, модели ранжирования проектов могут быть подвергнуты анализу чувствительности – определению того, какое изменение весовых коэффициентов требуется для получения значительного изменения приоритетов.
Преимущества и недостатки. Существует множество точек зрения на преимущества и недостатки модели ранжирования проектов. Рассмотрим, в частности, следующие преимущества:
• модель концептуально проста. Она сводит сложную процедуру выбора и принятия решения к удобному в практическом использовании набору конкретных вопросов и выдает на выходе единообразные оценки, что существенно облегчает отбор проектов. Возможно, именно это является главной причиной широкого распространения моделей ранжирования проектов;
• она полностью прозрачна. Любой человек может изучить модель, проверить результат ее применения и понять, почему рейтинг получился именно таким;
• похоже, она работает. Несколько проведенных исследований показали, что модель способствует принятию верных решений. Представители Procter & Gamble утверждают, что их компьютерные модели ранжирования проектов имеют 85%-ную предсказательную способность [1];
• ее легко использовать. Менеджеры, вовлеченные в процесс отбора проектов, охарактеризовали модели ранжирования как инструменты, отличающиеся наибольшей легкостью в использовании и в высшей степени подходящие для отбора проектов.
СОВЕТЫ ПО ИСПОЛЬЗОВАНИЮ МОДЕЛЕЙ РАНЖИРОВАНИЯ ПРОЕКТОВЕсли говорить о недостатках моделей ранжирования проектов, можно отметить следующее [2]:
Исходя из практических наблюдений, можно порекомендовать следующий подход к использованию моделей ранжирования проектов:
• оценивание должно проводить высшее руководство. Если определение оценок выполняется командами проектов, оно может оказаться предвзятым, возможно в пользу своих проектов;
• придать процессу вид дискуссии. Применение модели в режиме дискуссии обеспечивает участие руководителей высшего звена, поскольку они совместно рассматривают каждый проект, обсуждают его на соответствие каждому критерию, оценивают и добиваются консенсуса;
• использовать наглядную карту оценок. Когда каждому человеку, принимающему решение, предоставлена клавиатура, он может голосовать анонимно, но его голос будет немедленно введен в компьютер и результаты голосования появятся на большом экране.
• мнимая точность. Использование моделей неявно подразумевает, что полученные с их помощью результаты имеют высокую точность. На самом деле это отнюдь не так, и полученные оценки часто случайны. Именно поэтому моделями ранжирования проектов нельзя злоупотреблять, а их результаты не следует воспринимать как данность;
• потенциальная неэффективность распределения недостаточных ресурсов. Дело здесь в том, что модели ранжирования проектов не накладывают ограничений на требуемые ресурсы при максимизации оценки проекта – в отличие от ряда экономических методов, которые это делают;
• расход времени. Этот недостаток должен рассматриваться в свете важности принимаемых решений. В том случае, когда решения действительно являются ключевыми, на них следует потратить дополнительное время.
Вариации. Основные вариации в использовании моделей тесно связаны с такой их особенностью, как затраты времени. В попытках уменьшить время, необходимое на отбор проектов, компании ищут другие пути. Вместо того чтобы оценивать проекты силами высшего руководства и практиковать проведение дискуссий, в некоторых компаниях менеджеры сначала на совещании выполняют предварительную сортировку проектов и деление их на несколько групп по важности, а затем переходят к индивидуальному голосованию внутри групп. Другие опираются на оценки, выставленные отдельными лицами до проведения совещания. И хотя этот подход очень эффективен в смысле уменьшения затрат времени, он лишает людей, принимающих решение, возможности коллегиального изучения и обсуждения каждого фактора и достижения консенсуса. В редких случаях существует практика предварительного оценивания проектов силами самих проектных команд, после чего выставленные оценки выносятся на суд менеджеров, которые их принимают или опровергают.
Адаптация моделей ранжирования проектов под нужды пользователя. Хотя модели ранжирования проектов – это очень полезные инструменты, необходимо понимать, что рассмотренные нами варианты носят общий характер и, как следствие, требуют адаптации под конкретные особенности и проекты компании. Ниже мы приведем ряд тезисов, касающихся такой адаптации.
КОНТРОЛЬ МОДЕЛЕЙ РАНЖИРОВАНИЯ ПРОЕКТОВ
Такой контроль позволяет убедиться в том, что модель ранжирования проектов правильно структурирована и должным образом применяется. Он должен:
• основываться на проектных предложениях, стратегических и тактических планах, а также исторической информации;
• включать в себя уместные в данной ситуации критерии с весовыми коэффициентами и градуированными шкалами для оценки;
• оценивать каждый проект по каждому критерию, умножать значения критериев на их весовые коэффициенты, после чего суммировать результат по всем критериям;
• выдавать одиночную оценку для каждого проекта;
• обеспечивать возможность ранжирования проектов.
Резюме
В данном разделе были представлены модели ранжирования – инструмент отбора проектов. Эти модели посредством списка критериев помогают присваивать проектам оценки. Оценка (общий балл) является мерилом достоинств проекта. Более высокая оценка соответствует проекту с большими достоинствами. Хотя эти методы можно использовать для проекта любого типа, они особенно полезны в двух ситуациях: во-первых, на ранних фазах жизненного цикла проекта, когда принимаются основные решения и расставляются приоритеты, и, во-вторых, когда принимаются решения о продолжении/прекращении выполнения проекта.
Аналитический иерархический процесс
Что такое аналитический иерархический процесс?
Аналитический иерархический процесс (AHP), как и модель ранжирования, служит для ранжирования проектов. Однако модель ранжирования проектов – это одноуровневый процесс. Если один или несколько критериев состоят из подкритериев, которые комбинируются для получения общего значения этих критериев, то такое комбинирование должно выполняться за пределами модели. Аналитический иерархический процесс, напротив, включает в себя способы комбинирования этих подкритериев в явном виде. Таким образом, процедура использует иерархию, где каждый критерий подразделяется на подкритерии, соответствующие чьему-либо пониманию ситуации, в которой выполняется ранжирование проектов (см. рис. 2.3). Подобное разбиение дает возможность поиска причинно-следственных связей между целью (например, выбором наилучшего проекта), критериями (например, техническими достоинствами), подкритериями (например, вероятностью технического успеха) и проектами-кандидатами. Следующим шагом после установления иерархической структуры является взвешивание критериев и подкритериев с определением совокупных оценок каждого проекта на разных уровнях, а затем для всего проекта в целом. Совокупная оценка служит мерилом достоинств проекта: чем она выше, тем больше у проекта достоинств.
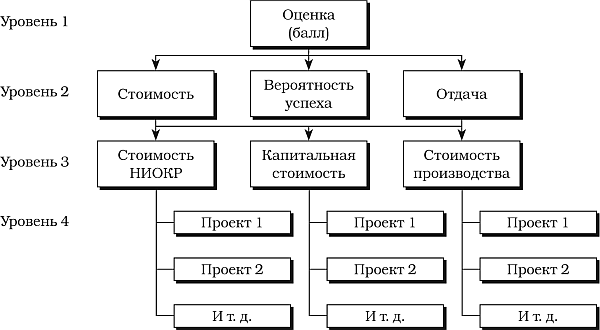Рис. 2.3. Пример иерархии решений AHP
Применение аналитического иерархического процесса
Описание АНР, к сожалению, в высшей степени абстрактно. Чтобы сделать его более конкретным, мы проиллюстрируем его с помощью того же «меню» исходных проектов и тех же критериев отбора, которые использовались и для модели ранжирования.
Определение проблемы (задачи) и цели. Первый шаг в процессе AHP – определить проблему (задачу) и цель. В нашем случае цель известна: нужно проранжировать новые и существующие проекты таким образом, чтобы иметь возможность выбирать для инициации лучшие из новых проектов и продолжать/прекращать те, которые уже выполняются.
Сбор исходной информации. Как и в моделях ранжирования проектов, аналитический иерархический процесс начинается с составления списка проектов-кандидатов и подбора исходной информации, на основе которой будет производиться ранжирование. Под исходной информацией понимаются:
• проектное предложение;
• стратегические и тактические планы;
• историческая информация.
Как уже было сказано в разделе «Модели ранжирования проектов», эта исходная информация обеспечивает понимание стратегии и целей компании, целей и содержания проекта, а также результатов решений, принятых по ходу отбора проектов в прошлом, и достигнутой ранее производительности проектов.
Формирование иерархической структуры. Как и в случае с любым другим методом выбора проектов, здесь необходимо решить, какие критерии следует применять для оценивания и ранжирования проектов. Особенность метода AHP состоит в том, что каждый критерий подразделяется на любое необходимое число подуровней. Чтобы проиллюстрировать это положение, мы будем использовать те же критерии, что и при рассмотрении модели ранжирования. Мы хотим проранжировать проекты в соответствии с их достоинствами с точки зрения стоимости, вероятности успеха и отдачи, причем критерий отдачи имеет вдвое больший вес, чем критерии вероятности успеха и стоимости. Иерархическая модель приведена на рис. 2.3. Поскольку в рассмотрение могут быть включены подкритерии, критерий «стоимость» был разделен. Однако, так как соответствующие данные в табл. 2.3 отсутствуют, при фактических вычислениях подкритерии учитываться не будут. Вместо этого проекты станут оцениваться по каждому из критериев наинизшего уровня – в нашем случае по стоимости, вероятности успеха и отдаче. Таким образом, при условии доступности соответствующих данных проекты были бы оценены по всем трем элементам стоимости, равно как и по вероятности успеха и отдаче.
Формирование матрицы для сравнения. На каждом уровне иерархии должна быть разработана матрица, элементы которой представляют собой относительное предпочтение (вес, весовой коэффициент, значимость и т. д.) каждого критерия данного уровня по сравнению с остальными критериями того же уровня. Записи в матрице (на пересечении строки и столбца матрицы) показывают степень предпочтительности фактора в данной строке над критерием в данном столбце.
В продолжение примера, используя данные из табл. 2.3, сформируем сравнительную матрицу первого уровня. На первом уровне этой матрицы расположены общая оценка и три фактора: стоимость, вероятность успеха и отдача.
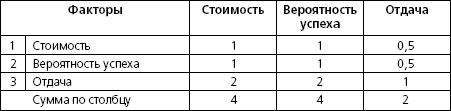Относительные весовые коэффициенты этих трех факторов представлены в верхней строке и в крайнем левом столбце. Степень предпочтения приведена в ячейках, ограниченных двойной линией. В строке «стоимость» показано, что критерий стоимости имеет вдвое более низкое предпочтение, чем отдача (в столбце «отдача»). Диагональные элементы, естественно, равны единице, а элементы, расположенные под диагональю, являются обратными по отношению к соответствующим элементам, расположенным над диагональю. Таким образом, в строке «отдача» элемент, находящийся на пересечении этой строки и столбца «стоимость», равен двум – то есть предпочтительность этого критерия вдвое выше, чем стоимости.
В этом примере имеются определенные значения для выражения относительных предпочтений. Однако во многих случаях элементы матрицы устанавливаются на основе рассуждений и здравого смысла. Процесс разработки каждой матрицы может быть очень времяемким. Впрочем, необязательно, чтобы все матрицы в иерархии формировались одними и теми же людьми. Например, в данной модели матрица относительной вероятности успеха проекта может быть заполнена техническими руководителями, матрица отдачи – отделом маркетинга, а матрица стоимости – руководителями отделов по работе с персоналом, закупкам и т. д.
Далее создается новая матрица, элементы которой – это элементы предыдущей матрицы, разделенные на сумму значений соответствующих столбцов.
Средние значения строк представляют собой весовые коэффициенты, которые будут использоваться при умножении результатов аналогичных операций на значения стоимости, вероятности успеха и отдачи для каждого проекта.
Определение проблемы (задачи) и цели. Первый шаг в процессе AHP – определить проблему (задачу) и цель. В нашем случае цель известна: нужно проранжировать новые и существующие проекты таким образом, чтобы иметь возможность выбирать для инициации лучшие из новых проектов и продолжать/прекращать те, которые уже выполняются.
Сбор исходной информации. Как и в моделях ранжирования проектов, аналитический иерархический процесс начинается с составления списка проектов-кандидатов и подбора исходной информации, на основе которой будет производиться ранжирование. Под исходной информацией понимаются:
• проектное предложение;
• стратегические и тактические планы;
• историческая информация.
Как уже было сказано в разделе «Модели ранжирования проектов», эта исходная информация обеспечивает понимание стратегии и целей компании, целей и содержания проекта, а также результатов решений, принятых по ходу отбора проектов в прошлом, и достигнутой ранее производительности проектов.
Формирование иерархической структуры. Как и в случае с любым другим методом выбора проектов, здесь необходимо решить, какие критерии следует применять для оценивания и ранжирования проектов. Особенность метода AHP состоит в том, что каждый критерий подразделяется на любое необходимое число подуровней. Чтобы проиллюстрировать это положение, мы будем использовать те же критерии, что и при рассмотрении модели ранжирования. Мы хотим проранжировать проекты в соответствии с их достоинствами с точки зрения стоимости, вероятности успеха и отдачи, причем критерий отдачи имеет вдвое больший вес, чем критерии вероятности успеха и стоимости. Иерархическая модель приведена на рис. 2.3. Поскольку в рассмотрение могут быть включены подкритерии, критерий «стоимость» был разделен. Однако, так как соответствующие данные в табл. 2.3 отсутствуют, при фактических вычислениях подкритерии учитываться не будут. Вместо этого проекты станут оцениваться по каждому из критериев наинизшего уровня – в нашем случае по стоимости, вероятности успеха и отдаче. Таким образом, при условии доступности соответствующих данных проекты были бы оценены по всем трем элементам стоимости, равно как и по вероятности успеха и отдаче.
Формирование матрицы для сравнения. На каждом уровне иерархии должна быть разработана матрица, элементы которой представляют собой относительное предпочтение (вес, весовой коэффициент, значимость и т. д.) каждого критерия данного уровня по сравнению с остальными критериями того же уровня. Записи в матрице (на пересечении строки и столбца матрицы) показывают степень предпочтительности фактора в данной строке над критерием в данном столбце.
В продолжение примера, используя данные из табл. 2.3, сформируем сравнительную матрицу первого уровня. На первом уровне этой матрицы расположены общая оценка и три фактора: стоимость, вероятность успеха и отдача.
В этом примере имеются определенные значения для выражения относительных предпочтений. Однако во многих случаях элементы матрицы устанавливаются на основе рассуждений и здравого смысла. Процесс разработки каждой матрицы может быть очень времяемким. Впрочем, необязательно, чтобы все матрицы в иерархии формировались одними и теми же людьми. Например, в данной модели матрица относительной вероятности успеха проекта может быть заполнена техническими руководителями, матрица отдачи – отделом маркетинга, а матрица стоимости – руководителями отделов по работе с персоналом, закупкам и т. д.
Далее создается новая матрица, элементы которой – это элементы предыдущей матрицы, разделенные на сумму значений соответствующих столбцов.