Страница:
К примеру, если мы предположим, что коэффициент резервирования или резервные требования c равны 10 %, что доля неиспользованных кредитов k равна 20 % (эта доля также включает влияние большого числа клиентов банка, а также другие факторы) и что сумма изначально внесенных в банк вкладов d равна 1 000 000 д.е., то, подставляя эти значения в формулу [3], получим:
[4]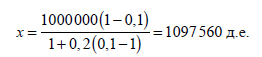
Отсюда мы видим, что банк, принявший вкладов до востребования на сумму 1 000 000 д.е., при поддержании 10 %-ного коэффициента резервирования и 20 %-ного k может предоставлять кредиты не на 900 000 д.е., как мы предполагали для иллюстрирования бухгалтерской записи (18) и последующих, а на значительно большую сумму 1 097 560 д.е. Следовательно, даже для случая изолированного банка способность к кредитной экспансии и созданию депозитов на 22 % выше, чем мы предположили в записи (18) и последующих[273]. Поэтому нам следует изменить наши прежние бухгалтерские записи, чтобы, следуя англосаксонской системе учета, отразить, что при c = 0,1 и k = 0,2 банк сможет расширить свой кредит до 1 097 560 д.е. вместо предполагаемых ранее 900 000 д.е., т. е. что способность банка к кредитной экспансии на 22 % выше. Измененные записи и соответствующий им баланс (ср. с записями (18) и (19)) будут выглядеть следующим образом:
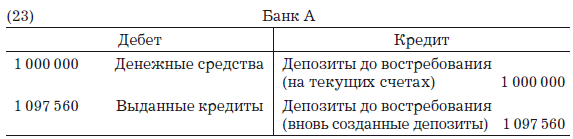
Эти записи соответствуют начальному вкладу в размере 1 000 000 д.е. и созданию изолированным банком из ничего кредитов и депозитов на сумму 1 097 560 д.е. Значение k (равное 0,2) указывает на то, что заемщики в среднем используют 80 % средств, которые они взяли в долг. Когда производится такое снятие денег со счета (и даже если снимается больший объем, при условии что несколько конечных получателей денег являются клиентами того же самого банка и хранят деньги в нем), производится следующая запись[274]:

При этом банковский баланс выглядит следующим образом:
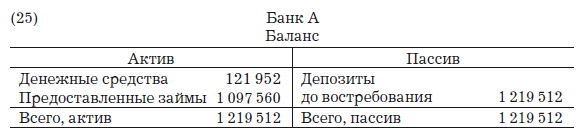
Очень маленький банк
Теперь рассмотрим особый вид изолированного банка – очень маленький, «лилипутский» банк, т. е. такой, для которого k = 0. Это означает, что заемщики немедленно изымают свои кредиты полностью, а те, кому они перечисляют платежи, не являются клиентами того же банка, что и заемщики. Если k = 0, то, подставляя это значение в формулу [3], получаем:
[5] x = d(1 – c).
И, поскольку в нашем примере d = 1 000 000 д.е., а c = 0,1, то:
x = 1 000 000(1–0,1) = 900 000 д.е.
Это в точности равно сумме депозитов, или фидуциарных средств обращения, созданных из ничего, которая отражена в записях (11) и (18). Однако в последнем разделе мы видели, что на практике, когда k лишь немногим отличается от нуля, изолированный банк может создавать значительно больший объем фидуциарных средств обращения. (Если k = 0,2, он может создать на 22 % больше, т. е. 1 097 560 д.е. вместо 900 000 д.е. в первом примере.) Это будет верно независимо от того, использует банк континентальную или англосаксонскую бухгалтерскую систему, и в изолированном банке созданная сумма может даже превышать объем начального депозита.
Вот почему банки столь жестко конкурируют, чтобы привлечь как можно больше депозитов и клиентов. Банкиры пытаются получить на депозиты столько денег, сколько это возможно, потому что способны к расширению кредита в объеме даже большем, чем суммы размещенных у них депозитов. Таким образом, чем больше объем [депозитов], тем более банк будет способен расширять соответствующий кредит. Банкиры стараются привлечь как можно больше клиентов, потому что чем больше у них клиентов, тем выше будет k, а чем выше k, тем больше их возможность расширять займы и генерировать депозиты. Но самое важное то, что банкиры технически неспособны различить, ведет ли реализуемая ими политика роста к расширению их индивидуальной сферы действий за счет других банков, или же в конечном итоге имеет результатом общую эскалацию кредитной экспансии, охватывающую всю банковскую систему, или и то и другое одновременно. Банки расширяют кредит и депозиты самостоятельно, но, кроме того, принимают участие в действиях, которые порождают еще более масштабную кредитно-депозитную экспансию в банковской системе в целом. Более того, в этом процессе банки прилагают максимум усилий, чтобы играть все более и более значительную роль по сравнению с другими банками, что постоянно дает новые стимулы для кредитной экспансии на уровне отдельных банков и в банковской системе в целом. В любом случае k представляет собой ключевой фактор, определяющий уровень доходов банка. Конкуренция между банками удерживает k на уровне, значительно меньшем единицы, но каждый банк борется за непрерывное повышение значения своего коэффициента k. Для этого банки используют собственные возможности (географическое расширение, способность вытеснять или поглощать конкурентов, развитие конкурентных преимуществ)[275]. Хотя для изолированного банка коэффициент k, равный единице, невозможен (за исключением случаев банка-монополиста), значение k, как правило, существенно выше нуля, и почти при любых обстоятельствах банки прилагают огромные усилия для его увеличения. Среди прочего, это объясняет постоянное давление к слиянию с другими банками.
Для наглядности мы составили следующую таблицу различных сочетаний c (коэффициента резервирования) и k (процента неиспользованных кредитов или клиентов одного и того же банка), которые позволяют изолированному банку в одиночку удваивать свою денежную массу (подставляя эти значения в формулу [3], получаем x = d).
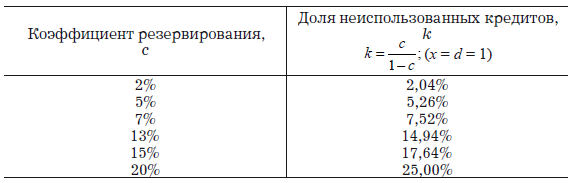
Кредитная экспансия и создание депозитов из ничего единственным банком-монополистом
Теперь предположим, что k = 1. Мы рассматриваем либо единственный банк-монополист, заемщики которого, за неимением других банков, вынуждены держать на депозитах все взятые ими кредиты, либо ситуацию, когда все конечные получатели платежей, сделанных заемщиками банка, тоже являются клиентами этого банка. (Эта «идеальная» цель была бы достигнута при слиянии всех остающихся мегабанков.) Подставив значение k = 1 в формулу [3], получим:
[6]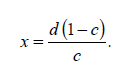
Возвращаясь к нашему примеру, в котором d = 1 000 000 д.е., а c = 0,1, подставим эти значения в полученную формулу:
[7]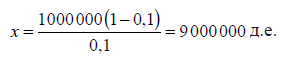
В этом случае банк самостоятельно может из ничего создать кредиты и депозиты, т. е фидуциарные средства обращения, на сумму 9 000 000 д.е., что означает следующее: он может увеличить предложение денег в 10 раз (первоначальный депозит 1 000 000 д.е. плюс 9 000 000 д.е. в форме фидуциарных средств обращения, или депозитов, созданных из ничего для обеспечения предоставленных банком кредитов).
Предположив вслед за Брешиани-Туррони[276], что все платежи выполняются между клиентами одного банка (либо занимающего монопольное положение, либо ввиду особых обстоятельств, определяющих такую ситуацию), рассмотрим бухгалтерские записи, которые покажут процесс продвижения к такому результату.
Мы будем следовать традиционной континентальной системе (противоположной англосаксонской), в которой все платежи отражаются на счете денежных средств. Нижеследующий пример представляет журнал на моменты времени t1, t2, t3… t9 и т. д. и отражает практику банка в каждой итерации предоставлять своим клиентам кредиты на сумму, равную 90 % получаемых банком денежных средств. Клиенты используют полученные кредиты полностью, но ввиду отсутствия у них счетов в других банках (или попросту из-за того, что другого банка в этом обществе нет), в конечном счете полученные ими деньги возвращаются в тот же банк. Это, в свою очередь, позволяет банку предоставлять новые кредиты и генерировать новые депозиты, причем процесс повторяется вновь и вновь:

Предположим, что U полностью использует полученный кредит и платит своему кредитору А. Являясь клиентом того же банка, что и U, А размещает полученные 900 000 д.е. на депозите в этом банке. В результате получаются следующие записи:

Предположим, что заемщик V снимает деньги со своего счета и платит кредитору В, который тоже клиент этого банка и тоже хранит в нем деньги. Этот повторяющийся процесс продолжается, отражаясь в следующих записях:

Так происходит снова и снова, пока в конце года общий объем банковских депозитов не достигает суммы:
[8] 1 000 000 + 1 000 000 ×0,9 + 1 000 000 ×0,92 +
+ 1 000 000 ×0,93 + 1 000 000 ×0,94 +… =
= 1 000 000 (1 + 0,9 + 0,92 + 0,93 + 0,94 +…)
Это выражение представляет собой сумму членов геометрической прогрессии. Она является возрастающей с коэффициентом 0,9[277].
В нашем примере r = 0,9; а = 1 000 000 д.е. и, следовательно, сумма членов прогрессии будет равна:
[13]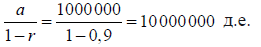
Если мы вспомним, что d представляет собой 1 000 000 д.е., первоначально внесенных на депозит, и что r = 1 – c, то есть r = 1–0,1 = 0,9, то ясно, что сумма всех банковских депозитов (первичных и производных) будет равна
[14]
Таким образом общий объем депозитов в банке-монополисте (или в банке, где все те, кто получает деньги от заемщиков банка, также имеют в нем счет) будет равен сумме первичных депозитов d, деленной на коэффициент резервирования c.
Формула [14] – простейшая версия так называемого банковского мультипликатора, и тождественна формуле [27], которая приводит к тому же результату для банковской системы из множества мелких банков. Эта формула впервые выведена, по-видимому, Альфредом Маршаллом в 1887 г.[278]
Чтобы вычислить чистый объем расширения кредитов, которые банк производит из ничего, – иными словами, депозитов или фидуциарных средств обращения, произведенных из ничего (для того, чтобы сделать возможной кредитную экспансию), – можно использовать следующую формулу:
[15]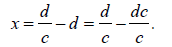
Теперь вынесем за скобки общий множитель:
[16]
Эта формула совпадает с формулой [6].
При d = 1 000 000 д.е. и c = 0,1 для нашего случая банка-монополиста чистая кредитная экспансия будет равна:
[17]
Поэтому баланс банка А, банка-монополиста, в конце концов будет выглядеть следующим образом:
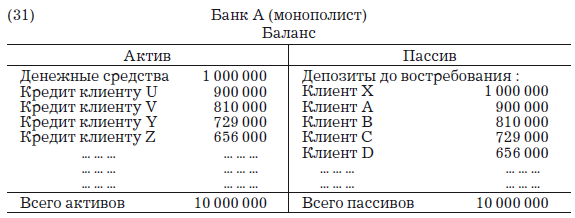
Располагая в своих хранилищах первичными депозитами в размере всего 1 000 000 д.е., банк А, занимающий монопольное положение, расширил кредит путем предоставления кредитов на сумму 9 000 000 д.е., в покрытие которых создав из ничего новых депозитов, или фидуциарных средств обращения, на сумму 9 000 000 д.е.[279]
5 Кредитная экспансия и создание новых депозитов в банковской системе в целом
6 Некоторые дополнительные сложные случаи
Этот теоретический аргумент побудил многих авторов, и в том числе Мюррея Ротбарда[283], при рассмотрении процесса кредитной экспансии в банковской системе исходить из того, что изолированный банк не теряет резервов при предоставлении все новых кредитов. Напротив, сохраняя резервы в неприкосновенности, изолированный банк изо всех сил пытается выдать новые кредиты на сумму, кратность которой по отношению к резервам обратно пропорциональна коэффициенту резервирования. Аргумент, объясняющий такой вид банковского мультипликатора, даже для случая изолированного банка, состоит в том, что банк будет пытаться избежать сокращения своих резервов в процессе предоставления кредитов (т. е. банкир не захочет оставить 100 000 д.е., а 900 000 д.е. ссудить). Напротив, для банка куда выгодней поддержание своего коэффициента резервирования путем предоставления кредитов на как можно более крупную сумму и сохранение начального резерва наличности в неприкосновенности (т. е. храня 1 000 000 д.е. наличными и создав из ничего новые кредиты на 9 000 000 д.е.). На практике уровень резервов наличности может быть обеспечен, если процесс кредитной экспансии протекает одновременно во всех банках. Это происходит оттого, что уменьшение наличности, которое банк испытывает после предоставления кредитов, компенсируется приемом новых депозитов, берущих начало из кредитов, взятых в других банках.
[4]
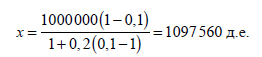
Отсюда мы видим, что банк, принявший вкладов до востребования на сумму 1 000 000 д.е., при поддержании 10 %-ного коэффициента резервирования и 20 %-ного k может предоставлять кредиты не на 900 000 д.е., как мы предполагали для иллюстрирования бухгалтерской записи (18) и последующих, а на значительно большую сумму 1 097 560 д.е. Следовательно, даже для случая изолированного банка способность к кредитной экспансии и созданию депозитов на 22 % выше, чем мы предположили в записи (18) и последующих[273]. Поэтому нам следует изменить наши прежние бухгалтерские записи, чтобы, следуя англосаксонской системе учета, отразить, что при c = 0,1 и k = 0,2 банк сможет расширить свой кредит до 1 097 560 д.е. вместо предполагаемых ранее 900 000 д.е., т. е. что способность банка к кредитной экспансии на 22 % выше. Измененные записи и соответствующий им баланс (ср. с записями (18) и (19)) будут выглядеть следующим образом:

Эти записи соответствуют начальному вкладу в размере 1 000 000 д.е. и созданию изолированным банком из ничего кредитов и депозитов на сумму 1 097 560 д.е. Значение k (равное 0,2) указывает на то, что заемщики в среднем используют 80 % средств, которые они взяли в долг. Когда производится такое снятие денег со счета (и даже если снимается больший объем, при условии что несколько конечных получателей денег являются клиентами того же самого банка и хранят деньги в нем), производится следующая запись[274]:

При этом банковский баланс выглядит следующим образом:

Очень маленький банк
Теперь рассмотрим особый вид изолированного банка – очень маленький, «лилипутский» банк, т. е. такой, для которого k = 0. Это означает, что заемщики немедленно изымают свои кредиты полностью, а те, кому они перечисляют платежи, не являются клиентами того же банка, что и заемщики. Если k = 0, то, подставляя это значение в формулу [3], получаем:
[5] x = d(1 – c).
И, поскольку в нашем примере d = 1 000 000 д.е., а c = 0,1, то:
x = 1 000 000(1–0,1) = 900 000 д.е.
Это в точности равно сумме депозитов, или фидуциарных средств обращения, созданных из ничего, которая отражена в записях (11) и (18). Однако в последнем разделе мы видели, что на практике, когда k лишь немногим отличается от нуля, изолированный банк может создавать значительно больший объем фидуциарных средств обращения. (Если k = 0,2, он может создать на 22 % больше, т. е. 1 097 560 д.е. вместо 900 000 д.е. в первом примере.) Это будет верно независимо от того, использует банк континентальную или англосаксонскую бухгалтерскую систему, и в изолированном банке созданная сумма может даже превышать объем начального депозита.
Вот почему банки столь жестко конкурируют, чтобы привлечь как можно больше депозитов и клиентов. Банкиры пытаются получить на депозиты столько денег, сколько это возможно, потому что способны к расширению кредита в объеме даже большем, чем суммы размещенных у них депозитов. Таким образом, чем больше объем [депозитов], тем более банк будет способен расширять соответствующий кредит. Банкиры стараются привлечь как можно больше клиентов, потому что чем больше у них клиентов, тем выше будет k, а чем выше k, тем больше их возможность расширять займы и генерировать депозиты. Но самое важное то, что банкиры технически неспособны различить, ведет ли реализуемая ими политика роста к расширению их индивидуальной сферы действий за счет других банков, или же в конечном итоге имеет результатом общую эскалацию кредитной экспансии, охватывающую всю банковскую систему, или и то и другое одновременно. Банки расширяют кредит и депозиты самостоятельно, но, кроме того, принимают участие в действиях, которые порождают еще более масштабную кредитно-депозитную экспансию в банковской системе в целом. Более того, в этом процессе банки прилагают максимум усилий, чтобы играть все более и более значительную роль по сравнению с другими банками, что постоянно дает новые стимулы для кредитной экспансии на уровне отдельных банков и в банковской системе в целом. В любом случае k представляет собой ключевой фактор, определяющий уровень доходов банка. Конкуренция между банками удерживает k на уровне, значительно меньшем единицы, но каждый банк борется за непрерывное повышение значения своего коэффициента k. Для этого банки используют собственные возможности (географическое расширение, способность вытеснять или поглощать конкурентов, развитие конкурентных преимуществ)[275]. Хотя для изолированного банка коэффициент k, равный единице, невозможен (за исключением случаев банка-монополиста), значение k, как правило, существенно выше нуля, и почти при любых обстоятельствах банки прилагают огромные усилия для его увеличения. Среди прочего, это объясняет постоянное давление к слиянию с другими банками.
Для наглядности мы составили следующую таблицу различных сочетаний c (коэффициента резервирования) и k (процента неиспользованных кредитов или клиентов одного и того же банка), которые позволяют изолированному банку в одиночку удваивать свою денежную массу (подставляя эти значения в формулу [3], получаем x = d).

Кредитная экспансия и создание депозитов из ничего единственным банком-монополистом
Теперь предположим, что k = 1. Мы рассматриваем либо единственный банк-монополист, заемщики которого, за неимением других банков, вынуждены держать на депозитах все взятые ими кредиты, либо ситуацию, когда все конечные получатели платежей, сделанных заемщиками банка, тоже являются клиентами этого банка. (Эта «идеальная» цель была бы достигнута при слиянии всех остающихся мегабанков.) Подставив значение k = 1 в формулу [3], получим:
[6]
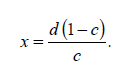
Возвращаясь к нашему примеру, в котором d = 1 000 000 д.е., а c = 0,1, подставим эти значения в полученную формулу:
[7]
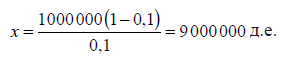
В этом случае банк самостоятельно может из ничего создать кредиты и депозиты, т. е фидуциарные средства обращения, на сумму 9 000 000 д.е., что означает следующее: он может увеличить предложение денег в 10 раз (первоначальный депозит 1 000 000 д.е. плюс 9 000 000 д.е. в форме фидуциарных средств обращения, или депозитов, созданных из ничего для обеспечения предоставленных банком кредитов).
Предположив вслед за Брешиани-Туррони[276], что все платежи выполняются между клиентами одного банка (либо занимающего монопольное положение, либо ввиду особых обстоятельств, определяющих такую ситуацию), рассмотрим бухгалтерские записи, которые покажут процесс продвижения к такому результату.
Мы будем следовать традиционной континентальной системе (противоположной англосаксонской), в которой все платежи отражаются на счете денежных средств. Нижеследующий пример представляет журнал на моменты времени t1, t2, t3… t9 и т. д. и отражает практику банка в каждой итерации предоставлять своим клиентам кредиты на сумму, равную 90 % получаемых банком денежных средств. Клиенты используют полученные кредиты полностью, но ввиду отсутствия у них счетов в других банках (или попросту из-за того, что другого банка в этом обществе нет), в конечном счете полученные ими деньги возвращаются в тот же банк. Это, в свою очередь, позволяет банку предоставлять новые кредиты и генерировать новые депозиты, причем процесс повторяется вновь и вновь:

Предположим, что U полностью использует полученный кредит и платит своему кредитору А. Являясь клиентом того же банка, что и U, А размещает полученные 900 000 д.е. на депозите в этом банке. В результате получаются следующие записи:

Предположим, что заемщик V снимает деньги со своего счета и платит кредитору В, который тоже клиент этого банка и тоже хранит в нем деньги. Этот повторяющийся процесс продолжается, отражаясь в следующих записях:

Так происходит снова и снова, пока в конце года общий объем банковских депозитов не достигает суммы:
[8] 1 000 000 + 1 000 000 ×0,9 + 1 000 000 ×0,92 +
+ 1 000 000 ×0,93 + 1 000 000 ×0,94 +… =
= 1 000 000 (1 + 0,9 + 0,92 + 0,93 + 0,94 +…)
Это выражение представляет собой сумму членов геометрической прогрессии. Она является возрастающей с коэффициентом 0,9[277].
В нашем примере r = 0,9; а = 1 000 000 д.е. и, следовательно, сумма членов прогрессии будет равна:
[13]
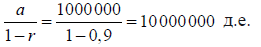
Если мы вспомним, что d представляет собой 1 000 000 д.е., первоначально внесенных на депозит, и что r = 1 – c, то есть r = 1–0,1 = 0,9, то ясно, что сумма всех банковских депозитов (первичных и производных) будет равна
[14]

Таким образом общий объем депозитов в банке-монополисте (или в банке, где все те, кто получает деньги от заемщиков банка, также имеют в нем счет) будет равен сумме первичных депозитов d, деленной на коэффициент резервирования c.
Формула [14] – простейшая версия так называемого банковского мультипликатора, и тождественна формуле [27], которая приводит к тому же результату для банковской системы из множества мелких банков. Эта формула впервые выведена, по-видимому, Альфредом Маршаллом в 1887 г.[278]
Чтобы вычислить чистый объем расширения кредитов, которые банк производит из ничего, – иными словами, депозитов или фидуциарных средств обращения, произведенных из ничего (для того, чтобы сделать возможной кредитную экспансию), – можно использовать следующую формулу:
[15]
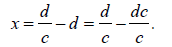
Теперь вынесем за скобки общий множитель:
[16]

Эта формула совпадает с формулой [6].
При d = 1 000 000 д.е. и c = 0,1 для нашего случая банка-монополиста чистая кредитная экспансия будет равна:
[17]

Поэтому баланс банка А, банка-монополиста, в конце концов будет выглядеть следующим образом:

Располагая в своих хранилищах первичными депозитами в размере всего 1 000 000 д.е., банк А, занимающий монопольное положение, расширил кредит путем предоставления кредитов на сумму 9 000 000 д.е., в покрытие которых создав из ничего новых депозитов, или фидуциарных средств обращения, на сумму 9 000 000 д.е.[279]
5 Кредитная экспансия и создание новых депозитов в банковской системе в целом
Мы рассмотрели огромные возможности изолированных банков в создании фидуциарных кредитов и депозитов. Самостоятельно они обычно могут удваивать предложение денег. Сейчас мы увидим, как банковская система с частичным резервированием, взятая как единое целое, создает из ничего значительно больший объем депозитов и вызывает куда более обширную кредитную экспансию. Действительно, в этом отношении система с частичным резервированием приводит к тем же последствиям, что и банк-монополист. Наш пример будет основан на более общем случае банковской системы, включающей группу обычных банков, каждый из которых поддерживает 10 %-ные денежные резервы c. Кроме того, каждый клиент в среднем не использует 20 % предоставленных кредитов (либо 20 % фидуциарных средств обращения возвращается в банк благодаря тому, что значительное число их конечных получателей также клиенты этого банка). Следовательно, k = 20 %.
Предположим, что г-н Х кладет в банк А на депозит 1 000 000 д.е. В этом случае банк делает следующую бухгалтерскую проводку:

Теперь банк А сможет создать и предоставить кредит клиенту Z на сумму, определяемую формулой [3], результатом чего станет такая запись:

И, так как k = 0,2, т. е. использовано 80 % выданных кредитов, будет сделана запись:

После этих записей баланс банка А будет выглядеть следующим образом:

Предположим, что когда Z изымает свой депозит, от платит Y, клиенту банка В, который открывает депозит в этом банке. Последуют три проводки, параллельно трем вышеприведенным. Для определения объемов снова используется формула [3].
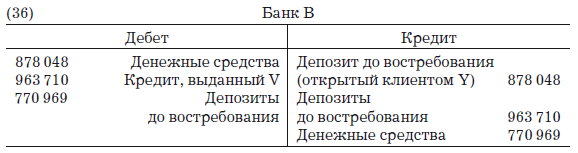
После этих действий баланс банка В будет выглядеть так:
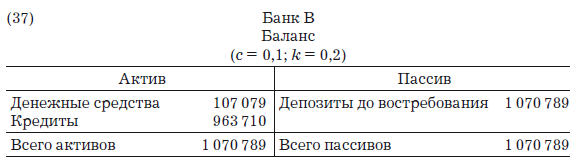
Представим, что V выплачивает долг U, который, в свою очередь, кладет полученные деньги на депозит в банке С, клиентом которого он является. Будут сделаны следующие проводки:
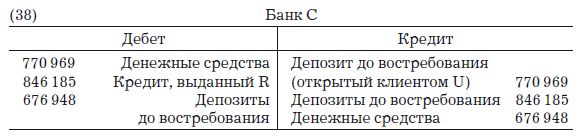
Последнюю запись банк С сделал, когда R изъял 80 % (k = 0,2) своего кредита, полученного от банка С, чтобы заплатить, например, кредитору Т. Как только эти операции будут выполнены, баланс банка С приобретет следующий вид.

И если кредитор Т по получении денег кладет их в банк D, клиентом которого он является, последуют записи:
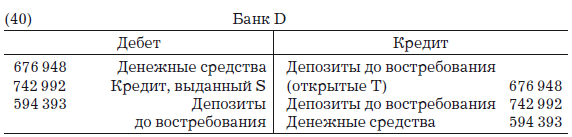
Последнюю запись банк сделает в своих регистрах, когда S заплатит своим кредиторам. В этот момент баланс банка D будет выглядеть так:

По мере продолжения этого процесса цепочка депозитов и кредитов расширяется на все банки системы. Когда полностью исчезнет воздействие первичного депозита в 1 000 000 д.е., общая сумма депозитов, созданных банковской системой, будет равна сумме последовательности:
[21] 1 219 512 + 1 219 512 · 0,878 + 1 219 512 · 0,8782 + … =
= a + ar + ar2 +… =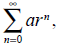
где: a = 1 219 512 д.е.,
а общий коэффициент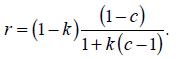
Так происходит оттого, что в нашем примере r будет равно 80 %, т. е. (1–k), от доли депозитов, вновь созданных каждым банком на каждой стадии. Эта доля, рассчитанная по формуле [3], равняется
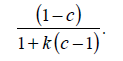
Отсюда
[22]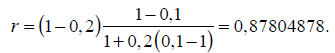
И, поскольку |r| < 1, можно применить формулы [11] и [12]:
[23]
Таким образом D, сумма депозитов в банковской системе, будет равна:
[24]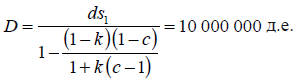
В этой формуле ds1 обозначает вторичные депозиты банка А и равна 1 219 512 д.е.
Чистая кредитная экспансия x в банковской системе в целом будет равна:
[25] x = D – d = 10 000 000 – 1 000 000 = 9 000 000 д.е.
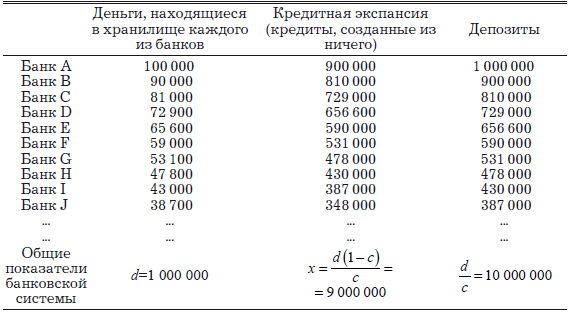
Общий итог сведен в табл. 4–1 и на рис. 4–1. Подробности даны для каждого банка – члена банковской системы.
Таблица 4-1
Система банков «обычного» размера
(k = 0,2; c = 0,1)

Примечание: последние три цифры округлены.
Когда в банк А сделан депозит до востребования в размере 1 000 000 д.е.:
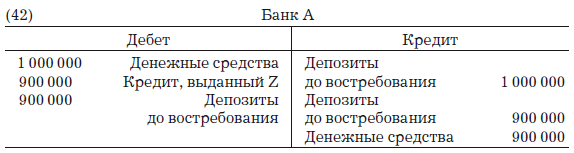

Рис. 4–1. кредитная экспансия в банковской системе *
Примечание: ввиду недостатка места области R и P не соответствуют их реальной величине.
* На основе рисунка из: C.A. Philips in Bank Credit, op. cit., p.61.
Когда Z снимает с депозита 900 000 д.е., чтобы заплатить Y, баланс банка А приобретает такой вид:

Если Y, в свою очередь, хранит полученные деньги в другом мелком банке В, у которого c = 0,1 и k = 0, то последуют проводки:
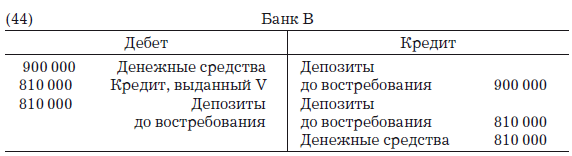
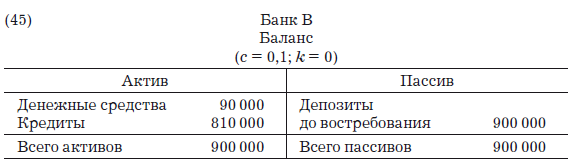
А баланс банка В будет выглядеть так:
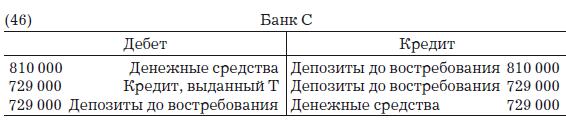
Теперь если V снимает с депозита в своем банке полученный кредит, чтобы уплатить U, а U хранит деньги уже в другом банке – банке С, столь же мелком, т. е. у которого k = 0, а c = 0,1, то в регистрах банка С будут отражены проводки:
А баланс банка С приобретет следующий вид:
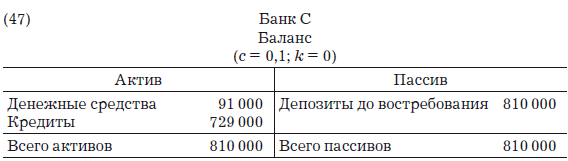
Когда Т заплатит своему кредитору S, при том что S хранит свои деньги в мелком банке D (у которого точно так же c = 0,1, а k = 0), будут сделаны бухгалтерские записи:
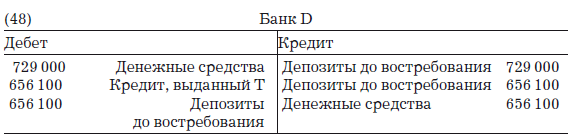
А баланс банка D станет выглядеть следующим образом:
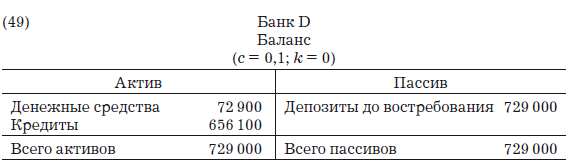
Общая сумма депозитов в системе очень малых банков равна сумме последовательности, отраженной в формуле [8], которая относится к банку-монополисту:
[26] 1 000 000 + 1 000 000 · 0,9 + 1 000 000 · 0,92 +1 000 000 · 0,93 + … =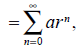
где: a = 1 000 000;
r = 0,9.
Как показано в прим. 27, эта сумма, в свою очередь, равна:
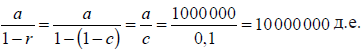
А поскольку a = d = 1 000 000 д.е., вложенных первоначально, то общую сумму депозитов можно рассчитать по формуле
[27]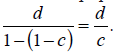
Эта формула идентична мультипликатору депозитов для случая банковской системы, состоящей из единственного банка-монополиста [14].
Теперь вспомним, что
[28]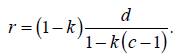
Так как банковская система в этом случае состоит из мелких банков и k = 0, то, подставив значение k в формулу [28], получим, что r = 1 – c = = 0,9, что нам уже известно. Поэтому банковская система, составленная из малых банков, порождает в общей сложности объем депозитов в размере 10 000 000 д.е. и чистую кредитную экспансию в размере 9 000 000 д.е., идентичные тем, что порождает монополистический банк с k = 1. Полученные результаты сведены в табл. 4–2.
Система мелких банков (где k = 0), конечно же, является исключением в рамках банковской системы вообще, где 0 < k < 1. Однако этот пример прост для понимания и поэтому обычно используется в учебниках для объяснения создания кредитных денег финансовой системой[280].
Таблица 4-2
Система мелких банков
(k = 0,2; c= 0,1)
Примечание: Последние три цифры округлены.
Верно также и то, что банковская система, состоящая из банка-монополиста (когда k = 1), – уникальный случай в рамках более широкой категории изолированных банков, расширяющих депозиты и кредиты.
В заключение отметим, что два частных случая ведут к идентичным результатам в том, что касается создания новых кредитов (9 000 000 д.е.) и общего объема депозитов (10 000 000 д.е.). В первом случае была рассмотрена система мелких банков с k = 0. Второй случай – изолированный банк с k = 1. С учетом того, что эти примеры просты для понимания, они обычно используются в учебниках для объяснения создания кредитов и объема депозитов, генерируемых банковской системой. Разные авторы ссылаются либо на систему крохотных банков, либо на единственный банк-монополист (или на банк, чьими клиентами являются конечные получатели кредитов)[281].
Предположим, что г-н Х кладет в банк А на депозит 1 000 000 д.е. В этом случае банк делает следующую бухгалтерскую проводку:

Теперь банк А сможет создать и предоставить кредит клиенту Z на сумму, определяемую формулой [3], результатом чего станет такая запись:

И, так как k = 0,2, т. е. использовано 80 % выданных кредитов, будет сделана запись:

После этих записей баланс банка А будет выглядеть следующим образом:

Предположим, что когда Z изымает свой депозит, от платит Y, клиенту банка В, который открывает депозит в этом банке. Последуют три проводки, параллельно трем вышеприведенным. Для определения объемов снова используется формула [3].

После этих действий баланс банка В будет выглядеть так:

Представим, что V выплачивает долг U, который, в свою очередь, кладет полученные деньги на депозит в банке С, клиентом которого он является. Будут сделаны следующие проводки:

Последнюю запись банк С сделал, когда R изъял 80 % (k = 0,2) своего кредита, полученного от банка С, чтобы заплатить, например, кредитору Т. Как только эти операции будут выполнены, баланс банка С приобретет следующий вид.

И если кредитор Т по получении денег кладет их в банк D, клиентом которого он является, последуют записи:

Последнюю запись банк сделает в своих регистрах, когда S заплатит своим кредиторам. В этот момент баланс банка D будет выглядеть так:

По мере продолжения этого процесса цепочка депозитов и кредитов расширяется на все банки системы. Когда полностью исчезнет воздействие первичного депозита в 1 000 000 д.е., общая сумма депозитов, созданных банковской системой, будет равна сумме последовательности:
[21] 1 219 512 + 1 219 512 · 0,878 + 1 219 512 · 0,8782 + … =
= a + ar + ar2 +… =
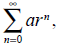
где: a = 1 219 512 д.е.,
а общий коэффициент
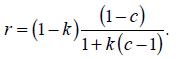
Так происходит оттого, что в нашем примере r будет равно 80 %, т. е. (1–k), от доли депозитов, вновь созданных каждым банком на каждой стадии. Эта доля, рассчитанная по формуле [3], равняется
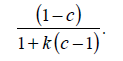
Отсюда
[22]
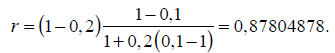
И, поскольку |r| < 1, можно применить формулы [11] и [12]:
[23]

Таким образом D, сумма депозитов в банковской системе, будет равна:
[24]
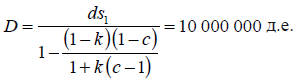
В этой формуле ds1 обозначает вторичные депозиты банка А и равна 1 219 512 д.е.
Чистая кредитная экспансия x в банковской системе в целом будет равна:
[25] x = D – d = 10 000 000 – 1 000 000 = 9 000 000 д.е.
Общий итог сведен в табл. 4–1 и на рис. 4–1. Подробности даны для каждого банка – члена банковской системы.
Таблица 4-1
Система банков «обычного» размера
(k = 0,2; c = 0,1)

Примечание: последние три цифры округлены.
Создание кредита в системе мелких банков
Теперь предположим, что система состоит только из очень мелких банков, для которых k = 0, а с = 0,1. Бухгалтерские проводки для такой банковской системы будут выглядеть следующим образом.Когда в банк А сделан депозит до востребования в размере 1 000 000 д.е.:


Рис. 4–1. кредитная экспансия в банковской системе *
Примечание: ввиду недостатка места области R и P не соответствуют их реальной величине.
* На основе рисунка из: C.A. Philips in Bank Credit, op. cit., p.61.
Когда Z снимает с депозита 900 000 д.е., чтобы заплатить Y, баланс банка А приобретает такой вид:

Если Y, в свою очередь, хранит полученные деньги в другом мелком банке В, у которого c = 0,1 и k = 0, то последуют проводки:

А баланс банка В будет выглядеть так:

Теперь если V снимает с депозита в своем банке полученный кредит, чтобы уплатить U, а U хранит деньги уже в другом банке – банке С, столь же мелком, т. е. у которого k = 0, а c = 0,1, то в регистрах банка С будут отражены проводки:

А баланс банка С приобретет следующий вид:

Когда Т заплатит своему кредитору S, при том что S хранит свои деньги в мелком банке D (у которого точно так же c = 0,1, а k = 0), будут сделаны бухгалтерские записи:

А баланс банка D станет выглядеть следующим образом:

Общая сумма депозитов в системе очень малых банков равна сумме последовательности, отраженной в формуле [8], которая относится к банку-монополисту:
[26] 1 000 000 + 1 000 000 · 0,9 + 1 000 000 · 0,92 +1 000 000 · 0,93 + … =
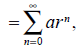
где: a = 1 000 000;
r = 0,9.
Как показано в прим. 27, эта сумма, в свою очередь, равна:
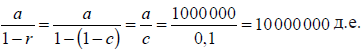
А поскольку a = d = 1 000 000 д.е., вложенных первоначально, то общую сумму депозитов можно рассчитать по формуле
[27]
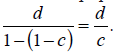
Эта формула идентична мультипликатору депозитов для случая банковской системы, состоящей из единственного банка-монополиста [14].
Теперь вспомним, что
[28]
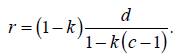
Так как банковская система в этом случае состоит из мелких банков и k = 0, то, подставив значение k в формулу [28], получим, что r = 1 – c = = 0,9, что нам уже известно. Поэтому банковская система, составленная из малых банков, порождает в общей сложности объем депозитов в размере 10 000 000 д.е. и чистую кредитную экспансию в размере 9 000 000 д.е., идентичные тем, что порождает монополистический банк с k = 1. Полученные результаты сведены в табл. 4–2.
Система мелких банков (где k = 0), конечно же, является исключением в рамках банковской системы вообще, где 0 < k < 1. Однако этот пример прост для понимания и поэтому обычно используется в учебниках для объяснения создания кредитных денег финансовой системой[280].
Таблица 4-2
Система мелких банков
(k = 0,2; c= 0,1)

Примечание: Последние три цифры округлены.
Верно также и то, что банковская система, состоящая из банка-монополиста (когда k = 1), – уникальный случай в рамках более широкой категории изолированных банков, расширяющих депозиты и кредиты.
В заключение отметим, что два частных случая ведут к идентичным результатам в том, что касается создания новых кредитов (9 000 000 д.е.) и общего объема депозитов (10 000 000 д.е.). В первом случае была рассмотрена система мелких банков с k = 0. Второй случай – изолированный банк с k = 1. С учетом того, что эти примеры просты для понимания, они обычно используются в учебниках для объяснения создания кредитов и объема депозитов, генерируемых банковской системой. Разные авторы ссылаются либо на систему крохотных банков, либо на единственный банк-монополист (или на банк, чьими клиентами являются конечные получатели кредитов)[281].
6 Некоторые дополнительные сложные случаи
Когда экспансию начинают все банки одновременно
В свете того факта, что в данном контексте мы вынуждены предложить упрощенный взгляд на процесс кредитной экспансии, необходимо отметить несколько дополнительных моментов, а также сделать некоторые пояснения. Начнем с того, что описанные нами процессы экспансии целиком и полностью возникают исключительно в результате увеличения количества денег, внесенных на вклад в начальном банке (в нашем примере d представляет 1 000 000 д.е., депонированных в банке А). Однако и исторически, по мере развития банков, и в настоящее время все процессы кредитной экспансии характеризуются тем, что новые деньги вливаются в банковскую систему не через один-единственный банк, а через множество банков (а то и в той или иной степени через все банки системы). Как показывает Ричард Липси[282], кредитная экспансия, подобная описанной нами – происходящая ex nihilo и поддерживаемая созданием необходимых банковских депозитов, – будет повторяться всякий раз, когда в любом из банков будет делаться вклад в размере 1 000 000 д.е. Поэтому общий процесс экспансии на деле является более существенным по масштабам и качественно более сложным, так как он происходит одновременно во многих банках и от множества депозитов. В нашем единственном примере с коэффициентом резервирования 10 % в итоге были созданы кредиты на сумму 9 000 000 д.е., что в девять раз превышает начальный депозит, и в результате денежное предложение увеличивается в 10 раз. Главный вывод, который отсюда следует, состоит в том, что если все банки одновременно получат новые денежные депозиты, они смогут расширить кредит без уменьшения своих денежных резервов, потому что, предоставляя кредиты, ведущие к изъятию денег (как мы до сих пор предполагали в наших бухгалтерских записях), они одновременно получают депозит в виде части денег, предоставленных в виде кредитов другими банками. Следовательно, на деле вовсе не обязательно происходит значительное сокращение резервов каждого из банков, и каждый банк, поддерживая свои резервы практически в неприкосновенности, будет способен выдавать кредиты и соответственно создавать депозиты, без особого риска.Этот теоретический аргумент побудил многих авторов, и в том числе Мюррея Ротбарда[283], при рассмотрении процесса кредитной экспансии в банковской системе исходить из того, что изолированный банк не теряет резервов при предоставлении все новых кредитов. Напротив, сохраняя резервы в неприкосновенности, изолированный банк изо всех сил пытается выдать новые кредиты на сумму, кратность которой по отношению к резервам обратно пропорциональна коэффициенту резервирования. Аргумент, объясняющий такой вид банковского мультипликатора, даже для случая изолированного банка, состоит в том, что банк будет пытаться избежать сокращения своих резервов в процессе предоставления кредитов (т. е. банкир не захочет оставить 100 000 д.е., а 900 000 д.е. ссудить). Напротив, для банка куда выгодней поддержание своего коэффициента резервирования путем предоставления кредитов на как можно более крупную сумму и сохранение начального резерва наличности в неприкосновенности (т. е. храня 1 000 000 д.е. наличными и создав из ничего новые кредиты на 9 000 000 д.е.). На практике уровень резервов наличности может быть обеспечен, если процесс кредитной экспансии протекает одновременно во всех банках. Это происходит оттого, что уменьшение наличности, которое банк испытывает после предоставления кредитов, компенсируется приемом новых депозитов, берущих начало из кредитов, взятых в других банках.
