Страница:
Отсюда, из наследственных структур и до самых отдаленных от поверхности сфер, вещество, упрощаясь, движется к равновесию, основанному на втором начале термодинамики (в соответствии с градиентом сложности и степенью диссимметрии). Стремление к уравновешенности соответствует всем физическим и термодинамическим правилам, оно являет собой аналог энтропии.
Но жизнь питается отрицательной энтропией. Иначе говоря, любая структура, поскольку она всегда может образовываться в правых и левых вариантах атомного строения, обязана состоять, согласно энтропии, из равного количества этих изомеров, то есть быть рацемичной. Рацемичной является почти любое косное вещество и на поверхности, и в недрах планеты. Почти, но не совсем, все вещество в целом – и живое, и неживое – располагается на некой лестнице рацемичности, обладает разными ее степенями, различным процентным соотношением неравенства в равенстве левого и правого вещества. Свойство гомохиральности играет важную роль в иерархии самоорганизующихся структур любого порядка и вида. Правые и левые изомеры энергетически неэквивалентны, левые слабее правых, поэтому их диссимметрия начинается на уровне сверхслабых взаимодействий в макроогранизме там, где «туман», то есть предполагаемая ось симметрии. «Туманное» место (то есть место предполагаемой оси симметрии) имеет вполне материальную базу, неравенство зеркальных энантиомеров начинается на уровне атомного ядра, числа нейтронов в нем. Граница симметрии – мировая линия – начинается с ядер атомов IV периода таблицы Д.И. Менделеева, так как здесь располагаются элементы, нейтрально относящиеся к мировой линии. К этому явлению мы будем обращаться не раз. Соединения, способные более эффективно обеспечить гомохиральность природных объектов, обладают энергетически выгодным «правым» свойством.
Тиозамещенные аналоги ДНК, в которые она входит в состав или замещает фосфатные группы скелета ДНК, резко отличаются от обычных молекул. Расчеты показали, что для них разность концентраций на три порядка превосходит ранее найденные значения, и при этом более энергетически выгодным оказывается энантиомер с естественной правой спиралью.
Второй шаг в описании диссимметрии сделал Пьер Кюри. В его биографии, написанной Марией Кюри, говорится об интересе, который вызвало у П. Кюри понятие симметрии. Ученый назвал ее состоянием «пространства» и относил к тем «первопричинам», которые определил Пастер. «Две среды, обладающие одинаковой диссимметрией, связаны между собой особым образом, и отсюда можно вывести некоторые физические следствия», – писал П. Кюри.
Пьер Кюри сформировал несколько теоретических абстрактных обобщений, которые определяли отношения диссимметрических объектов или фигур при их генетической связи. Одно из них гласит: «Когда некоторые причины производят некоторые действия, элементы симметрии причины должны обнаруживаться в этих произведенных действиях. Когда некоторые действия проявляют диссимметрию, то эта диссимметрия должна обнаруживаться и в причинах, их порождающих». А закон о диссимметрии он сформулировал так: «Некоторые элементы симметрии могут сосуществовать с некоторыми явлениями, но это не обязательно. Необходимо, чтобы некоторые элементы симметрии отсутствовали. Это и есть та диссимметрия, которая создает явление». П. Кюри писал о том, что понятие диссимметрии следует распространить на всю физику, потому что там, где есть диссимметрия, можно ожидать новые физические эффекты. Асимметрия порождает диссимметрию. Стало быть, нет никакой мистики в формировании формы предметов, этот процесс определяют физические законы.
Нельзя сказать, что идеи Пастера и их интерпретация Кюри были забыты. Они исследовались, но только в биохимическом аспекте, не выходя на уровень причин и следствий.
Истоки симметрии следует искать в фантомном пространстве, содержащем форму предмета, и в котором идут процессы структурообразования. Симметрия зависит от того, какие действия разрешается проводить над объектом. Например, билатеральную симметрию нельзя переставлять. Если ограничиться только физически выполнимыми операциями, то билатеральной симметрии не будет! Небольшая вариация объекта, как правило, уничтожает весь запас присущей ему симметрии. Именно поэтому природа выбрала для высших животных и растений на внешней огранке самую низшую, билатеральную симметрию. Симметрия вездесуща, ее энергия (скрытая) намного больше ядерной, однако в живых системах она находится под властью сверхслабых взаимодействий.
Если определение симметрии выбрано, то оно позволяет установить между изучаемыми объектами отношения эквивалентности. Все объекты делятся на классы. Все объекты, принадлежащие к одному и тому же классу, могут быть переведены друг в друга надлежаще выбранной операцией над симметрией. В то время как объекты, принадлежащие различным классам, ни одной операцией над симметрией друг в друга переведены быть не могут. Но если учесть, что здоровые клетки – неполносимметрические, то такой перевод возможен с помощью проводников, которыми в биологических системах являются белок в аллотропной фазе, вода, магнитные поля и УФ-фотоны. Перед нами стоит задача – определить лучшие из проводников, тем более что при лечении рака надо переводить кубическую симметрию в диссимметрию и в «золотое сечение».
Отметим влияние геометрии, чисел (в виде чисел Фибоначчи) золотого сечения, кристаллических классов, как на живое, так и неживое. И, как ни странно, живое в своем развитии вобрало все виды симметрии для решения внутренних дел и только несколько видов для огранки внешних форм. Что это, игра природы или закон, с которым мы не знакомы? Математически строгое представление о симметрии сформировалось сравнительно недавно – в ХIX веке. В трактовке известного немецкого математика Германа Вейля современное определение симметрии выглядит так: симметричным называется такой объект, который можно как-то изменять, получая в результате то же, с чего начали. Современное представление о симметрии предполагает неизменность объекта по отношению к каким-то преобразованиям, выполняемым над ним. Необходимо заметить, что в работах ведущих ученых имеется разночтение самих терминов «симметрия», «асимметрия», «антисимметрия» и «диссимметрия». В строгом понимании по Н.В. Тимофееву-Рессовскому и Ю.А. Урманцеву, «симметрия», упрощенно говоря, это строгая соразмерность в расположении чего-либо без малейших отклонений, «асимметрия» – полное отсутствие симметрии, «диссимметрия» – переходное состояние от симметрии к асимметрии, все промежуточные случаи отклонения от строгой симметрии. В этих терминах мы должны были бы говорить в нашей работе и о «флуктуирующей диссимметрии». Например, флуктуирующая симметрия, ее целесообразность в животном и растительном мире. Это не только отбор более симметричных и гармоничных особей, но и «выравнивание» особи относительно мировой линии. Смещение половины тела от нее вправо или влево больше допустимого ведет к вырождению породы… По этой линии самки ориентируются, кто будет их партнером в деле продолжения рода. Тот, кто ближе к «середине» и пропорционален, обречен на успех. Внешняя огранка – это отражение внутренней симметрии. Асимметрия и диссимметрия должны присутствовать в любом организме, но они должны быть гармоничными в пределах нормы.
Симметрия как таковая – это прерогатива математики и физики, но диссимметрия – биологии и физики. Геометрия теоретически решает пространственные задачи. Однако теория теорией, а решать, где же она переходит в реальность, материализуется, образует и формирует диссимметрию, необходимо, и как можно быстрее… Физики давно ищут место переходов симметрии в физике элементарных частиц. Интересной проблемой квантовой теории поля является включение в единую калибровочную схему и сильного взаимодействия («великое объединение»). Другим перспективным направлением объединения считается суперкалибровочная симметрия, или просто суперсимметрия. Предполагается, что вакуум является симметрией более высокого порядка, чем известные на сегодня виды симметрии. Нарушения симметрии, которые мы видим повсюду, не затрагивают динамическую симметрию вакуума. Динамическая симметрия вакуума не противоречит идее развития, потому что симметрия вакуума сохраняется и тогда, когда нарушаются другие виды симметрии.
В динамических системах процессы формообразования зависят от типа поведения системы, и от т. н. аттракторов. ГПК – это динамическая система с индивидуальными частотными характеристиками. Это система с обратной связью, то есть – она зациклена. Такие динамические системы могут иметь четыре типа поведения: состояние равновесия, периодическое движение, квазипериодическое и хаотическое движение. Этим типам решений соответствуют аттракторы системы в виде устойчивого равновесия, предельного цикла, квазипериодического аттрактора (p-мерного тора) и хаотического (или странного) аттрактора. Важным является то, что простейшие типы квазипериодических и хаотических аттракторов могут реализовываться в динамических системах с размерностью фазового пространства не менее трех. Эти данные указывают нам направление поиска истоков и механизмы сохранения диссимметриии в живом веществе.
Недавно появились работы, посвященные биологической симметрии, но ни математики, ни биологи не указывают, как формируются симметрия и диссимметрия на физическом уровне, какие физические факторы и законы движут ими, где места переходов симметрии в реальность, материю.
Симметрия предметов и ландшафта влияет на людей, и фэн-шуй не даром существует на белом свете уже несколько веков… Симметрия – это порождение квантового, очень странного мира. Это доказывает игра под названием «невозможное ожерелье». Каждая четная бусина зеленого цвета, нечетная красного и, что интересно, первая и последняя бусина всегда оказываются одинакового цвета. На плоскости можно изобразить и так называемые «невозможные» фигуры. Все это разные проявления одного и того же явления… Объяснение этим феноменам можно найти в геометродинамике и, надо полагать, в квантовой физике. Симметрия и асимметрия в семье порождает различные заболевания, в том числе рак, и это в тибетской медицине не вызывает сомнений. Тибетские врачи всегда лечат мужа и жену одновременно. Симметрию мы видим, щупаем, нюхаем, но точно определить, что это такое, пока не можем. Она дискретна (прерывиста) – то появляется, то исчезает в одном и том же объекте на разных уровнях. Возьмем, к примеру, хиральную – самую «сильную» симметрию в живых организмах. На уровне всего организма мы ее видим: есть правая и левая половины тела. Например, на уровне тканей она исчезает; мы не сможем определить из правой или левой ноги кусочек ткани. На уровне органов и клеток она появляется в «смазанном» виде, проявляя себя точно таким же «смутным» образом и на уровне систем. Симметрия почти «смазана» в аллотропной фазе протеинов, но в твердокристаллическом состоянии вновь проявляется отчетливо. То, как симметрия проявляет себя на разных уровнях организма, указывает нам, на каком уровне искать причину рака (рис. 1).
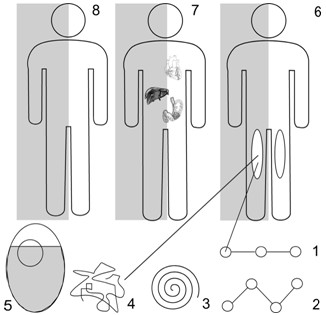
Рис. 1. Дискретное проявление хиральной симметрии.
1 – первичная структура белка; 2 – вторичная структура белка; 3 – третичная; 4 – глобулы; 5 – клетка; 6 – ткани; 7 – органы; 8 – организм.
Поэтому точнее будет сказать топологически, где отсутствует симметрия, и структурно, где нарушена диссимметрия, там появляется рак…
Симметрия связана с понятием середины и целого. В древнегреческой философии и искусстве понятие «середины, центра связано с представлением о цельности бытия». Середина – «избегание крайностей» (Аристотель) – отражает принцип уравновешенности. «Везде грек видел нечто цельное. А это и значит, что он, прежде всего, фиксировал центр наблюдаемого или постороннего предмета… Без понятия „середины“ немыслимо античное учение о пропорциях, мере, симметрии или гармонии». По всему выходит, что «середина» – это какая-то физическая сущность, не определяемая приборами, но видимая воочию. Это, конечно, парадокс. Если вспомнить, что устойчивость любому явлению передает только одно – периодизм, то «середина» – это настойчивое повторение одного и того же процесса, или материализация «центра» некоего фрактала этого явления. Надо полагать, вокруг «середины» всегда располагаются невидимые части фрактала, недостаточно повторяемые, но объективно существующие (что мы и обнаруживаем в виде «ауры»), которые существуют в виде полей… Создается такое впечатление, что физические законы в геометрии не действуют. Но значит ли это, что законы геометрии являются матрицей для физического, видимого мира? Вероятнее всего – да. В космологии – эволюция топологических дефектов Вселенной (Yurke, 1992) хорошо описывается фрактальной моделью – кластеризацией материи (Lucchin, 1985).
Как известно, чудо фрактальной геометрии заключается в том, что чрезвычайно сложные формы могут получаться в результате простых процессов генерирования. Еще один сюрприз преподносит нам учение о динамических системах: простые, детерминированные уравнения могут порождать такой хаос, при котором система никогда не возвращается в стабильное состояние. Часто такие системы ведут себя вполне нормально и до некоторого определенного значения ключевого параметра, потом происходит имеющий две возможности дальнейшего развития, потом четыре и, наконец, хаотический набор возможностей. Не кажется ли Вам, что эти переходы очень напоминают деление белка и изолецитального яйца, но в укороченном варианте?! Однако все живое имеет нехаотический, а вполне закономерный набор возможностей развития. Если учесть, что живой организм – это единый фрактал, то многое становится на свои места. Во-первых, математическое выражение превращается во фракталы, а они, в свою очередь, – в симметрию. Во-вторых, после следующей итерации эстафету подхватывает более «округлая» биологическая симметрия, которая сохраняет все предыдущие геометрические составляющие. Сложность рождается из простоты. Фракталы придают структуру и красоту хаосу. Поэтому нелинейность и фрактальность являются геометрией хаоса, а симметрия – геометрией порядка.
Хотя живая природа как бы отвергает симметрию, но следует ей. А хаос, как известно, тесно связан с порядком. Эта связь осуществляется с помощью указанных выше свойств фракталов. Но рак, казалось бы, хаотическая система, как ни странно, в упорядоченной системе (организме) создает хаос, но с элементами более упорядоченных структур. В Евклидовой геометрии приближающийся объект становится проще. У фракталов это свойство теряется. Трехмерный параллелепипед становится двухмерной плоскостью, затем одномерной линией и, наконец, точкой.
Многие структуры организмов устроены на принципах фракталов (в частности – энергообразующие и информопроводящие). Можно сказать, что деревообразность свойственна фрактальному скейлингу, или гипотезе самоподобия. Организм человека – тоже фрактал, и генетика начинается с этих скрытых пространственных структур, корни которых уходят также в фантомный мир.
Фракталы и симметрия несут на себе не только геометрическую нагрузку, но и пространственное отражение физических законов, физических полей, и им подчиняются химические реакции. Природа кодирует изображения живых и неживых объектов с помощью изощренных, но, в то же время, очень простых по сути способов. Фрактальные методы используются ею для сокращения объема хранимой информации самоподобием, при любом масштабе это так называемые вейвлет-методы, которые для сокращения объема хранимой информации о вейвлетно преобразованной области используют избыточность масштаба. То есть, природа вначале кодирует изображение, затем «обкусывает» лишнее. Кластеризация фракталов – это проявление временных совпадающих физических и пространственных характеристик, нужных объекту в данный промежуток времени (кластеры молекул воды и когерентное состояние молекул белковых структур тому подтверждение). Вот так просто функционируют «простые» методы природы. Многие объекты в природе (например, человеческое тело) состоят из множества фракталов, смешанных друг с другом, причем каждый фрактал имеет свою размерность, отличную от размерности остальных. Например, двухмерная поверхность человеческой сосудистой системы изгибается, ветвится, скручивается и сжимается так, что ее фрактальная размерность равна 3.0. Но если бы она была разделена на отдельные части, фрактальная размерность артерий была бы только 2.7, тогда как бронхиальные пути в легких имели бы фрактальную размерность 1.07. Фрактальная размерность клеточных мембран равна 3, а фрактальная размерность мембран раковых клеток понижена и, вероятнее всего, равна или ниже 1.0! Вопрос о природе фракталов остается открытым. То же самое мы испытываем, когда имеем дело с золотым сечением, симметрией, числами Фибоначчи. Эти явления, несомненно, имеют одну природу, и время создания общей теории, объединяющей их наподобие Общей Теории Относительности, давно назрело. Мало того, составляющие общей теории относительности и эти геометрические «невидимки» должны очень тесно взаимодействовать, ведь они вместе и составляют суть объективной реальности… В этой реальности: «…каждый последующий уровень опирается на предыдущий, причем реалии предыдущего уровня гораздо грубей реалий последующего» (Тибетская медицина). Строгая иерархия подчинения является основой живого, поэтому все в нем самоорганизуется, структурируется и упорядочивается.
Интуитивно симметрия в своих простых формах понятна любому человеку, и часто мы выделяем ее как элемент прекрасного и совершенного. В известной мере симметрия отражает степень упорядоченности системы. Например, окружность, ограничивающая каплю на плоскости, более упорядочена, чем размытое пятно на этой же площади, и, следовательно, более симметрична. Поэтому можно связать изменение энтропии как характеристики упорядочения с симметрией: чем более организовано вещество, тем выше симметрия и тем меньше энтропия. Одно из определений понятий симметрии и асимметрии дал В. Готт: «Симметрия – понятие, отражающее существующий в природе порядок, пропорциональность и соразмерность между элементами какой-либо системы или объекта природы, упорядоченность, равновесие системы, устойчивость, то есть, если хотите, некий элемент гармонии. Асимметрия – понятие противоположное симметрии, отражающее разупорядочение системы, нарушение равновесия и это связано с изменением, развитием системы». Таким образом, мы приходим к выводу, что развивающаяся динамическая система должна быть неравновесной и несимметричной. Этот тезис напрямую касается такого понятия, как жизнь. В ряде случаев симметрия является достаточно очевидным фактом. Например, для определенных геометрических фигур нетрудно увидеть эту симметрию и показать ее путем соответствующих преобразований, в результате которых фигура не изменит своего вида. Однако в общем смысле понятие симметрии гораздо шире, и ее можно понимать как неизменность (инвариантность) каких-либо свойств объекта по отношению к преобразованиям, операциям, выполняемым над этим объектом. Причем это может быть не только материальный объект, но и закон, математическая формула или уравнения, в том числе и нелинейные уравнения, которые, как мы уже знаем, играют большую роль в самоорганизующихся процессах. Дать более конкретное определение симметрии, чем у Готта, в общем случае затруднительно еще и потому, что она принимает свою форму в каждой сфере человеческой деятельности. Что касается математических построений, то там также имеют место симметричные многочлены, которые можно использовать для существенного упрощения решения алгебраических и дифференциальных уравнений. Особенно полезным оказалось использование симметрийных представлений в теории групп с введением инварианта, то есть такого преобразования, когда соотношения между переменными не изменяются. Отражением связи пространства, симметрии и законов сохранения может служить мысль великого французского математика А. Пуанкаре: «Пространство – это группа». Логика подсказывает – группа не может существовать одна. Отсюда следует – пространств множество, и иначе быть не может… Наиболее наглядное и непосредственное применение идей симметрии имеет место в кристаллографии и физике твердого тела, изучающих физические свойства кристаллов в зависимости от их строения. Даже непосвященному человеку хорошо видна здесь ассоциация с неким совершенством, порядком и гармонией. Симметрия является для мира кристаллов естественной базой их физической сущности. Один из создателей современной физики твердого тела Дж. Займен вообще считал, что вся теория твердых тел основана на трансляционной симметрии. Здесь симметрия проявляется при совмещении геометрических тел, например, правильных многогранников при повороте их в пространстве на определенные углы, а также при перемещениях в атомной решетке на определенные величины векторов трансляции, кратных периоду решетки. Более глубокое понимание и применение симметрии связано с изучением и обоснованием законов сохранения, отражающих фундаментальные свойства пространства-времени. Напомним, что симметрия относительно произвольного сдвига во времени приводит к закону сохранения энергии для консервативных (замкнутых) систем. Неизменность характеристик физической системы при произвольном перемещении ее как целого в пространстве на произвольный вектор приводит к закону сохранения импульса. И, наконец, симметрия относительно произвольных пространственных поворотов (изотропность пространства) связана с законом сохранения момента импульса. Так как категория симметрии относится к любому объекту или понятию, то она в полной мере применяется, например, к физическому закону. А поскольку суть физического закона – нахождение и вычисление идентичного в явлениях, то для инерциальных систем, согласно принципу относительности Галилея, эти физические законы будут во всех системах одинаковы. Следовательно, они инвариантны относительно описания явлений как в одной инерциальной системе, так и в другой, и тем самым сохраняют симметрию. В 1918 году были доказаны теоремы Нетер, смысл одной из которых состоит в том, что различным симметриям физических законов соответствуют определенные законы сохранения. Эта связь является настолько всеобщей, что ее можно считать наиболее полным отображением понятия сохранения субстанций и законов, их описывающих, в природе. Как сказал физик-теоретик Р. Фейнман: «Среди мудрейших и удивительных вещей в физике эта связь – одна из самых красивых и удивительных». Различие видов симметрии связано с разными способами пространственно-временного преобразования одной инерциальной системы в другую инерциальную систему. Остановимся на этом несколько подробнее. Каждому такому пространственно-временному преобразованию соответствует определенный вид симметрии. Так, перенос начала координат в произвольную точку пространства при неизменности физических свойств, связан с симметрией таких преобразований (это как раз и есть трансляционная симметрия), и означает физическую эквивалентность всех точек пространства, то есть его однородность. Поворот координатных осей в пространстве связан с физической эквивалентностью разных направлений в пространстве и означает изотропность пространства. Симметрия относительно переноса во времени связана с физической эквивалентностью различных моментов времени, что должно также отражать идею независимости хода времени от его начала (время протекает одинаково). Откуда, кстати, следует, что однородность времени проявляется в его равномерном течении. Такое заключение позволяет полагать, что относительная скорость всех процессов, протекающих в природе, одинакова. Этот факт равномерности течения времени был установлен экспериментально с точностью до 10-14 секунд за период ~10 миллионов лет. В качестве примера можно привести тот факт, что спектральный состав излучения атомов звезд, испущенного миллионы лет тому назад и воспринимаемого нами только сейчас, такой же, как спектральный состав таких же атомов на Земле. Заметим также, что проблемы симметрии-асимметрии оказываются связанными между собой глубже, чем это кажется, исходя из бинарной структуры этих понятий (да-нет). В качестве примера можно привести состояние человека во вращающейся центрифуге. Есть симметрия вращения (поворота), но относительность покоя и вращательного движения нарушается, и человек в такой центрифуге по своему состоянию (вестибулярные ощущения) может определить, что его вращающаяся закрытая (герметизированная) камера на центрифуге вращается. Таким образом, возникает ситуация, при которой физические законы не инвариантны относительно вращения, то есть налицо асимметрия. То же можно сказать и о так называемых преобразованиях подобия, связанных с изменением масштабов физических систем. Асимметрия относительно масштабных преобразований связана с тем, что порядок размеров атомов имеет одинаковое для всей Вселенной значение (~10-10 м). И если мы будем уменьшать размеры, например, изделий микроэлектроники, в том числе и пленочных, то характер поведения электронов в них изменится (возникают размерные эффекты), то есть опять-таки может возникнуть асимметричность процессов при таких размерах. Другой пример несимметрии относительно масштабов в биологии приводит Б. Свистунов: «Несмотря на похожесть окраски, нельзя, например, раскормить осу до размеров тигра, так как при массе 10-100 кг она потеряет способность летать – возникает другое качество».
Но жизнь питается отрицательной энтропией. Иначе говоря, любая структура, поскольку она всегда может образовываться в правых и левых вариантах атомного строения, обязана состоять, согласно энтропии, из равного количества этих изомеров, то есть быть рацемичной. Рацемичной является почти любое косное вещество и на поверхности, и в недрах планеты. Почти, но не совсем, все вещество в целом – и живое, и неживое – располагается на некой лестнице рацемичности, обладает разными ее степенями, различным процентным соотношением неравенства в равенстве левого и правого вещества. Свойство гомохиральности играет важную роль в иерархии самоорганизующихся структур любого порядка и вида. Правые и левые изомеры энергетически неэквивалентны, левые слабее правых, поэтому их диссимметрия начинается на уровне сверхслабых взаимодействий в макроогранизме там, где «туман», то есть предполагаемая ось симметрии. «Туманное» место (то есть место предполагаемой оси симметрии) имеет вполне материальную базу, неравенство зеркальных энантиомеров начинается на уровне атомного ядра, числа нейтронов в нем. Граница симметрии – мировая линия – начинается с ядер атомов IV периода таблицы Д.И. Менделеева, так как здесь располагаются элементы, нейтрально относящиеся к мировой линии. К этому явлению мы будем обращаться не раз. Соединения, способные более эффективно обеспечить гомохиральность природных объектов, обладают энергетически выгодным «правым» свойством.
Тиозамещенные аналоги ДНК, в которые она входит в состав или замещает фосфатные группы скелета ДНК, резко отличаются от обычных молекул. Расчеты показали, что для них разность концентраций на три порядка превосходит ранее найденные значения, и при этом более энергетически выгодным оказывается энантиомер с естественной правой спиралью.
Второй шаг в описании диссимметрии сделал Пьер Кюри. В его биографии, написанной Марией Кюри, говорится об интересе, который вызвало у П. Кюри понятие симметрии. Ученый назвал ее состоянием «пространства» и относил к тем «первопричинам», которые определил Пастер. «Две среды, обладающие одинаковой диссимметрией, связаны между собой особым образом, и отсюда можно вывести некоторые физические следствия», – писал П. Кюри.
Пьер Кюри сформировал несколько теоретических абстрактных обобщений, которые определяли отношения диссимметрических объектов или фигур при их генетической связи. Одно из них гласит: «Когда некоторые причины производят некоторые действия, элементы симметрии причины должны обнаруживаться в этих произведенных действиях. Когда некоторые действия проявляют диссимметрию, то эта диссимметрия должна обнаруживаться и в причинах, их порождающих». А закон о диссимметрии он сформулировал так: «Некоторые элементы симметрии могут сосуществовать с некоторыми явлениями, но это не обязательно. Необходимо, чтобы некоторые элементы симметрии отсутствовали. Это и есть та диссимметрия, которая создает явление». П. Кюри писал о том, что понятие диссимметрии следует распространить на всю физику, потому что там, где есть диссимметрия, можно ожидать новые физические эффекты. Асимметрия порождает диссимметрию. Стало быть, нет никакой мистики в формировании формы предметов, этот процесс определяют физические законы.
Нельзя сказать, что идеи Пастера и их интерпретация Кюри были забыты. Они исследовались, но только в биохимическом аспекте, не выходя на уровень причин и следствий.
Истоки симметрии следует искать в фантомном пространстве, содержащем форму предмета, и в котором идут процессы структурообразования. Симметрия зависит от того, какие действия разрешается проводить над объектом. Например, билатеральную симметрию нельзя переставлять. Если ограничиться только физически выполнимыми операциями, то билатеральной симметрии не будет! Небольшая вариация объекта, как правило, уничтожает весь запас присущей ему симметрии. Именно поэтому природа выбрала для высших животных и растений на внешней огранке самую низшую, билатеральную симметрию. Симметрия вездесуща, ее энергия (скрытая) намного больше ядерной, однако в живых системах она находится под властью сверхслабых взаимодействий.
Если определение симметрии выбрано, то оно позволяет установить между изучаемыми объектами отношения эквивалентности. Все объекты делятся на классы. Все объекты, принадлежащие к одному и тому же классу, могут быть переведены друг в друга надлежаще выбранной операцией над симметрией. В то время как объекты, принадлежащие различным классам, ни одной операцией над симметрией друг в друга переведены быть не могут. Но если учесть, что здоровые клетки – неполносимметрические, то такой перевод возможен с помощью проводников, которыми в биологических системах являются белок в аллотропной фазе, вода, магнитные поля и УФ-фотоны. Перед нами стоит задача – определить лучшие из проводников, тем более что при лечении рака надо переводить кубическую симметрию в диссимметрию и в «золотое сечение».
Отметим влияние геометрии, чисел (в виде чисел Фибоначчи) золотого сечения, кристаллических классов, как на живое, так и неживое. И, как ни странно, живое в своем развитии вобрало все виды симметрии для решения внутренних дел и только несколько видов для огранки внешних форм. Что это, игра природы или закон, с которым мы не знакомы? Математически строгое представление о симметрии сформировалось сравнительно недавно – в ХIX веке. В трактовке известного немецкого математика Германа Вейля современное определение симметрии выглядит так: симметричным называется такой объект, который можно как-то изменять, получая в результате то же, с чего начали. Современное представление о симметрии предполагает неизменность объекта по отношению к каким-то преобразованиям, выполняемым над ним. Необходимо заметить, что в работах ведущих ученых имеется разночтение самих терминов «симметрия», «асимметрия», «антисимметрия» и «диссимметрия». В строгом понимании по Н.В. Тимофееву-Рессовскому и Ю.А. Урманцеву, «симметрия», упрощенно говоря, это строгая соразмерность в расположении чего-либо без малейших отклонений, «асимметрия» – полное отсутствие симметрии, «диссимметрия» – переходное состояние от симметрии к асимметрии, все промежуточные случаи отклонения от строгой симметрии. В этих терминах мы должны были бы говорить в нашей работе и о «флуктуирующей диссимметрии». Например, флуктуирующая симметрия, ее целесообразность в животном и растительном мире. Это не только отбор более симметричных и гармоничных особей, но и «выравнивание» особи относительно мировой линии. Смещение половины тела от нее вправо или влево больше допустимого ведет к вырождению породы… По этой линии самки ориентируются, кто будет их партнером в деле продолжения рода. Тот, кто ближе к «середине» и пропорционален, обречен на успех. Внешняя огранка – это отражение внутренней симметрии. Асимметрия и диссимметрия должны присутствовать в любом организме, но они должны быть гармоничными в пределах нормы.
Симметрия как таковая – это прерогатива математики и физики, но диссимметрия – биологии и физики. Геометрия теоретически решает пространственные задачи. Однако теория теорией, а решать, где же она переходит в реальность, материализуется, образует и формирует диссимметрию, необходимо, и как можно быстрее… Физики давно ищут место переходов симметрии в физике элементарных частиц. Интересной проблемой квантовой теории поля является включение в единую калибровочную схему и сильного взаимодействия («великое объединение»). Другим перспективным направлением объединения считается суперкалибровочная симметрия, или просто суперсимметрия. Предполагается, что вакуум является симметрией более высокого порядка, чем известные на сегодня виды симметрии. Нарушения симметрии, которые мы видим повсюду, не затрагивают динамическую симметрию вакуума. Динамическая симметрия вакуума не противоречит идее развития, потому что симметрия вакуума сохраняется и тогда, когда нарушаются другие виды симметрии.
В динамических системах процессы формообразования зависят от типа поведения системы, и от т. н. аттракторов. ГПК – это динамическая система с индивидуальными частотными характеристиками. Это система с обратной связью, то есть – она зациклена. Такие динамические системы могут иметь четыре типа поведения: состояние равновесия, периодическое движение, квазипериодическое и хаотическое движение. Этим типам решений соответствуют аттракторы системы в виде устойчивого равновесия, предельного цикла, квазипериодического аттрактора (p-мерного тора) и хаотического (или странного) аттрактора. Важным является то, что простейшие типы квазипериодических и хаотических аттракторов могут реализовываться в динамических системах с размерностью фазового пространства не менее трех. Эти данные указывают нам направление поиска истоков и механизмы сохранения диссимметриии в живом веществе.
Недавно появились работы, посвященные биологической симметрии, но ни математики, ни биологи не указывают, как формируются симметрия и диссимметрия на физическом уровне, какие физические факторы и законы движут ими, где места переходов симметрии в реальность, материю.
Симметрия предметов и ландшафта влияет на людей, и фэн-шуй не даром существует на белом свете уже несколько веков… Симметрия – это порождение квантового, очень странного мира. Это доказывает игра под названием «невозможное ожерелье». Каждая четная бусина зеленого цвета, нечетная красного и, что интересно, первая и последняя бусина всегда оказываются одинакового цвета. На плоскости можно изобразить и так называемые «невозможные» фигуры. Все это разные проявления одного и того же явления… Объяснение этим феноменам можно найти в геометродинамике и, надо полагать, в квантовой физике. Симметрия и асимметрия в семье порождает различные заболевания, в том числе рак, и это в тибетской медицине не вызывает сомнений. Тибетские врачи всегда лечат мужа и жену одновременно. Симметрию мы видим, щупаем, нюхаем, но точно определить, что это такое, пока не можем. Она дискретна (прерывиста) – то появляется, то исчезает в одном и том же объекте на разных уровнях. Возьмем, к примеру, хиральную – самую «сильную» симметрию в живых организмах. На уровне всего организма мы ее видим: есть правая и левая половины тела. Например, на уровне тканей она исчезает; мы не сможем определить из правой или левой ноги кусочек ткани. На уровне органов и клеток она появляется в «смазанном» виде, проявляя себя точно таким же «смутным» образом и на уровне систем. Симметрия почти «смазана» в аллотропной фазе протеинов, но в твердокристаллическом состоянии вновь проявляется отчетливо. То, как симметрия проявляет себя на разных уровнях организма, указывает нам, на каком уровне искать причину рака (рис. 1).

Рис. 1. Дискретное проявление хиральной симметрии.
1 – первичная структура белка; 2 – вторичная структура белка; 3 – третичная; 4 – глобулы; 5 – клетка; 6 – ткани; 7 – органы; 8 – организм.
Поэтому точнее будет сказать топологически, где отсутствует симметрия, и структурно, где нарушена диссимметрия, там появляется рак…
Симметрия связана с понятием середины и целого. В древнегреческой философии и искусстве понятие «середины, центра связано с представлением о цельности бытия». Середина – «избегание крайностей» (Аристотель) – отражает принцип уравновешенности. «Везде грек видел нечто цельное. А это и значит, что он, прежде всего, фиксировал центр наблюдаемого или постороннего предмета… Без понятия „середины“ немыслимо античное учение о пропорциях, мере, симметрии или гармонии». По всему выходит, что «середина» – это какая-то физическая сущность, не определяемая приборами, но видимая воочию. Это, конечно, парадокс. Если вспомнить, что устойчивость любому явлению передает только одно – периодизм, то «середина» – это настойчивое повторение одного и того же процесса, или материализация «центра» некоего фрактала этого явления. Надо полагать, вокруг «середины» всегда располагаются невидимые части фрактала, недостаточно повторяемые, но объективно существующие (что мы и обнаруживаем в виде «ауры»), которые существуют в виде полей… Создается такое впечатление, что физические законы в геометрии не действуют. Но значит ли это, что законы геометрии являются матрицей для физического, видимого мира? Вероятнее всего – да. В космологии – эволюция топологических дефектов Вселенной (Yurke, 1992) хорошо описывается фрактальной моделью – кластеризацией материи (Lucchin, 1985).
Как известно, чудо фрактальной геометрии заключается в том, что чрезвычайно сложные формы могут получаться в результате простых процессов генерирования. Еще один сюрприз преподносит нам учение о динамических системах: простые, детерминированные уравнения могут порождать такой хаос, при котором система никогда не возвращается в стабильное состояние. Часто такие системы ведут себя вполне нормально и до некоторого определенного значения ключевого параметра, потом происходит имеющий две возможности дальнейшего развития, потом четыре и, наконец, хаотический набор возможностей. Не кажется ли Вам, что эти переходы очень напоминают деление белка и изолецитального яйца, но в укороченном варианте?! Однако все живое имеет нехаотический, а вполне закономерный набор возможностей развития. Если учесть, что живой организм – это единый фрактал, то многое становится на свои места. Во-первых, математическое выражение превращается во фракталы, а они, в свою очередь, – в симметрию. Во-вторых, после следующей итерации эстафету подхватывает более «округлая» биологическая симметрия, которая сохраняет все предыдущие геометрические составляющие. Сложность рождается из простоты. Фракталы придают структуру и красоту хаосу. Поэтому нелинейность и фрактальность являются геометрией хаоса, а симметрия – геометрией порядка.
Хотя живая природа как бы отвергает симметрию, но следует ей. А хаос, как известно, тесно связан с порядком. Эта связь осуществляется с помощью указанных выше свойств фракталов. Но рак, казалось бы, хаотическая система, как ни странно, в упорядоченной системе (организме) создает хаос, но с элементами более упорядоченных структур. В Евклидовой геометрии приближающийся объект становится проще. У фракталов это свойство теряется. Трехмерный параллелепипед становится двухмерной плоскостью, затем одномерной линией и, наконец, точкой.
Многие структуры организмов устроены на принципах фракталов (в частности – энергообразующие и информопроводящие). Можно сказать, что деревообразность свойственна фрактальному скейлингу, или гипотезе самоподобия. Организм человека – тоже фрактал, и генетика начинается с этих скрытых пространственных структур, корни которых уходят также в фантомный мир.
Фракталы и симметрия несут на себе не только геометрическую нагрузку, но и пространственное отражение физических законов, физических полей, и им подчиняются химические реакции. Природа кодирует изображения живых и неживых объектов с помощью изощренных, но, в то же время, очень простых по сути способов. Фрактальные методы используются ею для сокращения объема хранимой информации самоподобием, при любом масштабе это так называемые вейвлет-методы, которые для сокращения объема хранимой информации о вейвлетно преобразованной области используют избыточность масштаба. То есть, природа вначале кодирует изображение, затем «обкусывает» лишнее. Кластеризация фракталов – это проявление временных совпадающих физических и пространственных характеристик, нужных объекту в данный промежуток времени (кластеры молекул воды и когерентное состояние молекул белковых структур тому подтверждение). Вот так просто функционируют «простые» методы природы. Многие объекты в природе (например, человеческое тело) состоят из множества фракталов, смешанных друг с другом, причем каждый фрактал имеет свою размерность, отличную от размерности остальных. Например, двухмерная поверхность человеческой сосудистой системы изгибается, ветвится, скручивается и сжимается так, что ее фрактальная размерность равна 3.0. Но если бы она была разделена на отдельные части, фрактальная размерность артерий была бы только 2.7, тогда как бронхиальные пути в легких имели бы фрактальную размерность 1.07. Фрактальная размерность клеточных мембран равна 3, а фрактальная размерность мембран раковых клеток понижена и, вероятнее всего, равна или ниже 1.0! Вопрос о природе фракталов остается открытым. То же самое мы испытываем, когда имеем дело с золотым сечением, симметрией, числами Фибоначчи. Эти явления, несомненно, имеют одну природу, и время создания общей теории, объединяющей их наподобие Общей Теории Относительности, давно назрело. Мало того, составляющие общей теории относительности и эти геометрические «невидимки» должны очень тесно взаимодействовать, ведь они вместе и составляют суть объективной реальности… В этой реальности: «…каждый последующий уровень опирается на предыдущий, причем реалии предыдущего уровня гораздо грубей реалий последующего» (Тибетская медицина). Строгая иерархия подчинения является основой живого, поэтому все в нем самоорганизуется, структурируется и упорядочивается.
Интуитивно симметрия в своих простых формах понятна любому человеку, и часто мы выделяем ее как элемент прекрасного и совершенного. В известной мере симметрия отражает степень упорядоченности системы. Например, окружность, ограничивающая каплю на плоскости, более упорядочена, чем размытое пятно на этой же площади, и, следовательно, более симметрична. Поэтому можно связать изменение энтропии как характеристики упорядочения с симметрией: чем более организовано вещество, тем выше симметрия и тем меньше энтропия. Одно из определений понятий симметрии и асимметрии дал В. Готт: «Симметрия – понятие, отражающее существующий в природе порядок, пропорциональность и соразмерность между элементами какой-либо системы или объекта природы, упорядоченность, равновесие системы, устойчивость, то есть, если хотите, некий элемент гармонии. Асимметрия – понятие противоположное симметрии, отражающее разупорядочение системы, нарушение равновесия и это связано с изменением, развитием системы». Таким образом, мы приходим к выводу, что развивающаяся динамическая система должна быть неравновесной и несимметричной. Этот тезис напрямую касается такого понятия, как жизнь. В ряде случаев симметрия является достаточно очевидным фактом. Например, для определенных геометрических фигур нетрудно увидеть эту симметрию и показать ее путем соответствующих преобразований, в результате которых фигура не изменит своего вида. Однако в общем смысле понятие симметрии гораздо шире, и ее можно понимать как неизменность (инвариантность) каких-либо свойств объекта по отношению к преобразованиям, операциям, выполняемым над этим объектом. Причем это может быть не только материальный объект, но и закон, математическая формула или уравнения, в том числе и нелинейные уравнения, которые, как мы уже знаем, играют большую роль в самоорганизующихся процессах. Дать более конкретное определение симметрии, чем у Готта, в общем случае затруднительно еще и потому, что она принимает свою форму в каждой сфере человеческой деятельности. Что касается математических построений, то там также имеют место симметричные многочлены, которые можно использовать для существенного упрощения решения алгебраических и дифференциальных уравнений. Особенно полезным оказалось использование симметрийных представлений в теории групп с введением инварианта, то есть такого преобразования, когда соотношения между переменными не изменяются. Отражением связи пространства, симметрии и законов сохранения может служить мысль великого французского математика А. Пуанкаре: «Пространство – это группа». Логика подсказывает – группа не может существовать одна. Отсюда следует – пространств множество, и иначе быть не может… Наиболее наглядное и непосредственное применение идей симметрии имеет место в кристаллографии и физике твердого тела, изучающих физические свойства кристаллов в зависимости от их строения. Даже непосвященному человеку хорошо видна здесь ассоциация с неким совершенством, порядком и гармонией. Симметрия является для мира кристаллов естественной базой их физической сущности. Один из создателей современной физики твердого тела Дж. Займен вообще считал, что вся теория твердых тел основана на трансляционной симметрии. Здесь симметрия проявляется при совмещении геометрических тел, например, правильных многогранников при повороте их в пространстве на определенные углы, а также при перемещениях в атомной решетке на определенные величины векторов трансляции, кратных периоду решетки. Более глубокое понимание и применение симметрии связано с изучением и обоснованием законов сохранения, отражающих фундаментальные свойства пространства-времени. Напомним, что симметрия относительно произвольного сдвига во времени приводит к закону сохранения энергии для консервативных (замкнутых) систем. Неизменность характеристик физической системы при произвольном перемещении ее как целого в пространстве на произвольный вектор приводит к закону сохранения импульса. И, наконец, симметрия относительно произвольных пространственных поворотов (изотропность пространства) связана с законом сохранения момента импульса. Так как категория симметрии относится к любому объекту или понятию, то она в полной мере применяется, например, к физическому закону. А поскольку суть физического закона – нахождение и вычисление идентичного в явлениях, то для инерциальных систем, согласно принципу относительности Галилея, эти физические законы будут во всех системах одинаковы. Следовательно, они инвариантны относительно описания явлений как в одной инерциальной системе, так и в другой, и тем самым сохраняют симметрию. В 1918 году были доказаны теоремы Нетер, смысл одной из которых состоит в том, что различным симметриям физических законов соответствуют определенные законы сохранения. Эта связь является настолько всеобщей, что ее можно считать наиболее полным отображением понятия сохранения субстанций и законов, их описывающих, в природе. Как сказал физик-теоретик Р. Фейнман: «Среди мудрейших и удивительных вещей в физике эта связь – одна из самых красивых и удивительных». Различие видов симметрии связано с разными способами пространственно-временного преобразования одной инерциальной системы в другую инерциальную систему. Остановимся на этом несколько подробнее. Каждому такому пространственно-временному преобразованию соответствует определенный вид симметрии. Так, перенос начала координат в произвольную точку пространства при неизменности физических свойств, связан с симметрией таких преобразований (это как раз и есть трансляционная симметрия), и означает физическую эквивалентность всех точек пространства, то есть его однородность. Поворот координатных осей в пространстве связан с физической эквивалентностью разных направлений в пространстве и означает изотропность пространства. Симметрия относительно переноса во времени связана с физической эквивалентностью различных моментов времени, что должно также отражать идею независимости хода времени от его начала (время протекает одинаково). Откуда, кстати, следует, что однородность времени проявляется в его равномерном течении. Такое заключение позволяет полагать, что относительная скорость всех процессов, протекающих в природе, одинакова. Этот факт равномерности течения времени был установлен экспериментально с точностью до 10-14 секунд за период ~10 миллионов лет. В качестве примера можно привести тот факт, что спектральный состав излучения атомов звезд, испущенного миллионы лет тому назад и воспринимаемого нами только сейчас, такой же, как спектральный состав таких же атомов на Земле. Заметим также, что проблемы симметрии-асимметрии оказываются связанными между собой глубже, чем это кажется, исходя из бинарной структуры этих понятий (да-нет). В качестве примера можно привести состояние человека во вращающейся центрифуге. Есть симметрия вращения (поворота), но относительность покоя и вращательного движения нарушается, и человек в такой центрифуге по своему состоянию (вестибулярные ощущения) может определить, что его вращающаяся закрытая (герметизированная) камера на центрифуге вращается. Таким образом, возникает ситуация, при которой физические законы не инвариантны относительно вращения, то есть налицо асимметрия. То же можно сказать и о так называемых преобразованиях подобия, связанных с изменением масштабов физических систем. Асимметрия относительно масштабных преобразований связана с тем, что порядок размеров атомов имеет одинаковое для всей Вселенной значение (~10-10 м). И если мы будем уменьшать размеры, например, изделий микроэлектроники, в том числе и пленочных, то характер поведения электронов в них изменится (возникают размерные эффекты), то есть опять-таки может возникнуть асимметричность процессов при таких размерах. Другой пример несимметрии относительно масштабов в биологии приводит Б. Свистунов: «Несмотря на похожесть окраски, нельзя, например, раскормить осу до размеров тигра, так как при массе 10-100 кг она потеряет способность летать – возникает другое качество».
