Страница:
Формула Бейеса выступает здесь как силлогизм: из двух посылок ?( ?) и ?(y/ ?) с необходимостью следует текст с новой семантикой: ?(y/ ?).
Цель последующего изложения — указать аналогию, существующую между приведенным преобразованием смыслов в вероятностной модели языка и процессом измерения в квантовой механике и провести сопоставление между ними.
Как известно, состояние объекта в квантовой механике задается волновой функцией ?(q,t), которая определяет вероятности различных результатов измерения.
Существенно, что состояние объекта определяется именно зависимостью по координатам q.
Зависимость же по t описывает эволюцию этого состояния но времени.
Результат измерения связан лишь с зависимостью волновой функции от пространственных координат q.
По этой причине результаты измерения отнесены к состоянию в определенный момент времени t0 («замороженное время»).
Поэтому всюду ниже переменная t опускается.
Рассмотрим теперь подробнее процесс измерения.
Пусть для определенности производятся измерения величины у (или совокупности величин {у}) у объекта, находящегося в состоянии ?0(q).
Измерительные средства наблюдателя (приборы) играют роль фильтра у, с которым взаимодействует микрообъект. При этом разные измерения (измерения отличающихся наборов величин) будут соответствовать различным фильтрам в том смысле, в котором о них говорится в вероятностной модели смыслов (сокращенно ВМС).
Пусть выбрана конкретная измерительная процедура, соответствующая физической величине у и пусть {yn} — множество возможных значений этой величины, которые могут быть получены в этом измерении (для простоты записи полагаем, что это множество дискретно — в непрерывном случае существо выкладок сохраняется). Если в начальный момент (до взаимодействия с прибором) волновая функция объекта есть ?0(q), а прибора Y0( ?) (где + характеризует совокупность координат прибора), то волновая функция системы объект + прибор будет:
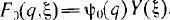После процесса взаимодействия (измерения) волновая функция системы объект + прибор станет(*170):
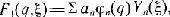где an — комплексная величина такая, что |а„|^2 —дает вероятность обнаружить в результате измерения величины у значение у„ (с волновой функцией прибора Yn( ?). В результате исхода уn объект окажется в состоянии ?n(q).
Таким образом, исходное состояние объекта ?0(q) трансформируется в результате измерения в состояние
Запись ?n(q/yn) выражает то обстоятельство, что возникшее состояние ?n(q) будет различным в зависимости от того, какое значение у„ будет получено в результате измерения величины у.
Вероятность появления этого состояния ?„(q/у„) описывается величиной \а„\^2 которая определяется лишь исходным состоянием ?0(q) и видом и результатом измерения:
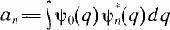где ?n — собственные функции оператора у, соответствующего физической величине у. В состоянии ?n(q) величина у с достоверностью имеет значение уn.
Сопоставим теперь описанный процесс измерения в квантовой механике с преобразованием функции ?( ?) при появлении фильтра у в вероятностной теории смыслов.
Множеству значений переменной ? (множеству смыслов) в ВМС соответствует множество значений переменной q — описывающей степени свободы физического объекта.
Функции ?( ?) отвечает функция ?0(q), или — более точно — | ?0(q)|2.
Фильтру ?(у/ ?) в ВМС. следует поставить в соответствие «измерительную установку» (прибор), реализующую измерение физической величины у.
Преобразованию ?( ?/y)=kp( ?)p(y/ ?) функции ?( ?) при спонтанном появлении фильтра у в ВМС соответствует преобразование волновой функции ?о(q)=» ?(q/yn) отвечающее измеренному значению уn величины у (фильтра). При этом появление того или иного значения yn в процессе измерения, а с ним и преобразование функции ?0(q) оказываются спонтанными.
Заключение.Сказанное выше позволяет сделать следующие выводы. Оперирование с текстами и смыслами в вероятностной модели смыслов и процесс измерения в квантовой теории имеют много общих черт, которые можно иллюстрировать таблицей.
Отличие может быть отмечено в том, что преобразование волновой функции ?0(q) в результате процесса измерения описывается более сложной процедурой, нежели преобразование функции ?( ?). Однако это отличие едва ли существенно при том, что общий характер вхождения величин, обусловливающих общие свойства преобразования, является сходным в обоих случаях(** 171).
Изложенное позволяет поставить вопрос о том, в какой степени квантово-механические процессы могут соответствовать процессам мышления, понимаемым так, как это представлено вероятностной моделью смыслов, опирающейся на представление о семантически насыщенном пространстве.
Вероятностная модель смыслов
Квантовая теория измерений
1 ? — переменная, описывающая множество смыслов (степени свободы текста)
1 q — переменная, описывающая степени свободы физического объекта.
2 Некоторый текст
2 Состояние физического объекта
3 ?( ?) — вероятностная функция, задающая спонтанную «распаковку» смыслов (обнаружение того или иного значения переменной ?
3 | ?(q)|^2 — функция вероятности,
4 у — фильтр (некоторый текст), с которым начинает взаимодействовать исходный текст
4 у — фильтр (измерительный прибор, известный объект, взаимодействие с которым дает измерение физической величины "у").
5 ?(у/ ?) = kp ( ?) ?( ?/у) — преобразование весовой функции смыслов
5 ?o (q) =» ? (q/yn) — преобразование функции состояния в процессе измерения
Приложение 2
Некоторые соображения о возможности построения пространственно-метрической логики
Приложение 3
О едином понимании естественного языка и языка музыкальных текстов с позиций вероятностной модели смыслов
Литература:
Цель последующего изложения — указать аналогию, существующую между приведенным преобразованием смыслов в вероятностной модели языка и процессом измерения в квантовой механике и провести сопоставление между ними.
Как известно, состояние объекта в квантовой механике задается волновой функцией ?(q,t), которая определяет вероятности различных результатов измерения.
Существенно, что состояние объекта определяется именно зависимостью по координатам q.
Зависимость же по t описывает эволюцию этого состояния но времени.
Результат измерения связан лишь с зависимостью волновой функции от пространственных координат q.
По этой причине результаты измерения отнесены к состоянию в определенный момент времени t0 («замороженное время»).
Поэтому всюду ниже переменная t опускается.
Рассмотрим теперь подробнее процесс измерения.
Пусть для определенности производятся измерения величины у (или совокупности величин {у}) у объекта, находящегося в состоянии ?0(q).
Измерительные средства наблюдателя (приборы) играют роль фильтра у, с которым взаимодействует микрообъект. При этом разные измерения (измерения отличающихся наборов величин) будут соответствовать различным фильтрам в том смысле, в котором о них говорится в вероятностной модели смыслов (сокращенно ВМС).
Пусть выбрана конкретная измерительная процедура, соответствующая физической величине у и пусть {yn} — множество возможных значений этой величины, которые могут быть получены в этом измерении (для простоты записи полагаем, что это множество дискретно — в непрерывном случае существо выкладок сохраняется). Если в начальный момент (до взаимодействия с прибором) волновая функция объекта есть ?0(q), а прибора Y0( ?) (где + характеризует совокупность координат прибора), то волновая функция системы объект + прибор будет:
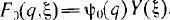
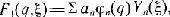
Таким образом, исходное состояние объекта ?0(q) трансформируется в результате измерения в состояние
Вероятность появления этого состояния ?„(q/у„) описывается величиной \а„\^2 которая определяется лишь исходным состоянием ?0(q) и видом и результатом измерения:
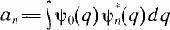
Сопоставим теперь описанный процесс измерения в квантовой механике с преобразованием функции ?( ?) при появлении фильтра у в вероятностной теории смыслов.
Множеству значений переменной ? (множеству смыслов) в ВМС соответствует множество значений переменной q — описывающей степени свободы физического объекта.
Функции ?( ?) отвечает функция ?0(q), или — более точно — | ?0(q)|2.
Фильтру ?(у/ ?) в ВМС. следует поставить в соответствие «измерительную установку» (прибор), реализующую измерение физической величины у.
Преобразованию ?( ?/y)=kp( ?)p(y/ ?) функции ?( ?) при спонтанном появлении фильтра у в ВМС соответствует преобразование волновой функции ?о(q)=» ?(q/yn) отвечающее измеренному значению уn величины у (фильтра). При этом появление того или иного значения yn в процессе измерения, а с ним и преобразование функции ?0(q) оказываются спонтанными.
Заключение.Сказанное выше позволяет сделать следующие выводы. Оперирование с текстами и смыслами в вероятностной модели смыслов и процесс измерения в квантовой теории имеют много общих черт, которые можно иллюстрировать таблицей.
Отличие может быть отмечено в том, что преобразование волновой функции ?0(q) в результате процесса измерения описывается более сложной процедурой, нежели преобразование функции ?( ?). Однако это отличие едва ли существенно при том, что общий характер вхождения величин, обусловливающих общие свойства преобразования, является сходным в обоих случаях(** 171).
Изложенное позволяет поставить вопрос о том, в какой степени квантово-механические процессы могут соответствовать процессам мышления, понимаемым так, как это представлено вероятностной моделью смыслов, опирающейся на представление о семантически насыщенном пространстве.
Вероятностная модель смыслов
Квантовая теория измерений
1 ? — переменная, описывающая множество смыслов (степени свободы текста)
1 q — переменная, описывающая степени свободы физического объекта.
2 Некоторый текст
2 Состояние физического объекта
3 ?( ?) — вероятностная функция, задающая спонтанную «распаковку» смыслов (обнаружение того или иного значения переменной ?
3 | ?(q)|^2 — функция вероятности,
4 у — фильтр (некоторый текст), с которым начинает взаимодействовать исходный текст
4 у — фильтр (измерительный прибор, известный объект, взаимодействие с которым дает измерение физической величины "у").
5 ?(у/ ?) = kp ( ?) ?( ?/у) — преобразование весовой функции смыслов
5 ?o (q) =» ? (q/yn) — преобразование функции состояния в процессе измерения
Приложение 2
Т. А. Перевозский Москва, Физико-технический институт
Некоторые соображения о возможности построения пространственно-метрической логики
Ранее в этой книге (гл. IV, §2) были высказаны некие общие соображения о том, что Бейесовский силлогизм может быть реинтерпретирован в терминах метрической логики, что естественно углубляет степень геометризации развиваемой концепции и открывает новые возможности для обсуждения сверхъединой теории поля, охватывающей как семантические, так и физические проявления Вселенной.
Остановимся на этом вопросе подробнее.
Если задан силлогизм Бейеса
то тем самым задано преобразование весовой функции, которое в краткой символической форме можно написать:
В (1)
?( ?) — преобразуется в некоторую новую функцию ?y( ?)
При выполнении достаточно общих условий вместе с преобразованием функций имеет место преобразование соответствующих производных
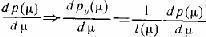В (2)
Здесь l( ?) — некоторая локально задаваемая (калибровочная) функция, которая определяется последним равенством, которому удобно придать несколько иную форму:
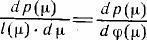Полагая ~ ? = ?( ?) можно написать ? = ?^-1(~ ?) где ?^-1—функция обратная к функции ?. Тогда можно написать
Иначе говоря, исходное преобразование (1), (2) можно выразить как преобразование индуцированное преобразованием ?-пространства ~ ? = ?( ?) которое «деформирует» метрику исходного ?-пространства, преобразуя его в ~ ?.-пространство. Отображение ~ ? = ?( ?) определяется довольно сложным образом силлогизмом Бейеса и не может быть здесь выписано явно. Важно, однако, отметить, что рассмотренные в предыдущих главах идеи в принципе могут быть изложены в терминах определенных преобразований над ?-пространством. Генератором группы этих преобразований, как ясно из сказанного, является соотношение силлогизма Бейеса.
Такой взгляд более тесно примыкает к языку современной физики, в котором фундаментальную роль играют теоретико-групповые методы.
Связанное, по сути, является указанием на некоторый язык, двойственный (сопряженный) тому, на котором велось все предыдущее изложение в книге. Подобная ситуация является довольно распространенной как в физике, так и в математике. Примерами могут служить различные представления уравнений квантовой механики, такие как Гейзенберговское представление, основанное на алгебре операторов и Шредингеровское представление, основанное на волновом уравнении [1]. Другим примером из физики могут служить теории близкодействия и дальнодействия в теории электрических и магнитных полей [2].
Примерами из математики могут служить сопряженные пространства, ковариантные и контрвариантные объекты в теории тензоров [3], теория информации и теория вероятностей (подробнее см. [4]).
Отметим здесь еще, что ВМС сближает с современной физикой представление о решающей роли наблюдателя. Текст не может быть воспринят читателем без его активного вмешательства. Воспринимаемый текст всегда должен быть реинтерпретирован. Аналогично наблюдение квантовой реальности осуществления совместно с актом неконтролируемого вмешательства наблюдателя в эту реальность [5].
Литература
В Ландау, Л. Д. и Лифшиц, Е. М. Квантовая механика.— М.: Гостехиздат, 1948.
Тамм И. Е. Основы теории электричества.— М.: Наука, 1966.
Гельфанд И. -М. Лекции по линейной алгебре.— М.: Наука, 1971.
Кульбак С. Теория информации и статистика.— М.: Наука, 1967.
Ахундов А. В. Вернер Гейзенберг и философия в кн.: Вернер Гейзенберг. Физика и философия. Часть и целое. М.: Наука, 1989.
Остановимся на этом вопросе подробнее.
Если задан силлогизм Бейеса
?( ?) — преобразуется в некоторую новую функцию ?y( ?)
При выполнении достаточно общих условий вместе с преобразованием функций имеет место преобразование соответствующих производных
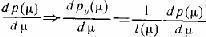
Здесь l( ?) — некоторая локально задаваемая (калибровочная) функция, которая определяется последним равенством, которому удобно придать несколько иную форму:
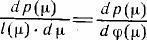
Такой взгляд более тесно примыкает к языку современной физики, в котором фундаментальную роль играют теоретико-групповые методы.
Связанное, по сути, является указанием на некоторый язык, двойственный (сопряженный) тому, на котором велось все предыдущее изложение в книге. Подобная ситуация является довольно распространенной как в физике, так и в математике. Примерами могут служить различные представления уравнений квантовой механики, такие как Гейзенберговское представление, основанное на алгебре операторов и Шредингеровское представление, основанное на волновом уравнении [1]. Другим примером из физики могут служить теории близкодействия и дальнодействия в теории электрических и магнитных полей [2].
Примерами из математики могут служить сопряженные пространства, ковариантные и контрвариантные объекты в теории тензоров [3], теория информации и теория вероятностей (подробнее см. [4]).
Отметим здесь еще, что ВМС сближает с современной физикой представление о решающей роли наблюдателя. Текст не может быть воспринят читателем без его активного вмешательства. Воспринимаемый текст всегда должен быть реинтерпретирован. Аналогично наблюдение квантовой реальности осуществления совместно с актом неконтролируемого вмешательства наблюдателя в эту реальность [5].
Литература
В Ландау, Л. Д. и Лифшиц, Е. М. Квантовая механика.— М.: Гостехиздат, 1948.
Тамм И. Е. Основы теории электричества.— М.: Наука, 1966.
Гельфанд И. -М. Лекции по линейной алгебре.— М.: Наука, 1971.
Кульбак С. Теория информации и статистика.— М.: Наука, 1967.
Ахундов А. В. Вернер Гейзенберг и философия в кн.: Вернер Гейзенберг. Физика и философия. Часть и целое. М.: Наука, 1989.
Приложение 3
Т. А. Перевозский
О едином понимании естественного языка и языка музыкальных текстов с позиций вероятностной модели смыслов
Вероятностная модель смыслов (ВМС) исходит из представления о континууме ? элементарных семантических элементов, над которыми задается весовая функция ?( ?), которая формируется соответствующим текстом. Иначе говоря, воспринимаемому через текст смыслу отвечает всякий раз некоторая весовая функция ?( ?).
Каково же значение отдельного элемента ?? Этот вопрос может быть пояснен аналогией, обращенной к музыке. Такое сопоставление тем более оправдано, что музыка в чистом виде представляет собой феномен сознания, ибо вне музыкального сознания нельзя говорить о музыке, но лишь только об акустике. Акустический феномен становится музыкальным лишь постольку, поскольку существует музыкальное сознание, ибо лишь в нем звук обретает музыкальный смысл.
Шкала смыслов ?, может быть уподоблена шкале музыкальных звуков.
Отдельно взятый звук не составляет еще музыки и сам по себе музыкальным смыслом не обладает. На основе одного только звука нельзя построить музыку.
Для того, чтобы музыкальный смысл возник, необходимо чтобы наряду с данным звуком существовали бы и другие. Иначе говоря, каждый звук лишь в той мере несет с собой музыкальный смысл, в какой он выражает собой отношение к другим звукам музыкальной системы.
В основе феномена музыки лежит понятие «тяготения» (1), которое, собственно, и есть начало музыкального движения. Каждый звук музыкален лишь в той мере, в какой он имеет тяготение к другому звуку, или же сам является центром тяготения для других звуков (в последнем случае его называют «тоникой» (1)).
Система звуков вместе с системой взаимных тяготений, имеющей место между звуками, задает то, что называют в музыке ладом. Например, существует мажорный лад, минорный лад — основные в европейской музыкальной культуре. Внутри лада каждый звук функционален, т. е. обладает ладовой функцией, что и сообщает ему то, что называют музыкальным смыслом.
Именно через посредство возникающих тяготений в процессе музыкального построения реализуется музыкальное развитие, т. е. музыкальная семантика. Возникающие тяготения не являются, вообще говоря, для нашего музыкального сознания однозначными, и это обстоятельство создает собственно напряжение в развитии музыкального произведения (текста), его, если угодно, драматургию, в которой новые звуки появляются сквозь это напряжение, на фоне такого напряжения (усиливая или ослабляя его), реализуя одну из многих возможностей тяготения или лишь сужая поле таких тяготений.
Поле тяготений может быть выражено в виде некоторой функции над звуками, и появление новых звуковых элементов во времени (или даже паузы) создает новую музыкальную ситуацию, в которой прежняя функция тяготения (аналог функции распределения ?( ?) в ВМС) преобразуется в новую (образуя новый «текст»).
Здесь появляющиеся новые звуки (аккорды, музыкальные элементы) играют роль «фильтров» в ВМС, под действием которых происходит преобразование музыкального контекста в нашем слуховом сознании.
Возникшее новое поле тяготений вызывает к проявлению новые звуки (музыкальные смыслы), и через это образуется продолжение музыкального смысла.
Таким образом, звук как акустический феномен обретает музыкальный смысл лишь благодаря существованию музыкального сознания, которое является носителем лада (ладовой, музыкальной организации звуков), благодаря чему в текущем звуке находят свое проявление другие звуки музыкальной системы, которые он «провоцирует» к появлению (проявлению) фактом своего звучания.
Лад, ладовая организация звуков как бы «встроена» в наше сознание подобно кантовской идее о пространстве и времени как априорных формах сознания(* 172).
Музыкальная система (шкала) звуков, являясь структурой, встроенной в наше сознание, может рассматриваться как феномен, характеризующий само сознание. Подобно этому семантическая шкала в ВМС должна рассматриваться как нечто, характеризующее природу нашего сознания и находящую свое выражение в языке.
Сказанное позволяет сделать вывод о том, что развитие семантики в тексте языка может быть уподоблено появлению музыкальной семантики в звуках.
Элементы музыкальной речи, отдельные фрагменты музыкальной конструкции совместно создают новую музыкальную семантику, так что любой музыкальный эпизод составлен из отдельных, более мелких составляющих, музыкально самостоятельных единиц, что полностью аналогично тому, как строится речь в естественном языке.
Мы видим, что существование полной музыкальной системы звуков как таковой является необходимой предпосылкой для того, чтобы какой-либо отдельно взятый звук мог бы иметь музыкальный смысл, отличный от просто акустического звучания.
Подобно этому в ВМС существование семантического упорядоченного континуума ? является изначально необходимым, чтобы существовала весовая функция ?( ?), задающая семантику текста. Такое сопоставление представляется тем более оправданным, что музыка почти во всех своих аспектах может быть уподоблена языку и являет собой как бы глубинную составляющую всякого естественного языка.
Бесспорно, вместе с тем, что с музыкой заведомо связано определенное состояние сознания. Именно поэтому кажется, что любое наше переживание может быть сопровождаемо соответствующим образом подобранной музыкой.
Нужно отметить то обстоятельство, что наш язык очень тесно связан с фонетической природой слова. Нашей речи свойственна интонация и притом в такой степени, что в зависимости от интонации смысл может меняться в самых широких пределах.
Пожалуй, именно благодаря фонетической, интонационной природе естественного языка наша речь обладает собственно эмоциональностью.
Письменный же язык таков, что, читая текст, мы неизменно должны проговаривать слова, т. е. воссоздавать мысленно их фонетический облик, подобно тому, как нотная запись — это письменный язык музыки.
Весьма вероятно, что музыка — это лишь усиленная форма выражения интонаций и их импульсов, которые глубоко заложены в нашем речевом поведении.
Особенность музыкального языка проявляется в том, что этот язык, в отличие от естественного языка, свободен от логических структур: он функционирует так же, как функционирует процесс предмышления в языке. (Предмышлением мы называем процесс спонтанного появления фильтров, сообщающих новое развитие мысли.)
На примере музыки мы отчетливо видим функционирование глубинных (предлогических) уровней сознания в их чистом
виде.
В заключение к сказанному приведем таблицу, иллюстрирующую характер обсуждаемой аналогии.
Вероятностная модель смыслов
Развитие музыкальной формы
1 Упорядоченная шкала смыслов ?
1 Упорядоченная система звуков музыкальной шкалы
2 Текст
2 Музыкальный текст
3 Весовая функция ?( ?)
3 Поле ладово-гармонических тяготений, задающее развитие музыкальной ситуации
4 Фильтр у
4 Спонтанное появление эпизода по ходу развития музыкального действия играет роль фильтра по отношению к предыдущему контексту
5 Преобразование весовой функции: ?( ?)=» ?( ?/y)
5 Преобразование тонально-ладовой и ладово-гармонической функций музыкального контекста под влиянием вновь возникшего фильтра y
6 Многомерность семантики
6 Многоголосие, гармония (одновременное звучание многих голосов) как проявление многомерности музыкальных текстов
Каково же значение отдельного элемента ?? Этот вопрос может быть пояснен аналогией, обращенной к музыке. Такое сопоставление тем более оправдано, что музыка в чистом виде представляет собой феномен сознания, ибо вне музыкального сознания нельзя говорить о музыке, но лишь только об акустике. Акустический феномен становится музыкальным лишь постольку, поскольку существует музыкальное сознание, ибо лишь в нем звук обретает музыкальный смысл.
Шкала смыслов ?, может быть уподоблена шкале музыкальных звуков.
Отдельно взятый звук не составляет еще музыки и сам по себе музыкальным смыслом не обладает. На основе одного только звука нельзя построить музыку.
Для того, чтобы музыкальный смысл возник, необходимо чтобы наряду с данным звуком существовали бы и другие. Иначе говоря, каждый звук лишь в той мере несет с собой музыкальный смысл, в какой он выражает собой отношение к другим звукам музыкальной системы.
В основе феномена музыки лежит понятие «тяготения» (1), которое, собственно, и есть начало музыкального движения. Каждый звук музыкален лишь в той мере, в какой он имеет тяготение к другому звуку, или же сам является центром тяготения для других звуков (в последнем случае его называют «тоникой» (1)).
Система звуков вместе с системой взаимных тяготений, имеющей место между звуками, задает то, что называют в музыке ладом. Например, существует мажорный лад, минорный лад — основные в европейской музыкальной культуре. Внутри лада каждый звук функционален, т. е. обладает ладовой функцией, что и сообщает ему то, что называют музыкальным смыслом.
Именно через посредство возникающих тяготений в процессе музыкального построения реализуется музыкальное развитие, т. е. музыкальная семантика. Возникающие тяготения не являются, вообще говоря, для нашего музыкального сознания однозначными, и это обстоятельство создает собственно напряжение в развитии музыкального произведения (текста), его, если угодно, драматургию, в которой новые звуки появляются сквозь это напряжение, на фоне такого напряжения (усиливая или ослабляя его), реализуя одну из многих возможностей тяготения или лишь сужая поле таких тяготений.
Поле тяготений может быть выражено в виде некоторой функции над звуками, и появление новых звуковых элементов во времени (или даже паузы) создает новую музыкальную ситуацию, в которой прежняя функция тяготения (аналог функции распределения ?( ?) в ВМС) преобразуется в новую (образуя новый «текст»).
Здесь появляющиеся новые звуки (аккорды, музыкальные элементы) играют роль «фильтров» в ВМС, под действием которых происходит преобразование музыкального контекста в нашем слуховом сознании.
Возникшее новое поле тяготений вызывает к проявлению новые звуки (музыкальные смыслы), и через это образуется продолжение музыкального смысла.
Таким образом, звук как акустический феномен обретает музыкальный смысл лишь благодаря существованию музыкального сознания, которое является носителем лада (ладовой, музыкальной организации звуков), благодаря чему в текущем звуке находят свое проявление другие звуки музыкальной системы, которые он «провоцирует» к появлению (проявлению) фактом своего звучания.
Лад, ладовая организация звуков как бы «встроена» в наше сознание подобно кантовской идее о пространстве и времени как априорных формах сознания(* 172).
Музыкальная система (шкала) звуков, являясь структурой, встроенной в наше сознание, может рассматриваться как феномен, характеризующий само сознание. Подобно этому семантическая шкала в ВМС должна рассматриваться как нечто, характеризующее природу нашего сознания и находящую свое выражение в языке.
Сказанное позволяет сделать вывод о том, что развитие семантики в тексте языка может быть уподоблено появлению музыкальной семантики в звуках.
Элементы музыкальной речи, отдельные фрагменты музыкальной конструкции совместно создают новую музыкальную семантику, так что любой музыкальный эпизод составлен из отдельных, более мелких составляющих, музыкально самостоятельных единиц, что полностью аналогично тому, как строится речь в естественном языке.
Мы видим, что существование полной музыкальной системы звуков как таковой является необходимой предпосылкой для того, чтобы какой-либо отдельно взятый звук мог бы иметь музыкальный смысл, отличный от просто акустического звучания.
Подобно этому в ВМС существование семантического упорядоченного континуума ? является изначально необходимым, чтобы существовала весовая функция ?( ?), задающая семантику текста. Такое сопоставление представляется тем более оправданным, что музыка почти во всех своих аспектах может быть уподоблена языку и являет собой как бы глубинную составляющую всякого естественного языка.
Бесспорно, вместе с тем, что с музыкой заведомо связано определенное состояние сознания. Именно поэтому кажется, что любое наше переживание может быть сопровождаемо соответствующим образом подобранной музыкой.
Нужно отметить то обстоятельство, что наш язык очень тесно связан с фонетической природой слова. Нашей речи свойственна интонация и притом в такой степени, что в зависимости от интонации смысл может меняться в самых широких пределах.
Пожалуй, именно благодаря фонетической, интонационной природе естественного языка наша речь обладает собственно эмоциональностью.
Письменный же язык таков, что, читая текст, мы неизменно должны проговаривать слова, т. е. воссоздавать мысленно их фонетический облик, подобно тому, как нотная запись — это письменный язык музыки.
Весьма вероятно, что музыка — это лишь усиленная форма выражения интонаций и их импульсов, которые глубоко заложены в нашем речевом поведении.
Особенность музыкального языка проявляется в том, что этот язык, в отличие от естественного языка, свободен от логических структур: он функционирует так же, как функционирует процесс предмышления в языке. (Предмышлением мы называем процесс спонтанного появления фильтров, сообщающих новое развитие мысли.)
На примере музыки мы отчетливо видим функционирование глубинных (предлогических) уровней сознания в их чистом
виде.
В заключение к сказанному приведем таблицу, иллюстрирующую характер обсуждаемой аналогии.
Вероятностная модель смыслов
Развитие музыкальной формы
1 Упорядоченная шкала смыслов ?
1 Упорядоченная система звуков музыкальной шкалы
2 Текст
2 Музыкальный текст
3 Весовая функция ?( ?)
3 Поле ладово-гармонических тяготений, задающее развитие музыкальной ситуации
4 Фильтр у
4 Спонтанное появление эпизода по ходу развития музыкального действия играет роль фильтра по отношению к предыдущему контексту
5 Преобразование весовой функции: ?( ?)=» ?( ?/y)
5 Преобразование тонально-ладовой и ладово-гармонической функций музыкального контекста под влиянием вновь возникшего фильтра y
6 Многомерность семантики
6 Многоголосие, гармония (одновременное звучание многих голосов) как проявление многомерности музыкальных текстов
Литература:
Августин Блаженный. 1978. Исповедь Блаженного Августина, Епископа Илонского, 71—264. Богословские труды, вып. 19. М.: Московская Патриархия, 264 с.
Адамар, Ж. 1970 Исследование психологии процесса изобретения в области математики. М.: Советское радио, 152 с.
Аристотель. 1976. О душе, 371—448. Собрание сочинений в четырех томах, т. 1. М.: Мысль, 550 с.
Аристотель. 1978. Первая аналитика, 117—254. Сочинения в четырех томах,т. II. М.: Мысль, 687 с.
Бёкке, Р. М. 1915. Космическое сознание. Петроград: изд. «Новый человек», 375 с.
Бердяев, Н. 1969. Смысл истории. Опыт философии человеческой судьбы. Париж, Imca-Press, 270 с.
Беспалько, И. Г. 1978. О некоторых аспектах теории установки и проблемы бессознательного, 56—61.
Бессознательное, т. 3. Тбилиси: Мецниереба, 797 с.
Бессознательное. 1978. Тбилиси: Мецниереба; т. I, 786 с.; т. 2, 686 с.;т. 3, 797 с.; т. 4 (1985), 462 с.
Богомолов, А. С. 1963. Неореализм и спекулятивная философия (А. Н. Уайтхед, с. 252—292). Современный объективный идеализм. Критические очерки.М.: Изд. социально-экономической литературы, 477 с.
Брагина, Н. Н. и Доброхотова, Т. А. 1981. Функциональные асимметрии человека. М.: Медицина, 288 с.
Бурбаки, Н. 1963. Очерки по истории математики. М.: ИЛ, 292 с. Буржуазная философская антропология XX века (ред. Б. Т. Григорьян).1986. М.: Наука, 295 с.
Вдовина, И. С. 1981. Эстетика французского персонализма. М.: Искусство, 189 с.
Вейль, Г. 1979. Гравитация и электричество, 513—528. Альберт Эйнштейн и теория гравитации. М.: Мир, 592 с.
Велихов, Е. П., Зинченко, В. П. и Лекторский, В. А. 1988. Сознание: опыт междисциплинарного подхода. Вопросы философии, 11,3—30.
Вернадский, В. И. 1977. Размышления натуралиста. Научная мысль как планетарное явление. Книга вторая. М.: Наука, 191 с.
Визгин, В. П. 1985. Единые теории поля в первой трети XX века. М.: Наука, 303 с.
Витгенштейн, Л. 1958. Логико-философский трактат. М.: ИЛ, 134 с. Габитова, Р. М. 1972. Человек и общество в немецком экзистенциализме. М.: Наука, 222 с.
Габитова, Р. М. \$78. Философия немецкого романтизма. М.: Наука, 288 с.
Гадамер, Х.-Г. 1988. Истина и метод. М.: Прогресс, 700 с.
Гегель, Г. В. Ф. 1977а. Философия религии (в двух томах), т. 2. М.: Мысль, 573 с.
Гегель, Г. В. Ф. 19776. Философия духа. Энциклопедия философских наук, т. 3. М.: Мысль, 471 с.Герменевтика: история и современность (критические очерки). 1985. М.: Мысль. 302 с.
Голосовкер, Я. Э. 1987. Логика мифа. М.: Наука, 218 с. Библиография составлена по принципу зарубежных изданий ав- тора.
Грюнбаум, А. 1969. Философские проблемы пространства и времени (пер.с английского). М.: Прогресс, 590 с.
Гусев, С. С. и Тульчинский, Г. Л. 1985. Проблема понимания в философии. М.: Политиздат, 191 с.
Гуссерль, Э. 1986. Кризис европейского человечества и философия. Вопросыфилософии, № 3, 101 — 116.
Декарт, Р. 1950а. Рассуждение о методе, 259—317. Избранные произведения(ред. В. В. Соколова). М.: Госполитиздат, 710 с.
Декарт, Р. 19506. Начала философии, 426—544. Избранные произведения(ред. В. В. Соколова). М.: Госполитиздат, 710 с.
Джемс, В. 1910. Многообразие религиозного опыта. М.: Типография Мамонтова (издание журнала «Русская мысль»), 518 с.
Достоевский, Ф. М. 1976. Братья Карамазовы. Полное собрание сочинений в тридцати томах, т. 15. Л.: Наука, 624 с.
Достоевский, Ф. М. 1983. Сон смешного человека. Фантастическая повесть, 104—119. Полное собрание сочинений в тридцати томах, т. 25, Дневник писателя за 1899 г. Л.: Наука, 470 с.
Ильин, И. П. 1983. Теория знака Ж. Дерриды и ее воздействие на современную критику США и Западной Европы, 108—125. Семиотика. Коммуникация. Стиль. М.: ИНИОН АН СССР, 204 с.
Казютинский, В. В. и Балашов, Ю. В. 1989. Антропный принцип: история и современность. Природа, 1, 23—32.
Кант, И. 1964. Критика чистого разума. Сочинения. В 6 томах, т. 3. М.:Мысль, 799 с.
Кант, И. 1966. Критика способности суждения. Сочинения. В 6 томах, т. 5. М.: Мысль, 564 с.
Караулов, Ю. К. 1976. Общая и русская идеография. М.: Наука, 355 с.
Козлова, М. С. 1972. Философия и язык (Критический анализ некоторых тенденций эволюции позитивизма XX в.). М.: Мысль, 254 с.
Котляр, Б. И. 1986. Пластичность нервной системы. М.: Изд. МГУ, 240 с. Кун, Т. 1977. Структура научных революций (2-е изд.). М.: Прогресс, 300 с.
Лейбниц, Г. В. 1983. Новые опыты о человеческом разумении автора системы предустановленной гармонии. Сочинения в четырех томах, т. 2. М.: Мысль, 686 с. Локк, Д. 1985. Опыт о человеческом разумении, 77—622. Сочинения в трех томах, т. 1. М.: Мысль. 622 с.
Лосев, А. Ф. 1964. Мера, 389—394. Философская энциклопедия, т. 3. М.: Изд. Советская энциклопедия, 584 с.
Лосев, А. Ф. 1967а. Плотин, 275—278. Философская энциклопедия, т 4. М.: Изд. Советская энциклопедия, 591 с.
Лосев, А. Ф. 1967b. Неоплатонизм, Философская энциклопедия, т. 4. М.: Изд. Советская энциклопедия, 591 с.
Лосев, А. Ф. 1969. История античной эстетики, том II. Софисты, Сократ, Платон. М.: Искусство, 714 с.
Манн, Т. 1960. Доктор Фаустус. Собрание сочинений, т. 5. М.: Художественная литература, 694 с.
Марголис, Дж. 1986. Личность и сознание. Перспективы нередуктивного материализма. М.: Прогресс, 420 с.
Маркс, К. 1955. Тезисы о Фейербахе, 1—4, К. Маркс и Ф. Энгельс. Сочинения, 2-е изд., т. 3. М.: Госполитиздат, 629 с.
Маркс, К. и Энгельс, Ф. 1955. Немецкая идеология, 7—544.
К Маркс и Ф. Энгельс. Сочинения, 2-е изд., т. 3. М.: Госполитиздат, 629 с..
Математическая энциклопедия, т. 1 —1977, 1151 с.; т. II—1979, 1103 с.; т. III —1982, 1183 с.; т. IV—1984, 1215 с.; т. V—1985, 1248 с. М.: Советская энциклопедия...
Махабхарата. II. 1960. Бхагавадгита. Ашхабад: Издательство Академии наук Туркменской ССР, 401 с.
Медников, Б. С. 1980 Геном как целое, 98—103. Уровни организации биологических систем. М.: Наука, 104 с.
Метерлинк, М. 1914. Смерть. С.-Петербург: Типография Корнфельда, 163 с.
Мотрошилова, Н. В. 1968. Принципы и противоречия феноменологической философии. М.: Высшая школа, 128 с.
Налимов, В. В. I960. Применение математической статистики при анализевещества. М.: Физматгиз, 430 с.
На английском языке: Nalimov, V. V.1963. The Application of Mathematical Statistics to Chemical Analysis. London: Pergamon Press (in USA distributed dy Addison-Wesley), 294 p.
Налимов, B. B. 1971. Теория эксперимента. M.: Наука, 207 с.
На немецком яз.:Nalimov, V. V. 1975, Theorie des Experiments. Berlin VEB Deutscher Landwirtschaftsverlag, 159 S.
Налимов, В. B. 1978. Непрерывность против дискретности в языке и мышлении. Тбилиси: изд. Тбилисского университета, 84 с.
Налимов, В. В. 1979. Вероятностная модель языка. М.: Наука, 303 с., 2-е расширенное издание (1-е изд.— 1974 г.).
На польском языке: Nalimow, W. W. 1976 Probabttistyczny model jezyka. Warszawa: Panstwowe Wydaynictwo Naukowe, 336 p.
На английском языке: Nalimov, V. V. 1981. In the Labyrinths of Language: A Mathematician's Journey. Philadelphia, Pa.: ISI-Press, 246 p.
Налимов B. B. 1981. О возможности метафорического использования математических представлений в психологии. Психологический журнал, 3, 39—47.
Налимов, В. В. 1986а. Природа смыслов в вероятностно ориентированной философии, 154—180. Язык. Наука. Философия (ред. Р. И. Павилёнис). Вильнюс: Институт философии, социологии и права Лит. СССР, 292 с.
Налимов, В. В. 19866. Вероятностный подход к описанию явлений, происходящих на глубинных уровнях сознания, 98—121. Труды семинара, посвященного 75-летию со дня рождения Д. И. Блохинцева. Дубна: Объединенный институт ядерных исследований, 21 I с.
Налимов, В. В. и Голикова, Т. И. 1976. Логические основания планирования эксперимента. М.: Металлургия, 128 с.; 2-е переработанное и расширенное издание— 1981, 151 с.
Налимов, В. В. и Дрогалина, Ж. А. 1978. Семантика ритма: ритм как непосредственное вхождение в континуальный поток образов, 292—298. Бессознательное, т. III. Тбилиси: Мецниереба, 797 с.
Налимов, В. В. и Дрогалина, Ж. А. 1984. Вероятностная модель бессознательного. Бессознательное как проявление семантической вселенной. Психологический журнал, 5; 6, 111 — 122.
Налимов, В. В. и Дрогалина, Ж. А. 1985. Как возможно построение модели бессознательного, 185—198 Бессознательное, т. IV. Тбилиси: Мецниереба, 462 с. На французском языке: Nalimov, V. amp; Drogalina, Zh. 1989. Comment Peut-On Construire Un Modele De L'Inconscient? p. 173—189. L'Inconscient. La Discussion Continue. M.: Progress, 374 p.
Налимов, В. В., Кузнецов, О. А. и Дрогалина, Ж. А. 1978. Видуализация семантических полей вербального текста в групповой «медитации» с. 70—709.
Бессознательное, т. III Тбилиси: Мецниереба, 797 с.
Налимов, В. В. и Мульченко,-3. М. 1969. Наукометрия. Изучение развития науки как информационного процесса. М.: Наука, 192 с.
На польском языке: Nalimow, W. W. amp; Mulczenko, Z. M. 1971. Naukometria. Warszawa: Wydawnictwo Naukowo-Techniczne, 170 p.
На венгерском языке: Nalimov, V. V. amp; Mulcszenko, Z. M. 1980. Tudomanymetria. Budapest: Akademiai Kiado, 271 p.
Адамар, Ж. 1970 Исследование психологии процесса изобретения в области математики. М.: Советское радио, 152 с.
Аристотель. 1976. О душе, 371—448. Собрание сочинений в четырех томах, т. 1. М.: Мысль, 550 с.
Аристотель. 1978. Первая аналитика, 117—254. Сочинения в четырех томах,т. II. М.: Мысль, 687 с.
Бёкке, Р. М. 1915. Космическое сознание. Петроград: изд. «Новый человек», 375 с.
Бердяев, Н. 1969. Смысл истории. Опыт философии человеческой судьбы. Париж, Imca-Press, 270 с.
Беспалько, И. Г. 1978. О некоторых аспектах теории установки и проблемы бессознательного, 56—61.
Бессознательное, т. 3. Тбилиси: Мецниереба, 797 с.
Бессознательное. 1978. Тбилиси: Мецниереба; т. I, 786 с.; т. 2, 686 с.;т. 3, 797 с.; т. 4 (1985), 462 с.
Богомолов, А. С. 1963. Неореализм и спекулятивная философия (А. Н. Уайтхед, с. 252—292). Современный объективный идеализм. Критические очерки.М.: Изд. социально-экономической литературы, 477 с.
Брагина, Н. Н. и Доброхотова, Т. А. 1981. Функциональные асимметрии человека. М.: Медицина, 288 с.
Бурбаки, Н. 1963. Очерки по истории математики. М.: ИЛ, 292 с. Буржуазная философская антропология XX века (ред. Б. Т. Григорьян).1986. М.: Наука, 295 с.
Вдовина, И. С. 1981. Эстетика французского персонализма. М.: Искусство, 189 с.
Вейль, Г. 1979. Гравитация и электричество, 513—528. Альберт Эйнштейн и теория гравитации. М.: Мир, 592 с.
Велихов, Е. П., Зинченко, В. П. и Лекторский, В. А. 1988. Сознание: опыт междисциплинарного подхода. Вопросы философии, 11,3—30.
Вернадский, В. И. 1977. Размышления натуралиста. Научная мысль как планетарное явление. Книга вторая. М.: Наука, 191 с.
Визгин, В. П. 1985. Единые теории поля в первой трети XX века. М.: Наука, 303 с.
Витгенштейн, Л. 1958. Логико-философский трактат. М.: ИЛ, 134 с. Габитова, Р. М. 1972. Человек и общество в немецком экзистенциализме. М.: Наука, 222 с.
Габитова, Р. М. \$78. Философия немецкого романтизма. М.: Наука, 288 с.
Гадамер, Х.-Г. 1988. Истина и метод. М.: Прогресс, 700 с.
Гегель, Г. В. Ф. 1977а. Философия религии (в двух томах), т. 2. М.: Мысль, 573 с.
Гегель, Г. В. Ф. 19776. Философия духа. Энциклопедия философских наук, т. 3. М.: Мысль, 471 с.Герменевтика: история и современность (критические очерки). 1985. М.: Мысль. 302 с.
Голосовкер, Я. Э. 1987. Логика мифа. М.: Наука, 218 с. Библиография составлена по принципу зарубежных изданий ав- тора.
Грюнбаум, А. 1969. Философские проблемы пространства и времени (пер.с английского). М.: Прогресс, 590 с.
Гусев, С. С. и Тульчинский, Г. Л. 1985. Проблема понимания в философии. М.: Политиздат, 191 с.
Гуссерль, Э. 1986. Кризис европейского человечества и философия. Вопросыфилософии, № 3, 101 — 116.
Декарт, Р. 1950а. Рассуждение о методе, 259—317. Избранные произведения(ред. В. В. Соколова). М.: Госполитиздат, 710 с.
Декарт, Р. 19506. Начала философии, 426—544. Избранные произведения(ред. В. В. Соколова). М.: Госполитиздат, 710 с.
Джемс, В. 1910. Многообразие религиозного опыта. М.: Типография Мамонтова (издание журнала «Русская мысль»), 518 с.
Достоевский, Ф. М. 1976. Братья Карамазовы. Полное собрание сочинений в тридцати томах, т. 15. Л.: Наука, 624 с.
Достоевский, Ф. М. 1983. Сон смешного человека. Фантастическая повесть, 104—119. Полное собрание сочинений в тридцати томах, т. 25, Дневник писателя за 1899 г. Л.: Наука, 470 с.
Ильин, И. П. 1983. Теория знака Ж. Дерриды и ее воздействие на современную критику США и Западной Европы, 108—125. Семиотика. Коммуникация. Стиль. М.: ИНИОН АН СССР, 204 с.
Казютинский, В. В. и Балашов, Ю. В. 1989. Антропный принцип: история и современность. Природа, 1, 23—32.
Кант, И. 1964. Критика чистого разума. Сочинения. В 6 томах, т. 3. М.:Мысль, 799 с.
Кант, И. 1966. Критика способности суждения. Сочинения. В 6 томах, т. 5. М.: Мысль, 564 с.
Караулов, Ю. К. 1976. Общая и русская идеография. М.: Наука, 355 с.
Козлова, М. С. 1972. Философия и язык (Критический анализ некоторых тенденций эволюции позитивизма XX в.). М.: Мысль, 254 с.
Котляр, Б. И. 1986. Пластичность нервной системы. М.: Изд. МГУ, 240 с. Кун, Т. 1977. Структура научных революций (2-е изд.). М.: Прогресс, 300 с.
Лейбниц, Г. В. 1983. Новые опыты о человеческом разумении автора системы предустановленной гармонии. Сочинения в четырех томах, т. 2. М.: Мысль, 686 с. Локк, Д. 1985. Опыт о человеческом разумении, 77—622. Сочинения в трех томах, т. 1. М.: Мысль. 622 с.
Лосев, А. Ф. 1964. Мера, 389—394. Философская энциклопедия, т. 3. М.: Изд. Советская энциклопедия, 584 с.
Лосев, А. Ф. 1967а. Плотин, 275—278. Философская энциклопедия, т 4. М.: Изд. Советская энциклопедия, 591 с.
Лосев, А. Ф. 1967b. Неоплатонизм, Философская энциклопедия, т. 4. М.: Изд. Советская энциклопедия, 591 с.
Лосев, А. Ф. 1969. История античной эстетики, том II. Софисты, Сократ, Платон. М.: Искусство, 714 с.
Манн, Т. 1960. Доктор Фаустус. Собрание сочинений, т. 5. М.: Художественная литература, 694 с.
Марголис, Дж. 1986. Личность и сознание. Перспективы нередуктивного материализма. М.: Прогресс, 420 с.
Маркс, К. 1955. Тезисы о Фейербахе, 1—4, К. Маркс и Ф. Энгельс. Сочинения, 2-е изд., т. 3. М.: Госполитиздат, 629 с.
Маркс, К. и Энгельс, Ф. 1955. Немецкая идеология, 7—544.
К Маркс и Ф. Энгельс. Сочинения, 2-е изд., т. 3. М.: Госполитиздат, 629 с..
Математическая энциклопедия, т. 1 —1977, 1151 с.; т. II—1979, 1103 с.; т. III —1982, 1183 с.; т. IV—1984, 1215 с.; т. V—1985, 1248 с. М.: Советская энциклопедия...
Махабхарата. II. 1960. Бхагавадгита. Ашхабад: Издательство Академии наук Туркменской ССР, 401 с.
Медников, Б. С. 1980 Геном как целое, 98—103. Уровни организации биологических систем. М.: Наука, 104 с.
Метерлинк, М. 1914. Смерть. С.-Петербург: Типография Корнфельда, 163 с.
Мотрошилова, Н. В. 1968. Принципы и противоречия феноменологической философии. М.: Высшая школа, 128 с.
Налимов, В. В. I960. Применение математической статистики при анализевещества. М.: Физматгиз, 430 с.
На английском языке: Nalimov, V. V.1963. The Application of Mathematical Statistics to Chemical Analysis. London: Pergamon Press (in USA distributed dy Addison-Wesley), 294 p.
Налимов, B. B. 1971. Теория эксперимента. M.: Наука, 207 с.
На немецком яз.:Nalimov, V. V. 1975, Theorie des Experiments. Berlin VEB Deutscher Landwirtschaftsverlag, 159 S.
Налимов, В. B. 1978. Непрерывность против дискретности в языке и мышлении. Тбилиси: изд. Тбилисского университета, 84 с.
Налимов, В. В. 1979. Вероятностная модель языка. М.: Наука, 303 с., 2-е расширенное издание (1-е изд.— 1974 г.).
На польском языке: Nalimow, W. W. 1976 Probabttistyczny model jezyka. Warszawa: Panstwowe Wydaynictwo Naukowe, 336 p.
На английском языке: Nalimov, V. V. 1981. In the Labyrinths of Language: A Mathematician's Journey. Philadelphia, Pa.: ISI-Press, 246 p.
Налимов B. B. 1981. О возможности метафорического использования математических представлений в психологии. Психологический журнал, 3, 39—47.
Налимов, В. В. 1986а. Природа смыслов в вероятностно ориентированной философии, 154—180. Язык. Наука. Философия (ред. Р. И. Павилёнис). Вильнюс: Институт философии, социологии и права Лит. СССР, 292 с.
Налимов, В. В. 19866. Вероятностный подход к описанию явлений, происходящих на глубинных уровнях сознания, 98—121. Труды семинара, посвященного 75-летию со дня рождения Д. И. Блохинцева. Дубна: Объединенный институт ядерных исследований, 21 I с.
Налимов, В. В. и Голикова, Т. И. 1976. Логические основания планирования эксперимента. М.: Металлургия, 128 с.; 2-е переработанное и расширенное издание— 1981, 151 с.
Налимов, В. В. и Дрогалина, Ж. А. 1978. Семантика ритма: ритм как непосредственное вхождение в континуальный поток образов, 292—298. Бессознательное, т. III. Тбилиси: Мецниереба, 797 с.
Налимов, В. В. и Дрогалина, Ж. А. 1984. Вероятностная модель бессознательного. Бессознательное как проявление семантической вселенной. Психологический журнал, 5; 6, 111 — 122.
Налимов, В. В. и Дрогалина, Ж. А. 1985. Как возможно построение модели бессознательного, 185—198 Бессознательное, т. IV. Тбилиси: Мецниереба, 462 с. На французском языке: Nalimov, V. amp; Drogalina, Zh. 1989. Comment Peut-On Construire Un Modele De L'Inconscient? p. 173—189. L'Inconscient. La Discussion Continue. M.: Progress, 374 p.
Налимов, В. В., Кузнецов, О. А. и Дрогалина, Ж. А. 1978. Видуализация семантических полей вербального текста в групповой «медитации» с. 70—709.
Бессознательное, т. III Тбилиси: Мецниереба, 797 с.
Налимов, В. В. и Мульченко,-3. М. 1969. Наукометрия. Изучение развития науки как информационного процесса. М.: Наука, 192 с.
На польском языке: Nalimow, W. W. amp; Mulczenko, Z. M. 1971. Naukometria. Warszawa: Wydawnictwo Naukowo-Techniczne, 170 p.
На венгерском языке: Nalimov, V. V. amp; Mulcszenko, Z. M. 1980. Tudomanymetria. Budapest: Akademiai Kiado, 271 p.