Страница:
Через двести лет Альберт Эйнштейн привел аналогичный аргумент в пользу существования атомов. Только он превзошел Лукреция и сформулировал математическое обоснование, позволившее ему точно описать, какими будут траектории движения частицы, если ее судорожные движения и вибрации действительно вызваны столкновениями с еще более мелкими частицами. В течение последующих шести лет французский физик Жан Батист Перрен разработал экспериментальный метод слежения за частицами, свободно плавающими в жидкости, обеспечивающий достаточную точность. Он подтвердил, что частицы и в самом деле движутся по траекториям, предсказанным Эйнштейном. Эксперимент убедил скептиков, что атомы действительно существуют[30]. Вклад в это дело Лукреция остался недооцененным.
Траектории Эйнштейна являли собой образец броуновского движения, получившего название по имени шотландского ботаника Роберта Броуна[31], который в 1826 году отметил хаотичное движение цветочной пыльцы, свободно плавающей в воде. Математическую трактовку броуновского движения[32] часто называют случайным блужданием, а иногда и более выразительно – «блужданием пьяницы». Представьте себе человека, выходящего из бара с открытой бутылкой в заднем кармане, из которой капает недопитая им выпивка. Он делает несколько шагов вперед, затем возникает большая вероятность, что он споткнется, покачнется. Пьяница пытается удержать равновесие, делает еще шаг, затем опять спотыкается. Направление, в котором этот человек споткнется, по сути, случайно, по крайней мере, оно никоим образом не связано с общим направлением движения, которое пьяница себе наметил. Если этот человек будет спотыкаться достаточно часто, то траектория его движения, нарисованная каплями на земле, пока он зигзагами плетется по направлению к своему отелю (или, что не менее вероятно, в абсолютно противоположном направлении), будет похожа на траекторию движения пылинки в луче солнечного света.
В сообществе физиков и химиков Эйнштейн получил признание за математическое объяснение броуновского движения потому, что его труд 1905 года оказался в руках Перрена[33].
Но на самом деле Эйнштейн опоздал со своим открытием на пять лет. Башелье описал математику случайных блужданий в своей диссертации еще в 1900 году. В отличие от Эйнштейна Башелье не интересовало случайное движение частичек пыли, возникающее от столкновения с атомами. Башелье интересовали случайные изменения цен на бирже.
Представьте себе, что пьяница добрел до своего отеля. Он выходит из лифта, перед ним длинный коридор. В одном конце коридора – номер 700; в другом конце – номер 799. Сам пьяница находится где-то посередине и не имеет представления, в какую сторону ему следует идти, чтобы попасть в свой номер. Он проходит, спотыкаясь и качаясь из стороны в сторону, полкоридора в одном направлении, затем полкоридора – в противоположном. Предположим, что каждый шаг, который делает пьяница, дает ему 50 %-ную вероятность того, что он немного приблизится к своему номеру 700, что в одном конце длинного коридора, или 50 %-ную вероятность того, что он немного приблизится к своему номеру 799 – в другом конце. Какова вероятность того, что, пройдя, скажем, сто или тысячу шагов, он окажется перед нужным номером?
Чтобы понять, как математика соотносится с финансовыми рынками, надо понять, что цена акции очень похожа на нашего пьяницу. В любой момент существует возможность того, что цена пойдет вверх, равно как и возможность того, что она пойдет вниз. Эти две возможности соответствуют действиям спотыкающегося пьяницы, бредущего к номеру 700 или 799, направляясь то в одну сторону, то в другую. Таким образом, вопрос, на который в данном случае может ответить математика, звучит следующим образом: если торги начинаются с определенной цены и эта цена совершает случайное блуждание, какова вероятность того, что она дойдет до какого-то определенного уровня через какой-то установленный промежуток времени? Другими словами, до какой двери, спотыкаясь, добредет цена через сто или тысячу разовых изменений на бирже?
Это – вопрос, на который Башелье ответил в своей диссертации. Он показал, что если цена акций совершает случайные блуждания, вероятность того, что она дойдет до какого-то установленного значения через определенный промежуток времени, будет соответствовать графику, известному сегодня как нормальная обобщенная функция (распределение Гаусса), или кривая нормального распределения (гауссова кривая)[34]. Эта кривая имеет форму колокола, закругленного в верхней части и расширяющегося книзу. Верхняя часть кривой располагается в районе стартовой цены, что означает, что, по наиболее вероятному сценарию, цена окажется где-то в районе стартовой. От центрального максимума кривая резко идет вниз, указывая на то, что существенные изменения цены менее вероятны. По мере того как цена на акции делает больше шагов случайного блуждания, кривая расширяется, становится в целом менее высокой. Это указывает на то, что со временем степень вероятности, что цена изменится по сравнению с первоначальной, повысится. В данном случае наглядное изображение просто бесценно, поэтому посмотрим на рисунок 1, чтобы понять, как это работает.
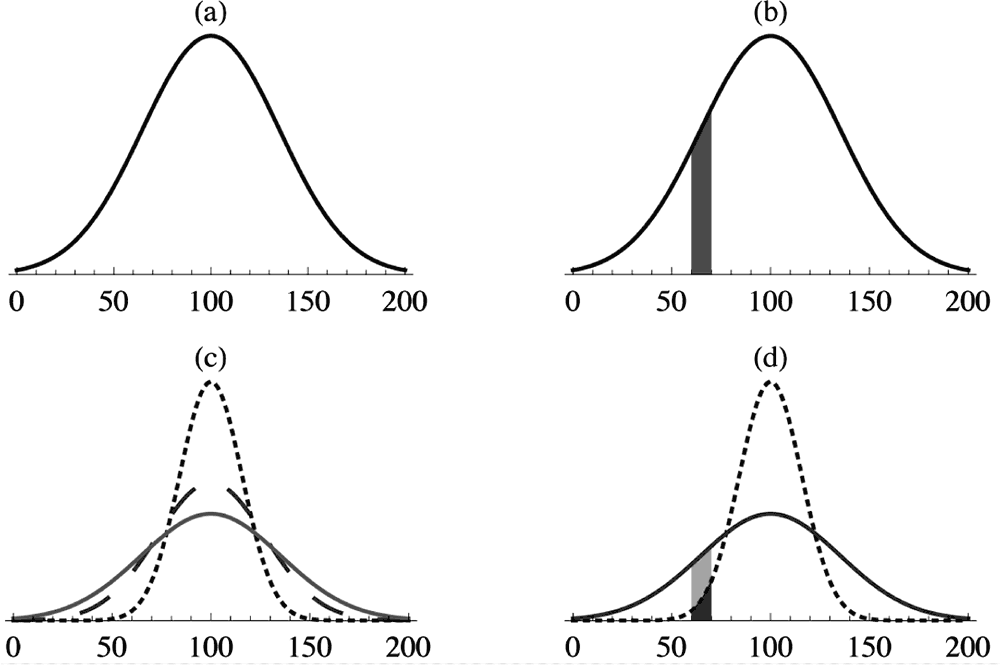Рис. 1. Вероятность в модели Башелье
Рисунок 1. Башелье обнаружил, что если цена на акции совершает случайные блуждания, вероятность того, что она достигнет определенного показателя в будущем, можно рассчитать по графику, известному как нормальная обобщенная функция. На представленных графиках показано, как это происходит в случае с акциями, цена которых в настоящий момент составляет 100 долларов. График (a) – это пример нормальной обобщенной функции, рассчитанной для конкретного момента времени в будущем, скажем, через пять лет. Вероятность того, что через пять лет цена на акции будет где-то в указанном диапазоне, обеспечивает область под графиком – так, например, заштрихованная область графика (b) соответствует вероятности того, что через пять лет акции будут стоить где-то в районе 60–70 долларов. Форма графика зависит от того, насколько отдаленное будущее вас интересует. На графике (c) пунктирная линия – это график на год с настоящего момента, линия, обозначенная штриховым пунктиром – на три года, а сплошная линия – на пять лет с настоящего момента. Вы можете заметить, что со временем графики становятся ниже и шире. Это означает, что вероятность того, что цена на акции будет сильно отличаться от своей начальной цены в 100 долларов, повышается, что видно на графике (d). Обращаем ваше внимание на то, что заштрихованная область под сплошной линией, соответствующая вероятности того, что через пять лет цена акции будет составлять 60–70 долларов, значительно больше, чем заштрихованная область под пунктирной линией, что соответствует одному году с настоящего момента.
Воспринимать динамику цен на акции в контексте случайного блуждания – это очень современно. Создается впечатление, что Башелье беспрецедентен в своем постижении тонкостей рынка[35]. Тем не менее в определенные моменты эта идея кажется сумасшедшей (что, возможно, объясняет, почему ее никто и не оценил). Вы можете сказать, что я просто чересчур верю в математику. Если изменение цен на акции носит случайный характер, то теория случайных блужданий прекрасна. Но почему вы, автор, считаете, что рынки блуждают случайно? Цены идут вверх в ответ на хорошие новости и вниз – в ответ на плохие. В этом нет ничего случайного. Основное предположение Башелье заключается в том, что степень вероятности того, что цена пойдет вверх в заданный момент, всегда равна степени вероятности того, что она пойдет вниз. А это – полный вздор.
Как человек, на практике знакомый с внутренними механизмами Парижской биржи, Башелье знал, как сильно информация может влиять на стоимость ценных бумаг. Оглядываясь в прошлое, легко указать на хорошие, равно как и на плохие новости и воспользоваться ими для объяснения динамики рынка. Башелье же было интересно понять, какова вероятность того, какими будут цены в будущем, когда вы не знаете, какие в тот момент будут новости. Некоторые будущие новости можно предсказать исходя из того, что уже известно. Профессиональные игроки достаточно хорошо умеют предсказывать такие вещи, как исход спортивных мероприятий, политических выборов. Это можно назвать умением прогнозировать степень вероятности того или иного исхода рискованных мероприятий, зависящих от воли случая. Но как прогнозируемость влияет на состояние рынка? Башелье размышлял следующим образом: любые прогнозируемые события уже отражены в текущей цене акции или облигации. Другими словами, если у вас есть основания полагать, что в будущем произойдет что-либо, в результате чего акция Microsoft станет стоить дороже (скажем, Microsoft изобретет новый компьютер или выиграет крупный иск), вы, вероятно, заплатите сейчас за акцию Microsoft больше, чем тот, кто не думает, что с Microsoft произойдет что-нибудь хорошее. Информация, благодаря которой позитивные события в будущем выглядят вероятными, повышает цены сейчас; и информация, благодаря которой негативные события в будущем выглядят вероятными, понижает цены тоже сейчас.
Но если эти аргументы справедливы, возражал Башелье, то цены на акции должны быть случайными. Представьте себе ситуацию: сделка совершена по установленной цене. Вот тут все и начинается. Осуществление сделки означает, что два человека – покупатель и продавец – сумели договориться о цене. И покупатель, и продавец ознакомились с имеющейся информацией и решили, насколько, на их взгляд, ценна для них акция. Но с важной оговоркой: покупатель, по крайней мере, в соответствии с логикой Башелье, покупает акцию по этой цене, так как думает, что, вполне вероятно, в будущем она вырастет. Тем временем продавец продает акцию по этой цене, потому что думает, что цена снизится. Забегая на шаг вперед: если на рынке множество информированных инвесторов, которые постоянно договариваются о ценах, по которым должны проводиться сделки, то текущая цена акции может интерпретироваться как цена, установленная с учетом всей возможной информации. Эта цена – итог спора информированных покупателей, считающих, что она будет повышаться, и продавцов, полагающих, что она будет понижаться. Другими словами, текущая цена в любой момент времени – это цена, при которой вся имеющаяся информация говорит, что вероятность того, что акции пойдут вверх и вниз, составляет 50 %. Если рынки работают так, как утверждал Башелье, то гипотеза о случайных блужданиях совсем не сумасшедшая. Это – неотъемлемая часть того, что заставляет рынки функционировать.
Этот взгляд на рынки сейчас известен как гипотеза об эффективности рынка. Основная идея заключается в том, что рыночные цены всегда отражают истинную стоимость вещей, выставляемых на торги, поскольку в этих ценах учтена вся имеющаяся информация. Башелье был первым, кто озвучил ее, но, как случилось со многими его глубочайшими выводами на тему финансовых рынков, мало кто оценил ее важность. Позднее, в 1965 году, гипотеза об эффективности рынка была заново предложена экономистом из Чикагского университета Юджином Фама[36]. Сегодня, конечно, эта гипотеза считается в высшей степени противоречивой. Некоторые экономисты, в особенности представители так называемой «чикагской школы», придерживаются ее как главной и неоспоримой истины. Но вам не понадобится прилагать слишком большие умственные усилия, чтобы понять, что она, мягко говоря, несколько неубедительна. Например, одним из следствий этой гипотезы является вывод, что на рынках не может быть никаких «пузырей», потому что «пузырь» может возникнуть, только если рыночная цена на некую вещь оказывается не привязанной к ее истинной цене. Любой, кто помнит бум и спад доткомов в конце 1990-х – начале 2000-х годов, кто пробовал, начиная примерно с 2006 года, продать свой дом, знает, что динамика цен не так рациональна, как уверяет нас «чикагская школа». На самом деле большинство обычных трейдеров, занимающихся этим бизнесом изо дня в день, с которыми я беседовал, находят эту идею попросту смехотворной.
Но даже если рынки не всегда эффективны, а это, конечно, так и есть, и даже если временами цены выходят далеко за рамки разумного, когда речь идет о стоимости торгуемых товаров (что тоже никем не оспаривается), гипотеза об эффективности рынка представляет собой исходную позицию в попытках понять, как работают рынки. Это – допущение, идеализация. Удачной аналогией здесь будет учебник по физике для старших классов школы, где в некоторых задачах дается допуск на отсутствие трения и силы притяжения. Конечно, такого в природе не существует. Но некоторых упрощающих допущений бывает достаточно, чтобы найти решение задачи, которая, если бы не эти допущения, оставалась неразрешимой. А уже когда вы решили упрощенную задачу, можно задаться вопросом, сколько вреда причиняют упрощающие допущения. Если вы хотите понять, что происходит при столкновении двух хоккейных шайб на катке, допустив при этом, что трение отсутствует, большой беды от этого допущения не будет. Но если допустить, что трение отсутствует при падении с велосипеда, это закончится сильными ссадинами. Аналогичная ситуация складывается и в случае, когда вы пытаетесь моделировать финансовые рынки: Башелье начинает с допущения – гипотезы об эффективности рынка – и добивается поразительных успехов. Следующий шаг, который Башелье оставил сделать будущим поколениям, пытающимся понять мир финансов, заключался в том, чтобы разобраться, когда допущение об эффективности рынка терпит неудачу.
Создается впечатление, что Самуэльсон был единственным получателем открытки Сэвиджа, который потрудился заглянуть в труды Башелье. Они произвели на него сильное впечатление, а Самуэльсон был достаточно влиятельной фигурой, чтобы довести их до внимания общественности. Работа Башелье, посвященная игре на бирже, стала пользоваться спросом у студентов МТИ, которые, в свою очередь, сделали имя Башелье известным в самых отдаленных уголках мира. Башелье официально канонизировали в 1964 году, когда коллега Самуэльсона по работе в МТИ Поль Кутнер включил диссертацию француза в сборник научных трудов «Случайный характер цен на фондовом рынке»[37]. На момент выхода сборника в свет гипотеза случайных блужданий была уже независимо друг от друга исследована и усовершенствована рядом ученых, однако ее рождение Кутнер однозначно приписал Башелье. По словам Кутнера, «работа [Башелье] настолько выдающаяся, что мы можем сказать: наука о спекулятивных ценах обрела славу в момент своего зарождения»[38].
Во многих отношениях Самуэльсон идеально подходил на роль человека, который должен был извлечь из забвения Башелье и эффективно распространить его идеи. Самуэльсон – один из наиболее влиятельных экономистов ХХ века. В 1970 году он получил вторую Нобелевскую премию по экономике за «повышение уровня анализа в экономической науке» и «превращение экономики в математическую дисциплину». Несмотря на то что он изучал экономику в Университете Чикаго и Гарварде, огромное влияние на него оказал Э. Б. Уилсон, специалист в области математической физики и статистики[39]. Самуэльсон познакомился с Уилсоном, будучи еще студентом. Уилсон в то время был профессором демографической статистики на факультете здравоохранения Гарвардского университета, но в первые двадцать лет своей карьеры он занимался физикой и инженерией в МТИ. Уилсон был студентом Дж. У. Гиббса, великого американского физика-математика, первым в США получившего в 1863 году в Йельском университете степень доктора технических наук. Наибольшую известность Гиббсу принесло то, что он положил начало математической теории термодинамики и статистической механике, которые пытаются дать объяснение поведению обычных объектов типа бочонка воды или автомобильного двигателя в разрезе их микроскопических частей[40].
Благодаря Уилсону Самуэльсон стал последователем традиции, заложенной Гиббсом. Его диссертация, написанная в 1940 году, была попыткой переложить экономику на язык математики, активно заимствуя идеи Гиббса из статистической термодинамики. Одна из основных задач термодинамики – дать описание того, как обобщить поведение отдельных частиц, чтобы описать крупные объекты. Основная часть этого анализа посвящена определению таких переменных, как температура или давление, которые не имеют смысла, когда речь идет об отдельных частицах, но могут использоваться для описания их коллективного поведения. Самуэльсон указал на то, что об экономике можно рассуждать подобным образом: экономика – это масса людей, которые общаются друг с другом и принимают решения. Чтобы понять крупномасштабную экономику (макроэкономику), следует определить переменные, характеризующие экономику в целом (уровень инфляции, например), а затем – зависимость между этими переменными и людьми. В 1947 году на основе своей гарвардской диссертации Самуэльсон опубликовал книгу. Она называлась «Основы экономического анализа»[41].
В определенном смысле книга Самуэльсона стала революционной, что не удалось диссертации Башелье. Когда Башелье работал над ней, экономика как наука, по сути, была подразделом политической философии. Цифры в ней до 1880-х годов не играли большой роли, да и тогда были введены в научный оборот только потому, что некоторые философы заинтересовались количественной оценкой экономик разных стран мира, чтобы их можно было сравнивать. Когда Башелье писал свою диссертацию, по существу, не было ни одного экономиста, способного понять и оценить математические методы, которыми он пользовался.
В следующие сорок лет экономика как наука пережила свой расцвет[42]. Преждевременные попытки определить количественные показатели уступили место более сложным методам их сравнения – отчасти благодаря работе Ирвинга Фишера[43], американского экономиста, еще одного студента Гиббса. В первые десятилетия ХХ века научные исследования в области экономики были единичными и проводились при поддержке европейских правительств, поскольку потребности военного строительства подталкивали их к тому, чтобы придать законную силу попыткам увеличить объемы производства. Но как научная дисциплина экономика полностью обрела свое лицо только в начале 1930-х годов, одновременно с началом Великой депрессии. Политические лидеры Европы и Соединенных Штатов тогда считали, что в мировой экономике произошла какая-то катастрофа, и обратились за советом к экспертам. Неожиданно резко увеличилось финансирование научных исследований, что привело к образованию большого числа вакансий в университетах. Самуэльсон приехал в Гарвард на гребне этой интересной новой волны. Когда была опубликована его книга, уже сформировалось научное сообщество, способное понять истинное значение этой работы. Книга Самуэльсона и изданный впоследствии учебник, который со временем стал бестселлером всех времен среди книг по экономике, помогли остальным оценить, что же на самом деле совершил Башелье почти полвека назад.
Выражаясь современным языком, в своей диссертации Башелье представил модель того, как меняются рыночные цены со временем. Сейчас бы мы назвали ее моделью случайных блужданий. Термин «модель» вошел в экономику в 1930-х годах с работой еще одного физика, переквалифицировавшегося в экономиста, Яна Тинбергена (Самуэльсон был вторым человеком, получившим Нобелевскую премию по экономике; а Тинберген – первым)[44]. Этот термин уже использовался в физике, чтобы сказать о чем-то, немного меньшем, чем полноценная физическая теория. Теория – по крайней мере, как ее обычно представляют физики – это попытка полностью и точно описать какое-то свойство мира. Модель же – что-то вроде упрощенного изображения того, как работают определенные физические процессы или системы. Тинберген воспользовался этим термином в экономике, несмотря на то что его модели были предназначены для того, чтобы придумать способы прогнозировать зависимость между экономическими переменными, например, между процентными ставками и инфляцией или между зарплатами и производительностью труда (широко известно суждение Тинбергена о том, что компания менее продуктивна, если доход самого высокооплачиваемого работника будет более чем в пять раз превышать доход самого низкооплачиваемого работника – золотое правило, которое сегодня в значительной степени забыто). В отличие от физики, где люди работают с четко сформулированными теориями, математическая экономика имеет дело почти исключительно с моделями[45].
К моменту публикации книги Кутнера в 1964 году идея о том, что рыночные цены подвержены случайным блужданиям, уже хорошо укоренилась, и многие экономисты признавали, что ответственность за это лежала на Башелье. Но модель случайных блужданий не была кульминацией его диссертации. Он рассматривал ее как подготовительную работу, служащую его истинно главной цели – созданию моделей опционного ценообразования. Опцион – это вид дериватива, дающий владельцу опциона право купить (или иногда продать) конкретную ценную бумагу, например акцию или облигацию, по заранее установленной цене (которая называется «цена-страйк») в какой-то момент в будущем (дата истечения срока опциона). Когда вы покупаете опцион, вы не покупаете напрямую акции, вы покупаете право торговать этими акциями в какой-то момент в будущем, но по цене, на которую согласны в настоящий момент. Цена опциона должна соответствовать стоимости права на покупку чего-либо в определенный момент в будущем.
Траектории Эйнштейна являли собой образец броуновского движения, получившего название по имени шотландского ботаника Роберта Броуна[31], который в 1826 году отметил хаотичное движение цветочной пыльцы, свободно плавающей в воде. Математическую трактовку броуновского движения[32] часто называют случайным блужданием, а иногда и более выразительно – «блужданием пьяницы». Представьте себе человека, выходящего из бара с открытой бутылкой в заднем кармане, из которой капает недопитая им выпивка. Он делает несколько шагов вперед, затем возникает большая вероятность, что он споткнется, покачнется. Пьяница пытается удержать равновесие, делает еще шаг, затем опять спотыкается. Направление, в котором этот человек споткнется, по сути, случайно, по крайней мере, оно никоим образом не связано с общим направлением движения, которое пьяница себе наметил. Если этот человек будет спотыкаться достаточно часто, то траектория его движения, нарисованная каплями на земле, пока он зигзагами плетется по направлению к своему отелю (или, что не менее вероятно, в абсолютно противоположном направлении), будет похожа на траекторию движения пылинки в луче солнечного света.
В сообществе физиков и химиков Эйнштейн получил признание за математическое объяснение броуновского движения потому, что его труд 1905 года оказался в руках Перрена[33].
Но на самом деле Эйнштейн опоздал со своим открытием на пять лет. Башелье описал математику случайных блужданий в своей диссертации еще в 1900 году. В отличие от Эйнштейна Башелье не интересовало случайное движение частичек пыли, возникающее от столкновения с атомами. Башелье интересовали случайные изменения цен на бирже.
Представьте себе, что пьяница добрел до своего отеля. Он выходит из лифта, перед ним длинный коридор. В одном конце коридора – номер 700; в другом конце – номер 799. Сам пьяница находится где-то посередине и не имеет представления, в какую сторону ему следует идти, чтобы попасть в свой номер. Он проходит, спотыкаясь и качаясь из стороны в сторону, полкоридора в одном направлении, затем полкоридора – в противоположном. Предположим, что каждый шаг, который делает пьяница, дает ему 50 %-ную вероятность того, что он немного приблизится к своему номеру 700, что в одном конце длинного коридора, или 50 %-ную вероятность того, что он немного приблизится к своему номеру 799 – в другом конце. Какова вероятность того, что, пройдя, скажем, сто или тысячу шагов, он окажется перед нужным номером?
Чтобы понять, как математика соотносится с финансовыми рынками, надо понять, что цена акции очень похожа на нашего пьяницу. В любой момент существует возможность того, что цена пойдет вверх, равно как и возможность того, что она пойдет вниз. Эти две возможности соответствуют действиям спотыкающегося пьяницы, бредущего к номеру 700 или 799, направляясь то в одну сторону, то в другую. Таким образом, вопрос, на который в данном случае может ответить математика, звучит следующим образом: если торги начинаются с определенной цены и эта цена совершает случайное блуждание, какова вероятность того, что она дойдет до какого-то определенного уровня через какой-то установленный промежуток времени? Другими словами, до какой двери, спотыкаясь, добредет цена через сто или тысячу разовых изменений на бирже?
Это – вопрос, на который Башелье ответил в своей диссертации. Он показал, что если цена акций совершает случайные блуждания, вероятность того, что она дойдет до какого-то установленного значения через определенный промежуток времени, будет соответствовать графику, известному сегодня как нормальная обобщенная функция (распределение Гаусса), или кривая нормального распределения (гауссова кривая)[34]. Эта кривая имеет форму колокола, закругленного в верхней части и расширяющегося книзу. Верхняя часть кривой располагается в районе стартовой цены, что означает, что, по наиболее вероятному сценарию, цена окажется где-то в районе стартовой. От центрального максимума кривая резко идет вниз, указывая на то, что существенные изменения цены менее вероятны. По мере того как цена на акции делает больше шагов случайного блуждания, кривая расширяется, становится в целом менее высокой. Это указывает на то, что со временем степень вероятности, что цена изменится по сравнению с первоначальной, повысится. В данном случае наглядное изображение просто бесценно, поэтому посмотрим на рисунок 1, чтобы понять, как это работает.
Рисунок 1. Башелье обнаружил, что если цена на акции совершает случайные блуждания, вероятность того, что она достигнет определенного показателя в будущем, можно рассчитать по графику, известному как нормальная обобщенная функция. На представленных графиках показано, как это происходит в случае с акциями, цена которых в настоящий момент составляет 100 долларов. График (a) – это пример нормальной обобщенной функции, рассчитанной для конкретного момента времени в будущем, скажем, через пять лет. Вероятность того, что через пять лет цена на акции будет где-то в указанном диапазоне, обеспечивает область под графиком – так, например, заштрихованная область графика (b) соответствует вероятности того, что через пять лет акции будут стоить где-то в районе 60–70 долларов. Форма графика зависит от того, насколько отдаленное будущее вас интересует. На графике (c) пунктирная линия – это график на год с настоящего момента, линия, обозначенная штриховым пунктиром – на три года, а сплошная линия – на пять лет с настоящего момента. Вы можете заметить, что со временем графики становятся ниже и шире. Это означает, что вероятность того, что цена на акции будет сильно отличаться от своей начальной цены в 100 долларов, повышается, что видно на графике (d). Обращаем ваше внимание на то, что заштрихованная область под сплошной линией, соответствующая вероятности того, что через пять лет цена акции будет составлять 60–70 долларов, значительно больше, чем заштрихованная область под пунктирной линией, что соответствует одному году с настоящего момента.
Воспринимать динамику цен на акции в контексте случайного блуждания – это очень современно. Создается впечатление, что Башелье беспрецедентен в своем постижении тонкостей рынка[35]. Тем не менее в определенные моменты эта идея кажется сумасшедшей (что, возможно, объясняет, почему ее никто и не оценил). Вы можете сказать, что я просто чересчур верю в математику. Если изменение цен на акции носит случайный характер, то теория случайных блужданий прекрасна. Но почему вы, автор, считаете, что рынки блуждают случайно? Цены идут вверх в ответ на хорошие новости и вниз – в ответ на плохие. В этом нет ничего случайного. Основное предположение Башелье заключается в том, что степень вероятности того, что цена пойдет вверх в заданный момент, всегда равна степени вероятности того, что она пойдет вниз. А это – полный вздор.
Как человек, на практике знакомый с внутренними механизмами Парижской биржи, Башелье знал, как сильно информация может влиять на стоимость ценных бумаг. Оглядываясь в прошлое, легко указать на хорошие, равно как и на плохие новости и воспользоваться ими для объяснения динамики рынка. Башелье же было интересно понять, какова вероятность того, какими будут цены в будущем, когда вы не знаете, какие в тот момент будут новости. Некоторые будущие новости можно предсказать исходя из того, что уже известно. Профессиональные игроки достаточно хорошо умеют предсказывать такие вещи, как исход спортивных мероприятий, политических выборов. Это можно назвать умением прогнозировать степень вероятности того или иного исхода рискованных мероприятий, зависящих от воли случая. Но как прогнозируемость влияет на состояние рынка? Башелье размышлял следующим образом: любые прогнозируемые события уже отражены в текущей цене акции или облигации. Другими словами, если у вас есть основания полагать, что в будущем произойдет что-либо, в результате чего акция Microsoft станет стоить дороже (скажем, Microsoft изобретет новый компьютер или выиграет крупный иск), вы, вероятно, заплатите сейчас за акцию Microsoft больше, чем тот, кто не думает, что с Microsoft произойдет что-нибудь хорошее. Информация, благодаря которой позитивные события в будущем выглядят вероятными, повышает цены сейчас; и информация, благодаря которой негативные события в будущем выглядят вероятными, понижает цены тоже сейчас.
Но если эти аргументы справедливы, возражал Башелье, то цены на акции должны быть случайными. Представьте себе ситуацию: сделка совершена по установленной цене. Вот тут все и начинается. Осуществление сделки означает, что два человека – покупатель и продавец – сумели договориться о цене. И покупатель, и продавец ознакомились с имеющейся информацией и решили, насколько, на их взгляд, ценна для них акция. Но с важной оговоркой: покупатель, по крайней мере, в соответствии с логикой Башелье, покупает акцию по этой цене, так как думает, что, вполне вероятно, в будущем она вырастет. Тем временем продавец продает акцию по этой цене, потому что думает, что цена снизится. Забегая на шаг вперед: если на рынке множество информированных инвесторов, которые постоянно договариваются о ценах, по которым должны проводиться сделки, то текущая цена акции может интерпретироваться как цена, установленная с учетом всей возможной информации. Эта цена – итог спора информированных покупателей, считающих, что она будет повышаться, и продавцов, полагающих, что она будет понижаться. Другими словами, текущая цена в любой момент времени – это цена, при которой вся имеющаяся информация говорит, что вероятность того, что акции пойдут вверх и вниз, составляет 50 %. Если рынки работают так, как утверждал Башелье, то гипотеза о случайных блужданиях совсем не сумасшедшая. Это – неотъемлемая часть того, что заставляет рынки функционировать.
Этот взгляд на рынки сейчас известен как гипотеза об эффективности рынка. Основная идея заключается в том, что рыночные цены всегда отражают истинную стоимость вещей, выставляемых на торги, поскольку в этих ценах учтена вся имеющаяся информация. Башелье был первым, кто озвучил ее, но, как случилось со многими его глубочайшими выводами на тему финансовых рынков, мало кто оценил ее важность. Позднее, в 1965 году, гипотеза об эффективности рынка была заново предложена экономистом из Чикагского университета Юджином Фама[36]. Сегодня, конечно, эта гипотеза считается в высшей степени противоречивой. Некоторые экономисты, в особенности представители так называемой «чикагской школы», придерживаются ее как главной и неоспоримой истины. Но вам не понадобится прилагать слишком большие умственные усилия, чтобы понять, что она, мягко говоря, несколько неубедительна. Например, одним из следствий этой гипотезы является вывод, что на рынках не может быть никаких «пузырей», потому что «пузырь» может возникнуть, только если рыночная цена на некую вещь оказывается не привязанной к ее истинной цене. Любой, кто помнит бум и спад доткомов в конце 1990-х – начале 2000-х годов, кто пробовал, начиная примерно с 2006 года, продать свой дом, знает, что динамика цен не так рациональна, как уверяет нас «чикагская школа». На самом деле большинство обычных трейдеров, занимающихся этим бизнесом изо дня в день, с которыми я беседовал, находят эту идею попросту смехотворной.
Но даже если рынки не всегда эффективны, а это, конечно, так и есть, и даже если временами цены выходят далеко за рамки разумного, когда речь идет о стоимости торгуемых товаров (что тоже никем не оспаривается), гипотеза об эффективности рынка представляет собой исходную позицию в попытках понять, как работают рынки. Это – допущение, идеализация. Удачной аналогией здесь будет учебник по физике для старших классов школы, где в некоторых задачах дается допуск на отсутствие трения и силы притяжения. Конечно, такого в природе не существует. Но некоторых упрощающих допущений бывает достаточно, чтобы найти решение задачи, которая, если бы не эти допущения, оставалась неразрешимой. А уже когда вы решили упрощенную задачу, можно задаться вопросом, сколько вреда причиняют упрощающие допущения. Если вы хотите понять, что происходит при столкновении двух хоккейных шайб на катке, допустив при этом, что трение отсутствует, большой беды от этого допущения не будет. Но если допустить, что трение отсутствует при падении с велосипеда, это закончится сильными ссадинами. Аналогичная ситуация складывается и в случае, когда вы пытаетесь моделировать финансовые рынки: Башелье начинает с допущения – гипотезы об эффективности рынка – и добивается поразительных успехов. Следующий шаг, который Башелье оставил сделать будущим поколениям, пытающимся понять мир финансов, заключался в том, чтобы разобраться, когда допущение об эффективности рынка терпит неудачу.
Создается впечатление, что Самуэльсон был единственным получателем открытки Сэвиджа, который потрудился заглянуть в труды Башелье. Они произвели на него сильное впечатление, а Самуэльсон был достаточно влиятельной фигурой, чтобы довести их до внимания общественности. Работа Башелье, посвященная игре на бирже, стала пользоваться спросом у студентов МТИ, которые, в свою очередь, сделали имя Башелье известным в самых отдаленных уголках мира. Башелье официально канонизировали в 1964 году, когда коллега Самуэльсона по работе в МТИ Поль Кутнер включил диссертацию француза в сборник научных трудов «Случайный характер цен на фондовом рынке»[37]. На момент выхода сборника в свет гипотеза случайных блужданий была уже независимо друг от друга исследована и усовершенствована рядом ученых, однако ее рождение Кутнер однозначно приписал Башелье. По словам Кутнера, «работа [Башелье] настолько выдающаяся, что мы можем сказать: наука о спекулятивных ценах обрела славу в момент своего зарождения»[38].
Во многих отношениях Самуэльсон идеально подходил на роль человека, который должен был извлечь из забвения Башелье и эффективно распространить его идеи. Самуэльсон – один из наиболее влиятельных экономистов ХХ века. В 1970 году он получил вторую Нобелевскую премию по экономике за «повышение уровня анализа в экономической науке» и «превращение экономики в математическую дисциплину». Несмотря на то что он изучал экономику в Университете Чикаго и Гарварде, огромное влияние на него оказал Э. Б. Уилсон, специалист в области математической физики и статистики[39]. Самуэльсон познакомился с Уилсоном, будучи еще студентом. Уилсон в то время был профессором демографической статистики на факультете здравоохранения Гарвардского университета, но в первые двадцать лет своей карьеры он занимался физикой и инженерией в МТИ. Уилсон был студентом Дж. У. Гиббса, великого американского физика-математика, первым в США получившего в 1863 году в Йельском университете степень доктора технических наук. Наибольшую известность Гиббсу принесло то, что он положил начало математической теории термодинамики и статистической механике, которые пытаются дать объяснение поведению обычных объектов типа бочонка воды или автомобильного двигателя в разрезе их микроскопических частей[40].
Благодаря Уилсону Самуэльсон стал последователем традиции, заложенной Гиббсом. Его диссертация, написанная в 1940 году, была попыткой переложить экономику на язык математики, активно заимствуя идеи Гиббса из статистической термодинамики. Одна из основных задач термодинамики – дать описание того, как обобщить поведение отдельных частиц, чтобы описать крупные объекты. Основная часть этого анализа посвящена определению таких переменных, как температура или давление, которые не имеют смысла, когда речь идет об отдельных частицах, но могут использоваться для описания их коллективного поведения. Самуэльсон указал на то, что об экономике можно рассуждать подобным образом: экономика – это масса людей, которые общаются друг с другом и принимают решения. Чтобы понять крупномасштабную экономику (макроэкономику), следует определить переменные, характеризующие экономику в целом (уровень инфляции, например), а затем – зависимость между этими переменными и людьми. В 1947 году на основе своей гарвардской диссертации Самуэльсон опубликовал книгу. Она называлась «Основы экономического анализа»[41].
В определенном смысле книга Самуэльсона стала революционной, что не удалось диссертации Башелье. Когда Башелье работал над ней, экономика как наука, по сути, была подразделом политической философии. Цифры в ней до 1880-х годов не играли большой роли, да и тогда были введены в научный оборот только потому, что некоторые философы заинтересовались количественной оценкой экономик разных стран мира, чтобы их можно было сравнивать. Когда Башелье писал свою диссертацию, по существу, не было ни одного экономиста, способного понять и оценить математические методы, которыми он пользовался.
В следующие сорок лет экономика как наука пережила свой расцвет[42]. Преждевременные попытки определить количественные показатели уступили место более сложным методам их сравнения – отчасти благодаря работе Ирвинга Фишера[43], американского экономиста, еще одного студента Гиббса. В первые десятилетия ХХ века научные исследования в области экономики были единичными и проводились при поддержке европейских правительств, поскольку потребности военного строительства подталкивали их к тому, чтобы придать законную силу попыткам увеличить объемы производства. Но как научная дисциплина экономика полностью обрела свое лицо только в начале 1930-х годов, одновременно с началом Великой депрессии. Политические лидеры Европы и Соединенных Штатов тогда считали, что в мировой экономике произошла какая-то катастрофа, и обратились за советом к экспертам. Неожиданно резко увеличилось финансирование научных исследований, что привело к образованию большого числа вакансий в университетах. Самуэльсон приехал в Гарвард на гребне этой интересной новой волны. Когда была опубликована его книга, уже сформировалось научное сообщество, способное понять истинное значение этой работы. Книга Самуэльсона и изданный впоследствии учебник, который со временем стал бестселлером всех времен среди книг по экономике, помогли остальным оценить, что же на самом деле совершил Башелье почти полвека назад.
Выражаясь современным языком, в своей диссертации Башелье представил модель того, как меняются рыночные цены со временем. Сейчас бы мы назвали ее моделью случайных блужданий. Термин «модель» вошел в экономику в 1930-х годах с работой еще одного физика, переквалифицировавшегося в экономиста, Яна Тинбергена (Самуэльсон был вторым человеком, получившим Нобелевскую премию по экономике; а Тинберген – первым)[44]. Этот термин уже использовался в физике, чтобы сказать о чем-то, немного меньшем, чем полноценная физическая теория. Теория – по крайней мере, как ее обычно представляют физики – это попытка полностью и точно описать какое-то свойство мира. Модель же – что-то вроде упрощенного изображения того, как работают определенные физические процессы или системы. Тинберген воспользовался этим термином в экономике, несмотря на то что его модели были предназначены для того, чтобы придумать способы прогнозировать зависимость между экономическими переменными, например, между процентными ставками и инфляцией или между зарплатами и производительностью труда (широко известно суждение Тинбергена о том, что компания менее продуктивна, если доход самого высокооплачиваемого работника будет более чем в пять раз превышать доход самого низкооплачиваемого работника – золотое правило, которое сегодня в значительной степени забыто). В отличие от физики, где люди работают с четко сформулированными теориями, математическая экономика имеет дело почти исключительно с моделями[45].
К моменту публикации книги Кутнера в 1964 году идея о том, что рыночные цены подвержены случайным блужданиям, уже хорошо укоренилась, и многие экономисты признавали, что ответственность за это лежала на Башелье. Но модель случайных блужданий не была кульминацией его диссертации. Он рассматривал ее как подготовительную работу, служащую его истинно главной цели – созданию моделей опционного ценообразования. Опцион – это вид дериватива, дающий владельцу опциона право купить (или иногда продать) конкретную ценную бумагу, например акцию или облигацию, по заранее установленной цене (которая называется «цена-страйк») в какой-то момент в будущем (дата истечения срока опциона). Когда вы покупаете опцион, вы не покупаете напрямую акции, вы покупаете право торговать этими акциями в какой-то момент в будущем, но по цене, на которую согласны в настоящий момент. Цена опциона должна соответствовать стоимости права на покупку чего-либо в определенный момент в будущем.