§ 3. Строго разделительный силлогизм
Читатель может возразить: «Умозаключение, которое вы обозначили как необоснованное, зачастую рассматривается как раз в качестве обоснованного. Допустим, вы точно не знаете месяц, в котором родился Шекспир, но при этом вы можете сделать утверждение: «Он родился в апреле или в мае». Затем вы можете узнать, что он родился все-таки в апреле. Не выведете ли вы из этого, что Шекспир не родился в мае? и если да, то не нарушите ли вы собственное правило, согласно которому в разделительном силлогизме меньшая посылка должна отрицать один из дизъюнктов?»
Читатель совершенно прав. Однако является ли данный пример в действительности опровержением установленного нами правила? На поверку оказывается, что нет. Данное умозаключение является обоснованным только при подразумеваемой посылке, гласящей, что один из дизъюнктов исключает другого. Бо′льшая посылка в примере, приведенном читателем, будучи сформулированной в полном виде, будет выглядеть так: «Шекспир родился в апреле или в мае, и он не родился в апреле и одновременно в мае». Данное суждение является конъюнктивным, и та его часть, которая является посылкой в аргументе читателя, представляет конъюнкт, утверждающий строгую дизъюнкцию. Такие дизъюнктивные суждения зачастую понимаются без дополнительных объяснений и поэтому не выражаются в явной форме. Тем не менее, для прояснения посылок, входящих в аргумент, эти суждения следует проявить.
В этом смысле строго дизъюнктивные силлогизмы рекомендуется рассматривать отдельно. В них большей посылкой является строго дизъюнктивное суждение, а меньшей – простое категорическое суждение. Отыщем условия, необходимые для обоснованности такого силлогизма.
Допустим, нам известна истинность следующего: «Неверно, что мои часы идут точно» и «Поведение всех механизмов подвержено воздействию климата». Утверждение истинности строго дизъюнктивного суждения означает утверждение того, что, по крайней мере, один из дизъюнктов является ложным. Следовательно, если мы утверждаем суждение «поведение всех механизмов подвержено воздействию климата», мы также должны утверждать и суждение «мои часы не идут точно». Однако будет неверным утверждать, что если один из членов строгой дизъюнкции ложен, то другой истинен. Строго разделительный силлогизм является обоснованным, если в меньшей посылке утверждается один из дизъюнктов, а в заключении отрицается другой.
Схематическая форма данного аргумента такова: неверно, что одновременно А есть В и С есть D; А есть В; следовательно, С не есть D. Или: (p . q)′; p; ∴ q′. Считается, что данное умозаключение стоит в модусе «modus ponendo tollens», поскольку, утверждая (в меньшей посылке), мы отрицаем (в большей).
Теперь можно подытожить обоснованные и необоснованные умозаключения, которые мы рассмотрели в данной главе.

Читатель совершенно прав. Однако является ли данный пример в действительности опровержением установленного нами правила? На поверку оказывается, что нет. Данное умозаключение является обоснованным только при подразумеваемой посылке, гласящей, что один из дизъюнктов исключает другого. Бо′льшая посылка в примере, приведенном читателем, будучи сформулированной в полном виде, будет выглядеть так: «Шекспир родился в апреле или в мае, и он не родился в апреле и одновременно в мае». Данное суждение является конъюнктивным, и та его часть, которая является посылкой в аргументе читателя, представляет конъюнкт, утверждающий строгую дизъюнкцию. Такие дизъюнктивные суждения зачастую понимаются без дополнительных объяснений и поэтому не выражаются в явной форме. Тем не менее, для прояснения посылок, входящих в аргумент, эти суждения следует проявить.
В этом смысле строго дизъюнктивные силлогизмы рекомендуется рассматривать отдельно. В них большей посылкой является строго дизъюнктивное суждение, а меньшей – простое категорическое суждение. Отыщем условия, необходимые для обоснованности такого силлогизма.
Допустим, нам известна истинность следующего: «Неверно, что мои часы идут точно» и «Поведение всех механизмов подвержено воздействию климата». Утверждение истинности строго дизъюнктивного суждения означает утверждение того, что, по крайней мере, один из дизъюнктов является ложным. Следовательно, если мы утверждаем суждение «поведение всех механизмов подвержено воздействию климата», мы также должны утверждать и суждение «мои часы не идут точно». Однако будет неверным утверждать, что если один из членов строгой дизъюнкции ложен, то другой истинен. Строго разделительный силлогизм является обоснованным, если в меньшей посылке утверждается один из дизъюнктов, а в заключении отрицается другой.
Схематическая форма данного аргумента такова: неверно, что одновременно А есть В и С есть D; А есть В; следовательно, С не есть D. Или: (p . q)′; p; ∴ q′. Считается, что данное умозаключение стоит в модусе «modus ponendo tollens», поскольку, утверждая (в меньшей посылке), мы отрицаем (в большей).
Теперь можно подытожить обоснованные и необоснованные умозаключения, которые мы рассмотрели в данной главе.

§ 4. Сведение смешанных силлогизмов
Некоторые из указанных выше принципов, несомненно, знакомы читателю. Читатель мог использовать их всю свою жизнь, не формулируя при этом в явной форме, но осуществляя при этом умозаключения именно с помощью этих принципов. Однако ни то, что мы с ними знакомы, ни то, что они, по сути, являются несложными, не умаляет их важности. Эти принципы являются основополагающими для всей логической теории. Они раз за разом возникают в любом исследовании, связанном с обоснованностью суждений, используемых для обоснования последующих суждений.
При этом эти принципы не являются независимыми друг от друга. Если читатель вспомнит эквивалентности, установленные между сложными суждениями, ему не составит труда свести аргумент, стоящий в одном модусе, к аргументу в любом другом модусе. Поэтому мы без лишних комментариев перечислим эквивалентности между четырьмя модусами в нижеследующей таблице.
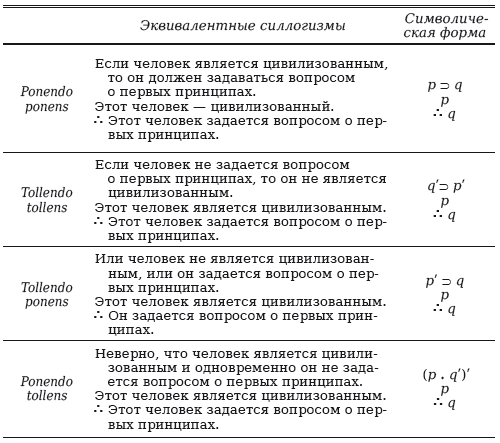
При этом эти принципы не являются независимыми друг от друга. Если читатель вспомнит эквивалентности, установленные между сложными суждениями, ему не составит труда свести аргумент, стоящий в одном модусе, к аргументу в любом другом модусе. Поэтому мы без лишних комментариев перечислим эквивалентности между четырьмя модусами в нижеследующей таблице.

§ 5. ЧИСТЫЙ УСЛОВНЫЙ И РАЗДЕЛИТЕЛЬНЫЙ СИЛЛОГИЗМЫ
Теперь нам предстоит рассмотреть чисто разделительные силлогизмы, с которыми мы познакомились в начале главы. Рассмотрим следующий аргумент:
Если снижены издержки на производство товара, то на данный товар увеличивается экономический спрос.
Если товар производится в большом количестве, то издержки на производство единицы товара снижаются.
∴ Если товар производится в большом количестве, то на него увеличивается экономический спрос.
Вместе первые два принципа имплицируют заключение так, что относительно них оно является подчиненным. Посылка, в которой в качестве компоненты содержится консеквент заключения, называется большей посылкой; посылка, содержащая антецедент заключения, называется меньшей посылкой. Очевидно, что правильность данного силлогизма зависит от транзитивности отношения «если…, то», или импликации.
Схематически данный силлогизм можно записать следующим образом: если С есть D, то Е есть F; если А есть B, то С есть D; следовательно, если А есть B, то Е есть F. Или более абстрактно: q ⊃ r; p ⊃ q; ∴ p ⊃ r.
Теперь рассмотрим другой силлогизм:
Если человек здоров, то его организм не страдает от недоедания.
Если человек беден, то его организм страдает от недоедания.
∴ Если человек здоров, то он не беден.
В данном силлогизме сначала записана меньшая посылка. Данный аргумент является обоснованным, хотя его форма и несколько отличается от силлогизма в первом примере. Схематически его можно записать следующим образом: если А есть В, С не есть D; если Е есть F, С есть D; следовательно, если А есть В, Е не есть F. Или же: r ⊃ q′; p ⊃ q; ∴ r ⊃ p′. Зависимость правильности данного аргумента от транзитивности отношения «если…, то» в данном примере уже не столь очевидна. Тем не менее, данное условие все еще обеспечивает правильность силлогизма. Это можно показать, сведя форму данного силлогизма к форме первого силлогизма. Для этого суждение в большей посылке следует заменить на эквивалентное контрапозитивное суждение:
Если организм человека не страдает от недоедания, то этот человек не беден.
Если человек здоров, то его организм не страдает от недоедания.
∴ Если человек здоров, то он не беден.
Не все чистые условные силлогизмы являются правильными. Примером тому служит нижеследующий силлогизм:
Если рабочие объединяются, то их условия труда становятся удовлетворительными.
Если рабочие не сознают своих общих интересов, они не объединяются.
∴ Если рабочие не сознают своих общих интересов, их условия труда не становятся удовлетворительными.
Читатель может самостоятельно убедиться в том, что форма данных силлогизмов отличается от двух рассмотренных форм правильных силлогизмов, а также и в том, что ее невозможно свести к какой-либо из этих правильных форм.
Умозаключения, в которых посылки представлены двумя дизъюнктивными суждениями, называются чистыми разделительными силлогизмами. Они встречаются довольно редко. Рассмотрим следующий силлогизм:
Или люди трусливы, или они протестуют против несправедливого обращения.
Или люди не трусливы, или они не защищают собственные экономические интересы.
∴ Или люди не защищают свои собственные экономические интересы, или они протестуют против несправедливого обращения.
Данный силлогизм является правильным. Однако у нас нет необходимости проверять условия истинности данного силлогизма, поскольку читатель может проверить правильность любого чистого разделительного силлогизма, сведя его к форме чисто условного силлогизма. На примере вышеприведенного силлогизма такое сведение будет выглядеть следующим образом:
Если люди не трусливы, то они протестуют против несправедливого обращения.
Если люди защищают собственные экономические интересы, то они не трусливы.
∴ Если люди защищают собственные экономические интересы, то они протестуют против несправедливого обращения.
Очевидно, что в данном чистом условном силлогизме заключение эквивалентно заключению вышеприведенного чистого разделительного силлогизма.
Если снижены издержки на производство товара, то на данный товар увеличивается экономический спрос.
Если товар производится в большом количестве, то издержки на производство единицы товара снижаются.
∴ Если товар производится в большом количестве, то на него увеличивается экономический спрос.
Вместе первые два принципа имплицируют заключение так, что относительно них оно является подчиненным. Посылка, в которой в качестве компоненты содержится консеквент заключения, называется большей посылкой; посылка, содержащая антецедент заключения, называется меньшей посылкой. Очевидно, что правильность данного силлогизма зависит от транзитивности отношения «если…, то», или импликации.
Схематически данный силлогизм можно записать следующим образом: если С есть D, то Е есть F; если А есть B, то С есть D; следовательно, если А есть B, то Е есть F. Или более абстрактно: q ⊃ r; p ⊃ q; ∴ p ⊃ r.
Теперь рассмотрим другой силлогизм:
Если человек здоров, то его организм не страдает от недоедания.
Если человек беден, то его организм страдает от недоедания.
∴ Если человек здоров, то он не беден.
В данном силлогизме сначала записана меньшая посылка. Данный аргумент является обоснованным, хотя его форма и несколько отличается от силлогизма в первом примере. Схематически его можно записать следующим образом: если А есть В, С не есть D; если Е есть F, С есть D; следовательно, если А есть В, Е не есть F. Или же: r ⊃ q′; p ⊃ q; ∴ r ⊃ p′. Зависимость правильности данного аргумента от транзитивности отношения «если…, то» в данном примере уже не столь очевидна. Тем не менее, данное условие все еще обеспечивает правильность силлогизма. Это можно показать, сведя форму данного силлогизма к форме первого силлогизма. Для этого суждение в большей посылке следует заменить на эквивалентное контрапозитивное суждение:
Если организм человека не страдает от недоедания, то этот человек не беден.
Если человек здоров, то его организм не страдает от недоедания.
∴ Если человек здоров, то он не беден.
Не все чистые условные силлогизмы являются правильными. Примером тому служит нижеследующий силлогизм:
Если рабочие объединяются, то их условия труда становятся удовлетворительными.
Если рабочие не сознают своих общих интересов, они не объединяются.
∴ Если рабочие не сознают своих общих интересов, их условия труда не становятся удовлетворительными.
Читатель может самостоятельно убедиться в том, что форма данных силлогизмов отличается от двух рассмотренных форм правильных силлогизмов, а также и в том, что ее невозможно свести к какой-либо из этих правильных форм.
Умозаключения, в которых посылки представлены двумя дизъюнктивными суждениями, называются чистыми разделительными силлогизмами. Они встречаются довольно редко. Рассмотрим следующий силлогизм:
Или люди трусливы, или они протестуют против несправедливого обращения.
Или люди не трусливы, или они не защищают собственные экономические интересы.
∴ Или люди не защищают свои собственные экономические интересы, или они протестуют против несправедливого обращения.
Данный силлогизм является правильным. Однако у нас нет необходимости проверять условия истинности данного силлогизма, поскольку читатель может проверить правильность любого чистого разделительного силлогизма, сведя его к форме чисто условного силлогизма. На примере вышеприведенного силлогизма такое сведение будет выглядеть следующим образом:
Если люди не трусливы, то они протестуют против несправедливого обращения.
Если люди защищают собственные экономические интересы, то они не трусливы.
∴ Если люди защищают собственные экономические интересы, то они протестуют против несправедливого обращения.
Очевидно, что в данном чистом условном силлогизме заключение эквивалентно заключению вышеприведенного чистого разделительного силлогизма.
§ 6. Дилемма
Условные и дизъюнктивные суждения могут сочетаться множеством способов, предлагая и более сложные аргументы. Мы не можем рассматривать все из них, и поэтому мы остановимся лишь на одном из них, называющимся «дилеммой». Читателю следует учесть, что дилемма не вводит никакого нового логического принципа и рассматривается отдельно лишь в силу существующей традиции и интересных вариантов применения. Никаких иных причин для выделения дилеммы из множества других сложных форм рассуждения нет.
Дилемма – это такой аргумент, в котором одна посылка (большая) является конъюнкцией двух условных суждений, а вторая посылка (меньшая) является дизъюнктивным суждением. В меньшей посылке либо утверждаются антецеденты, либо отрицаются консеквенты большей посылки.
Дилеммы, в которых меньшая посылка утверждает антецеденты в большей посылке, называются конструктивными. Дилеммы, в которых меньшая посылка отрицает антецеденты в большей посылке, называются деструктивными. В конструктивных дилеммах антецеденты большей посылки должны быть представлены различными суждениями, тогда как консеквенты могут быть либо различными суждениями, либо одним и тем же суждением. В первом случае дилемма является сложной конструктивной, во втором – простой конструктивной. В деструктивной дилемме консеквенты в большей посылке должны быть различными суждениями, тогда как антецеденты могут быть представлены различными суждениями или же одним и тем же суждением. В первом случае дилемма является сложной деструктивной, во втором – простой деструктивной. Таким образом, существует четыре различных вида дилемм. Проиллюстрируем каждый из них.
1. Сложная конструктивная дилемма
Если женщины приукрашиваются напоказ, то они самовлюбленны. Если женщины приукрашиваются для того, чтобы привлекать мужчин, то они аморальны.
Женщины приукрашиваются напоказ или для того, чтобы привлекать мужчин.
∴ Женщины самовлюбленны или аморальны.
2. Простая конструктивная дилемма
Если допустить, что сумма углов треугольника равна сумме двух прямых углов, то пятый постулат Евклида доказуем. Если допустить, что существуют два подобных треугольника с разной площадью, то постулат Евклида доказуем.
Допускается, что сумма углов треугольника равна сумме двух прямых углов, или что существуют два подобных треугольника с неравной площадью.
Дилемма – это такой аргумент, в котором одна посылка (большая) является конъюнкцией двух условных суждений, а вторая посылка (меньшая) является дизъюнктивным суждением. В меньшей посылке либо утверждаются антецеденты, либо отрицаются консеквенты большей посылки.
Дилеммы, в которых меньшая посылка утверждает антецеденты в большей посылке, называются конструктивными. Дилеммы, в которых меньшая посылка отрицает антецеденты в большей посылке, называются деструктивными. В конструктивных дилеммах антецеденты большей посылки должны быть представлены различными суждениями, тогда как консеквенты могут быть либо различными суждениями, либо одним и тем же суждением. В первом случае дилемма является сложной конструктивной, во втором – простой конструктивной. В деструктивной дилемме консеквенты в большей посылке должны быть различными суждениями, тогда как антецеденты могут быть представлены различными суждениями или же одним и тем же суждением. В первом случае дилемма является сложной деструктивной, во втором – простой деструктивной. Таким образом, существует четыре различных вида дилемм. Проиллюстрируем каждый из них.
1. Сложная конструктивная дилемма
Если женщины приукрашиваются напоказ, то они самовлюбленны. Если женщины приукрашиваются для того, чтобы привлекать мужчин, то они аморальны.
Женщины приукрашиваются напоказ или для того, чтобы привлекать мужчин.
∴ Женщины самовлюбленны или аморальны.
2. Простая конструктивная дилемма
Если допустить, что сумма углов треугольника равна сумме двух прямых углов, то пятый постулат Евклида доказуем. Если допустить, что существуют два подобных треугольника с разной площадью, то постулат Евклида доказуем.
Допускается, что сумма углов треугольника равна сумме двух прямых углов, или что существуют два подобных треугольника с неравной площадью.
Конец бесплатного ознакомительного фрагмента
