Страница:
В параметре E учитывается только информация, необходимая для задачи, и информация, вводимая пользователем. Два или более методов действия могут иметь одинаковую производительность E, но иметь разное время выполнения. Возможно даже, что один метод имеет более высокий показатель E, но действует медленнее, чем другой метод, – например M K M K и M K K K. В этом примере при использовании первого метода должно быть введено только два символа. При использовании второго метода требуется ввести три символа, но времени на все действие тратится меньше. Трудно привести другие примеры из обычной жизни, в которых происходит аналогичная перестановка скорости и информационной производительности. [22]Как правило, чем более производительным является интерфейс, тем более продуктивным и более человекоориентированным он является.
Информация измеряется в битах. Один бит, который представляет собой один из двух альтернативных вариантов (таких как 0 или 1, да или нет), является единицей информации. [23]Например, чтобы выбрать один из каких-либо четырех объектов, потребуется 2 бита информации. Если объекты обозначить как A, B, C и D, первый бит информации определит выбор между A и B или C и D. Когда первый выбор сделан (например, C и D), второй бит определит выбор между следующими двумя элементами (либо C, либо D). Двух двоичных выборов, или двух битов, достаточно для выбора одного элемента из четырех. Чтобы сделать выбор из группы восьми элементов, потребуется 3 бита. Из шестнадцати элементов – 4 бита, и т. д. В общем случае при количестве n равновероятных вариантов суммарное количество передаваемой информации определяется как степень 2, равная n:
\log_2 n
Количество информации для каждого варианта определяется как
(1/n) \log_2 n (1)
Если вероятности для каждой альтернативы не являются равными и i – я альтернатива имеет вероятность p(i), то информация, передаваемая этой альтернативой, определяется как
p(i) \log_2(1/p(i)) (2)
Количество информации является суммой (по всем вариантам) выражения (2), которое при равновероятных вариантах сводится к выражению (1). Отсюда следует, что информационное содержание интерфейса, в котором возможно сделать только нажатие единственной клавиши (а ненажатие клавиши не допускается), составляет 0 бит:
1 \log_2(1) = 0 (3)
Однако может показаться, что нажатие единственной клавиши способно, например, вызвать подрыв динамита для разрушения здания. Таким образом, передает ли это нажатие какую-нибудь информацию? На самом деле нет, потому что ненажатие кнопки не было предусмотрено как альтернатива – интерфейс допускает «только нажатие единственной клавиши». Если же нажатие клавиши не производится в течение 5-минутного периода, когда подрыв возможен, то здание не будет разрушено, и поэтому нажатие или ненажатие передает до 1 бита информации, так как в этом случае имеется альтернатива из двух вариантов. Из выражения (2) следует, что в вычислениях используется вероятность (p) того, что здание будет разрушено. Таким образом, вероятность того, что оно не будет разрушено, составляет 1-p. С помощью выражения (2) мы можем вычислить информационное содержание данного интерфейса:
p \log_2(1/p) + (1-p) \log_2(1/(1-p)) (4)
При p=S результат выражения (4) составит:
S*1 + S*1 = S + S = 1
Значение выражения (4) будет меньше 1, если p<> S. В частности при p = 0 или p = 1 оно составит 0, как это видно из выражения (3).
Этот пример показывает важный момент, который заключается в том, что мы можем оценить объем информации, содержащейся в сообщении, только в контексте всего набора возможных сообщений. Чтобы подсчитать количество информации, передаваемой некоторым полученным сообщением, необходимо знать в частности вероятность, с которой это сообщение может быть отправлено. Количество информации в любом сообщении не зависит от других сообщений, которые были в прошлом или могут быть в будущем, не связано со временем или продолжительностью и не зависит от каких-либо иных событий, так же как результат подбрасывания симметричной монеты не зависит от результата предыдущих подбрасываний или от времени дня, когда это подбрасывание производится.
Кроме того, важно учитывать, что:
«нельзя путать понятие информации с понятием смысла…информация является мерой свободы выбора сообщения… Следует отметить, что при наличии только двух возможных сообщений утверждать, что какое-то сообщение передает какой-то объем [1 бит] информации, неправильно. Понятие информации не применимо к отдельным сообщениям (в отличие от понятия смыла), но применимо к ситуации в целом; при этом единица информации показывает, что в данной ситуации имеется некоторый объем свободы в выборе сообщения, который удобно обозначать как стандартный или единичный объем информации»Однако действия, которые совершает пользователь при выполнении задачи, можно с большей точностью смоделировать в виде процесса Маркова, в котором вероятность последующих действий зависит от уже совершенных пользователем действий. Тем не менее, для данного рассмотрения достаточно использовать упомянутые вероятности отдельных, единичных событий, при этом будем исходить из того, что все сообщения являются независимыми друг от друга и равновероятными.
(Shannon и Weaver, 1963, с. 9).
Также можно вычислить количество информации, которое передается с помощью устройств, отличающихся от клавиатуры. Если экран дисплея разделен на две области – со словом «Да» в одной области и словом «Нет» – в другой, то один клик, совершенный в одной из областей, будет передавать 1 бит информации. Если имеется n равновероятных объектов, то нажатием на один из них сообщается \log_2 n бит информации. Если объекты имеют разные размеры, то количество информации, сообщаемой каждым из них, не изменяется, но увеличивается время перемещения ГУВ к более мелким объектам (далее мы покажем способ вычисления этого времени). Если объекты имеют разные вероятности, формула остается аналогичной той, которая была дана для случая ввода с клавиатуры разновероятных данных. Различие состоит только в том, что для нажатия клавиши может потребоваться 0.2 с. тогда как для нажатия кнопки, изображенной на экране, в среднем может потребоваться около 1.3 с (без учета времени перемещения руки пользователя с клавиатуры на ГУВ).
В случае голосового ввода информации его информационное содержание можно вычислить, если рассматривать речь как последовательность вводимых символов, а не как непрерывный поток определенного диапазона и продолжительности.
Данный подход к теории информации и ее связи с разработкой интерфейсов является упрощенным. Но даже в такой упрощенной форме, которую мы также использовали при рассмотрении модели GOMS, теория информации может дать нам общий критерий оценки качества интерфейса.
4.3.1. Производительность интерфейса для Хола
Аккуратный подсчет есть путь к знаниям всех существующих вещей и тайных секретов.
Папирусы Рхинда, 1650 г. до н. э.
Аккуратный подсчет есть путь к знаниям всех существующих вещей и тайных секретов.
Полезно подробно рассмотреть пример вычисления среднего количества информации, требуемого для некоего интерфейса. Для этого я снова использую пример интерфейса для перевода температур из одной шкалы в другую. В соответствии с условиями требуется, чтобы количество символов, вводимых в температурный преобразователь, равнялось в среднем 4. Кроме того, по условиям задачи десятичная точка используется однократно в 90 % вводимых данных, а в 10 % – вообще не встречается; знак минус появляется один раз в 25 % данных и совсем не встречается в остальных 75 % данных. Из соображений простоты, а также потому, что не требуется ответ с точностью до 1 %, я буду исходить из того, что все остальные цифры встречаются с одинаковой частотой, и не буду учитывать те 10 % данных, которые не содержат десятичной точки.
Требуется определить множество возможных вариантов ввода и их вероятности. Возможны 5 вариантов (d означает цифру):
1. -.dd
2. -d.d
3. .ddd
4. d.dd
5. dd.d
Первые два варианта встречаются в 12.5 % случаев, и количество каждого из них составляет 100. Каждый из последних трех вариантов встречается в 25 % случаев, и количество каждого из них составляет почти 1000. [24]Вероятность каждого из первых двух вариантов ввода составляет (0.125/100)=0.00125. Вероятность любого из последних трех вариантов ввода составляет (0.75/3000)=0.00025. Сумма вероятностей, как это и должно быть, составляет 1.
Количество информации (в битах), передаваемое каждым вариантом, определяется выражением (2): [25]
p(i) \log_2(1/p(i))
Значение этого выражения составляет приблизительно 0.012 для отрицательных значений ввода и 0.003 – для положительных. 200*0.00674+3000*0.003 дает в сумме 11.4 бита для каждого варианта ввода.
Важно учесть вероятности вариантов. Если использовать простой подход, в котором все 12 символов (минус, десятичная точка и 10 цифр) принять как равновероятные, то вероятность каждого символа составит 1/12, а количество информации, содержащейся в 4-значном варианте ввода, составит приблизительно
4 \log_2(12)H14 бит
В теории информации есть теорема, в которой утверждается, что максимум информации передается при условии, что все символы равновероятны. Поэтому если принять все варианты как равновероятные, то общее значение будет равно количеству информации в каждом отдельном варианте или превышать его. Очевидно, что такое допущение позволяет упростить вычисление информационного содержания. Если же результирующее значение приближенного вычисления меньше количества информации, которое пользователь должен ввести в интерфейс, то проводить еще более точные вычисления уже нет необходимости.
Мы только что выяснили, что каждый раз, когда Холу требуется провести преобразование температурных значений, он должен ввести в среднем около 11 бит информации. Мы можем разделить это количество на то количество информации, которое требуется ввести в интерфейс, что мы сейчас и сделаем. В результате мы получим производительность (эффективность) данного интерфейса.
Другим упрощением, позволяющим провести быстрый анализ интерфейса, является вычисление различных жестов на основе количества информации, передаваемого одним нажатием клавиши или одной операцией ГУВ. При передаче информации нажатием клавиши ее количество зависит от общего количества клавиш и относительной частоты использования каждой из них. Таким образом, нажатия клавиши могут использоваться как приблизительная мера информации. Если на клавиатуре имеется 128 клавиш, и каждая из них используется с одинаковой частотой, то нажатие любой из них будет передавать 7 бит информации. В действительности частота использования клавиш субщественно различается. Например, пробел или буква е используются чаще, чем й или \, поэтому в большинстве приложений на каждое нажатие клавиши приходится в среднем около 5 битов. По условиям нашей задачи среднее число символов вводимых температурных значений не должно превышать 4.
Для данного анализа удобнее использовать более простую меру, чем теоретическая информационная производительность. Символьная эффективностьчасто имеет такую же практическую ценность, что и информационная производительность. Она определяется как минимальное количество символов, необходимое для выполнения задачи, отнесенное к количеству символов, которое в данном интерфейсе требуется ввести пользователем.
Если в нашем интерфейсе потребуется вводить в среднем 4 символа, то символьная эффективность такого интерфейса составит 100 %. При добавлении еще одной клавиши, обозначающей шкалу перевода температурного значения, а также еще одной для разделения, средняя длина ввода возрастет до 6 символов, а символьная эффективность снизится до 67 %. Если в качестве устройства ввода Хол будет использовать числовую клавиатуру, состоящую из 16 клавиш, то каждой отдельной клавишей будет передаваться 4 бита информации, и поэтому производительность интерфейса возрастет. (Однако по условиям задачи такой возможности не предусмотрено.)
Поскольку любая задача в соответствии с анализом GOMS требует как минимум одного ментального оператора, наиболее производительный интерфейс с использованием клавиатуры для перевода температурных значений из одной шкалы в другую будет теоретически иметь следующее среднее время использования:
M + K + K + K + K = 2.15 с
Таким образом, он будет значительно быстрее, чем любой из двух уже рассмотренных вариантов. Однако введение 4 символов с помощью стандартной клавиатуры дает, по крайней мере, 20 бит информации, тогда как требуется только 10. Следовательно, теоретическая информационная производительность составляет 55 %, а значит, существует возможность улучшения. Как мы уже видели, использование стандартной числовой клавиатуры вместо полной клавиатуры снижает объем информации, вводимой на каждые 4 символа, до 16 бит, что повышает производительность до 60 %. Желаемая числовая клавиатура, содержащая только цифры, знак минус и десятичную точку, позволит немного повысить производительность – до 70 %. Дальнейшее повышение производительности возможно через использование особых кодировок обозначений температуры и изобретение новых устройств ввода, но здесь возникают трудности, связанные с обучением и лишними расходами, поэтому остановимся на варианте с 70 % теоретической информационной производительности. Независимо от того, могут ли теоретические границы быть достигнуты на практике или нет, они дают нам направление в разработке интерфейса.
4.3.2. Другие решения интерфейса для Хола
В разделе 4.3.1 мы приостановили дальнейшие попытки улучшения интерфейса, достигнув 70 % теоретической информационной производительности. Данная производительность определена для пока еще неизвестного, теоретического интерфейса, в котором каким-то образом можно получить 100 % эффективность использования клавиш. Давайте посмотрим, насколько мы можем приблизиться к этому идеалу с помощью стандартной клавиатуры и ГУВ.
Рассмотрим интерфейс, в котором используется клавиатура со всеми символами. В таком интерфейсе на экране появляется следующее сообщение:
M K K K K K M K
Среднее время составит 3.9 с.
Мы можем уменьшить это время, если сами символы C и F будем использовать в качестве разделителей. Рассмотрим интерфейс, в котором появляется следующая инструкция:
GOMS-анализ показывает, что для интерфейса с символами C и F в качестве разделителей запись будет следующей:
M K K K K M K
Среднее время составит 3.7 с. Если бы мы не знали, что теоретически минимальное время составляет 2.15 с, то это решение могло бы показаться удачным. Оно является значительно более эффективным, чем ранее рассмотренные, поэтому мы могли бы на нем остановиться. Однако теоретический минимум подстегивает нас к поиску еще более быстрой интерфейсной модели. Рассмотрим интерфейс, изображенный на рис. 4.5. Такой интерфейс можно назвать разветвленным. В нем один ввод дает в результате два вывода.
Рис. 4.5. Интерфейс, в котором не используется разделитель. Более эффективным является вариант, в котором выполняется посимвольная обработка вводимых данных и одновременное преобразование в обеих шкалах
В разветвленном интерфейсе нет необходимости в разделителе. Кроме того, пользователю не нужно указывать, какое именно преобразование требуется провести. GOMS-анализ показывает, что для 4 символов, которые в среднем будут вводиться, запись будет следующей:
M K K K K
В разветвленном интерфейсе достигается минимальное время 2.15 с, и его символьная эффективность составляет 100 %.
Если, как в нашем примере, в месте вывода происходит изменение результата в тот момент, когда символы вводятся, это колебание цифр не отвлекает пользователя, потому что в локусе его внимания находится именно ввод данных. Непрерывно изменяемые значения на выводе могут быть даже полезными – после нескольких применений пользователь будет замечать эти колебания только краем глаза, что будет служить подсказкой о том, что система отвечает на вводимые данные. Если используется посимвольный режим работы интерфейса, то для большей эффективности такая система должна реагировать довольно быстро. В частности скорость реакции не должна быть меньше скорости ввода. Такая проблема может возникать только при сетевом использовании интерфейса.
Хотя это и не входит в условие задачи, но может возникнуть вопрос о том, как происходит очистка полей в преобразователе для выполнения следующего преобразования. Добавляет ли операция очистки еще одно нажатие клавиши? Необязательно. Например, мы можем разработать интерфейс таким образом, что каждый раз, когда оператор возвращается к своему основному занятию или переходит к другой задаче, значения, указанные в преобразователе, могут автоматически затеняться, а сам температурный преобразователь становиться неактивным; причем в это время все значения могут оставаться в своих полях так, что при необходимости их можно было бы опять увидеть, но уже при следующем вводе все они будут стерты.
Разветвленный интерфейс не обязательно является самым лучшим из тех, что уже были рассмотрены – или из тех, что возможны, – только потому, что он имеет оптимальную скорость работы и является весьма эффективным. Кроме скорости есть и другие параметры, которые также являются важными: частота появления ошибок; время, необходимое для изучения интерфейса; возможность длительного запоминания способа использования интерфейса. Особенно следует обратить внимание на частоту появления ошибок в разветвленном интерфейсе, поскольку есть вероятность того, что Хол может прочитать результат не из того поля. Это важно особенно потому, что когда он услышал, например слово Цельсий, ему необходимо прочитать значение из поля шкалы Фаренгейта. Тем не менее, разветвленный температурный преобразователь определенно входит в небольшое число тех интерфейсов, которые можно рассматривать как рабочие варианты для программы преобразования температурных значений из одной шкалы в другую. Другие рассмотренные нами примеры, которые могли бы показаться удачными, если бы мы не проводили с ними GOMS-анализ, на самом деле не являются таковыми.
Используемая как в простом анализе временных затрат на нажатия клавиш, так и в полном информационно-теоретическом исследовании, квантификация теоретического интерфейса с минимальным временем использования или с минимальным количеством используемых символов, или с минимальным количеством используемой информации может быть полезна с точки зрения разработки интерфейса. Без количественных ориентиров мы можем только догадываться о том, насколько хорошо мы разработали интерфейс и есть ли возможность его улучшения.
Рассмотрим интерфейс, в котором используется клавиатура со всеми символами. В таком интерфейсе на экране появляется следующее сообщение:
Для перевода температуры из одной шкалы в другую укажите нужную шкалу с помощью символа C (шкала Цельсия) или F (шкала Фаренгейта). Введите числовое значение температуры, затем нажмите клавишу Enter. Результат преобразования будет отображен на экране.GOMS-анализ показывает, что пользователь должен сделать 6 нажатий клавиш. По правилам расстановки операторов M получаем. следующую запись:
M K K K K K M K
Среднее время составит 3.9 с.
Мы можем уменьшить это время, если сами символы C и F будем использовать в качестве разделителей. Рассмотрим интерфейс, в котором появляется следующая инструкция:
Для перевода температуры из одной шкалы в другую введите числовое значение температуры и следом поставьте символ C, если оно в шкале Цельсия, или F, если оно в шкале Фаренгейта. Результат преобразования будет отображен на экране.В данном примере нажимать на клавишу «Enter» не требуется. Некоторые примитивные средства разработки интерфейсов требуют, чтобы пользователь обязательно использовал клавишу «Enter», и поэтому в них невозможно использовать символы C и F в качестве разделителей. Такие инструменты не подходят для разработки человекоориентированных интерфейсов.
GOMS-анализ показывает, что для интерфейса с символами C и F в качестве разделителей запись будет следующей:
M K K K K M K
Среднее время составит 3.7 с. Если бы мы не знали, что теоретически минимальное время составляет 2.15 с, то это решение могло бы показаться удачным. Оно является значительно более эффективным, чем ранее рассмотренные, поэтому мы могли бы на нем остановиться. Однако теоретический минимум подстегивает нас к поиску еще более быстрой интерфейсной модели. Рассмотрим интерфейс, изображенный на рис. 4.5. Такой интерфейс можно назвать разветвленным. В нем один ввод дает в результате два вывода.
В разветвленном интерфейсе нет необходимости в разделителе. Кроме того, пользователю не нужно указывать, какое именно преобразование требуется провести. GOMS-анализ показывает, что для 4 символов, которые в среднем будут вводиться, запись будет следующей:
M K K K K
В разветвленном интерфейсе достигается минимальное время 2.15 с, и его символьная эффективность составляет 100 %.
Если, как в нашем примере, в месте вывода происходит изменение результата в тот момент, когда символы вводятся, это колебание цифр не отвлекает пользователя, потому что в локусе его внимания находится именно ввод данных. Непрерывно изменяемые значения на выводе могут быть даже полезными – после нескольких применений пользователь будет замечать эти колебания только краем глаза, что будет служить подсказкой о том, что система отвечает на вводимые данные. Если используется посимвольный режим работы интерфейса, то для большей эффективности такая система должна реагировать довольно быстро. В частности скорость реакции не должна быть меньше скорости ввода. Такая проблема может возникать только при сетевом использовании интерфейса.
Хотя это и не входит в условие задачи, но может возникнуть вопрос о том, как происходит очистка полей в преобразователе для выполнения следующего преобразования. Добавляет ли операция очистки еще одно нажатие клавиши? Необязательно. Например, мы можем разработать интерфейс таким образом, что каждый раз, когда оператор возвращается к своему основному занятию или переходит к другой задаче, значения, указанные в преобразователе, могут автоматически затеняться, а сам температурный преобразователь становиться неактивным; причем в это время все значения могут оставаться в своих полях так, что при необходимости их можно было бы опять увидеть, но уже при следующем вводе все они будут стерты.
Разветвленный интерфейс не обязательно является самым лучшим из тех, что уже были рассмотрены – или из тех, что возможны, – только потому, что он имеет оптимальную скорость работы и является весьма эффективным. Кроме скорости есть и другие параметры, которые также являются важными: частота появления ошибок; время, необходимое для изучения интерфейса; возможность длительного запоминания способа использования интерфейса. Особенно следует обратить внимание на частоту появления ошибок в разветвленном интерфейсе, поскольку есть вероятность того, что Хол может прочитать результат не из того поля. Это важно особенно потому, что когда он услышал, например слово Цельсий, ему необходимо прочитать значение из поля шкалы Фаренгейта. Тем не менее, разветвленный температурный преобразователь определенно входит в небольшое число тех интерфейсов, которые можно рассматривать как рабочие варианты для программы преобразования температурных значений из одной шкалы в другую. Другие рассмотренные нами примеры, которые могли бы показаться удачными, если бы мы не проводили с ними GOMS-анализ, на самом деле не являются таковыми.
Используемая как в простом анализе временных затрат на нажатия клавиш, так и в полном информационно-теоретическом исследовании, квантификация теоретического интерфейса с минимальным временем использования или с минимальным количеством используемых символов, или с минимальным количеством используемой информации может быть полезна с точки зрения разработки интерфейса. Без количественных ориентиров мы можем только догадываться о том, насколько хорошо мы разработали интерфейс и есть ли возможность его улучшения.
4.4. Закон Фитса и закон Хика
Основы знаний надлежит искать в математике.
Роджер Бэкон «Opus Majus», XIII в.
Различные количественные законы, имеющие отношение к разработке интерфейсов, имеют хорошее когнитивное обоснование, и их правильность была неоднократно проверена. Эти законы часто дают нам дополнительные данные, на основе которых можно принимать те или иные решения, связанные с разработкой интерфейсов. Закон Фитса (Fitts' Law) позволяет определить количественно тот факт, что чем дальше находится объект от текущей позиции курсора или чем меньше размеры этого объекта, тем больше времени потребуется пользователю для перемещения к нему курсора. Закон Хика (Hick's Law) позволяет количественно определить наблюдение, заключающееся в том, что чем больше количество вариантов заданного типа вы предоставляете, тем больше времени требуется на выбор.
4.4.1. Закон Фитса
Представим, что вы перемещаете курсор к кнопке, изображенной на экране. Кнопка является
цельюданного перемещения. Длина прямой линии, соединяющей начальную позицию курсора и ближайшую точку целевого объекта, определяется в законе Фитса как
дистанция. На основе данных о размерах объекта и дистанции
закон Фитсапозволяет найти среднее время, за которое пользователь сможет переместить курсор к кнопке.
В одномерном случае, при котором размер объекта вдоль линии перемещения курсора обозначается как S, а дистанция от начальной позиции курсора до объекта – как D (рис. 4.6), закон Фитса формулируется следующим образом:
Время (мс) = a + b \log_2(D/S+1)
(Константы a и b устанавливаются опытным путем по параметрам производительности человека.) [26]
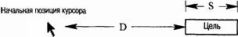Рис. 4.6. Расстояния, которые используются в законе Фитса для определения времени, необходимого для перемещения курсора к цели
Вычисляемое время отсчитывается от момента, когда курсор начинает движение по прямой линии, до момента, когда пользователь щелкает мышью по целевому объекту. Логарифм по основанию 2 является мерой трудности задачи в количестве бит информации, которое требуется для описания (одномерного) пути перемещения курсора.
Для вычисления времени можно использовать любые единицы измерения дистанции, т. к. D/S является отношением двух дистанций и поэтому не зависит от единицы измерения. Отсюда следует, что хотя указательное устройство может переместиться на расстояние большее или меньшее, чем то расстояние, на которое переместится на экране курсор, закон все равно работает, при условии, что соотношение между движением ГУВ и курсора является линейным. Закон Фитса может применяться только к тем типам перемещения, которые совершаются при использовании большинства человеко-машинных интерфейсов, т. е. к таким перемещениям, которые невелики относительно размеров человеческого тела и которые являются непрерывными (совершаемыми одним движением). Для приближенных вычислений я использую следующие значения констант в уравнении закона Фитса: a=50, b=150.
Также проводились тестирования с законом Фитса, дополненным некоторыми более сложными параметрами, такими, например, как перемещение курсора между прямыми или искривленными границами (Accot и Zhai, 1997). Для двумерных целей обычно можно получить корректное приближенное значение времени, необходимого для перемещения курсора к объекту, используя в качестве параметра S наименьшее из значений размеров объекта по горизонтали или по вертикали (Mackenzie, 1995).
Рис. 4.7. Меню в Macintosh, расположенное у верхней границы экрана, увеличивается в размере, что является более эффективным по сравнению с меню, которое всплывает из-за границы экрана
Закон Фитса позволяет объяснить, например, почему переместить курсор к меню в стиле Apple Macintosh, располагающемуся на границе экрана (рис. 4.7), намного быстрее, чем переместить курсор к меню в стиле Microsoft Windows, которое всплывает из-за границы экрана (рис. 4.8). Размер S меню в Windows на моем экране составляет 5 мм. Эффективный размер меню в Macintosh является довольно большим, потому что пользователю не требуется останавливаться в пределах полосы меню; он может просто передвинуть ГУВ на любое расстояние превышающее расстояние, необходимое для размещения курсора в пределах меню, – курсор в любом случае остановится на границе экрана.
Рис. 4.8. Меню в Windows находится под верхней границей экрана, поэтому пользователю нужно более точно подводить курсор к меню, чтобы, можно было вызвать подменю
Ряд выполненных мной тестов помог установить, что пользователи Macintosh обычно останавливаются в пределах 50 мм от границы экрана, поэтому для Macintosh мы можем принять 50 мм как S. При использовании 14-дюймового плоского монитора среднее расстояние, на которое требуется переместить курсор, чтобы достичь панели меню, составляет 80 мм. Таким образом, время перемещения курсора к какому-либо из элементов меню в Macintosh будет:
50 + 150 \log_2(80/50+1) = 256 мс
Это время является намного меньшим, чем то, которое требуется на перемещение курсора к необходимому элементу меню в Windows:
50 + 150 \log_2(80/5+1) = 663 мс
Полученные значения времени относятся только лишь к перемещению курсора. Щелчок по целевому объекту, к которому перемещался курсор, добавляет в среднем еще 0.1 с. (Значение оператора K=0.2, принятое в модели GOMS, учитывает и нажатие кнопки, и ее отпускание, в то время как указанное значение учитывает только нажатие кнопки.) При проведении обычного эксперимента вам придется добавить еще 0.25 с, чтобы учесть время человеческой реакции в начале движения курсора. С учетом всех этих факторов мы получим именно те значения, которые я получил экспериментальным путем: в среднем пользователю требуется около 0.6 с, чтобы открыть Apple-меню, в то время как для открытия Windows-меню требуется более 1 с. Таким образом, этот анализ объясняет, почему при разработке интерфейса Macintosh меню были намеренно помещены на границе экрана.
В одномерном случае, при котором размер объекта вдоль линии перемещения курсора обозначается как S, а дистанция от начальной позиции курсора до объекта – как D (рис. 4.6), закон Фитса формулируется следующим образом:
Время (мс) = a + b \log_2(D/S+1)
(Константы a и b устанавливаются опытным путем по параметрам производительности человека.) [26]
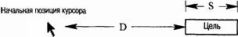
Вычисляемое время отсчитывается от момента, когда курсор начинает движение по прямой линии, до момента, когда пользователь щелкает мышью по целевому объекту. Логарифм по основанию 2 является мерой трудности задачи в количестве бит информации, которое требуется для описания (одномерного) пути перемещения курсора.
Для вычисления времени можно использовать любые единицы измерения дистанции, т. к. D/S является отношением двух дистанций и поэтому не зависит от единицы измерения. Отсюда следует, что хотя указательное устройство может переместиться на расстояние большее или меньшее, чем то расстояние, на которое переместится на экране курсор, закон все равно работает, при условии, что соотношение между движением ГУВ и курсора является линейным. Закон Фитса может применяться только к тем типам перемещения, которые совершаются при использовании большинства человеко-машинных интерфейсов, т. е. к таким перемещениям, которые невелики относительно размеров человеческого тела и которые являются непрерывными (совершаемыми одним движением). Для приближенных вычислений я использую следующие значения констант в уравнении закона Фитса: a=50, b=150.
Также проводились тестирования с законом Фитса, дополненным некоторыми более сложными параметрами, такими, например, как перемещение курсора между прямыми или искривленными границами (Accot и Zhai, 1997). Для двумерных целей обычно можно получить корректное приближенное значение времени, необходимого для перемещения курсора к объекту, используя в качестве параметра S наименьшее из значений размеров объекта по горизонтали или по вертикали (Mackenzie, 1995).
Закон Фитса позволяет объяснить, например, почему переместить курсор к меню в стиле Apple Macintosh, располагающемуся на границе экрана (рис. 4.7), намного быстрее, чем переместить курсор к меню в стиле Microsoft Windows, которое всплывает из-за границы экрана (рис. 4.8). Размер S меню в Windows на моем экране составляет 5 мм. Эффективный размер меню в Macintosh является довольно большим, потому что пользователю не требуется останавливаться в пределах полосы меню; он может просто передвинуть ГУВ на любое расстояние превышающее расстояние, необходимое для размещения курсора в пределах меню, – курсор в любом случае остановится на границе экрана.
Ряд выполненных мной тестов помог установить, что пользователи Macintosh обычно останавливаются в пределах 50 мм от границы экрана, поэтому для Macintosh мы можем принять 50 мм как S. При использовании 14-дюймового плоского монитора среднее расстояние, на которое требуется переместить курсор, чтобы достичь панели меню, составляет 80 мм. Таким образом, время перемещения курсора к какому-либо из элементов меню в Macintosh будет:
50 + 150 \log_2(80/50+1) = 256 мс
Это время является намного меньшим, чем то, которое требуется на перемещение курсора к необходимому элементу меню в Windows:
50 + 150 \log_2(80/5+1) = 663 мс
Полученные значения времени относятся только лишь к перемещению курсора. Щелчок по целевому объекту, к которому перемещался курсор, добавляет в среднем еще 0.1 с. (Значение оператора K=0.2, принятое в модели GOMS, учитывает и нажатие кнопки, и ее отпускание, в то время как указанное значение учитывает только нажатие кнопки.) При проведении обычного эксперимента вам придется добавить еще 0.25 с, чтобы учесть время человеческой реакции в начале движения курсора. С учетом всех этих факторов мы получим именно те значения, которые я получил экспериментальным путем: в среднем пользователю требуется около 0.6 с, чтобы открыть Apple-меню, в то время как для открытия Windows-меню требуется более 1 с. Таким образом, этот анализ объясняет, почему при разработке интерфейса Macintosh меню были намеренно помещены на границе экрана.