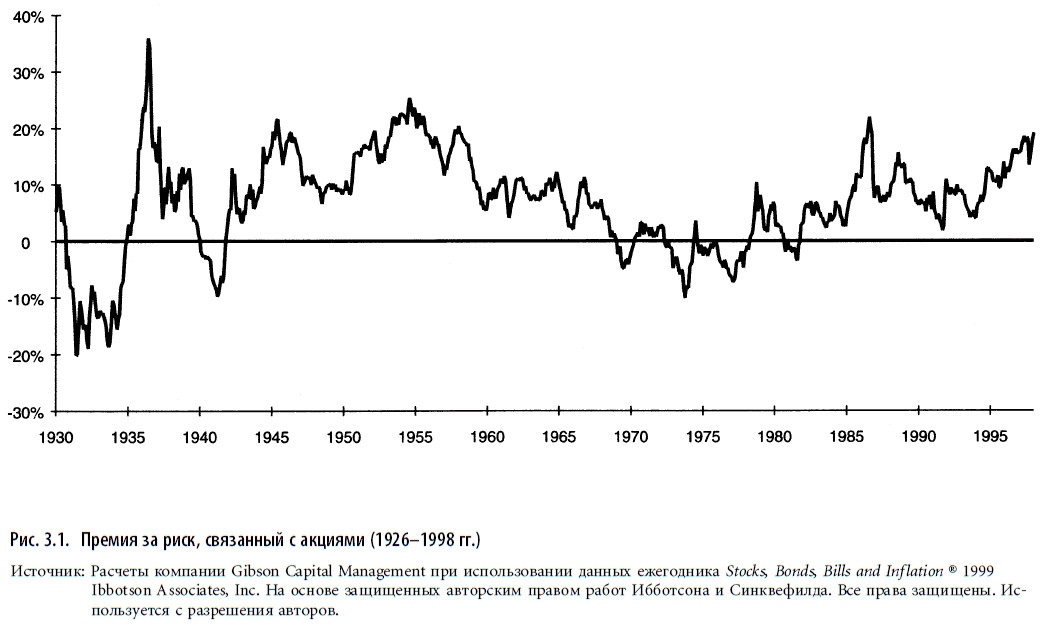
За рассмотренный нами 73-летний период акции крупных компаний имели годовую доходность в сложных процентах 11,2 %, что на 7,4 % больше годовой доходности казначейских векселей (3,8 %). Разница между доходностью акций крупных компаний и доходностью казначейских векселей называется премией за риск, связанный с акциями. Если предположить, что волатильность акций крупных компаний в будущем существенно не изменится и они будут оцениваться на рынке таким образом, что компенсация за волатильность в будущем не будет отличаться от ее исторического значения, то премия за риск, связанный с акциями, в размере 7,4 % будет вполне оправданна в будущем. Таким образом, можно построить простую модель оценки доходности в сложных процентах акций крупных компаний:
Доходность казначейских векселей = х%
Плюс премия за риск, связанный с акциями = +7,4%
Равно будущей доходности в сложных процентах акций крупных компаний = (х + 7,4)%
Наконец, предположив, что историческое значение премии за акции мелких компаний будет соответствовать будущему значению, наша модель оценки доходности в сложных процентах акций мелких компаний будет следующей:
Доходность казначейских векселей = х%
Плюс премия за риск, связанный с акциями = +7,4%
Равно будущей доходности в сложных процентах акций крупных компаний = (х + 7,4)%
Плюс премия за акции мелких компаний = +1,2%
Равно будущей доходности в сложных процентах акций мелких компаний = (х + 8,6)%
Важно подчеркнуть, что эти модели основаны на долгосрочных исторических взаимосвязях между инвестиционными инструментами. Соответственно они отражают средние значения нескольких существенно отличающихся друг от друга подпериодов, в течение которых действительные результаты значительно отличались от того, что можно было бы вычислить с помощью этих моделей. Например, на рис. 2.4 видно, что кривая доходности обычно положительная, восходящая, но бывали периоды, когда она была плоской или отрицательной. В этом случае данные модели требуют корректировки[10].
Взаимосвязи, отраженные в этих моделях, очень важны и являются основой для объяснения клиенту инвестиционного риска и доходности. Они также дают хороший ориентир, который помогает клиентам сформировать более реалистичное ожидание относительно будущей эффективности инвестиций.
Выводы и пояснения
Клиенты часто ошибочно воспринимают риск, с которым они сталкиваются при инвестировании средств. Если это не исправить, высока вероятность, что решения относительно инвестиционного портфеля будут не в их пользу. Клиент, полностью понимающий суть инфляции, процентного риска, кредитного риска, риска, связанного с акциями, с гораздо большей вероятностью будет принимать разумные инвестиционные решения, наиболее соответствующие поставленным финансовым целям.
В табл. 3.1 дана краткая сводка эффективности рассмотренных нами основных инвестиционных инструментов[11]. В колонке «Среднегеометрическое» дается сравнение исторической годовой доходности в сложных процентах различных инструментов. Понятно, что в долгосрочной перспективе инвестирование в любые акции, например в обыкновенные, принесет больший доход, чем в облигации, и гораздо больший, чем в казначейские векселя. Соответственно, сравнивая стандартные отклонения, можно увидеть, что большая доходность связана с большей волатильностью.
Сравнивая доходность инвестиционных инструментов, клиенты часто удивляются, какое значение для накопления состояния имеет небольшая растущая доходность. Например, 1 долл., инвестированный в казначейские векселя с годовой доходностью в сложных процентах 3,8 %, к концу 1998 г. превратился в 14,94 долл. Для сравнения: 1 долл., инвестированный в акции крупных компаний, годовая доходность в сложных процентах которых всего на 7,4 % больше, за тот же период превратился в 2350,89 долл. Точно так же инвестирование 1 долл. в акции мелких компаний, годовая доходность которых всего на 1,2 % превышает доходность акций крупных компаний, дало поразительные результаты – 5116,65 долл. к концу 1998 г. Это наглядно демонстрирует «чудо сложных процентов».
Если вычисленная в сложных процентах годовая доходность разных инвестиционных инструментов различается незначительно, то разница в стандартных отклонениях доходности может быть огромной. Например, из табл. 3.1 видно, что казначейские векселя, историческая доходность которых была наименьшей, имели самое маленькое стандартное отклонение. Однако историческую изменчивость доходности казначейских векселей нельзя считать краткосрочным измерителем неопределенности доходности. Это обусловлено двумя причинами. Во-первых, средняя доходность казначейских векселей имела тенденцию к повышению в течение нескольких десятилетий начиная с 1930 г. и достигла пика в 1981 г. Эта долговременная тенденция повышения средней доходности казначейских векселей стала причиной более высоких отклонений относительно долгосрочной средней, чем относительно средней за более короткий период. В этом смысле долгосрочное стандартное отклонение казначейских векселей превышает их историческую краткосрочную волатильность. Во-вторых, можно полностью устранить краткосрочную неопределенность доходности, покупая векселя со сроком погашения один год и фиксируя таким образом доход. Поэтому нельзя считать долгосрочное стандартное отклонение казначейских векселей показателем краткосрочной волатильности.
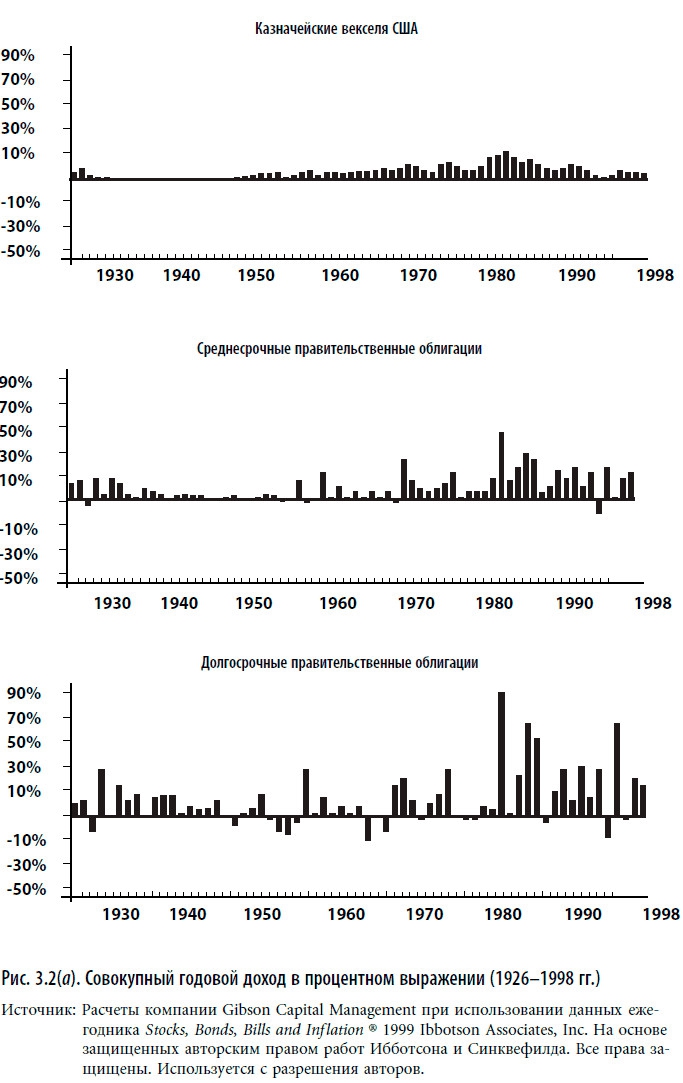
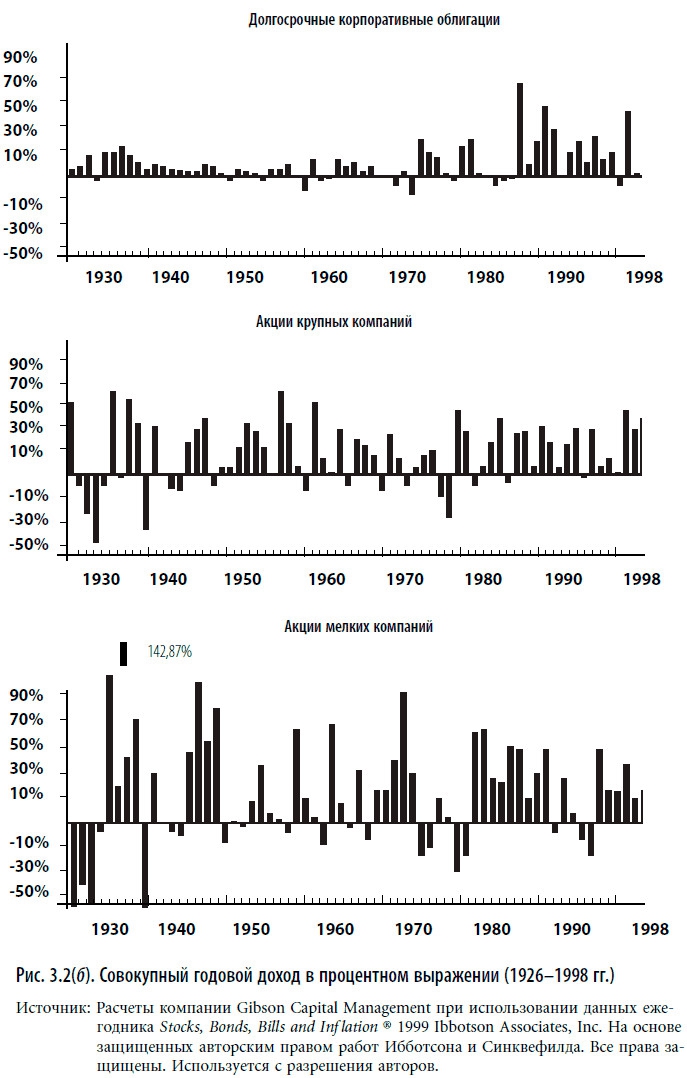
Хотя многие значения стандартного отклонения, представленные в табл. 3.1, позволяют сравнить относительную волатильность, прямое сравнение еще более удивительно. На рис. 3.2(а) и (б) даны профили совокупной годовой доходности различных инвестиционных инструментов в сравнении друг с другом в серии графиков с одинаковой вертикальной шкалой. Такой способ представления информации способствует лучшему пониманию относительной волатильности.
В табл. 3.1 стандартное отклонение совокупной доходности акций крупных компаний разбивается на компоненты: доход и прирост капитала. Интересно, что компонент «прирост капитала» имеет стандартное отклонение 19,6 % по сравнению с 1,4 % компонента «доход». Ясно, что изменчивость доходности акций крупных компаний почти полностью связана с изменением цен при относительно стабильном доходе от дивидендов.
Одно из возможных объяснений заключается в структуре дивидендной политики большинства корпораций. Прибыль компании из года в год меняется. Однако вместо того, чтобы менять размер дивидендов в зависимости от прибыли, корпорации стремятся установить размер дивидендов на таком уровне, чтобы их было удобно выплачивать из прибыли и в удачные, и в неудачные годы. Размер дивидендов обычно не уменьшают, кроме случаев, когда это абсолютно необходимо; увеличение возможно, только когда руководство компании уверено, что относительно постоянное увеличение прибыли компенсирует более высокие дивидендные выплаты[12]. В результате дивиденды выплачиваются стабильно, их размер постепенно увеличивается.
Из табл. 3.1 видно, что компонент «прирост капитала» доходности акций крупных компаний составляет 6,5 %. Это больше, чем совокупная доходность самого эффективного инструмента, генерирующего процентный доход, – долгосрочных корпоративных облигаций. По сути, исторически инвестирование в обыкновенные акции гарантировало долгосрочный прирост капитала, достаточный не только для поддержания, но и для увеличения его покупательной способности. Это позволяет использовать поток дивидендов на покрытие текущих жизненных расходов. Поскольку портфель обыкновенных акций может не отставать от уровня инфляции в среднем в долгосрочной перспективе, так же будет вести себя и поток дивидендов (выделено курсивом, потому что в краткосрочной перспективе более высокая волатильность обыкновенных акций приводит к значительной неопределенности годовой доходности). Поэтому краткосрочные и среднесрочные результаты могут существенно отличаться от «нормальных взаимосвязей», выявленных при исследовании эффективности в большие периоды времени.
Способность портфеля обыкновенных акций давать относительно стабильный растущий поток дивидендов важна для инвесторов, которые не хотят отставать от инфляции. Если бы 50-летняя женщина (см. табл. 2.1) вложила часть своих средств в акции, ее портфель не был бы так чувствителен к разрушительному влиянию инфляции.
Изучая табл. 3.1 вместе с клиентом, важно подчеркнуть, что доходность одного инвестиционного инструмента следует оценивать в сравнении с доходностью другого. Например, при сравнении годовой доходности в сложных процентах казначейских векселей (3,8 %) и акций крупных компаний (11,2 %) наиболее наглядным будет показатель спрэда между ними (7,4 %). Иногда взаимосвязь между ними ошибочно считают мультипликативной, т. е. неверно думать, что годовая доходность акций крупных компаний (11,2 %) в 2,9 раза больше, чем годовая доходность казначейских векселей (3,8 %). (Обзор моделей доходности ценных бумаг, которые мы разработали для каждого инвестиционного инструмента, отчетливо демонстрирует взаимосвязь в виде арифметической разницы, или спрэда.)
Подобная проблема возникает при рассмотрении доходности вне исторического контекста. В период с конца 1970-х до начала 1980-х процентные ставки были на уровне двузначных чисел. У клиентов часто возникал резонный вопрос: «Зачем мне вкладывать деньги в рискованные акции, чтобы получить годовой доход в сложных процентах в размере 11,2 %, если можно не рискуя получить 12 %, инвестируя в казначейские векселя?» В таком случае можно сказать, что доходность акций была 11,2 % в то время, когда доходность казначейских векселей находилась на уровне 3,8 % при среднем уровне инфляции 3,1 %. На основе разработанной нами модели оценки доходности обыкновенных акций можно утверждать, что, когда доходность казначейских векселей составляет 12 %, растущая доходность акций в сложных процентах равна 7,4 %, а совокупная доходность – 19,4 %[13].
В табл. 3.1 дана краткая сводка эффективности рассмотренных нами основных инвестиционных инструментов[11]. В колонке «Среднегеометрическое» дается сравнение исторической годовой доходности в сложных процентах различных инструментов. Понятно, что в долгосрочной перспективе инвестирование в любые акции, например в обыкновенные, принесет больший доход, чем в облигации, и гораздо больший, чем в казначейские векселя. Соответственно, сравнивая стандартные отклонения, можно увидеть, что большая доходность связана с большей волатильностью.
Сравнивая доходность инвестиционных инструментов, клиенты часто удивляются, какое значение для накопления состояния имеет небольшая растущая доходность. Например, 1 долл., инвестированный в казначейские векселя с годовой доходностью в сложных процентах 3,8 %, к концу 1998 г. превратился в 14,94 долл. Для сравнения: 1 долл., инвестированный в акции крупных компаний, годовая доходность в сложных процентах которых всего на 7,4 % больше, за тот же период превратился в 2350,89 долл. Точно так же инвестирование 1 долл. в акции мелких компаний, годовая доходность которых всего на 1,2 % превышает доходность акций крупных компаний, дало поразительные результаты – 5116,65 долл. к концу 1998 г. Это наглядно демонстрирует «чудо сложных процентов».
Если вычисленная в сложных процентах годовая доходность разных инвестиционных инструментов различается незначительно, то разница в стандартных отклонениях доходности может быть огромной. Например, из табл. 3.1 видно, что казначейские векселя, историческая доходность которых была наименьшей, имели самое маленькое стандартное отклонение. Однако историческую изменчивость доходности казначейских векселей нельзя считать краткосрочным измерителем неопределенности доходности. Это обусловлено двумя причинами. Во-первых, средняя доходность казначейских векселей имела тенденцию к повышению в течение нескольких десятилетий начиная с 1930 г. и достигла пика в 1981 г. Эта долговременная тенденция повышения средней доходности казначейских векселей стала причиной более высоких отклонений относительно долгосрочной средней, чем относительно средней за более короткий период. В этом смысле долгосрочное стандартное отклонение казначейских векселей превышает их историческую краткосрочную волатильность. Во-вторых, можно полностью устранить краткосрочную неопределенность доходности, покупая векселя со сроком погашения один год и фиксируя таким образом доход. Поэтому нельзя считать долгосрочное стандартное отклонение казначейских векселей показателем краткосрочной волатильности.
Хотя многие значения стандартного отклонения, представленные в табл. 3.1, позволяют сравнить относительную волатильность, прямое сравнение еще более удивительно. На рис. 3.2(а) и (б) даны профили совокупной годовой доходности различных инвестиционных инструментов в сравнении друг с другом в серии графиков с одинаковой вертикальной шкалой. Такой способ представления информации способствует лучшему пониманию относительной волатильности.
Одно из возможных объяснений заключается в структуре дивидендной политики большинства корпораций. Прибыль компании из года в год меняется. Однако вместо того, чтобы менять размер дивидендов в зависимости от прибыли, корпорации стремятся установить размер дивидендов на таком уровне, чтобы их было удобно выплачивать из прибыли и в удачные, и в неудачные годы. Размер дивидендов обычно не уменьшают, кроме случаев, когда это абсолютно необходимо; увеличение возможно, только когда руководство компании уверено, что относительно постоянное увеличение прибыли компенсирует более высокие дивидендные выплаты[12]. В результате дивиденды выплачиваются стабильно, их размер постепенно увеличивается.
Из табл. 3.1 видно, что компонент «прирост капитала» доходности акций крупных компаний составляет 6,5 %. Это больше, чем совокупная доходность самого эффективного инструмента, генерирующего процентный доход, – долгосрочных корпоративных облигаций. По сути, исторически инвестирование в обыкновенные акции гарантировало долгосрочный прирост капитала, достаточный не только для поддержания, но и для увеличения его покупательной способности. Это позволяет использовать поток дивидендов на покрытие текущих жизненных расходов. Поскольку портфель обыкновенных акций может не отставать от уровня инфляции в среднем в долгосрочной перспективе, так же будет вести себя и поток дивидендов (выделено курсивом, потому что в краткосрочной перспективе более высокая волатильность обыкновенных акций приводит к значительной неопределенности годовой доходности). Поэтому краткосрочные и среднесрочные результаты могут существенно отличаться от «нормальных взаимосвязей», выявленных при исследовании эффективности в большие периоды времени.
Способность портфеля обыкновенных акций давать относительно стабильный растущий поток дивидендов важна для инвесторов, которые не хотят отставать от инфляции. Если бы 50-летняя женщина (см. табл. 2.1) вложила часть своих средств в акции, ее портфель не был бы так чувствителен к разрушительному влиянию инфляции.
Изучая табл. 3.1 вместе с клиентом, важно подчеркнуть, что доходность одного инвестиционного инструмента следует оценивать в сравнении с доходностью другого. Например, при сравнении годовой доходности в сложных процентах казначейских векселей (3,8 %) и акций крупных компаний (11,2 %) наиболее наглядным будет показатель спрэда между ними (7,4 %). Иногда взаимосвязь между ними ошибочно считают мультипликативной, т. е. неверно думать, что годовая доходность акций крупных компаний (11,2 %) в 2,9 раза больше, чем годовая доходность казначейских векселей (3,8 %). (Обзор моделей доходности ценных бумаг, которые мы разработали для каждого инвестиционного инструмента, отчетливо демонстрирует взаимосвязь в виде арифметической разницы, или спрэда.)
Подобная проблема возникает при рассмотрении доходности вне исторического контекста. В период с конца 1970-х до начала 1980-х процентные ставки были на уровне двузначных чисел. У клиентов часто возникал резонный вопрос: «Зачем мне вкладывать деньги в рискованные акции, чтобы получить годовой доход в сложных процентах в размере 11,2 %, если можно не рискуя получить 12 %, инвестируя в казначейские векселя?» В таком случае можно сказать, что доходность акций была 11,2 % в то время, когда доходность казначейских векселей находилась на уровне 3,8 % при среднем уровне инфляции 3,1 %. На основе разработанной нами модели оценки доходности обыкновенных акций можно утверждать, что, когда доходность казначейских векселей составляет 12 %, растущая доходность акций в сложных процентах равна 7,4 %, а совокупная доходность – 19,4 %[13].
Приложение. Статистические понятия
Среднегеометрическое и среднеарифметическое
В первой колонке табл. 3.1 приведены среднегеометрические значения, или годовая доходность в сложных процентах. Среднеарифметическое, показанное во второй колонке, означает простое среднее значение доходности серии.
Проиллюстрируем различия на примере. Предположим, мы инвестируем 100 долл. в акции, которые в течение первого года превращаются в 125 долл., имея совокупную доходность +25 %. За второй год доходность акций составила –20 %, как следствие, капитал уменьшился со 125 долл. США до 100 долл. Чтобы получить среднеарифметическое доходности этих двух годов, нужно разделить их сумму на 2:
Доходность первого года = +25%
Доходность второго года = –20%
Сумма = +5%
Среднеарифметическое = Сумма: 2 = 2,5%
Однако среднегеометрическое (годовая доходность в сложных процентах) будет равно 0, т. е. если изначально было инвестировано 100 долл. и через два года капитал остался равен 100 долл., то среднегеометрическое доходности составит 0. Для любых серий чисел среднеарифметическое всегда будет выше, чем среднегеометрическое, или равно ему. Разница между средним арифметическим и средним геометрическим будет больше в серии значительно изменяющихся чисел. Только в случае, когда числа в серии будут постоянными, среднеарифметическое и среднегеометрическое будут равны. Неравенство этих двух измерений следует из того, что для покрытия эффективности ниже средней эффективность выше средней должна быть больше в процентном выражении.
Среднеарифметическое подходит для измерения типичного результата за один период времени. Среднегеометрическое больше подходит для сравнения доходности нескольких временных периодов, поскольку отражает уровень роста инвестиций в сложных процентах. Часто модели доходности различных инвестиционных инструментов являются моделями одного временного периода, включающими среднеарифметическое[14]. Поскольку целью данной главы является разработка структуры для определения долгосрочной инвестиционной политики (на несколько периодов), для сравнения относительной исторической эффективности и моделей доходности будущих инвестиций будет использоваться среднегеометрическое (годовая доходность в сложных процентах).
Премии за риски и доходность с поправкой на инфляцию
В данной книге для вычисления премий за риски или доходности с поправкой на инфляцию среднегеометрическое одного инвестиционного инструмента арифметически вычитается из среднего геометрического другого инструмента или из уровня инфляции. Например, если вычесть среднегеометрическое акций крупных компаний (11,2 %) из среднего геометрического казначейских векселей (3,8 %), премия за риск, связанный с акциями, составит 7,4 %. Компания Ibbotson Associates, предоставившая исторические данные доходности казначейских векселей, облигаций и акций, используемые в настоящей книге, предпочитает определять премии за риски и доходность с поправкой на инфляцию как геометрическую разность различных серий доходности. Например, геометрическая разность между 5 и 12 % будет равна не 7 %, а 6,7 %. Вычисления выглядят следующим образом:
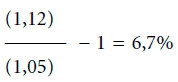Модели, разработанные в настоящей книге, помогут понять инвестиционную эффективность и консультанту, и клиенту. При разработке моделей использовалась арифметическая, а не геометрическая разность, чтобы клиенту было легче следить за ходом рассуждений. (Большинство людей считает, что разница между 5 и 12 % будет равна 7 %, а не 6,7 %.) Такой упрощенный подход не уменьшает концептуальной значимости модели, но позволяет избежать трудностей при объяснении различий между геометрической и арифметической разницей.
Ожидаемая доходность и стандартное отклонение
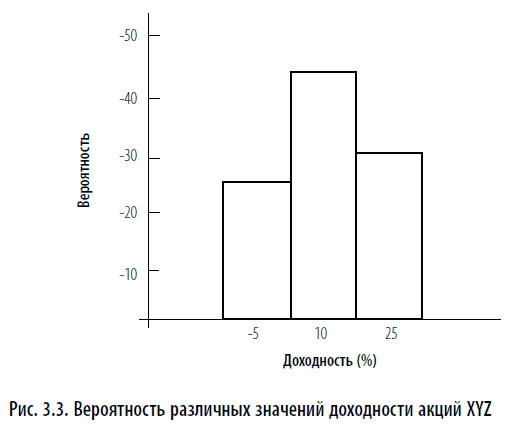
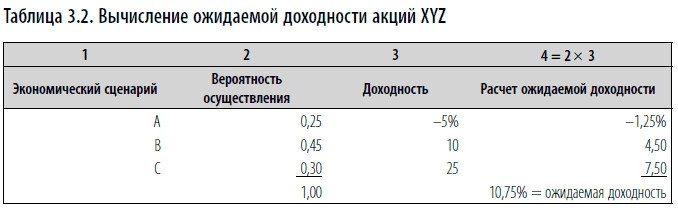
Ожидаемая доходность инвестиций вычисляется как средневзвешенное возможных доходностей, где весом является соответствующая вероятность доходности. Таким образом, в одной статистике учитывается и размер каждой возможной доходности, и ее вероятность. Например, рис. 3.3 показывает эффективность инвестирования в акции XYZ, которые в зависимости от трех возможных экономических сценариев будут иметь доходность –5 %, 10 % или 25 %. Вероятность развития каждого из экономических сценариев можно выразить в десятичных дробях. Например, сценарий А имеет вероятность осуществления 25 %, поэтому ему соответствует вероятность 0,25. В табл. 3.2 показан математический расчет ожидаемой доходности инвестиции в акции XYZ, составляющей 10,75 %.
Инвестиционные инструменты различаются по ожидаемой доходности, но это только одна сторона будущей эффективности. Также важно учитывать волатильность инвестиций. Чем больше доходность инвестиций может отличаться от ожидаемой, тем больше ее волатильность. Для измерения волатильности обычно используют стандартное отклонение. Для его вычисления необходимо вычесть ожидаемую доходность из каждой возможной доходности. Данные отклонения затем возводят в квадрат и умножают на соответствующие им вероятности, после чего результаты складывают. Полученная сумма называется дисперсией (среднеквадратичным отклонением, средневзвешенным по вероятности). Стандартное отклонение получается путем извлечения квадратного корня из дисперсии. В нашем примере стандартное отклонение доходности составляет 11,1 и рассчитывается, как показано в табл. 3.3.
Распределение вероятности
В реальной жизни возможные доходности инвестиций обычно нельзя строго разделить на три возможности, как в предыдущем примере. Скорее ряд возможных значений доходности образует бесконечную кривую, или распределение вероятности, подобное тому, что изображено на рис. 3.4. Поскольку распределение доходности непрерывно, вероятности описываются для различных групп результатов. Например, вероятность того, что доходность акций АВС составит от 5 % до 10 %, можно определить, подсчитав площадь под кривой, ограниченную с боков вертикалями, опущенными к значениям горизонтальной оси 5 % и 10 %. Если, например, площадь области, закрашенной черным, составляет 9 % от площади всей области под кривой, тогда вероятность, что доходность акций АВС будет от 5 % до 10 %, равна 9 % (или 0,09).
В первой колонке табл. 3.1 приведены среднегеометрические значения, или годовая доходность в сложных процентах. Среднеарифметическое, показанное во второй колонке, означает простое среднее значение доходности серии.
Проиллюстрируем различия на примере. Предположим, мы инвестируем 100 долл. в акции, которые в течение первого года превращаются в 125 долл., имея совокупную доходность +25 %. За второй год доходность акций составила –20 %, как следствие, капитал уменьшился со 125 долл. США до 100 долл. Чтобы получить среднеарифметическое доходности этих двух годов, нужно разделить их сумму на 2:
Доходность первого года = +25%
Доходность второго года = –20%
Сумма = +5%
Среднеарифметическое = Сумма: 2 = 2,5%
Однако среднегеометрическое (годовая доходность в сложных процентах) будет равно 0, т. е. если изначально было инвестировано 100 долл. и через два года капитал остался равен 100 долл., то среднегеометрическое доходности составит 0. Для любых серий чисел среднеарифметическое всегда будет выше, чем среднегеометрическое, или равно ему. Разница между средним арифметическим и средним геометрическим будет больше в серии значительно изменяющихся чисел. Только в случае, когда числа в серии будут постоянными, среднеарифметическое и среднегеометрическое будут равны. Неравенство этих двух измерений следует из того, что для покрытия эффективности ниже средней эффективность выше средней должна быть больше в процентном выражении.
Среднеарифметическое подходит для измерения типичного результата за один период времени. Среднегеометрическое больше подходит для сравнения доходности нескольких временных периодов, поскольку отражает уровень роста инвестиций в сложных процентах. Часто модели доходности различных инвестиционных инструментов являются моделями одного временного периода, включающими среднеарифметическое[14]. Поскольку целью данной главы является разработка структуры для определения долгосрочной инвестиционной политики (на несколько периодов), для сравнения относительной исторической эффективности и моделей доходности будущих инвестиций будет использоваться среднегеометрическое (годовая доходность в сложных процентах).
Премии за риски и доходность с поправкой на инфляцию
В данной книге для вычисления премий за риски или доходности с поправкой на инфляцию среднегеометрическое одного инвестиционного инструмента арифметически вычитается из среднего геометрического другого инструмента или из уровня инфляции. Например, если вычесть среднегеометрическое акций крупных компаний (11,2 %) из среднего геометрического казначейских векселей (3,8 %), премия за риск, связанный с акциями, составит 7,4 %. Компания Ibbotson Associates, предоставившая исторические данные доходности казначейских векселей, облигаций и акций, используемые в настоящей книге, предпочитает определять премии за риски и доходность с поправкой на инфляцию как геометрическую разность различных серий доходности. Например, геометрическая разность между 5 и 12 % будет равна не 7 %, а 6,7 %. Вычисления выглядят следующим образом:
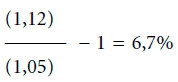
Ожидаемая доходность и стандартное отклонение
Ожидаемая доходность инвестиций вычисляется как средневзвешенное возможных доходностей, где весом является соответствующая вероятность доходности. Таким образом, в одной статистике учитывается и размер каждой возможной доходности, и ее вероятность. Например, рис. 3.3 показывает эффективность инвестирования в акции XYZ, которые в зависимости от трех возможных экономических сценариев будут иметь доходность –5 %, 10 % или 25 %. Вероятность развития каждого из экономических сценариев можно выразить в десятичных дробях. Например, сценарий А имеет вероятность осуществления 25 %, поэтому ему соответствует вероятность 0,25. В табл. 3.2 показан математический расчет ожидаемой доходности инвестиции в акции XYZ, составляющей 10,75 %.
Распределение вероятности
В реальной жизни возможные доходности инвестиций обычно нельзя строго разделить на три возможности, как в предыдущем примере. Скорее ряд возможных значений доходности образует бесконечную кривую, или распределение вероятности, подобное тому, что изображено на рис. 3.4. Поскольку распределение доходности непрерывно, вероятности описываются для различных групп результатов. Например, вероятность того, что доходность акций АВС составит от 5 % до 10 %, можно определить, подсчитав площадь под кривой, ограниченную с боков вертикалями, опущенными к значениям горизонтальной оси 5 % и 10 %. Если, например, площадь области, закрашенной черным, составляет 9 % от площади всей области под кривой, тогда вероятность, что доходность акций АВС будет от 5 % до 10 %, равна 9 % (или 0,09).
Конец бесплатного ознакомительного фрагмента