В общем виде математическая постановка экстремальной задачи состоит в определении наибольшего или наименьшего значения целевой функции f (x1, x2,…, xj…, xn) при условиях gj (x1, x2…, xj…, xn) ≤ b (i = 1… m), где f, g i – заданные функции; xj(j = 1… n) – искомь 2 е переменные; bj (i = 1… m) – некоторые действительные числа.
В зависимости от свойств функций f и gi экономико-математические методы рассматривают как ряд самостоятельных разделов, изучающих методы решения определенных классов задач.
Прежде всего экономико-математические методы подразделяют на методы решения задач линейного и нелинейного программирования. При этом если все функции f и gi – линейные или не содержат произведения искомых переменных, то соответствующая задача – это задача линейного программирования.
Если хотя бы одна из этих функций – нелинейная или содержит произведения искомых переменных, то соответствующая задача – это задача нелинейного программирования. Среди них наиболее изучены задачи выпуклого программирования, в результате решения которых определяют минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом замкнутом множестве.
Из задач выпуклого программирования подробно разработаны задачи квадратичного программирования, в которых требуется найти максимум (или минимум) квадратичной функции при условии, что ее переменные удовлетворяют некоторой системе линейных уравнений.
Отдельные разделы экономико-математических методов изучают методы решения задач целочисленного, параметрического, дробно-линейного программирования.
В задачах целочисленного программирования неизвестные могут принимать только целочисленные значения.
В задачах параметрического программирования целевая функция и/или функции, определяющие область возможных изменений переменных, зависят от некоторых параметров.
В задачах дробно-линейного программирования целевая функция – это отношение двух линейных функций, а функции, определяющие область возможных изменений переменных, линейны.
7.2. Однопродуктовая модель
7.3. Основная производственная задача Л. В. Канторовича
7.4. Модель развития экономики (модель Харрода)
7.5. Распределение ресурсов
7.6. Формирование производственной программы
7.7. Задача о назначениях
7.8. Транспортная задача
7.9. Задача составления смесей
7.10. Задача о ранце
7.11. Задача коммивояжера
7.12. Распределение капитальных вложений
7.13. Игровая модель обмена товарами (модель Эджворта)
Глава 8
8.1. Регрессионный анализ
В зависимости от свойств функций f и gi экономико-математические методы рассматривают как ряд самостоятельных разделов, изучающих методы решения определенных классов задач.
Прежде всего экономико-математические методы подразделяют на методы решения задач линейного и нелинейного программирования. При этом если все функции f и gi – линейные или не содержат произведения искомых переменных, то соответствующая задача – это задача линейного программирования.
Если хотя бы одна из этих функций – нелинейная или содержит произведения искомых переменных, то соответствующая задача – это задача нелинейного программирования. Среди них наиболее изучены задачи выпуклого программирования, в результате решения которых определяют минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом замкнутом множестве.
Из задач выпуклого программирования подробно разработаны задачи квадратичного программирования, в которых требуется найти максимум (или минимум) квадратичной функции при условии, что ее переменные удовлетворяют некоторой системе линейных уравнений.
Отдельные разделы экономико-математических методов изучают методы решения задач целочисленного, параметрического, дробно-линейного программирования.
В задачах целочисленного программирования неизвестные могут принимать только целочисленные значения.
В задачах параметрического программирования целевая функция и/или функции, определяющие область возможных изменений переменных, зависят от некоторых параметров.
В задачах дробно-линейного программирования целевая функция – это отношение двух линейных функций, а функции, определяющие область возможных изменений переменных, линейны.
7.2. Однопродуктовая модель
Однопродуктовая модель предназначена для оптимизации распределения объемов производства по способам производства. Постановка задачи может выполняться с различными экономическими оценками.
Определяемые величины обозначим через x (i) – величина планируемого производства продукции по i – му способу производства.
Основное ограничение предусматривает необходимость выполнения общего плана производства:
x (1) + x (2) +… + x (n) = V.
Здесь n – число способов производства, V – общий план производства. Каждая из величин x (i) должна быть больше нулялибо равна нулю:
x (i) > 0.
Оптимизационная оценка вариантов решения задачи имеет вид
f(x (1)) + f(x (2)) +… + f(x (n)).
Способ решения задачи зависит от вида функции f. При линейной функции методом решения будет линейное программирование, при нелинейной функции – возможно привлечение метода множителей Лагранжа либо динамического программирования.
Определяемые величины обозначим через x (i) – величина планируемого производства продукции по i – му способу производства.
Основное ограничение предусматривает необходимость выполнения общего плана производства:
x (1) + x (2) +… + x (n) = V.
Здесь n – число способов производства, V – общий план производства. Каждая из величин x (i) должна быть больше нулялибо равна нулю:
x (i) > 0.
Оптимизационная оценка вариантов решения задачи имеет вид
f(x (1)) + f(x (2)) +… + f(x (n)).
Способ решения задачи зависит от вида функции f. При линейной функции методом решения будет линейное программирование, при нелинейной функции – возможно привлечение метода множителей Лагранжа либо динамического программирования.
7.3. Основная производственная задача Л. В. Канторовича
Одна из первых математических моделей была разработана в 1939 г. Л. В. Канторовичем. Пусть имеется некий производственный процесс, предназначенный для выпуска n видов продукции. По каждому из видов продукции заданы ограничения на объем выпуска и нормы расхода привлекаемых ресурсов. Поставка продукции потребителю осуществляется комплектами, и поэтому требуется сформировать плановый ассортимент выпуска продукции, обеспечивающий максимальное число комплектов поставки продукции.
Формализуя математическую постановку задачи, введем следующие ограничения:
x(i) > 0;
a(s,1)x(1) + a(s,2)x(2) +… + a(s,n)x(n) ‹V(s).
Оптимизационная оценка имеет вид

Здесь k(i) – количество единиц i – го продукта в комплекте. Решается задача методом линейного программирования, который фактически и появился как алгоритм решения этой математической задачи в 1939 г.
Формализуя математическую постановку задачи, введем следующие ограничения:
x(i) > 0;
a(s,1)x(1) + a(s,2)x(2) +… + a(s,n)x(n) ‹V(s).
Оптимизационная оценка имеет вид

Здесь k(i) – количество единиц i – го продукта в комплекте. Решается задача методом линейного программирования, который фактически и появился как алгоритм решения этой математической задачи в 1939 г.
7.4. Модель развития экономики (модель Харрода)
Одна из первых упрощенных моделей развития экономики страны была предложена английским экономистом Р. Харродом. В модели учитывается один определяемый фактор – капитальные вложения, а состояние экономики оценивается через размер национального дохода.
Для математической постановки задачи введем следующие обозначения:
y (t) – национальный доход в год t;
k (t) – производственные фонды в год t;
c (t) – объем потребления в год t;
s (t) – объем накопления в год t;
ν (t) – капитальные вложения в год t.
Будем предполагать, что функционирование экономики происходит при выполнении следующих условий:
y (t) = c (t) + s (t) – условие баланса доходов и расходов за каждый год;
s (t) = v (t) – условие исключения пролеживания капитала;
s (t) = ay (t) – условие пропорционального деления национального годового дохода.
Два условия принимаются для характеристики внутренних экономических процессов. Первое условие характеризует связь капитальных вложений и общей суммы производственных фондов, второе – связь национального годового дохода и производственных фондов. Капитальные вложения в год t могут рассматриваться как прирост производственных фондов или производная от функции, «производственные фонды» принимаются как капитальные годовые вложения:
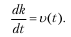
Национальный доход в каждый год принимается как отдача производственных фондов с соответствующим нормативным коэффициентом фондоотдачи:

Соединяя условия задачи, можно получить следующее соотношение:

Отсюда следует итоговое уравнение Харрода:

Его решением является экспоненциальное изменение национального дохода по годовым интервалам:
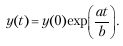
Несмотря на упрощенный вид математической модели, ее результат может быть использован для укрупненного анализа национальной экономики. Параметры a и b могут стать параметрами управления при выборе плановой стратегии развития с целью максимального приближения к предпочтительной траектории изменения национального дохода или для выбора минимального интервала времени достижения заданного уровня национального дохода.
Для математической постановки задачи введем следующие обозначения:
y (t) – национальный доход в год t;
k (t) – производственные фонды в год t;
c (t) – объем потребления в год t;
s (t) – объем накопления в год t;
ν (t) – капитальные вложения в год t.
Будем предполагать, что функционирование экономики происходит при выполнении следующих условий:
y (t) = c (t) + s (t) – условие баланса доходов и расходов за каждый год;
s (t) = v (t) – условие исключения пролеживания капитала;
s (t) = ay (t) – условие пропорционального деления национального годового дохода.
Два условия принимаются для характеристики внутренних экономических процессов. Первое условие характеризует связь капитальных вложений и общей суммы производственных фондов, второе – связь национального годового дохода и производственных фондов. Капитальные вложения в год t могут рассматриваться как прирост производственных фондов или производная от функции, «производственные фонды» принимаются как капитальные годовые вложения:
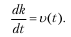
Национальный доход в каждый год принимается как отдача производственных фондов с соответствующим нормативным коэффициентом фондоотдачи:

Соединяя условия задачи, можно получить следующее соотношение:

Отсюда следует итоговое уравнение Харрода:

Его решением является экспоненциальное изменение национального дохода по годовым интервалам:
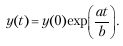
Несмотря на упрощенный вид математической модели, ее результат может быть использован для укрупненного анализа национальной экономики. Параметры a и b могут стать параметрами управления при выборе плановой стратегии развития с целью максимального приближения к предпочтительной траектории изменения национального дохода или для выбора минимального интервала времени достижения заданного уровня национального дохода.
7.5. Распределение ресурсов
Пусть имеется m видов ресурсов, каждый i – й ресурс в количестве bi(i = 1… m). Эти ресурсы нужно использовать для n видов продукции. Для выпуска единицы j – го вида продукции необходимо aij единиц i – го вида ресурса. Требуется определить, сколько каждого вида продукции следует произвести, чтобы такой выпуск был наилучшим для принятого критерия оптимальности.
В реальных задачах суммарное количество основных xj(j = 1… n) и дополнительных yi (i = 1… m) переменных всегда больше, чем число зависимостей m, поэтому система (1) ограничений имеет бесчисленное множество решений. Из этого бесчисленного множества следует выбрать одно – оптимальное, соответствующее критерию – цели решения задачи.
Цель задачи распределения ресурсов определяется какой-либо одной из двух взаимоисключающих постановок:
1. При заданных ресурсах максимизировать получаемый результат.
2. При заданном результате минимизировать потребные ресурсы.
Первая постановка аналитически будет сформулирована следующим образом:

где xj – количество выпускаемой продукции j – го вида – искомая переменная (j = = 1… n); n – количество наименований продукции; с. – величина, показывающая, какой вклад в результат дает единица продукции j – го вида; bi – заданное количество ресурса i – го вида (i = 1… m); m – количество наименований ресурсов; aij – норма расхода ресурса, т. е. количество ресурса i – го вида, потребляемого на производство единицы j – го вида продукции.
Решение задачи (1) дает нахождение таких значений xj, которые обеспечивают при заданных ресурсах получение максимального результата.
Вторая постановка задачи будет иметь вид:
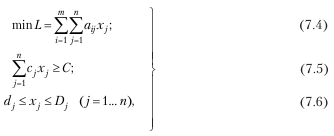
где C – минимально допустимое значение потребного результата.
Совместимость ограничивающих условий В общую постановку задачи оптимизации входят неравенства вида
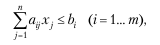
где n – число неизвестных; m – число неравенств.
Если в каждое неравенство добавить неотрицательное неизвестное y ≥ 0 (i = 1… m), то от системы неравенств можно перейти к системе уравнений
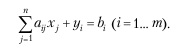
В этой системе общее число неизвестных N = n + m, где n – число основных неизвестных xj; m – число дополнительных неизвестных yi, которое равно числу уравнений.
Возможны три варианта соотношения величин N и m.
1. Число неизвестных меньше, чем число уравнений: N < m. Например, N = 1, m = 2.
Очевидно, эта система решения не имеет, т. е. нет таких значений x 1, которые бы удовлетворяли обоим уравнениям. В этом случае говорят, что система условий несовместна. Значит, если число неизвестных N меньше числа уравнений m, то система решения не имеет и является несовместной.
2. Число неизвестных равно числу уравнений: N = m.
Например, нетрудно вычислить, что решением этой системы будут значения x1 = 2, x2 = 1. Таким образом, линейная система, в которой число неизвестных N равно числу уравнений m, имеет одно решение.
3. Число неизвестных больше числа уравнений: N > m.
Например, 2x1 + x2 = 2. Очевидно, что все значения x1 и x2, лежащие на прямой этого уравнения, являются его решением. Если в системе число неизвестных N больше числа уравнений m, то такая система имеет бесчисленное множество решений.
В реальных задачах суммарное количество основных xj(j = 1… n) и дополнительных yi (i = 1… m) переменных всегда больше, чем число зависимостей m, поэтому система (1) ограничений имеет бесчисленное множество решений. Из этого бесчисленного множества следует выбрать одно – оптимальное, соответствующее критерию – цели решения задачи.
Цель задачи распределения ресурсов определяется какой-либо одной из двух взаимоисключающих постановок:
1. При заданных ресурсах максимизировать получаемый результат.
2. При заданном результате минимизировать потребные ресурсы.
Первая постановка аналитически будет сформулирована следующим образом:

где xj – количество выпускаемой продукции j – го вида – искомая переменная (j = = 1… n); n – количество наименований продукции; с. – величина, показывающая, какой вклад в результат дает единица продукции j – го вида; bi – заданное количество ресурса i – го вида (i = 1… m); m – количество наименований ресурсов; aij – норма расхода ресурса, т. е. количество ресурса i – го вида, потребляемого на производство единицы j – го вида продукции.
Решение задачи (1) дает нахождение таких значений xj, которые обеспечивают при заданных ресурсах получение максимального результата.
Вторая постановка задачи будет иметь вид:
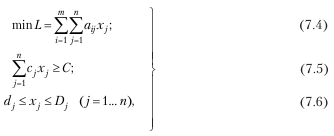
где C – минимально допустимое значение потребного результата.
Совместимость ограничивающих условий В общую постановку задачи оптимизации входят неравенства вида
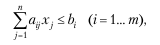
где n – число неизвестных; m – число неравенств.
Если в каждое неравенство добавить неотрицательное неизвестное y ≥ 0 (i = 1… m), то от системы неравенств можно перейти к системе уравнений
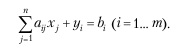
В этой системе общее число неизвестных N = n + m, где n – число основных неизвестных xj; m – число дополнительных неизвестных yi, которое равно числу уравнений.
Возможны три варианта соотношения величин N и m.
1. Число неизвестных меньше, чем число уравнений: N < m. Например, N = 1, m = 2.
Очевидно, эта система решения не имеет, т. е. нет таких значений x 1, которые бы удовлетворяли обоим уравнениям. В этом случае говорят, что система условий несовместна. Значит, если число неизвестных N меньше числа уравнений m, то система решения не имеет и является несовместной.
2. Число неизвестных равно числу уравнений: N = m.
Например, нетрудно вычислить, что решением этой системы будут значения x1 = 2, x2 = 1. Таким образом, линейная система, в которой число неизвестных N равно числу уравнений m, имеет одно решение.
3. Число неизвестных больше числа уравнений: N > m.
Например, 2x1 + x2 = 2. Очевидно, что все значения x1 и x2, лежащие на прямой этого уравнения, являются его решением. Если в системе число неизвестных N больше числа уравнений m, то такая система имеет бесчисленное множество решений.
7.6. Формирование производственной программы
Рассмотрим производственный участок, выпускающий два типа деталей. Исходная заготовка при изготовлении деталей первого типа проходит две операции (токарную и сверлильную) при трудоемкости 20 и 30 ч/шт. соответственно. При изготовлении детали второго типа необходимы три операции (токарная, сверлильная, шлифовальная) при трудоемкости 40, 30, 20 ч/шт. соответственно. Прибыль от продажи деталей равна 1,5 руб./шт. для деталей первого типа и 1 руб./шт. для деталей второго типа.
На плановый период ресурс рабочего времени по операциям в часах составляет: токарная – 1000, сверлильная – 900, шлифовальная – 400 ч. Необходимо подобрать производственную программу выпуска деталей, обеспечивающую максимальную прибыль.
Обозначим количество деталей первого типа, принимаемых для выпуска, через y, второго типа – х. Математическая постановка задачи определения у и х имеет вид
40 х + 20 у = 1000;
30 х + 30 у = 900;
20 х = 400;
х > 0, y > 0;
J = 1,5 y + 1 x → max.
На плановый период ресурс рабочего времени по операциям в часах составляет: токарная – 1000, сверлильная – 900, шлифовальная – 400 ч. Необходимо подобрать производственную программу выпуска деталей, обеспечивающую максимальную прибыль.
Обозначим количество деталей первого типа, принимаемых для выпуска, через y, второго типа – х. Математическая постановка задачи определения у и х имеет вид
40 х + 20 у = 1000;
30 х + 30 у = 900;
20 х = 400;
х > 0, y > 0;
J = 1,5 y + 1 x → max.
7.7. Задача о назначениях
Пусть имеются n работ и n кандидатов для их выполнения. Назначению i – го кандидата (i = 1… n) на j – ю работу (j = 1… n) соответствуют определенная эффективность (прибыль, производительность) или затраты какого-либо ресурса Требуется назначить на выполнение всех видов работ таких кандидатов, которые обеспечат наибольшую эффективность, т. е. минимум суммарных затрат или максимум прибыли (производительности). Каждого кандидата можно назначить только на одну должность, и каждая работа может быть выполнена только одним кандидатом.
Математическая постановка задачи имеет вид:
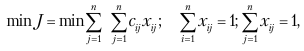
где xj – искомая переменная: Xj = 1, если i – й кандидат распределяется на j – ю работу; 0 – в противном случае.
В такой постановке данная задача относится к классу комбинаторных.
Математическая постановка задачи имеет вид:
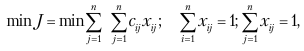
где xj – искомая переменная: Xj = 1, если i – й кандидат распределяется на j – ю работу; 0 – в противном случае.
В такой постановке данная задача относится к классу комбинаторных.
7.8. Транспортная задача
Транспортная задача – это задача о выборе плана перевозок однородного продукта из пунктов производства в пункты потребления. Пусть имеется m пунктов отправления и n пунктов назначения. Ресурсы продукта в пунктах отправления обозначим через a (i), потребность в продукте в пункте потребления – b (j). Расходы на доставку единицы продукта от поставщика i к потребителю j равняются c (i, j). Балансовое условие производства и потребления имеет вид:
a (1) + a (2) +… + a (n) = b (1) + b (2) +… + b (m).
Требуется определить x (i, j) – количество продукта, доставляемое от пункта производства i к пункту потребления j. Обязательными условиями являются:
необходимость вывоза всего произведенного продукта:
x(i, 1) + x(i, 2) +… + x (i, m) = a(i) для всех значений i;
необходимость удовлетворения всех потребителей:
x (1, j) + x (2, j) +.·· + x (n, j) = b (j) для всех значений j.
Оптимальный план доставки продукта должен обеспечить минимум общей суммы затрат на доставку:
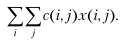
Решаются транспортные задачи методами линейного программирования.
a (1) + a (2) +… + a (n) = b (1) + b (2) +… + b (m).
Требуется определить x (i, j) – количество продукта, доставляемое от пункта производства i к пункту потребления j. Обязательными условиями являются:
необходимость вывоза всего произведенного продукта:
x(i, 1) + x(i, 2) +… + x (i, m) = a(i) для всех значений i;
необходимость удовлетворения всех потребителей:
x (1, j) + x (2, j) +.·· + x (n, j) = b (j) для всех значений j.
Оптимальный план доставки продукта должен обеспечить минимум общей суммы затрат на доставку:
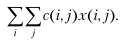
Решаются транспортные задачи методами линейного программирования.
7.9. Задача составления смесей
Задачи составления рациона корма, состава шихты при выплавке стали, состава цементной смеси относятся к группе задач составления смесей. В такой задаче задается набор исходных материалов, характеризующихся содержанием контролируемых компонентов а(i,j) – содержание i – го компонента в j – м виде исходного материала.
Требуется определить x (j) – количество j – го материала, принимаемого для подготовки комплексной смеси. Совокупность ограничений включает условия вида:
x (j) < X (j);
x (1) + x (2) +… + x(n) < Y;
a(i, 1) x (1) + a(i, 2) x (2) +… + a(i, n) x(n) > A(i).
Здесь X (j) – допустимое для использования количество j – го материала, Y – общее ограничение на массу исходного материала, A (i) – минимально необходимое содержание i – го компонента в конечном продукте.
Оценкой вариантов решения задачи является сумма затрат на состав материалов в формируемой смеси:
J = c (1) x (1) + c (2) x (2) +… + c (n) x (n),
где c (j) – расходы на единицу j – го материала.
Требуется определить x (j) – количество j – го материала, принимаемого для подготовки комплексной смеси. Совокупность ограничений включает условия вида:
x (j) < X (j);
x (1) + x (2) +… + x(n) < Y;
a(i, 1) x (1) + a(i, 2) x (2) +… + a(i, n) x(n) > A(i).
Здесь X (j) – допустимое для использования количество j – го материала, Y – общее ограничение на массу исходного материала, A (i) – минимально необходимое содержание i – го компонента в конечном продукте.
Оценкой вариантов решения задачи является сумма затрат на состав материалов в формируемой смеси:
J = c (1) x (1) + c (2) x (2) +… + c (n) x (n),
где c (j) – расходы на единицу j – го материала.
7.10. Задача о ранце
Пусть имеется некоторый объем V, который необходимо заполнить различными предметами. Предметов имеется несколько видов, отличающихся объемом v (i) и ценностью c (i).
Требуется определить вариант заполнения предметами объема V, чтобы их суммарная ценность оказалась наибольшей. Неизвестные переменные задачи – это x (i) – число предметов i – го вида, выбранных для размещения в ранце. Ограничения задачи имеют вид:
x (1) v (1) + x (2) v (2) +… + x (n) v (n) < V;
x (i) > 0.
Оценка вариантов решения задачи – это сумма
J = x (1) c (1) + x (2) c (2) +… + x (n) c (n),
которая должна иметь максимальное значение.
Требуется определить вариант заполнения предметами объема V, чтобы их суммарная ценность оказалась наибольшей. Неизвестные переменные задачи – это x (i) – число предметов i – го вида, выбранных для размещения в ранце. Ограничения задачи имеют вид:
x (1) v (1) + x (2) v (2) +… + x (n) v (n) < V;
x (i) > 0.
Оценка вариантов решения задачи – это сумма
J = x (1) c (1) + x (2) c (2) +… + x (n) c (n),
которая должна иметь максимальное значение.
7.11. Задача коммивояжера
Обычно эта задача формулируется следующим образом. Коммивояжер должен побывать в ряде городов. Известны расстояния между каждой парой городов (время или стоимость проезда). Необходимо выбрать кратчайший маршрут, проходящий один раз через каждый город. Если расстояние между городами не зависит от направления движения, то задача называется симметричной. Если стоимость проезда меняется при изменении направления движения, задача называется несимметричной.
Для задачи коммивояжера при необходимости посещения только двух городов выбора нет. При посещении трех городов и заданном начальном пункте возможны 2 маршрута. Если городов четыре, то имеется 6 маршрутов, а при одиннадцати городах – более 3,5 млн допустимых маршрутов. В общем случае при n городах имеется (n -1)! маршрутов.
К подобному типу задач сводится множество реальных ситуаций. Например, выбор очередности обработки разнородных изделий, маршрута автотранспорта, задачи выбора маршрута в сетях систем связи.
Пример. Пусть имеется 5 пунктов, соединенных между собой дорогами так, что из любого пункта можно проехать в любой другой пункт. Известно время перевозки из пункта i в пункт j (табл. 7.1).
Таблица 7.1
Время переезда, ед.

Требуется найти маршрут с наименьшей продолжительностью, начинающийся в данном пункте, проходящий через все пункты и заканчивающийся в пункте выезда.
Решение. Введем обозначения: i и j – номера пунктов выезда и въезда; t. – время переезда из пункта i в пункт j. В общем случае tij может быть не равно времени переезда в обратном направлении
– tij ≠ tji (например, когда один пункт на вершине горы, а другой – у ее подножия). Введем булевы переменные:

Составим модель (рис. 7.1). Из пункта 1 можно выехать в любой из пунктов: 2, или 5, или 3, или 4, или остаться в пункте 1. Но при этом можно выехать только в одном-единственном направлении. Это условие можно записать так:
δ11 + δ12 + δ13 + δ14 + δ15 = 1
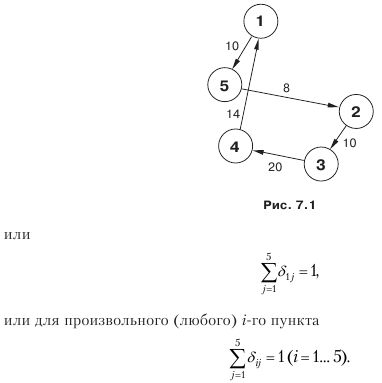
Эти зависимости обеспечивают выполнение условия, согласно которому из каждого пункта выезд производится только один раз и только в одном направлении.
Условие въезда в пункт 1 аналогично условию выезда из пункта 1. Требование минимальной продолжительности маршрута запишется в виде целевой функции:
min L = t11δ11+ t12δ12 + t13δ13 + t14δ14 + t15δ15 + t21δ21 + t22δ22 +… + t55δ55
где tij берутся из исходной таблицы, а δij – искомые переменные.
Математическую постановку задачи можно сформулировать в виде:

В результате решения системы получим следующие значения (рис. 7.2):
δ110 = δ520 = δ230 = δ340 = δ410 = 1, остальные δij0 = 0;
min L = 10 + 8 + 10 +20 + 14 = 62.
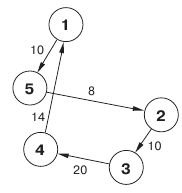
Рис. 7.2
Переходя от частной постановки к общей, задачу коммивояжера можно сформулировать так:
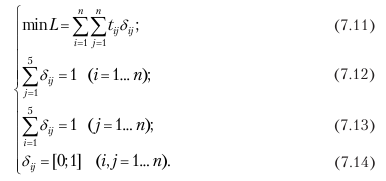
Для задачи коммивояжера при необходимости посещения только двух городов выбора нет. При посещении трех городов и заданном начальном пункте возможны 2 маршрута. Если городов четыре, то имеется 6 маршрутов, а при одиннадцати городах – более 3,5 млн допустимых маршрутов. В общем случае при n городах имеется (n -1)! маршрутов.
К подобному типу задач сводится множество реальных ситуаций. Например, выбор очередности обработки разнородных изделий, маршрута автотранспорта, задачи выбора маршрута в сетях систем связи.
Пример. Пусть имеется 5 пунктов, соединенных между собой дорогами так, что из любого пункта можно проехать в любой другой пункт. Известно время перевозки из пункта i в пункт j (табл. 7.1).
Таблица 7.1
Время переезда, ед.

Требуется найти маршрут с наименьшей продолжительностью, начинающийся в данном пункте, проходящий через все пункты и заканчивающийся в пункте выезда.
Решение. Введем обозначения: i и j – номера пунктов выезда и въезда; t. – время переезда из пункта i в пункт j. В общем случае tij может быть не равно времени переезда в обратном направлении
– tij ≠ tji (например, когда один пункт на вершине горы, а другой – у ее подножия). Введем булевы переменные:

Составим модель (рис. 7.1). Из пункта 1 можно выехать в любой из пунктов: 2, или 5, или 3, или 4, или остаться в пункте 1. Но при этом можно выехать только в одном-единственном направлении. Это условие можно записать так:
δ11 + δ12 + δ13 + δ14 + δ15 = 1

Эти зависимости обеспечивают выполнение условия, согласно которому из каждого пункта выезд производится только один раз и только в одном направлении.
Условие въезда в пункт 1 аналогично условию выезда из пункта 1. Требование минимальной продолжительности маршрута запишется в виде целевой функции:
min L = t11δ11+ t12δ12 + t13δ13 + t14δ14 + t15δ15 + t21δ21 + t22δ22 +… + t55δ55
где tij берутся из исходной таблицы, а δij – искомые переменные.
Математическую постановку задачи можно сформулировать в виде:

В результате решения системы получим следующие значения (рис. 7.2):
δ110 = δ520 = δ230 = δ340 = δ410 = 1, остальные δij0 = 0;
min L = 10 + 8 + 10 +20 + 14 = 62.

Рис. 7.2
Переходя от частной постановки к общей, задачу коммивояжера можно сформулировать так:
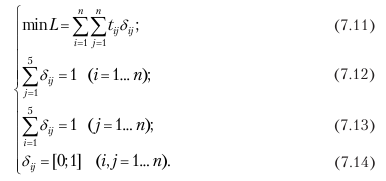
7.12. Распределение капитальных вложений
Пусть известны возможные значения эффективности (например, прирост прибыли, выпуск продукции и др.) на каждом из четырех предприятий отрасли в результате расширения действующих мощностей (табл. 7.2).
Требуется составить план распределения ограниченных капиталовложений по этим предприятиям (К = 200 ден. ед.), максимизирующий общий прирост выпуска при заданной номенклатуре и структуре отраслевого плана производства продукции.
Таблица 7.2 Возможные значения эффективности предприятий в результате расширения действующих мощностей

Решение.
Данная задача может быть решена методом динамического программирования. Обозначим: g i (x) – прирост выпуска продукции на i – м предприятии при x единиц капиталовложений на реконструкцию или расширение активной части его основных фондов; F (K) – максимально возможный прирост выпуска продукции при распределении суммы К между четырьмя предприятиями.
Тогда, согласно основному функциональному уравнению Беллмана:
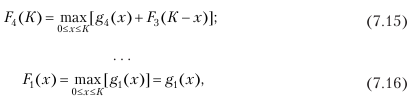
т. е. максимальный прирост выпуска продукции на первом предприятии при распределении для него (и только для него) единиц капиталовложений x (0 ‹x ‹K) будет соответствовать значениям графы 2 исходных данных.
Реализация задачи будет заключаться в последовательном решении уравнений Беллмана, описывающих максимальный прирост выпуска при распределении К = 200 между двумя предприятиями, затем тремя и четырьмя. В процессе вычислений x меняется от 0 до К с шагом Δ = 50:

и т. д. (табл. 7.3).
Из анализа результатов расчетов следует, что наибольший достижимый прирост продукции составит
F4 (200) = g4 (150) + F3 (50) = 110 + 36 = 146,
т. е. четвертому предприятию должно быть выделено 150, а первым трем – 50 ед. средств.
Таблица 7.3

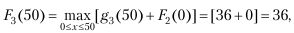
т. е. все оставшиеся 50 ед. выделяются третьему заводу.
Итак, решение задачи: x10 = x20 = 0; x30 = 50; x40= 150ден. ед.
Требуется составить план распределения ограниченных капиталовложений по этим предприятиям (К = 200 ден. ед.), максимизирующий общий прирост выпуска при заданной номенклатуре и структуре отраслевого плана производства продукции.
Таблица 7.2 Возможные значения эффективности предприятий в результате расширения действующих мощностей

Решение.
Данная задача может быть решена методом динамического программирования. Обозначим: g i (x) – прирост выпуска продукции на i – м предприятии при x единиц капиталовложений на реконструкцию или расширение активной части его основных фондов; F (K) – максимально возможный прирост выпуска продукции при распределении суммы К между четырьмя предприятиями.
Тогда, согласно основному функциональному уравнению Беллмана:
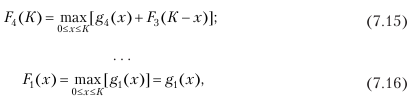
т. е. максимальный прирост выпуска продукции на первом предприятии при распределении для него (и только для него) единиц капиталовложений x (0 ‹x ‹K) будет соответствовать значениям графы 2 исходных данных.
Реализация задачи будет заключаться в последовательном решении уравнений Беллмана, описывающих максимальный прирост выпуска при распределении К = 200 между двумя предприятиями, затем тремя и четырьмя. В процессе вычислений x меняется от 0 до К с шагом Δ = 50:

и т. д. (табл. 7.3).
Из анализа результатов расчетов следует, что наибольший достижимый прирост продукции составит
F4 (200) = g4 (150) + F3 (50) = 110 + 36 = 146,
т. е. четвертому предприятию должно быть выделено 150, а первым трем – 50 ед. средств.
Таблица 7.3

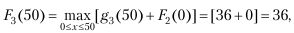
т. е. все оставшиеся 50 ед. выделяются третьему заводу.
Итак, решение задачи: x10 = x20 = 0; x30 = 50; x40= 150ден. ед.
7.13. Игровая модель обмена товарами (модель Эджворта)
Рассмотрим «игру» двух лиц, обладающих некоторой суммой, не равной нулю. «Игрок» А имеет а единиц одного товара, «игрок» В – b единиц второго товара. При обмене товарами каждый из «игроков» стремится извлечь пользу.
Для участника А итог обмена обозначим через (x, y), для участника В итог деятельности будет (а – x, b – y). Для определяемых величин x и y учитываются ограничивающие условия. Значение x находится в пределах от 0 до а, значение y – в пределах от 0 до b.
В координатах x, y для прямоугольника допустимых значений искомых неизвестных строятся линии равной выгодности. Для участника А – это совокупность параллельных выпуклых функций, для участника В – это совокупность параллельных вогнутых функций. Точки возможных условий контракта – это точки касания функций полезности результата для участников.
Для участника А итог обмена обозначим через (x, y), для участника В итог деятельности будет (а – x, b – y). Для определяемых величин x и y учитываются ограничивающие условия. Значение x находится в пределах от 0 до а, значение y – в пределах от 0 до b.
В координатах x, y для прямоугольника допустимых значений искомых неизвестных строятся линии равной выгодности. Для участника А – это совокупность параллельных выпуклых функций, для участника В – это совокупность параллельных вогнутых функций. Точки возможных условий контракта – это точки касания функций полезности результата для участников.
Глава 8
МЕТОДЫ РЕШЕНИЯ УПРАВЛЕНЧЕСКИХ ЗАДАЧ
8.1. Регрессионный анализ
Событие – всякий факт, который может произойти или не произойти в результате опыта как результат предпринятого действия (действий). Признаком отнесенности факта к разряду событий является ответ «да» либо «нет» на вопрос: «Произошло ли событие?» Событиями можно назвать как падение монеты гербом вверх при бросании («орел» или «решка»?), так и своевременную поставку сырья и др.
События могут быть достоверными, возможными и невозможными.
Достоверное событие – событие, которое непременно должно произойти, например выпадение любого количества очков на игральной кости, расход ресурсов при выпуске продукции.
Возможное – событие, которое может произойти или не произойти: падение монеты гербом вверх, выполнение плана на 100 % и др.
Невозможное – событие, которое не может произойти: появление (у игрока) двух тузов при вытаскивании одной карты, выпуск сверхплановой продукции без использования дополнительных ресурсов и др.
Для выражения возможности события используют численную меру. Численную меру возможности события называют вероятностью. Вероятность события A, т. е. P (A), можно вычислить:
P (A) = m/n
где m – число случаев, когда событие A может произойти; n – общее число случаев.

Вероятность P (A) характеризует возможность появления события А в будущем. Для оценки того, как часто события уже происходили, используют понятие частоты. Частоту события А обозначают
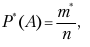
где m* показывает, сколько раз событие произошло; n – общее число произведенных испытаний.
Несовместными называют события, исключающие друг друга. Так, падение монеты вверх гербом и цифрами – это два несовместных события. Очевидно, что сумма вероятностей всех несовместных событий равна 1.
Случайные события можно характеризовать числами. Такие числа называют случайными величинами. Случайная величина может принять то или иное значение, заранее не известное. Например, случайными величинами являются объем поставленных материалов, трудоемкость операции или работы.
Леонид Витальевич Канторович – лауреат Нобелевской премии. Родился в 1912 г. в Санкт-Петербурге в семье врача. В 18 лет закончил математический факультет Ленинградского университета и уже через четыре года получил звание профессора. В 1935 г. ему была присуждена ученая степень доктора физико-математических наук. Л. В. Канторович является основателем российской школы функционального анализа, вычислительной математики, языков программирования. Крупнейшим его открытием стало введение в математическую и экономическую науки понятия «линейное программирование» (1939). Это универсальная математическая модель решения многих экономических задач. Им были введены «двойственные оценки» ресурсов, показывающие ценность этих ресурсов для общества. Двойственные оценки получили разнообразное толкование в зависимости от рассматриваемого круга задач. Одной из разработок Л. В. Канторовича была теория дифференциальной ренты. Рентные оценки позволяют измерить стоимость пользования природными ресурсами (землей, водой, воздухом и т. п.).
За короткий период Л. В. Канторовичу удалось построить разветвленную теорию на базе линейного программирования, а также создать основы математической теории. Им были разработаны транспортная задача, задача раскроя материалов. В 1965 г. Л. В. Канторович совместно с В. С Немчиновым и В. В. Новожиловым получил Ленинскую премию за разработку оптимизационного подхода к плановому управлению экономикой.
В 1975 г. Л. В. Канторович за разработку теории оптимального использования ресурсов был удостоен Нобелевской премии.
Конкретное измеренное значение случайной величины называют ее реализацией. Различные реализации случайной величины относят к несовместным событиям. Действительно, если трудоемкость изготовления детали составила 100 человеко-часов, то она не может быть равна 105 или иметь любое другое значение.
События могут быть достоверными, возможными и невозможными.
Достоверное событие – событие, которое непременно должно произойти, например выпадение любого количества очков на игральной кости, расход ресурсов при выпуске продукции.
Возможное – событие, которое может произойти или не произойти: падение монеты гербом вверх, выполнение плана на 100 % и др.
Невозможное – событие, которое не может произойти: появление (у игрока) двух тузов при вытаскивании одной карты, выпуск сверхплановой продукции без использования дополнительных ресурсов и др.
Для выражения возможности события используют численную меру. Численную меру возможности события называют вероятностью. Вероятность события A, т. е. P (A), можно вычислить:
P (A) = m/n
где m – число случаев, когда событие A может произойти; n – общее число случаев.

Вероятность P (A) характеризует возможность появления события А в будущем. Для оценки того, как часто события уже происходили, используют понятие частоты. Частоту события А обозначают
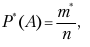
где m* показывает, сколько раз событие произошло; n – общее число произведенных испытаний.
Несовместными называют события, исключающие друг друга. Так, падение монеты вверх гербом и цифрами – это два несовместных события. Очевидно, что сумма вероятностей всех несовместных событий равна 1.
Случайные события можно характеризовать числами. Такие числа называют случайными величинами. Случайная величина может принять то или иное значение, заранее не известное. Например, случайными величинами являются объем поставленных материалов, трудоемкость операции или работы.
Леонид Витальевич Канторович – лауреат Нобелевской премии. Родился в 1912 г. в Санкт-Петербурге в семье врача. В 18 лет закончил математический факультет Ленинградского университета и уже через четыре года получил звание профессора. В 1935 г. ему была присуждена ученая степень доктора физико-математических наук. Л. В. Канторович является основателем российской школы функционального анализа, вычислительной математики, языков программирования. Крупнейшим его открытием стало введение в математическую и экономическую науки понятия «линейное программирование» (1939). Это универсальная математическая модель решения многих экономических задач. Им были введены «двойственные оценки» ресурсов, показывающие ценность этих ресурсов для общества. Двойственные оценки получили разнообразное толкование в зависимости от рассматриваемого круга задач. Одной из разработок Л. В. Канторовича была теория дифференциальной ренты. Рентные оценки позволяют измерить стоимость пользования природными ресурсами (землей, водой, воздухом и т. п.).
За короткий период Л. В. Канторовичу удалось построить разветвленную теорию на базе линейного программирования, а также создать основы математической теории. Им были разработаны транспортная задача, задача раскроя материалов. В 1965 г. Л. В. Канторович совместно с В. С Немчиновым и В. В. Новожиловым получил Ленинскую премию за разработку оптимизационного подхода к плановому управлению экономикой.
В 1975 г. Л. В. Канторович за разработку теории оптимального использования ресурсов был удостоен Нобелевской премии.
Конкретное измеренное значение случайной величины называют ее реализацией. Различные реализации случайной величины относят к несовместным событиям. Действительно, если трудоемкость изготовления детали составила 100 человеко-часов, то она не может быть равна 105 или иметь любое другое значение.
