Случайная величина не может быть описана одним конкретным числом. Ее можно описать либо количественными характеристиками, либо законом распределения. Наиболее распространенными характеристиками случайной величины являются: математическое ожидание, дисперсия, среднее квадратическое отклонение, коэффициент вариабельности.
Математическое ожидание характеризует среднее значение случайной величины и обозначается M x, или M [x], или x:
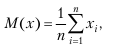
где n – число реализаций; xi – значение случайной величины в i – й реализации. Дисперсия D [x] (или D x) характеризует разброс значений случайной величины:
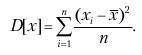
Так как размерность дисперсии равна квадрату размерности самой случайной величины, использовать дисперсию для относительной оценки разброса случайной величины нельзя.
Поэтому разброс оценивают средним квадратическим отклонением:
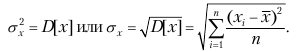
Удобной характеристикой случайной величины является коэффициент вариабельности, который показывает относительное значение разброса случайной величины.
Пример. Пусть наличие некоторого i – го ресурса в каждом квартале bi – случайная величина. Реализация этой случайной величины – фактический объем ресурса в каждом квартале (по отчету за прошлый год и три квартала текущего) (табл. 8.1).
Таблица 8.1
Объем ресурса в каждом квартале
Решение. Математическое ожидание случайной величины bi:
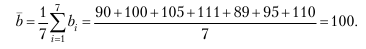
Среднеквадратическое отклонение:
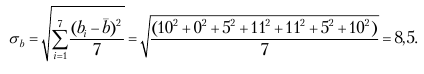
Коэффициент вариабельности:
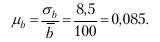
Наиболее полная характеристика случайной величины – закон ее распределения. Он показывает, какова вероятность появления каждого возможного значения случайной величины или каким образом суммарная вероятность появления случайной величины, равная единице, распределена между ее возможными значениями. То есть закон распределения устанавливает связь между возможными значениями случайной величины и вероятностями их появления.
Из множества законов наиболее распространен нормальный закон распределения, с помощью которого решают различные задачи оптимизации, в том числе и в условиях неопределенности.
Нормальный закон распределения имеет две формы представления: плотность распределения (рис. 8.1, а) и функцию распределения (рис. 8.1, б).
С помощью графика (а) можно определить, например, чему равна вероятность принятия случайной величиной x, изменяющейся в интервале значений A, B (A ≤ x ≤ B), значения не больше величины a, т. е. P (x ≤ a). Оказывается, эта вероятность равна заштрихованной площади.
Зная P (x ≤ a), можно предположить, что x будет не меньше величины а, т. е. P (x ≤ a).
Очевидно, что P (x ≤ a) + P (x ≤ a) = 1 (как сумма несовместных событий), тогда P (x ≥ a) = 1 – P (x ≥ a), что соответствует незаштрихованной площади (рис. 8.1, а).
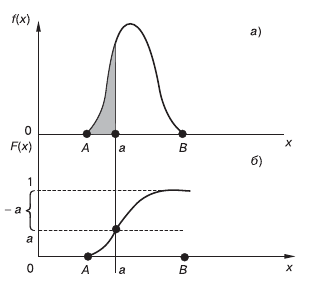
Рис. 8.1. Плотность распределения (а) и функция распределения (б) Большое распространение получила другая форма распределения (потому что площадь криволинейной фигуры трудно вычислить) – функция распределения F (x) (рис. 8.1 б). Здесь вероятность P (x ≤ a) равна ординате кривой F (x). Следова тельно, P(x ≤ a) = F(a), т. е. P(x ≤ a) = 1 – F(a). Для обеспечения расчетов по нормальному закону распределения от реальной случайной величины x переходят к нормированной (центрированной) случайной величине t = (x – x)
При этом P (x ≤ a) = F (t). Для определения F (t) используют специальные таблицы, по данным которых можно построить график функции распределения (табл. 8.2, рис. 8.2).
Таблица 8.2
Данные для построения графика функции распределения
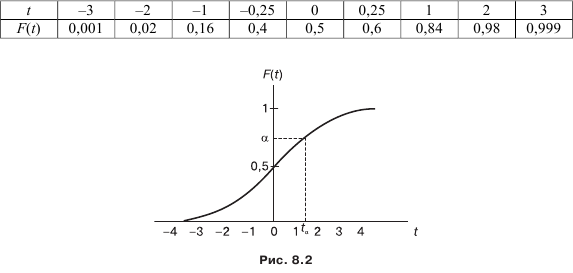По графику F(t) можно определить интересующие нас величины. Например, какова вероятность того, что наличный ресурс будет не менее 98.
Очевидно, что
P(x ≥ 98) = 1 – P(x ≤ 98).
Для данного примера
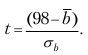
Ранее установили, что b = 100; σb = 9.
Следовательно,
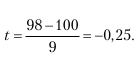
Так как
P(x ≤ a) = F(t), то P(x ≤ 98) = F(–0,25) = 0,4;
то
P(x ≥ 98) = 1 – P(x ≤ 98) = 1–0,4 = 0,6.
Можно поставить и обратную задачу: при каком значении tα вероятность появления случайной величины удовлетворяла условию P(t ≤ tα) = α – заданный уровень вероятности. Если a задать 0,6, то tα = 0,25.
Регрессионный анализ представляет собой статистическую процедуру для математического расчета среднего соотношения зависимой и независимой переменных. Выделяют два вида регрессии – простую и множественную. Простая регрессия включает одну независимую переменную, множественная – две и более.
Для характеристики метода построения регрессионной зависимости рассмотрим совокупность двух величин x (i) и y (i). Требуется на базе этих данных построить зависимость
y = a + bx.
Коэффициенты a и b следует подобрать так, чтобы расчетные значения y по уравнению были наиболее близки к заданным значениям y (i). Условие близости формулируется как сумма квадратов отклонений по каждому из значений y.
Значение коэффициентов a и b определяется из соотношений:
b = (nR(x, y)– m(x)m(y))/(nD(x)– m(x)m(x));
a = m(y)– bm(x).
Здесь использованы следующие предварительно вычисленные параметры: n – количество пар значений рассматриваемых переменных; m (y) – сумма значений y; m (x) – сумма значений x; D (x) – сумма квадратов значений x; R (x, y) – сумма произведений значений x (i) и y (i).
Сумма квадратов расхождений значений y, вычисленных по расчетному соотношению, и значений по исходным данным называется стандартной ошибкой регрессионного уравнения.
8.2. Метод Лагранжа
8.3. Метод Гаусса
Математическое ожидание характеризует среднее значение случайной величины и обозначается M x, или M [x], или x:
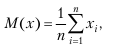
где n – число реализаций; xi – значение случайной величины в i – й реализации. Дисперсия D [x] (или D x) характеризует разброс значений случайной величины:
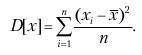
Так как размерность дисперсии равна квадрату размерности самой случайной величины, использовать дисперсию для относительной оценки разброса случайной величины нельзя.
Поэтому разброс оценивают средним квадратическим отклонением:
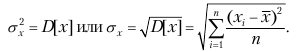
Удобной характеристикой случайной величины является коэффициент вариабельности, который показывает относительное значение разброса случайной величины.
Пример. Пусть наличие некоторого i – го ресурса в каждом квартале bi – случайная величина. Реализация этой случайной величины – фактический объем ресурса в каждом квартале (по отчету за прошлый год и три квартала текущего) (табл. 8.1).
Таблица 8.1
Объем ресурса в каждом квартале
Решение. Математическое ожидание случайной величины bi:
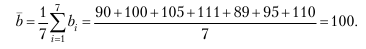
Среднеквадратическое отклонение:
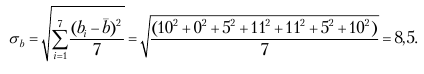
Коэффициент вариабельности:
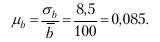
Наиболее полная характеристика случайной величины – закон ее распределения. Он показывает, какова вероятность появления каждого возможного значения случайной величины или каким образом суммарная вероятность появления случайной величины, равная единице, распределена между ее возможными значениями. То есть закон распределения устанавливает связь между возможными значениями случайной величины и вероятностями их появления.
Из множества законов наиболее распространен нормальный закон распределения, с помощью которого решают различные задачи оптимизации, в том числе и в условиях неопределенности.
Нормальный закон распределения имеет две формы представления: плотность распределения (рис. 8.1, а) и функцию распределения (рис. 8.1, б).
С помощью графика (а) можно определить, например, чему равна вероятность принятия случайной величиной x, изменяющейся в интервале значений A, B (A ≤ x ≤ B), значения не больше величины a, т. е. P (x ≤ a). Оказывается, эта вероятность равна заштрихованной площади.
Зная P (x ≤ a), можно предположить, что x будет не меньше величины а, т. е. P (x ≤ a).
Очевидно, что P (x ≤ a) + P (x ≤ a) = 1 (как сумма несовместных событий), тогда P (x ≥ a) = 1 – P (x ≥ a), что соответствует незаштрихованной площади (рис. 8.1, а).
Рис. 8.1. Плотность распределения (а) и функция распределения (б) Большое распространение получила другая форма распределения (потому что площадь криволинейной фигуры трудно вычислить) – функция распределения F (x) (рис. 8.1 б). Здесь вероятность P (x ≤ a) равна ординате кривой F (x). Следова тельно, P(x ≤ a) = F(a), т. е. P(x ≤ a) = 1 – F(a). Для обеспечения расчетов по нормальному закону распределения от реальной случайной величины x переходят к нормированной (центрированной) случайной величине t = (x – x)
При этом P (x ≤ a) = F (t). Для определения F (t) используют специальные таблицы, по данным которых можно построить график функции распределения (табл. 8.2, рис. 8.2).
Таблица 8.2
Данные для построения графика функции распределения
Очевидно, что
P(x ≥ 98) = 1 – P(x ≤ 98).
Для данного примера
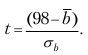
Ранее установили, что b = 100; σb = 9.
Следовательно,
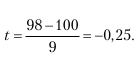
Так как
P(x ≤ a) = F(t), то P(x ≤ 98) = F(–0,25) = 0,4;
то
P(x ≥ 98) = 1 – P(x ≤ 98) = 1–0,4 = 0,6.
Можно поставить и обратную задачу: при каком значении tα вероятность появления случайной величины удовлетворяла условию P(t ≤ tα) = α – заданный уровень вероятности. Если a задать 0,6, то tα = 0,25.
Регрессионный анализ представляет собой статистическую процедуру для математического расчета среднего соотношения зависимой и независимой переменных. Выделяют два вида регрессии – простую и множественную. Простая регрессия включает одну независимую переменную, множественная – две и более.
Для характеристики метода построения регрессионной зависимости рассмотрим совокупность двух величин x (i) и y (i). Требуется на базе этих данных построить зависимость
y = a + bx.
Коэффициенты a и b следует подобрать так, чтобы расчетные значения y по уравнению были наиболее близки к заданным значениям y (i). Условие близости формулируется как сумма квадратов отклонений по каждому из значений y.
Значение коэффициентов a и b определяется из соотношений:
b = (nR(x, y)– m(x)m(y))/(nD(x)– m(x)m(x));
a = m(y)– bm(x).
Здесь использованы следующие предварительно вычисленные параметры: n – количество пар значений рассматриваемых переменных; m (y) – сумма значений y; m (x) – сумма значений x; D (x) – сумма квадратов значений x; R (x, y) – сумма произведений значений x (i) и y (i).
Сумма квадратов расхождений значений y, вычисленных по расчетному соотношению, и значений по исходным данным называется стандартной ошибкой регрессионного уравнения.
8.2. Метод Лагранжа
Вся совокупность методов решения управленческих задач делится на две группы: аналитические и численные. При выборе метода решения конкретной задачи следует учесть, что аналитическое решение всегда предпочтительнее численного, так как оно позволяет исследовать влияние различных факторов на оптимальное решение. Однако при решении практических задач не всегда удается получить аналитическое решение.
Общего метода решения всех управленческих задач не существует.
В зависимости от вида оценки вариантов решения задачи, состава и вида ограничивающих условий могут применяться различные методы поиска оптимального решения. Иногда одна задача может решаться разными методами. Аналитические методы решения управленческих задач опираются на дифференциальное исчисление. Наиболее универсальными среди численных методов являются методы линейного и динамического программирования. Для численных методов решения необходимо иметь четкую область ограничений. Чем меньше эта область, тем проще поиск оптимального решения.
Дифференциальное исчисление – метод поиска оптимального решения через вычисление производных оптимизируемой функции. Для отыскания экстремума (максимума, минимума) функции одной переменной J (x) необходимо найти решение уравнения
dJ / dx = 0.
Если вторая производная меньше нуля, то имеет место максимум функции, если вторая производная больше нуля, то имеет место минимум функции.
В случае функции нескольких переменных задача оптимизации сводится к решению систем уравнений, каждое из которых является производной по одной из переменных.
Необходимым условием применения метода дифференциального исчисления является дифференцируемость выражения J(x) и в общем случае – отсутствие ограничений.
Метод Лагранжа – метод дифференциального исчисления, применяемый при наличии ограничивающих условий. Этот метод позволяет перейти от оптимизационной задачи с ограничениями к альтернативной оптимизационной задаче без ограничений при совпадении решений. Фактически математическая задача на условный экстремум заменяется задачей на безусловный экстремум, но с увеличением числа неизвестных.
Первоначальная задача:
с(x) → min;
A(x) > 0.
Альтернативная задача:
с(x) + λA(x) → min.
Условиями экстремума при решении данной задачи являются условия равенства нулю производной по x и λ.
Коэффициент λ называется множителем Лагранжа. Если в исходной задаче имеется набор ограничений, то в альтернативной задаче во втором слагаемом появляется сумма слагаемых с коэффициентами λ(i). Если ограничение по i – му ресурсу в точке экстремума обращаются в равенство, то множитель Лагранжа для них не равен нулю. Если ограничения в точке экстремума не оказывают влияние на решение, то множитель Лагранжа для них равен нулю.
При общей постановке оптимизационной задачи в виде
max (min) f (x1, x2…, xn); gi (x1, x2…, xn) = bi (i =1… m),
функция Лагранжа имеет вид:
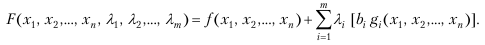
Для ее оптимизации находят частные производные
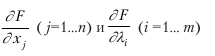
и рассматривают систему n + m уравнений:
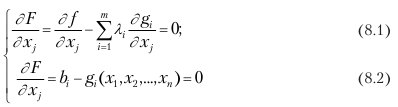
с n + m неизвестными x1, x2…., xn, λ1, λ2…, λm.
Всякое решение системы определяет точку x = (x10, x20…, x0n), в которой может иметь место экстремум функции f (x1, x2…, xn) Следовательно, решив систему уравнений, получим все точки, в которых функция Лагранжа может иметь экстремальные значения.
Пример. Известен рыночный спрос на определенное изделие в количестве 180 шт. Это изделие может быть изготовлено двумя предприятиями одного концерна по различным технологиям. При производстве x 1 изделий первым предприятием его затраты составят 4x1 + x12 руб., а при изготовлении x 2 изделий вторым предприятием – 8x2 + x22 руб. Требуется определить, сколько изделий, изготовленных по каждой технологии, может предложить концерн, чтобы общие издержки его производства были минимальны.
Решение. Запишем математическую постановку задачи в виде:
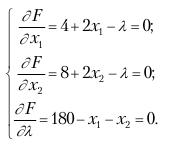
Для нахождения минимального значения целевой функции составим функцию Лагранжа
F (x1, x2, λ) = 4x1 +x12 + 8x2 + x22 + λ(180 – x1 – x2),
вычислим ее частные производные по x1, x2, λ и приравняем их к нулю:
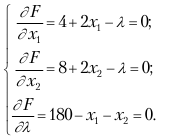
Отсюда 4 + 2x1 = 8 + 2x2, или x1 + x2 = 2. Решая это уравнение совместно с x1 + x2 = 180, находим x10 =91; x20=89, т. е. получаем координаты точки, подозрительной на экстремум. Используя вторые частные производные, можно показать, что в этой точке функция f имеет условный минимум.
Общего метода решения всех управленческих задач не существует.
В зависимости от вида оценки вариантов решения задачи, состава и вида ограничивающих условий могут применяться различные методы поиска оптимального решения. Иногда одна задача может решаться разными методами. Аналитические методы решения управленческих задач опираются на дифференциальное исчисление. Наиболее универсальными среди численных методов являются методы линейного и динамического программирования. Для численных методов решения необходимо иметь четкую область ограничений. Чем меньше эта область, тем проще поиск оптимального решения.
Дифференциальное исчисление – метод поиска оптимального решения через вычисление производных оптимизируемой функции. Для отыскания экстремума (максимума, минимума) функции одной переменной J (x) необходимо найти решение уравнения
dJ / dx = 0.
Если вторая производная меньше нуля, то имеет место максимум функции, если вторая производная больше нуля, то имеет место минимум функции.
В случае функции нескольких переменных задача оптимизации сводится к решению систем уравнений, каждое из которых является производной по одной из переменных.
Необходимым условием применения метода дифференциального исчисления является дифференцируемость выражения J(x) и в общем случае – отсутствие ограничений.
Метод Лагранжа – метод дифференциального исчисления, применяемый при наличии ограничивающих условий. Этот метод позволяет перейти от оптимизационной задачи с ограничениями к альтернативной оптимизационной задаче без ограничений при совпадении решений. Фактически математическая задача на условный экстремум заменяется задачей на безусловный экстремум, но с увеличением числа неизвестных.
Первоначальная задача:
с(x) → min;
A(x) > 0.
Альтернативная задача:
с(x) + λA(x) → min.
Условиями экстремума при решении данной задачи являются условия равенства нулю производной по x и λ.
Коэффициент λ называется множителем Лагранжа. Если в исходной задаче имеется набор ограничений, то в альтернативной задаче во втором слагаемом появляется сумма слагаемых с коэффициентами λ(i). Если ограничение по i – му ресурсу в точке экстремума обращаются в равенство, то множитель Лагранжа для них не равен нулю. Если ограничения в точке экстремума не оказывают влияние на решение, то множитель Лагранжа для них равен нулю.
При общей постановке оптимизационной задачи в виде
max (min) f (x1, x2…, xn); gi (x1, x2…, xn) = bi (i =1… m),
функция Лагранжа имеет вид:
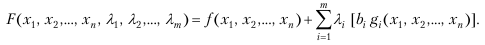
Для ее оптимизации находят частные производные
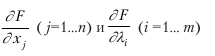
и рассматривают систему n + m уравнений:
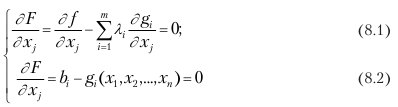
с n + m неизвестными x1, x2…., xn, λ1, λ2…, λm.
Всякое решение системы определяет точку x = (x10, x20…, x0n), в которой может иметь место экстремум функции f (x1, x2…, xn) Следовательно, решив систему уравнений, получим все точки, в которых функция Лагранжа может иметь экстремальные значения.
Пример. Известен рыночный спрос на определенное изделие в количестве 180 шт. Это изделие может быть изготовлено двумя предприятиями одного концерна по различным технологиям. При производстве x 1 изделий первым предприятием его затраты составят 4x1 + x12 руб., а при изготовлении x 2 изделий вторым предприятием – 8x2 + x22 руб. Требуется определить, сколько изделий, изготовленных по каждой технологии, может предложить концерн, чтобы общие издержки его производства были минимальны.
Решение. Запишем математическую постановку задачи в виде:
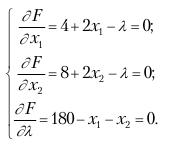
Для нахождения минимального значения целевой функции составим функцию Лагранжа
F (x1, x2, λ) = 4x1 +x12 + 8x2 + x22 + λ(180 – x1 – x2),
вычислим ее частные производные по x1, x2, λ и приравняем их к нулю:
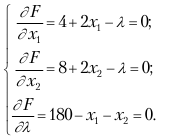
Отсюда 4 + 2x1 = 8 + 2x2, или x1 + x2 = 2. Решая это уравнение совместно с x1 + x2 = 180, находим x10 =91; x20=89, т. е. получаем координаты точки, подозрительной на экстремум. Используя вторые частные производные, можно показать, что в этой точке функция f имеет условный минимум.
8.3. Метод Гаусса
Метод Гаусса – это последовательное изменение состава опорного решения до получения оптимального варианта, не допускающего улучшения, это способ решения оптимизационной задачи, у которой оценка и ограничения являются линейными функциями. Рассмотрим алгоритм метода Гаусса на числовом примере. Постановка задачи: максимизировать
Конец бесплатного ознакомительного фрагмента