Страница:
— Закусите в кафе «Абракадабра».
— Как туда попасть?
— Для этого надо познакомиться с обычаями нашей страны.
— Мы уже познакомились, — не выдержал я.
— Молодой человек, — вспылил автомат, — вы даже не успели до конца разобраться в правилах движения на монорельсовой дороге!
— Как это — не успели? — обиделся я. — Мы уже знаем сложение и вычитание положительных и отрицательных чисел.
— И это все?! А умножение? А деление? А дробные числа? А мнимые? А…
И тут он пошел говорить такие слова, каких я и не слыхивал. Мы стали переспрашивать. Тогда автомат еще пуще раскипятился:
— Вот видите! Вы не понимаете самых обыкновенных вещей. Нет, нам положительно не о чем разговаривать!
И замолчал. Напрасно мы задавали ему всякие вопросы, он и ухом не повел. Но Таня все-таки его разжалобила — девчонки это умеют.
— Милый автомат, — сказала она, — не сердитесь, пожалуйста! Мы ведь еще такие неопытные. Лучше помогите нам!
Автомат нерешительно хмыкнул.
— Так и быть, — проворчал он. — Возьмите с подноса жетон и опустите в щель под динамиком.
Наконец-то! Сейчас мы узнаем тайну зеленого стручка!
Я так разволновался, что никак не мог опустить жетон. И все зря. Из широкого отверстия в щите выпали две картонки. На них были фотографии тех самых букв, которых мы видели в парке. На каждой фотографии по две буквы. Одна большая, другая маленькая. А внизу — имя. Ну, прямо как на ежегодном снимке учеников нашего класса.
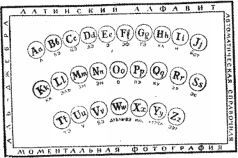Я чуть не заплакал с досады. Но автомат (и как он только все замечает?) заворчал, что на первый раз хватит и этого и что, пока мы не будем знать каждую букву в лицо и по имени, лучше нам к нему не обращаться.
— Почтенный автомат, — сказал Олег, — мы готовы выучить все, что угодно, но объясните, пожалуйста, что это за буквы?
— Так бы и спрашивали, — подобрел тот, — от этого я никогда не отказываюсь. На первой картонке вы видите основных жителей Аль-Джебры — двадцать шесть букв латинского алфавита. Этот алфавит употребляется во многих странах. Ведь он был принят еще в Древнем Риме, и многие народы пользуются им до наших дней. Поэтому тем из вас, кто изучает какой-нибудь иностранный язык — английский, немецкий, французский, — эти буквы уже знакомы. Зато вряд ли вы знаете буквы, изображенные на другой картонке.
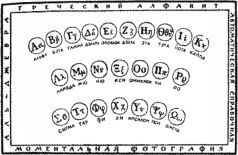Это двадцать четыре представителя греческого алфавита. В Аль-Джебре они встречаются не так уж часто, но знакомство с ними вам еще пригодится.
Ну, мы рассмотрели и те и эти фотографии. Латинские буквы ничего себе, а греческие мне не особенно понравились. По-моему, они ужасные кривляки. Взять хотя бы Кси: прямо змея!
А потом за нами пришла мама Двойка. Мы простились с автоматом и вернулись на монорельсовую дорогу, чтобы раз и навсегда разделаться с этими трудными правилами воздушного движения.
Напоследок я успел опустить в щель еще один жетон и снова получил две картонки с фотографиями. Посылаю их тебе: пригодятся для следующих уроков.
А пока — кси-пси! Привет.
Сева.
Нулики подрались
В тесноте, да не в обиде
Молотобойцы
Нулик-пограничник
Пламенный привет от Нулика-Пограничника! Теперь наша школа называется пограничной. Мы не пропускаем ни одной цифры, пока не узнаем, какой у нее знак отличия: плюс или минус. Один Нулик даже не пустил домой собственную маму, потому что она рассердилась и не хотела отвечать на его вопросы. Кончилось тем, что мама его наказала, пожаловалась моей маме и нашу школу чуть не закрыли.
Хорошо еще, что у меня такая добрая мама. Она меня простила и даже подарила силомер. Получше вашего-то: волшебный! Выбираешь число, задумываешь, в какую степень его возвести, бьешь молотком, и гирька сама показывает ответ.
Я принес силомер в школу, и все стали возводить нуль в разные степени. Но как мы ни старались, гирька ни разу не поднялась выше нуля. Словно ее приклеили. Как вы думаете, отчего это? Может, у нас сил не хватает, чтобы ударить как следует?
Потом я надумал сделать то, чего вы не успели: возвести целое положительное число в отрицательную степень.
Но и от этого толку мало: какое число ни возьмешь, гирька хоть и поднимается, но очень немножко, не выше единицы. Тогда мы взяли большущее число 1000 и возвели его в минус третью степень: 1000—3. Ухватились за молоток сообща и как трахнем! А противная гирька почти не сдвинулась с места. Что ж это такое? Неужели мама подарила мне испорченный силомер?
Я на нее очень обиделся, но она только рассмеялась. Она вообще любит смеяться. А потом сказала, что если возводить целое положительное число в целую отрицательную степень, то больше единицы никогда не получится. И чем большее число возводишь, тем меньшее число получается. Вот силомер и показал всего — навсего одну миллиардную: 0,000000001.
Пришлось поверить на слово. Потому что, отчего это происходит, мама не объяснила. Зато она сказала, что число, которое возводится в степень, называется основанием степени, число, в которое возводится это основание, — показателем степени, а уж сама степень получается только в ответе.
На этом основании я могу сказать, что не только вы меня, но и я вас могу кое-чему научить. Вот как!
Нулик-Пограничник.
P.S. Когда же вы напишете про кафе «Абракадабра»?
Карнавал
— Как туда попасть?
— Для этого надо познакомиться с обычаями нашей страны.
— Мы уже познакомились, — не выдержал я.
— Молодой человек, — вспылил автомат, — вы даже не успели до конца разобраться в правилах движения на монорельсовой дороге!
— Как это — не успели? — обиделся я. — Мы уже знаем сложение и вычитание положительных и отрицательных чисел.
— И это все?! А умножение? А деление? А дробные числа? А мнимые? А…
И тут он пошел говорить такие слова, каких я и не слыхивал. Мы стали переспрашивать. Тогда автомат еще пуще раскипятился:
— Вот видите! Вы не понимаете самых обыкновенных вещей. Нет, нам положительно не о чем разговаривать!
И замолчал. Напрасно мы задавали ему всякие вопросы, он и ухом не повел. Но Таня все-таки его разжалобила — девчонки это умеют.
— Милый автомат, — сказала она, — не сердитесь, пожалуйста! Мы ведь еще такие неопытные. Лучше помогите нам!
Автомат нерешительно хмыкнул.
— Так и быть, — проворчал он. — Возьмите с подноса жетон и опустите в щель под динамиком.
Наконец-то! Сейчас мы узнаем тайну зеленого стручка!
Я так разволновался, что никак не мог опустить жетон. И все зря. Из широкого отверстия в щите выпали две картонки. На них были фотографии тех самых букв, которых мы видели в парке. На каждой фотографии по две буквы. Одна большая, другая маленькая. А внизу — имя. Ну, прямо как на ежегодном снимке учеников нашего класса.
— Почтенный автомат, — сказал Олег, — мы готовы выучить все, что угодно, но объясните, пожалуйста, что это за буквы?
— Так бы и спрашивали, — подобрел тот, — от этого я никогда не отказываюсь. На первой картонке вы видите основных жителей Аль-Джебры — двадцать шесть букв латинского алфавита. Этот алфавит употребляется во многих странах. Ведь он был принят еще в Древнем Риме, и многие народы пользуются им до наших дней. Поэтому тем из вас, кто изучает какой-нибудь иностранный язык — английский, немецкий, французский, — эти буквы уже знакомы. Зато вряд ли вы знаете буквы, изображенные на другой картонке.
Ну, мы рассмотрели и те и эти фотографии. Латинские буквы ничего себе, а греческие мне не особенно понравились. По-моему, они ужасные кривляки. Взять хотя бы Кси: прямо змея!
А потом за нами пришла мама Двойка. Мы простились с автоматом и вернулись на монорельсовую дорогу, чтобы раз и навсегда разделаться с этими трудными правилами воздушного движения.
Напоследок я успел опустить в щель еще один жетон и снова получил две картонки с фотографиями. Посылаю их тебе: пригодятся для следующих уроков.
А пока — кси-пси! Привет.
Сева.
Нулики подрались
(Нулик — отряду РВТ)
Здравствуйте, ребята! Не знаю, может, вы и правы, что отрицательных пирожных не бывает, зато отрицательные Нулики встречаются. Сегодня утром один такой отрицательный Нулик напал на другого, который до сих пор считался очень положительным. Ну и драка была! Еще немного — и они бы взаимоуничтожились. Я уж думал, не рассадить ли их по разным загонам — ну, как эти самые… абсолютные значения. Но тут их растащили другие Нулики. Из этого я сделал вывод, что положительный Нулик только прикидывался положительным. На деле он самый что ни на есть отрицательный! И я им обоим поставил по поведению жирный минус.
В нашей школе занятия продолжаются.
Греческие буквы трудные. Мы их пока отложили. Зато латинский алфавит всем понравился. Только как туда попали русские буквы? И почему некоторые из них называются по-другому: Р — Пэ, В — Бэ? А вот «О» молодчина! И там и тут пишется одинаково. Это потому, что оно похоже на меня.
Если снова побываете у автомата, непременно спросите: куда ведет воздушная монорельсовая дорога? Не к тем ли Великанам, которых вызывают, когда мы безобразничаем? И где эти Великаны живут? Справа или слева от Нулевой станции?
Нулик-Профессор.
В нашей школе занятия продолжаются.
Греческие буквы трудные. Мы их пока отложили. Зато латинский алфавит всем понравился. Только как туда попали русские буквы? И почему некоторые из них называются по-другому: Р — Пэ, В — Бэ? А вот «О» молодчина! И там и тут пишется одинаково. Это потому, что оно похоже на меня.
Нулик-Профессор.
В тесноте, да не в обиде
(Таня — Нулику)
Бедный, бедный Нулик! Ну и каша у тебя в голове! Сначала изобрел какие-то отрицательные пирожные, потом — положительных и отрицательных Нуликов!
Запомни раз и навсегда: нуль — единственное число, которое не бывает ни положительным, ни отрицательным. Это что-то вроде пограничника, который стоит на рубеже между положительными и отрицательными числами.
Конечно, в твоей школе тоже есть положительные и отрицательные Нулики. Но это ведь совсем другое дело. Просто одни из них хорошие, а другие — плохие.
Второй твой вопрос — о Великанах — очень интересный. Но ответил на него не автомат, а мама Двойка. Она говорит, что ты любознательный ребенок.
Оба конца монорельсовой дороги и вправду ведут в Бесконечность. А в Бесконечности, понятно, живут числа — Великаны. Бесконечность тоже бывает положительная и отрицательная. Только там свои, особые законы. Положительные и отрицательные Великаны прекрасно уживаются. Но как это им удается, мы не узнали. Это как раз один из тех вопросов, на которые мама Двойка отвечает: «Всякому овощу свое время».
А теперь танцуй! Мы научились умножать и делить отрицательные числа.
Ты ведь знаешь, что умножение можно рассматривать как сложение. Умножить два на три — все равно что сложить три двойки:
+ + + + + +
2 * 3 = 2 + 2 + 2 = 6
То же самое происходит, когда отрицательное число умножают на положительное. Разве умножить минус два на плюс три — это не то же самое, что сложить три отрицательные двойки? А так как при сложении отрицательных чисел вагончики двигаются влево от Нулевой станции, то и произведение будет отрицательное — минус шесть:
— + — — — —
2 * 3 = 2 + 2 + 2 = 6
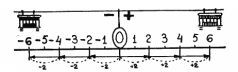— Ну, а если умножить минус три на плюс два? — спросил Сева. — Тогда что?
— Какая же разница? — сказала мама Двойка. — Как было минус шесть, так и останется минус шесть. Вот смотрите:
— + — — —
3 * 2 = 3 + 3 = 6
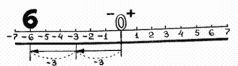— Ясно! — кивнул Сева. — Пусть себе множители меняются знаками сколько хотят, произведение все равно остается то же. Оно всегда будет отрицательным, если мы перемножаем два числа с разными знаками. — Сева важно посмотрел на всех. Он был страшно собой доволен. — Все поняли? Тогда поехали дальше. Выясним теперь, что получится, если оба множителя отрицательные?
— Ну что ж, выясняйте, — сказала мама Двойка, — мы с удовольствием вас послушаем.
— Вы меня не поняли, — смутился Сева. — Это я вас собирался послушать.
— Ах вот оно что! Тогда другое дело.
Всем нам стало неловко за Севу. Мы подумали, что мама Двойка обиделась, но она посмотрела на нас смеющимися глазами и продолжала:
— Вы хотели знать, что происходит при перемножении двух отрицательных чисел? Нетрудно догадаться. Чтобы умножить любое число на положительное, надо отложить его на монорельсе в ту же сторону от Нулевой станции, с какой оно находится. Это мы только что видели.
Когда же мы умножаем любое число на отрицательное, все происходит наоборот. Вы ведь знаете, какие упрямцы эти отрицательные числа! Поэтому умножаемое откладывается не с той стороны, где оно находится, а по другую сторону от нуля:
+ — —
2 * 4 = 8
Теперь нетрудно понять, что получится при умножении отрицательного числа на отрицательное; в этом случае умножаемое надо откладывать вправо от нуля:
— — +
2 * 4 = 8
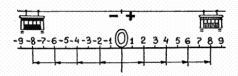— Вот те раз! — Брови у Севы стали прямо как два вопросительных знака. — Отрицательное число, умноженное на отрицательное, становится положительным?! Чудеса!
— Такие чудеса случаются у нас в Аль-Джебре на каждом шагу, — ответила мама Двойка.
— Ну, если так, расскажите нам поскорее про деление. Там, наверное, будут какие-нибудь новые чудеса?
— Ничуть не бывало. Деление — действие, обратное умножению. Стало быть, и правила знаков не меняются:
— + —
6 : 3 = 2
— — —
6 : 3 = 2
Мы почувствовали себя ужасно образованными. А пуще всех — Сева.
— Теперь нам все нипочем! — заявил он. — Мы знаем эту дорогу как свои пять пальцев!
— Ошибаетесь, — сказала мама Двойка, — вы познакомились только с целыми числами.
— А разве здесь есть и другие?
— А как же!
— Вы, наверное, подразумеваете дробные числа, — предположил Олег.
— Не только. Дробные числа — это те, что расположены между целыми числами. — Мама Двойка указала на палочки ограды, которые мы недавно пересчитывали. — Здесь расстояние между двумя целыми числами разделено на десять равных частей. Каждая из них составляет одну десятую единицы. Но ведь этих делений может быть и гораздо больше. Мысленно мы можем разделить это расстояние на любое число частей.
— Значит, вагончик может останавливаться не только у целого числа, но и у любой дроби, то есть между станциями?
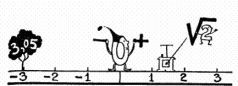— Ну конечно! В любом месте, по первому требованию!
Мы тут же вызвали вагончик и заставили его остановиться сперва против числа 2,5, а потом против 3,44… Этого нам показалось мало. Мы назвали число минус пять и четыре миллионных: —5,000 004, и красный вагончик, миновав Нулевую станцию, превратился в синий и остановился на волосок дальше станции минус 5.
— Выходит, — неуверенно сказал Сева, — вся эта бесконечная дорога сплошь заполнена числами?
— Именно сплошь! — ответила мама Двойка. — Можно сказать, непрерывно. У нас очень большая плотность населения. На всем пути не сыскать ни одной точечки, не заселенной каким-нибудь числом. Есть среди этих чисел и такие, величину которых мы никогда не можем вычислить точно.
— Что ж это за число, которое нельзя вычислить?
— Ну, хотя бы корень квадратный из двух: √2. Попробуйте найти число, которое при возведении в квадрат давало бы два.
Сева наморщил лоб, подумал немного, потом махнул рукой и засмеялся:
— И много таких чисел?
— Бесконечное множество. Их называют иррациональными в отличие от рациональных. Латинское слово «рацио» значит «разум». Следовательно, рациональные числа — это разумные числа, то есть числа, постижимые разумом.
Сева прямо задохнулся от смеха:
— Ой, умираю! Рациональные — значит разумные. А иррациональные — сумасшедшие, что ли?
— Ну, зачем же так! — обиделась мама Двойка. — Просто они не поддаются точному вычислению. Поэтому их долгое время не признавали числами. Но с тех пор как у нас появилась воздушная монорельсовая дорога (или числовая прямая — так ее называют по-другому), иррациональные числа после долгих скитаний получили, наконец, точный адрес. Вычислить их по-прежнему можно только приближенно. Зато легко указать место на монорельсовой дороге, где они живут. Вместе с числами рациональными они образуют дружную семью действительных чисел, — закончила мама Двойка и снова заставила нас удивиться.
— А разве бывают и недействительные?
— Конечно. Есть числа мнимые, есть комплексные…
Сева не дал ей договорить.
— Вспомнил! — заорал он. — И Мнимая Единица может на что-нибудь пригодиться!
— Да, да, — подтвердила я, — так ответил автомат маленькой буковке с зонтиком: i.
— Оно и понятно, — сказала мама Двойка, — латинской буквой i (по-русски — И) в Аль-Джебре обозначается Мнимая Единица.
— Но почему мнимая? Она что, воображаемая?
— Настолько воображаемая, что ей, как и другим мнимым числам, не нашлось местечка на всей бесконечной монорельсовой дороге.
— Так вот почему она была такая грустная! — смекнул Сева.
— А где же тогда живут мнимые числа? — спросил Олег.
— Всякому овощу свое время.
Пришлось спрятать любопытство в карман. Мы распрощались с мамой Двойкой и пошли… Куда бы ты думал? Конечно, в Парк Науки и Отдыха.
Как мы там отдыхали, узнаешь из следующего письма.
Таня.
Запомни раз и навсегда: нуль — единственное число, которое не бывает ни положительным, ни отрицательным. Это что-то вроде пограничника, который стоит на рубеже между положительными и отрицательными числами.
Конечно, в твоей школе тоже есть положительные и отрицательные Нулики. Но это ведь совсем другое дело. Просто одни из них хорошие, а другие — плохие.
Второй твой вопрос — о Великанах — очень интересный. Но ответил на него не автомат, а мама Двойка. Она говорит, что ты любознательный ребенок.
Оба конца монорельсовой дороги и вправду ведут в Бесконечность. А в Бесконечности, понятно, живут числа — Великаны. Бесконечность тоже бывает положительная и отрицательная. Только там свои, особые законы. Положительные и отрицательные Великаны прекрасно уживаются. Но как это им удается, мы не узнали. Это как раз один из тех вопросов, на которые мама Двойка отвечает: «Всякому овощу свое время».
А теперь танцуй! Мы научились умножать и делить отрицательные числа.
Ты ведь знаешь, что умножение можно рассматривать как сложение. Умножить два на три — все равно что сложить три двойки:
+ + + + + +
2 * 3 = 2 + 2 + 2 = 6
То же самое происходит, когда отрицательное число умножают на положительное. Разве умножить минус два на плюс три — это не то же самое, что сложить три отрицательные двойки? А так как при сложении отрицательных чисел вагончики двигаются влево от Нулевой станции, то и произведение будет отрицательное — минус шесть:
— + — — — —
2 * 3 = 2 + 2 + 2 = 6
— Какая же разница? — сказала мама Двойка. — Как было минус шесть, так и останется минус шесть. Вот смотрите:
— + — — —
3 * 2 = 3 + 3 = 6
— Ну что ж, выясняйте, — сказала мама Двойка, — мы с удовольствием вас послушаем.
— Ах вот оно что! Тогда другое дело.
Всем нам стало неловко за Севу. Мы подумали, что мама Двойка обиделась, но она посмотрела на нас смеющимися глазами и продолжала:
— Вы хотели знать, что происходит при перемножении двух отрицательных чисел? Нетрудно догадаться. Чтобы умножить любое число на положительное, надо отложить его на монорельсе в ту же сторону от Нулевой станции, с какой оно находится. Это мы только что видели.
Когда же мы умножаем любое число на отрицательное, все происходит наоборот. Вы ведь знаете, какие упрямцы эти отрицательные числа! Поэтому умножаемое откладывается не с той стороны, где оно находится, а по другую сторону от нуля:
+ — —
2 * 4 = 8
Теперь нетрудно понять, что получится при умножении отрицательного числа на отрицательное; в этом случае умножаемое надо откладывать вправо от нуля:
— — +
2 * 4 = 8
— Такие чудеса случаются у нас в Аль-Джебре на каждом шагу, — ответила мама Двойка.
— Ну, если так, расскажите нам поскорее про деление. Там, наверное, будут какие-нибудь новые чудеса?
— Ничуть не бывало. Деление — действие, обратное умножению. Стало быть, и правила знаков не меняются:
— + —
6 : 3 = 2
— — —
6 : 3 = 2
Мы почувствовали себя ужасно образованными. А пуще всех — Сева.
— Теперь нам все нипочем! — заявил он. — Мы знаем эту дорогу как свои пять пальцев!
— Ошибаетесь, — сказала мама Двойка, — вы познакомились только с целыми числами.
— А разве здесь есть и другие?
— А как же!
— Вы, наверное, подразумеваете дробные числа, — предположил Олег.
— Не только. Дробные числа — это те, что расположены между целыми числами. — Мама Двойка указала на палочки ограды, которые мы недавно пересчитывали. — Здесь расстояние между двумя целыми числами разделено на десять равных частей. Каждая из них составляет одну десятую единицы. Но ведь этих делений может быть и гораздо больше. Мысленно мы можем разделить это расстояние на любое число частей.
— Значит, вагончик может останавливаться не только у целого числа, но и у любой дроби, то есть между станциями?
Мы тут же вызвали вагончик и заставили его остановиться сперва против числа 2,5, а потом против 3,44… Этого нам показалось мало. Мы назвали число минус пять и четыре миллионных: —5,000 004, и красный вагончик, миновав Нулевую станцию, превратился в синий и остановился на волосок дальше станции минус 5.
— Выходит, — неуверенно сказал Сева, — вся эта бесконечная дорога сплошь заполнена числами?
— Именно сплошь! — ответила мама Двойка. — Можно сказать, непрерывно. У нас очень большая плотность населения. На всем пути не сыскать ни одной точечки, не заселенной каким-нибудь числом. Есть среди этих чисел и такие, величину которых мы никогда не можем вычислить точно.
— Что ж это за число, которое нельзя вычислить?
— Ну, хотя бы корень квадратный из двух: √2. Попробуйте найти число, которое при возведении в квадрат давало бы два.
Сева наморщил лоб, подумал немного, потом махнул рукой и засмеялся:
— И много таких чисел?
— Бесконечное множество. Их называют иррациональными в отличие от рациональных. Латинское слово «рацио» значит «разум». Следовательно, рациональные числа — это разумные числа, то есть числа, постижимые разумом.
Сева прямо задохнулся от смеха:
— Ой, умираю! Рациональные — значит разумные. А иррациональные — сумасшедшие, что ли?
— Ну, зачем же так! — обиделась мама Двойка. — Просто они не поддаются точному вычислению. Поэтому их долгое время не признавали числами. Но с тех пор как у нас появилась воздушная монорельсовая дорога (или числовая прямая — так ее называют по-другому), иррациональные числа после долгих скитаний получили, наконец, точный адрес. Вычислить их по-прежнему можно только приближенно. Зато легко указать место на монорельсовой дороге, где они живут. Вместе с числами рациональными они образуют дружную семью действительных чисел, — закончила мама Двойка и снова заставила нас удивиться.
— А разве бывают и недействительные?
— Конечно. Есть числа мнимые, есть комплексные…
Сева не дал ей договорить.
— Вспомнил! — заорал он. — И Мнимая Единица может на что-нибудь пригодиться!
— Да, да, — подтвердила я, — так ответил автомат маленькой буковке с зонтиком: i.
— Оно и понятно, — сказала мама Двойка, — латинской буквой i (по-русски — И) в Аль-Джебре обозначается Мнимая Единица.
— Но почему мнимая? Она что, воображаемая?
— Настолько воображаемая, что ей, как и другим мнимым числам, не нашлось местечка на всей бесконечной монорельсовой дороге.
— Так вот почему она была такая грустная! — смекнул Сева.
— А где же тогда живут мнимые числа? — спросил Олег.
— Всякому овощу свое время.
Пришлось спрятать любопытство в карман. Мы распрощались с мамой Двойкой и пошли… Куда бы ты думал? Конечно, в Парк Науки и Отдыха.
Как мы там отдыхали, узнаешь из следующего письма.
Таня.
Молотобойцы
(Сева — Нулику)
Здравствуй, старик! Не удивляйся, что вместо Олега пишу тебе я. Мне так захотелось самому рассказать, как я здорово отличился, что он уступил мне свою очередь.
Говорят, великие люди занимались физическим трудом и спортом. Лев Толстой косил траву, шил сапоги. Ученый Павлов играл в городки. А я решил стать молотобойцем.
Здесь в парке есть занятный аттракцион — силомер. Такие встречаются и у нас, но этот устроен немного по-другому.
У нас ударяешь молотом по наковальне, и гирька подскакивает вверх. Чем сильнее ударишь, тем выше она поднимется. На таком силомере меряются силами. На здешнем — знаниями.
Рейка, вдоль которой движется гиря, очень похожа на монорельсовую дорогу. Только числовая прямая здесь расположена по-другому: не в длину, а в вышину. И числа на ней, начиная с нуля, только положительные. На этом силомере возводят числа в степень.
Задумываешь число, возводишь в уме в какую-нибудь степень, а потом, чтобы проверить себя, бьешь молотком по наковальне. Гирька долетает до вычисленной степени. Если ты возвел правильно, у этого числа зажигается зеленый огонек, ошибся — красный.
Первый удар предоставили Тане. Ничего не поделаешь: девочка! Она возвела два в третью степень. У нее получилось восемь. Таня стукнула молотком, гирька взлетела к восьмерке, и зажглась зеленая лампочка.
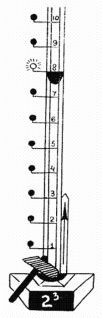Потом стукнул Олег. Он возвел два в десятую степень. Получилось 1024. И когда гирька долетела до этого числа, снова зажглась зеленая лампочка. Все это показалось мне очень уж обыкновенным. Захотелось отмочить что-нибудь такое, чтобы все ахнули. Я объявил, что сделаю удар в честь моего друга Нулика-Профессора.
Возвел двойку в нулевую степень. У меня получился нуль.
Я изо всей силы трахнул молотком по наковальне, и-ха-ха! — гирька осталась на нуле. Этого-то я и хотел! Но как же я удивился, когда вместо зеленого огонька зажегся красный! Может быть, я так сильно ударил, что силомер испортился? Но почему же тогда все кругом засмеялись?
Я не знал что и подумать, но тут какая-то латинская буковка — не то Эн, не то Эм — сказала, что таких ошибок у них даже дети не делают и что любое число, возведенное в нулевую степень, всегда равно не нулю, а единице. Я несколько раз проверил это на силомере — правильно! И пять, и сто, и двести — все они в нулевой степени равны единице.
Тогда я решил возвести в нулевую степень нуль. Я рассуждал так: коли нуль — это число, а все числа в нулевой степени равны единице, то и нуль в нулевой степени тоже равен единице. Ударил по наковальне и…
Лучше бы я этого никогда не делал!
Гирька словно взбесилась: сперва взвилась под облака, потом ушла куда-то под землю, потом опять взмыла вверх. И так она металась туда-сюда, пока кто-то не догадался выключить силомер.
Тут уж никто не смеялся. У всех были испуганные лица — почти как на том представлении, где твой тезка, Нулик, стащил знак умножения. Я и сам-то перепугался до смерти.
Страшнее всего было то, что гиря все время куда-то проваливалась. Оказалось, числовая прямая уходит другим концом в бездонный колодец, где помещаются отрицательные числа.
Наверное, у меня был очень несчастный вид, потому что та же буква — не то Эм, не то Эн — подошла ко мне и стала утешать.
— Успокойтесь, — сказала она, — так может быть со всяким, кто впервые в Аль-Джебре. Нуль и в самом деле число, но совсем особенное. Вы ведь помните, что оно не бывает ни положительным, ни отрицательным. Поэтому обращаться с ним надо осторожно. А когда возводишь нуль, да еще в нулевую степень, нужно быть осторожным вдвойне. Потому что при этом получается неопределенное число. Оно может быть и пятеркой, и миллионом, и бесконечностью, и положительным, и отрицательным, и даже нулем! Поэтому гирька до того растерялась и разнервничалась, что силомер испортился.
Славная буковка! Мне захотелось сказать ей что-нибудь приятное. Вообще-то у меня это плохо получается. Но я вовремя вспомнил, как тетя Нина разговаривает с гостями.
— Ах, ах, это в высшей степени интересно! — сказал я самым что ни на есть разлюбезным голосом.
— Благодарю вас, — засмеялась буковка. — Но не советую употреблять выражение «в высшей степени» в Аль-Джебре. Как бы ни была высока степень, всегда найдется еще более высокая. Ведь числа бесконечны.
Эх, подвела меня тетя!
Тут силомер снова наладили, и Тане вздумалось возвести число не в целую степень, а в дробную.
— Если возвести четыре в половинную степень, по-моему, получится два, — сказала она.
— С чего это ты взяла? — спросил я.
— А вот с чего: четыре в нулевой степени равно единице. Четыре в первой степени — четырем. Значит, четыре в половинной степени равно половине от четырех, то есть двум.
Таня стукнула молотком. Гирька остановилась у числа два, и вспыхнула зеленая лампочка. Тогда и мне захотелось попробовать.
— Возвожу девять в половинную степень, — объявил я. — Рассуждаю так: девять в нулевой степени — это единица. Девять в первой степени — девять. Значит, девять в половинной степени равно четырем с половиной.
Я торжественно стукнул молотком, гирька остановилась на четырех с половиной, и… вспыхнула красная лампочка. Я прямо обалдел. Несчастный я человек! Ну почему, почему мне так не везет? Ведь я рассуждал точно так же, как Таня!
И снова на помощь мне пришла та же буковка (а я так и не запомнил — Эм она или Эн!).
— Дело в том, — сказала она, — что эта девочка допустила ошибку, а вы ее повторили. Девять в половинной степени и вправду находится между единицей и девяткой. Но оно вовсе не равно половине от девяти. Для того чтобы возвести число в половинную степень, надо не делить его на два, а извлечь из него корень второй степени. А корень второй степени из девяти равен трем, а не четырем с половиной.
— Так почему же у Тани получилось правильно?
— Да потому, что корень второй степени из четырех равен двум, а два и есть как раз половина от четырех. И это — простое совпадение.
Таня, конечно, покраснела, а Олег (он всегда ее выручает), чтобы отвлечь от нее внимание, сделал вывод:
— Значит, возвести число в степень, равную одной пятой — это все равно что извлечь из этого числа корень пятой степени.
Например: 31/5 = 5√3.
— Ваша правда, — подтвердила буковка.
— Тогда, наверное, и обратно, — продолжал Олег. — Возвести число в пятую степень — это все равно что извлечь из него корень степени одна пятая: 35 = 1/5√3.
Что ты скажешь! Он и на этот раз попал в самую точку!
Тут мне пришло в голову, что если можно возводить числа в положительные степени, то почему бы не попробовать в отрицательные? Буковка посмотрела на меня пристально:
— Уж очень вы торопитесь! Аль-Джебра — государство большое. Для того чтобы с ним как следует познакомиться, нужны не дни, не недели, а годы…
Еще чего! А как же Черная Маска? Так и останется без лица?
Посовещались немного и решили, что довольно ходить вокруг да около. Пора приниматься за дело. Но прежде неплохо бы закусить! То-то мне стали вспоминаться гостеприимные обжоры…
Буковка словно угадала мои мысли:
— Может быть, вы проголодались? Тогда советую зайти в кафе «Абракадабра».
А нам только того и надо!
Хочешь знать, что дальше? Потерпи немножко. Всякому овощу…
Сева.
Говорят, великие люди занимались физическим трудом и спортом. Лев Толстой косил траву, шил сапоги. Ученый Павлов играл в городки. А я решил стать молотобойцем.
Здесь в парке есть занятный аттракцион — силомер. Такие встречаются и у нас, но этот устроен немного по-другому.
У нас ударяешь молотом по наковальне, и гирька подскакивает вверх. Чем сильнее ударишь, тем выше она поднимется. На таком силомере меряются силами. На здешнем — знаниями.
Рейка, вдоль которой движется гиря, очень похожа на монорельсовую дорогу. Только числовая прямая здесь расположена по-другому: не в длину, а в вышину. И числа на ней, начиная с нуля, только положительные. На этом силомере возводят числа в степень.
Задумываешь число, возводишь в уме в какую-нибудь степень, а потом, чтобы проверить себя, бьешь молотком по наковальне. Гирька долетает до вычисленной степени. Если ты возвел правильно, у этого числа зажигается зеленый огонек, ошибся — красный.
Первый удар предоставили Тане. Ничего не поделаешь: девочка! Она возвела два в третью степень. У нее получилось восемь. Таня стукнула молотком, гирька взлетела к восьмерке, и зажглась зеленая лампочка.
Возвел двойку в нулевую степень. У меня получился нуль.
Я изо всей силы трахнул молотком по наковальне, и-ха-ха! — гирька осталась на нуле. Этого-то я и хотел! Но как же я удивился, когда вместо зеленого огонька зажегся красный! Может быть, я так сильно ударил, что силомер испортился? Но почему же тогда все кругом засмеялись?
Я не знал что и подумать, но тут какая-то латинская буковка — не то Эн, не то Эм — сказала, что таких ошибок у них даже дети не делают и что любое число, возведенное в нулевую степень, всегда равно не нулю, а единице. Я несколько раз проверил это на силомере — правильно! И пять, и сто, и двести — все они в нулевой степени равны единице.
Тогда я решил возвести в нулевую степень нуль. Я рассуждал так: коли нуль — это число, а все числа в нулевой степени равны единице, то и нуль в нулевой степени тоже равен единице. Ударил по наковальне и…
Лучше бы я этого никогда не делал!
Гирька словно взбесилась: сперва взвилась под облака, потом ушла куда-то под землю, потом опять взмыла вверх. И так она металась туда-сюда, пока кто-то не догадался выключить силомер.
Тут уж никто не смеялся. У всех были испуганные лица — почти как на том представлении, где твой тезка, Нулик, стащил знак умножения. Я и сам-то перепугался до смерти.
Страшнее всего было то, что гиря все время куда-то проваливалась. Оказалось, числовая прямая уходит другим концом в бездонный колодец, где помещаются отрицательные числа.
Наверное, у меня был очень несчастный вид, потому что та же буква — не то Эм, не то Эн — подошла ко мне и стала утешать.
— Успокойтесь, — сказала она, — так может быть со всяким, кто впервые в Аль-Джебре. Нуль и в самом деле число, но совсем особенное. Вы ведь помните, что оно не бывает ни положительным, ни отрицательным. Поэтому обращаться с ним надо осторожно. А когда возводишь нуль, да еще в нулевую степень, нужно быть осторожным вдвойне. Потому что при этом получается неопределенное число. Оно может быть и пятеркой, и миллионом, и бесконечностью, и положительным, и отрицательным, и даже нулем! Поэтому гирька до того растерялась и разнервничалась, что силомер испортился.
Славная буковка! Мне захотелось сказать ей что-нибудь приятное. Вообще-то у меня это плохо получается. Но я вовремя вспомнил, как тетя Нина разговаривает с гостями.
— Ах, ах, это в высшей степени интересно! — сказал я самым что ни на есть разлюбезным голосом.
— Благодарю вас, — засмеялась буковка. — Но не советую употреблять выражение «в высшей степени» в Аль-Джебре. Как бы ни была высока степень, всегда найдется еще более высокая. Ведь числа бесконечны.
Эх, подвела меня тетя!
Тут силомер снова наладили, и Тане вздумалось возвести число не в целую степень, а в дробную.
— Если возвести четыре в половинную степень, по-моему, получится два, — сказала она.
— С чего это ты взяла? — спросил я.
— А вот с чего: четыре в нулевой степени равно единице. Четыре в первой степени — четырем. Значит, четыре в половинной степени равно половине от четырех, то есть двум.
Таня стукнула молотком. Гирька остановилась у числа два, и вспыхнула зеленая лампочка. Тогда и мне захотелось попробовать.
— Возвожу девять в половинную степень, — объявил я. — Рассуждаю так: девять в нулевой степени — это единица. Девять в первой степени — девять. Значит, девять в половинной степени равно четырем с половиной.
Я торжественно стукнул молотком, гирька остановилась на четырех с половиной, и… вспыхнула красная лампочка. Я прямо обалдел. Несчастный я человек! Ну почему, почему мне так не везет? Ведь я рассуждал точно так же, как Таня!
И снова на помощь мне пришла та же буковка (а я так и не запомнил — Эм она или Эн!).
— Дело в том, — сказала она, — что эта девочка допустила ошибку, а вы ее повторили. Девять в половинной степени и вправду находится между единицей и девяткой. Но оно вовсе не равно половине от девяти. Для того чтобы возвести число в половинную степень, надо не делить его на два, а извлечь из него корень второй степени. А корень второй степени из девяти равен трем, а не четырем с половиной.
— Так почему же у Тани получилось правильно?
— Да потому, что корень второй степени из четырех равен двум, а два и есть как раз половина от четырех. И это — простое совпадение.
Таня, конечно, покраснела, а Олег (он всегда ее выручает), чтобы отвлечь от нее внимание, сделал вывод:
— Значит, возвести число в степень, равную одной пятой — это все равно что извлечь из этого числа корень пятой степени.
Например: 31/5 = 5√3.
— Ваша правда, — подтвердила буковка.
— Тогда, наверное, и обратно, — продолжал Олег. — Возвести число в пятую степень — это все равно что извлечь из него корень степени одна пятая: 35 = 1/5√3.
Что ты скажешь! Он и на этот раз попал в самую точку!
Тут мне пришло в голову, что если можно возводить числа в положительные степени, то почему бы не попробовать в отрицательные? Буковка посмотрела на меня пристально:
— Уж очень вы торопитесь! Аль-Джебра — государство большое. Для того чтобы с ним как следует познакомиться, нужны не дни, не недели, а годы…
Еще чего! А как же Черная Маска? Так и останется без лица?
Посовещались немного и решили, что довольно ходить вокруг да около. Пора приниматься за дело. Но прежде неплохо бы закусить! То-то мне стали вспоминаться гостеприимные обжоры…
Буковка словно угадала мои мысли:
— Может быть, вы проголодались? Тогда советую зайти в кафе «Абракадабра».
А нам только того и надо!
Хочешь знать, что дальше? Потерпи немножко. Всякому овощу…
Сева.
Нулик-пограничник
(Нулик — отряду РВТ)
Хорошо еще, что у меня такая добрая мама. Она меня простила и даже подарила силомер. Получше вашего-то: волшебный! Выбираешь число, задумываешь, в какую степень его возвести, бьешь молотком, и гирька сама показывает ответ.
Я принес силомер в школу, и все стали возводить нуль в разные степени. Но как мы ни старались, гирька ни разу не поднялась выше нуля. Словно ее приклеили. Как вы думаете, отчего это? Может, у нас сил не хватает, чтобы ударить как следует?
Но и от этого толку мало: какое число ни возьмешь, гирька хоть и поднимается, но очень немножко, не выше единицы. Тогда мы взяли большущее число 1000 и возвели его в минус третью степень: 1000—3. Ухватились за молоток сообща и как трахнем! А противная гирька почти не сдвинулась с места. Что ж это такое? Неужели мама подарила мне испорченный силомер?
Я на нее очень обиделся, но она только рассмеялась. Она вообще любит смеяться. А потом сказала, что если возводить целое положительное число в целую отрицательную степень, то больше единицы никогда не получится. И чем большее число возводишь, тем меньшее число получается. Вот силомер и показал всего — навсего одну миллиардную: 0,000000001.
На этом основании я могу сказать, что не только вы меня, но и я вас могу кое-чему научить. Вот как!
Нулик-Пограничник.
P.S. Когда же вы напишете про кафе «Абракадабра»?
Карнавал
(Олег — Нулику)
Здравствуй, дружище! Ты просишь рассказать про кафе «Абракадабра», но так случилось, что мы опять туда не попали. Заколдованное оно, что ли? Мы уже были совсем близко, но тут дорогу нам преградило веселое карнавальное шествие.
Впереди всех шли цифры. Многие держали на плечах маленьких Нуликов. Прямо как у нас на первомайской демонстрации.
Вслед за цифрами дружно выступали латинские и греческие буквы.
Четким строевым шагом прошли знаки равенства, за ними — действующие знаки.
Легко подпрыгивали разноцветные точки, похожие на целлулоидовые мячики. Некоторые плавали в воздухе, как воздушные шары.
Вот промелькнули, кувыркаясь на ходу, ловкие гимнасты: знаки сложения и вычитания. Проковыляли на ходулях радикалы. Над ними — ни дать ни взять рой бабочек — порхали показатели корней.
А потом пошли скобки, скобки, скобки… Круглые, квадратные, фигурные…
Позади маршировал сводный оркестр восклицательных знаков.
— Слава доблестным факториалам! — закричали в толпе. Мы хотели спросить, что за слово такое, но тут эти самые факториалы грянули марш. Разом ударились друг о друга десятки медных тарелок, загремели трубы. Защебетали, словно стая ласточек, флейты, и все кругом запели.
Так никто нам и не объяснил, что такое факториал и что вообще происходит.
— Может быть, это праздник Кирилла и Мефодия? — сказала Таня.
Ее мама недавно была в Болгарии. Там каждый год устраивают торжества в честь создателей славянской письменности. В этот день жители надевают свои лучшие платья и выходят на улицу, чтобы посмотреть парад букв. В параде участвуют школьники. Каждый из них изображает какую-нибудь букву.
— При чем тут Кирилл и Мефодий? — фыркнул Сева. — Аль-Джебра — государство математическое. Не пойму только, как сюда попали буквы? Наверное, по недоразумению?
Он, как всегда, сказал это чересчур громко. Вот когда нас наконец услышали!
— Как это — по недоразумению? — возмутились толпившиеся кругом буквы. — Это мы-то по недоразумению? Нас оскорбляют! Нас унижают!
— Да знаете ли вы, — кипятилась латинская буква Тэ, — знаете ли вы, что без нас, может, и не было бы никакой Аль-Джебры!
— Может, и не было бы! — подтвердили хором другие буквы.
Мне с трудом удалось объяснить им, что Сева не хотел никого обидеть. Просто мы здесь впервые и многого еще не знаем. Буквы сменили гнев на милость и стали наперебой что-то нам объяснять. Но они так волновались и галдели, что ничего нельзя было разобрать.
— Граждане буквы, — сказал я, — говорите по очереди! Так мы легче поймем друг друга.
Тогда из толпы вышел важный Дэ.
— Пусть каждый из вас, — сказал он, — задумает какое-нибудь число. Задумали? Хорошо. Теперь умножьте его на три. Так. Прибавьте четыре. Готово? Теперь пусть каждый скажет, какое число у него получилось.
— Десять! — объявила Таня.
— Нет, девятнадцать! — возразил Сева.
— А у меня шестьдесят четыре, — сказал я.
— Видите, вас трое, и у каждого получилось по-разному.
Но в этой игре могут быть тысячи, миллионы участников. Каждый может задумать любое число, и мы получим целую гору ответов. Для того только чтобы прочитать их — не то что записать, — понадобится уйма времени. А я вот записал на этом клочке бумаги все возможные ответы.
И Дэ показал нам свою запись: 3а + 4.
— Позвольте, где же девятнадцать? — всполошился Сева.
Впереди всех шли цифры. Многие держали на плечах маленьких Нуликов. Прямо как у нас на первомайской демонстрации.
Вслед за цифрами дружно выступали латинские и греческие буквы.
Четким строевым шагом прошли знаки равенства, за ними — действующие знаки.
Легко подпрыгивали разноцветные точки, похожие на целлулоидовые мячики. Некоторые плавали в воздухе, как воздушные шары.
Вот промелькнули, кувыркаясь на ходу, ловкие гимнасты: знаки сложения и вычитания. Проковыляли на ходулях радикалы. Над ними — ни дать ни взять рой бабочек — порхали показатели корней.
А потом пошли скобки, скобки, скобки… Круглые, квадратные, фигурные…
Позади маршировал сводный оркестр восклицательных знаков.
— Слава доблестным факториалам! — закричали в толпе. Мы хотели спросить, что за слово такое, но тут эти самые факториалы грянули марш. Разом ударились друг о друга десятки медных тарелок, загремели трубы. Защебетали, словно стая ласточек, флейты, и все кругом запели.
Так никто нам и не объяснил, что такое факториал и что вообще происходит.
— Может быть, это праздник Кирилла и Мефодия? — сказала Таня.
Ее мама недавно была в Болгарии. Там каждый год устраивают торжества в честь создателей славянской письменности. В этот день жители надевают свои лучшие платья и выходят на улицу, чтобы посмотреть парад букв. В параде участвуют школьники. Каждый из них изображает какую-нибудь букву.
— При чем тут Кирилл и Мефодий? — фыркнул Сева. — Аль-Джебра — государство математическое. Не пойму только, как сюда попали буквы? Наверное, по недоразумению?
Он, как всегда, сказал это чересчур громко. Вот когда нас наконец услышали!
— Как это — по недоразумению? — возмутились толпившиеся кругом буквы. — Это мы-то по недоразумению? Нас оскорбляют! Нас унижают!
— Да знаете ли вы, — кипятилась латинская буква Тэ, — знаете ли вы, что без нас, может, и не было бы никакой Аль-Джебры!
— Может, и не было бы! — подтвердили хором другие буквы.
Мне с трудом удалось объяснить им, что Сева не хотел никого обидеть. Просто мы здесь впервые и многого еще не знаем. Буквы сменили гнев на милость и стали наперебой что-то нам объяснять. Но они так волновались и галдели, что ничего нельзя было разобрать.
— Граждане буквы, — сказал я, — говорите по очереди! Так мы легче поймем друг друга.
Тогда из толпы вышел важный Дэ.
— Десять! — объявила Таня.
— Нет, девятнадцать! — возразил Сева.
— А у меня шестьдесят четыре, — сказал я.
— Видите, вас трое, и у каждого получилось по-разному.
Но в этой игре могут быть тысячи, миллионы участников. Каждый может задумать любое число, и мы получим целую гору ответов. Для того только чтобы прочитать их — не то что записать, — понадобится уйма времени. А я вот записал на этом клочке бумаги все возможные ответы.
И Дэ показал нам свою запись: 3а + 4.
— Позвольте, где же девятнадцать? — всполошился Сева.