Страница:
Фокусник подал знак, и буквы а в сопровождении индексов быстро расселись на палке:
— Внимание! Приступаю к выводу формулы. В этом ряду под а1 и а2 можно подразумевать любые числа.
— Ну конечно, — сказал Сева, — так же как и под всеми остальными.
— Думайте, думайте, молодой человек! — возразил фокусник. — Ведь все эти а — члены одной арифметической прогрессии. Поэтому произвольно могут быть взяты только первые два а. Величины остальных зависят от разности между двумя первыми. Итак, обозначаю разность буквой d. Ведь разность прогрессии постоянна. Тогда a2 = а1 + d; а3 = а2 + d; a4 = a3 + d.
И так до конца прогрессии. Понятно?
— Понятно, понятно! — закричали все.
— Продолжаю! Надеюсь, все заметили, что в этой прогрессии восемь членов. Или четыре пары. Сумму крайних членов записываю так: а1 + а8.
Обозначаю сумму всех членов большой латинской буквой Эс — S. Ведь слово «сумма» начинается с этой буквы! Значит, S = 4(а1 + a8).
Кто-то спросил:
— А если в прогрессии десять членов? Как тогда вычислить сумму?
— Точно так же, — ответил фокусник. — Только пар станет уже не четыре, а пять, и последний член прогрессии будет a10: S = 5 (a1 + a10).
— Стало быть, это справедливо для любого числа членов? — не унимался дотошный зритель.
— Какое число членов вам угодно сложить?
— Пять! Двадцать! Сто семьдесят пять! Двести сорок! Миллион семьсот тысяч! — неслось со всех сторон.
Фокусник закрыл уши руками:
— Тише, тише! Сейчас все ваши просьбы будут исполнены.
Он подождал, когда все успокоятся, и снова заговорил:
— Обозначаю число членов буквой Эн — n. Тогда последний член прогрессии будет а энное — an, а сумма крайних членов a1 + an.
Нетрудно догадаться, что число пар будет в два раза меньше числа n, то есть n/2. Вот и выходит, что сумма членов запишется так: S = (a1 + an) * n/2.
— Разрешите спросить, — сказал Олег, — если число членов прогрессии нечетное, как вы его разобьете на пары?
— А уж над этим вы подумайте сами. Но поверьте честному слову фокусника — формула нисколько не изменится.
Он еще раз сложил свою палку, и она тут же исчезла. Все захлопали, засмеялись. Фокусник тоже сложился пополам и исчез так же неожиданно, как его палка.
Вот какие фокусы показывают в Аль-Джебре.
Таня.
Последняя калитка
Простота и невероятность
Новые открытия Нулика
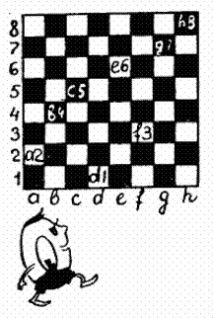Здравствуйте, ребята! Ну и работу вы нам задали! Теперь мы только и делаем, что играем в шахматы. Каждый сам смастерил себе доску и фигуры. Играем с утра до вечера — то друг с другом, а то и каждый сам с собой. Но я все-таки успел сделать открытие: по шахматной доске сразу видно, что Карликания и Аль-Джебра друзья. Ведь каждая шахматная клетка имеет свое обозначение, которое состоит из цифр и букв. Например, е5, а4, d8. Разве это не доказательство дружбы?
Задачу с зернами все-таки решили проверить. Конечно, без риса. Просто все стали писать на своих досках, сколько надо положить рисинок на каждую клетку: 1, 2, 4, 8, 16, 32, 64, 128… Когда заполнили первый ряд, выяснилось, что одни пишут слева направо, а другие справа налево.
Стали спорить, как надо писать. Положили две доски одну под другой. На одной числа написаны внизу, слева направо, на другой — вверху, справа налево. Числа, одинаково отстоящие от края, оказались друг против друга. Прямо как на палке у фокусника!
Я попробовал сложить каждую пару, но одинаковых чисел не получилось. Понятно: ведь прогрессия-то не арифметическая, а геометрическая! Тогда я их перемножил и сделал второе открытие: все произведения оказались совершенно одинаковые:
1 Х 128 = 128;
2 X 64 = 128;
4 X 32 = 128;
8 X 16 = 128.
Да, теперь я уже не тот Нулик, что прежде. Меня и вправду не узнать. А все ваши письма!
Дальше считать зерна никто не захотел — кому же охота писать такие огромные числа? Но один Нулик задал интересный вопрос: если на шестьдесят четвертую клетку надо положить девять с лишним квинтиллионов зерен, то сколько всего зерен будет на доске, если, конечно, заполнить все клетки?
— Что тут думать! — сказал другой Нулик. — Всего на доске будет зерен два в шестьдесят третьей степени. То есть вот эти девять квинтиллионов.
— Ничего подобного, — возразил третий, — девять квинтиллионов будет только на последней клетке, а на всей доске во много раз больше.
Они заспорили, а я снова посмотрел на свою шахматную доску, где в первом ряду написана геометрическая прогрессия: 1, 2, 4, 8, 16, 32, 64, 128. После треугольника Паскаля я вообще стал очень внимательно рассматривать числа — все время ищу закономерности! Вот и сейчас сложил первый член прогрессии со вторым: 1 + 2 = 3. Сумма их оказалась на единицу меньше третьего члена — четверки. Потом я сложил 1 + 2 + 4. Получилось семь. А это на единицу меньше восьми. 1 + 2 + 4 + 8 = 15. И это тоже меньше шестнадцати на единицу. Выходит, сумма всех предыдущих членов этой геометрической прогрессии меньше последующего всегда на единицу. А это значит, что на шестидесяти трех клетках шахматной доски будет столько же зерен, сколько на последней, шестьдесят четвертой, только на одно зернышко меньше. А всего на доске зерен будет в два раза больше, чем на последней клетке, минус единица: 2 * 263 — 1. А это ведь все равно что 264 — 1.
Так я сделал третье открытие. И для этого мне не понадобилось ни писать всю прогрессию до конца, ни умножать девять квинтиллионов с хвостиком на два. Хорошая штука алгебра!
Нулик-Шахматист.
Волшебная практика
Весовая
— Внимание! Приступаю к выводу формулы. В этом ряду под а1 и а2 можно подразумевать любые числа.
— Ну конечно, — сказал Сева, — так же как и под всеми остальными.
И так до конца прогрессии. Понятно?
— Понятно, понятно! — закричали все.
— Продолжаю! Надеюсь, все заметили, что в этой прогрессии восемь членов. Или четыре пары. Сумму крайних членов записываю так: а1 + а8.
Обозначаю сумму всех членов большой латинской буквой Эс — S. Ведь слово «сумма» начинается с этой буквы! Значит, S = 4(а1 + a8).
Кто-то спросил:
— А если в прогрессии десять членов? Как тогда вычислить сумму?
— Точно так же, — ответил фокусник. — Только пар станет уже не четыре, а пять, и последний член прогрессии будет a10: S = 5 (a1 + a10).
— Стало быть, это справедливо для любого числа членов? — не унимался дотошный зритель.
— Какое число членов вам угодно сложить?
— Пять! Двадцать! Сто семьдесят пять! Двести сорок! Миллион семьсот тысяч! — неслось со всех сторон.
Фокусник закрыл уши руками:
— Тише, тише! Сейчас все ваши просьбы будут исполнены.
Он подождал, когда все успокоятся, и снова заговорил:
— Обозначаю число членов буквой Эн — n. Тогда последний член прогрессии будет а энное — an, а сумма крайних членов a1 + an.
Нетрудно догадаться, что число пар будет в два раза меньше числа n, то есть n/2. Вот и выходит, что сумма членов запишется так: S = (a1 + an) * n/2.
— Разрешите спросить, — сказал Олег, — если число членов прогрессии нечетное, как вы его разобьете на пары?
— А уж над этим вы подумайте сами. Но поверьте честному слову фокусника — формула нисколько не изменится.
Он еще раз сложил свою палку, и она тут же исчезла. Все захлопали, засмеялись. Фокусник тоже сложился пополам и исчез так же неожиданно, как его палка.
Вот какие фокусы показывают в Аль-Джебре.
Таня.
Последняя калитка
(Нулик — отряду РВТ)
Здравствуйте, ребята! Письмо Тани нам ужасно понравилось. И все мои ученики сразу захотели стать фокусниками. Но я сказал, что фокусником буду я, а они — моими ассистентами. Их дело — сидеть на палке.
Сначала на палке никто сидеть не хотел. А когда я их уговорил, оказалось, что сидеть не на чем. Потому что мы нигде не могли найти палку, которая складывается. Я очень расстроился, а все, наоборот, обрадовались и побежали кататься на калитке. Это у нас игра такая. В Арабелле давно уже нет никаких заборов. Случайно остался один по дороге в Римскую провинцию. Там еще такая скрипучая калитка. Сядешь на нее и ездишь. Вперед-назад, вперед-назад!
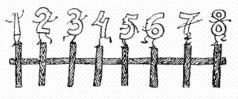Ну, я тоже поплелся. Все стали кататься, а я стоял в сторонке и смотрел. А потом догадался: вот она, палка, которая складывается! То есть не палка, а забор с калиткой. Ведь калитка, если ее открыть, доходит до самого забора! А забор сделан из редких поперечных планок. В калитке четыре поперечные планки. Отсчитать еще четыре на заборе. Выбрать восемь ассистентов — на каждой планке по одному — и открыть калитку до самого конца. Мое предложение понравилось. На палке не хотел сидеть никто, зато на заборе захотели сидеть все. Чтобы не было скандала, я отобрал восемь ассистентов по порядку: Единицу, Двойку, Тройку, Четверку, Пятерку, Шестерку, Семерку и Восьмерку.
Сказать по правде, я думал, что это никакая не прогрессия, а натуральный ряд чисел, но у меня другого выхода не было, иначе все бы передрались.
Числа стали на планки. Несколько других ассистентов ухватились за калитку. Я взмахнул рукой, калитка со страшным скрипом поехала к забору… И вот уже у нас получились четыре пары чисел:
4 и 5; 3 и 6; 2 и 7; 1 и 8.
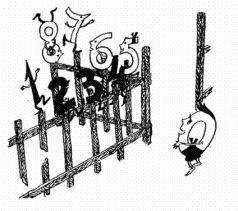Сложили каждую пару — получилось девять. Вот так штука! Выходит, я сделал открытие: натуральный ряд чисел тоже прогрессия. И разность ее равна единице.
Я сложил все числа натурального ряда от единицы до двухсот. Прямо в уме! Вот где мне пригодилась формула фокусника.
Первый член прогрессии a1 = l, а последний an = 200. Значит, сумма прогрессии равна:
S = (1 + 200) * 200/2 = 201 * 100 = 20100.
Двадцать тысяч сто! Вот здорово! От радости я изо всех сил ухватился за калитку и стал ее раскачивать вместе с ассистентами. И тут ржавые петли не выдержали, калитка отвалилась, и все попадали на землю. Настроение сразу испортилось. Еще бы! У кого синяк под глазом, у кого штаны порваны… И мы пошли домой.
По дороге я придумал еще одну прогрессию: 1 + 1 + 1 + 1 + 1 + 1 + 1 + …
И так до тысячи. В этой прогрессии разность равна нулю. Ведь нуль все-таки число! Подставил числа в формулу, и получилось: S = (1 + 1) * 1000/2 = 2 * 500 = 1000.
А дома мне здорово влетело от мамы — ей уже успели на меня нажаловаться.
— Это еще что за фокусы? — сказала она. — Никаких калиток! Чтобы больше этого не было!
Больше и не будет. Потому что кататься все равно не на чем. Калитка-то отвалилась, а она ведь была последняя!
Привет.
Нулик-Фокусник.
Сначала на палке никто сидеть не хотел. А когда я их уговорил, оказалось, что сидеть не на чем. Потому что мы нигде не могли найти палку, которая складывается. Я очень расстроился, а все, наоборот, обрадовались и побежали кататься на калитке. Это у нас игра такая. В Арабелле давно уже нет никаких заборов. Случайно остался один по дороге в Римскую провинцию. Там еще такая скрипучая калитка. Сядешь на нее и ездишь. Вперед-назад, вперед-назад!
Сказать по правде, я думал, что это никакая не прогрессия, а натуральный ряд чисел, но у меня другого выхода не было, иначе все бы передрались.
Числа стали на планки. Несколько других ассистентов ухватились за калитку. Я взмахнул рукой, калитка со страшным скрипом поехала к забору… И вот уже у нас получились четыре пары чисел:
4 и 5; 3 и 6; 2 и 7; 1 и 8.
Я сложил все числа натурального ряда от единицы до двухсот. Прямо в уме! Вот где мне пригодилась формула фокусника.
Первый член прогрессии a1 = l, а последний an = 200. Значит, сумма прогрессии равна:
S = (1 + 200) * 200/2 = 201 * 100 = 20100.
Двадцать тысяч сто! Вот здорово! От радости я изо всех сил ухватился за калитку и стал ее раскачивать вместе с ассистентами. И тут ржавые петли не выдержали, калитка отвалилась, и все попадали на землю. Настроение сразу испортилось. Еще бы! У кого синяк под глазом, у кого штаны порваны… И мы пошли домой.
По дороге я придумал еще одну прогрессию: 1 + 1 + 1 + 1 + 1 + 1 + 1 + …
И так до тысячи. В этой прогрессии разность равна нулю. Ведь нуль все-таки число! Подставил числа в формулу, и получилось: S = (1 + 1) * 1000/2 = 2 * 500 = 1000.
А дома мне здорово влетело от мамы — ей уже успели на меня нажаловаться.
— Это еще что за фокусы? — сказала она. — Никаких калиток! Чтобы больше этого не было!
Больше и не будет. Потому что кататься все равно не на чем. Калитка-то отвалилась, а она ведь была последняя!
Привет.
Нулик-Фокусник.
Простота и невероятность
(Олег — Нулику)
Вот мы и расстались с «Абракадаброй». Директор подробно объяснил, как нам завтра пройти на строительство. Мы поблагодарили его за угощение и пошли побродить.
Был уже вечер. Ярко светились огни домов, вспыхивали и гасли разноцветные вывески. Из раскрытых окон доносилась музыка. Там за накрытыми столами собрались жители Аль-Джебры, чтобы отметить свой праздник.
Нам вдруг стало не по себе. Почему-то захотелось домой. Но тут совсем близко раздался голос из репродуктора: «Внимание! Внимание! Через пять минут в Павильоне невероятных задач начнется праздничное состязание. Председателем жюри единогласно избран всемирно известный барон Мюнхгаузен. Желающих принять участие просят поторопиться!»
Ты, уж наверное, догадался: мы снова очутились рядом с Парком Науки и Отдыха. Можно подумать, ноги несли нас туда сами!
Вот и Павильон невероятных задач. С трудом отыскали свободные места. На эстраду вышли судьи. Мюнхгаузена встретили громкими аплодисментами. Кстати, роль его исполняла буква Ка. Барон учтиво раскланялся и начал:
— Уважаемая публика! Разрешите мне объяснить правила предстоящего состязания. Каждый участник должен придумать задачу. На первый взгляд она должна быть очень простой — такой простой, чтобы всем показалось, что решить ее легче легкого. Это — первое условие. Второе… О, второе условие — невероятность решения! Разумеется, я не говорю о решении на бумаге. Наоборот, задача должна быть решена в числах, но практически она должна быть невыполнима.
Итак, повторяю: условие состязания — простота и невероятность. Я мог бы для примера рассказать вам что-нибудь из своей практики. Но, к сожалению, все истории, которые со мной случались, были не только просты, но и вполне вероятны. Почему высмеетесь? Все знают, что барон Мюнхгаузен самый правдивый человек на свете. Разве не правда, что я верхом на пушечном ядре влетел в неприятельский город? Разве не правда, что я нанизал на бечевку целую стаю живых уток и вместе с ними взлетел в воздух? Таких правдоподобных историй у меня сколько угодно. Ваше же дело — придумать задачу, не выполнимую на практике. Не подумайте только, что она должна быть бессмысленной. За бессмысленные задачи участники платят штраф и вызывают из состязания. Ну что ж, начнем? Попрошу желающих. На сцену поднялись пухлая Шестерка и латинская буква Эн. Барон Мюнхгаузен предложил им тянуть жребий. Первой получила слово Шестерка. Вот что она рассказала:
— В давние времена, на Востоке, жил могущественный и грозный шах. Он был несметно богат. Все трепетали перед ним. Приближенные не только исполняли, но и предупреждали любое его желание. Сначала это нравилось шаху. Но настал день, когда все ему наскучило. Не радовали его больше ни наряды, ни яства, привезенные со всех концов света…
День ото дня становился он все угрюмее. Напрасно поэты слагали в его честь стихи. Напрасно пели для него самые искусные певцы, танцевали самые прославленные красавицы. Ничто не могло развлечь скучающего владыку. Целыми часами сидел он в своих роскошных покоях, бессмысленно глядя в одну точку. Дошло до того, что он заболел.
Врачи сменялись у его ложа чародеями и предсказателями. Но все их старания ни к чему не приводили. От шаха осталась одна тень. И все поняли, что дни его сочтены.
И вот у решетки шахского дворца появился странник. Босые ноги его были изранены, сквозь грязные лохмотья просвечивало тело. Странник сказался искусным врачом и потребовал, чтобы его пустили к шаху. Стража грубо оттолкнула оборванца. Тот поднял отчаянный крик. Услыхал его вопли шах и пожелал видеть безумца, который осмелился нарушить его покой. Нищего впустили.
— О великий шах, — сказал он, — я пришел, чтобы излечить тебя от тяжкого недуга.
— Чтобы излечить, надо знать причину болезни, — возразил шах. — Откуда знать тебе то, чего я и сам не знаю?
— Ошибаешься, — сказал странник, — причина твоей болезни — скука. Скука — бич богатых. Им нечего желать, потому что желания их тут же исполняются. Им не о чем думать, потому что за них думают другие. Я принес тебе лекарство, которое заставит тебя думать.
Странник достал из-под рваного плаща небольшую доску, расчерченную черными и белыми квадратами. Он положил ее на низенький столик рядом с шахским ложем и выстроил на ней черные и белые фигурки.
— Эту игру, — сказал он, — я назвал шахматами: ведь ей предстоит излечить шаха.
С этой минуты шах ни о чем, кроме шахмат, и знать не хотел. Целые дни проводил он вместе со странником за шахматной доской и подолгу размышлял над каждым ходом. Здоровье его заметно улучшилось. А когда ему удалось впервые выиграть партию, он почувствовал себя совершенно исцеленным.
— Требуй у меня всего, чего пожелаешь, — сказал он своему спасителю. — Захочешь, подарю тебе гору золота, захочешь — табун чистокровных арабских скакунов…
— О шах, — перебил его странник, — не надо мне ни золота, ни скакунов. В твоей стране столько голодных! Накорми их, — это будет для меня лучшим подарком.
— Какое мне дело до других! — воскликнул разгневанный шах. — Я обещал одарить тебя.
— Для себя мне немного нужно, — улыбнулся странник. — Видишь эту шахматную доску? На ней шестьдесят четыре клетки. Положи на первую клетку одно зернышко риса, на вторую — два зернышка, на третью — четыре, на четвертую — восемь. И так удваивай число зерен на каждой следующей клетке, до тех пор, пока не заполнишь последнюю. Вот и все.
— Только-то?! — облегченно вздохнул шах. — Мало же ты просишь! Я бы потребовал больше.
Принесли мешок риса, и шах сам начал выкладывать зерна. На первую клетку положил одно, на вторую — два, на третью — четыре…
Уже на седьмой клетке для шестидесяти четырех зерен не хватило места.
— Что же, — сказал странник, — вели ссыпать зерна в мешок.
Но шаху быстро наскучило считать. Он кликнул слуг. Теперь стали отсчитывать зерна они: шестьдесят четыре, сто двадцать восемь, двести пятьдесят шесть, пятьсот двенадцать, тысяча двадцать четыре…
Но это была еще только одиннадцатая клетка!
Стемнело. Зажгли светильники. Слуги чуть не падали от усталости. Когда они дошли до семнадцатой клетки, им нужно было отсчитать шестьдесят пять тысяч пятьсот тридцать шесть зерен. Но тут они сбились со счета. Несмотря на то что была уже глубокая ночь, шах велел разбудить мудрецов. Теперь он уже не смеялся, — побледнел, осунулся…
Прошли сутки, и еще одни сутки, и еще одни сутки, а мудрецы все считали… Вот уже и они стали валиться от усталости, а конца все еще не было видно. Слуги вносили все новые и новые мешки…
Но вот вбежал насмерть перепуганный хранитель шахских запасов. Он доложил, что в амбарах не осталось ни одного рисового зернышка.
— Негодяй! — закричал шах страннику. — Ты разорил меня!
— Я просил тебя накормить голодных, — ответил странник, — ты не захотел этого. Тогда я изменил свою просьбу. И ты счел меня глупцом. Попробуй теперь сосчитать, сколько зерен нужно положить на последнюю, шестьдесят четвертую клетку, и ты поймешь, кто из нас глупец. Опустоши все рисовые поля на свете — тебе и этого не хватит, чтобы со мной расквитаться.
— Ах так! — в бешенстве закричал шах. — Сейчас ты узнаешь, умею ли я платить сполна. Отрубить ему голову!
— Такова шахская справедливость, — закончила свой рассказ Шестерка. — А теперь прошу вас убедиться, что задача эта очень проста, но практически невыполнима. Число рисовых зерен росло по такому правилу: 1, 2, 4, 8, 16, 32, и так далее. Каждое последующее число больше предыдущего в два раза.
Такой ряд чисел называется геометрической прогрессией. Только, пожалуйста, не путайте ее с арифметической. В арифметической прогрессии каждое последующее число больше предыдущего на одно и то же число — оно называется разностью прогрессии. В геометрической прогрессии каждое последующее число больше предыдущего в одно и то же число раз, и число это называется знаменателем прогрессии.
В нашей задаче знаменатель прогрессии равен двум. Если хотите, эту прогрессию можно записать и так:
20, 21, 22, 23, 24, 25, 26…
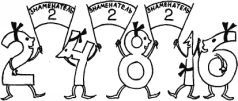Нетрудно догадаться, что на шестьдесят четвертой клетке должно быть 263 — два в шестьдесят третьей степени зерен, потому что на первую клетку приходится 20 — два в нулевой степени зерен, то есть одно зерно. Но если вы попробуете сосчитать, чему равно два в шестьдесят третьей степени, вы ужаснетесь. Такого огромного количества зерен никогда не смог бы раздобыть жестокий шах. Он не смог бы даже прочитать это число. Вот оно: 9 223 372 036 854 775 808 — девять квинтиллионов двести двадцать три квадриллиона триста семьдесят два триллиона тридцать шесть миллиардов восемьсот пятьдесят четыре миллиона семьсот семьдесят пять тысяч восемьсот восемь… Уф!
Попробуйте подсчитать, сколько это килограммов риса, если каждое зернышко в среднем весит 0,0182 грамма. Знаете, что получится? Больше ста шестидесяти семи триллионов килограммов! Стоит ли доказывать, что моя задача хоть и проста, но практически невыполнима?
Шестерка поклонилась и села. Ей долго хлопали. Потом поднялась латинская буква Эн. Она сказала так:
— Уважаемая Шестерка познакомила нас с геометрической прогрессией, где все числа непрерывно растут. Такая прогрессия называется возрастающей. Я позволю себе занять ваше внимание сразу двумя геометрическими прогрессиями — возрастающей и убывающей. И сделаю это на одном и том же примере. Задача моя будет так же проста, как предыдущая, и так же невыполнима. Моя предшественница рассказала прелестную сказку об изобретателе шахмат и коварном шахе. Позвольте и мне задать вам задачу, связанную с шахматами.
Эн вынула из кармана платок, развернула его и показала публике. На платке были нарисованы шестьдесят четыре квадрата, черные и белые, — как на шахматной доске.
— Будем считать, — продолжала Эн, — что этот платок заменяет нам шахматную доску. Обратите внимание — толщина платка равна 0,1 — одной десятой миллиметра. Складываю платок пополам. Теперь его толщина стала вдвое больше: две десятых миллиметра. Зато и площадь его стала меньше в два раза. Складываю платок еще раз вдвое. Теперь его толщина в четыре раза больше первоначальной, но и площадь уменьшилась в четыре раза. Я предлагаю складывать этот платок вдвое до тех пор, пока возможно. А потом продолжайте складывать мысленно.
Эн бросила платок в зал, кто-то его подхватил и стал перегибать: раз, второй, третий… Перегнул в шестой и крикнул:
— Готово! Теперь видна только одна клетка. Толщина платка увеличилась в шестьдесят четыре раза. Ничего невозможного тут нет.
— Вы сложили платок только шесть раз, — возразила Эн самонадеянному зрителю, — а надо было шестьдесят четыре! Понимаете разницу? Если бы вам удалось это сделать, толщина платка стала бы такой большой, что он перерос бы горы, миновал солнце и уперся бы в какую-нибудь отдаленную звезду.
— А вы докажите! — крикнули в зале.
Тогда Эн стала решать задачу на доске.
— Неужели вы не догадались, что я почти повторила предыдущую задачу? После каждого перегибания толщина платка увеличивается вдвое и возрастает по закону геометрической прогрессии: 2, 4, 8, 16, 32, 64 и так далее. Разница только в том, что после шестидесяти четырех перегибаний толщина платка станет больше не в 263, а в 264 раз. Оно и понятно: ведь эта прогрессия начинается не с 20 — двух в нулевой, а с 21 — двух в первой степени. Толщина развернутого платка 0,1 миллиметра. Чтобы вычислить толщину сложенного платка, надо 0,1 умножить на 264. Получается 1 844 674 407 371 километр.
Один триллион восемьсот сорок четыре миллиарда шестьсот семьдесят четыре миллиона четыреста семь тысяч триста семьдесят один километр.
А ведь расстояние от Земли до Солнца всего-навсего около ста пятидесяти миллионов километров!
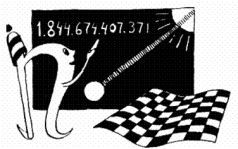Кажется, условие состязания выполнено: задача проста и практически невыполнима.
— А где же обещанная убывающая прогрессия? — спросил Сева.
— Да здесь же, — ответила Эн. — Ведь в то время как толщина платка увеличивается, площадь его все время уменьшается: 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, и так далее. Это и есть убывающая геометрическая прогрессия. После шестидесяти четырех перегибаний площадь станет в 1/264 раз — в одну вторую, взятую в шестьдесят четвертой степени раз, меньше первоначальной. И если бы мы складывали платок дальше, то она все время приближалась бы к нулю, а толщина (или высота) стремилась бы к Великанам в Бесконечность. Вы согласны? Тогда благодарю за внимание.
В зале снова зашумели, захлопали. Барон Мюнхгаузен позвонил в колокольчик и сказал:
— Жюри одинаково восхищено и той и другой задачей. Обеим участницам вручается первый приз.
Он передал победительницам шахматные доски с красивыми фигурами из слоновой кости и добавил:
— Меня так заинтересовали оба выступления, что следующее путешествие я совершу в Бесконечность. А потом — кто знает? — может быть, доберусь и до Нуля!
Барон поклонился. Соревнования кончились, и мы отправились спать. Ведь завтра нам идти на строительство! А перед этим не мешает хорошенько отдохнуть.
Олег.
Был уже вечер. Ярко светились огни домов, вспыхивали и гасли разноцветные вывески. Из раскрытых окон доносилась музыка. Там за накрытыми столами собрались жители Аль-Джебры, чтобы отметить свой праздник.
Ты, уж наверное, догадался: мы снова очутились рядом с Парком Науки и Отдыха. Можно подумать, ноги несли нас туда сами!
Вот и Павильон невероятных задач. С трудом отыскали свободные места. На эстраду вышли судьи. Мюнхгаузена встретили громкими аплодисментами. Кстати, роль его исполняла буква Ка. Барон учтиво раскланялся и начал:
— Уважаемая публика! Разрешите мне объяснить правила предстоящего состязания. Каждый участник должен придумать задачу. На первый взгляд она должна быть очень простой — такой простой, чтобы всем показалось, что решить ее легче легкого. Это — первое условие. Второе… О, второе условие — невероятность решения! Разумеется, я не говорю о решении на бумаге. Наоборот, задача должна быть решена в числах, но практически она должна быть невыполнима.
Итак, повторяю: условие состязания — простота и невероятность. Я мог бы для примера рассказать вам что-нибудь из своей практики. Но, к сожалению, все истории, которые со мной случались, были не только просты, но и вполне вероятны. Почему высмеетесь? Все знают, что барон Мюнхгаузен самый правдивый человек на свете. Разве не правда, что я верхом на пушечном ядре влетел в неприятельский город? Разве не правда, что я нанизал на бечевку целую стаю живых уток и вместе с ними взлетел в воздух? Таких правдоподобных историй у меня сколько угодно. Ваше же дело — придумать задачу, не выполнимую на практике. Не подумайте только, что она должна быть бессмысленной. За бессмысленные задачи участники платят штраф и вызывают из состязания. Ну что ж, начнем? Попрошу желающих. На сцену поднялись пухлая Шестерка и латинская буква Эн. Барон Мюнхгаузен предложил им тянуть жребий. Первой получила слово Шестерка. Вот что она рассказала:
— В давние времена, на Востоке, жил могущественный и грозный шах. Он был несметно богат. Все трепетали перед ним. Приближенные не только исполняли, но и предупреждали любое его желание. Сначала это нравилось шаху. Но настал день, когда все ему наскучило. Не радовали его больше ни наряды, ни яства, привезенные со всех концов света…
День ото дня становился он все угрюмее. Напрасно поэты слагали в его честь стихи. Напрасно пели для него самые искусные певцы, танцевали самые прославленные красавицы. Ничто не могло развлечь скучающего владыку. Целыми часами сидел он в своих роскошных покоях, бессмысленно глядя в одну точку. Дошло до того, что он заболел.
Врачи сменялись у его ложа чародеями и предсказателями. Но все их старания ни к чему не приводили. От шаха осталась одна тень. И все поняли, что дни его сочтены.
И вот у решетки шахского дворца появился странник. Босые ноги его были изранены, сквозь грязные лохмотья просвечивало тело. Странник сказался искусным врачом и потребовал, чтобы его пустили к шаху. Стража грубо оттолкнула оборванца. Тот поднял отчаянный крик. Услыхал его вопли шах и пожелал видеть безумца, который осмелился нарушить его покой. Нищего впустили.
— О великий шах, — сказал он, — я пришел, чтобы излечить тебя от тяжкого недуга.
— Чтобы излечить, надо знать причину болезни, — возразил шах. — Откуда знать тебе то, чего я и сам не знаю?
— Ошибаешься, — сказал странник, — причина твоей болезни — скука. Скука — бич богатых. Им нечего желать, потому что желания их тут же исполняются. Им не о чем думать, потому что за них думают другие. Я принес тебе лекарство, которое заставит тебя думать.
Странник достал из-под рваного плаща небольшую доску, расчерченную черными и белыми квадратами. Он положил ее на низенький столик рядом с шахским ложем и выстроил на ней черные и белые фигурки.
— Эту игру, — сказал он, — я назвал шахматами: ведь ей предстоит излечить шаха.
С этой минуты шах ни о чем, кроме шахмат, и знать не хотел. Целые дни проводил он вместе со странником за шахматной доской и подолгу размышлял над каждым ходом. Здоровье его заметно улучшилось. А когда ему удалось впервые выиграть партию, он почувствовал себя совершенно исцеленным.
— Требуй у меня всего, чего пожелаешь, — сказал он своему спасителю. — Захочешь, подарю тебе гору золота, захочешь — табун чистокровных арабских скакунов…
— О шах, — перебил его странник, — не надо мне ни золота, ни скакунов. В твоей стране столько голодных! Накорми их, — это будет для меня лучшим подарком.
— Какое мне дело до других! — воскликнул разгневанный шах. — Я обещал одарить тебя.
— Для себя мне немного нужно, — улыбнулся странник. — Видишь эту шахматную доску? На ней шестьдесят четыре клетки. Положи на первую клетку одно зернышко риса, на вторую — два зернышка, на третью — четыре, на четвертую — восемь. И так удваивай число зерен на каждой следующей клетке, до тех пор, пока не заполнишь последнюю. Вот и все.
— Только-то?! — облегченно вздохнул шах. — Мало же ты просишь! Я бы потребовал больше.
Принесли мешок риса, и шах сам начал выкладывать зерна. На первую клетку положил одно, на вторую — два, на третью — четыре…
Уже на седьмой клетке для шестидесяти четырех зерен не хватило места.
— Что же, — сказал странник, — вели ссыпать зерна в мешок.
Но шаху быстро наскучило считать. Он кликнул слуг. Теперь стали отсчитывать зерна они: шестьдесят четыре, сто двадцать восемь, двести пятьдесят шесть, пятьсот двенадцать, тысяча двадцать четыре…
Но это была еще только одиннадцатая клетка!
Стемнело. Зажгли светильники. Слуги чуть не падали от усталости. Когда они дошли до семнадцатой клетки, им нужно было отсчитать шестьдесят пять тысяч пятьсот тридцать шесть зерен. Но тут они сбились со счета. Несмотря на то что была уже глубокая ночь, шах велел разбудить мудрецов. Теперь он уже не смеялся, — побледнел, осунулся…
Прошли сутки, и еще одни сутки, и еще одни сутки, а мудрецы все считали… Вот уже и они стали валиться от усталости, а конца все еще не было видно. Слуги вносили все новые и новые мешки…
Но вот вбежал насмерть перепуганный хранитель шахских запасов. Он доложил, что в амбарах не осталось ни одного рисового зернышка.
— Негодяй! — закричал шах страннику. — Ты разорил меня!
— Ах так! — в бешенстве закричал шах. — Сейчас ты узнаешь, умею ли я платить сполна. Отрубить ему голову!
— Такова шахская справедливость, — закончила свой рассказ Шестерка. — А теперь прошу вас убедиться, что задача эта очень проста, но практически невыполнима. Число рисовых зерен росло по такому правилу: 1, 2, 4, 8, 16, 32, и так далее. Каждое последующее число больше предыдущего в два раза.
Такой ряд чисел называется геометрической прогрессией. Только, пожалуйста, не путайте ее с арифметической. В арифметической прогрессии каждое последующее число больше предыдущего на одно и то же число — оно называется разностью прогрессии. В геометрической прогрессии каждое последующее число больше предыдущего в одно и то же число раз, и число это называется знаменателем прогрессии.
В нашей задаче знаменатель прогрессии равен двум. Если хотите, эту прогрессию можно записать и так:
20, 21, 22, 23, 24, 25, 26…
Попробуйте подсчитать, сколько это килограммов риса, если каждое зернышко в среднем весит 0,0182 грамма. Знаете, что получится? Больше ста шестидесяти семи триллионов килограммов! Стоит ли доказывать, что моя задача хоть и проста, но практически невыполнима?
Шестерка поклонилась и села. Ей долго хлопали. Потом поднялась латинская буква Эн. Она сказала так:
— Уважаемая Шестерка познакомила нас с геометрической прогрессией, где все числа непрерывно растут. Такая прогрессия называется возрастающей. Я позволю себе занять ваше внимание сразу двумя геометрическими прогрессиями — возрастающей и убывающей. И сделаю это на одном и том же примере. Задача моя будет так же проста, как предыдущая, и так же невыполнима. Моя предшественница рассказала прелестную сказку об изобретателе шахмат и коварном шахе. Позвольте и мне задать вам задачу, связанную с шахматами.
Эн вынула из кармана платок, развернула его и показала публике. На платке были нарисованы шестьдесят четыре квадрата, черные и белые, — как на шахматной доске.
— Будем считать, — продолжала Эн, — что этот платок заменяет нам шахматную доску. Обратите внимание — толщина платка равна 0,1 — одной десятой миллиметра. Складываю платок пополам. Теперь его толщина стала вдвое больше: две десятых миллиметра. Зато и площадь его стала меньше в два раза. Складываю платок еще раз вдвое. Теперь его толщина в четыре раза больше первоначальной, но и площадь уменьшилась в четыре раза. Я предлагаю складывать этот платок вдвое до тех пор, пока возможно. А потом продолжайте складывать мысленно.
Эн бросила платок в зал, кто-то его подхватил и стал перегибать: раз, второй, третий… Перегнул в шестой и крикнул:
— Готово! Теперь видна только одна клетка. Толщина платка увеличилась в шестьдесят четыре раза. Ничего невозможного тут нет.
— Вы сложили платок только шесть раз, — возразила Эн самонадеянному зрителю, — а надо было шестьдесят четыре! Понимаете разницу? Если бы вам удалось это сделать, толщина платка стала бы такой большой, что он перерос бы горы, миновал солнце и уперся бы в какую-нибудь отдаленную звезду.
— А вы докажите! — крикнули в зале.
Тогда Эн стала решать задачу на доске.
— Неужели вы не догадались, что я почти повторила предыдущую задачу? После каждого перегибания толщина платка увеличивается вдвое и возрастает по закону геометрической прогрессии: 2, 4, 8, 16, 32, 64 и так далее. Разница только в том, что после шестидесяти четырех перегибаний толщина платка станет больше не в 263, а в 264 раз. Оно и понятно: ведь эта прогрессия начинается не с 20 — двух в нулевой, а с 21 — двух в первой степени. Толщина развернутого платка 0,1 миллиметра. Чтобы вычислить толщину сложенного платка, надо 0,1 умножить на 264. Получается 1 844 674 407 371 километр.
Один триллион восемьсот сорок четыре миллиарда шестьсот семьдесят четыре миллиона четыреста семь тысяч триста семьдесят один километр.
А ведь расстояние от Земли до Солнца всего-навсего около ста пятидесяти миллионов километров!
— А где же обещанная убывающая прогрессия? — спросил Сева.
— Да здесь же, — ответила Эн. — Ведь в то время как толщина платка увеличивается, площадь его все время уменьшается: 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, и так далее. Это и есть убывающая геометрическая прогрессия. После шестидесяти четырех перегибаний площадь станет в 1/264 раз — в одну вторую, взятую в шестьдесят четвертой степени раз, меньше первоначальной. И если бы мы складывали платок дальше, то она все время приближалась бы к нулю, а толщина (или высота) стремилась бы к Великанам в Бесконечность. Вы согласны? Тогда благодарю за внимание.
В зале снова зашумели, захлопали. Барон Мюнхгаузен позвонил в колокольчик и сказал:
— Жюри одинаково восхищено и той и другой задачей. Обеим участницам вручается первый приз.
Он передал победительницам шахматные доски с красивыми фигурами из слоновой кости и добавил:
— Меня так заинтересовали оба выступления, что следующее путешествие я совершу в Бесконечность. А потом — кто знает? — может быть, доберусь и до Нуля!
Барон поклонился. Соревнования кончились, и мы отправились спать. Ведь завтра нам идти на строительство! А перед этим не мешает хорошенько отдохнуть.
Олег.
Новые открытия Нулика
(Нулик — отряду РВТ)
Задачу с зернами все-таки решили проверить. Конечно, без риса. Просто все стали писать на своих досках, сколько надо положить рисинок на каждую клетку: 1, 2, 4, 8, 16, 32, 64, 128… Когда заполнили первый ряд, выяснилось, что одни пишут слева направо, а другие справа налево.
Я попробовал сложить каждую пару, но одинаковых чисел не получилось. Понятно: ведь прогрессия-то не арифметическая, а геометрическая! Тогда я их перемножил и сделал второе открытие: все произведения оказались совершенно одинаковые:
1 Х 128 = 128;
2 X 64 = 128;
4 X 32 = 128;
8 X 16 = 128.
Да, теперь я уже не тот Нулик, что прежде. Меня и вправду не узнать. А все ваши письма!
Дальше считать зерна никто не захотел — кому же охота писать такие огромные числа? Но один Нулик задал интересный вопрос: если на шестьдесят четвертую клетку надо положить девять с лишним квинтиллионов зерен, то сколько всего зерен будет на доске, если, конечно, заполнить все клетки?
— Что тут думать! — сказал другой Нулик. — Всего на доске будет зерен два в шестьдесят третьей степени. То есть вот эти девять квинтиллионов.
— Ничего подобного, — возразил третий, — девять квинтиллионов будет только на последней клетке, а на всей доске во много раз больше.
Они заспорили, а я снова посмотрел на свою шахматную доску, где в первом ряду написана геометрическая прогрессия: 1, 2, 4, 8, 16, 32, 64, 128. После треугольника Паскаля я вообще стал очень внимательно рассматривать числа — все время ищу закономерности! Вот и сейчас сложил первый член прогрессии со вторым: 1 + 2 = 3. Сумма их оказалась на единицу меньше третьего члена — четверки. Потом я сложил 1 + 2 + 4. Получилось семь. А это на единицу меньше восьми. 1 + 2 + 4 + 8 = 15. И это тоже меньше шестнадцати на единицу. Выходит, сумма всех предыдущих членов этой геометрической прогрессии меньше последующего всегда на единицу. А это значит, что на шестидесяти трех клетках шахматной доски будет столько же зерен, сколько на последней, шестьдесят четвертой, только на одно зернышко меньше. А всего на доске зерен будет в два раза больше, чем на последней клетке, минус единица: 2 * 263 — 1. А это ведь все равно что 264 — 1.
Так я сделал третье открытие. И для этого мне не понадобилось ни писать всю прогрессию до конца, ни умножать девять квинтиллионов с хвостиком на два. Хорошая штука алгебра!
Нулик-Шахматист.
Волшебная практика
(Сева — Нулику)
Мы чуть не опоздали к началу рабочего дня. И все из-за Тани. На стройках, говорит, всегда пыль и грязь. Как бы мне, говорит, там не испортить любимого платья в оборочках. Наконец она появилась в комбинезоне и сапогах, на голове косынка, защитные очки. Прямо хоть снимай для газеты: «Знатная электросварщица Татьяна Н.».
Девчонок хлебом не корми — дай надеть какую-нибудь обновку. Я-то знаю, что не платья ей жалко, — просто захотелось покрасоваться в комбинезоне.
Ну и лицо у нее было, когда она увидела, что строительство больше похоже на ухоженную детскую площадку, где ребята заняты разными техническими играми — пилят, вырезают, конструируют… Только «игрушки» здесь были гораздо крупнее. Кружевные стрельчатые краны легко передвигали в воздухе разноцветные пластикатные детали.
К нам подошла нарядная латинская буква Эф. Она удивленно покосилась на Танин костюм:
— Хотите познакомиться с нашим экспериментальным строительством? Я вас провожу.
Первым долгом поинтересовались, что здесь строят.
— Да все, что угодно, — ответила Эф. — Дома, машины, бассейны…
Мы залюбовались высоким домом из разноцветных кубиков… Он вырос прямо на наших глазах — ни дать ни взять воздушный замок. И как же мне жалко стало, когда этот замок вдруг рассыпался, а на его месте возникло длинное двухэтажное здание с плоской крышей.
— Охота была строить, а потом разрушать! — подосадовал я.
Но Эф объяснила, что здесь не просто строят, а делают расчеты, которые тут же проверяют на практике. Я подумал, что если это и практика, то, во всяком случае, волшебная.
К нам подошел солидный карликан, Девятка.
— Здравствуйте, — обратился он к Эф. — Мы строим дом. Нам надо вырыть котлован для фундамента. Имеются три экскаватора. Первый может вырыть котлован за четыре часа, второй — за три, третий — за двенадцать. Через сколько часов будет готов котлован, если все три экскаватора работают одновременно? Это очень важно! Без этого я не смогу составить график строительства.
— Обратитесь к Главному Составителю, — ответила Эф.
Мы переглянулись.
— Нельзя ли и нам повидать Главного Составителя? — спросила Таня.
— А вы разве умеете решать уравнения? — поинтересовалась Эф.
Таня только покраснела. А я сказал напрямки, что мы об этом понятия не имеем.
— В таком случае вам придется начать с азов! Чтобы решить уравнение, следует прежде всего познакомиться с отрицательными числами.
Ну, это-то мы знали!
Эф облегченно вздохнула:
— Тогда я могу зачислить вас на строительство в качестве практикантов.
— И мы сейчас же начнем составлять уравнения? — брякнул я.
— О, до этого далеко. Сперва придется поработать в весовой.
Что ты скажешь? Опять отсрочка! В кармане лежит готовая задача, а ты, изволь радоваться, работай весовщиком!
Эф заметила, как мне досадно.
— В нашем деле лучше не торопиться, — сказала она, — это верный способ сэкономить время.
Ничего не поделаешь, пошли в весовую. Кстати, я давно не взвешивался. А в этой Аль-Джебре похудеешь!
Сева.
Девчонок хлебом не корми — дай надеть какую-нибудь обновку. Я-то знаю, что не платья ей жалко, — просто захотелось покрасоваться в комбинезоне.
Ну и лицо у нее было, когда она увидела, что строительство больше похоже на ухоженную детскую площадку, где ребята заняты разными техническими играми — пилят, вырезают, конструируют… Только «игрушки» здесь были гораздо крупнее. Кружевные стрельчатые краны легко передвигали в воздухе разноцветные пластикатные детали.
К нам подошла нарядная латинская буква Эф. Она удивленно покосилась на Танин костюм:
— Хотите познакомиться с нашим экспериментальным строительством? Я вас провожу.
Первым долгом поинтересовались, что здесь строят.
— Да все, что угодно, — ответила Эф. — Дома, машины, бассейны…
Мы залюбовались высоким домом из разноцветных кубиков… Он вырос прямо на наших глазах — ни дать ни взять воздушный замок. И как же мне жалко стало, когда этот замок вдруг рассыпался, а на его месте возникло длинное двухэтажное здание с плоской крышей.
— Охота была строить, а потом разрушать! — подосадовал я.
Но Эф объяснила, что здесь не просто строят, а делают расчеты, которые тут же проверяют на практике. Я подумал, что если это и практика, то, во всяком случае, волшебная.
К нам подошел солидный карликан, Девятка.
— Здравствуйте, — обратился он к Эф. — Мы строим дом. Нам надо вырыть котлован для фундамента. Имеются три экскаватора. Первый может вырыть котлован за четыре часа, второй — за три, третий — за двенадцать. Через сколько часов будет готов котлован, если все три экскаватора работают одновременно? Это очень важно! Без этого я не смогу составить график строительства.
— Обратитесь к Главному Составителю, — ответила Эф.
Мы переглянулись.
— Нельзя ли и нам повидать Главного Составителя? — спросила Таня.
— А вы разве умеете решать уравнения? — поинтересовалась Эф.
Таня только покраснела. А я сказал напрямки, что мы об этом понятия не имеем.
— В таком случае вам придется начать с азов! Чтобы решить уравнение, следует прежде всего познакомиться с отрицательными числами.
Ну, это-то мы знали!
Эф облегченно вздохнула:
— Тогда я могу зачислить вас на строительство в качестве практикантов.
— И мы сейчас же начнем составлять уравнения? — брякнул я.
— О, до этого далеко. Сперва придется поработать в весовой.
Что ты скажешь? Опять отсрочка! В кармане лежит готовая задача, а ты, изволь радоваться, работай весовщиком!
Эф заметила, как мне досадно.
— В нашем деле лучше не торопиться, — сказала она, — это верный способ сэкономить время.
Ничего не поделаешь, пошли в весовую. Кстати, я давно не взвешивался. А в этой Аль-Джебре похудеешь!
Сева.
Весовая
(Таня — Нулику)
Что ни говори, Нулик, Аль-Джебра — удивительное государство! Вчера были в современном кафе, сегодня на сверхскоростном строительстве, и вот, не успели опомниться, как попали в гости к древнему восточному кудеснику.
Как ты себе представляешь весовую? Большой амбар, тяжелые неуклюжие весы. У весов — дюжий весовщик в брезентовом фартуке и рукавицах. А вокруг — мешки, ящики, корзины…
Как ты себе представляешь весовую? Большой амбар, тяжелые неуклюжие весы. У весов — дюжий весовщик в брезентовом фартуке и рукавицах. А вокруг — мешки, ящики, корзины…