Страница:
Так вот, ничего подобного не было. Нас ввели в полутемный сводчатый зал с тонкими витыми колоннами, такой высоченный, что потолка не видно. Будто над тобой ночное небо, только без луны и звезд. Вместо них в полумраке светятся какие-то закорючки и загогулины. Должно быть, восточные письмена. Посреди зала — большие старинные весы: тяжелые медные чашки, подвешенные на цепях к концам металлического коромысла. Весы тоже сплошь в закорючках и загогулинах. Они парят в воздухе, как большая диковинная птица. А между чашками, словно глазок радиоприемника, сверкает зеленый кошачий глаз.
— Садитесь, — шепнула Эф.
Мы оглянулись: ни стульев, ни кресел. Только несколько пестрых ковриков на полу. Эф уселась на одном из них, скрестив ноги. Мы сделали то же самое.
Бам! Что-то зазвенело — будто стукнулись два медных подноса, — и из темноты вынырнула фигура в длинном черном балахоне с желтыми разводами. На голове — белая шелковая башня. Называется «тюрбан». И борода у него тоже белая и шелковистая.
— Главный Весовщик, — шепнула Эф. — Следите за ним внимательно.
Весовщик приложил руку к сердцу и поклонился. Мы тоже приложили руки к сердцу и поклонились. Потом он взмахнул палочкой, и на каждой чашке весов появилось по Семерке. — обе в светящихся костюмах. Я так на них загляделась — даже не заметила, что в кошачьем глазке засветились две черточки. Эф легонько толкнула меня локтем:
— Это знак равенства. Семь равно семи, — негромко сказала она.
— Уж конечно, не восьми, — фыркнул Сева.
Но тут Весовщик снова взмахнул палочкой, и на правой чашке весов вместо Семерки оказалась Восьмерка. Чашка сразу опустилась. Мы взглянули на зеленый глазок: черточки знака равенства соединились слева и образовали уголок: 7 « 8.
— А вот знак неравенства. Он обозначает, что семь меньше восьми, — пояснила Эф.
Тут Восьмерка и Семерка поменялись местами. Теперь уже опустилась левая чашка. Черточки в кошачьем глазке снова задвигались и соединились правыми концами: 8 » 7.
— Понятно, — сказал Олег, — этот знак показывает, что восемь больше семи. Выходит, там, где палочки сходятся, стоит меньшее число, а там, где они расходятся, — большее.
— Детские игрушки, — проворчал Сева.
Весовщик не обратил внимания на его дерзость. Он взмахнул палочкой, и вот уже вместо чисел на весах засветились буквы: слева а + b, справа с. Между ними загорелся знак равенства: а + b = с.
Но в Севу точно бес вселился! Все ему не нравилось.
— Почему это, — придрался он, — Весовщик думает, что а + b равно с?
— А он вовсе и не думает — он требует этого, — ответила Эф. — Наверное, ему для какой-то задачи понадобилось, чтобы левая часть непременно была равна правой.
— А может быть, он все-таки ошибается? — заупрямился Сева. — Ведь под буквой можно подразумевать любое число! Вот я сейчас попрошу заменить все три буквы числами.
Он встал и подошел к Весовщику. Признаться, я очень испугалась: вдруг Весовщик рассердится и превратит Севу в какое-нибудь неравенство? Но он вовсе не рассердился. Наоборот, прижал руку к сердцу, и вот уже на левой чашке весов вместо буквы а стоит число Четыре, вместо b — Пять, а на другой чашке вместо с — Девятка: 4 + 5 = 9.
Но Сева не унимался.
— Нет, так не пойдет, уважаемый Главный Весовщик! Вы просто поставили те числа, которые вам выгодно. Позвольте, я сам!
Он назвал другие числа. Весовщик улыбнулся и снова пустил в ход свою палочку. Коромысло закачалось, в глазке зажегся знак неравенства. И мы увидели вот что: 6 + 7 « 20.
— Что я говорил! — закричал Сева. — Выходит, а плюс b не равно с.
И тут молчаливый Весовщик не выдержал.
— О неразумный отрок! — заговорил он тонким скрипучим голосом. — Если ты хочешь стать мудрецом, не болтай языком, не подумав. Под буквами действительно можно подразумевать произвольные числа. Но только до тех пор, пока они не связаны знаком равенства. В равенстве а + b = с можно произвольно заменить числами не три, а только две буквы. Величина третьей выяснится сама собой. Замени две из этих букв числами.
Сева подумал, пошевелил губами…
— Пусть а будет равно пяти, а с — двенадцати. На весах появилось выражение: 5 + b = 12.
— Скажи теперь, — улыбнулся Весовщик, — можно ли вместо b подставить любое число?
Но Сева не успел и рот открыть, как на весах вместо буквы b засветилась Семерка: 5 + 7 = 12.
Сева почесал за ухом.
— Да! С этими равенствами не разгуляешься. Зато уж в неравенстве подставляй что душе угодно — так неравенством и останется.
Весовщик укоризненно покачал головой:
— Опять говоришь не подумав. Неравенство неравенству рознь.
Oн взмахнул палочкой. На левой чашке весов появились c + d, на правой е, а между ними — знак неравенства: c + d « e.
Правая чашка весов опустилась.
— Назови вместо этих букв любые числа, — предложил Весовщик.
Сева назвал. И на левой чашке весов мы увидели 4 + 8, а на правой 9. Левая чашка опустилась, и знак неравенства повернулся острием вправо: 4 + 8 » 9.
— Ага! Неравенство сохранилось, — обрадовался Сева.
— Да, — сказал Весовщик, — но теперь левая часть стала больше правой, а не меньше, как мы условились.
— Почтенный Весовщик, — вмешался Олег, — вы хотите сказать, что, подставив в левую часть этого неравенства 4 + 8, справа можно подставить любое число, но при одном условии: оно должно быть больше двенадцати. Тогда левая часть всегда будет меньше правой.
— Вот именно, вот именно! — умилился Весовщик и так закивал головой, что вот-вот борода отвалится! Потом он перестал кивать и взглянул на Севу. Тот стоял надутый, взъерошенный, как воробей после драки.
— Вижу, — сказал Весовщик, — тебе во что бы то ни стало хочется подставлять любые числа под все буквы. Так и быть, попробуй еще разок.
На весах засветилось равенство: 3а + 2b = 2а + 3b — b + а.
— Нет уж, спасибо! — Сева даже руками замахал. — Теперь меня не проведешь.
— Зря отказываешься. В этом примере можно подставлять вместо а и b любые числа, какие вздумается.
Весовщик подставил вместо а Четверку, вместо b — Тройку: 3 * 4 — 2 * 3 = 2 * 4 + 3 * 3 — 3 + 4.
И сейчас же числа эти исчезли, уступив место числу 18 на каждой чашке весов: 18 = 18.
Сева растерянно поморгал глазами. Опять он попал впросак. Но почему?
— Да потому, — ответил Весовщик, — что это равенство особое. Оно называется тождеством. Какими числами ни заменяй буквы в тождестве, равенство все равно сохранится.
— Но как отличить тождество от обычного равенства, не подставляя чисел вместо букв? — спросила я.
— Для этого надо обе части равенства сделать совершенно одинаковыми. Смотрите!
Мы увидели на весах прежнее тождество: 3а + 2b = 2а + 3b — b + а.
Тут Весовщик протянул руки к правой чашке весов и как закричит:
— Подобные, приведитесь!
И сейчас же 2а в правой части соединились еще с одним а, 3b, из которых вычли одно b, превратились в 2b, и на весах образовалось другое выражение: За + 2b = 3а + 2b.
Покончив с тождеством, Весовщик взмахнул палочкой, и на ней очутился металлический обруч. С таким у нас занимаются художественной гимнастикой.
Я чуть не фыркнула: неужели Весовщик собирается танцевать с обручем? Вот будет весело! Но танцевать он не стал, а достал веревочку и измерил ширину круга в самом его широком месте.
— Эта ширина называется диаметром круга, — пояснил он. Хотя кто же этого не знает?
Потом Весовщик стал укладывать этот веревочный диаметр по обручу, чтобы измерить длину окружности. Сделал отметку, уложил веревочку один раз, второй, третий, но до отметки все еще не дошел. Выходит, длина окружности больше, чем три ее диаметра. Весовщик стал откладывать веревочку в четвертый раз, но ее оказалось слишком много. На глаз получалось, что надо отложить только одну пятую веревочки. Весовщик отрезал одну пятую, но и этот кусочек оказался длиннее, чем нужно. Значит, длина окружности меньше чем три и одна пятая диаметра.
Тогда Весовщик разрезал этот кусочек веревки пополам, и он стал равен одной десятой диаметра. Но теперь его не хватило до отметки. Значит, длина окружности меньше чем три и одна пятая, но больше чем три и одна десятая диаметра.
Долго Весовщик возился с этой задачей, а потом улыбнулся и сказал:
— О мои юные друзья, я пошутил. Я и раньше знал, что решить эту задачу точно невозможно. Мне только хотелось, чтобы вы убедились в этом сами. Во сколько раз длина окружности больше своего диаметра, можно подсчитать только приближенно. Вычислите это число с точностью хоть до миллиона знаков, оно все равно не будет совершенно точным.
— Значит, это — иррациональное число? — спросил Олег.
— Конечно! — подтвердила Эф. — Мы можем указать, где оно живет на монорельсовой дороге, но выразить его точным числом нельзя. В Аль-Джебре его обозначают греческой буквой Пи. Смотрите, вот оно.
На левую чашку весов вспорхнула буковка, слегка напоминающая русское «п», а на правой появилось число 3,14.
— Число Пи приближенно равно трем целым и четырнадцати сотым, — объяснил Весовщик.
Он взмахнул палочкой. Чашка с буквой Пи чуть-чуть опустилась, а в кошачьем глазке появились две волнистые линии:
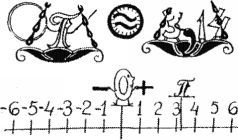— Это знак приближенного равенства, — пояснила Эф. — На самом деле Пи немножко больше чем 3,14. Поэтому левая чашка слегка перевешивает.
Снова стукнулись два медных подноса, и Главный Весовщик исчез. Прямо-таки растаял.
— Перерыв на пятнадцать минут! — объявила Эф.
Как ты думаешь, может, и мне объявить небольшой перерыв?
Таня.
Аль-Джебр!
Вверх-вниз!
Мнимая карусель
— Садитесь, — шепнула Эф.
Мы оглянулись: ни стульев, ни кресел. Только несколько пестрых ковриков на полу. Эф уселась на одном из них, скрестив ноги. Мы сделали то же самое.
Бам! Что-то зазвенело — будто стукнулись два медных подноса, — и из темноты вынырнула фигура в длинном черном балахоне с желтыми разводами. На голове — белая шелковая башня. Называется «тюрбан». И борода у него тоже белая и шелковистая.
— Главный Весовщик, — шепнула Эф. — Следите за ним внимательно.
Весовщик приложил руку к сердцу и поклонился. Мы тоже приложили руки к сердцу и поклонились. Потом он взмахнул палочкой, и на каждой чашке весов появилось по Семерке. — обе в светящихся костюмах. Я так на них загляделась — даже не заметила, что в кошачьем глазке засветились две черточки. Эф легонько толкнула меня локтем:
— Это знак равенства. Семь равно семи, — негромко сказала она.
— Уж конечно, не восьми, — фыркнул Сева.
Но тут Весовщик снова взмахнул палочкой, и на правой чашке весов вместо Семерки оказалась Восьмерка. Чашка сразу опустилась. Мы взглянули на зеленый глазок: черточки знака равенства соединились слева и образовали уголок: 7 « 8.
— А вот знак неравенства. Он обозначает, что семь меньше восьми, — пояснила Эф.
Тут Восьмерка и Семерка поменялись местами. Теперь уже опустилась левая чашка. Черточки в кошачьем глазке снова задвигались и соединились правыми концами: 8 » 7.
— Понятно, — сказал Олег, — этот знак показывает, что восемь больше семи. Выходит, там, где палочки сходятся, стоит меньшее число, а там, где они расходятся, — большее.
— Детские игрушки, — проворчал Сева.
Весовщик не обратил внимания на его дерзость. Он взмахнул палочкой, и вот уже вместо чисел на весах засветились буквы: слева а + b, справа с. Между ними загорелся знак равенства: а + b = с.
Но в Севу точно бес вселился! Все ему не нравилось.
— Почему это, — придрался он, — Весовщик думает, что а + b равно с?
— А он вовсе и не думает — он требует этого, — ответила Эф. — Наверное, ему для какой-то задачи понадобилось, чтобы левая часть непременно была равна правой.
— А может быть, он все-таки ошибается? — заупрямился Сева. — Ведь под буквой можно подразумевать любое число! Вот я сейчас попрошу заменить все три буквы числами.
Он встал и подошел к Весовщику. Признаться, я очень испугалась: вдруг Весовщик рассердится и превратит Севу в какое-нибудь неравенство? Но он вовсе не рассердился. Наоборот, прижал руку к сердцу, и вот уже на левой чашке весов вместо буквы а стоит число Четыре, вместо b — Пять, а на другой чашке вместо с — Девятка: 4 + 5 = 9.
Но Сева не унимался.
— Нет, так не пойдет, уважаемый Главный Весовщик! Вы просто поставили те числа, которые вам выгодно. Позвольте, я сам!
Он назвал другие числа. Весовщик улыбнулся и снова пустил в ход свою палочку. Коромысло закачалось, в глазке зажегся знак неравенства. И мы увидели вот что: 6 + 7 « 20.
— Что я говорил! — закричал Сева. — Выходит, а плюс b не равно с.
И тут молчаливый Весовщик не выдержал.
— О неразумный отрок! — заговорил он тонким скрипучим голосом. — Если ты хочешь стать мудрецом, не болтай языком, не подумав. Под буквами действительно можно подразумевать произвольные числа. Но только до тех пор, пока они не связаны знаком равенства. В равенстве а + b = с можно произвольно заменить числами не три, а только две буквы. Величина третьей выяснится сама собой. Замени две из этих букв числами.
Сева подумал, пошевелил губами…
— Пусть а будет равно пяти, а с — двенадцати. На весах появилось выражение: 5 + b = 12.
— Скажи теперь, — улыбнулся Весовщик, — можно ли вместо b подставить любое число?
Но Сева не успел и рот открыть, как на весах вместо буквы b засветилась Семерка: 5 + 7 = 12.
Сева почесал за ухом.
— Да! С этими равенствами не разгуляешься. Зато уж в неравенстве подставляй что душе угодно — так неравенством и останется.
Весовщик укоризненно покачал головой:
— Опять говоришь не подумав. Неравенство неравенству рознь.
Oн взмахнул палочкой. На левой чашке весов появились c + d, на правой е, а между ними — знак неравенства: c + d « e.
Правая чашка весов опустилась.
— Назови вместо этих букв любые числа, — предложил Весовщик.
Сева назвал. И на левой чашке весов мы увидели 4 + 8, а на правой 9. Левая чашка опустилась, и знак неравенства повернулся острием вправо: 4 + 8 » 9.
— Ага! Неравенство сохранилось, — обрадовался Сева.
— Да, — сказал Весовщик, — но теперь левая часть стала больше правой, а не меньше, как мы условились.
— Почтенный Весовщик, — вмешался Олег, — вы хотите сказать, что, подставив в левую часть этого неравенства 4 + 8, справа можно подставить любое число, но при одном условии: оно должно быть больше двенадцати. Тогда левая часть всегда будет меньше правой.
— Вот именно, вот именно! — умилился Весовщик и так закивал головой, что вот-вот борода отвалится! Потом он перестал кивать и взглянул на Севу. Тот стоял надутый, взъерошенный, как воробей после драки.
— Вижу, — сказал Весовщик, — тебе во что бы то ни стало хочется подставлять любые числа под все буквы. Так и быть, попробуй еще разок.
На весах засветилось равенство: 3а + 2b = 2а + 3b — b + а.
— Нет уж, спасибо! — Сева даже руками замахал. — Теперь меня не проведешь.
— Зря отказываешься. В этом примере можно подставлять вместо а и b любые числа, какие вздумается.
Весовщик подставил вместо а Четверку, вместо b — Тройку: 3 * 4 — 2 * 3 = 2 * 4 + 3 * 3 — 3 + 4.
И сейчас же числа эти исчезли, уступив место числу 18 на каждой чашке весов: 18 = 18.
Сева растерянно поморгал глазами. Опять он попал впросак. Но почему?
— Да потому, — ответил Весовщик, — что это равенство особое. Оно называется тождеством. Какими числами ни заменяй буквы в тождестве, равенство все равно сохранится.
— Но как отличить тождество от обычного равенства, не подставляя чисел вместо букв? — спросила я.
— Для этого надо обе части равенства сделать совершенно одинаковыми. Смотрите!
Мы увидели на весах прежнее тождество: 3а + 2b = 2а + 3b — b + а.
Тут Весовщик протянул руки к правой чашке весов и как закричит:
— Подобные, приведитесь!
И сейчас же 2а в правой части соединились еще с одним а, 3b, из которых вычли одно b, превратились в 2b, и на весах образовалось другое выражение: За + 2b = 3а + 2b.
Покончив с тождеством, Весовщик взмахнул палочкой, и на ней очутился металлический обруч. С таким у нас занимаются художественной гимнастикой.
Я чуть не фыркнула: неужели Весовщик собирается танцевать с обручем? Вот будет весело! Но танцевать он не стал, а достал веревочку и измерил ширину круга в самом его широком месте.
— Эта ширина называется диаметром круга, — пояснил он. Хотя кто же этого не знает?
Потом Весовщик стал укладывать этот веревочный диаметр по обручу, чтобы измерить длину окружности. Сделал отметку, уложил веревочку один раз, второй, третий, но до отметки все еще не дошел. Выходит, длина окружности больше, чем три ее диаметра. Весовщик стал откладывать веревочку в четвертый раз, но ее оказалось слишком много. На глаз получалось, что надо отложить только одну пятую веревочки. Весовщик отрезал одну пятую, но и этот кусочек оказался длиннее, чем нужно. Значит, длина окружности меньше чем три и одна пятая диаметра.
Тогда Весовщик разрезал этот кусочек веревки пополам, и он стал равен одной десятой диаметра. Но теперь его не хватило до отметки. Значит, длина окружности меньше чем три и одна пятая, но больше чем три и одна десятая диаметра.
Долго Весовщик возился с этой задачей, а потом улыбнулся и сказал:
— О мои юные друзья, я пошутил. Я и раньше знал, что решить эту задачу точно невозможно. Мне только хотелось, чтобы вы убедились в этом сами. Во сколько раз длина окружности больше своего диаметра, можно подсчитать только приближенно. Вычислите это число с точностью хоть до миллиона знаков, оно все равно не будет совершенно точным.
— Значит, это — иррациональное число? — спросил Олег.
— Конечно! — подтвердила Эф. — Мы можем указать, где оно живет на монорельсовой дороге, но выразить его точным числом нельзя. В Аль-Джебре его обозначают греческой буквой Пи. Смотрите, вот оно.
На левую чашку весов вспорхнула буковка, слегка напоминающая русское «п», а на правой появилось число 3,14.
— Число Пи приближенно равно трем целым и четырнадцати сотым, — объяснил Весовщик.
Он взмахнул палочкой. Чашка с буквой Пи чуть-чуть опустилась, а в кошачьем глазке появились две волнистые линии:
Снова стукнулись два медных подноса, и Главный Весовщик исчез. Прямо-таки растаял.
— Перерыв на пятнадцать минут! — объявила Эф.
Как ты думаешь, может, и мне объявить небольшой перерыв?
Таня.
Аль-Джебр!
(Сева — Нулику)
Знаешь, Нулик, напрасно я злился на этого Весовщика. Он даже почище фокусника. Фокусников и у нас пруд пруди. А настоящего живого чародея днем с огнем не сыщешь.
В перерыве я подговаривал ребят смыться. Сколько можно возиться с неравенствами, равенствами и всякими Пи? Пришли составлять уравнение, так чего там!… Но Олег сказал, что сперва неплохо бы выяснить, что такое уравнение. Ах да! Я и позабыл.
Снова стукнулись медные подносы, вернулась наша Эф, и мы опять уселись на коврики.
Только я хотел спросить, где же Весовщик, а он уж тут как тут! Сидит под весами, словно никуда не исчезал.
Весовщик взмахнул палочкой, и над каждой чашкой весов появилось по числу 14. В глазке засверкал знак равенства.
«Здравствуйте! — подумал я. — Все сначала!»
Но я ошибался. Кроме чисел 14, на каждой чашке весов появилось по Пятерке: 14 + 5 = 14 + 5.
Чашки не дрогнули, глазок по-прежнему показывал равенство. Потом вместо этих чисел на весы стали две суммы: а + b = с + d.
И снова подле каждой из них засветились одинаковые числа, на этот раз Тройки: a + b + 3 = c + d + 3.
Чашки не шелохнулись.
— Видите, — сказал Главный Весовщик, — если к обеим частям прибавить по одинаковому числу, равенство не нарушится. Понятно, что можно не только прибавить, но и вычесть по одинаковому числу. Можно умножить обе части или разделить их на одинаковые числа, — равенство все равно сохранится.
— А если прибавить не числа, а одинаковые буквы? — спросил я.
— На здоровье! — ответил Весовщик. — Ведь буква — то же число. Вот смотрите.
Теперь к суммам на весах прибавились буквы n. Равенство не исчезло: a + b + 3 + n = c + d + 3 + n.
Ox, и заскучал я от этих равенств, даже спать захотелось! Но тут случилось такое, что сон с меня как ветром сдуло.
На левой чашке весов засветилась буква, на которую я до сих пор и внимания не обращал, — Икс из латинского алфавита: x. Ты ее знаешь, она точь-в-точь знак умножения или русское Ха. Ставь ее на голову, поворачивай спиной — со всех сторон одинаковая! Рядом с Иксом засветилась Тройка, между ними вспыхнул знак минус, а на правой чашке весов оказался твой тезка, Нулик: х — 3 = 0.
В кошачьем глазке появился знак равенства и… Только не пугайся! Икс быстро обернулся (он, оказывается, стоял к нам спиной), и мы увидели, что на нем черная маска. Вот так история! Подумать только, под Черной Маской скрывается Икс!
Тут мы все повскакали, бросились к этому Иксу, схватили его за руки — а вдруг опять убежит? А он и не думает убегать. Стоит себе, глазами хлопает.
— В чем дело? — спрашивает. — Мы как будто незнакомы.
— Как? Разве не вы та самая Черная Маска, которая подбросила Нулику зеленый стручок? И разве не вас мы должны расколдовать?
— Нет, я не тот, кого вы ищете. Ведь в Аль-Джебре нас, Иксов, как капель в море. Этой буквой обозначается неизвестное число.
Пришлось нам извиниться и вернуться на свои коврики. Но кое-что мы все-таки разузнали: Черная Маска — неизвестное число.
А Весовщик продолжал как ни в чем не бывало:
— Перед вами равенство х — 3 = 0. Но оно немного отличается от тех, что я вам показывал до сих пор. Это не тождество, не просто равенство, а уравнение первой степени.
«Давно бы так!» — подумал я.
— В чем его особенность? — продолжал Весовщик. — Если в тождестве можно заменить любыми числами все буквы, а в обычном равенстве — только некоторые, то в уравнении первой степени вместо буквы Икс может стоять только одно-единственное число. Иначе равенство нарушится. Найти это единственное неизвестное число и значит решить уравнение. Пока уравнение не решено, никто не знает, чему равен Икс. Потому-то он и надевает черную маску. Стоит решить уравнение, и маска упадет сама собой.
С этой минуты скуки моей как не бывало. Я вдруг понял, что все, что мы до сих пор узнавали в Аль-Джебре, нужно, чтобы решить уравнение и расколдовать Черную Маску. Не зря мы дрожали от страха в темном подземелье, не зря торчали на воздушной монорельсовой дороге, корпели над шифром в «Абракадабре», не зря и сейчас слушаем этого кудесника с белой башней на голове. А в том, что он кудесник, можешь не сомневаться. Разве простой человек заставил бы меня полюбить то, что я терпеть не мог?
Теперь Весовщик говорил, а я смотрел ему в рот, боялся словечко пропустить.
— Как же решается уравнение х — 3 = 0? Это очень простое уравнение. Чтобы решить его, достаточно, пожалуй, одного заклинания.
Он распахнул руки в широченных шелковых рукавах и завопил:
— Аль-джебр!
— Аль-джебр, аль-джебр! — отозвалось где-то наверху. И сейчас же на весах появилось равенство: х — 3 + 3 = 3.
— Вы уже знаете, — пояснил Весовщик, — если прибавить к обеим частям равенства по одинаковому числу, ничего не изменится. Вот я и поставил на каждую чашку весов по числу Три.
Но тут обе Тройки слева от знака равенства исчезли.
— Куда это они? — удивился я.
— Неужели ты забыл правила движения на монорельсовой дороге? Минус Три и плюс Три — числа с разными знаками. Значит, они взаимоуничтожаются. Получается, что Икс равен Трем:
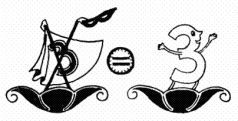На весах появилось новое равенство: х = 3.
Черная маска, закрывавшая лицо Икса, свалилась. Икс низко поклонился и убежал.
— Занятно! — Олег задумчиво поглядел на весы. — В уравнении х — 3 = 0 Тройка была на левой чашке весов. Теперь она очутилась на правой.
— Правильно, — подтвердил Весовщик. — Но слева она была со знаком минус, а справа оказалась со знаком плюс. Хоть он там и не стоит, но подразумевается.
— Зачем же тогда добавлять к обеим частям уравнения по Тройке? — сказал Олег. — Можно ведь просто перенести Тройку с левой чашки весов на правую, только с обратным знаком.
— Твои слова для меня как мед! — поклонился Весовщик. — Именно так и решают уравнения. А Тройки я прибавил лишь затем, чтобы вы поняли, почему можно переносить число с одной стороны на другую. Да будет вам известно, что перенос отрицательного числа из одной части равенства в другую называется восстановлением. Название это осталось у нас с тех самых пор, когда отрицательные числа считались бессмысленными. Перенос отрицательного числа в другую часть равенства с обратным знаком как бы восстанавливал его в правах, превращал в положительное число. Восстановление — по-арабски «аль-джебр». Это волшебное слово завещал нам великий ученый Мухаммед ибн Муса аль-Хварезми. Оно есть в заглавии написанной им книги, которая положила начало нашему государству и называется «Книга восстановлений и противопоставлений».
Он указал на светящиеся в полумраке арабские письмена и прочитал: «Китаб аль-джебр валь-мукабала».
— Большое вам спасибо, — сказал Олег. — Что такое восстановление, мы как будто поняли. Но что такое противопоставление?
Тут снова стукнулись медные подносы. Весовщик загадочно улыбнулся и растаял в темноте. Мне послышался голос мамы Двойки: «Всякому овощу свое время!» С тех пор как мы здесь, эта пословица так и звенит у меня в ушах!
Даже не верится: неужели настанет день, когда мы сядем рядом, возьмем задачу зеленого стручка и решим ее сами, без всяких провожатых и весовщиков?
Сева.
В перерыве я подговаривал ребят смыться. Сколько можно возиться с неравенствами, равенствами и всякими Пи? Пришли составлять уравнение, так чего там!… Но Олег сказал, что сперва неплохо бы выяснить, что такое уравнение. Ах да! Я и позабыл.
Снова стукнулись медные подносы, вернулась наша Эф, и мы опять уселись на коврики.
Только я хотел спросить, где же Весовщик, а он уж тут как тут! Сидит под весами, словно никуда не исчезал.
Весовщик взмахнул палочкой, и над каждой чашкой весов появилось по числу 14. В глазке засверкал знак равенства.
«Здравствуйте! — подумал я. — Все сначала!»
Но я ошибался. Кроме чисел 14, на каждой чашке весов появилось по Пятерке: 14 + 5 = 14 + 5.
Чашки не дрогнули, глазок по-прежнему показывал равенство. Потом вместо этих чисел на весы стали две суммы: а + b = с + d.
И снова подле каждой из них засветились одинаковые числа, на этот раз Тройки: a + b + 3 = c + d + 3.
Чашки не шелохнулись.
— Видите, — сказал Главный Весовщик, — если к обеим частям прибавить по одинаковому числу, равенство не нарушится. Понятно, что можно не только прибавить, но и вычесть по одинаковому числу. Можно умножить обе части или разделить их на одинаковые числа, — равенство все равно сохранится.
— А если прибавить не числа, а одинаковые буквы? — спросил я.
— На здоровье! — ответил Весовщик. — Ведь буква — то же число. Вот смотрите.
Теперь к суммам на весах прибавились буквы n. Равенство не исчезло: a + b + 3 + n = c + d + 3 + n.
Ox, и заскучал я от этих равенств, даже спать захотелось! Но тут случилось такое, что сон с меня как ветром сдуло.
На левой чашке весов засветилась буква, на которую я до сих пор и внимания не обращал, — Икс из латинского алфавита: x. Ты ее знаешь, она точь-в-точь знак умножения или русское Ха. Ставь ее на голову, поворачивай спиной — со всех сторон одинаковая! Рядом с Иксом засветилась Тройка, между ними вспыхнул знак минус, а на правой чашке весов оказался твой тезка, Нулик: х — 3 = 0.
В кошачьем глазке появился знак равенства и… Только не пугайся! Икс быстро обернулся (он, оказывается, стоял к нам спиной), и мы увидели, что на нем черная маска. Вот так история! Подумать только, под Черной Маской скрывается Икс!
Тут мы все повскакали, бросились к этому Иксу, схватили его за руки — а вдруг опять убежит? А он и не думает убегать. Стоит себе, глазами хлопает.
— В чем дело? — спрашивает. — Мы как будто незнакомы.
— Как? Разве не вы та самая Черная Маска, которая подбросила Нулику зеленый стручок? И разве не вас мы должны расколдовать?
— Нет, я не тот, кого вы ищете. Ведь в Аль-Джебре нас, Иксов, как капель в море. Этой буквой обозначается неизвестное число.
Пришлось нам извиниться и вернуться на свои коврики. Но кое-что мы все-таки разузнали: Черная Маска — неизвестное число.
А Весовщик продолжал как ни в чем не бывало:
— Перед вами равенство х — 3 = 0. Но оно немного отличается от тех, что я вам показывал до сих пор. Это не тождество, не просто равенство, а уравнение первой степени.
«Давно бы так!» — подумал я.
— В чем его особенность? — продолжал Весовщик. — Если в тождестве можно заменить любыми числами все буквы, а в обычном равенстве — только некоторые, то в уравнении первой степени вместо буквы Икс может стоять только одно-единственное число. Иначе равенство нарушится. Найти это единственное неизвестное число и значит решить уравнение. Пока уравнение не решено, никто не знает, чему равен Икс. Потому-то он и надевает черную маску. Стоит решить уравнение, и маска упадет сама собой.
С этой минуты скуки моей как не бывало. Я вдруг понял, что все, что мы до сих пор узнавали в Аль-Джебре, нужно, чтобы решить уравнение и расколдовать Черную Маску. Не зря мы дрожали от страха в темном подземелье, не зря торчали на воздушной монорельсовой дороге, корпели над шифром в «Абракадабре», не зря и сейчас слушаем этого кудесника с белой башней на голове. А в том, что он кудесник, можешь не сомневаться. Разве простой человек заставил бы меня полюбить то, что я терпеть не мог?
Теперь Весовщик говорил, а я смотрел ему в рот, боялся словечко пропустить.
— Как же решается уравнение х — 3 = 0? Это очень простое уравнение. Чтобы решить его, достаточно, пожалуй, одного заклинания.
Он распахнул руки в широченных шелковых рукавах и завопил:
— Аль-джебр!
— Аль-джебр, аль-джебр! — отозвалось где-то наверху. И сейчас же на весах появилось равенство: х — 3 + 3 = 3.
— Вы уже знаете, — пояснил Весовщик, — если прибавить к обеим частям равенства по одинаковому числу, ничего не изменится. Вот я и поставил на каждую чашку весов по числу Три.
Но тут обе Тройки слева от знака равенства исчезли.
— Куда это они? — удивился я.
— Неужели ты забыл правила движения на монорельсовой дороге? Минус Три и плюс Три — числа с разными знаками. Значит, они взаимоуничтожаются. Получается, что Икс равен Трем:
Черная маска, закрывавшая лицо Икса, свалилась. Икс низко поклонился и убежал.
— Занятно! — Олег задумчиво поглядел на весы. — В уравнении х — 3 = 0 Тройка была на левой чашке весов. Теперь она очутилась на правой.
— Правильно, — подтвердил Весовщик. — Но слева она была со знаком минус, а справа оказалась со знаком плюс. Хоть он там и не стоит, но подразумевается.
— Зачем же тогда добавлять к обеим частям уравнения по Тройке? — сказал Олег. — Можно ведь просто перенести Тройку с левой чашки весов на правую, только с обратным знаком.
— Твои слова для меня как мед! — поклонился Весовщик. — Именно так и решают уравнения. А Тройки я прибавил лишь затем, чтобы вы поняли, почему можно переносить число с одной стороны на другую. Да будет вам известно, что перенос отрицательного числа из одной части равенства в другую называется восстановлением. Название это осталось у нас с тех самых пор, когда отрицательные числа считались бессмысленными. Перенос отрицательного числа в другую часть равенства с обратным знаком как бы восстанавливал его в правах, превращал в положительное число. Восстановление — по-арабски «аль-джебр». Это волшебное слово завещал нам великий ученый Мухаммед ибн Муса аль-Хварезми. Оно есть в заглавии написанной им книги, которая положила начало нашему государству и называется «Книга восстановлений и противопоставлений».
— Большое вам спасибо, — сказал Олег. — Что такое восстановление, мы как будто поняли. Но что такое противопоставление?
Тут снова стукнулись медные подносы. Весовщик загадочно улыбнулся и растаял в темноте. Мне послышался голос мамы Двойки: «Всякому овощу свое время!» С тех пор как мы здесь, эта пословица так и звенит у меня в ушах!
Даже не верится: неужели настанет день, когда мы сядем рядом, возьмем задачу зеленого стручка и решим ее сами, без всяких провожатых и весовщиков?
Сева.
Вверх-вниз!
(Олег — Нулику)
Что ты скажешь, Нулик, не дают нам лететь вперед сломя голову!
Вышли из весовой, спрашиваем у Эф:
— Когда начнем составлять уравнения?
А она:
— Сперва научитесь решать.
— Вот те раз! Сперва решать, а составлять потом?
— В Аль-Джебре считают, что так целесообразней.
Что ж, решать так решать. Чем скорее, тем лучше.
— Как раз наоборот, — отвечает Эф, — чем скорее, тем хуже. На сегодня довольно. Ваш рабочий день кончился. Отдохните, а завтра приходите снова.
И мы пошли отдыхать. В общем, это не так уж плохо, особенно если под боком Парк Науки и Отдыха.
В парке, как всегда, было полно народу.
Стали думать, куда пойти. Сева непременно хотел посмотреть что-нибудь новенькое. Тане не терпелось опять побывать у силомера. Но я их помирил: предложил пойти к силомеру и все-таки увидать кое-что новое. Потому что мы ведь не успели заглянуть в колодец, где живут отрицательные числа!
Когда мы подошли к молотку, какой-то чудак возводил в квадрат квадратные корни. Задумает, например, корень квадратный из трех и возведет его в квадрат. Понятно, ничего, кроме трех, при этом получиться не может. Потому что извлечение корня и возведение в степень — действия взаимоуничтожающиеся.
√(32) = 3.
Представь себе, что к какому-нибудь числу прибавили пять и тут же снова вычли. От этого число не изменилось.
Точно так же не изменится число, если из него сперва извлекут корень квадратный, а потом снова возведут в квадрат.
Покончив с квадратными корнями, чудак стал возводить в третью степень корень третьей степени из пяти и, конечно, получил пять: 3√(53) = 5.
Он долго стучал молотком, и каждый раз зажигалась зеленая лампочка.
Сева спросил у него, зачем он зря тратит время. Чудак неодобрительно хмыкнул:
— Погостите у нас — узнаете, что без этого иной раз не проживешь.
Наконец он устал и отошел в сторону. А молоток взяла крохотная буковка Вэ — v. Она возвела в квадрат число 41. Гирька взлетела высоко-высоко, к числу 1681, и зажглась зеленая лампочка. Малютка Вэ запрыгала от радости: ничего, мол, что росточком не вышла, зато гирьку вон куда забросила!
Подошла очередь Севы.
— Дайте-ка мне возвести в квадрат отрицательное число. Возведу, а потом загляну в колодец. Только гирьки, пожалуй, там и не увидишь. Ведь чем больше число, тем глубже она уходит в колодец. А я возьму число не маленькое. Ну, хотя бы минус сорок один. Насколько я понимаю, минус сорок один в квадрате равно минус тысяче шестистам восьмидесяти одному.
Кругом зашептались. Сева стукнул молотком, гирька ушла вниз. Мы заглянули в колодец: где-то там, в темной глубине, зажглась красная лампочка.
— В чем дело? — всполошился Сева. — Что-нибудь не так?
— Конечно, — пропищала крошка Вэ, — вы забыли переменить знак. Ведь отрицательное число, возведенное в квадрат, становится положительным.
Сева схватился за голову.
— Какой же я осел! Ведь возвести в квадрат — значит помножить число само на себя! А минус на минус дает плюс.
Он отошел, уступив место Тане.
Она возвела в квадрат минус три. Получилось плюс девять. Гирька подскочила и загорелся зеленый огонек. Потом Таня возвела минус три в третью степень. Получилось минус двадцать семь. Гирька ушла в колодец, и там снова вспыхнула зеленая лампочка.
— Дай-ка мне!
Я взял у Тани молоток и стал возводить минус три в четвертую степень, пятую, шестую, седьмую…
Гирька по очереди то подпрыгивала все выше и выше, то уходила все глубже в колодец. И каждый раз загорался зеленый огонек. Тут-то я и понял, что, когда отрицательное число возводишь в четную степень, ответ получается положительный, а когда в нечетную — отрицательный. Хочешь знать почему? Возьми карандаш и разберись сам.
Наконец мы решили, что достаточно углубили свои знания в колодце, и отправились дальше.
По дороге нам повстречалась старая знакомая — та самая Мнимая Единичка, которая спрашивала у автомата, найдется ли ей место в жизни. Мы ее сразу узнали по маленькому красному зонтику.
— Здравствуйте, как поживаете?
— Отлично, — ответила она. — Автомат сказал правду: и Мнимая Единица может на что-нибудь пригодиться.
— Неужели вы нашли себе место на воздушной монорельсовой дороге?
— Конечно, но не на той ветке, где живут действительные числа. У нас, Мнимых Единиц, собственная дорога. Она пересекает воздушную монорельсовую как раз на Нулевой станции.
— Как же мы ее не заметили? — спросил Сева.
— Так ведь наша дорога мнимая и не сразу бросается в глаза.
— Жаль, что не сразу! — сердито отрезал Сева. — Теперь придется возвращаться, чтобы посмотреть на нее.
— Возвращаться к старому иногда полезно, — заметила Мнимая Единичка. — Но с небольшим кусочком мнимой дороги вы можете познакомиться и здесь. В парке построен новый аттракцион. Он называется «Мнимая карусель». Я там работаю. Хотите взглянуть?
Хотим ли мы взглянуть на карусель, да еще мнимую? Как ты думаешь?
Олег.
Вышли из весовой, спрашиваем у Эф:
— Когда начнем составлять уравнения?
А она:
— Сперва научитесь решать.
— Вот те раз! Сперва решать, а составлять потом?
— В Аль-Джебре считают, что так целесообразней.
Что ж, решать так решать. Чем скорее, тем лучше.
— Как раз наоборот, — отвечает Эф, — чем скорее, тем хуже. На сегодня довольно. Ваш рабочий день кончился. Отдохните, а завтра приходите снова.
И мы пошли отдыхать. В общем, это не так уж плохо, особенно если под боком Парк Науки и Отдыха.
В парке, как всегда, было полно народу.
Стали думать, куда пойти. Сева непременно хотел посмотреть что-нибудь новенькое. Тане не терпелось опять побывать у силомера. Но я их помирил: предложил пойти к силомеру и все-таки увидать кое-что новое. Потому что мы ведь не успели заглянуть в колодец, где живут отрицательные числа!
Когда мы подошли к молотку, какой-то чудак возводил в квадрат квадратные корни. Задумает, например, корень квадратный из трех и возведет его в квадрат. Понятно, ничего, кроме трех, при этом получиться не может. Потому что извлечение корня и возведение в степень — действия взаимоуничтожающиеся.
√(32) = 3.
Представь себе, что к какому-нибудь числу прибавили пять и тут же снова вычли. От этого число не изменилось.
Точно так же не изменится число, если из него сперва извлекут корень квадратный, а потом снова возведут в квадрат.
Покончив с квадратными корнями, чудак стал возводить в третью степень корень третьей степени из пяти и, конечно, получил пять: 3√(53) = 5.
Он долго стучал молотком, и каждый раз зажигалась зеленая лампочка.
Сева спросил у него, зачем он зря тратит время. Чудак неодобрительно хмыкнул:
— Погостите у нас — узнаете, что без этого иной раз не проживешь.
Подошла очередь Севы.
— Дайте-ка мне возвести в квадрат отрицательное число. Возведу, а потом загляну в колодец. Только гирьки, пожалуй, там и не увидишь. Ведь чем больше число, тем глубже она уходит в колодец. А я возьму число не маленькое. Ну, хотя бы минус сорок один. Насколько я понимаю, минус сорок один в квадрате равно минус тысяче шестистам восьмидесяти одному.
Кругом зашептались. Сева стукнул молотком, гирька ушла вниз. Мы заглянули в колодец: где-то там, в темной глубине, зажглась красная лампочка.
— В чем дело? — всполошился Сева. — Что-нибудь не так?
— Конечно, — пропищала крошка Вэ, — вы забыли переменить знак. Ведь отрицательное число, возведенное в квадрат, становится положительным.
Сева схватился за голову.
— Какой же я осел! Ведь возвести в квадрат — значит помножить число само на себя! А минус на минус дает плюс.
Он отошел, уступив место Тане.
Она возвела в квадрат минус три. Получилось плюс девять. Гирька подскочила и загорелся зеленый огонек. Потом Таня возвела минус три в третью степень. Получилось минус двадцать семь. Гирька ушла в колодец, и там снова вспыхнула зеленая лампочка.
— Дай-ка мне!
Я взял у Тани молоток и стал возводить минус три в четвертую степень, пятую, шестую, седьмую…
Гирька по очереди то подпрыгивала все выше и выше, то уходила все глубже в колодец. И каждый раз загорался зеленый огонек. Тут-то я и понял, что, когда отрицательное число возводишь в четную степень, ответ получается положительный, а когда в нечетную — отрицательный. Хочешь знать почему? Возьми карандаш и разберись сам.
Наконец мы решили, что достаточно углубили свои знания в колодце, и отправились дальше.
По дороге нам повстречалась старая знакомая — та самая Мнимая Единичка, которая спрашивала у автомата, найдется ли ей место в жизни. Мы ее сразу узнали по маленькому красному зонтику.
— Здравствуйте, как поживаете?
— Отлично, — ответила она. — Автомат сказал правду: и Мнимая Единица может на что-нибудь пригодиться.
— Неужели вы нашли себе место на воздушной монорельсовой дороге?
— Конечно, но не на той ветке, где живут действительные числа. У нас, Мнимых Единиц, собственная дорога. Она пересекает воздушную монорельсовую как раз на Нулевой станции.
— Как же мы ее не заметили? — спросил Сева.
— Так ведь наша дорога мнимая и не сразу бросается в глаза.
— Жаль, что не сразу! — сердито отрезал Сева. — Теперь придется возвращаться, чтобы посмотреть на нее.
— Возвращаться к старому иногда полезно, — заметила Мнимая Единичка. — Но с небольшим кусочком мнимой дороги вы можете познакомиться и здесь. В парке построен новый аттракцион. Он называется «Мнимая карусель». Я там работаю. Хотите взглянуть?
Хотим ли мы взглянуть на карусель, да еще мнимую? Как ты думаешь?
Олег.
Мнимая карусель
(Таня — Нулику)
Вот тебе, Нулик, наши последние новости.
По дороге к аттракциону все чаще мелькали рекламные плакаты:
ПЕРВАЯ В МИРЕ МНИМАЯ КАРУСЕЛЬ!
ИСКЛЮЧИТЕЛЬНО ДЛЯ МНИМЫХ ЕДИНИЦ!
ЕДИНСТВЕННОЕ МЕСТО,
ГДЕ МНИМЫЕ ЕДИНИЦЫ МОГУТ СТАТЬ
ДЕЙСТВИТЕЛЬНЫМИ!
Мнимые Единицы, кружитесь на здоровье!
Наша симпатичная подружка щебетала без умолку и рассказала кучу интересного.
Оказывается, Мнимая Единица — это просто-напросто корень квадратный из отрицательной единицы: √—1.
— А разве из минус единицы нельзя извлечь корень? — спросил Сева. — Ведь корень квадратный из единицы всегда равен единице.
— Ой-ой-ой! — ужаснулась Мнимая Единичка. — Это касается только положительной единицы. Ведь что значит извлечь корень квадратный, скажем, из девяти?
— Это значит найти такое число, которое при возведении в квадрат равнялось бы девяти, — ответил Олег. — Это число три.
— Верно. А теперь попробуйте найти число, которое при возведении в квадрат дает минус единицу!
Мнимая Единичка тоненько засмеялась.
Сева озадаченно взъерошил волосы:
— М-да! Такого числа нет. Какое число ни возводи в квадрат, положительное или отрицательное, ответ все равно получится положительный. Уж я-то знаю!
— Вот видите. Потому-то корень квадратный из минус единицы называется мнимой единицей.
— Выходит, мнимые единицы совсем особые числа. Наверное, и дорога у вас устроена как-нибудь особенно.
— Ничуть. Наша дорога очень похожа на ту, где живут действительные числа, только расположена она под прямым углом к ней. Это такая же бесконечная прямая, в центре которой находится все та же Нулевая станция.
— Раз у вас есть Нулевая станция, значит есть положительные и отрицательные числа?
— Что вы! Разве мнимые числа могут быть положительными и отрицательными? Просто на нашей дороге, так же как и на дороге действительных чисел, есть два направления от нуля. Одно из них условились обозначать знаком плюс, другое — знаком минус.
— Но как же мнимые числа отличают от действительных?
— С помощью буквы i: 2i, 5i, —8i, —12i.
— Вот как! У вас, как и у других букв в Аль-Джебре, тоже есть коэффициенты?
— Конечно.
— А где же ваш коэффициент? — ляпнул Сева.
И когда только он научится вести себя в обществе? Хорошо еще, воспитанная Единичка сделала вид, что не заметила его бестактности.
— Мой коэффициент — единица, и он, как всегда, невидимка.
Но Сева уже закусил удила. Ужасный он спорщик!
— Вот вы говорите, что мнимая монорельсовая дорога похожа на действительную. Значит, и правила движения на ней те же. Так ведь? Тогда при чем здесь карусель? Ведь на обычной монорельсовой дороге движение идет по прямой, а карусель-то кружится?
— Вы отчасти правы, — ответила Мнимая Единичка. — Правила движений у нас более разнообразны. При сложении и вычитании вагончики на мнимой дороге движутся по прямой и по тем же правилам, что и действительные числа; 2i + 3i = 5i; 8i — 15i = — 7i, или вот еще: —3i + 9i = 6i, ну и конечно: 5i — 5i = 0.
Мнимые Единички с разными знаками и одинаковыми коэффициентами взаимоуничтожаются на Нулевой станции.
Иное дело — умножение, деление, возведение в степень… Тут уж Мнимые Единицы двигаются не только по прямой, но и по кривой. Именно это вы сейчас и увидите.
По дороге к аттракциону все чаще мелькали рекламные плакаты:
ПЕРВАЯ В МИРЕ МНИМАЯ КАРУСЕЛЬ!
ИСКЛЮЧИТЕЛЬНО ДЛЯ МНИМЫХ ЕДИНИЦ!
ЕДИНСТВЕННОЕ МЕСТО,
ГДЕ МНИМЫЕ ЕДИНИЦЫ МОГУТ СТАТЬ
ДЕЙСТВИТЕЛЬНЫМИ!
Мнимые Единицы, кружитесь на здоровье!
Наша симпатичная подружка щебетала без умолку и рассказала кучу интересного.
Оказывается, Мнимая Единица — это просто-напросто корень квадратный из отрицательной единицы: √—1.
— А разве из минус единицы нельзя извлечь корень? — спросил Сева. — Ведь корень квадратный из единицы всегда равен единице.
— Ой-ой-ой! — ужаснулась Мнимая Единичка. — Это касается только положительной единицы. Ведь что значит извлечь корень квадратный, скажем, из девяти?
— Это значит найти такое число, которое при возведении в квадрат равнялось бы девяти, — ответил Олег. — Это число три.
— Верно. А теперь попробуйте найти число, которое при возведении в квадрат дает минус единицу!
Мнимая Единичка тоненько засмеялась.
Сева озадаченно взъерошил волосы:
— Вот видите. Потому-то корень квадратный из минус единицы называется мнимой единицей.
— Выходит, мнимые единицы совсем особые числа. Наверное, и дорога у вас устроена как-нибудь особенно.
— Ничуть. Наша дорога очень похожа на ту, где живут действительные числа, только расположена она под прямым углом к ней. Это такая же бесконечная прямая, в центре которой находится все та же Нулевая станция.
— Раз у вас есть Нулевая станция, значит есть положительные и отрицательные числа?
— Что вы! Разве мнимые числа могут быть положительными и отрицательными? Просто на нашей дороге, так же как и на дороге действительных чисел, есть два направления от нуля. Одно из них условились обозначать знаком плюс, другое — знаком минус.
— Но как же мнимые числа отличают от действительных?
— С помощью буквы i: 2i, 5i, —8i, —12i.
— Вот как! У вас, как и у других букв в Аль-Джебре, тоже есть коэффициенты?
— Конечно.
— А где же ваш коэффициент? — ляпнул Сева.
И когда только он научится вести себя в обществе? Хорошо еще, воспитанная Единичка сделала вид, что не заметила его бестактности.
— Мой коэффициент — единица, и он, как всегда, невидимка.
Но Сева уже закусил удила. Ужасный он спорщик!
— Вот вы говорите, что мнимая монорельсовая дорога похожа на действительную. Значит, и правила движения на ней те же. Так ведь? Тогда при чем здесь карусель? Ведь на обычной монорельсовой дороге движение идет по прямой, а карусель-то кружится?
— Вы отчасти правы, — ответила Мнимая Единичка. — Правила движений у нас более разнообразны. При сложении и вычитании вагончики на мнимой дороге движутся по прямой и по тем же правилам, что и действительные числа; 2i + 3i = 5i; 8i — 15i = — 7i, или вот еще: —3i + 9i = 6i, ну и конечно: 5i — 5i = 0.
Мнимые Единички с разными знаками и одинаковыми коэффициентами взаимоуничтожаются на Нулевой станции.
Иное дело — умножение, деление, возведение в степень… Тут уж Мнимые Единицы двигаются не только по прямой, но и по кривой. Именно это вы сейчас и увидите.