В настоящем разделе рассматривается механизм общественного выбора в условиях прямой и представительной демократии. Одна из важнейших проблем общественного выбора состоит в том, ведет ли этот механизм к результату, который отражает интересы и взгляды электората.
Рассматривая в принципе возможность ранжирования доступных вариантов общественного выбора (раздел 2.4), мы познакомились с теоремой о невозможности. Предполагалось, что способ ранжирования должен опираться на какие-то разумные и нравственно приемлемые принципы, следовать этим принципам. Эту проблему исследовал Кеннет Эрроу. Он исходил из того, что функция общественного выбора должна быть полной (законченной) и транзитивной в ранжировании вариантов, подчиняться таким критериям, как принципы единогласия, универсальности, отсутствия «диктатора», независимости от посторонних альтернатив.
К. Эрроу доказал свою известную теорему о невозможности. Теорема утверждает, что не существует функции общественного выбора, удовлетворяющего одновременно всем четырем требованиям.
Иллюстрацией того, что названные выше критерии являются несовместимыми, является парадокс Кондорсе, или парадокс циклического голосования. Он состоит в том, что транзитивность общественного выбора, т. е. его последовательность и непротиворечивость, при голосовании по принципу простого большинства не соблюдается. Таким образом, последовательный и непротиворечивый общественный выбор невозможен. Парадокс Кондорсе иллюстрирует теорему о невозможности К. Эрроу. (Парадокс Кондорсе называют также «парадоксом циклического голосования».)
Вернемся к парадоксу Кондорсе, который мы рассмотрели в главе 2, но сформулируем его в общем виде, без привязки вариантов к каким-то конкретным проектам.
Таблица 6.2
Парадокс Кондорсе
В табл. 6.2 приведены трое голосующих А, В, С со своими предпочтениями в отношении вариантов выбора х, у, z.
При последовательном голосовании вариантов по парам результаты голосования по принципу большинства будут следующими:
1. Голосуются х и у: выбирается вариант х, так как за него выступает большинство (А и С ).
2. Голосуются у и z: выбирается вариант у, так как за него выступает большинство (А и В ).
3. Голосуются z и x: выбирается вариант z, так как за него выступает большинство (B и С).
Результаты голосования (результаты коллективного выбора) являются непоследовательными и противоречивыми. Рациональность и транзитивность коллективного выбора предполагают выбор варианта х в сравнении с вариантом z. Если бы А был диктатором, то это бы и случилось. Но в условиях демократического выбора результат выборов непоследователен.
Вместе с тем голосование по принципу простого большинства не всегда ведет к парадоксу Кондорсе. В частности, в случае с примером в табл. 6.1 последовательный и непротиворечивый результат голосования может получиться, если, во-первых, изменить процедуру голосования и, во-вторых, предпочтения голосующего С будут другими.
Приведем два варианта предпочтений избирателей Р и Р2 (табл. 6.3).
Таблица 6.3
Предпочтения избирателей (выбор большинством голосов)
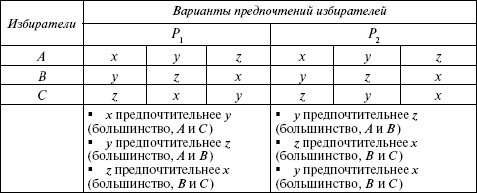При варианте выбора Р1 отсутствует его транзитивность, т. е. последовательность и непротиворечивость (если бы оно было транзитивным, то х должно быть предпочтительнее z).
В случае с вариантом предпочтений Р2 голосование по принципу большинства является транзитивным. Разница между этими двумя вариантами состоит в том, что в первом случае предпочтения являются многовершинными, во втором – одновершинными. (Термины «многовершинные предпочтения» и «одновершинные предпочтения» возникли в связи с особенностями графического изображения предпочтений.)
Различия между вариантами предпочтений Р1 и Р2 графически изображены на рис. 6.1. На нем представлены предпочтения трех избирателей (x, y, z) путем ранжирования этих предпочтений (1 – наиболее предпочтительный выбор, 3 – наименее предпочтительный).
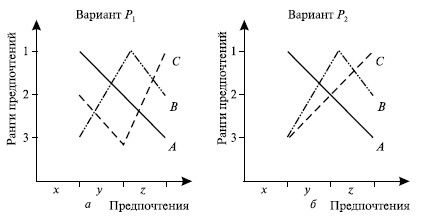
Рис. 6.1. Многовершинные (а) и одновершинные (б) предпочтения
Одновершинные предпочтения (с одной точкой максимума) имеют место тогда, когда все их варианты расположены на линии таким образом, что ни один из голосующих не предпочитает х и z варианту у, если у находится между х и z.
Многовершинные предпочтения (с точками максимума более одной) имеют место тогда, когда при любом расположении их вариантов на линии хотя бы один голосующий не имеет одновершинных предпочтений.
В первом варианте предпочтений на рис. 6.1 избиратели А и В имеют одновершинные предпочтения, в то время как голосующий С отличается многовершинными предпочтениями (график его предпочтений имеет F-образную форму), неравномерно распределенными по шкале предпочтений. Как правило, это предпочтения по принципу «или все, или ничего». Это и ведет к возникновению парадокса Кондорсе, т. е. к парадоксу циклического голосования.
Во втором варианте все голосующие имеют одновершинные предпочтения, равномерно распределенные по шкале предпочтений. Если можно было бы избавиться от многовершинных предпочтений, то обнаружилось бы, что голосование по принципу большинства уже не подвержено парадоксу Кондорсе.
Таким образом, в ситуации, когда предпочтения избирателей являются одновершинными (с одной точкой максимума), равномерно распределенными по шкале предпочтений, голосование по принципу большинства является транзитивным, т. е. последовательным и непротиворечивым.
Рассмотрим пример, в котором имеются три варианта государственного бюджета:
• вариант х – это большой государственный бюджет;
• вариант у – бюджет средних размеров;
• вариант z – небольшой бюджет.
Для тех избирателей, которые выбирают вариант х, естественно предположить, что вторым по значимости выбором будет вариант у, а наименее значимым будет вариант z.
Точно так же для тех, кто выбирает вариант z, следующими по значимости вариантами будут у, а затем х.
В случае нетранзитивного голосования избирателя С его варианты расположены в следующей последовательности: z – небольшой бюджет; х – большой бюджет; у – бюджет средних размеров. Такие предпочтения можно назвать по принципу «все или ничего».
Вероятность таких предпочтений у голосующих незначительна, поэтому можно исключить возможность многовершинных предпочтений в нашем примере. Это выглядит логично в данном примере, где сравниваются разные уровни затрат.
Другая ситуация возникает, если сравниваются не разные уровни, а разные виды государственных расходов. В этом случае нельзя не принимать во внимание голосующих с многовершинными предпочтениями, их нельзя исключить, как в предыдущем примере.
Приведем пример голосования по поводу использования восстановленных земель в пойме р. Клязьмы. Предлагаемые для голосования варианты включали следующее:
х – создание городского парка;
у – строительство муниципального жилья;
z – распродажа земель для частного строительства.
Участвовавшие в голосовании представители различных партий имели следующие предпочтения:
либеральные демократы – х, у, z;
коммунисты – у, z, х;
союз правых сил – z, х, у.
В данном случае предпочтения союза правых сил являются многовершинными, но их нельзя сбросить со счетов как не имеющие значения. Они реальны. И в данном случае речь идет не о разных уровнях государственных расходов, а об их разных видах вперемешку с вариантом, где имеются в виду, по существу, доходы.
Последний пример дает возможность обратить внимание на один из упомянутых выше аспектов парадокса Кондорсе. При наличии нескольких вариантов для голосования (больше двух вариантов) и многовершинных предпочтений у кого-то из голосующих результат голосования будет зависеть от процедуры голосования. В частности, если в рассматриваемом примере сначала голосуются варианты городского парка и муниципального жилья, а затем варианты муниципального и частного жилья, то выбор будет сделан в пользу городского парка.
Действительно, сначала парк признается лучшей альтернативой по сравнению с муниципальным жильем (2 голоса против 1). Затем вариант частного строительства признается худшим по сравнению с вариантом муниципального жилья (1 голос против 2). В итоге наилучший вариант – это городской парк, он лучше муниципального жилья и тем более лучше частного строительства. Но если бы мы сначала поставили на голосование городской парк и муниципальное жилье, а затем городской парк и частное строительство и на этом остановились, то результат был бы противоположным.
6.3. Теорема медианного избирателя
6.4. Проблемы мажоритарного голосования в условиях прямой демократии
Рассматривая в принципе возможность ранжирования доступных вариантов общественного выбора (раздел 2.4), мы познакомились с теоремой о невозможности. Предполагалось, что способ ранжирования должен опираться на какие-то разумные и нравственно приемлемые принципы, следовать этим принципам. Эту проблему исследовал Кеннет Эрроу. Он исходил из того, что функция общественного выбора должна быть полной (законченной) и транзитивной в ранжировании вариантов, подчиняться таким критериям, как принципы единогласия, универсальности, отсутствия «диктатора», независимости от посторонних альтернатив.
К. Эрроу доказал свою известную теорему о невозможности. Теорема утверждает, что не существует функции общественного выбора, удовлетворяющего одновременно всем четырем требованиям.
Иллюстрацией того, что названные выше критерии являются несовместимыми, является парадокс Кондорсе, или парадокс циклического голосования. Он состоит в том, что транзитивность общественного выбора, т. е. его последовательность и непротиворечивость, при голосовании по принципу простого большинства не соблюдается. Таким образом, последовательный и непротиворечивый общественный выбор невозможен. Парадокс Кондорсе иллюстрирует теорему о невозможности К. Эрроу. (Парадокс Кондорсе называют также «парадоксом циклического голосования».)
Вернемся к парадоксу Кондорсе, который мы рассмотрели в главе 2, но сформулируем его в общем виде, без привязки вариантов к каким-то конкретным проектам.
Таблица 6.2
Парадокс Кондорсе
При последовательном голосовании вариантов по парам результаты голосования по принципу большинства будут следующими:
1. Голосуются х и у: выбирается вариант х, так как за него выступает большинство (А и С ).
2. Голосуются у и z: выбирается вариант у, так как за него выступает большинство (А и В ).
3. Голосуются z и x: выбирается вариант z, так как за него выступает большинство (B и С).
Результаты голосования (результаты коллективного выбора) являются непоследовательными и противоречивыми. Рациональность и транзитивность коллективного выбора предполагают выбор варианта х в сравнении с вариантом z. Если бы А был диктатором, то это бы и случилось. Но в условиях демократического выбора результат выборов непоследователен.
Вместе с тем голосование по принципу простого большинства не всегда ведет к парадоксу Кондорсе. В частности, в случае с примером в табл. 6.1 последовательный и непротиворечивый результат голосования может получиться, если, во-первых, изменить процедуру голосования и, во-вторых, предпочтения голосующего С будут другими.
Приведем два варианта предпочтений избирателей Р и Р2 (табл. 6.3).
Таблица 6.3
Предпочтения избирателей (выбор большинством голосов)
В случае с вариантом предпочтений Р2 голосование по принципу большинства является транзитивным. Разница между этими двумя вариантами состоит в том, что в первом случае предпочтения являются многовершинными, во втором – одновершинными. (Термины «многовершинные предпочтения» и «одновершинные предпочтения» возникли в связи с особенностями графического изображения предпочтений.)
Различия между вариантами предпочтений Р1 и Р2 графически изображены на рис. 6.1. На нем представлены предпочтения трех избирателей (x, y, z) путем ранжирования этих предпочтений (1 – наиболее предпочтительный выбор, 3 – наименее предпочтительный).
Рис. 6.1. Многовершинные (а) и одновершинные (б) предпочтения
Одновершинные предпочтения (с одной точкой максимума) имеют место тогда, когда все их варианты расположены на линии таким образом, что ни один из голосующих не предпочитает х и z варианту у, если у находится между х и z.
Многовершинные предпочтения (с точками максимума более одной) имеют место тогда, когда при любом расположении их вариантов на линии хотя бы один голосующий не имеет одновершинных предпочтений.
В первом варианте предпочтений на рис. 6.1 избиратели А и В имеют одновершинные предпочтения, в то время как голосующий С отличается многовершинными предпочтениями (график его предпочтений имеет F-образную форму), неравномерно распределенными по шкале предпочтений. Как правило, это предпочтения по принципу «или все, или ничего». Это и ведет к возникновению парадокса Кондорсе, т. е. к парадоксу циклического голосования.
Во втором варианте все голосующие имеют одновершинные предпочтения, равномерно распределенные по шкале предпочтений. Если можно было бы избавиться от многовершинных предпочтений, то обнаружилось бы, что голосование по принципу большинства уже не подвержено парадоксу Кондорсе.
Таким образом, в ситуации, когда предпочтения избирателей являются одновершинными (с одной точкой максимума), равномерно распределенными по шкале предпочтений, голосование по принципу большинства является транзитивным, т. е. последовательным и непротиворечивым.
Рассмотрим пример, в котором имеются три варианта государственного бюджета:
• вариант х – это большой государственный бюджет;
• вариант у – бюджет средних размеров;
• вариант z – небольшой бюджет.
Для тех избирателей, которые выбирают вариант х, естественно предположить, что вторым по значимости выбором будет вариант у, а наименее значимым будет вариант z.
Точно так же для тех, кто выбирает вариант z, следующими по значимости вариантами будут у, а затем х.
В случае нетранзитивного голосования избирателя С его варианты расположены в следующей последовательности: z – небольшой бюджет; х – большой бюджет; у – бюджет средних размеров. Такие предпочтения можно назвать по принципу «все или ничего».
Вероятность таких предпочтений у голосующих незначительна, поэтому можно исключить возможность многовершинных предпочтений в нашем примере. Это выглядит логично в данном примере, где сравниваются разные уровни затрат.
Другая ситуация возникает, если сравниваются не разные уровни, а разные виды государственных расходов. В этом случае нельзя не принимать во внимание голосующих с многовершинными предпочтениями, их нельзя исключить, как в предыдущем примере.
Приведем пример голосования по поводу использования восстановленных земель в пойме р. Клязьмы. Предлагаемые для голосования варианты включали следующее:
х – создание городского парка;
у – строительство муниципального жилья;
z – распродажа земель для частного строительства.
Участвовавшие в голосовании представители различных партий имели следующие предпочтения:
либеральные демократы – х, у, z;
коммунисты – у, z, х;
союз правых сил – z, х, у.
В данном случае предпочтения союза правых сил являются многовершинными, но их нельзя сбросить со счетов как не имеющие значения. Они реальны. И в данном случае речь идет не о разных уровнях государственных расходов, а об их разных видах вперемешку с вариантом, где имеются в виду, по существу, доходы.
Последний пример дает возможность обратить внимание на один из упомянутых выше аспектов парадокса Кондорсе. При наличии нескольких вариантов для голосования (больше двух вариантов) и многовершинных предпочтений у кого-то из голосующих результат голосования будет зависеть от процедуры голосования. В частности, если в рассматриваемом примере сначала голосуются варианты городского парка и муниципального жилья, а затем варианты муниципального и частного жилья, то выбор будет сделан в пользу городского парка.
Действительно, сначала парк признается лучшей альтернативой по сравнению с муниципальным жильем (2 голоса против 1). Затем вариант частного строительства признается худшим по сравнению с вариантом муниципального жилья (1 голос против 2). В итоге наилучший вариант – это городской парк, он лучше муниципального жилья и тем более лучше частного строительства. Но если бы мы сначала поставили на голосование городской парк и муниципальное жилье, а затем городской парк и частное строительство и на этом остановились, то результат был бы противоположным.
6.3. Теорема медианного избирателя
В условиях голосования по принципу простого большинства ключом к успеху является политика привлечения медианного избирателя. Избиратели, находящиеся в середине избирательного спектра, играют особую роль.
Медиана – это центральное или срединное значение вариационного признака; другими словами, вариант, находящийся в центре ранжированного ряда.
Медианный избиратель – это избиратели, голосующие за средние, а не за крайние варианты того или иного общественного проекта, избиратели, находящиеся в середине избирательного спектра.
Вернемся к примеру с различными вариантами предлагаемого для голосования государственного бюджета: вариант х – это большой государственный бюджет; вариант у – бюджет средних размеров; вариант z – небольшой бюджет.
Предположим, что имеют место одновершинные предпочтения (например, вариант Р2 в табл. 6.3 и на рис. 6.1). В этом случае В – медианный избиратель, его выбор – это вариант у, т. е. государственный бюджет средних размеров. Данный вариант – это также второй по значению вариант для всех остальных избирателей. В конечном итоге наиболее предпочтительным при мажоритарном голосовании будет вариант у.
Иллюстрация той власти, которой обладает медианный избиратель, дана на рис. 6.2. При количестве голосующих (n) медианный избиратель будет голосовать за уровень государственных расходов, равный Gn/2 (срединный вариант). Сравним этот уровень с любым другим уровнем расходов.
1. При голосовании вариантов Gn/2 и G1 (первый вариант) победит вариант медианного избирателя, так как за него будут голосовать также и те, кто предпочитает более высокий уровень государственных расходов.
2. При голосовании вариантов Gn/2 и Gn (последний вариант) также победит вариант медианного избирателя, так как за него будут голосовать в том числе и те, кто предпочитает более низкий уровень государственных расходов.
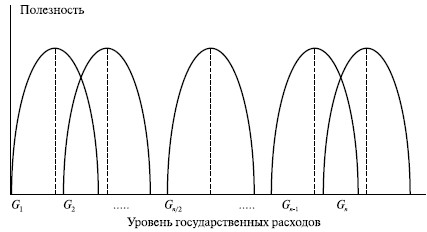
Рис. 6.2. Власть медианного избирателя
Таким образом, при голосовании по принципу большинства выбор медианного избирателя будет поддержан большинством избирателей. Этот вывод получил название теоремы медианного избирателя.
Теорема медианного избирателя: при мажоритарном голосовании победит тот вариант, который предпочитает медианный избиратель.
Вместе с тем необходимо иметь в виду, что теорема медианного избирателя в основном применима к условиям представительной демократии и неприменима к условиям прямой демократии. Практическое значение теоремы медианного избирателя в условиях представительной демократии широко известно. Политические партии формулируют свои программы таким образом, чтобы привлекать не только крайние политические группы, но прежде всего электорат, находящийся в середине политического спектра.
Медиана – это центральное или срединное значение вариационного признака; другими словами, вариант, находящийся в центре ранжированного ряда.
Медианный избиратель – это избиратели, голосующие за средние, а не за крайние варианты того или иного общественного проекта, избиратели, находящиеся в середине избирательного спектра.
Вернемся к примеру с различными вариантами предлагаемого для голосования государственного бюджета: вариант х – это большой государственный бюджет; вариант у – бюджет средних размеров; вариант z – небольшой бюджет.
Предположим, что имеют место одновершинные предпочтения (например, вариант Р2 в табл. 6.3 и на рис. 6.1). В этом случае В – медианный избиратель, его выбор – это вариант у, т. е. государственный бюджет средних размеров. Данный вариант – это также второй по значению вариант для всех остальных избирателей. В конечном итоге наиболее предпочтительным при мажоритарном голосовании будет вариант у.
Иллюстрация той власти, которой обладает медианный избиратель, дана на рис. 6.2. При количестве голосующих (n) медианный избиратель будет голосовать за уровень государственных расходов, равный Gn/2 (срединный вариант). Сравним этот уровень с любым другим уровнем расходов.
1. При голосовании вариантов Gn/2 и G1 (первый вариант) победит вариант медианного избирателя, так как за него будут голосовать также и те, кто предпочитает более высокий уровень государственных расходов.
2. При голосовании вариантов Gn/2 и Gn (последний вариант) также победит вариант медианного избирателя, так как за него будут голосовать в том числе и те, кто предпочитает более низкий уровень государственных расходов.
Рис. 6.2. Власть медианного избирателя
Таким образом, при голосовании по принципу большинства выбор медианного избирателя будет поддержан большинством избирателей. Этот вывод получил название теоремы медианного избирателя.
Теорема медианного избирателя: при мажоритарном голосовании победит тот вариант, который предпочитает медианный избиратель.
Вместе с тем необходимо иметь в виду, что теорема медианного избирателя в основном применима к условиям представительной демократии и неприменима к условиям прямой демократии. Практическое значение теоремы медианного избирателя в условиях представительной демократии широко известно. Политические партии формулируют свои программы таким образом, чтобы привлекать не только крайние политические группы, но прежде всего электорат, находящийся в середине политического спектра.
6.4. Проблемы мажоритарного голосования в условиях прямой демократии
Одной из проблем теории общественного выбора является повышение эффективности общественного выбора путем мажоритарного голосования. Вопрос заключается в том, дает ли эта система эффективный результат, т. е., отражают ли результаты прямого голосования взгляды избирателей. Речь идет о мажоритарном голосовании в условиях прямой демократии. Как мы увидим при дальнейшем рассмотрении этой проблемы, мажоритарное голосование даже в условиях прямой демократии может привести к неэффективному результату.
Можно привести простые примеры неэффективности выбора мажоритарным голосованием – неэффективности в том смысле, что при голосовании выбирается не самый оптимальный, т. е. эффективный, объем производства общественных благ.
На рис. 6.3 приведен пример результатов неэффективного голосования «за» – левая часть рис. 6.3, б и неэффективного голосования «против» – правая часть рис. 6.3, а. По вертикали отмечены частные выгоды (В ) каждого голосующего и уплачиваемый налог (Т = 300). По горизонтали отмечены голосующие А, В, С.
Можно привести простые примеры неэффективности выбора мажоритарным голосованием – неэффективности в том смысле, что при голосовании выбирается не самый оптимальный, т. е. эффективный, объем производства общественных благ.
На рис. 6.3 приведен пример результатов неэффективного голосования «за» – левая часть рис. 6.3, б и неэффективного голосования «против» – правая часть рис. 6.3, а. По вертикали отмечены частные выгоды (В ) каждого голосующего и уплачиваемый налог (Т = 300). По горизонтали отмечены голосующие А, В, С.
Конец бесплатного ознакомительного фрагмента