Страница:
Эта цитата, касающаяся еще одного числа, опять-таки привлекает внимание к тому смыслу, который древние египтяне вкладывали в повторение чисел. В данном случае числа ясно показывают, что количество статуй, ниш, колонн или чего бы там ни было, могло быть подсчитано. В пропорциях же пирамиды они подразумеваются или скрыты. После сооружения пирамиды, эти числа могли быть открыты заново теми, кто был способен сделать новые замеры и вычислить пропорции.
Стоит еще раз назвать пропорции трех главных пирамид Гизы. Напомним, что речь идет о соотношениях единиц измерения, использованных при строительстве, а не о самих единицах. Отношения высоты к основанию каждой пирамиды и образованные ими углы можно изобразить следующим образом (рис. 26):
Пирамида Хуфу =7:11 =51°5'
Пирамида Хафры =4:6 = 53°8'
Пирамида Менкаура = 11:18 = 50°43'
Для пирамиды Хафры я дал отношение 4:6 вместо 2:3 потому, что первое подразумевает треугольник 3:4:5. Число 5 неясно присутствует в длине склона пирамиды.
Математика и фараоны
Глава 6
С вященная геометрия и пирамиды гизы
Священная геометрия
Круг, треугольник и квадрат
С помощью круга и сетки
Комплекс Гизы
Стоит еще раз назвать пропорции трех главных пирамид Гизы. Напомним, что речь идет о соотношениях единиц измерения, использованных при строительстве, а не о самих единицах. Отношения высоты к основанию каждой пирамиды и образованные ими углы можно изобразить следующим образом (рис. 26):
Пирамида Хафры =4:6 = 53°8'
Пирамида Менкаура = 11:18 = 50°43'
Для пирамиды Хафры я дал отношение 4:6 вместо 2:3 потому, что первое подразумевает треугольник 3:4:5. Число 5 неясно присутствует в длине склона пирамиды.
Математика и фараоны
Я пришел к указанным пропорциям прежде, чем обнаружил, что именно эту систему использовали древние египтяне. Благодаря находке нескольких математических папирусов, египтологи узнали кое-что о древнеегипетских системах исчисления и мер. Содержавшиеся в них задачи решались писцами. Одним из самых известных является «Риндский математический папирус», хранящийся ныне в Британском музее. Изучая эти задачки, египтологи узнали, как древние египтяне справлялись с различными количествами, возникавшими при вычислении мер веса, длины и объема, в которых часто использовались дроби, а также как они управлялись с углами.
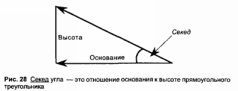
Сегодня для измерения углов используют транспортир, делящий круг на 360 градусов. Каждый градус делится на 60 минут, которые в свою очередь подразделяются на 60 секунд. Древние же египтяне использовали совершенно иной способ вычисления углов – на основе отношения высоты к основанию прямоугольного треугольника. На самом деле они выражали любой угол на языке градиента. Аналогичная система использовалась до недавнего времени на английских дорожных знаках, предупреждавших о крутом спуске или подъеме впереди. Эти знаки давали градиент холма в числовом отношении, например 1 к 6. Это означало, что на шесть единиц по горизонтали приходится одна единица подъема по вертикали.
Точно так же в Древнем Египте градиент склона выражался отношением целого числа, называвшимся «секед» угла (рис. 28). В книге «Математика во времена фараонов» Ричард Гиллингс объясняет:
«Секед правильной пирамиды – это наклон любой из четырех треугольных граней к плоскости основания, измеряемый энным числом горизонтальных единиц на одну вертикальную единицу подъема. Таким образом, эта единица измерения эквивалентна нашему современному котангенсу угла наклона. В целом секед пирамиды – это своего рода дробь, выраженная в стольких-то ладонях (единицах из мерения) горизонтально на каждый локоть вертикального подъема, где 7 ладоней равны одному локтю. Египетское слово „секед“ таким образом родственно нашему современному слову „градиент“».
Понимание этой простой системы стало ключевым моментом в определении техники съемки древних бриттов в Марлборо-Даунс.
Благодаря пониманию метода древних египтян, стало ясно, откуда взялись «странные» углы склона вроде 51°51', как в Великой пирамиде. Он является производным от простого числового отношения высоты и основания пирамиды, которое в случае Великой пирамиды равно 7:11. Это справедливо для всех пирамид. Но упоминаний этого простого факта я не нашел ни в одной книге, прочитанной по этой тематике. Числовой ключ к пирамидам заключен в отношении их высоты к основанию.
В практическом плане – а древние египтяне, несомненно, были людьми практичными это наилегчайший способ изготовления шаблонов, необходимых для постоянной проверки правильности угла наклона на протяжении всего строительства пирамиды.
Тут же возникли новые вопросы почему в Гизе древние египтяне выбирали разные углы наклона для каждой пирамиды? Что такого значимого в разных пропорциях? Не практичнее ли было бы возводить все пирамиды по формуле, найденной для Великой пирамиды?
Египтологи были бы рады убедить нас в том, что каждый фараон жаждал выразить свою индивидуальность, оттого и различия. Но могла быть и иная причина. Возможно, все они желали воплотить разные символические ассоциации, скрытые в различных пропорциях.
Есть по крайней мере еще одна пирамида, построенная на отношении 7:11. Она находится в Мейдуме – более чем в 160 километрах (100 милях) к югу от Гизы и приписывается Снофру (Снеферу) – отцу Хуфу. У другой пирамиды в Абусире, приписываемой Сахуре – одному из фараонов V династии, угол наклона составляет 51°42' и лишь на какую-то долю отличается от угла Великой пирамиды. И здесь, вероятно, использовано то же отношение – 7:11. Проблема с пирамидой Сахуры, как и со многими другими пирамидами в Египте, заключает ся в том, что из-за снятой облицовки трудно определить с точностью истинный угол.
Угол наклона пирамиды Хафры повторяется в пирамиде Пепи II – одного из фараонов VI династии, правившего с 2278 по 2184 год до н. э. Пирамида разрушена, но угол ее наклона определили по остаткам внешней облицовки. Конструкция более поздних египетских пирамид значительно уступала комплексу Гизы. Изначальное отношение пирамиды Хафры следует принять 4:6, четные числа которого выражают женское начало – Исиду.
В третьей пирамиде – Менкаура присутствуют и мужское число 11, и женское – 18. Последнее же можно представить как 6+6+6 или еще одно проявление числа 666. Третье божество троицы – мужчина Гор, которого я ассоциирую с пирамидой Менкаура и который, согласно мифам, вел постоянную войну со злым дядей Сетом. Мог ли он быть тем зверем, о котором говорится в «Откровении апостола Иоанна»?
Древние египтяне видели в своих фараонах воплощение бога Гора, задача которого на Земле и состояла в создании порядка из хаоса. В символическом плане фараон также мог представлять наше духовное «я» в борьбе с самыми низменными сторонами нашей человеческой натуры.
С богом Сетом ассоциировался красный цвет, и поэтому вполне возможно, что двухцветная композиция пирамиды Менкаура с ее верхними ярусами из белого известняка и нижними из необтесанного красного гранита была призвана изображать борьбу Гора с Сетом, порядка с хаосом, нашего духовного начала с нашим телесным естеством.
Древний Египет называли «Две земли» – Верхний и Нижний Египет. Белый цвет символизировал Верхний Египет, а красный – Нижний. Использование двух цветов в пирамиде Менкаура также могло устанавливать символическую связь с «Двумя землями». В своей книге «Фараоны и пирамиды» Джордж Харт обращает на это внимание:
«Таким образом, даже будучи меньшим по размерам на плато Гиза, памятник Менкаура являл собой привлекательное зрелище, благодаря цветовому контрасту белого известняка и красного гранита. И вновь зрителя поражает… глубокий дуализм египетских символов. Ибо в пирамиде Менкаура больше, чем в любой другой, линия смены цвета… подчеркивала его роль „Властелина Двух земель“ даже облицовочными блоками его погребального памятника».
С другой стороны, использование в пирамиде Менкаура чисел 11 и 18 могло также выражать необходимость уравновесить мужской и женский элементы в душе.
Традиция «магических» чисел делает еще один шаг вперед, складывая отдельные цифры в любое число, что бы привести последнее к его первоначальной форме. Обычно речь могла идти о любом числе от 1 до 9. Например, число 18 можно привести к числу 9, сложив две цифры: 1+8=9. Существовали некоторые исключения из этой системы. Древние придавали большое значение числам с повторяющимися цифрами – 11, 22, 33, 44 и т п. Так, число 11 (1+1) обычно не могло быть сведено к 2.
Подобное понятие не имеет места в современной на уке и рассматривается как суеверный вздор. Древние же египтяне высоко ценили свой критерий мер и пропорций, породивший весьма своеобразные формы их искусства. По мнению Платона, сохранение такой гармоничной системы пропорций было основной причиной процветания египетской цивилизации на протяжении долгих тысячелетий. Из учения Пифагора, посвященного в египетское жречество, можно заключить, что жрецы широко пользовались «наукой» о магических числах, принципом приведения чисел к их первичной форме. Следовательно, этот принцип необходимо понять, если мы желаем проникнуть в их образ мышления и разгадать некоторые концепции, заключенные в конструкции пирамид.
Применительно к трем пирамидам этот принцип дает следующие соотношения
Хуфу (7:11), 7+11=18, 1+8=9;
Хафра (4:6), 4+6=10;
Менкаура(11:18), 11+18=29, 2+9=11.
Становится очевидно, что образцы чисел, в частности 11 и 18, включены в конституцию. Гармония чисел 9, 10 и 11, отражающая последовательность строительства пирамид (Хуфу, Хафры и Менкаура), дает в сумме 30 (9+10+11), что можно выразить так 3х10. В гематрии (еврейской системе привязывания чисел к буквам) число 10 соответствует древнееврейской букве «h». В иудаизме 10 – это число Бога, буквой «h» оканчиваются все слова (например, Иегова = Jehovah), служащие отражением божества. Через эту традицию и числовой символизм мы прослеживаем косвенную связь трех пирамид с божественным. (Традиционные значения различных чисел даются в Приложении 2).
Соотношения, включенные в пирамиды Гизы, проливают дополнительный свет на ассоциации, скрытые в этих памятниках. Также можно считать, что они символически выражают вечные истины, присутствующие в мифах и религиозных верованиях древних египтян. Пирамиды Гизы могут быть несколько больше связаны с возвеличиванием трех фараонов и обеспечением их загробной жизни, чем великие соборы средневековой Европы с прославлением отдельных королей христианского мира, построивших их и часто похороненных в них. Средневековые короли могли финансировать строительство этих больших храмов и использовать их в качестве своего последнего пристанища, но не это было их главной целью. Точно так же приписывание пирамидам имен построивших их фараонов может затемнить их истинное религиозное предназначение.
Все это, конечно же, лишь догадки и одновременно решительный отказ от того, что хотели бы навязать нам ортодоксальные египтологи Но это подразумевает последовательность в замысле комплекса Гизы, которая была признана только после того, как работа Бьювэла и Джилберта связала его с тремя-звездами Пояса Ориона, и отсюда начинается новый путь изучения значения пирамид.
Какими бы важными ни были числа для древних культур, они не были первоначальным источником математического знания. Платон утверждал, что все вечные истины могут быть получены с помощью циркуля и линейки. Иными словами, чистая геометрия лежит в центре всех вещей. Чистая геометрия может быть определена как рисунки, полученные с помощью циркуля и линейки безотносительно к числам и мерам. Еще один ключ к головоломке дает геометрическая основа ориентационного плана комплекса Гизы. Для понимания смысла схемы, обнаруженной в Марлборо-Даунс, и ее связи с Великой пирамидой Египта необходимо прежде исследовать концепции священной геометрии.
Сегодня для измерения углов используют транспортир, делящий круг на 360 градусов. Каждый градус делится на 60 минут, которые в свою очередь подразделяются на 60 секунд. Древние же египтяне использовали совершенно иной способ вычисления углов – на основе отношения высоты к основанию прямоугольного треугольника. На самом деле они выражали любой угол на языке градиента. Аналогичная система использовалась до недавнего времени на английских дорожных знаках, предупреждавших о крутом спуске или подъеме впереди. Эти знаки давали градиент холма в числовом отношении, например 1 к 6. Это означало, что на шесть единиц по горизонтали приходится одна единица подъема по вертикали.
Точно так же в Древнем Египте градиент склона выражался отношением целого числа, называвшимся «секед» угла (рис. 28). В книге «Математика во времена фараонов» Ричард Гиллингс объясняет:
«Секед правильной пирамиды – это наклон любой из четырех треугольных граней к плоскости основания, измеряемый энным числом горизонтальных единиц на одну вертикальную единицу подъема. Таким образом, эта единица измерения эквивалентна нашему современному котангенсу угла наклона. В целом секед пирамиды – это своего рода дробь, выраженная в стольких-то ладонях (единицах из мерения) горизонтально на каждый локоть вертикального подъема, где 7 ладоней равны одному локтю. Египетское слово „секед“ таким образом родственно нашему современному слову „градиент“».
Понимание этой простой системы стало ключевым моментом в определении техники съемки древних бриттов в Марлборо-Даунс.
Благодаря пониманию метода древних египтян, стало ясно, откуда взялись «странные» углы склона вроде 51°51', как в Великой пирамиде. Он является производным от простого числового отношения высоты и основания пирамиды, которое в случае Великой пирамиды равно 7:11. Это справедливо для всех пирамид. Но упоминаний этого простого факта я не нашел ни в одной книге, прочитанной по этой тематике. Числовой ключ к пирамидам заключен в отношении их высоты к основанию.
Тут же возникли новые вопросы почему в Гизе древние египтяне выбирали разные углы наклона для каждой пирамиды? Что такого значимого в разных пропорциях? Не практичнее ли было бы возводить все пирамиды по формуле, найденной для Великой пирамиды?
Египтологи были бы рады убедить нас в том, что каждый фараон жаждал выразить свою индивидуальность, оттого и различия. Но могла быть и иная причина. Возможно, все они желали воплотить разные символические ассоциации, скрытые в различных пропорциях.
Есть по крайней мере еще одна пирамида, построенная на отношении 7:11. Она находится в Мейдуме – более чем в 160 километрах (100 милях) к югу от Гизы и приписывается Снофру (Снеферу) – отцу Хуфу. У другой пирамиды в Абусире, приписываемой Сахуре – одному из фараонов V династии, угол наклона составляет 51°42' и лишь на какую-то долю отличается от угла Великой пирамиды. И здесь, вероятно, использовано то же отношение – 7:11. Проблема с пирамидой Сахуры, как и со многими другими пирамидами в Египте, заключает ся в том, что из-за снятой облицовки трудно определить с точностью истинный угол.
Угол наклона пирамиды Хафры повторяется в пирамиде Пепи II – одного из фараонов VI династии, правившего с 2278 по 2184 год до н. э. Пирамида разрушена, но угол ее наклона определили по остаткам внешней облицовки. Конструкция более поздних египетских пирамид значительно уступала комплексу Гизы. Изначальное отношение пирамиды Хафры следует принять 4:6, четные числа которого выражают женское начало – Исиду.
В третьей пирамиде – Менкаура присутствуют и мужское число 11, и женское – 18. Последнее же можно представить как 6+6+6 или еще одно проявление числа 666. Третье божество троицы – мужчина Гор, которого я ассоциирую с пирамидой Менкаура и который, согласно мифам, вел постоянную войну со злым дядей Сетом. Мог ли он быть тем зверем, о котором говорится в «Откровении апостола Иоанна»?
Древние египтяне видели в своих фараонах воплощение бога Гора, задача которого на Земле и состояла в создании порядка из хаоса. В символическом плане фараон также мог представлять наше духовное «я» в борьбе с самыми низменными сторонами нашей человеческой натуры.
С богом Сетом ассоциировался красный цвет, и поэтому вполне возможно, что двухцветная композиция пирамиды Менкаура с ее верхними ярусами из белого известняка и нижними из необтесанного красного гранита была призвана изображать борьбу Гора с Сетом, порядка с хаосом, нашего духовного начала с нашим телесным естеством.
Древний Египет называли «Две земли» – Верхний и Нижний Египет. Белый цвет символизировал Верхний Египет, а красный – Нижний. Использование двух цветов в пирамиде Менкаура также могло устанавливать символическую связь с «Двумя землями». В своей книге «Фараоны и пирамиды» Джордж Харт обращает на это внимание:
«Таким образом, даже будучи меньшим по размерам на плато Гиза, памятник Менкаура являл собой привлекательное зрелище, благодаря цветовому контрасту белого известняка и красного гранита. И вновь зрителя поражает… глубокий дуализм египетских символов. Ибо в пирамиде Менкаура больше, чем в любой другой, линия смены цвета… подчеркивала его роль „Властелина Двух земель“ даже облицовочными блоками его погребального памятника».
С другой стороны, использование в пирамиде Менкаура чисел 11 и 18 могло также выражать необходимость уравновесить мужской и женский элементы в душе.
Традиция «магических» чисел делает еще один шаг вперед, складывая отдельные цифры в любое число, что бы привести последнее к его первоначальной форме. Обычно речь могла идти о любом числе от 1 до 9. Например, число 18 можно привести к числу 9, сложив две цифры: 1+8=9. Существовали некоторые исключения из этой системы. Древние придавали большое значение числам с повторяющимися цифрами – 11, 22, 33, 44 и т п. Так, число 11 (1+1) обычно не могло быть сведено к 2.
Подобное понятие не имеет места в современной на уке и рассматривается как суеверный вздор. Древние же египтяне высоко ценили свой критерий мер и пропорций, породивший весьма своеобразные формы их искусства. По мнению Платона, сохранение такой гармоничной системы пропорций было основной причиной процветания египетской цивилизации на протяжении долгих тысячелетий. Из учения Пифагора, посвященного в египетское жречество, можно заключить, что жрецы широко пользовались «наукой» о магических числах, принципом приведения чисел к их первичной форме. Следовательно, этот принцип необходимо понять, если мы желаем проникнуть в их образ мышления и разгадать некоторые концепции, заключенные в конструкции пирамид.
Применительно к трем пирамидам этот принцип дает следующие соотношения
Хуфу (7:11), 7+11=18, 1+8=9;
Хафра (4:6), 4+6=10;
Менкаура(11:18), 11+18=29, 2+9=11.
Становится очевидно, что образцы чисел, в частности 11 и 18, включены в конституцию. Гармония чисел 9, 10 и 11, отражающая последовательность строительства пирамид (Хуфу, Хафры и Менкаура), дает в сумме 30 (9+10+11), что можно выразить так 3х10. В гематрии (еврейской системе привязывания чисел к буквам) число 10 соответствует древнееврейской букве «h». В иудаизме 10 – это число Бога, буквой «h» оканчиваются все слова (например, Иегова = Jehovah), служащие отражением божества. Через эту традицию и числовой символизм мы прослеживаем косвенную связь трех пирамид с божественным. (Традиционные значения различных чисел даются в Приложении 2).
Соотношения, включенные в пирамиды Гизы, проливают дополнительный свет на ассоциации, скрытые в этих памятниках. Также можно считать, что они символически выражают вечные истины, присутствующие в мифах и религиозных верованиях древних египтян. Пирамиды Гизы могут быть несколько больше связаны с возвеличиванием трех фараонов и обеспечением их загробной жизни, чем великие соборы средневековой Европы с прославлением отдельных королей христианского мира, построивших их и часто похороненных в них. Средневековые короли могли финансировать строительство этих больших храмов и использовать их в качестве своего последнего пристанища, но не это было их главной целью. Точно так же приписывание пирамидам имен построивших их фараонов может затемнить их истинное религиозное предназначение.
Все это, конечно же, лишь догадки и одновременно решительный отказ от того, что хотели бы навязать нам ортодоксальные египтологи Но это подразумевает последовательность в замысле комплекса Гизы, которая была признана только после того, как работа Бьювэла и Джилберта связала его с тремя-звездами Пояса Ориона, и отсюда начинается новый путь изучения значения пирамид.
Какими бы важными ни были числа для древних культур, они не были первоначальным источником математического знания. Платон утверждал, что все вечные истины могут быть получены с помощью циркуля и линейки. Иными словами, чистая геометрия лежит в центре всех вещей. Чистая геометрия может быть определена как рисунки, полученные с помощью циркуля и линейки безотносительно к числам и мерам. Еще один ключ к головоломке дает геометрическая основа ориентационного плана комплекса Гизы. Для понимания смысла схемы, обнаруженной в Марлборо-Даунс, и ее связи с Великой пирамидой Египта необходимо прежде исследовать концепции священной геометрии.
Глава 6
С вященная геометрия и пирамиды гизы
Большая галерея пирамиды выстроена на одной линии с центром одного из кругов.
Надпись над входом в Академию Платона в Афинах гласила: «Пусть войдет сюда сведущий в геометрии». Для древних греков чистая геометрия была центром всех вещей. Она была способом примирения мира божественного с формой видимого мира. Золотая пропорция, например, может быть описана на языке геометрии, но не чисел. Она может быть начертана, но не может быть записана, поскольку имеет бесконечное число десятичных знаков. Геометрию можно считать способом определения того, что иначе неопределимо.
Об использовании чистой геометрии в Древнем Египте мы знаем очень мало. Мы не располагаем папирусами, дававшими бы геометрический эквивалент уравнений Платона, Фалеса и Эвклида, олицетворяющих древнегреческую мысль. Тем не менее Платон считал, что Египет владел совокупностью глубоких знании, основанных на гармонии и пропорции. Мы можем сделать вывод, что древние египтяне не менее искусно владели циркулем и линейкой, чем их греческие коллеги. Эти знания должны были повлиять на их искусство и архитектуру. Разгадка того, как египтяне выбирали использовавшиеся ими пропорции, является способом возвращения к истокам их цивилизации.
Узоры на Марлборо-Даунс также представляются основанными на чистой геометрии. Нашим следующим шагом поэтому станет сближение этих несоизмеримых частей головоломки и открытие геометрии, лежащей в их основе и объединяющей их.
Надпись над входом в Академию Платона в Афинах гласила: «Пусть войдет сюда сведущий в геометрии». Для древних греков чистая геометрия была центром всех вещей. Она была способом примирения мира божественного с формой видимого мира. Золотая пропорция, например, может быть описана на языке геометрии, но не чисел. Она может быть начертана, но не может быть записана, поскольку имеет бесконечное число десятичных знаков. Геометрию можно считать способом определения того, что иначе неопределимо.
Об использовании чистой геометрии в Древнем Египте мы знаем очень мало. Мы не располагаем папирусами, дававшими бы геометрический эквивалент уравнений Платона, Фалеса и Эвклида, олицетворяющих древнегреческую мысль. Тем не менее Платон считал, что Египет владел совокупностью глубоких знании, основанных на гармонии и пропорции. Мы можем сделать вывод, что древние египтяне не менее искусно владели циркулем и линейкой, чем их греческие коллеги. Эти знания должны были повлиять на их искусство и архитектуру. Разгадка того, как египтяне выбирали использовавшиеся ими пропорции, является способом возвращения к истокам их цивилизации.
Узоры на Марлборо-Даунс также представляются основанными на чистой геометрии. Нашим следующим шагом поэтому станет сближение этих несоизмеримых частей головоломки и открытие геометрии, лежащей в их основе и объединяющей их.
Священная геометрия
Термин «священная геометрия» может ввести в заблуждение, поскольку основы геометрической пропорции широко распространены в природе, а также в искусстве и архитектуре. Почему одни элементы священны, а другие нет? Нелегко ответить на этот вопрос. Тем не менее стало уже традицией делать особый акцент на определенных геометрических отношениях и пропорциях, чаще всего использовавшихся в проектах построек религиозного предназначения. Обычному наблюдателю эти пропорции просто приятны. В художественном плане они аналогичны музыке. С помощью различных сочетаний нот и свойств можно получить гармоничные и резонирующие звуки. Определенные мелодии вроде григорианских хоралов навевают возвышенные чувства. Другая музыка позволяет нам соприкоснуться непосред ственно с собственными эмоциями.
Великий же философ Пифагор показал связи между музыкой, звуком, числом и формой.
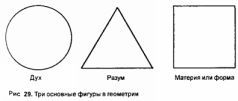
В религиозной традиции центральными являются три основные геометрические фигуры, круг, треугольник и квадрат (рис. 29). Считалось, что они представляют три уровня нашего бытия: дух, разум и тело. Никому не известно, кто первым использовал циркуль, как и системы счета. Вероятно, первоначально речь шла о шнурке на двух колышках, которые и проложили путь символическому исследованию царства идей и форм. Все правильные геометрические фигуры могут быть получены с помощью циркуля Бога, которого порой называли «Великим Геометром», часто изображали пользующимся циркулем.
С геометрией было связано и изучение чисел. Идеальными считали целые числа – в них виделась законченность. Дроби же представляли собой числа в стадии становления В этом смысле они порой рассматривались как динамическая сила божественного в движении через мироздание. Целые числа познаваемы, но такие отношения, как число пи (π), могут быть только аппроксимациями и потому непознаваемы. То была непостижимая рука Бога, проникающая во все вещи.
Поскольку отдельные числа являются либо рациональными (целые числа), либо иррациональными (дробные числа), геометрия может навести мосты между ними. Круг может представлять как принцип рационального целого числа в своем диаметре, так и иррациональную функцию в своей окружности. Квадрат и его диагональ также дают похожий феномен. Например, диагональ квадрата со стороной, равной одной единице, равна корню квадратному из 2 (рис. 33).
Термин «корень» в выражении «корень квадратный» имеет древнее происхождение и под разумевает понятие, взятое из природы. Корень растения спрятан, но порождает и питает то, что на поверхности.
Точно так же скрыты и корни квадратных чисел, и все они подразумеваются в них. Например, корень квадратный из 16 равен 4 (4×4=16). Корень же квадратный из 15 представляет собой иррациональное число, которое не так легко вычислить. Извлечение квадратных корней было главным занятием древних математиков. Когда же корень квадратный какого-либо числа нельзя было изобразить в цифрах, его всегда можно было воспроизвести геометрически. Этим и объясняется власть геометрии в античном мире. Геометрия считалась воротами в высшие сферы человеческого сознания, и поэтому ее принципы стали включаться в культовое искусство и архитектуру. Отталкиваясь от пропорций священного искусства и архитектуры, мы получаем концепцию священной геометрии, которую, пожалуй, лучше всего определить как геометрию, скрытую в религиозных постройках и духовных формах.
В религиозной традиции центральными являются три основные геометрические фигуры, круг, треугольник и квадрат (рис. 29). Считалось, что они представляют три уровня нашего бытия: дух, разум и тело. Никому не известно, кто первым использовал циркуль, как и системы счета. Вероятно, первоначально речь шла о шнурке на двух колышках, которые и проложили путь символическому исследованию царства идей и форм. Все правильные геометрические фигуры могут быть получены с помощью циркуля Бога, которого порой называли «Великим Геометром», часто изображали пользующимся циркулем.
С геометрией было связано и изучение чисел. Идеальными считали целые числа – в них виделась законченность. Дроби же представляли собой числа в стадии становления В этом смысле они порой рассматривались как динамическая сила божественного в движении через мироздание. Целые числа познаваемы, но такие отношения, как число пи (π), могут быть только аппроксимациями и потому непознаваемы. То была непостижимая рука Бога, проникающая во все вещи.
Поскольку отдельные числа являются либо рациональными (целые числа), либо иррациональными (дробные числа), геометрия может навести мосты между ними. Круг может представлять как принцип рационального целого числа в своем диаметре, так и иррациональную функцию в своей окружности. Квадрат и его диагональ также дают похожий феномен. Например, диагональ квадрата со стороной, равной одной единице, равна корню квадратному из 2 (рис. 33).
Точно так же скрыты и корни квадратных чисел, и все они подразумеваются в них. Например, корень квадратный из 16 равен 4 (4×4=16). Корень же квадратный из 15 представляет собой иррациональное число, которое не так легко вычислить. Извлечение квадратных корней было главным занятием древних математиков. Когда же корень квадратный какого-либо числа нельзя было изобразить в цифрах, его всегда можно было воспроизвести геометрически. Этим и объясняется власть геометрии в античном мире. Геометрия считалась воротами в высшие сферы человеческого сознания, и поэтому ее принципы стали включаться в культовое искусство и архитектуру. Отталкиваясь от пропорций священного искусства и архитектуры, мы получаем концепцию священной геометрии, которую, пожалуй, лучше всего определить как геометрию, скрытую в религиозных постройках и духовных формах.
Круг, треугольник и квадрат
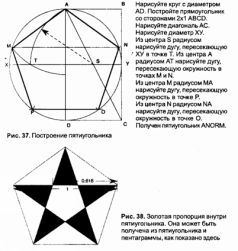
Легче других геометрических форм изобразить круг. Для этого достаточно циркуля или шнурка, колышка и маркера. Два взаимосвязанных круга можно получить, передвинув кончик циркуля на окружность первого круга и нарисовав второй равного размера. В образовавшейся весике могут быть получены три самых важных «корня»(√2, √3 и √5) (рис. 31).
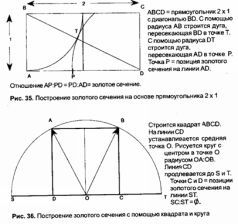
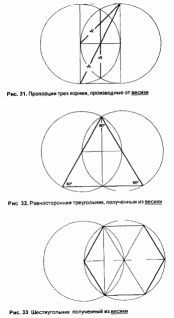Если принять радиус кругов за 1, тогда корень квадратный из двух (√2) может быть получен из диагонали квадрата, образованного линией между двумя центрами и двумя перпендикулярными к ней радиусами. Корень квадратный из трех (√3) образуется линией, соединяющей две точки пересечения кругов весики. Корень квадратный из пяти (√5) дает диагональ прямоугольника со сторонами 2 и 1. Этот прямоугольник можно использовать для обнаружения золотой пропорции (см. рис 35, на рис. 36, 37 и 38 показаны другие способы получения золотой пропорции). Позже мы увидим, что весика и пря моугольник со сторонами 2 и 1 служили ключом к получению древних единиц измерения.
Треугольник рассматривался как переходная форма между квадратом и кругом. Со временем он стал изображать триаду богов и богинь, обычно – как в Египте – отца, мать и сына. Эта концепция служит центральным стержнем многих религиозных систем и проявляет себя в христианстве в виде Бога Отца, Сына и Святого духа.
Идеальным считался равносторонний треугольник, в котором равны все стороны и углы. Широко использовался и другой треугольник, обычно приписываемый Пифагору, но явно существовавший задолго до него. Этот треугольник имеет стороны, выраженные целыми числами 3: 4: 5. Он является простейшим вариантом прямоугольного треугольника (90°) со сторонами, выражаемыми целыми числами. Благодаря простым отношениям чисел его использовали в топографии, а также в искусстве и скульптуре. На нем основана пирамида Хафры.
Круг, треугольник, квадрат и прямоугольник образуют основу культовой архитектуры. Они традиционно были связаны друг с другом особыми пропорциями. Последние призваны были отобразить собственную гармонию космоса.
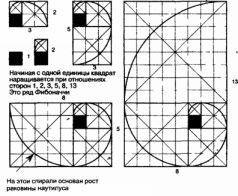
Одна такая пропорция – «гномон» была определена Аристотелем следующим образом: «Любая фигура, которая, будучи добавленной к исконной фигуре, дает в результате фигуру, подобную исконной». Иными словами, сохраняются соотношения между всеми дополнительными шагами. Примером этого служит золотое сечение, которое может быть выражено числами 1, 1, 2, 3, 5, 8, 13, 23 и т д., где отношения между любыми двумя соседними числами быстро сходятся в одной точке по мере движения по ряду. Ряд Фибоначчи является самым известным примером гномонического отношения, но есть и другие.
Изучая «гномоны» с разными отношениями, я сделал важное открытие «Гномон», основанный на отношении 1:3, имеет непосредственное отношение к пирамидам Гизы. Получается, что из этого отношения могут быть получены основные пропорции пирамид Хуфу, Хафры и Менкаура (рис. 40). Все начинается с трех квадратов, соединенных в линию и образующих прямоугольник со сторонами 3 и 1. Затем чертится квадрат на длинной стороне на каждом этапе увеличения.
Первый квадрат образует прямоугольник с отношением сторон 3:4. При его удвоении получается отношение пирамиды Хафры – 6:4. При добавлении еще двух последовательных квадратов к прямоугольнику 3:4 получаем отношение пирамиды Хуфу – 7:11. Еще один добавленный квадрат дает пропорции пирамиды Менкаура – 11:18. Этот прием добавления квадратов к прямоугольнику 3:1 драматическим образом обнаруживает, что пирамиды отражают естественную математическую прогрессию в отношениях их высоты к основанию. Так или иначе, но они связаны гармоничным геометрическим рядом.
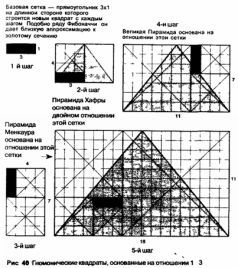Что примечательного могло быть в отношении 3:1? Может быть, оно отражало символизм египетской троицы – Осириса, Исиды и Гора. Возможно, мы никогда этого не узнаем наверняка, но этот рисунок позволяет нам лучше понять методы египтян.
Это открытие согласуется с тем, что нам известно о египетских методах проектирования, которые, похоже, всегда основывались на схемах квадратной сетки. В египетском искусстве имеются многочисленные примеры, показывающие, что художники и скульпторы сначала рисовали сетку на стене, которую предстояло расписать или вырезать, для того чтобы сохранить установленные пропорции. Простые числовые отношения этих сеток служат сердцевиной всех великих художественных произведений египтян.
Тот же метод использовался многими художниками Возрождения, в том числе и Леонардо да Винчи. В Древнем Египте это нашло своевоплощение в Великой пирамиде, что и подкрепляется ее тесной связью с узором на Марлборо-Даунс.
Треугольник рассматривался как переходная форма между квадратом и кругом. Со временем он стал изображать триаду богов и богинь, обычно – как в Египте – отца, мать и сына. Эта концепция служит центральным стержнем многих религиозных систем и проявляет себя в христианстве в виде Бога Отца, Сына и Святого духа.
Круг, треугольник, квадрат и прямоугольник образуют основу культовой архитектуры. Они традиционно были связаны друг с другом особыми пропорциями. Последние призваны были отобразить собственную гармонию космоса.
Рис. 39. Гномоничесжие спирали, построенные из отношения квадрата 2:1
В своей книге «Священная геометрия» Роберт Лолор приводит примеры «гномонических» спиралей, подобных основанной на ряде Фибоначчи, полученной из отношения 1:2. Эти расширяющиеся схемы иногда называют «завихренными квадратами», поскольку они дают спирали, которые часто встречаются в природе (рис. 39).Изучая «гномоны» с разными отношениями, я сделал важное открытие «Гномон», основанный на отношении 1:3, имеет непосредственное отношение к пирамидам Гизы. Получается, что из этого отношения могут быть получены основные пропорции пирамид Хуфу, Хафры и Менкаура (рис. 40). Все начинается с трех квадратов, соединенных в линию и образующих прямоугольник со сторонами 3 и 1. Затем чертится квадрат на длинной стороне на каждом этапе увеличения.
Первый квадрат образует прямоугольник с отношением сторон 3:4. При его удвоении получается отношение пирамиды Хафры – 6:4. При добавлении еще двух последовательных квадратов к прямоугольнику 3:4 получаем отношение пирамиды Хуфу – 7:11. Еще один добавленный квадрат дает пропорции пирамиды Менкаура – 11:18. Этот прием добавления квадратов к прямоугольнику 3:1 драматическим образом обнаруживает, что пирамиды отражают естественную математическую прогрессию в отношениях их высоты к основанию. Так или иначе, но они связаны гармоничным геометрическим рядом.
Это открытие согласуется с тем, что нам известно о египетских методах проектирования, которые, похоже, всегда основывались на схемах квадратной сетки. В египетском искусстве имеются многочисленные примеры, показывающие, что художники и скульпторы сначала рисовали сетку на стене, которую предстояло расписать или вырезать, для того чтобы сохранить установленные пропорции. Простые числовые отношения этих сеток служат сердцевиной всех великих художественных произведений египтян.
Тот же метод использовался многими художниками Возрождения, в том числе и Леонардо да Винчи. В Древнем Египте это нашло своевоплощение в Великой пирамиде, что и подкрепляется ее тесной связью с узором на Марлборо-Даунс.
С помощью круга и сетки
На Марлборо-Даунс размещены два взаимосвязанных круга, каждый диаметром в 19,3 километра (12 миль). В данном случае круги не образуют подлинный узор весики и поэтому не имеют явного отношения к известным геометрическим фигурам.
Как мне предстояло со временем открыть, размещение этих кругов не было произвольным, а подчинялось особому отношению, найденному в Великой пирамиде Хуфу. При наложении поперечного сечения Великой пирамиды на карту (рис. 21) обнаруживается геометрическое объяснение линейного построения галерей, ходов и камер пирамиды, в частности, ориентации Большой галереи пирамиды на центр одного из кругов.
Это позволяло объяснить местоположение и размеры всех внутренних камер и галерей Великой пирамиды на языке чистой геометрии и открывало волнующую перспективу. Для разгадки этой тайны необходимо было вы яснить, как египтяне могли прийти к проекту Великой пирамиды с помощью чистой геометрии прежде, чем приспособить его к сетке 7:11.
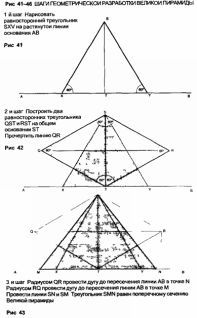
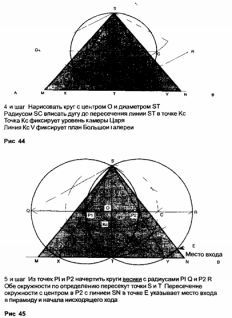
В рисунке Марлборо-Даунс ключом служил равносторонний треугольник. Взяв его за основу, свойственную пирамиде Хуфу, геометрию можно показать с помощью рисунков 41-46. Такой поэтапный чертеж фиксирует местоположение всех камер и ходов Великой пирамиды.
Однако чистая геометрия создает иррациональные пропорции. Установив базовую структуру, дальше следовало превратить ее в такую форму, которую можно было бы выразить рациональными или целыми числами. В этом заключается большая ценность сетки. При ее наложении на геометрию могут быть считаны точные измерения. Можно сделать вывод, что именно так была спроектирована Великая пирамида, поскольку чистая геометрия должна была дать угол склона чуть меньше, чем мы видим на практике.
При использовании сетки с точной пропорцией 7:11 все аккуратно становится на место и достигается идеальный компромисс между чистой геометрией и ее гармоничным выражением в мире формы.
Наложение сетки 7:11 на пирамиду показывает, что камера Царя расположена на два квадрата (на 2/7 ее высоты) выше уровня земли, а камера Царицы – на один квадрат выше уровня земли, то есть на 1/7 высоты пирамиды (рис. 47). Вход в пирамиду, на мой взгляд, был рассчитан на основе поделенного пополам квадранта первого квадрата в том месте, где он пересекает сторону пирамиды.
Углы наклона восходящего и нисходящего ходов равны 26º31'23». На первый взгляд, он кажется весьма странным, но на самом деле является простым градиентом, образованным отношением 2:1. Иными словами, ход поднимается на один квадрат при горизонтальном перемещении на каждые два квадрата, образуя диагональ прямоугольника с отношением сторон 2:1. Его можно было легко построить, и его, без сомнения, использовали благодаря месту этого прямоугольника в священной геометрии, в частности, в получении золотого сечения.
Если прибегнуть к этим методам, то можно показать, что все внутренние ходы и покои основаны на простых геометрических пропорциях, хотя так называемые вентиляционные шахты не совсем совпадают с этой схемой.
Это наводит на мысль о том, что они были созданы с астрономическими целями, как это и предположили Бьювэл и Джилберт в «Тайне Ориона».
Как только были установлены первичные параметры сетки, не составило труда соорудить угловые шаблоны, которые обеспечивали с помощью отвеса высокую точность градиентов различных ходов.
Как мне предстояло со временем открыть, размещение этих кругов не было произвольным, а подчинялось особому отношению, найденному в Великой пирамиде Хуфу. При наложении поперечного сечения Великой пирамиды на карту (рис. 21) обнаруживается геометрическое объяснение линейного построения галерей, ходов и камер пирамиды, в частности, ориентации Большой галереи пирамиды на центр одного из кругов.
Это позволяло объяснить местоположение и размеры всех внутренних камер и галерей Великой пирамиды на языке чистой геометрии и открывало волнующую перспективу. Для разгадки этой тайны необходимо было вы яснить, как египтяне могли прийти к проекту Великой пирамиды с помощью чистой геометрии прежде, чем приспособить его к сетке 7:11.
В рисунке Марлборо-Даунс ключом служил равносторонний треугольник. Взяв его за основу, свойственную пирамиде Хуфу, геометрию можно показать с помощью рисунков 41-46. Такой поэтапный чертеж фиксирует местоположение всех камер и ходов Великой пирамиды.
Однако чистая геометрия создает иррациональные пропорции. Установив базовую структуру, дальше следовало превратить ее в такую форму, которую можно было бы выразить рациональными или целыми числами. В этом заключается большая ценность сетки. При ее наложении на геометрию могут быть считаны точные измерения. Можно сделать вывод, что именно так была спроектирована Великая пирамида, поскольку чистая геометрия должна была дать угол склона чуть меньше, чем мы видим на практике.
При использовании сетки с точной пропорцией 7:11 все аккуратно становится на место и достигается идеальный компромисс между чистой геометрией и ее гармоничным выражением в мире формы.
Наложение сетки 7:11 на пирамиду показывает, что камера Царя расположена на два квадрата (на 2/7 ее высоты) выше уровня земли, а камера Царицы – на один квадрат выше уровня земли, то есть на 1/7 высоты пирамиды (рис. 47). Вход в пирамиду, на мой взгляд, был рассчитан на основе поделенного пополам квадранта первого квадрата в том месте, где он пересекает сторону пирамиды.
Если прибегнуть к этим методам, то можно показать, что все внутренние ходы и покои основаны на простых геометрических пропорциях, хотя так называемые вентиляционные шахты не совсем совпадают с этой схемой.
Это наводит на мысль о том, что они были созданы с астрономическими целями, как это и предположили Бьювэл и Джилберт в «Тайне Ориона».
Как только были установлены первичные параметры сетки, не составило труда соорудить угловые шаблоны, которые обеспечивали с помощью отвеса высокую точность градиентов различных ходов.
Комплекс Гизы
Египтологи постоянно твердили, что в размещении пирамид на плато Гиза нет единого плана. Не понимаю, как они умудрились прийти к такому выводу. Достаточно приложить известные принципы древнеегипетской системы мер к плато Гиза, чтобы понять лежащую в его основе схему. Египтяне использовали именно сетчатую систему. Мне оставалось лишь найти сетку, которая наилучшим образом соответствовала бы комплексу Гизы.