Страница:
Это было написано в 1960 годах – еще до того, как стали очень популярными идеи о столкновениях Земли с кометами и астероидами.
Глава 8
В родах и локтях
Унифицированные единицы измерения
Земные меры
Мегалитический ярд
Радиус
Канон мер
Стандартные английские единицы измерения и окружность
Фарлонг
Род
Мегалитический ярд и короткий фарлонг
Короткий фарлонг и экваториальная окружность
Широта и долгота
Глава 8
В родах и локтях
Закодированное послание из прошлого ждет расшифровки людьми будущего поколения.
В Европе мы приняли метрическую систему за основу наших мер. Эта система была учреждена в ходе наполеоновских реформ, с тем чтобы упорядочить крайне запу анные единицы измерения дореволюционной Франции. Специальная комиссия в конце концов решила взять за основу новой системы мер расстояние между северным полюсом и экватором по линии парижского меридиана. В 1801 году за новую единицу измерения – метр была принята одна десятимиллионная часть квадранта этого меридиана.
То был знаменательный шаг, привязавший систему мер к размерам планеты Земля. Однако круги на Марлборо-Даунс подсказывают, что такая связь была установлена раньше. Мы уже показали, что древние вычислили окружность экватора. Я также могу доказать, что они вычислили и меридиан. Благодаря моему исследованию кругов на Марлборо-Даунс, я могу показать связь многих – если не всех – древних мер западного мира с пропорциями планеты. Это заявление может показаться нелепым, но мое исследование подтверждает ее.
В Европе мы приняли метрическую систему за основу наших мер. Эта система была учреждена в ходе наполеоновских реформ, с тем чтобы упорядочить крайне запу анные единицы измерения дореволюционной Франции. Специальная комиссия в конце концов решила взять за основу новой системы мер расстояние между северным полюсом и экватором по линии парижского меридиана. В 1801 году за новую единицу измерения – метр была принята одна десятимиллионная часть квадранта этого меридиана.
То был знаменательный шаг, привязавший систему мер к размерам планеты Земля. Однако круги на Марлборо-Даунс подсказывают, что такая связь была установлена раньше. Мы уже показали, что древние вычислили окружность экватора. Я также могу доказать, что они вычислили и меридиан. Благодаря моему исследованию кругов на Марлборо-Даунс, я могу показать связь многих – если не всех – древних мер западного мира с пропорциями планеты. Это заявление может показаться нелепым, но мое исследование подтверждает ее.
Унифицированные единицы измерения
Многие исследователи античного мира интуитивно чувствовали, что должна была существовать некая основа, объединяющая древние меры, и что мог существовать их общий источник. В «Секретах Великой пирамиды» Ливио Стеккини отмечает: «Все меры длины, объема и веса античного мира, в том числе Китая и Индии, образовывали рациональную и органичную систему, которая может быть воспроизведена, отталкиваясь от основной единицы длины».
Во второй половине 19-го столетия известный специалист в этой области Фридрих Хульти утверждал, что все древние меры могли быть произведены от египечского фута, равного 300 миллиметрам (11,8 дюйма), и локтя, равного 450 миллиметрам (17,7 дюйма). Изучив соотношение египетского и римского футов, Стеккини пришел к выводу, что истинной основой был географический или греческий фут, равный 307,7957 миллиметра (12,1 дюйма).
Многие ломали головы над происхождением как древних, так и современных мер. Я, естественно, задался вопросом, а нельзя ли найти разгадку в пропорциях двойных кругов на Марлборо-Даунс. Много лет потребовалось, чтобы разгадать эту тайну. Первым делом я решил нащупать какую-либо связь древних мер с радиусом и окружностью моих кругов.
Во второй половине 19-го столетия известный специалист в этой области Фридрих Хульти утверждал, что все древние меры могли быть произведены от египечского фута, равного 300 миллиметрам (11,8 дюйма), и локтя, равного 450 миллиметрам (17,7 дюйма). Изучив соотношение египетского и римского футов, Стеккини пришел к выводу, что истинной основой был географический или греческий фут, равный 307,7957 миллиметра (12,1 дюйма).
Многие ломали головы над происхождением как древних, так и современных мер. Я, естественно, задался вопросом, а нельзя ли найти разгадку в пропорциях двойных кругов на Марлборо-Даунс. Много лет потребовалось, чтобы разгадать эту тайну. Первым делом я решил нащупать какую-либо связь древних мер с радиусом и окружностью моих кругов.
Земные меры
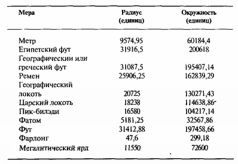
К счастью, Ливио Стеккини уже вычислил номинальные метрические величины ряда важных мер Древнего Египта и остального античного мира. Ниже приводится их список:
В дополнение к вышеназванным я решил также рассмотреть две стандартные английские меры – фут (0,3048 метра) и фарлонг (201,168 метра), считающиеся древними, и открытый профессором Томом мегалитический ярд (0,829 метра).
Когда я перевел размеры моих кругов в эти древние меры, стало ясно, что нужно снова немного подогнать их номинальный радиус – с 9576,78 метра до 9574,95 метра. Это не выходит за рамки погрешности. Окружность была вычислена, исходя из древнеегипетского номинального значения пи, равного 22/7, что дает размеры кругов в различных единицах измерения:
Когда я перевел размеры моих кругов в эти древние меры, стало ясно, что нужно снова немного подогнать их номинальный радиус – с 9576,78 метра до 9574,95 метра. Это не выходит за рамки погрешности. Окружность была вычислена, исходя из древнеегипетского номинального значения пи, равного 22/7, что дает размеры кругов в различных единицах измерения:
Мегалитический ярд
Этот список, казалось, открывал ряд интересных возможностей, но больше всего меня поразило число мегалитических ярдов в радиусе (11 550) и в окружнос ти (72 600), поскольку я получил целые числа, делимые на 10. Это показалось мне необычным и заслуживающим дополнительного исследования.
Значение чисел в подобных обстоятельствах лучше всего оценивать, приводя индивидуальные числа к их первичным множителям. Этот процесс изучается в школе и означает деление числа на его наименьший делимый множитель. Этот процесс повторяется до тех пор, пока не будут использованы все множители, выраженные целыми числами. Например, число двенадцать можно разделить на два и получить шесть. Шесть можно затем разделить на два и получить три, а три – разделить на три и получить один. Значит, множителями двенадцати являются 2×2×3×1. Число один обычно не принимается во внимание, поскольку все числа можно разделить на единицу.
Чтобы сделать этот процесс понятнее, я пройду его шаг за шагом и рассмотрю выводы, которые могут быть сделаны. Числа мегалитических ярдов в радиусе окружности могут быть разложены на множители следующим образом:
Радиус (11 550) Окружность (72 600)
11550:2=5775 72600 2=36300
5775:3=1925 36300:2=18150
1925:5=385 18150:2=9075
385:5=77 9075:3=3025
77:7=11 3025:5=605
11:11=1 605:5=121
121:11=11
11:11=1
Этот процесс дает следующие множители радиуса 2×3×5×5×7×11 Множители окружности, 2×2×2×3×5×5×11×11. Если разделить и радиус, и окружность на число общих множителей 2×3×5×5×11 (или 1650), то получится:
Радиус Окружность
11550:1650=7 72600:1650=44(2×22)
Отношение 7:11 неизбежно возникает из того факта, что я выбрал значение пи (π) = 22:7, которое использовалось в Древнем Египте. Формула вычисления длины окружности из ее радиуса: 2πr, где r – длина радиуса. В случае круга с радиусом в семь единиц мы получаем 2×(22:7)×7. Семерки сокращаются, и окружность оказывается равной 2×22 = 44 единицы. Этими единицами могут быть миллиметры, мили или километры – не имеет зна чения, что именно. Принцип остается неизменным. Любой круг радиусом в 7 единиц даст окружность в 44 единицы, если значение пи равно 22:7.
Как мы уже видели, древние предпочитали получать отношения целых чисел в своих памятниках и постройках. В данном случае они использовали мегалитические ярды, выбрав целое число радиуса, делимое на 7, и таким образом длина окружности также выражается целым числом.
Для практических целей топографии идеальна базовая единица измерения где-то между 0,5 метра и 1 метром, которая поддается дальнейшему делению. В эту категорию попадают стандартный английский ярд, царский локоть и мегалитический ярд профессора Тома. Как мы знаем, круги Марлборо выдержаны в пропорции целых чисел к размерам Земли, а мегалитический ярд – в про порции целых чисел к кругам, следовательно, мегалитическии ярд находится в пропорции целых чисел к размерам Земли. Он является единственной сопоставимой мерой, отвечающей этим критериям.
Том получил свою единицу измерения в результате статистического анализа примерно 300 каменных кругов по всей Британии. В его книге «Мегалитические сооружения в Британии» 1 мегалитический ярд равен 2,720 ± 0,003 фута, или 829,04 ± 0,91438 миллиметра. Значение открытия Тома просто поразительно. Оно подразумевает, что все круги были сооружены с помощью одной и той же системы мер, очевидна связь замысла и конструкции каменных кругов по всей стране на протяжении болee чем тысячелетия, но археологи до сих пор не желают признать это.
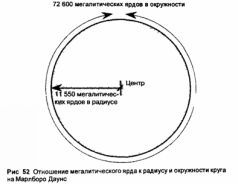
Картина дополняется моим собственным открытием того, что мегалитический ярд находится в отношении целых чисел как с радиусом, так и с окружностью кругов Марлборо-Даунс (рис. 52) и, стедовательно с Землеи. Том считает, что древние бритты искали именно это отношение целых чисел радиусов с окружностью когда сооружали свои эллиптические и овальные каменные памятники.
Благодаря соотношению мегалитического ярда с pадиусом и окружностью Земли теперь становится ясно что строители Эивбери, Стоунхенджа и других каменных круглых памятников точно определили пропорции Земли и с большой точностью привязали к ним свою единицу измерения.
Использование мегалитического ярда в создании кругов Марлборо-Даунс привязывает их к культуре каменных кругов, возникшей в Британии около 3100 года до н. э. Это было хорошее начало, но впереди меня ждали новые сюрпризы.
Ради систематичности своего исследования различных древних мер я должен был проанализировать по очереди каждую в их соотношениях с радиусом и окружностью кругов Марлборо-Даунс. Только тогда можно было получить полную картину.
Значение чисел в подобных обстоятельствах лучше всего оценивать, приводя индивидуальные числа к их первичным множителям. Этот процесс изучается в школе и означает деление числа на его наименьший делимый множитель. Этот процесс повторяется до тех пор, пока не будут использованы все множители, выраженные целыми числами. Например, число двенадцать можно разделить на два и получить шесть. Шесть можно затем разделить на два и получить три, а три – разделить на три и получить один. Значит, множителями двенадцати являются 2×2×3×1. Число один обычно не принимается во внимание, поскольку все числа можно разделить на единицу.
Чтобы сделать этот процесс понятнее, я пройду его шаг за шагом и рассмотрю выводы, которые могут быть сделаны. Числа мегалитических ярдов в радиусе окружности могут быть разложены на множители следующим образом:
Радиус (11 550) Окружность (72 600)
11550:2=5775 72600 2=36300
5775:3=1925 36300:2=18150
1925:5=385 18150:2=9075
385:5=77 9075:3=3025
77:7=11 3025:5=605
11:11=1 605:5=121
121:11=11
11:11=1
Этот процесс дает следующие множители радиуса 2×3×5×5×7×11 Множители окружности, 2×2×2×3×5×5×11×11. Если разделить и радиус, и окружность на число общих множителей 2×3×5×5×11 (или 1650), то получится:
Радиус Окружность
11550:1650=7 72600:1650=44(2×22)
Отношение 7:11 неизбежно возникает из того факта, что я выбрал значение пи (π) = 22:7, которое использовалось в Древнем Египте. Формула вычисления длины окружности из ее радиуса: 2πr, где r – длина радиуса. В случае круга с радиусом в семь единиц мы получаем 2×(22:7)×7. Семерки сокращаются, и окружность оказывается равной 2×22 = 44 единицы. Этими единицами могут быть миллиметры, мили или километры – не имеет зна чения, что именно. Принцип остается неизменным. Любой круг радиусом в 7 единиц даст окружность в 44 единицы, если значение пи равно 22:7.
Как мы уже видели, древние предпочитали получать отношения целых чисел в своих памятниках и постройках. В данном случае они использовали мегалитические ярды, выбрав целое число радиуса, делимое на 7, и таким образом длина окружности также выражается целым числом.
Для практических целей топографии идеальна базовая единица измерения где-то между 0,5 метра и 1 метром, которая поддается дальнейшему делению. В эту категорию попадают стандартный английский ярд, царский локоть и мегалитический ярд профессора Тома. Как мы знаем, круги Марлборо выдержаны в пропорции целых чисел к размерам Земли, а мегалитический ярд – в про порции целых чисел к кругам, следовательно, мегалитическии ярд находится в пропорции целых чисел к размерам Земли. Он является единственной сопоставимой мерой, отвечающей этим критериям.
Том получил свою единицу измерения в результате статистического анализа примерно 300 каменных кругов по всей Британии. В его книге «Мегалитические сооружения в Британии» 1 мегалитический ярд равен 2,720 ± 0,003 фута, или 829,04 ± 0,91438 миллиметра. Значение открытия Тома просто поразительно. Оно подразумевает, что все круги были сооружены с помощью одной и той же системы мер, очевидна связь замысла и конструкции каменных кругов по всей стране на протяжении болee чем тысячелетия, но археологи до сих пор не желают признать это.
Картина дополняется моим собственным открытием того, что мегалитический ярд находится в отношении целых чисел как с радиусом, так и с окружностью кругов Марлборо-Даунс (рис. 52) и, стедовательно с Землеи. Том считает, что древние бритты искали именно это отношение целых чисел радиусов с окружностью когда сооружали свои эллиптические и овальные каменные памятники.
Благодаря соотношению мегалитического ярда с pадиусом и окружностью Земли теперь становится ясно что строители Эивбери, Стоунхенджа и других каменных круглых памятников точно определили пропорции Земли и с большой точностью привязали к ним свою единицу измерения.
Использование мегалитического ярда в создании кругов Марлборо-Даунс привязывает их к культуре каменных кругов, возникшей в Британии около 3100 года до н. э. Это было хорошее начало, но впереди меня ждали новые сюрпризы.
Ради систематичности своего исследования различных древних мер я должен был проанализировать по очереди каждую в их соотношениях с радиусом и окружностью кругов Марлборо-Даунс. Только тогда можно было получить полную картину.
Радиус
На первый взгляд, казалось, что нет никакого особого отношения между другими древними единицами измерения и кругами Марлборо-Даунс, и я не особенно-то волновался, когда начал разлагать их на их индивидуальные множители. Но то, что выяснилось, побудило меня взять другой след, оказавшийся самым захватывающим в моих поисках. Понадобилось несколько лет, чтобы пожать плоды. Честно говоря, это объяснялось не сложностью вопроса, а собственной неспособностью увидеть то, что бросалось в глаза.
В порядке оправдания могу лишь сказать, что мое исследование кругов Марлборо-Даунс растянулось на многие годы. Биты информации рассеяны по разным файлам. И только после их соединения различными способами, как частей головоломки, начала вырисовываться полная картина.
Я начал с разложения на множители 16 580 пик-билэди:
16 580: 2 = 8290 8290: 2 = 4145 4145: 5 = 820
Получаем множители: 2×2×5×829. Множители 18 238 царских локтей:
18238:2=9119 9119:11=829 или 2×11×829.
Обратим внимание на то, что отношение между пик-билэди и царским локтем равно 10:11. Позже будет показана его значимость.
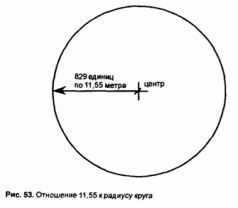
Как это ни невероятно, выяснилось, что число 829 является общим множителем в большинстве измерений радиуса кругов Марлборо-Даунс:
Это наглядно подтверждает мысль Стеккини о том, что некое объединяющее измерение связывает вместе эти древние меры, причем не малой, как он думал, а крупной единицей. Деление радиуса кругов Марлборо в метрах на 829 дает 11,55 метра. Следует заметить, что все меры объединены достаточно большим общим знаменателем, а не таким малым, как 11,55 метра.
Что же было такого особенного в этом расстоянии? Оно не было единицей измерения, дающей целое число для окружности круга Марлборо-Даунс или полярного меридиана. Оно, конечно же, соотнесено с экваториальным радиусом Земли (829 × 666 × 11,55), но это оказалось не очень-то полезным.
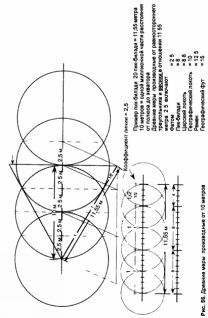
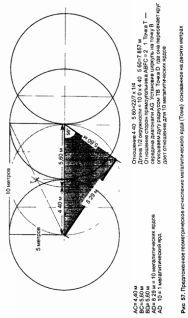
Я задавался вопросом, связано ли оно с измерением времени и вращения Земли. Работа Стеккийи предпола… …колышков провести по земле линию длиной в 10 метров, то есть равную одной миллионной части расстояния от полюсов до экватора, и построить равносторонний треугольник, который эта линия делила бы пополам, то длина каждой стороны треугольника составит 11,55 метра (см. рис. 55).
Итак, Стеккини был прав, когда утверждал, что древние меры являются производными от расстояния между полюсом и экватором, но не впрямую, как он полагал. Тайный неписаный закон, пронизавший эти древние меры, призван был испочьзовать не прямое и очевидное расстояние, которое мы применяем сегодня в метрической системе – расстояние между полюсом и экватором, а основанное на нем отношение, взятое из равностороннего треугольника.
Мы можем лишь строить догадки о тайных побудительных причинах. Они предполагают, что равносторонний треугольник имел некую впечатляющую символическую значимость. Тот же треугольник позволил мне создать схему пирамиды на Марлборо-Даунс, и его же можно найти включенным в геометрию стадий проектирования Великой пирамиды. Сейчас уже очевидно, что тот же самый треугольник послужил основой для целого ряда древних мер.
Он также убедительно доказывает, что французы отнюдь не были первыми изобретателями метра. Когда-то в далеком прошлом некая цивилизация точно вычислила расстояние между полюсом и экватором и установила незыблемую базовую меру в десять метров – одну миллионную часть этого расстояния. Производными от нее были и древнеегипетские, и древнегреческие меры. Хотя вычисленный Томом мегалитический ярд соотнесен с окружностью экватора, со временем я открыл способ примирить и его с полярным меридианом.
После расшифровки закодированного соотношения метра с такими древними мерами, как ремен и пик-билэди, стало совершенно ясно, как каждая из этих мер была произведена от 11,55 метра с помощью чистой геометрии (Кстати, слово «геометрия» означает «измерение земли» и является поэтому подходящим термином).
Дальнейший анализ показал, что большинство этих мер объединял еще один множитель, хоть и не выр женный целым числом.Это 2,5:
6,25 фатома = 2,5×2,5
20 пик-билэди = 2,5×8
22 царских локтя = 2,5×8,8
25 географических локтей =2,5×10
31,25ремена = 2,5×12,5
37,5 географического фута =2,5×15
Коэффициент 2,5 – производное от деления круга с помощью композиции весика писцес. Например, на рисунке 53 показано, как пик-билэди можно точно определить с помощью простых геометрических методов, как только было установлено постоянное расстояние в 10 метров. На практике это проделывалось, вероятно, с по мощью двух колышков и шнурка в качестве циркуля. Используя эту систему и простое деление, можно открыть различные древние меры.
Мегалитический ярд может быть вписан в ту же схему иным образом, но опять-таки на основе 10 метров (см. рис. 56). Получается линия длиной в 8,29 метра (27,2 фута), которая затем может быть поделена на десятые для по лучения мегалитического ярда. Последний не только точно соотносится с размерами экватора, но и может быть произведен от полярного меридиана.
В порядке оправдания могу лишь сказать, что мое исследование кругов Марлборо-Даунс растянулось на многие годы. Биты информации рассеяны по разным файлам. И только после их соединения различными способами, как частей головоломки, начала вырисовываться полная картина.
Я начал с разложения на множители 16 580 пик-билэди:
16 580: 2 = 8290 8290: 2 = 4145 4145: 5 = 820
Получаем множители: 2×2×5×829. Множители 18 238 царских локтей:
18238:2=9119 9119:11=829 или 2×11×829.
Как это ни невероятно, выяснилось, что число 829 является общим множителем в большинстве измерений радиуса кругов Марлборо-Даунс:
Что же было такого особенного в этом расстоянии? Оно не было единицей измерения, дающей целое число для окружности круга Марлборо-Даунс или полярного меридиана. Оно, конечно же, соотнесено с экваториальным радиусом Земли (829 × 666 × 11,55), но это оказалось не очень-то полезным.
Я задавался вопросом, связано ли оно с измерением времени и вращения Земли. Работа Стеккийи предпола… …колышков провести по земле линию длиной в 10 метров, то есть равную одной миллионной части расстояния от полюсов до экватора, и построить равносторонний треугольник, который эта линия делила бы пополам, то длина каждой стороны треугольника составит 11,55 метра (см. рис. 55).
Итак, Стеккини был прав, когда утверждал, что древние меры являются производными от расстояния между полюсом и экватором, но не впрямую, как он полагал. Тайный неписаный закон, пронизавший эти древние меры, призван был испочьзовать не прямое и очевидное расстояние, которое мы применяем сегодня в метрической системе – расстояние между полюсом и экватором, а основанное на нем отношение, взятое из равностороннего треугольника.
Мы можем лишь строить догадки о тайных побудительных причинах. Они предполагают, что равносторонний треугольник имел некую впечатляющую символическую значимость. Тот же треугольник позволил мне создать схему пирамиды на Марлборо-Даунс, и его же можно найти включенным в геометрию стадий проектирования Великой пирамиды. Сейчас уже очевидно, что тот же самый треугольник послужил основой для целого ряда древних мер.
Он также убедительно доказывает, что французы отнюдь не были первыми изобретателями метра. Когда-то в далеком прошлом некая цивилизация точно вычислила расстояние между полюсом и экватором и установила незыблемую базовую меру в десять метров – одну миллионную часть этого расстояния. Производными от нее были и древнеегипетские, и древнегреческие меры. Хотя вычисленный Томом мегалитический ярд соотнесен с окружностью экватора, со временем я открыл способ примирить и его с полярным меридианом.
После расшифровки закодированного соотношения метра с такими древними мерами, как ремен и пик-билэди, стало совершенно ясно, как каждая из этих мер была произведена от 11,55 метра с помощью чистой геометрии (Кстати, слово «геометрия» означает «измерение земли» и является поэтому подходящим термином).
Дальнейший анализ показал, что большинство этих мер объединял еще один множитель, хоть и не выр женный целым числом.Это 2,5:
6,25 фатома = 2,5×2,5
20 пик-билэди = 2,5×8
22 царских локтя = 2,5×8,8
25 географических локтей =2,5×10
31,25ремена = 2,5×12,5
37,5 географического фута =2,5×15
Коэффициент 2,5 – производное от деления круга с помощью композиции весика писцес. Например, на рисунке 53 показано, как пик-билэди можно точно определить с помощью простых геометрических методов, как только было установлено постоянное расстояние в 10 метров. На практике это проделывалось, вероятно, с по мощью двух колышков и шнурка в качестве циркуля. Используя эту систему и простое деление, можно открыть различные древние меры.
Мегалитический ярд может быть вписан в ту же схему иным образом, но опять-таки на основе 10 метров (см. рис. 56). Получается линия длиной в 8,29 метра (27,2 фута), которая затем может быть поделена на десятые для по лучения мегалитического ярда. Последний не только точно соотносится с размерами экватора, но и может быть произведен от полярного меридиана.
Канон мер
Выясненные до сих пор факты подтверждают пред ставление о том, что в античные времена существовал передовой народ, сумевший составить систему мер в гармонии с пропорциями Земли. Этого можно было добиться только путем точного вычисления экваториальной окружности и полярного меридиана Земли.
Находки можно подытожить следующим образом:
1) Мегалитический ярд, равный 0,829 метра, – это единственная мера сопоставимого размера, которая соответствует в соотношении целых чисел экваториальной окружности и радиусу Земли. Радиус Земли измеряется 666 × 1650 × 7 мегалитическими ярдами, а ее окружность – 666 × 1650 × 22 × 2 мегалитическими ярдами.
2) В какое-то время в отдаленном прошлом расстояние между полюсом и экватором было тщательно измерено и, поделенное на миллион частей, дало расстояние ровно в десять метров. С помощью этой стандартной меры в виде линии деления пополам равностороннего треугольника было установлено еще одно расстояние – 11,55 метра как длина одной стороны треугольника. Исходя из этой длины были образованы древнеегипетские и классические меры.
Так появилось убедительное доказательство того, что круги Марлборо-Даунс не были статистической аномалией, а были спланированы умышленно на ландшафте. Прежде чем пытаться определить, как некая культура смогла добиться столь поразительного мастерства, да и знания точных размеров и пропорций Земли, нам предстоит сделать еще один шаг в нашем математическом анализе систем мер.
1) Мегалитический ярд, равный 0,829 метра, – это единственная мера сопоставимого размера, которая соответствует в соотношении целых чисел экваториальной окружности и радиусу Земли. Радиус Земли измеряется 666 × 1650 × 7 мегалитическими ярдами, а ее окружность – 666 × 1650 × 22 × 2 мегалитическими ярдами.
2) В какое-то время в отдаленном прошлом расстояние между полюсом и экватором было тщательно измерено и, поделенное на миллион частей, дало расстояние ровно в десять метров. С помощью этой стандартной меры в виде линии деления пополам равностороннего треугольника было установлено еще одно расстояние – 11,55 метра как длина одной стороны треугольника. Исходя из этой длины были образованы древнеегипетские и классические меры.
Так появилось убедительное доказательство того, что круги Марлборо-Даунс не были статистической аномалией, а были спланированы умышленно на ландшафте. Прежде чем пытаться определить, как некая культура смогла добиться столь поразительного мастерства, да и знания точных размеров и пропорций Земли, нам предстоит сделать еще один шаг в нашем математическом анализе систем мер.
Стандартные английские единицы измерения и окружность
До сих пор мы не рассматривали стандартные английские меры – ярд, фут и фарлонг. Эти единицы измерения менялись с течением времени. Нынешний стандарт ярда был установлен лишь в 1824 году. В эпоху Тюдоров он был несколько короче и равнялся 35,963 современного дюйма или 2,99692 современного фута. Таким образом Тюдоровский фут составлял 11,988 современного дюйма. В Британии при римлянах, когда, как считается, возникли британские меры, фут составлял всего 11,65 современного дюйма. Сравните: Стандартный английский фут (с 1824 года)= 12 дюймам; Тюдоровский фут (Генриха VII)= 11,988 дюйма; Римско-британский фут = 11,65 дюйма.
Когда я измерил круги Марлборо в стандартных единицах, меня поразил тот факт, что окружность насчитывает 299,12 фарлонга, что почти равняется 300.
Сегодня мы привычно делим круг на 360 градусов, и эта система была взята из Древней Месопотамии. Каждый градус подразделяется на 60 минут, а каждая минута – на 60 секунд, что указывает на соотношение времени и угловой меры, а этот обычай заимствован из астрономических наблюдений.
360 это 6×60. С другой стороны, 300 это 5×60. Основанная на шести угловая мера, которой мы пользуемся сегодня, имеет немалое общее значение при вычислении углов, но ведь можно привести доводы и в пользу меры, основанной на пяти, которую можно получить, разделив окружность круга на 300, а не на 360 градусов. Это значительно облегчило бы построение пятиугольных геометрических фигур. Мы уже убедились, что пятиугольник включает золотую пропорцию, так что могла иметься эзотерическая причина для деления окружности на 300 единиц.
Современный фарлонг чуть великоват для того, что бы вместиться 300 раз в окружности кругов Марлборо.
60171,27 метра:300 = 200,571 метра, а стандартный фарлонг равен 201,168 метра.
Для точной подгонки современный фарлонг должен был бы быть на 59,7 сантиметра (23,5 дюйма) короче. Исходя из того, что сохраняются все те же отношения дюймов к футу (12), футов к ярду (3) и ярдов к фарлонгу (220), ярд должен был быть сокращен до 2,991 фута, а фут до 11,964 дюйма.
Таким образом, фут оказался бы на 0,024 дюйма, или на 1/42 дюйма, короче фута, введенного Генрихом VII. Эта разница едва различима и может стать очевидной только при умножении для получения более крупных единиц измерения.
Для облегчения ссылки я буду называть эту новую меру «1/300 окружности круга Марлборо», или «короткий фарлонг» (КФ). Соответственно получаем короткий ярд (КЯ) и короткий фут (КФ) (рис. 58).
Когда я измерил круги Марлборо в стандартных единицах, меня поразил тот факт, что окружность насчитывает 299,12 фарлонга, что почти равняется 300.
Сегодня мы привычно делим круг на 360 градусов, и эта система была взята из Древней Месопотамии. Каждый градус подразделяется на 60 минут, а каждая минута – на 60 секунд, что указывает на соотношение времени и угловой меры, а этот обычай заимствован из астрономических наблюдений.
360 это 6×60. С другой стороны, 300 это 5×60. Основанная на шести угловая мера, которой мы пользуемся сегодня, имеет немалое общее значение при вычислении углов, но ведь можно привести доводы и в пользу меры, основанной на пяти, которую можно получить, разделив окружность круга на 300, а не на 360 градусов. Это значительно облегчило бы построение пятиугольных геометрических фигур. Мы уже убедились, что пятиугольник включает золотую пропорцию, так что могла иметься эзотерическая причина для деления окружности на 300 единиц.
Современный фарлонг чуть великоват для того, что бы вместиться 300 раз в окружности кругов Марлборо.
60171,27 метра:300 = 200,571 метра, а стандартный фарлонг равен 201,168 метра.
Для точной подгонки современный фарлонг должен был бы быть на 59,7 сантиметра (23,5 дюйма) короче. Исходя из того, что сохраняются все те же отношения дюймов к футу (12), футов к ярду (3) и ярдов к фарлонгу (220), ярд должен был быть сокращен до 2,991 фута, а фут до 11,964 дюйма.
Таким образом, фут оказался бы на 0,024 дюйма, или на 1/42 дюйма, короче фута, введенного Генрихом VII. Эта разница едва различима и может стать очевидной только при умножении для получения более крупных единиц измерения.
Фарлонг
Слово «фарлонг» саксонского происхождения, оно означает «длиной с борозду», поскольку эта мера использовалась для определения длины вспаханных полос земли. В своей книге «Единицы веса и меры Англии» Р.Д. Коннор указывает, что фарлонг – производный от «рода» – единицы измерения, равной 5,5 ярда. Сорок родов составляют один фарлонг. Другие авторы называют разные способы образования фарлонга, но в целом считалось, что он был введен для практического использования в сельском хозяйстве и оценки площади земли, поскольку он соотносится с акром (1 фарлонг×4 рода = 1 акр). Прослеживается и его связь с римским стадием. Восемь стадий со ставляют одну римскую милю, а 8 фарлонгов равны 1 стандартной английской мили. И все же короткий фарлонг, едва превышающий 658 футов, не совсем совпадает со стадием, который насчитывает только 600 футов.
Род
Род, который Р. Д. Коннор считает одной из базовых британских единиц измерения, – производное от саксонского слова «джирд». Точная оценка древних измерений весьма затруднена из-за незначительных местных колебаний. Как мы уже видели, даже официальные стандартные меры изменялись на протяжении последних 500 лет, что становится очевидным при точном измерении старых зданий. Просматриваются два истока рода. Континентальный друзский фут, равный 0,333 метра, и естественный фут, равный 9,9 дюйма, или 0,2515 метра.
Если взять короткий фарлонг за изначальную точную меру, тогда короткий род оказывается равным 5,014 метра (200,5709:40 = 5,014 метра). Если точна признанная длина друзского и естественного футов, тогда при делении короткого рода на них получаем:
1 род:1 друзский фут = 15,06 (5,014: 0,333 = 15,06). 1 род:1 естественный фут = 19,976 (5,014:0,251 = 19,976).
Оба эти отношения близки к целым числам. Для корректировки этих мер с тем, чтобы род равнялся ровно 15 друзским футам и 20 естественным, друзский фут пришлось бы увеличить на один миллиметр до 0,334 метра, а естественный фут уменьшить на 0,8 миллиметра до 0,2507 метра. Это в пределах допустимой погрешности для обеих мер. На самом деле эти слегка подправленные друзский и естественный футы гораздо лучше соотносятся с коротким родом, чем нескорректированные меры с нынешним стандартным родом.
Тот факт, похоже, побуждает к использованию короткого фарлонга. Иными словами, благодаря изменениям в точных величинах английских стандартов представляется в высшей степени резонным теоретически допустить меру, основанную на делении круга Марлборо на 300 единиц, меру, которую мы назвали коротким фарлонгом.
Если взять короткий фарлонг за изначальную точную меру, тогда короткий род оказывается равным 5,014 метра (200,5709:40 = 5,014 метра). Если точна признанная длина друзского и естественного футов, тогда при делении короткого рода на них получаем:
1 род:1 друзский фут = 15,06 (5,014: 0,333 = 15,06). 1 род:1 естественный фут = 19,976 (5,014:0,251 = 19,976).
Оба эти отношения близки к целым числам. Для корректировки этих мер с тем, чтобы род равнялся ровно 15 друзским футам и 20 естественным, друзский фут пришлось бы увеличить на один миллиметр до 0,334 метра, а естественный фут уменьшить на 0,8 миллиметра до 0,2507 метра. Это в пределах допустимой погрешности для обеих мер. На самом деле эти слегка подправленные друзский и естественный футы гораздо лучше соотносятся с коротким родом, чем нескорректированные меры с нынешним стандартным родом.
Тот факт, похоже, побуждает к использованию короткого фарлонга. Иными словами, благодаря изменениям в точных величинах английских стандартов представляется в высшей степени резонным теоретически допустить меру, основанную на делении круга Марлборо на 300 единиц, меру, которую мы назвали коротким фарлонгом.
Мегалитический ярд и короткий фарлонг
После определения длины короткого фарлонга – 200,5709 метра, или одной трехсотой части окружности круга Марлборо, становится очевидным его значимое соотношение с мегалитическим ярдом. В окружности насчитываются 72 600 мегалитических ярдов (72 600: 300 = 242). Иными словами:
1 короткий фарлонг (КФ) = 242 мегалитическим ярдам.
Это примечательно, ибо 242 имеет множители: 11×22, или 11×11×2.
Современный фарлонг равен 220 стандартным ярдам. Множители числа 220: 10×22, или 11×10×2.
Таким образом существует отношение 10:11 между мегалитическим ярдом и коротким– стандартным ярдом. Это отношение точно повторяет отношение между уже упомянутыми двумя египетскими мерами – пик-билэди и царским локтем.
Отношение 10:11 имеет важное значение при вычислении и согласовании площадей и объемов. Согласно Стеккини, меры с таким отношением широко использовались в античном мире. Поэтому вполне возможно, что в древние времена использовались два варианта ярда – мегалитический ярд профессора Тома и короткий стандартный ярд, от которого произведены нынешние британские меры. Эти единицы измерения соотносятся, по скольку и короткий фарлонг, и мегалитический ярд находятся в выраженной целыми числами пропорции с экваториальной окружностью Земли.
1 короткий фарлонг (КФ) = 242 мегалитическим ярдам.
Это примечательно, ибо 242 имеет множители: 11×22, или 11×11×2.
Современный фарлонг равен 220 стандартным ярдам. Множители числа 220: 10×22, или 11×10×2.
Отношение 10:11 имеет важное значение при вычислении и согласовании площадей и объемов. Согласно Стеккини, меры с таким отношением широко использовались в античном мире. Поэтому вполне возможно, что в древние времена использовались два варианта ярда – мегалитический ярд профессора Тома и короткий стандартный ярд, от которого произведены нынешние британские меры. Эти единицы измерения соотносятся, по скольку и короткий фарлонг, и мегалитический ярд находятся в выраженной целыми числами пропорции с экваториальной окружностью Земли.
Короткий фарлонг и экваториальная окружность
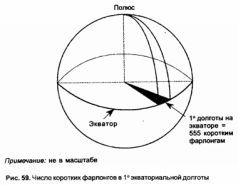
Происходит нечто любопытное, когда мы используем короткий фарлонг для измерения экваториальной окружности Земли. Каждый градус долготы на экваторе равен 69,170971 мили (24901,55: 360 = 69,170971). Это эквивалентно 555 коротким фарлонгам. Или, скажем иначе: 1 градус экваториальной долготы равен 555 коротким фарлонгам.
Множители числа 555: 37×15. Таким образом мы по лучаем отражение числа 666, множителями которого являются 37 и 18. Таким образом получаем отношение 15 к 18, или 5:6. Ему предстояло стать весьма значимым, когда я начал вникать в системы съемки местности, применявшиеся строителями мегалитов.
Множители числа 555: 37×15. Таким образом мы по лучаем отражение числа 666, множителями которого являются 37 и 18. Таким образом получаем отношение 15 к 18, или 5:6. Ему предстояло стать весьма значимым, когда я начал вникать в системы съемки местности, применявшиеся строителями мегалитов.
Широта и долгота
В соответствии с формой Земли длина одного градуса долготы на экваторе превышает длину одного градуса широты. Однако длина градуса широты pacтет по мере удаления от экватора к полюсу. Длины одного градуса широты и одного градуса долготы оказываются равными на 55° широты, на которой почти точно расположена Стена Хэдриена в Англии. Здесь один градус широты и один градус долготы равны 555 коротким фарлонгам. Может ли быть простым совпадением то, что длины градусов широты и долготы уравниваются на пятьдесят пятой параллели (55°) и оказываются делимыми на символически взаимодействующее число 555? Полагаю, что нет.
Все эти соотношения подтверждают постулат Стеккини:
«Изучая античную географию, я убедился в том, что на нашей планете жил народ с передовой математической и астрономической наукой еще за несколько тысячелетий до классической Греции».
Мое исследование придает дополнительный вес этому предположению. Мыслимо ли, что все факты, выявившиеся при изучении двойных кругов на Марлборо-Даунс, обязаны своим существованием лишь случайности? Несомненно, они были созданы умышленно. И мне предстояло открыть, как и почему они были созданы.
Выбрав расстояние чуть меньшее 9,6 километров (6 миль) в качестве радиуса для каждого из двойных кругов Марлборо-Даунс, создатели этой композиции установили гармоничное соотношение между мегалитическим ярдом и другими древними мерами, привязав их к радиусу, экваториальной окружности и полярному меридиану Земли. Это ошеломляющее достижение указывает на ясное представление о размерах Земли.
Два круга содержат достаточно информации, чтобы убедить нас в том, что их создатели обладали глубокими знаниями математики. Это что-то вроде закодированного послания из прошлого, ждущего своей расшифровки теми представителями будущего поколения, которые окажутся достаточно умелыми, чтобы раскрыть заключенные в них тайны. Открытия, последовавшие за моим допущением, что размер каждого круга был умышленно при равнен к 1/666 части окружности Земли, с лихвой – на мой взгляд – оправдали такой выбор.
Несмотря на уже сделанные мной волнующие открытия, мне предстояло еще решить ряд сложнейших задач. Я уже не сомневался в том, что двойные круги Марлборо-Даунс были созданы преднамеренно, но еще следо вало определить, как это было сделано. Есть кое-какие данные о появлении золотых изделий около 2800 года до н. э., а бронза появилась лишь несколько столетий спустя – около 2500 года до н. э. Следовательно, топографы мегалитических кругов не имели металлических инструментов. Им пришлось создавать свои ландшафтные ком позиции с помощью простейшего оборудования вроде «реек визирования». Следующим шагом моих поисков стало изучение техники типографической съемки древне-британских землемеров.
Все эти соотношения подтверждают постулат Стеккини:
«Изучая античную географию, я убедился в том, что на нашей планете жил народ с передовой математической и астрономической наукой еще за несколько тысячелетий до классической Греции».
Мое исследование придает дополнительный вес этому предположению. Мыслимо ли, что все факты, выявившиеся при изучении двойных кругов на Марлборо-Даунс, обязаны своим существованием лишь случайности? Несомненно, они были созданы умышленно. И мне предстояло открыть, как и почему они были созданы.
Выбрав расстояние чуть меньшее 9,6 километров (6 миль) в качестве радиуса для каждого из двойных кругов Марлборо-Даунс, создатели этой композиции установили гармоничное соотношение между мегалитическим ярдом и другими древними мерами, привязав их к радиусу, экваториальной окружности и полярному меридиану Земли. Это ошеломляющее достижение указывает на ясное представление о размерах Земли.
Два круга содержат достаточно информации, чтобы убедить нас в том, что их создатели обладали глубокими знаниями математики. Это что-то вроде закодированного послания из прошлого, ждущего своей расшифровки теми представителями будущего поколения, которые окажутся достаточно умелыми, чтобы раскрыть заключенные в них тайны. Открытия, последовавшие за моим допущением, что размер каждого круга был умышленно при равнен к 1/666 части окружности Земли, с лихвой – на мой взгляд – оправдали такой выбор.
Несмотря на уже сделанные мной волнующие открытия, мне предстояло еще решить ряд сложнейших задач. Я уже не сомневался в том, что двойные круги Марлборо-Даунс были созданы преднамеренно, но еще следо вало определить, как это было сделано. Есть кое-какие данные о появлении золотых изделий около 2800 года до н. э., а бронза появилась лишь несколько столетий спустя – около 2500 года до н. э. Следовательно, топографы мегалитических кругов не имели металлических инструментов. Им пришлось создавать свои ландшафтные ком позиции с помощью простейшего оборудования вроде «реек визирования». Следующим шагом моих поисков стало изучение техники типографической съемки древне-британских землемеров.