все», а нераспределённый – квантору «
некоторые»; что соприкасающиеся на схеме Эйлера круги соответствуют связке «
является», а несоприкасающиеся – связке «
не является». Например, требуется совершить три операции преобразования с суждением: «
Все учебники являются книгами». Изобразим субъект «
учебники», предикат «
книги» и непредикат «
не книги» круговой схемой и установим распределённость этих терминов (рис. 30):
 Получившуюся круговую схему можно прочитать четырьмя способами:
Получившуюся круговую схему можно прочитать четырьмя способами:
1. Все учебники являются книгами(исходное суждение).
2. Некоторые книги являются учебниками(обращение).
3. Все учебники не являются не книгами(превращение).
4. Все не книги не являются учебниками(противопоставление предикату).
Рассмотрим ещё один пример. Надо преобразовать тремя способами суждение: « Все планеты не являются звёздами». Изобразим кругами Эйлера субъект « планеты», предикат « звёзды» и непредикат « не звёзды». Обратите внимание на то, что понятия « планеты» и « не звёзды» находятся в отношении подчинения: планета – это обязательно не звезда, но небесное тело, которое не является звездой – это не обязательно планета. Установим распределённость этих терминов (рис. 31):
 Получившуюся круговую схему можно прочитать четырьмя разными способами:
Получившуюся круговую схему можно прочитать четырьмя разными способами:
1. Все планеты не являются звёздами(исходное суждение).
2. Все звёзды не являются планетами(обращение).
3. Все планеты являются не звёздами(превращение).
4. Некоторые не звёзды являются планетами(противопоставление предикату).
2. Что такое превращение? Возьмите три любых суждения и совершите с каждым из них операцию превращения.
3. Что представляет собой операция противопоставления предикату? Возьмите три каких-нибудь суждения и преобразуйте каждое из них путём противопоставления предикату.
4. Каким образом знания о распределённости терминов в простых суждениях и умение её устанавливать с помощью круговых схем может помочь в проведении операций преобразования суждений?
5. Возьмите какое-нибудь суждение вида Aи совершите с ним все операции преобразования с помощью круговых схем и установления распределённости терминов. Сделайте то же самое с каким-нибудь суждением вида E.
2.5. Логический квадрат
2.6. Сложное суждение
2.7. Логические формулы

1. Все учебники являются книгами(исходное суждение).
2. Некоторые книги являются учебниками(обращение).
3. Все учебники не являются не книгами(превращение).
4. Все не книги не являются учебниками(противопоставление предикату).
Рассмотрим ещё один пример. Надо преобразовать тремя способами суждение: « Все планеты не являются звёздами». Изобразим кругами Эйлера субъект « планеты», предикат « звёзды» и непредикат « не звёзды». Обратите внимание на то, что понятия « планеты» и « не звёзды» находятся в отношении подчинения: планета – это обязательно не звезда, но небесное тело, которое не является звездой – это не обязательно планета. Установим распределённость этих терминов (рис. 31):

1. Все планеты не являются звёздами(исходное суждение).
2. Все звёзды не являются планетами(обращение).
3. Все планеты являются не звёздами(превращение).
4. Некоторые не звёзды являются планетами(противопоставление предикату).
Проверьте себя:
1. Каким образом осуществляется операция обращения? Возьмите три каких-нибудь суждения и произведите с каждым из них обращение. Как происходит обращение во всех видах простых суждений и во всех случаях отношений между их субъектом и предикатом? Какие суждения не поддаются обращению?2. Что такое превращение? Возьмите три любых суждения и совершите с каждым из них операцию превращения.
3. Что представляет собой операция противопоставления предикату? Возьмите три каких-нибудь суждения и преобразуйте каждое из них путём противопоставления предикату.
4. Каким образом знания о распределённости терминов в простых суждениях и умение её устанавливать с помощью круговых схем может помочь в проведении операций преобразования суждений?
5. Возьмите какое-нибудь суждение вида Aи совершите с ним все операции преобразования с помощью круговых схем и установления распределённости терминов. Сделайте то же самое с каким-нибудь суждением вида E.
2.5. Логический квадрат
Простые суждения делятся на сравнимые и несравнимые.
Сравнимые (идентичные по материалу)суждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками. Например, суждения: « Все школьники изучают математику», « Некоторые школьники не изучают математику», – являются сравнимыми: у них совпадают субъекты и предикаты, а кванторы и связки различаются. Несравнимыесуждения имеют разные субъекты и предикаты. Например, суждения: « Все школьники изучают математику», « Некоторые спортсмены – это олимпийские чемпионы», – являются несравнимыми: субъекты и предикаты у них не совпадают.
Сравнимые суждения бывают, как и понятия, совместимыми и несовместимыми и могут находиться в различных отношениях между собой.
Совместимыминазываются суждения, которые могут быть одновременно истинными. Например, суждения: « Некоторые люди – это спортсмены», « Некоторые люди – это не спортсмены», – являются одновременно истинными и представляют собой совместимые суждения.
Несовместимыминазываются суждения, которые не могут быть одновременно истинными: истинность одного из них обязательно означает ложность другого. Например, суждения: « Все школьники изучают математику», «Некоторые школьники не изучают математику», – не могут быть одновременно истинными и являются несовместимыми (истинность первого суждения с неизбежностью приводит к ложности второго).
Совместимые суждения могут находиться в следующих отношениях:
1. Равнозначность– это отношение между двумя суждениями, у которых и субъекты, и предикаты, и связки, и кванторы совпадают. Например, суждения: « Москва является древним городом»,
« Столица России является древним городом», – находятся в отношении равнозначности.
2. Подчинение– это отношение между двумя суждениями, у которых предикаты и связки совпадают, а субъекты находятся в отношении вида и рода. Например, суждения: « Все растения являются живыми организмами», « Все цветы (некоторые растения) являются живыми организмами», – находятся в отношении подчинения.
3. Частичное совпадение (субконтрарность)– это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения: « Некоторые грибы являются съедобными», « Некоторые грибы не являются съедобными», – находятся в отношении частичного совпадения. Необходимо отметить, что в этом отношении находятся только частные суждения – частноутвердительные ( I) и частноотрицательные ( O).
Несовместимые суждения могут находиться в следующих отношениях.
1. Противоположность (контрарность)– это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения: « Все люди являются правдивыми», « Все люди не являются правдивыми», – находятся в отношении противоположности. В этом отношении могут быть только общие суждения – общеутвердительные ( A) и общеотрицательные ( E). Важным признаком противоположных суждений является то, что они не могут быть одновременно истинными, но могут быть одновременно ложными. Так, два приведённых противоположных суждения не могут быть одновременно истинными, но могут быть одновременно ложными: неправда, что все люди являются правдивыми, но также неправда, что все люди не являются правдивыми.
Противоположные суждения могут быть одновременно ложными, потому что между ними, обозначающими какие-то крайние варианты, всегда есть третий, средний, промежуточный вариант. Если этот средний вариант будет истинным, то два крайних окажутся ложными. Между противоположными (крайними) суждениями: « Все люди являются правдивыми», « Все люди не являются правдивыми», – есть третий, средний вариант: « Некоторые люди являются правдивыми, а некоторые не являются таковыми», – который, будучи истинным суждением, обусловливает одновременную ложность двух крайних, противоположных суждений.
2. Противоречие (контрадикторность)– это отношение между двумя суждениями, у которых предикаты совпадают, связки различны, а субъекты отличаются своими объёмами, т. е. находятся в отношении подчинения (вида и рода). Например, суждения: « Все люди являются правдивыми», «Некоторые люди не являются правдивыми», – находятся в отношении противоречия. Важным признаком противоречащих суждений, в отличие от противоположных, является то, что между ними не может быть третьего, среднего, промежуточного варианта. В силу этого два противоречащих суждения не могут быть одновременно истинными и не могут быть одновременно ложными: истинность одного из них обязательно означает ложность другого, и наоборот – ложность одного обусловливает истинность другого. К противоположным и противоречащим суждениям мы ещё вернёмся, когда речь пойдёт о логических законах противоречия и исключённого третьего.
Рассмотренные отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата (рис. 32), который был разработан ещё средневековыми логиками:
 Вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так, суждения вида
Aи вида
I, а также суждения вида
Eи вида
Oнаходятся в отношении подчинения. Суждения вида
Aи вида
Eнаходятся в отношении противоположности, а суждения вида
Iи вида
O– частичного совпадения. Суждения вида
Aи вида
O, а также суждения вида
Eи вида
Iнаходятся в отношении противоречия. Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями
Aи
A,
Iи
I,
Eи
E,
Oи
O. Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения: «
Все люди изучали логику», «
Некоторые люди не изучали логику». Видя, что первое суждение является общеутвердительным (
A), а второе частноотрицательным (
O), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Суждения: «
Все люди изучали логику (A)», «
Некоторые люди изучали логику (I)», находятся в отношении подчинения, а суждения: «
Все люди изучали логику (A)», «
Все люди не изучали логику (E)», – находятся в отношении противоположности.
Вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так, суждения вида
Aи вида
I, а также суждения вида
Eи вида
Oнаходятся в отношении подчинения. Суждения вида
Aи вида
Eнаходятся в отношении противоположности, а суждения вида
Iи вида
O– частичного совпадения. Суждения вида
Aи вида
O, а также суждения вида
Eи вида
Iнаходятся в отношении противоречия. Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями
Aи
A,
Iи
I,
Eи
E,
Oи
O. Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения: «
Все люди изучали логику», «
Некоторые люди не изучали логику». Видя, что первое суждение является общеутвердительным (
A), а второе частноотрицательным (
O), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Суждения: «
Все люди изучали логику (A)», «
Некоторые люди изучали логику (I)», находятся в отношении подчинения, а суждения: «
Все люди изучали логику (A)», «
Все люди не изучали логику (E)», – находятся в отношении противоположности.
Как уже говорилось, важным свойством суждений, в отличие от понятий, является то, что они могут быть истинными или ложными.
Что касается сравнимых суждений, то истинностные значения каждого из них определённым образом связаны с истинностными значениями остальных. Так, если суждение вида Aявляется истинным или ложным, то три других ( I, E, O), сравнимых с ним суждения (имеющих сходные с ним субъекты и предикаты), в зависимости от этого (от истинности или ложности суждения вида A) тоже являются истинными или ложными. Например, если суждение вида A: « Все тигры – это хищники», – является истинным, то суждение вида I: « Некоторые тигры – это хищники», – также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида E: « Все тигры – это не хищники», – является ложным, и суждение вида O: « Некоторые тигры – это не хищники», – также является ложным. Таким образом, в данном случае из истинности суждения вида Aвытекает истинность суждения вида Iи ложность суждений вида Eи вида O(разумеется, речь идёт о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
2. Что такое совместимые и несовместимые суждения? Приведите по три примера совместимых и несовместимых суждений.
3. В каких отношениях могут быть совместимые суждения? Приведите по два примера для отношений равнозначности, подчинения и частичного совпадения.
4. В каких отношениях могут быть несовместимые суждения?
Приведите по три примера для отношений противоположности и противоречия. Почему противоположные суждения могут быть одновременно ложными, а противоречащие не могут?
5. Что представляет собой логический квадрат? Каким образом он изображает отношения между суждениями? Почему логический квадрат не изображает отношение равнозначности? Как с помощью логического квадрата определять отношение между двумя простыми сравнимыми суждениями?
6. Возьмите какое-нибудь истинное или ложное суждения вида Aи сделайте из него выводы об истинности сравнимых с ним суждений видов E, I, O. Возьмите какое-нибудь истинное или ложное суждения вида Eи сделайте из него выводы об истинности сравнимых с ним суждений A, I, O.
Сравнимые (идентичные по материалу)суждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками. Например, суждения: « Все школьники изучают математику», « Некоторые школьники не изучают математику», – являются сравнимыми: у них совпадают субъекты и предикаты, а кванторы и связки различаются. Несравнимыесуждения имеют разные субъекты и предикаты. Например, суждения: « Все школьники изучают математику», « Некоторые спортсмены – это олимпийские чемпионы», – являются несравнимыми: субъекты и предикаты у них не совпадают.
Сравнимые суждения бывают, как и понятия, совместимыми и несовместимыми и могут находиться в различных отношениях между собой.
Совместимыминазываются суждения, которые могут быть одновременно истинными. Например, суждения: « Некоторые люди – это спортсмены», « Некоторые люди – это не спортсмены», – являются одновременно истинными и представляют собой совместимые суждения.
Несовместимыминазываются суждения, которые не могут быть одновременно истинными: истинность одного из них обязательно означает ложность другого. Например, суждения: « Все школьники изучают математику», «Некоторые школьники не изучают математику», – не могут быть одновременно истинными и являются несовместимыми (истинность первого суждения с неизбежностью приводит к ложности второго).
Совместимые суждения могут находиться в следующих отношениях:
1. Равнозначность– это отношение между двумя суждениями, у которых и субъекты, и предикаты, и связки, и кванторы совпадают. Например, суждения: « Москва является древним городом»,
« Столица России является древним городом», – находятся в отношении равнозначности.
2. Подчинение– это отношение между двумя суждениями, у которых предикаты и связки совпадают, а субъекты находятся в отношении вида и рода. Например, суждения: « Все растения являются живыми организмами», « Все цветы (некоторые растения) являются живыми организмами», – находятся в отношении подчинения.
3. Частичное совпадение (субконтрарность)– это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения: « Некоторые грибы являются съедобными», « Некоторые грибы не являются съедобными», – находятся в отношении частичного совпадения. Необходимо отметить, что в этом отношении находятся только частные суждения – частноутвердительные ( I) и частноотрицательные ( O).
Несовместимые суждения могут находиться в следующих отношениях.
1. Противоположность (контрарность)– это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения: « Все люди являются правдивыми», « Все люди не являются правдивыми», – находятся в отношении противоположности. В этом отношении могут быть только общие суждения – общеутвердительные ( A) и общеотрицательные ( E). Важным признаком противоположных суждений является то, что они не могут быть одновременно истинными, но могут быть одновременно ложными. Так, два приведённых противоположных суждения не могут быть одновременно истинными, но могут быть одновременно ложными: неправда, что все люди являются правдивыми, но также неправда, что все люди не являются правдивыми.
Противоположные суждения могут быть одновременно ложными, потому что между ними, обозначающими какие-то крайние варианты, всегда есть третий, средний, промежуточный вариант. Если этот средний вариант будет истинным, то два крайних окажутся ложными. Между противоположными (крайними) суждениями: « Все люди являются правдивыми», « Все люди не являются правдивыми», – есть третий, средний вариант: « Некоторые люди являются правдивыми, а некоторые не являются таковыми», – который, будучи истинным суждением, обусловливает одновременную ложность двух крайних, противоположных суждений.
2. Противоречие (контрадикторность)– это отношение между двумя суждениями, у которых предикаты совпадают, связки различны, а субъекты отличаются своими объёмами, т. е. находятся в отношении подчинения (вида и рода). Например, суждения: « Все люди являются правдивыми», «Некоторые люди не являются правдивыми», – находятся в отношении противоречия. Важным признаком противоречащих суждений, в отличие от противоположных, является то, что между ними не может быть третьего, среднего, промежуточного варианта. В силу этого два противоречащих суждения не могут быть одновременно истинными и не могут быть одновременно ложными: истинность одного из них обязательно означает ложность другого, и наоборот – ложность одного обусловливает истинность другого. К противоположным и противоречащим суждениям мы ещё вернёмся, когда речь пойдёт о логических законах противоречия и исключённого третьего.
Рассмотренные отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата (рис. 32), который был разработан ещё средневековыми логиками:

Как уже говорилось, важным свойством суждений, в отличие от понятий, является то, что они могут быть истинными или ложными.
Что касается сравнимых суждений, то истинностные значения каждого из них определённым образом связаны с истинностными значениями остальных. Так, если суждение вида Aявляется истинным или ложным, то три других ( I, E, O), сравнимых с ним суждения (имеющих сходные с ним субъекты и предикаты), в зависимости от этого (от истинности или ложности суждения вида A) тоже являются истинными или ложными. Например, если суждение вида A: « Все тигры – это хищники», – является истинным, то суждение вида I: « Некоторые тигры – это хищники», – также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида E: « Все тигры – это не хищники», – является ложным, и суждение вида O: « Некоторые тигры – это не хищники», – также является ложным. Таким образом, в данном случае из истинности суждения вида Aвытекает истинность суждения вида Iи ложность суждений вида Eи вида O(разумеется, речь идёт о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
Проверьте себя:
1. Какие суждения называются сравнимыми и какие – несравнимыми?2. Что такое совместимые и несовместимые суждения? Приведите по три примера совместимых и несовместимых суждений.
3. В каких отношениях могут быть совместимые суждения? Приведите по два примера для отношений равнозначности, подчинения и частичного совпадения.
4. В каких отношениях могут быть несовместимые суждения?
Приведите по три примера для отношений противоположности и противоречия. Почему противоположные суждения могут быть одновременно ложными, а противоречащие не могут?
5. Что представляет собой логический квадрат? Каким образом он изображает отношения между суждениями? Почему логический квадрат не изображает отношение равнозначности? Как с помощью логического квадрата определять отношение между двумя простыми сравнимыми суждениями?
6. Возьмите какое-нибудь истинное или ложное суждения вида Aи сделайте из него выводы об истинности сравнимых с ним суждений видов E, I, O. Возьмите какое-нибудь истинное или ложное суждения вида Eи сделайте из него выводы об истинности сравнимых с ним суждений A, I, O.
2.6. Сложное суждение
В зависимости от союза, с помощью которого простые суждения соединяются в сложные, выделяется пять видов сложных суждений:
1. Конъюнктивное суждение (конъюнкция)– это сложное суждение с соединительным союзом «и», который обозначается в логике условным знаком «?». С помощью этого знака конъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a? b(читается « aи b»), где aи b– это два каких-либо простых суждения. Например, сложное суждение: « Сверкнула молния, и загремел гром», – является конъюнкцией (соединением) двух простых суждений: «Сверкнула молния», «Загремел гром». Конъюнкция может состоять не только из двух, но и из большего числа простых суждений. Например: « Сверкнула молния, и загремел гром, и пошёл дождь( a? b? c)».
2. Дизъюнктивное суждение (дизъюнкция)– это сложное суждение с разделительным союзом «или». Вспомним, что, говоря о логических операциях сложения и умножения понятий, мы отмечали неоднозначность этого союза – он может использоваться как в нестрогом (неисключающем) значении, так и в строгом (исключающем). Неудивительно поэтому, что дизъюнктивные суждения делятся на два вида:
1. Нестрогая дизъюнкция– это сложное суждение с разделительным союзом «или» в его нестрогом (неисключающем) значении, который обозначается условным знаком «?». С помощью этого знака нестрогое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a? b(читается « aили b»), где aи b– это два простых суждения. Например, сложное суждение: « Он изучает английский, или он изучает немецкий», – является нестрогой дизъюнкцией (разделением) двух простых суждений: «Он изучает английский», «Он изучает немецкий».Эти суждения друг друга не исключают, ведь возможно изучать и английский, и немецкий одновременно, поэтому данная дизъюнкция является нестрогой.
2. Строгая дизъюнкция– это сложное суждение с разделительным союзом «или» в его строгом (исключающем) значении, который обозначается условным знаком «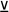 ». С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a
». С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a
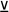 b(читается «или
a, или
b»), где
aи
b– это два простых суждения. Например, сложное суждение: «
Он учится в 9 классе, или он учится в 11 классе», – является строгой дизъюнкцией (разделением) двух простых суждений:
«Он учится в 9 классе», «Он учится в 11 классе». Обратим внимание на то, что эти суждения друг друга исключают, ведь невозможно одновременно учиться и в 9, и в 11 классе (если он учится в 9 классе, то точно не учится в 11 классе, и наоборот), в силу чего данная дизъюнкция является строгой.
b(читается «или
a, или
b»), где
aи
b– это два простых суждения. Например, сложное суждение: «
Он учится в 9 классе, или он учится в 11 классе», – является строгой дизъюнкцией (разделением) двух простых суждений:
«Он учится в 9 классе», «Он учится в 11 классе». Обратим внимание на то, что эти суждения друг друга исключают, ведь невозможно одновременно учиться и в 9, и в 11 классе (если он учится в 9 классе, то точно не учится в 11 классе, и наоборот), в силу чего данная дизъюнкция является строгой.
Как нестрогая, так и строгая дизъюнкции могут состоять не только из двух, но и из большего числа простых суждений. Например: « Он изучает английский, или он изучает немецкий, или он изучает французский (a ? b ? c)», « Он учится в 9 классе, или он учится в 10 классе, или он учится в 11 классе (a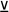 b
b
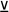 c)».
c)».
3. Импликативное суждение (импликация)– это сложное суждение с условным союзом «если … то», который обозначается условным знаком «?». С помощью этого знака импликативное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a? b(читается «если a, то b»), где aи b– это два простых суждения. Например, сложное суждение: « Если вещество является металлом, то оно электропроводно», – представляет собой импликативное суждение (причинно-следственную связь) двух простых суждений: «Вещество является металлом», «Вещество электропроводно». В данном случае эти два суждения связаны таким образом, что из первого вытекает второе (если вещество – металл, то оно обязательно электропроводно), однако из второго не вытекает первое (если вещество электропроводно, то это вовсе не означает, что оно является металлом). Первая часть импликации называется основанием, а вторая – следствием; из основания вытекает следствие, но из следствия не вытекает основание. Формулу импликации: a? b, можно прочитать так: «если a, то обязательно b, но если b, то не обязательно a».
4. Эквивалентное суждение (эквиваленция)– это сложное суждение с союзом «если … то» не в его условном значении (как в случае с импликацией), а в тождественном (эквивалентном). В данном случае этот союз обозначается условным знаком «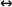 », с помощью которого эквивалентное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a
», с помощью которого эквивалентное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a
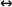 b(читается «если
a, то
b, и если
b, то
a»), где
aи
b– это два простых суждения. Например, сложное суждение: «
Если число является чётным, то оно делится без остатка на 2», – представляет собой эквивалентное суждение (равенство, тождество) двух простых суждений:
«Число является чётным», «Число делится без остатка на 2». Нетрудно заметить, что в данном случае два суждения связаны так, что из первого вытекает второе, а из второго – первое: если число чётное, то оно обязательно делится без остатка на 2, а если число делится без остатка на 2, то оно обязательно чётное. Понятно, что в эквиваленции, в отличие от импликации, не может быть ни основания, ни следствия, т. к. две её части являются равнозначными суждениями.
b(читается «если
a, то
b, и если
b, то
a»), где
aи
b– это два простых суждения. Например, сложное суждение: «
Если число является чётным, то оно делится без остатка на 2», – представляет собой эквивалентное суждение (равенство, тождество) двух простых суждений:
«Число является чётным», «Число делится без остатка на 2». Нетрудно заметить, что в данном случае два суждения связаны так, что из первого вытекает второе, а из второго – первое: если число чётное, то оно обязательно делится без остатка на 2, а если число делится без остатка на 2, то оно обязательно чётное. Понятно, что в эквиваленции, в отличие от импликации, не может быть ни основания, ни следствия, т. к. две её части являются равнозначными суждениями.
5. Отрицательное суждение (отрицание)– это сложное суждение с союзом «неверно, что…», который обозначается условным знаком «¬». С помощью этого знака отрицательное суждение можно представить в виде формулы: ¬ a(читается «неверно, что a»), где a– это простое суждение. Здесь может возникнуть вопрос – где же вторая часть сложного суждения, которую мы обычно обозначали символом b? В записи: ¬ a, уже присутствуют два простых суждения: a– это какое-то утверждение, а знак «¬» – его отрицание. Перед нами как бы два простых суждения – одно утвердительное, другое – отрицательное. Пример отрицательного суждения: « Неверно, что все мухи являются птицами».
Итак, мы рассмотрели пять видов сложных суждений: конъюнкцию, дизъюнкцию (нестрогую и строгую), импликацию, эквиваленцию и отрицание.
Союзов в естественном языке много, но все они по смыслу сводятся к рассмотренным пяти видам, и любое сложное суждение относится к одному из них. Например, сложное суждение: « Уж полночь близится, а Германа всё нет», – является конъюнкцией, потому что в нём союз « а» употребляется в роли соединительного союза «и». Сложное суждение, в котором вообще нет союза: « Посеешь ветер, пожнёшь бурю», – является импликацией, т. к. два простых суждения в нём связаны по смыслу условным союзом «если…то».
Любое сложное суждение является истинным или ложным в зависимости от истинности или ложности входящих в него простых суждений. Приведена табл. 6 истинности всех видов сложных суждений в зависимости от всех возможных наборов истинностных значений двух входящих в них простых суждений (таких наборов всего четыре): оба простых суждения истинные; первое суждение истинное, а второе ложное; первое суждение ложное, а второе истинное; оба суждения ложные).
 Как видим, конъюнкция истинна только тогда, когда истинны оба входящих в неё простых суждения. Надо отметить, что конъюнкция, состоящая не из двух, а из большего числа простых суждений, также истинна только в том случае, когда истинны все входящие в неё суждения. Во всех остальных случаях она является ложной. Нестрогая дизъюнкция, наоборот, истинна во всех случаях за исключением того, когда оба входящих в неё простых суждения ложны. Нестрогая дизъюнкция, состоящая не из двух, а из большего числа простых суждений, также ложна только тогда, когда ложны все входящие в неё простые суждения. Строгая дизъюнкция истинна только тогда, когда одно входящее в неё простое суждение истинно, а другое ложно. Строгая дизъюнкция, состоящая не из двух, а из большего числа простых суждений, истинна только в том случае, если истинно только одно из входящих в неё простых суждений, а все остальные ложны. Импликация ложна только в одном случае – когда её основание является истинным, а следствие ложным. Во всех остальных случаях она истинна. Эквиваленция истинна тогда, когда два составляющих её простых суждения истинны или когда оба являются ложными. Если одна часть эквиваленции истинна, а другая ложна, то эквиваленция ложна. Проще всего определяется истинность отрицания: когда утверждение истинно, его отрицание ложно; когда утверждение ложно, его отрицание истинно.
Как видим, конъюнкция истинна только тогда, когда истинны оба входящих в неё простых суждения. Надо отметить, что конъюнкция, состоящая не из двух, а из большего числа простых суждений, также истинна только в том случае, когда истинны все входящие в неё суждения. Во всех остальных случаях она является ложной. Нестрогая дизъюнкция, наоборот, истинна во всех случаях за исключением того, когда оба входящих в неё простых суждения ложны. Нестрогая дизъюнкция, состоящая не из двух, а из большего числа простых суждений, также ложна только тогда, когда ложны все входящие в неё простые суждения. Строгая дизъюнкция истинна только тогда, когда одно входящее в неё простое суждение истинно, а другое ложно. Строгая дизъюнкция, состоящая не из двух, а из большего числа простых суждений, истинна только в том случае, если истинно только одно из входящих в неё простых суждений, а все остальные ложны. Импликация ложна только в одном случае – когда её основание является истинным, а следствие ложным. Во всех остальных случаях она истинна. Эквиваленция истинна тогда, когда два составляющих её простых суждения истинны или когда оба являются ложными. Если одна часть эквиваленции истинна, а другая ложна, то эквиваленция ложна. Проще всего определяется истинность отрицания: когда утверждение истинно, его отрицание ложно; когда утверждение ложно, его отрицание истинно.
2. Охарактеризуйте все виды сложных суждений: название, союз, условное обозначение, формула, пример. Чем отличается нестрогая дизъюнкция от строгой? Как отличить импликацию от эквиваленции?
3. Каким образом можно определить вид сложного суждения, если в нём вместо союзов «и», «или», «если… то» употребляются какие-либо другие союзы?
4. Приведите по три примера для каждого вида сложных суждений, не используя при этом союзов «и», «или», «если…то».
5. Определите, к какому виду относятся следующие сложные суждения:
1. Живое существо является человеком только тогда, когда оно обладает мышлением.
2. Человечество может погибнуть то ли от истощения земных ресурсов, то ли от экологической катастрофы, то ли в результате третьей мировой войны.
3. Вчера он получил двойку не только по математике, но ещё и по русскому.
4. Проводник нагревается, когда через него проходит электрический ток.
5. Окружающий нас мир либо познаваем, либо нет.
6. Или же он совершенно бездарен, или же полный лентяй.
7. Когда человек льстит, он лжёт.
8. Вода превращается в лёд лишь при температуре от 0 °C и ниже.
6. От чего зависит истинность сложных суждений? Какие значения истинности принимают конъюнкция, нестрогая и строгая дизъюнкция, импликация, эквиваленция и отрицание в зависимости от всех наборов истинностных значений входящих в них простых суждений?
1. Конъюнктивное суждение (конъюнкция)– это сложное суждение с соединительным союзом «и», который обозначается в логике условным знаком «?». С помощью этого знака конъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a? b(читается « aи b»), где aи b– это два каких-либо простых суждения. Например, сложное суждение: « Сверкнула молния, и загремел гром», – является конъюнкцией (соединением) двух простых суждений: «Сверкнула молния», «Загремел гром». Конъюнкция может состоять не только из двух, но и из большего числа простых суждений. Например: « Сверкнула молния, и загремел гром, и пошёл дождь( a? b? c)».
2. Дизъюнктивное суждение (дизъюнкция)– это сложное суждение с разделительным союзом «или». Вспомним, что, говоря о логических операциях сложения и умножения понятий, мы отмечали неоднозначность этого союза – он может использоваться как в нестрогом (неисключающем) значении, так и в строгом (исключающем). Неудивительно поэтому, что дизъюнктивные суждения делятся на два вида:
1. Нестрогая дизъюнкция– это сложное суждение с разделительным союзом «или» в его нестрогом (неисключающем) значении, который обозначается условным знаком «?». С помощью этого знака нестрогое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a? b(читается « aили b»), где aи b– это два простых суждения. Например, сложное суждение: « Он изучает английский, или он изучает немецкий», – является нестрогой дизъюнкцией (разделением) двух простых суждений: «Он изучает английский», «Он изучает немецкий».Эти суждения друг друга не исключают, ведь возможно изучать и английский, и немецкий одновременно, поэтому данная дизъюнкция является нестрогой.
2. Строгая дизъюнкция– это сложное суждение с разделительным союзом «или» в его строгом (исключающем) значении, который обозначается условным знаком «
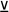 ». С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a
». С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a
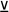 b(читается «или
a, или
b»), где
aи
b– это два простых суждения. Например, сложное суждение: «
Он учится в 9 классе, или он учится в 11 классе», – является строгой дизъюнкцией (разделением) двух простых суждений:
«Он учится в 9 классе», «Он учится в 11 классе». Обратим внимание на то, что эти суждения друг друга исключают, ведь невозможно одновременно учиться и в 9, и в 11 классе (если он учится в 9 классе, то точно не учится в 11 классе, и наоборот), в силу чего данная дизъюнкция является строгой.
b(читается «или
a, или
b»), где
aи
b– это два простых суждения. Например, сложное суждение: «
Он учится в 9 классе, или он учится в 11 классе», – является строгой дизъюнкцией (разделением) двух простых суждений:
«Он учится в 9 классе», «Он учится в 11 классе». Обратим внимание на то, что эти суждения друг друга исключают, ведь невозможно одновременно учиться и в 9, и в 11 классе (если он учится в 9 классе, то точно не учится в 11 классе, и наоборот), в силу чего данная дизъюнкция является строгой.Как нестрогая, так и строгая дизъюнкции могут состоять не только из двух, но и из большего числа простых суждений. Например: « Он изучает английский, или он изучает немецкий, или он изучает французский (a ? b ? c)», « Он учится в 9 классе, или он учится в 10 классе, или он учится в 11 классе (a
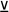
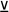
3. Импликативное суждение (импликация)– это сложное суждение с условным союзом «если … то», который обозначается условным знаком «?». С помощью этого знака импликативное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a? b(читается «если a, то b»), где aи b– это два простых суждения. Например, сложное суждение: « Если вещество является металлом, то оно электропроводно», – представляет собой импликативное суждение (причинно-следственную связь) двух простых суждений: «Вещество является металлом», «Вещество электропроводно». В данном случае эти два суждения связаны таким образом, что из первого вытекает второе (если вещество – металл, то оно обязательно электропроводно), однако из второго не вытекает первое (если вещество электропроводно, то это вовсе не означает, что оно является металлом). Первая часть импликации называется основанием, а вторая – следствием; из основания вытекает следствие, но из следствия не вытекает основание. Формулу импликации: a? b, можно прочитать так: «если a, то обязательно b, но если b, то не обязательно a».
4. Эквивалентное суждение (эквиваленция)– это сложное суждение с союзом «если … то» не в его условном значении (как в случае с импликацией), а в тождественном (эквивалентном). В данном случае этот союз обозначается условным знаком «
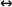 », с помощью которого эквивалентное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a
», с помощью которого эквивалентное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a
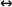 b(читается «если
a, то
b, и если
b, то
a»), где
aи
b– это два простых суждения. Например, сложное суждение: «
Если число является чётным, то оно делится без остатка на 2», – представляет собой эквивалентное суждение (равенство, тождество) двух простых суждений:
«Число является чётным», «Число делится без остатка на 2». Нетрудно заметить, что в данном случае два суждения связаны так, что из первого вытекает второе, а из второго – первое: если число чётное, то оно обязательно делится без остатка на 2, а если число делится без остатка на 2, то оно обязательно чётное. Понятно, что в эквиваленции, в отличие от импликации, не может быть ни основания, ни следствия, т. к. две её части являются равнозначными суждениями.
b(читается «если
a, то
b, и если
b, то
a»), где
aи
b– это два простых суждения. Например, сложное суждение: «
Если число является чётным, то оно делится без остатка на 2», – представляет собой эквивалентное суждение (равенство, тождество) двух простых суждений:
«Число является чётным», «Число делится без остатка на 2». Нетрудно заметить, что в данном случае два суждения связаны так, что из первого вытекает второе, а из второго – первое: если число чётное, то оно обязательно делится без остатка на 2, а если число делится без остатка на 2, то оно обязательно чётное. Понятно, что в эквиваленции, в отличие от импликации, не может быть ни основания, ни следствия, т. к. две её части являются равнозначными суждениями.5. Отрицательное суждение (отрицание)– это сложное суждение с союзом «неверно, что…», который обозначается условным знаком «¬». С помощью этого знака отрицательное суждение можно представить в виде формулы: ¬ a(читается «неверно, что a»), где a– это простое суждение. Здесь может возникнуть вопрос – где же вторая часть сложного суждения, которую мы обычно обозначали символом b? В записи: ¬ a, уже присутствуют два простых суждения: a– это какое-то утверждение, а знак «¬» – его отрицание. Перед нами как бы два простых суждения – одно утвердительное, другое – отрицательное. Пример отрицательного суждения: « Неверно, что все мухи являются птицами».
Итак, мы рассмотрели пять видов сложных суждений: конъюнкцию, дизъюнкцию (нестрогую и строгую), импликацию, эквиваленцию и отрицание.
Союзов в естественном языке много, но все они по смыслу сводятся к рассмотренным пяти видам, и любое сложное суждение относится к одному из них. Например, сложное суждение: « Уж полночь близится, а Германа всё нет», – является конъюнкцией, потому что в нём союз « а» употребляется в роли соединительного союза «и». Сложное суждение, в котором вообще нет союза: « Посеешь ветер, пожнёшь бурю», – является импликацией, т. к. два простых суждения в нём связаны по смыслу условным союзом «если…то».
Любое сложное суждение является истинным или ложным в зависимости от истинности или ложности входящих в него простых суждений. Приведена табл. 6 истинности всех видов сложных суждений в зависимости от всех возможных наборов истинностных значений двух входящих в них простых суждений (таких наборов всего четыре): оба простых суждения истинные; первое суждение истинное, а второе ложное; первое суждение ложное, а второе истинное; оба суждения ложные).

Проверьте себя:
1. На каком основании выделяются виды сложных суждений?2. Охарактеризуйте все виды сложных суждений: название, союз, условное обозначение, формула, пример. Чем отличается нестрогая дизъюнкция от строгой? Как отличить импликацию от эквиваленции?
3. Каким образом можно определить вид сложного суждения, если в нём вместо союзов «и», «или», «если… то» употребляются какие-либо другие союзы?
4. Приведите по три примера для каждого вида сложных суждений, не используя при этом союзов «и», «или», «если…то».
5. Определите, к какому виду относятся следующие сложные суждения:
1. Живое существо является человеком только тогда, когда оно обладает мышлением.
2. Человечество может погибнуть то ли от истощения земных ресурсов, то ли от экологической катастрофы, то ли в результате третьей мировой войны.
3. Вчера он получил двойку не только по математике, но ещё и по русскому.
4. Проводник нагревается, когда через него проходит электрический ток.
5. Окружающий нас мир либо познаваем, либо нет.
6. Или же он совершенно бездарен, или же полный лентяй.
7. Когда человек льстит, он лжёт.
8. Вода превращается в лёд лишь при температуре от 0 °C и ниже.
6. От чего зависит истинность сложных суждений? Какие значения истинности принимают конъюнкция, нестрогая и строгая дизъюнкция, импликация, эквиваленция и отрицание в зависимости от всех наборов истинностных значений входящих в них простых суждений?
2.7. Логические формулы
Любое высказывание или целое рассуждение можно подвергнуть формализации. Это значит отбросить его содержание и оставить только его логическую форму, выразив её с помощью уже известных нам условных обозначений конъюнкции, нестрогой и строгой дизъюнкции, импликации, эквиваленции и отрицания.
Например, чтобы формализовать следующее высказывание: « Он занимается живописью, или музыкой, или литературой», – надо сначала выделить входящие в него простые суждения и установить вид логической связи между ними. В приведённое высказывание входят три простых суждения: «Он занимается живописью», «Он занимается музыкой», «Он занимается литературой».
Эти суждения объединены разделительной связью, однако они друг друга не исключают (можно заниматься и живописью, и музыкой, и литературой), следовательно, перед нами – нестрогая дизъюнкция, форму которой можно представить следующей условной записью: a? b? c, где a, b, c– указанные выше простые суждения. Форму: a? b? c, можно наполнить каким угодно содержанием, например: « Цицерон был политиком, или оратором, или писателем», «Он изучает английский, или немецкий, или французский», «Люди передвигаются наземным, или воздушным, или водным транспортом».
Формализуем рассуждение: « Он учится в 9 классе, или в 10 классе, или в 11 классе. Однако, известно, что он не учится ни в 10, ни в 11 классе. Следовательно, он учится в 9 классе». Выделим простые высказывания, входящие в это рассуждение и обозначим их маленькими буквами латинского алфавита: «Он учится в 9 классе (a)», «Он учится в 10 классе (b)», «Он учится в 11 классе (c)». Первая часть рассуждения представляет собой строгую дизъюнкцию этих трёх высказываний: a? b? c. Вторая часть рассуждения является отрицанием второго: ¬ b, и третьего: ¬ c, высказываний, причём эти два отрицания соединяются, т. е. связаны конъюнктивно: ¬ b? ¬ c. Конъюнкция отрицаний присоединяется к упомянутой выше строгой дизъюнкции трёх простых суждений: ( a? b? c) ? (¬ b? ¬ c), и уже из этой новой конъюнкции как следствие вытекает утверждение первого простого суждения: « Он учится в 9 классе». Логическое следование, как мы уже знаем, представляет собой импликацию. Таким образом, результат формализации нашего рассуждения выражается формулой: (( a? b? c) ? (¬ b?¬ c)) ? a. Эту логическую форму можно наполнить любым содержанием. Например: « Впервые человек полетел в космос в 1957 г., или в 1959 г., или в 1961 г. Однако, известно, что впервые человек полетел в космос не в 1957 г. и не в 1959 г.. Следовательно, впервые человек полетел в космос в 1961 г.» Ещё один вариант: « Философский трактат «Критика чистого разума» написал то ли Иммануил Кант, то ли Георг Гегель, то ли Карл Маркс. Однако, ни Гегель, ни Маркс не являются авторами этого трактата. Следовательно, его написал Кант».
Результатом формализации любого рассуждения, как мы увидели, является какая-либо формула, состоящая из маленьких букв латинского алфавита, выражающих входящие в рассуждение простые высказывания, и условных обозначений логических связей между ними (конъюнкции, дизъюнкции и др.). Все формулы делятся в логике на три вида:
1. Тождественно-истинные формулыявляются истинными при всех наборах истинностных значений входящих в них переменных (простых суждений). Любая тождественно-истинная формула представляет собой логический закон.
Например, чтобы формализовать следующее высказывание: « Он занимается живописью, или музыкой, или литературой», – надо сначала выделить входящие в него простые суждения и установить вид логической связи между ними. В приведённое высказывание входят три простых суждения: «Он занимается живописью», «Он занимается музыкой», «Он занимается литературой».
Эти суждения объединены разделительной связью, однако они друг друга не исключают (можно заниматься и живописью, и музыкой, и литературой), следовательно, перед нами – нестрогая дизъюнкция, форму которой можно представить следующей условной записью: a? b? c, где a, b, c– указанные выше простые суждения. Форму: a? b? c, можно наполнить каким угодно содержанием, например: « Цицерон был политиком, или оратором, или писателем», «Он изучает английский, или немецкий, или французский», «Люди передвигаются наземным, или воздушным, или водным транспортом».
Формализуем рассуждение: « Он учится в 9 классе, или в 10 классе, или в 11 классе. Однако, известно, что он не учится ни в 10, ни в 11 классе. Следовательно, он учится в 9 классе». Выделим простые высказывания, входящие в это рассуждение и обозначим их маленькими буквами латинского алфавита: «Он учится в 9 классе (a)», «Он учится в 10 классе (b)», «Он учится в 11 классе (c)». Первая часть рассуждения представляет собой строгую дизъюнкцию этих трёх высказываний: a? b? c. Вторая часть рассуждения является отрицанием второго: ¬ b, и третьего: ¬ c, высказываний, причём эти два отрицания соединяются, т. е. связаны конъюнктивно: ¬ b? ¬ c. Конъюнкция отрицаний присоединяется к упомянутой выше строгой дизъюнкции трёх простых суждений: ( a? b? c) ? (¬ b? ¬ c), и уже из этой новой конъюнкции как следствие вытекает утверждение первого простого суждения: « Он учится в 9 классе». Логическое следование, как мы уже знаем, представляет собой импликацию. Таким образом, результат формализации нашего рассуждения выражается формулой: (( a? b? c) ? (¬ b?¬ c)) ? a. Эту логическую форму можно наполнить любым содержанием. Например: « Впервые человек полетел в космос в 1957 г., или в 1959 г., или в 1961 г. Однако, известно, что впервые человек полетел в космос не в 1957 г. и не в 1959 г.. Следовательно, впервые человек полетел в космос в 1961 г.» Ещё один вариант: « Философский трактат «Критика чистого разума» написал то ли Иммануил Кант, то ли Георг Гегель, то ли Карл Маркс. Однако, ни Гегель, ни Маркс не являются авторами этого трактата. Следовательно, его написал Кант».
Результатом формализации любого рассуждения, как мы увидели, является какая-либо формула, состоящая из маленьких букв латинского алфавита, выражающих входящие в рассуждение простые высказывания, и условных обозначений логических связей между ними (конъюнкции, дизъюнкции и др.). Все формулы делятся в логике на три вида:
1. Тождественно-истинные формулыявляются истинными при всех наборах истинностных значений входящих в них переменных (простых суждений). Любая тождественно-истинная формула представляет собой логический закон.
