Страница:
Ледяные торосы в несколько метров высоты разбиваются энергией многократных ударов прочной носовой части ледокола.
Участник знаменитого перехода «Сибирякова» в 1932 г., моряк-полярник Н. Марков, так описывает работу этого ледокола:
«Среди сотен ледяных скал, среди сплошного покрова льда „Сибиряков“ начал битву. Пятьдесят два часа подряд стрелка машинного телеграфа прыгала от „полного назад“ к „полному вперед“. Тринадцать четырехчасовых морских вахт „Сибиряков“ с разгона врезался в лед, крошил его носом, влезал на лед, ломал его и снова отходил назад. Лед, толщиной в три четверти метра, с трудом уступал дорогу. С каждым ударом пробивались на треть корпуса».
Самыми крупными и мощными в мире ледоколами располагает СССР.
Мнение это разделял, по-видимому, даже автор «20 тысяч лье под водой»; в одной из глав этого романа Жюль Верн описывает неподвижно висящее в воде затонувшее судно, а в другой упоминает о кораблях, «догнивающих, свободно вися в воде».
Правильно ли подобное утверждение?
Некоторое основание для него, как будто, имеется, так как давление воды в глубинах океана действительно достигает огромных степеней. На глубине 10 м вода давит с силой 1 кг на 1 см2 погруженного тела. На глубине 20 м это давление равно уже 2 кг, на глубине 100 м — 10 кг, 1000 м — 100 кг. Океан же во многих местах имеет глубину в несколько километров, достигая в самых глубоких частях Великого океана более 11 км (Марианская впадина). Легко вычислить, какое огромное давление должны испытывать вода и погруженные в нее предметы на этих огромных глубинах.
Если порожнюю закупоренную бутылку опустить на значительную глубину и затем извлечь вновь, то обнаружится, что давление воды вогнало пробку внутрь бутылки и вся посудина полна воды. Знаменитый океанограф Джон Меррей в своей книге «Океан» рассказывает, что был проделан такой опыт: три стеклянные трубки различных размеров, с обоих концов запаянные, были завернуты в холст и помещены в медный цилиндр с отверстиями для свободного пропуска воды. Цилиндр был спущен на глубину 5 км. Когда его извлекли оттуда, оказалось, что холст наполнен снегообразной массой: это было раздробленное стекло. Куски дерева, опущенные на подобную глубину, после извлечения тонули в воде, как кирпич, — настолько они были сдавлены.
Естественно, казалось бы, ожидать, что столь чудовищное давление должно настолько уплотнить воду на больших глубинах, что даже тяжелые предметы не будут в ней тонуть, как не тонет железная гиря в ртути.
Однако подобное мнение совершенно не обосновано. Опыт показывает, что вода, как и все вообще жидкости, мало поддается сжатию. Сдавливаемая с силой 1 кг на 1 см2 вода сжимается всего только на 1/22 000 долю своего объема и примерно так же сжимается при дальнейшем возрастании давления на каждый килограмм. Если бы мы пожелали довести воду до такой плотности, чтобы в ней плавало железо, необходимо было бы уплотнить ее в 8 раз. Между тем для уплотнения только вдвое, т. е. для сокращения объема наполовину, необходимо давление в 11 000 кг на 1 см2 (если бы только упомянутая мера сжатия имела место для таких огромных давлений). Это соответствует глубине 110 км под уровнем океана!
Отсюда ясно, что говорить о сколько-нибудь заметном уплотнении воды в глубине океанов совершенно не приходится. В самом глубоком их место вода уплотнена лишь на 1100/22000, т. е. на 1/20 нормальной своей плотности, всего на 5%[34]. Это почти не может повлиять на условия плавания в ней различных тел, — тем более, что твердые предметы, погруженные в такую воду, также подвергаются этому давлению и, следовательно, тоже уплотняются.
Не может быть поэтому ни малейшего сомнения в том, что затонувшие суда покоятся на дне океана. «Все, что тонет в стакане воды, — говорит Меррей, — должно пойти ко дну и в самом глубоком океане».
Мне приходилось слышать против этого такое возражение. Если осторожно погрузить стакан вверх дном в воду, он может остаться в этом положении, так как будет вытеснять объем воды, весящий столько же, сколько стакан. Более тяжелый металлический стакан может удержаться в подобном положении и ниже уровня воды, не опускаясь на дно. Точно так же, будто бы, может остановиться на полпути и опрокинутый вверх килем крейсер или другое судно. Если в некоторых помещениях судна воздух окажется плотно запертым, то судно погрузится на определенную глубину и там остановится.
Не мало ведь судов идет ко дну в перевернутом состоянии — и возможно, что некоторые из них так и не достигают дна, оставаясь висеть в темных глубинах океана. Достаточно было бы легкого толчка, чтобы вывести такое судно из равновесия, перевернуть, наполнить водою и заставить упасть на дно, — по откуда взяться толчкам в глубине океана, где вечно царит тишина и спокойствие и куда не проникают даже отголоски бурь?
Все эти доводы основаны на физической ошибке. Перевернутый стакан не погружается в воду сам — его надо внешней силой погрузить в воду, как кусок дерева или пустую закупоренную бутылку. Точно так же и опрокинутый килем вверх корабль вовсе и не начнет тонуть, а останется на поверхности воды. Очутиться на полпути между уровнем океана и его дном он никак не может.
Переход от портов Франции до острова Мадагаскара этот подводный крейсер мог совершать, не заходя по пути ни в один порт. По комфортабельности жилых помещений «Сюркуф», быть может, не уступал «Наутилусу». Далее, «Сюркуф» имел перед кораблем капитана Немо и то несомненное преимущество, что на верхней палубе крейсера устроен был водонепроницаемый ангар для разведывательного гидросамолета. Отметим также, что Жюль Верн не снабдил «Наутилус» перископом, дающим лодке возможность обозревать горизонт из-под воды.
В одном лишь отношении реальные подводные корабли долю еще будут далеко отставать от создания фантазии французского романиста: в глубине погружения. Однако приходится отметить, что в этом пункте фантазия Жюля Верна перешла границы правдоподобия. «Капитан Немо, — читаем в одном месте романа, — достигал глубины в три, четыре, пять, семь, девять и десять тысяч метров под поверхностью океана». А однажды «Наутилус» опустился даже на небывалую глубину — в 16 тысяч метров! «Я чувствовал, — рассказывает герой романа, — как содрогаются скрепы железной обшивки подводного судна, как изгибаются его распоры, как подаются внутрь окна, уступая давлению воды Если бы корабль наш не обладал прочностью сплошною литого тела, его мгновенно сплющило бы в лепешку».
Опасение вполне уместное, потому что на глубине 16 км (если бы такая глубина имелась в океане) давление воды должно было бы достигать 16 000: 10 = 1600 кг на 1 см2, или 1600 технических атмосфер; такое усилие не раздробляет железа, но безусловно смяло бы конструкцию. Однако подобной глубины современная океанография не знает. Преувеличенные представления о глубинах океана, господствовавшие в эпоху Жюля Верна (роман написан в 1869 г.), объясняются несовершенством способов измерения глубины. В те времена для линь-лота употреблялась не проволока, а пеньковая веревка; такой лот задерживался трением о воду тем сильнее, чем глубже он погружался; на значительной глубине трение возрастало до того, что лот вовсе переставал опускаться, сколько ни травили линь: пеньковая веревка лишь спутывалась, создавая впечатление огромной глубины.
Подводные корабли нашего времени способны выдерживать давление не более 25 атмосфер; это определяет наибольшую глубину их погружения: 250 м. Гораздо большей глубины удалось достигнуть в особом аппарате, названном «батисферой» (рис. 51) и предназначенном специально для изучения фауны океанских пучин. Этот аппарат напоминает, однако, не «Наутилус» Жюля Верна, а фантастическое создание другого романиста — глубоководный шар Уэллса, описанный в рассказе «В морской глубине». Герой этого рассказа спустился до дна океана на глубину 9 км в толстостенном стальном шаре; аппарат погружался без троса, но со съемным грузом; достигнув дна океана, шар освободился здесь от увлекавшего его груза и стремительно взлетел на поверхность воды.
В батисфере ученые достигли глубины более 900 м. Батисфера спускается на тросе с судна, с которым сидящие в шаре поддерживают телефонную связь[36].
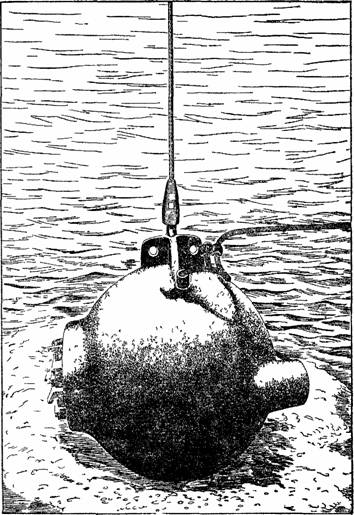Рисунок 51. Стальной шарообразный аппарат «батисфера» для спуска в глубокие слои океана. В этом аппарате Вильям Бийб достиг в 1934 г глубины 923 м. Толщина стенок шара — около 4 см, диаметр 1,5 м, вес 2, 5 тонны.
Техника подъема была всецело основана на применении закона Архимеда. Под корпусом затонувшего судна в грунте морского дна водолазы прорыли 12 туннелей и протянули сквозь каждый из них прочное стальное полотенце. Концы полотенец были прикреплены к понтонам, намеренно потопленным подле ледокола. Вся эта работа выполнена была на глубине 25 м под уровнем моря.
Понтонами (рис. 52) служили полые непроницаемые железные цилиндры 11 м длиной и 5,5 м в диаметре. Порожний понтон весил 50 тонн. По правилам геометрии легко вычислить его объем: около 250 кубометров. Ясно, что такой цилиндр порожняком должен плавать на воде: он вытесняет 250 тонн воды, сам же весит только 50; грузоподъемность его равна разности между 250 и 50, т. е. 200 тонн. Чтобы заставить понтон опуститься на дно, его заполняют водой.
Когда (см. рис. 52) концы стальных строп были прочно прикреплены к потопленным понтонам, в цилиндры стали с помощью шлангов нагнетать сжатый воздух. На глубине 25 м вода давит с силой 25/10 + 1, т. е. 3,5 атмосферы. Воздух же подавался в цилиндры под давлением около 4 атмосфер и, следовательно, должен был вытеснять воду из понтонов. Облегченные цилиндры с огромной силою выталкивались окружающей водою на поверхность моря. Они всплывали в воде, как аэростат в воздухе. Совместная подъемная их сила при полном вытеснении из них воды равнялась бы 200 х 12, т. е. 2400 тонн. Это превышает вес затонувшего «Садко», так что ради более плавного подъема понтоны были освобождены от воды только частично.
Рисунок 52. Схема подъема «Садко»; показан разрез ледокола, понтоны и стропы.
Тем не менее подъем осуществлен был лишь после нескольких неудачных попыток. «Четыре аварии терпела на нем спасательная партия, пока добилась успеха, — пишет руководивший работами главный корабельный инженер ЭПРОН Т. И. Бобрицкий[37]. — Три раза, напряженно ожидая судна, мы видели вместо поднимающегося ледокола стихийно вырывающиеся наверх, в хаосе волн и пены, понтоны и разорванные, змеями извивающиеся шланги. Два раза показывался и снова исчезал в пучине моря ледокол, прежде чем всплыл и окончательно удержался на поверхности».
Как же действует эта установка? Каждый, знакомый с законом Архимеда, сообразит, что ящики, находясь в воде, будут стремиться всплыть вверх. Их увлекает вверх сила, равная весу воды, вытесняемой ящиками, т. е. весу одного кубического метра воды, повторенному столько раз, сколько ящиков погружено в воду. Из рисунков видно, что в воде оказывается всегда шесть ящиков. Значит, сила, увлекающая погруженные ящики вверх, равна весу 6 м3 воды, т. е. 6 тоннам. Вниз же их тянет собственный вес ящиков, который, однако, уравновешивается грузом из шести ящиков, свободно свисающих на наружной стороне каната.
Итак, канат, перекинутый указанным образом, будет всегда подвержен тяге в 6 тонн, приложенной к одной его стороне и направленной вверх. Ясно, что сила эта заставит канат безостановочно вращаться, скользя по шкивам, и при каждом обороте совершать работу в 6000 * 20 = 120 000 кгм.
Теперь понятно, что если усеять страну такими башнями, то мы сможем получать от них безграничное количество работы, достаточное для покрытия всех нужд народного хозяйства. Башни будут вращать якоря динамомашин и давать электрическую энергию в любом количестве.
Однако если разобраться внимательно в этом проекте, то легко убедиться, что ожидаемого движения каната происходить вовсе не должно.
Чтобы бесконечный канат вращался, ящики должны входить в водяной бассейн башни снизу и покидать его сверху. Но ведь, вступая в бассейн, ящик должен преодолеть давление столба воды в 20 м высотой! Это давление на квадратный метр площади ящика равно ни много, ни мало двадцати тоннам (весу 20м3 воды). Тяга же вверх составляет всего только 6 тонн, т. е. явно недостаточна, чтобы втащить ящик в бассейн.
Среди многочисленных образчиков водяных «вечных» двигателей, сотни которых придуманы были изобретателями-неудачниками, можно найти очень простые и остроумные варианты.
Рисунок 53. Проект мнимого «вечного» водяного двигателя.
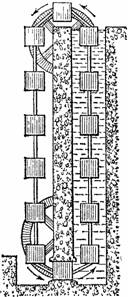Рисунок 54. Уcтpoйствo башни предыдущего рисунка.
Взгляните на рис. 55. Часть деревянного барабана, укрепленного на оси, все время погружена в воду. Если справедлив закон Архимеда, то погруженная в воду часть должна всплывать и, коль скоро выталкивающая сила больше силы трения на оси барабана, вращение никогда не прекратится…
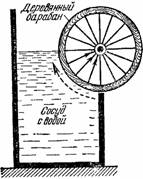Рисунок 55. Еще один проект «вечного» водяного двигателя.
Не спешите с постройкой этого «вечного» двигателя! Вас непременно постигнет неудача: барабан не сдвинется с места. В чем же дело, в чем ошибка наших рассуждений? Оказывается, мы не учли направления действующих сил. А направлены они будут всегда по перпендикуляру к поверхности барабана, т. е. по радиусу к оси. Из повседневного опыта каждый знает, что невозможно заставить колесо вращаться, прикладывая усилия вдоль радиуса колеса. Чтобы вызвать вращение, надо приложить усилие перпендикулярно к радиусу, т. е. по касательной к окружности колеса. Теперь уже нетрудно понять, почему и в этом случае закончится неудачей попытка осуществить «вечное» движение.
Закон Архимеда давал соблазнительную пищу уму искателей «вечного» двигателя и побуждал придумывать хитроумные приспособления для использования кажущейся потери веса в целях получения вечного источника механической энергии.
«Такой пар я назвал газ, потому что он почти не отличается от хаоса древних» (первоначальный смысл слова «хаос» — сияющее пространство).
Однако повое словечко долго после этого не употреблялось и было возрождено лишь знаменитым Лавуазье в 1789 г. Оно получило широкое распространение, когда всюду заговорили о полетах братьев Монгольфье на первых воздушных шарах.
Ломоносов в своих сочинениях употреблял другое наименование для газообразных тел — «упругие жидкости» (остававшееся в употреблении еще и тогда, когда я учился в школе). Заметим, кстати, что Ломоносову принадлежит заслуга введения в русскую речь ряда названий, ставших теперь стандартными словами научного языка:
атмосфера
манометр
барометр
микрометр
воздушный насос
оптика, оптический
вязкость
э (е) лектрический
кристаллизация
э (е) фир
материя
и др.
Гениальный родоначальник русского естествознания писал по этому поводу: «Принужден я был искать слов для наименования некоторых физических инструментов, действий и натуральных вещей, которые (т. е. слова) хотя сперва покажутся несколько странны, однако надеюсь, что они со временем через употребление знакомее будут».
Как мы знаем, надежды Ломоносова вполне оправдались.
Напротив, предложенные впоследствии В. И. Далем (известным составителем «Толкового словаря») слова для замены «атмосферы» — неуклюжие «мироколица» или «колоземица» — совершенно не привились, как не привился его «небозём» вместо горизонта и другие новые слова.
Казалось бы, здесь детски-простая арифметическая задача: один стакан вытекает в 0,5 минуты, — значит, 30 стаканов выльются в 15 минут.
Но сделайте опыт. Окажется, что самовар опоражнивается не в четверть часа, как вы ожидали, а в полчаса.
В чем же дело? Ведь расчет так прост!
Прост, но неверен. Нельзя думать, что скорость истечения с начала до конца остается одна и та же. Когда первый стакан вытек из самовара, струя течет уже под меньшим давлением, так как уровень воды в самоваре понизился; понятно, что второй стакан наполнится в больший срок, чем в полминуты; третий вытечет еще ленивее, и т. д.
Скорость истечения всякой жидкости из отверстия в открытом сосуде находится в прямой зависимости от высоты столба жидкости, стоящего над отверстием. Гениальный Торичелли, ученик Галилея, первый указал на эту зависимость и выразил ее простой формулой:
где v — скорость истечения, g — ускорение силы тяжести, a h — высота уровня жидкости над отверстием. Из этой формулы следует, что скорость вытекающей струи совершенно не зависит от плотности жидкости: легкий спирт и тяжеловесная ртуть при одинаковом уровне вытекают из отверстия одинаково быстро (рис. 56). Из формулы видно, что на Луне, где сила тяжести в 6 раз меньше, чем на Земле, потребовалось бы для наполнения стакана примерно в 2,5 раза больше времени, нежели на Земле.
Но возвратимся к нашей задаче. Если после истечения из самовара 20 стаканов уровень воды в нем (считая от отверстия крана) понизился в четыре раза, то 21-й стакан наполнится вдвое медленнее, чем 1-й. И если в дальнейшем уровень воды понизится в 9 раз, то для наполнения последних стаканов понадобится уже втрое больше времени, чем для наполнения первого. Все знают, как вяло вытекает вода из крана самовара, который уже почти опорожнен. Решая эту задачу приемами высшей математики, можно доказать, что время, нужное на полное опорожнение сосуда, с два раза больше срока, в течение которого вылился бы такой же объем жидкости при неизменном первоначальном уровне.
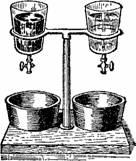Рисунок 56. Что скорее выльется: ртуть или спирт? Уровень жидкости в сосудах одинаков.
«В бассейн проведены две трубы. Через одну первую пустой бассейн может наполниться в 5 часов; через одну вторую полный бассейн может опорожниться в 10 часов. Во сколько часов наполнится пустой бассейн, если открыть обе трубы сразу?»
Задачи этого рода имеют почтенную давность — без малого 20 веков, восходя к Герону Александрийскому. Вот одна из героновых задач, — не столь, правда, замысловатая, как ее потомки:
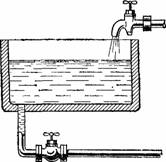Рисунок 57. Задача о бассейне.
Между тем это вполне осуществимо. Банка, изображенная на рис. 58, — именно такой удивительный сосуд. Это обыкновенная банка с узким горлом, через пробку которой вдвинута стеклянная трубка. Если вы откроете кран С ниже конца трубки, то жидкость будет литься из него неослабевающей струёй до тех пор, пока уровень воды не опустится в сосуде до нижнего конца трубки. Вдвинув трубку почти до уровня крана, вы можете заставить всю жидкость, находящуюся выше уровня отверстия, вытечь равномерной, хотя и очень слабой струёй.
Участник знаменитого перехода «Сибирякова» в 1932 г., моряк-полярник Н. Марков, так описывает работу этого ледокола:
«Среди сотен ледяных скал, среди сплошного покрова льда „Сибиряков“ начал битву. Пятьдесят два часа подряд стрелка машинного телеграфа прыгала от „полного назад“ к „полному вперед“. Тринадцать четырехчасовых морских вахт „Сибиряков“ с разгона врезался в лед, крошил его носом, влезал на лед, ломал его и снова отходил назад. Лед, толщиной в три четверти метра, с трудом уступал дорогу. С каждым ударом пробивались на треть корпуса».
Самыми крупными и мощными в мире ледоколами располагает СССР.
Где находятся затонувшие суда?
Распространено мнение, — даже среди моряков, — будто суда, затонувшие в океане, не достигают морского дна, а висят недвижно на некоторой глубине, где вода «соответственно уплотнена давлением вышележащих слоев».Мнение это разделял, по-видимому, даже автор «20 тысяч лье под водой»; в одной из глав этого романа Жюль Верн описывает неподвижно висящее в воде затонувшее судно, а в другой упоминает о кораблях, «догнивающих, свободно вися в воде».
Правильно ли подобное утверждение?
Некоторое основание для него, как будто, имеется, так как давление воды в глубинах океана действительно достигает огромных степеней. На глубине 10 м вода давит с силой 1 кг на 1 см2 погруженного тела. На глубине 20 м это давление равно уже 2 кг, на глубине 100 м — 10 кг, 1000 м — 100 кг. Океан же во многих местах имеет глубину в несколько километров, достигая в самых глубоких частях Великого океана более 11 км (Марианская впадина). Легко вычислить, какое огромное давление должны испытывать вода и погруженные в нее предметы на этих огромных глубинах.
Если порожнюю закупоренную бутылку опустить на значительную глубину и затем извлечь вновь, то обнаружится, что давление воды вогнало пробку внутрь бутылки и вся посудина полна воды. Знаменитый океанограф Джон Меррей в своей книге «Океан» рассказывает, что был проделан такой опыт: три стеклянные трубки различных размеров, с обоих концов запаянные, были завернуты в холст и помещены в медный цилиндр с отверстиями для свободного пропуска воды. Цилиндр был спущен на глубину 5 км. Когда его извлекли оттуда, оказалось, что холст наполнен снегообразной массой: это было раздробленное стекло. Куски дерева, опущенные на подобную глубину, после извлечения тонули в воде, как кирпич, — настолько они были сдавлены.
Естественно, казалось бы, ожидать, что столь чудовищное давление должно настолько уплотнить воду на больших глубинах, что даже тяжелые предметы не будут в ней тонуть, как не тонет железная гиря в ртути.
Однако подобное мнение совершенно не обосновано. Опыт показывает, что вода, как и все вообще жидкости, мало поддается сжатию. Сдавливаемая с силой 1 кг на 1 см2 вода сжимается всего только на 1/22 000 долю своего объема и примерно так же сжимается при дальнейшем возрастании давления на каждый килограмм. Если бы мы пожелали довести воду до такой плотности, чтобы в ней плавало железо, необходимо было бы уплотнить ее в 8 раз. Между тем для уплотнения только вдвое, т. е. для сокращения объема наполовину, необходимо давление в 11 000 кг на 1 см2 (если бы только упомянутая мера сжатия имела место для таких огромных давлений). Это соответствует глубине 110 км под уровнем океана!
Отсюда ясно, что говорить о сколько-нибудь заметном уплотнении воды в глубине океанов совершенно не приходится. В самом глубоком их место вода уплотнена лишь на 1100/22000, т. е. на 1/20 нормальной своей плотности, всего на 5%[34]. Это почти не может повлиять на условия плавания в ней различных тел, — тем более, что твердые предметы, погруженные в такую воду, также подвергаются этому давлению и, следовательно, тоже уплотняются.
Не может быть поэтому ни малейшего сомнения в том, что затонувшие суда покоятся на дне океана. «Все, что тонет в стакане воды, — говорит Меррей, — должно пойти ко дну и в самом глубоком океане».
Мне приходилось слышать против этого такое возражение. Если осторожно погрузить стакан вверх дном в воду, он может остаться в этом положении, так как будет вытеснять объем воды, весящий столько же, сколько стакан. Более тяжелый металлический стакан может удержаться в подобном положении и ниже уровня воды, не опускаясь на дно. Точно так же, будто бы, может остановиться на полпути и опрокинутый вверх килем крейсер или другое судно. Если в некоторых помещениях судна воздух окажется плотно запертым, то судно погрузится на определенную глубину и там остановится.
Не мало ведь судов идет ко дну в перевернутом состоянии — и возможно, что некоторые из них так и не достигают дна, оставаясь висеть в темных глубинах океана. Достаточно было бы легкого толчка, чтобы вывести такое судно из равновесия, перевернуть, наполнить водою и заставить упасть на дно, — по откуда взяться толчкам в глубине океана, где вечно царит тишина и спокойствие и куда не проникают даже отголоски бурь?
Все эти доводы основаны на физической ошибке. Перевернутый стакан не погружается в воду сам — его надо внешней силой погрузить в воду, как кусок дерева или пустую закупоренную бутылку. Точно так же и опрокинутый килем вверх корабль вовсе и не начнет тонуть, а останется на поверхности воды. Очутиться на полпути между уровнем океана и его дном он никак не может.
Как осуществились мечты Жюля Верна и Уэллса
Реальные подводные лодки нашего времени в некоторых отношениях не только догнали фантастический «Наутилус» Жюля Верпа, но даже превзошли его. Правда, скорость хода нынешних подводных крейсеров вдвое меньше быстроты «Наутилуса»: 24 узла против 50 у Жюля Верна (узел — около 1,8 км в час). Самый длинный переход современного подводного корабля — кругосветное путешествие, между тем как капитан Немо совершил поход вдвое длиннее. Зато «Наутилус» обладал водоизмещением только в 1500 тонн, имел на борту команду всего из двух-трех десятков человек и способен был оставаться под водой без перерыва не более сорока восьми часов. Подводный крейсер «Сюркуф», построенный в 1929 г. и принадлежавший французскому флоту, имел 3200 тонн водоизмещения, управлялся командой из ста пятидесяти человек и способен был держаться под водой, не всплывая, до ста двадцати часов[35].Переход от портов Франции до острова Мадагаскара этот подводный крейсер мог совершать, не заходя по пути ни в один порт. По комфортабельности жилых помещений «Сюркуф», быть может, не уступал «Наутилусу». Далее, «Сюркуф» имел перед кораблем капитана Немо и то несомненное преимущество, что на верхней палубе крейсера устроен был водонепроницаемый ангар для разведывательного гидросамолета. Отметим также, что Жюль Верн не снабдил «Наутилус» перископом, дающим лодке возможность обозревать горизонт из-под воды.
В одном лишь отношении реальные подводные корабли долю еще будут далеко отставать от создания фантазии французского романиста: в глубине погружения. Однако приходится отметить, что в этом пункте фантазия Жюля Верна перешла границы правдоподобия. «Капитан Немо, — читаем в одном месте романа, — достигал глубины в три, четыре, пять, семь, девять и десять тысяч метров под поверхностью океана». А однажды «Наутилус» опустился даже на небывалую глубину — в 16 тысяч метров! «Я чувствовал, — рассказывает герой романа, — как содрогаются скрепы железной обшивки подводного судна, как изгибаются его распоры, как подаются внутрь окна, уступая давлению воды Если бы корабль наш не обладал прочностью сплошною литого тела, его мгновенно сплющило бы в лепешку».
Опасение вполне уместное, потому что на глубине 16 км (если бы такая глубина имелась в океане) давление воды должно было бы достигать 16 000: 10 = 1600 кг на 1 см2, или 1600 технических атмосфер; такое усилие не раздробляет железа, но безусловно смяло бы конструкцию. Однако подобной глубины современная океанография не знает. Преувеличенные представления о глубинах океана, господствовавшие в эпоху Жюля Верна (роман написан в 1869 г.), объясняются несовершенством способов измерения глубины. В те времена для линь-лота употреблялась не проволока, а пеньковая веревка; такой лот задерживался трением о воду тем сильнее, чем глубже он погружался; на значительной глубине трение возрастало до того, что лот вовсе переставал опускаться, сколько ни травили линь: пеньковая веревка лишь спутывалась, создавая впечатление огромной глубины.
Подводные корабли нашего времени способны выдерживать давление не более 25 атмосфер; это определяет наибольшую глубину их погружения: 250 м. Гораздо большей глубины удалось достигнуть в особом аппарате, названном «батисферой» (рис. 51) и предназначенном специально для изучения фауны океанских пучин. Этот аппарат напоминает, однако, не «Наутилус» Жюля Верна, а фантастическое создание другого романиста — глубоководный шар Уэллса, описанный в рассказе «В морской глубине». Герой этого рассказа спустился до дна океана на глубину 9 км в толстостенном стальном шаре; аппарат погружался без троса, но со съемным грузом; достигнув дна океана, шар освободился здесь от увлекавшего его груза и стремительно взлетел на поверхность воды.
В батисфере ученые достигли глубины более 900 м. Батисфера спускается на тросе с судна, с которым сидящие в шаре поддерживают телефонную связь[36].
Как был поднят «Садко»?
В широком просторе океана гибнут ежегодно тысячи крупных и мелких судов, особенно в военное время. Наиболее ценные и доступные из затонувших кораблей стали извлекать со дна моря. Советские инженеры и водолазы, входящие в состав ЭПРОН (т. е. «Экспедиции подводных работ особого назначения»), прославились на весь мир успешным подъемом более чем 150 крупных судов. Среди них одно из самых больших — ледокол «Садко», затонувший на Белом море в 1916 г. из-за халатности капитана. Пролежав на морском дне 17 лет, этот превосходный ледокол был поднят работниками ЭПРОН и вступил опять в строй.Техника подъема была всецело основана на применении закона Архимеда. Под корпусом затонувшего судна в грунте морского дна водолазы прорыли 12 туннелей и протянули сквозь каждый из них прочное стальное полотенце. Концы полотенец были прикреплены к понтонам, намеренно потопленным подле ледокола. Вся эта работа выполнена была на глубине 25 м под уровнем моря.
Понтонами (рис. 52) служили полые непроницаемые железные цилиндры 11 м длиной и 5,5 м в диаметре. Порожний понтон весил 50 тонн. По правилам геометрии легко вычислить его объем: около 250 кубометров. Ясно, что такой цилиндр порожняком должен плавать на воде: он вытесняет 250 тонн воды, сам же весит только 50; грузоподъемность его равна разности между 250 и 50, т. е. 200 тонн. Чтобы заставить понтон опуститься на дно, его заполняют водой.
Когда (см. рис. 52) концы стальных строп были прочно прикреплены к потопленным понтонам, в цилиндры стали с помощью шлангов нагнетать сжатый воздух. На глубине 25 м вода давит с силой 25/10 + 1, т. е. 3,5 атмосферы. Воздух же подавался в цилиндры под давлением около 4 атмосфер и, следовательно, должен был вытеснять воду из понтонов. Облегченные цилиндры с огромной силою выталкивались окружающей водою на поверхность моря. Они всплывали в воде, как аэростат в воздухе. Совместная подъемная их сила при полном вытеснении из них воды равнялась бы 200 х 12, т. е. 2400 тонн. Это превышает вес затонувшего «Садко», так что ради более плавного подъема понтоны были освобождены от воды только частично.
Тем не менее подъем осуществлен был лишь после нескольких неудачных попыток. «Четыре аварии терпела на нем спасательная партия, пока добилась успеха, — пишет руководивший работами главный корабельный инженер ЭПРОН Т. И. Бобрицкий[37]. — Три раза, напряженно ожидая судна, мы видели вместо поднимающегося ледокола стихийно вырывающиеся наверх, в хаосе волн и пены, понтоны и разорванные, змеями извивающиеся шланги. Два раза показывался и снова исчезал в пучине моря ледокол, прежде чем всплыл и окончательно удержался на поверхности».
«Вечный» водяной двигатель
Среди множества проектов «вечного двигателя» было немало и таких, которые основаны на всплывании тел в воде. Высокая башня в 20 м высоты наполнена водой. Наверху и внизу башни установлены шкивы, через которые перекинут прочный канат в виде бесконечного ремня. К канату прикреплено 14 полых кубических ящиков в метр высоты, склепанных из железных листов так, что внутрь ящиков вода проникнуть не может. Наши рис. 53 и 54 изображают внешний вид такой башни и ее продольный разрез.Как же действует эта установка? Каждый, знакомый с законом Архимеда, сообразит, что ящики, находясь в воде, будут стремиться всплыть вверх. Их увлекает вверх сила, равная весу воды, вытесняемой ящиками, т. е. весу одного кубического метра воды, повторенному столько раз, сколько ящиков погружено в воду. Из рисунков видно, что в воде оказывается всегда шесть ящиков. Значит, сила, увлекающая погруженные ящики вверх, равна весу 6 м3 воды, т. е. 6 тоннам. Вниз же их тянет собственный вес ящиков, который, однако, уравновешивается грузом из шести ящиков, свободно свисающих на наружной стороне каната.
Итак, канат, перекинутый указанным образом, будет всегда подвержен тяге в 6 тонн, приложенной к одной его стороне и направленной вверх. Ясно, что сила эта заставит канат безостановочно вращаться, скользя по шкивам, и при каждом обороте совершать работу в 6000 * 20 = 120 000 кгм.
Теперь понятно, что если усеять страну такими башнями, то мы сможем получать от них безграничное количество работы, достаточное для покрытия всех нужд народного хозяйства. Башни будут вращать якоря динамомашин и давать электрическую энергию в любом количестве.
Однако если разобраться внимательно в этом проекте, то легко убедиться, что ожидаемого движения каната происходить вовсе не должно.
Чтобы бесконечный канат вращался, ящики должны входить в водяной бассейн башни снизу и покидать его сверху. Но ведь, вступая в бассейн, ящик должен преодолеть давление столба воды в 20 м высотой! Это давление на квадратный метр площади ящика равно ни много, ни мало двадцати тоннам (весу 20м3 воды). Тяга же вверх составляет всего только 6 тонн, т. е. явно недостаточна, чтобы втащить ящик в бассейн.
Среди многочисленных образчиков водяных «вечных» двигателей, сотни которых придуманы были изобретателями-неудачниками, можно найти очень простые и остроумные варианты.
Взгляните на рис. 55. Часть деревянного барабана, укрепленного на оси, все время погружена в воду. Если справедлив закон Архимеда, то погруженная в воду часть должна всплывать и, коль скоро выталкивающая сила больше силы трения на оси барабана, вращение никогда не прекратится…
Не спешите с постройкой этого «вечного» двигателя! Вас непременно постигнет неудача: барабан не сдвинется с места. В чем же дело, в чем ошибка наших рассуждений? Оказывается, мы не учли направления действующих сил. А направлены они будут всегда по перпендикуляру к поверхности барабана, т. е. по радиусу к оси. Из повседневного опыта каждый знает, что невозможно заставить колесо вращаться, прикладывая усилия вдоль радиуса колеса. Чтобы вызвать вращение, надо приложить усилие перпендикулярно к радиусу, т. е. по касательной к окружности колеса. Теперь уже нетрудно понять, почему и в этом случае закончится неудачей попытка осуществить «вечное» движение.
Закон Архимеда давал соблазнительную пищу уму искателей «вечного» двигателя и побуждал придумывать хитроумные приспособления для использования кажущейся потери веса в целях получения вечного источника механической энергии.
Кто придумал слова «газ» и «атмосфера»?
Слово «газ» принадлежит к числу слов, придуманных учеными наряду с такими словами, как «термометр», «электричество», «гальванометр», «телефон» и прежде всего «атмосфера». Из всех придуманных слов «газ» — безусловно самое короткое. Старинный голландский химик и врач Гельмонт, живший с 1577 по 1644 г. (современник Галилея), произвел «газ» от греческого слова «хаос». Открыв, что воздух состоит из двух частей, из которых одна поддерживает горение и сгорает, остальная же часть не обладает этими свойствами, Гельмонт писал:«Такой пар я назвал газ, потому что он почти не отличается от хаоса древних» (первоначальный смысл слова «хаос» — сияющее пространство).
Однако повое словечко долго после этого не употреблялось и было возрождено лишь знаменитым Лавуазье в 1789 г. Оно получило широкое распространение, когда всюду заговорили о полетах братьев Монгольфье на первых воздушных шарах.
Ломоносов в своих сочинениях употреблял другое наименование для газообразных тел — «упругие жидкости» (остававшееся в употреблении еще и тогда, когда я учился в школе). Заметим, кстати, что Ломоносову принадлежит заслуга введения в русскую речь ряда названий, ставших теперь стандартными словами научного языка:
атмосфера
манометр
барометр
микрометр
воздушный насос
оптика, оптический
вязкость
э (е) лектрический
кристаллизация
э (е) фир
материя
и др.
Гениальный родоначальник русского естествознания писал по этому поводу: «Принужден я был искать слов для наименования некоторых физических инструментов, действий и натуральных вещей, которые (т. е. слова) хотя сперва покажутся несколько странны, однако надеюсь, что они со временем через употребление знакомее будут».
Как мы знаем, надежды Ломоносова вполне оправдались.
Напротив, предложенные впоследствии В. И. Далем (известным составителем «Толкового словаря») слова для замены «атмосферы» — неуклюжие «мироколица» или «колоземица» — совершенно не привились, как не привился его «небозём» вместо горизонта и другие новые слова.
Как будто простая задача
Самовар, вмещающий 30 стаканов, полон воды. Вы подставляете стакан под его кран и с часами в руках следите по секундной стрелке, во сколько времени стакан наполняется до краев. Допустим, что в полминуты. Теперь зададим вопрос: во сколько времени опорожнится весь самовар, если оставить кран открытым?Казалось бы, здесь детски-простая арифметическая задача: один стакан вытекает в 0,5 минуты, — значит, 30 стаканов выльются в 15 минут.
Но сделайте опыт. Окажется, что самовар опоражнивается не в четверть часа, как вы ожидали, а в полчаса.
В чем же дело? Ведь расчет так прост!
Прост, но неверен. Нельзя думать, что скорость истечения с начала до конца остается одна и та же. Когда первый стакан вытек из самовара, струя течет уже под меньшим давлением, так как уровень воды в самоваре понизился; понятно, что второй стакан наполнится в больший срок, чем в полминуты; третий вытечет еще ленивее, и т. д.
Скорость истечения всякой жидкости из отверстия в открытом сосуде находится в прямой зависимости от высоты столба жидкости, стоящего над отверстием. Гениальный Торичелли, ученик Галилея, первый указал на эту зависимость и выразил ее простой формулой:
Но возвратимся к нашей задаче. Если после истечения из самовара 20 стаканов уровень воды в нем (считая от отверстия крана) понизился в четыре раза, то 21-й стакан наполнится вдвое медленнее, чем 1-й. И если в дальнейшем уровень воды понизится в 9 раз, то для наполнения последних стаканов понадобится уже втрое больше времени, чем для наполнения первого. Все знают, как вяло вытекает вода из крана самовара, который уже почти опорожнен. Решая эту задачу приемами высшей математики, можно доказать, что время, нужное на полное опорожнение сосуда, с два раза больше срока, в течение которого вылился бы такой же объем жидкости при неизменном первоначальном уровне.
Задача о бассейне
От сказанного один шаг к пресловутым задачам о бассейне, без которых не обходится ни один арифметический и алгебраический задачник. Всем памятны классически-скучные, схоластические задачи вроде следующей:«В бассейн проведены две трубы. Через одну первую пустой бассейн может наполниться в 5 часов; через одну вторую полный бассейн может опорожниться в 10 часов. Во сколько часов наполнится пустой бассейн, если открыть обе трубы сразу?»
Задачи этого рода имеют почтенную давность — без малого 20 веков, восходя к Герону Александрийскому. Вот одна из героновых задач, — не столь, правда, замысловатая, как ее потомки:
Две тысячи лет решаются задачи о бассейнах и — такова сила рутины! — две тысячи лет решаются неправильно. Почему неправильно — вы поймете сами после того, что сейчас сказано было о вытекании воды. Как учат решать задачи о бассейнах? Первую, например, задачу решают так. В 1 час первая труба наливает 0,2 бассейна, вторая выливает 0,1 бассейна; значит, при действии обоих труб в бассейн ежечасно поступает 0,2 — 0,1 = 0,1 откуда для времени наполнения бассейна получается 10 часов. Это рассуждение неверно: если втекание воды можно считать происходящим под постоянным давлением и, следовательно, равномерным, то ее вытекание происходит при изменяющемся уровне и, значит, неравномерно. Из того, что второй трубой бассейн опоражнивается в 10 часов, вовсе не следует, что ежечасно вытекает 0,1 доля бассейна; школьный прием решения, как видим, ошибочен. Решить задачу правильно средствами элементарной математики нельзя, а потому задачам о бассейне (с вытекающей водой) вовсе не место в арифметических задачниках[38].
Четыре фонтана дано. Обширный дан водоем.
За сутки первый фонтан до краев его наполняет.
Два дня и две ночи второй над тем же должен работать.
Третий втрое, чем первый, слабей.
В четверо суток последний за ним поспевает.
Ответить мне, скоро ли будет он полон,
Если во время одно все их открыть?
Удивительный сосуд
Возможно ли устроить такой сосуд, из которого вода вытекала бы все время равномерной струёй, не замедляя своего течения, несмотря на то, что уровень жидкости понижается? После того, что вы узнали из предыдущих статей, вы, вероятно, готовы счесть подобную задачу неразрешимой.Между тем это вполне осуществимо. Банка, изображенная на рис. 58, — именно такой удивительный сосуд. Это обыкновенная банка с узким горлом, через пробку которой вдвинута стеклянная трубка. Если вы откроете кран С ниже конца трубки, то жидкость будет литься из него неослабевающей струёй до тех пор, пока уровень воды не опустится в сосуде до нижнего конца трубки. Вдвинув трубку почти до уровня крана, вы можете заставить всю жидкость, находящуюся выше уровня отверстия, вытечь равномерной, хотя и очень слабой струёй.