161 E. 80 r.
Положение «тяжесть тем быстрее движется, чем дольше падает» является 5-м в сочинении о тяжести (Opusculum de ponderositate), приписываемом знаменитому механику Средневековья Иордану из Неморы (XII в.) и изданном Курцием Траяном в Венеции в 1565 г. Дюэм предполагал, что в этом произведении объединены сочинения трех авторов: Иордана, анонимного «предшественника Леонардо» и анонимного «предшественника Стевина». Однако Марколонго (1932) считает возможным приписать его целиком Иордану. «Предшественник Леонардо» (или Иордан) утверждает, что тяжелое тело, падающее в воздухе, увлекает находящийся за ним воздух и толкает воздух, находящийся впереди; от этого сопротивление воздуха убывает, а «тяжесть» становится больше; среда получает все больший импульс и начинает не только испытывать действие падающей тяжести, но и увлекать ее.
Воздух, облекающий тела, движется ли вместе с этими телами? Воздух, окружающий тела, движется вместе с этими телами, что показывает нам опыт, когда конь бежит по пыльным дорогам.
Движение воздуха быстрее ли того, что приводит его в движение? Воздух никогда не будет равной скорости с тем, что приводит его в движение, и это показывают нам движения уже названной, следующей за бегом коня пыли, которая в кратчайший промежуток движения поворачивает назад вихревым движением и в нем расточает до конца свой импульс.
162 H2. 6 r.
Характерное для Леонардо переплетение абстрактно-объяснительных и чувственно-наглядных моментов.
Верхняя вода будет более быстро опускаться, чем нижняя.
163 Т. А. V, 5.
Ср. Т. А. V, 4.
Во всяком течении воды вблизи ее падения изгиб склона начнется раньше на поверхности, чем на дне. Доказывается предыдущим, так как если верхняя вода аb быстрее нижней cd, то вода еа будет быстрее увлекаема водою ab, нежели вода fс водою cd, и, следовательно, изгиб склона ранее начнется на поверхности, в точке g, нежели на дне, где он начинается в точке с.

164 С. А. 126 v. а.
Доказывается предыдущим – см. предыдущий отрывок.
Спрашивается здесь: если сосуд будет продырявлен на дне равными отверстиями наподобие решета, то какое из отверстий выльет больше воды в равный промежуток времени? Ты так поступишь для проверки на опыте и установления правила. Открывай одно отверстие зараз и определяй, сколько весит вода, вытекшая с высоты одного локтя – или большей, или меньшей, как угодно, – и затем закрой его, и то же сделай с другими, закрывая одно за другим те, с которыми ты опыт уже произвел. Но позаботься, чтобы в сосуд доливалась другая вода без всякого толчка, дабы нигде не производить давления на дно принимающего ее сосуда, и чтобы в сосуде этом было по весу всегда столько же воды; и для этого надобно, чтобы сосуд, принимающий воду, был отделен от того, из которого она наливается.
165 F. 53 r.
То же в Т. А. VIII, 2, где имеется следующее заключение: «Сделав вышеуказанный опыт, ты скажешь на основании предыдущего, что отверстие в той части дна, которая более удалена от центра поверхности воды, выльет воды более. И это потому, что она более будет толкаема, как доказано». Ссылка на предыдущее имеет в виду Т. А. VIII, 1, которой соответствует А. 25 v., где читаем: «Всякое жидкое тело, которое будет способно к движению, будет больше ударять и толкать ту часть окружающей его стенки, которая более будет удалена от центра его поверхности – более, чем любая другая часть его сосуда».
У воды, уровень которой не опускается ниже определенной высоты, количество выливающейся через данное отверстие в данное время воды будет таково, какова высота этого отверстия. Я утверждаю, что если b выливает в определенное время определенное количество воды, то с выльет в то же самое время воды вдвое больше; ибо над с тяжесть воды вдвое бóльшая. И соотношения между весами здесь не такие, какие у плотных и цельных предметов, падающих в воздухе, так как вода, ударяя о воздух, делает в нем сплошное отверстие. А вещь плотная и цельная, постепенно опускающаяся в воздухе, рассекает перед собою воздух, который оказывает некоторое сопротивление и потому несколько сгущается и потому не дает прохода движущемуся телу определенной длины, как воде, имеющей длину неопределенную.
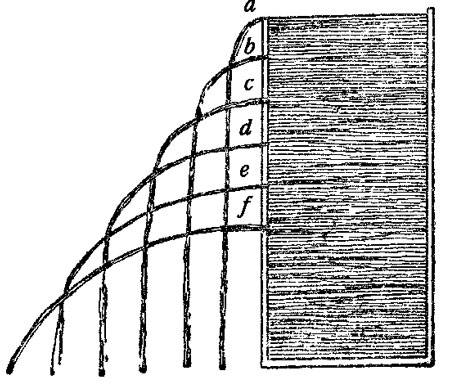
То же в Т. А. VIII, 17. Как известно, истинное соотношение определяется из формулы: Q = µ × ω × 2gH, где Q – расход жидкости, µ – коэффициент расхода, ω – площадь отверстия и H – напор или высота жидкости.
Отсюда
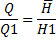
а не
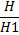
166 А. 59 r.
как утверждает Леонардо.
Что такое пена воды? Вода, которая падает с высоты в другую воду, заключает в себе известное количество воздуха, каковой благодаря удару погружается вместе с нею и вновь быстрым движением взлетает вверх, достигая покинутой поверхности, будучи облеченным тонкой влагой в сферическое тело, распространяясь кругообразно от первого удара.
Или, вернее, вода, которая падает на другую, удаляется от своего места и разнообразными и различными ветвлениями, двоящимися и загибающимися, идет, сплетаясь и переплетаясь, и, когда они отражаются на поверхности воды силою тяжести и удара, этой водой произведенного, у воздуха из-за крайней быстроты нет времени вырваться к своей стихии, но погружается он вышеуказанным способом.
167 I2. 61 r. – 60 v.
То же в Т. А. V, 44. Один из многочисленных гидродинамических отрывков Леонардо с характерным чувственно-наглядным описанием.
Вода, что падает с высоты одного локтя, никогда не вернется на подобную высоту, разве что мелкими каплями, которые взлетят гораздо выше, так как отраженное движение будет гораздо более быстрым, нежели движение падающее. В самом деле, когда вода падает, она погружает вместе с собою большое количество воздуха, и, после того как вода испытала удар, она отскакивает к своей поверхности с импульсом, делающим движение почти столь же быстрым, сколь было движение падения. Однако столь же быстрым не будет оно по причине, указанной во 2-й [главе] 7-й [книги], гласящей: движение отражения никогда не будет столь же быстрым, сколько было падение вещи, которая отражается, и поэтому последующее отражение никогда не будет равно своему предшествующему. Так что отражение, совершаемое водою, уходит от дна, где было произведено, с быстротой не совсем той же, с какой произведено было; но к этому прибавляется вторая скорость, которая это движение увеличивает, и это тот воздух, который погружается вместе с падением воды, воздух, который, будучи облекаем водою, бурно взлетает, и к своей взметается стихии, наподобие ветра, нагнетаемого кузнечным мехом, и с собой уносит последнюю, граничащую с поверхностью, воду, и благодаря такому приращению заставляет ее взметаться гораздо выше, чем она должна бы по своей природе.
168 С. А. 209 v.
То же в Т. А. V, 51, где сравнение с кузнечным мехом отсутствует. В другом отрывке (I2. 21 v. – Т. А. V, 52) Леонардо с обычной для него образностью говорит о воздухе, который выходит из воды, как молния из туч.
Всякое трущееся тело оказывает сопротивление в том месте, где трется, четвертою частью своей тяжести (gravezza).
169 C. A. 198 v.
Из других текстов видно, что Леонардо считал этот коэффициент приблизительным. Для трения дерева о дерево, о камень и о железо, с чем преимущественно приходилось иметь дело, коэффициент в общем правилен.
Трение гладких тел тем меньшего сопротивления будет и тем большей грузности, чем менее наклонно место, по которому совершается движение, – в случае когда движущее находится выше движимого. Трение гладких тел будет тем меньшего сопротивления и грузности, чем менее наклонно место, по которому совершается движение, – в случае когда движущее находится ниже движимого.
Если гладкий наклон располагает гладкое тяжелое тело действовать одною четвертою его тяжести по линии его движения, тогда тяжесть эта сама по себе расположена к движению вниз.
170 F. 56. v.
Наклон плоскости Леонардо измеряет отношением длины к вертикали.
Ему известно также, что составляющая силы тяжести, параллельная плоскости (то, что Леонардо называет «грузностью», или peso), обратно пропорциональна наклону. В первом случае (движущее выше движимого) тело тянут вверх, во втором (движущее ниже движимого) его тянут вниз, следовательно, приложенная сила имеет или противоположный знак с «грузностью», или одинаковый с ней. Таким образом, она вынуждена или преодолевать «грузность», или суммироваться с ней. Вот почему в первом случае «грузность», чем больше наклон, тем больше, во втором тем меньше.
О трении небес, – производит ли оно звук или нет. Всякий звук причиняется воздухом, ударяющимся о плотное тело, и если будет произведен двумя тяжелыми телами совместно, то происходит это благодаря воздуху, который их окружает, и такое трение стирает трущиеся тела. Отсюда следовало бы, что небеса при своем трении, не имея между собою воздуха, звука не произвели бы, и, существуй такое трение в самом деле, за столько столетий, в течение коих эти небеса вращаются, они были бы истерты столь огромной быстротой, совершающейся изо дня в день. И если бы они звук все же производили, то распространяться он не мог бы; ибо звук столкновения и под водой малоощутителен, а в плотных телах мало или совсем не ощущался бы. Кроме того, в гладких телах трение их не производит звука, что равным образом привело бы к отсутствию звука при соприкасании или, вернее, трении небес. И если небеса эти не были отполированы при соприкасании своего трения, следует, что будут они бугристы и шероховаты; поэтому соприкасание их не сплошное, а если так, то образуется пустота, которой, как заключают, в природе нет. Итак, следует, что трение уже стерло бы границы каждого неба и, насколько быстрее движется небо у середины, чем у полюсов, настолько быстрее оно у середины, нежели у полюсов, стиралось бы; а потому больше уже не терлось бы, и звук прекратился бы, и танцоры остановились, разве что небеса вращались бы одно к востоку, а другое к западу.
Дюэм усматривал в этом отрывке, как и во многих других, влияние Альберта Саксонского, у которого читаем, что быстрое движение производит звук при наличии трения, сотрясения воздуха и др. условий; но в небесных телах трения нет, потому что они гладки и ровны, нет также сотрясения воздуха. Гораздо вероятнее, однако, непосредственное влияние Ристоро д’Ареццо (La composizione del mondo, 1282), который также в своей аргументации говорит об отсутствии воздуха и о гладкости небесных тел.
О законах статики
171 C. A. 93 v.
Отрывок 171 подводит нас к проблемам статики: к закону рычага (172—174), понятию статического момента (175—178), вопросам сложения и разложения сил (179—185), блоков и полиспастов (186—190), центру тяжести тел (191), сопротивлению материалов (192—198) и статике сооружений (199), одна из теорем которой находит приложение к «равновесию, или балансированию, людей» (200).
Наука о тяжестях вводима в заблуждение своею практикою, которая во многих частях не находится с этою наукою в согласии, причем и невозможно привести ее к согласию, и это происходит от полюсов весов, благодаря которым создается наука об этих тяжестях, полюсов, которые, по мнению древних философов, были полюсами, имеющими природу математической линии, и в некоторых местах математическими точками – точками и линиями, которые бестелесны; практика же полагает их телесными, потому что так велит необходимость, раз они должны поддерживать груз этих весов вместе с взвешиваемыми на них грузами.
Я нашел, что древние эти ошибались в этом суждении о тяжестях и что ошибка эта произошла оттого, что они в значительной части своей науки пользовались телесными полюсами и в значительной – полюсами математическими, то есть духовными или, вернее, бестелесными.
172 Br. M. I r – I v.
Полюс (polo) – т. е. точка опоры.
Бестелесными – непротяженными, т. е. представляемыми как математическая точка.
Умножь деления рычага на фунты к нему прикрепленного груза и результат раздели на деления противорычага, и частное будет противовес, который, находясь на противорычаге, противится опусканию груза, на указанном рычаге находящегося.
Умножь большее плечо весов на груз, им поддерживаемый, и раздели результат на меньшее плечо, и частное будет груз, который, находясь на меньшем плече, противится опусканию большего плеча в случае равновесия плеч весов.
173 А. 47 r.
Под рычагом Леонардо разумеет то плечо, к которому приложена сила, под противорычагом – второе плечо, к которому приложена другая, противодействующая сила.
Закон рычага был известен уже древним (Аристотель, Архимед).
Тяжесть, привешенная к одному плечу рычага, сделанного из любого материала, во столько раз большую тяжесть поднимает на конце противоположного плеча, во сколько раз одно плечо больше другого.
174 А. 22 v.
Если хочешь, чтобы груз b поднял груз а при равных плечах весов, необходимо, чтобы b было тяжелее а. Если бы ты захотел, чтобы груз d поднял груз с, более тяжелый, чем он, нужно было бы заставить его при опускании совершить более длинный путь, нежели путь, совершаемый с при подъеме; и, если он опускается больше, следует, что плечо весов, опускающееся с ним, должно быть длиннее другого. И если бы ты захотел, чтобы незначительный груз f поднял большой е, грузу пришлось бы двигаться по более длинному пути и быстрее, нежели грузу е.
175 Е. 72 v.
Чертеж не приводится ввиду ясности рассуждения.
Отношение между пространством mn и пространством nb то же, что между весом, опустившимся в d, и весом, которым обладало это d в положении b.
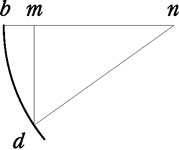
176 А. 45 r.
То же отношение, которое будет между длиною рычага и противорычага, найдешь ты и в их грузах, и, сходно, в медленности движения, и в пути, совершаемом их концами, когда они достигают постоянной высоты своего полюса.
177 Ash. I, 3 r.
Эту проекцию плеча рычага на горизонталь, проходящую через точку опоры рычага, Леонардо называет потенциальным рычагом, в отличие от самого плеча, которое он называет рычагом реальным. Отношение, о котором он говорит здесь и в следующем отрывке, есть отношение обратной пропорциональности.
Когда они достигают постоянной высоты... – т. е. когда они достигают положения равновесия.
В каком отношении линия сb будет находиться к линии ас, в таком будет находиться вес и длина cm к весу cn.
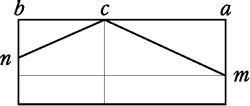
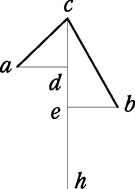
Многими исследователями указывалось, что здесь Леонардо формулирует понятие статического момента относительно точки, являющегося произведением силы на перпендикуляр, опущенный из данной точки на направление силы. Другие обращали, однако, внимание на то, что Леонардо пользуется не произведением груза на «потенциальный рычаг», а отношениями между теми и другими, т. е. понятием момента в чистом виде еще не пользуется. Аналогичные леонардовским понятия встречаем уже у Иордана и в Opusculum de ponderositate (о нем см. примеч. 160), который формулирует свои положения приблизительно так: если у коленчатого рычага асb (см. чертеж) на обоих концах находятся неравные грузы, то он примет такое положение, что расстояния точек a и b от вертикали ch, проведенной через точку опоры, окажутся в обратном отношении к величине грузов, в этих точках находящихся. Подобный же чертеж имеется в приведенном отрывке Леонардо.
178 Вr. М. 1 v.
По 6-й [главе] 9-й [книги], тяжесть распределяется между реальными плечами весов не в том отношении, какое существует между этими плечами, но в отношении, какое имеют между собою потенциальные плечи.
Конец бесплатного ознакомительного фрагмента
