71 S. K. M. III, 43 v.
Необходимость – наставница и пестунья природы. Необходимость – тема и изобретательница природы, и узда, и вечный закон.
72 С. А. 112 v.
И столь природа усладительна и неистощима в разнообразии, что среди деревьев одной и той же породы ни одного не найдется растения, которое вполне походило бы на другое, и не только растения, но и ветвей, и листьев, и плода не найдется ни одного, который бы в точности походил на другой.
73 S. K. M. III, 20 v.
Яркой параллелью к мысли о неистощимом разнообразии природы могут служить многочисленные наблюдения Леонардо над растительным миром, собранные в «Трактате о живописи» и обнаруживающие его стремление охватить растительное многообразие во всех его бесконечных и неисчерпаемых особенностях.
Кажется, что здесь природа для многих животных была скорее мачехой жестокой, нежели матерью, а для некоторых не мачехой, а матерью сердобольной.
74 W. An. A. 13 v.
Ты видел здесь, с каким тщанием природа расположила нервы, артерии и вены в пальцах по бокам, а не посредине, дабы при работе как-нибудь не укололись и не порезались они.
75 Вr. М. 156 v.
Почему природа не запретила одному животному жить смертью другого? Природа, стремясь и находя радость постоянно творить и производить жизни и формы, зная, что в этом рост ее земной материи, гораздо охотнее и быстрее творит, чем время разрушает; и потому положила она, чтобы многие животные служили пищей одни другим; и, так как это не удовлетворяет подобное желание, часто насылает она некие ядовитые и губительные испарения на большие множества и скопления животных, и прежде всего на людей, прирост коих велик, поскольку ими не питаются другие животные, и по устранении причин устраняются следствия. Итак, эта земля ищет прекращения своей жизни, желая непрестанного умножения на указанном и доказанном тобою основании; часто следствия походят на свои причины, животные служат примером мировой жизни.
76 С. А. 208 r. b.
Интересно отметить, что природа (la natura) превращается в конце отрывка в землю (questa terra).
В первый год крыса за 12 месяцев приносит 72 детеныша, по 6 зараз, в 12 пометов, по 6 на приплод, хотя иногда она производит больше или меньше; если бы половина была самок, то, мы скажем, что в течение месяца [следующего года] могло бы получиться 36 приплодов и один от первой матери, что дает 37 за месяц… Первый приплод дает за 3 месяца 3 приплода по 6 детенышей, откуда по 3 самки в каждом [т. е. 27 самок], и, если бы на протяжении этого года новорожденные детеныши не рожали, мы получим [от первого приплода] 12 пометов в год, которые каждый месяц давали бы 9, [итого] получим 108 детенышей [самок].
77 С. А. 12 v. а.
Аристотель, а вслед за ним Плиний, утверждал, что одна мышь в короткое время дала потомство в 120 мышей.
В течение месяца... – Имеется в виду первый месяц по истечении года, также и дальше, когда речь о 3 месяцах.
Первый приплод, т. е. 3 самки дают в течение этих месяцев по 3 приплода, в каждом по 3 самки, т. е. 3 × 3 × 3 = 27. Итого имеем с самками первого года 27 + 36 = 63. В конце отрывка то же вычисление повторяется для 12 месяцев, т. е. 3 × 3 × 12 = 108.
О время, истребитель вещей и старость завистливая, ты разрушаешь все вещи и все вещи пожираешь твердыми зубами годов мало-помалу, медленной смертью. Елена, когда смотрелась в зеркало, видя досадные морщины своего лица, соделанные старостью, жалуется и думает наедине, зачем два раза была похищена.
78 С. А. 346 v. а.
Это почти буквальный перевод из «Метаморфоз» Овидия (XV, 232—236).
Смертный дым. Возьми мышьяк и смешай с серой или реальгар. Способ розовая вода. Отстоянная жаба, а именно наземная. Пена бешеной собаки и отстоянный кизил. Тарантул тарентский. Порошок медянки или извести ядовитой для бросания на корабли.
79 С. А. 12 r. а.
Реальгар (risagallo) – As2S2, сернистый мышьяк, известный в то время также под названием красного мышьяка. Что при обжигании последнего получается ядовитый белый мышьяк (As2O2), было известно уже Абу Мансуру и псевдо-Геберу.
Способ розовая вода. – У арабских алхимиков за некоторыми приборами и приемами, применявшимися при изготовлении розовой воды, сохранилось это обозначение в качестве более общего технического термина. Отсюда и Альберт Великий, напр., говорит о возгонке вина «по образцу розовой воды». Нечто подобное, возможно, имеет в виду и Леонардо.
Жаба, rospo, – считалась ядовитой. Ср. у Челлини – rospo velenoso.
Отстоенная, stillato, – по-видимому, «дистиллированный» (профильтрованный) настой.
Если сделать сверлом отверстие в молодом дереве и вогнать туда мышьяку и реальгару, сублимированных и растворенных в водке, то это имеет силу сделать ядовитыми плоды его или его иссушить. Но следует названному отверстию быть большим, и доходить до сердцевины, и быть сделанным в пору созревания плодов, а названную ядовитую воду следует впускать в такое отверстие при помощи насоса и затыкать крепким куском дерева. То же самое может быть сделано, когда молодые деревья находятся в соку.
80 С. А. 373 r. а.
Сублимированных – подвергнутых возгонке.
Amatis.
Amor omnia vincit et nos cedamus amori.
81 H2. 41 v.
Т. е.: Все побеждает любовь, и мы любви покоримся. Стих из «Буколик» Вергилия (X, 69). В рукописях Леонардо встречается целый ряд примеров латинских склонений и спряжений, списки латинских слов, отрывки из грамматики Доната и т. п. По-видимому, и эта строчка относится к той же категории выписок, в особенности следует обратить внимание на вышестоящую глагольную форму Amatis. Ольшки, считая маловероятным, чтобы Леонардо до 40–45 лет не владел латынью, полагает, что в подобного рода отрывках следует видеть эскизы к элементарной латинской грамматике.
Жизнь нашу создаем мы смертью других. В мертвой вещи остается бессознательная жизнь, которая, вновь попадая в желудок живых, вновь обретает жизнь чувствующую и разумную.
82 W. An. B. 28 r.
Тело всякой питающейся вещи беспрерывно умирает и беспрерывно рождается вновь; ибо пища войти может только туда, откуда прежняя пища вышла, и, когда она вышла, жизни больше нет, и, если пищу исчезнувшую не возместить таким же количеством новой, жизнь лишится своего здравия, и если ты их этой пищи лишишь [вовсе], то жизнь вовсе окажется разрушенной. Но если будешь возмещать столько, сколько разрушается за день, то будет вновь рождаться столько жизни, сколько тратится, наподобие света свечи, питаемого влагой этой свечи, который, благодаря весьма быстрому притоку снизу, непрерывно восстанавливает то, что наверху, умирая, уничтожается и, умирая, из блестящего света в темный обращается дым; смерть эта беспрерывна, как беспрерывен и этот дым, и беспрерывность этого дыма та же, что беспрерывность питания, и мгновенно свет весь мертв и весь родился вновь, вместе с движением пищи своей.
Вряд ли стоит к этому картинному и яркому описанию внутренних противоречий природной жизни подыскивать литературные параллели и источники. Начиная с Гераклита Темного, а может быть ранее, в разных вариациях повторяется все та же мысль.
Питаемого влагой свечи – в основе лежит учение о переходе стихий друг в друга, т. е. в данном случае воды и воздуха в огонь.

83 Вr. М. 156 v.
Смотри же, надежда и желание водвориться на свою родину и вернуться в первое свое состояние уподобляется бабочке в отношении света, и человек, который всегда с непрекращающимся желанием, полный ликования, ожидает новой весны, всегда нового лета и всегда новых месяцев и новых годов (причем кажется ему, будто желанные предметы слишком медлят прийти), не замечает, что собственного желает разрушения! А желание это есть квинтэссенция, дух стихий, который, оказываясь заточенным душой человеческого тела, всегда стремится вернуться к пославшему его. И хочу, чтобы ты знал, что это именно желание есть квинтэссенция – спутница природы, а человек – образец мира.
84 Tr. 40 v.
Квинтэссенция – пятая стихия, т. е. небесный эфир, считалась неуничтожимой и неразрушимой. Дюэм перед словом «квинтэссенция» ставит в квадратных скобках celui de la, тогда текст приобретает такой смысл: «но это желание есть желание квинтэссенции – духа стихий, которая…» и: «это именно желание есть желание квинтэссенции, спутницы природы…» Истинный смысл уясняется в особенности при сопоставлении с 131, 132 или 166, трактующими о природе тяжестей и движении стихий.
Душа никогда не может разрушиться при разрушении тела, но действует в теле наподобие ветра, производящего звук в органе, в котором, если испорчена трубка, не получится больше от ветра хорошего действия.
85 С. А. 59 r.
Каждая часть хочет быть в своем целом, в коем лучше себя сохраняет.
Каждая часть имеет склонность вновь соединиться со своим целым, дабы избежать своего несовершенства.
Душа хочет находиться со своим телом, потому что без органических орудий этого тела она ничего не может совершить и ощущать.
86 С. А. 385 v.
Из этого и предыдущего отрывка видно, что в сущности душа без тела оказывается бездеятельной и физически сведенной к нулю. Ср. аргументацию против возможности деятельности духов в природе (46—47).
Анаксагор. Любая вещь происходит из любой вещи, и любая вещь становится любой вещью, и любая вещь возвращается в любую вещь, ибо то, что есть в стихиях, сделано из этих стихий.
87 F. 74 v.
Все во всем (quodlibet in quolibet) – одна из аксиом алхимии псевдо-Раймунда Луллия и философии Николая Кузанского. В тех же выражениях мысль повторена у Дж. Бруно (De umbris idearum).
Ни одна неодушевленная вещь не движется сама собою, но движение ее производится другими.
88 К. 101 v.
Это положение вполне совпадает с принципами Аристотелевой механики. Книги VII и VIII Аристотелевой «Физики» целиком построены на положении, что всякая неодушевленная вещь движима отличным от нее источником движения, который ей необходимо сопутствует и находится с ней в непосредственном контакте. Иными словами, движение длится, только пока приложена сила (источник движения), и прекращается с прекращением силы. Сила является, таким образом, у Аристотеля и его школы не причиной ускорения, а причиной самого движения (т. е. скорости).
Вода, движущаяся в реке, или призываема, или гонима, или движется сама. Если призываема или требуема – кто требующий? Если гонима, кто тот, кто гонит ее? Если движется сама, то показывает, что у нее есть сознание. Но в телах непрерывно меняющейся формы невозможно быть сознанию, ибо в таких телах нет суждения.
89 А. 22 v.
Против постоянного движения. Никакая неодушевленная вещь не сможет двигаться сама собою; следовательно, если она движется, то приводима в движение неравной силой, то есть силой неравной продолжительности и движения или неравной грузности. И с прекращением желания в первом двигателе тотчас же остановится второй.
90 А. 34 v.
Грузности – в подл. peso. В отличие от тяжести (gravezza) как свойства тела, peso означает часто или самый груз, или «грузность» – тяжесть в определенных условиях: величину нагрузки, натяжения веревки, вес тела в жидкости и т. п. Эта изменчивость peso сближает его с акцидентальной тяжестью (ср. о теории тяжести, зависящей от положения, прим. 181). Следует заметить, однако, что терминологическое различие peso и gravezza (или peso и grave) не выдерживается строго и вполне.
Ни одна неодушевленная вещь не может толкать или тянуть, не сопровождая движимой вещи; такими причинами движения могут быть лишь сила и тяжесть. Если толкает или тянет тяжесть, то производит это движение в вещи только потому, что хочет покоя, и, поскольку никакая вещь, двигающаяся падающим движением, не способна вернуться на первоначальную высоту, движение кончается.
И если движущее другую вещь есть сила, эта сила также сопровождает двигаемую ею вещь и движет ее так, что сама себя уничтожает; и когда уничтожится – никакая приводившаяся ею в движение вещь не в состоянии вновь произвести ее. Следовательно, никакая двигаемая вещь не может иметь длительного действия, потому что по устранении причины исчезают и следствия.
И в этом отрывке мы имеем дело с перипатетическим Nullum violentum potest esse perpetuum («Ничто насильственное не может быть вечным»).
О силе, движении, времени и бесконечном
91 F. 26 r.
Предшествующие отрывки подвели нас вплотную к основным проблемам механики, в первую очередь к проблеме движущей силы, силы – источника движения. Теоретические размышления о мере этой силы (91) параллельны практическим размышлениям о соотношении между силой артиллерийского орудия и дальностью полета ядра (92). Продолжая эти разыскания, Леонардо приходит к заключению, что есть разница между мысленным делением силы до бесконечности и физическим ее делением, доходящим до определенных «минимумов», далее неделимых (93—97). К проблемам бесконечной делимости Леонардо подходит и с другой стороны, анализируя понятие точки (98—99) и времени (100—101). С этим суждением о бесконечно малом связаны и его суждения о бесконечном (102), и отзвуки старых споров о minimum in quod sic, поднимавших вопросы о бесконечном приближении переменных величин к пределу (103).
1. Если сила двигает тело в известное время на известное расстояние, та же самая сила половину этого тела передвинет в то же время на двойное расстояние.
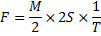
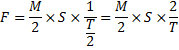
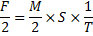

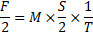
Это различные варианты основной аксиомы перипатетической механики, где сила (ср. примеч. 87) является причиной не ускорения, а скорости.
След., вместо обычной формулы:
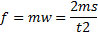
имеем f = mv или
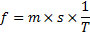
Как нетрудно видеть, от Леонардо ускользает правильное соотношение между t, с одной стороны, f и m – с другой. Поэтому в положениях 1, 3 и 5, где t принимается постоянным, даны правильные соотношения между m и s, f и m, f и s, тогда как во втором случае времена относятся к действительности не как 2⁄1, а как √2⁄1, а в четвертом не как 1⁄2, а как 1⁄√2.
У самого Аристотеля аксиома выражена в виде:

или

92 I. 130 r.
или словами: «Скорость по весу меньшего относится к скорости большего, как более тяжелое тело к менее тяжелому» (De coelo, III, 2). Впрочем, есть и формулировка f ⁄ f 1 = v ⁄v 1:
«Если сила движет тело с известной скоростью, то потребуется вдвое бóльшая сила, чтобы двигать его с удвоенной скоростью» (ср. Phys. VI, 5; De coelo, III, 2).
Первое и третье положения буквально совпадают с первым и пятым заключениями в трактате о пропорциях Альберта Саксонского, на который Леонардо ссылается в I, 120 r., а также с положениями в гл. 5-й кн. 7-й Физики Аристотеля.
Если бомбарда выбрасывает с наибольшей своей силой ядро в 100 фунтов на 3 мили, то на какое расстояние выбросит она ядро в 200 или 300 или другой какой груз, больший или меньший 100?
Если бомбарда 4 фунтами пороха выбрасывает 4-фунтовое ядро с наибольшей своей силой на 2 мили, то сколько следует прибавить пороху, чтобы выстрелить им на 4 мили? Если бомбарда 4 фунтами пороха гонит ядро в 4 фунта на 2 мили, на какое расстояние будут гнать его 6 фунтов пороха?
93 F. 51 v.
Внимательно изучая условия взрыва в орудии, Леонардо, в сущности, ориентируется на предыдущую аксиому.
Если сила движет тело в известное время на известное расстояние, не обязательно, чтобы такая сила двигала двойную тяжесть в течение двойного времени на двойное расстояние [?]; потому что, может быть, такая сила не способна будет двигать движимое.
Если сила движет тело в определенное время на определенное расстояние, не обязательно, чтобы половина этой силы двигала то же движимое в то же время на половину этого расстояния, потому что может случиться, что она не способна будет двигать его вовсе.
94 I. 120 v.
Приведенный отрывок дает ограничение предыдущей аксиоме. Ср. у Аристотеля (Физика, VII, 5): «Если Е движет Z в течение D на [расстояние] Т, не необходимо, чтобы Е в равное время двигало вдвое большее Z на половину Т… Ибо может случиться, [что] вообще двигать не будет… Иначе [и] один [человек] двигал бы корабль, если [только совокупные] силы волочащих корабль разделить на число [людей] и [так же] длину, на которую передвигали все» (т. е. силу и путь разделить на число двигавших).
…На двойное расстояние – очевидная ошибка, вместо «на то же расстояние».
О движении. Говорит Альберт Саксонский в своем сочинении «О пропорциях», что если сила движет движимое с определенной скоростью, то половину его будет двигать с двойной скоростью, что, мне кажется, не так.
95 I. 102 v.
О «Трактате о пропорциях» и Альберте Саксонском см. примеч. к 8. Принцип Альберта есть тот же аристотелевский принцип (примеч. 91), но без оговорки 93.
И если некоторые говорили, что чем меньше приводимое в движение тело, тем более его гонит движущее, постоянно увеличивая скорость движения пропорционально уменьшению его до бесконечности, то отсюда следовало бы, что атом был бы почти столь же быстр, сколь воображение или глаз, который мгновенно достигает звездной высоты. Поэтому путь его был бы бесконечен, так как вещь, которая может уменьшаться бесконечно, делалась бы бесконечно быстрой и двигалась бы по бесконечному пути, поскольку всякая непрерывная величина делима до бесконечности. Мнение это отвергается разумом, а следовательно, и опытом.
96 Е. 60 r.
Мысль о том, что физическое деление имеет естественные пределы, преступая которые мы разрушаем свойства данной вещи, т. е., иными словами, теория своего рода естественных минимумов (minima naturalia) определенно высказывалась и развивалась уже Эгидием Римским (1247–1316). Зачатки ее находим у Аверроэса (1126–1198) и у Роберта Большеголового (1175–1235), учителя Роджера Бэкона.
То, что в акте делимо, делимо и в потенции; хотя это и не значит, что делимое в потенции делимо и в акте. И если деления, совершаемые потенциально в бесконечность, меняют субстанцию делимой материи, то деления эти вернутся к составу своего целого при воссоединении частей по тем же стадиям, по которым они делились. Возьмем, например, лед и будем делить в бесконечность: он превратится в воду, из воды в воздух, и если воздух опять уплотнится, то станет водой и из воды градом и т. д.
97 С. А. 119 v. b.
Хотя то, что делимо актуально, делимо и потенциально, однако не все величины, делимые потенциально, будут делимы актуально.
98 М. 87 v.
Уже в Средние века хорошо было известно, что потенциально до бесконечности делимый континуум (in infinitum divisibile) не является еще актуально разделенным или разделимым на актуально бесконечное число частей (divisibile in infinitum).
Если угол есть встреча двух линий, то, поскольку линии кончаются в точке, бесконечные линии могут иметь начало в такой точке и, наоборот, бесконечные линии могут вместе в этой точке кончаться; следовательно, точка может быть общей началу и концу бесчисленных линий.
И кажется здесь странным, что раз треугольник кончается точкой в вершине угла, противолежащей основанию, и можно его разделить с концов основания на бесконечное число частей, что точка, будучи общим пределом всех названных делений, вместе с треугольником окажется делимой до бесконечности.
99 Вr. М. 131 r.
Разделить с концов основания – разделить бесконечным числом линий, проходящих через все точки основания, расположенные между его концами.
Наименьшая физическая точка больше всех математических точек, и следует это из того, что физическая точка есть величина непрерывная, а все непрерывное делимо до бесконечности, а точка математическая неделима, потому что не есть величина.
Всякая непрерывная величина мысленно делима до бесконечности.
(Среди всех вещей, существующих меж нас, существование ничто занимает первое место, и ведение его простирается на вещи, не имеющие существования, и сущность его обретается во времени в прошлом и будущем и ничего не имеет от настоящего. В этом ничто часть равна целому, и целое части, и делимое неделимому, и дает оно при делении тот же результат, что при умножении, и при сложении тот же, что при вычитании, как видно это у арифметиков из десятой их цифры, изображающей ничто; и власть его не простирается на вещи природы.
То, что называется ничто, обретается только во времени и словах; во времени обретается оно среди прошлого и будущего и ничего не удерживает от настоящего; также и в словах – в том, о чем говорится, что его нет или что оно невозможно.)
Во времени ничто находится в прошлом и будущем, и ничего не имеет от настоящего, и в природе сближается с невозможным, отчего, по сказанному, не имеет существования, поскольку там, где было бы ничто, должна была бы налицо быть пустота.
Среди великих вещей, которые находятся меж нас, существование ничто – величайшее. Оно пребывает во времени и в прошлое и будущее простирает свои члены, коими захватывает все минувшие дела и грядущие, как [неодушевленной] природы, так и существ одушевленных, и ничего не имеет от неделимого настоящего. Оно не распространяется на сущность какой-либо вещи.
100 Вr. М. 173 v.
Обретается среди прошлого и будущего и т. д. – Дюэм неверно переводит: son essence réside entre le passé et le futur, et la grandeur nulle est en possession du présent, – сближая мысль Леонардо с мыслями Николая Кузанского и Бергсона: точка, настоящее, покой – чистые невозможности и с тем вместе единственно доступны интеллекту. Так как перевод неточен (ср. след. абзац), то отпадает и комментарий.
Члены – первоначально было «руки». В круглых скобках – зачеркнутое самим Леонардо.
Хотя время и причисляют к непрерывным величинам, однако оно, будучи незримым и без тела, не целиком подпадает власти геометрии, которая делит на фигуры и тела бесконечного разнообразия, как мы видим, что это делается с видимыми и телесными вещами; но совпадает оно только с первыми началами ее, то есть с точкой и линией: точка во времени должна быть приравнена мгновению, а линия имеет сходство с длительностью известного количества времени, и подобно тому как точки суть начало и конец вышеназванной линии, так мгновения суть предел и начало каждого данного промежутка времени, и если линия делима до бесконечности, то промежуток времени не чужд такого деления, и если части, на которые разделена линия, соизмеримы друг с другом, то также и части времени будут друг с другом соизмеримы.
101 Br. M. 176 r.
Напиши о свойстве времени отдельно от геометрии.
102 С. А. 131 v.
Что за вещь, которая не существует и которая, существуй она, не существовала бы? Бесконечное, которое, если бы могло существовать, было бы ограниченно и конечно, так как то, что может существовать, имеет пределы в вещи, которая окружает его границы, и то, что не может существовать, есть то, что не имеет пределов.
103 К. 62 (14).
Петр имеет силу в 12 [единиц], и, если ему дано 12 [единиц] веса, он их не движет, потому что равные между собою вещи не одолевают одна другую. Но 11 он понесет, потому что из неравных сил бóльшая одолевает меньшую, так что 12 будут двигать 11. И здесь имеет место замечательный случай, а именно: если эти 12 могут двигать 11, оказывается, что эти 12 будут двигать тяжесть бесконечно бóльшую 11, потому что всякая непрерывная величина делима до бесконечности. Единица между 11 и 12 может бесконечно делиться, ибо можно сказать, 12 способно двигать 11 и будет еще двигать 111⁄2, и затем 2/3, и затем 113⁄4, и так до бесконечности может в том же порядке возрастать, деля на новые части остаток, так что последним будет тот из наименьших грузов, которого он не сможет более нести, то есть тот, который дополняет до 12. Так что здесь выходят две вещи, которые, казалось, невозможно предположить, а именно что человек будет в силах нести на себе груза бесконечно больше, чем может нести, и что минимальный груз выше того, который он нести может, будет тот, который он нести не может. Пример: 4 на весах уравновешивают 4, но двигать не могут; однако с успехом будут они двигать 3 и бесконечно больше груза, чем три, но груз равный 4 никогда, потому что от 3 к 4 одна единица, которая непрерывна, а всякая непрерывная величина делима до бесконечности.
