Страница:
Илл. 4.5. Распределение цены базового контракта при экспирации
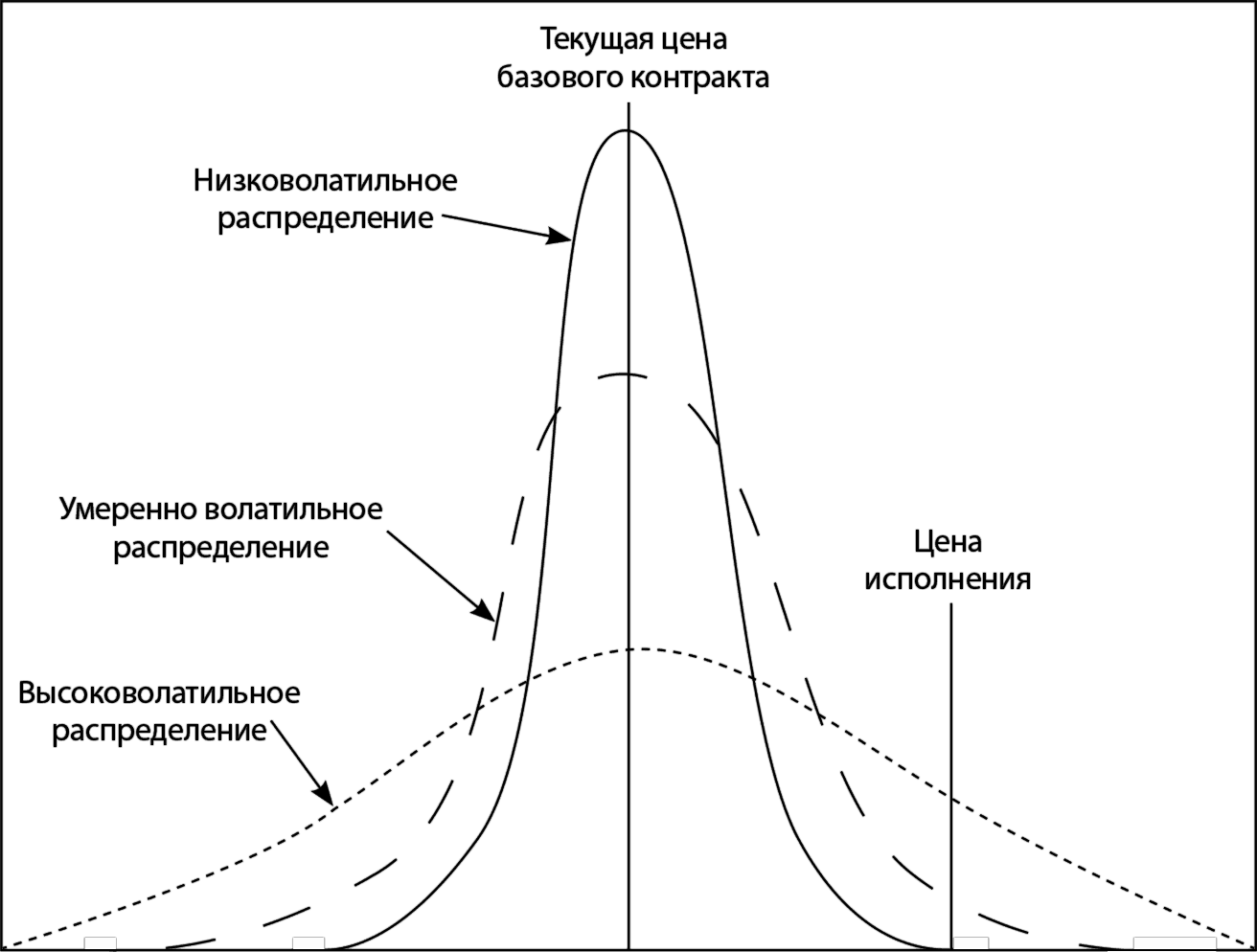
С этим и связано важное различие между оценкой базового контракта и оценкой опциона. Если предположить, что значения цены базового контракта подчиняются нормальному распределению, то стоимость базового контракта определяется местоположением пика кривой, изображающей это распределение, в то время как стоимость опциона зависит от «узости» или «широты» распределения.
Математическое ожидание и стандартное отклонение
Допустим, мы решили ввести представление о нормальном распределении возможных значений цены в модель для определения стоимости опциона. Для этого нужно описать нашу кривую. Поскольку модель математическая, кривую необходимо представить в количественном выражении.
К счастью, кривую нормального распределения можно охарактеризовать с помощью двух параметров – математического ожидания и стандартного отклонения. Если мы знаем, что распределение нормально, и нам известны оба этих параметра, то мы знаем все характеристики данного распределения.
Графически математическое ожидание соответствует точке расположения пика кривой, а стандартное отклонение показывает, насколько быстро или медленно убывают ее хвосты. У кривых, хвосты которых убывают медленно (илл. 4.4), стандартное отклонение больше, чем у кривых, хвосты которых убывают быстро (илл. 4.3).
Математическое ожидание – это не что иное, как средний результат, и потому знакомо многим трейдерам, а вот понятие стандартного отклонения менее известно. На самом деле, чтобы успешно торговать опционами, совершенно не обязательно знать, как рассчитываются эти параметры (для интересующихся детальный расчет представлен в приложении B). Что имеет значение для опционного трейдера, так это интерпретация параметров, особенно с точки зрения возможного изменения цены.
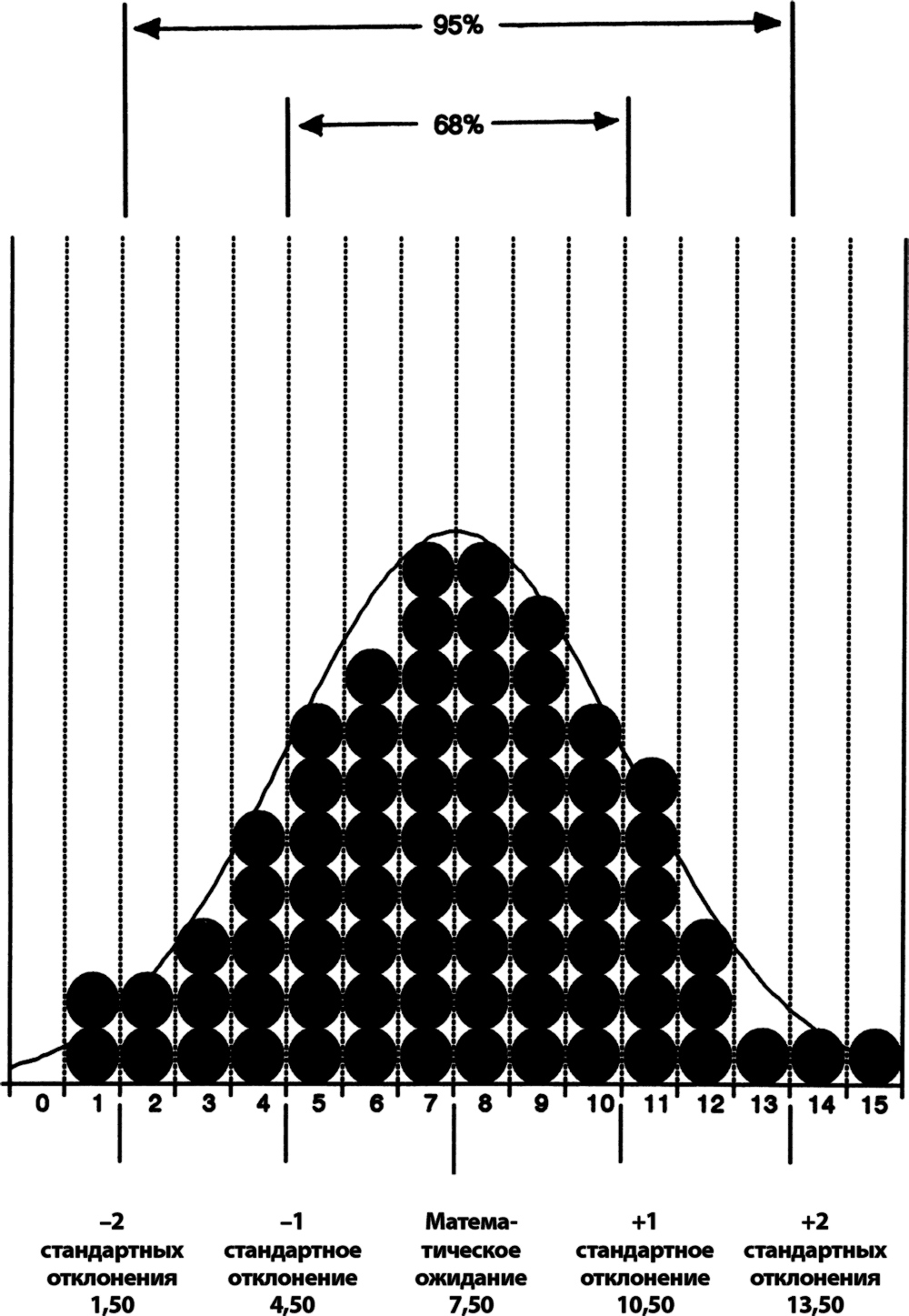
Вернемся к илл. 4.2 и рассмотрим находящиеся внизу игрового поля лунки с номерами от 0 до 15. В нашем варианте они показывают, сколько раз выпала решка при подбрасывании монетки 15 раз. С равным успехом они могут показывать, сколько раз шарик отклонился вправо, наткнувшись на очередной штырек при движении по игровому полю. Первой лунке присваивается нулевое значение, поскольку любой попавший в нее шарик должен был все время отклоняться влево. Последней лунке присваивается значение 15, поскольку попавший в нее шарик должен был все время отклоняться вправо.
Доустим, нам говорят, что математическое ожидание и стандартное отклонение на илл. 4.2 составляют соответственно 7,50 и 3,00. Как это характеризует распределение? (На самом деле эти параметры составляют 7,51 и 2,99, как показано в приложении B, но мы для простоты округлили их до 7,50 и 3,00.) Математическое ожидание показывает средний результат. Если мы сложим все результаты и разделим их на количество попыток, то получим 7,50. Если говорить о лунках, то средний результат окажется где-то посредине между 7-й и 8-й лунками (на самом деле это невозможно; как отмечалось в главе 3, средний результат не обязательно является реально возможным).
Стандартное отклонение характеризует не только степень пологости кривой, но и вероятность того, что шарик окажется в той или иной лунке или группе лунок. В частности, стандартное отклонение говорит о вероятности попадания шарика в лунку на определенном расстоянии от среднего. Например, мы можем узнать вероятность того, что шарик окажется в лунке с номером от 0 до 4 или от 11 до 15. Для получения ответа нужно узнать, на сколько стандарт ных отклонений шарик должен отклониться от среднего, а затем определить вероятность, соответствующую этому числу стандартных отклонений.
Вероятность, соответствующую любому числу стандартных отклонений, определяют по таблицам, которые приводятся в большинстве книг по статистике. Или же ее рассчитывают по соответствующим формулам (см. приложение B). Опционным трейдерам полезно знать, что:
• отклонения на ±1 стандартное отклонение наблюдаются примерно в 68,3 % (около 2/3) всех случаев;
• отклонения на ±2 стандартных отклонения наблюдаются примерно в 95,4 % (около 19/20) всех случаев;
• отклонения на ±3 стандартных отклонения наблюдаются примерно в 99,7 % (около 369/370) всех случаев.
Обратите внимание, что число стандартных отклонений указывается со знаком «плюс» или «минус». Поскольку нормальные распределения симметричны, вероятность повышательного и понижательного изменения одинакова.
Попробуем теперь ответить на вопрос о вероятности попадания шарика в лунки с номерами от 0 до 4 или от 11 до 15. Поместим перегородку между лунками 7 и 8, чтобы обозначить среднее значение 7½. Если стандартное отклонение – 3, то какие лунки находятся в пределах одного стандартного отклонения от среднего значения? Одно стандартное отклонение от среднего – это 7½ ±3, т. е. 4½ и 10½. Если представить ½ как перегородку между лунками, то мы увидим, что лунки с пятой по десятую находятся в пределах одного стандартного отклонения от среднего. Мы знаем, что на одно стандартное отклонение приходится 2/3 всех случаев, т. е. из каждых трех брошенных шариков два попадут в лунки с пятой по десятую. Остальные попадут в лунки с номерами 0–4 и 11–15. Таким образом, в ответ на исходный вопрос можно сказать, что вероятность попадания шарика в лунки с номерами от 0 до 4 или от 11 до 15 составляет один к трем или около 30 % (точный ответ: 100 % – 68,3 % = 31,7 %). Именно это показано на илл. 4.6.
Возможен и другой метод расчета. Представим себе, что держим пари. Допустим, кто-то считает, что вероятность непопадания шарика в лунку 14 или 15 составляет тридцать к одному. Стоит ли нам с ним спорить? Одна из особенностей стандартных отклонений заключается в том, что их можно просто складывать. В нашем примере, если одно стандартное отклонение – 3, то два стандартных отклонения – 6. Поэтому два стандартных отклонения от математического ожидания – это 7,5 ± 6 = 1,5 или 13,5. На илл. 4.6 видно, что лунки 14 и 15 лежат за пределами двух стандартных отклонений. Поскольку вероятность получения результата в пределах двух стандартных отклонений примерно равна 19 из 20, то вероятность получения результата за пределами двух стандартных отклонений – 1 к 20. Предложенные условия пари могут показаться весьма благо приятными, однако не следует забывать, что за пределами двух стандартных отклонений находятся также лунки 0 и 1. Поскольку нормальное распределение симметрично, вероятность попадания шарика в лунки 14 или 15 должна составлять половину от вероятности 1 к 20, т. е. 1 к 40. Таким образом, ставка 30 к 1 нам не подходит, поскольку риск в данном случае не оправдан.
Илл. 4.6. Вероятность, соответствующая 1, 2 и 3 стандартным отклонениям
Математическое ожидание – 7,50
Стандартное отклонение – 3,00
±1 стандартное отклонение – 68,3 % (2/3)
±2 стандартных отклонения – 95,4 % (19/20)
±3 стандартных отклонения – 99,7 % (369/370)
В главе 3 мы говорили, что один из логичных подходов к оценке опциона состоит в присвоении вероятностей бесконечному числу возможных значений цены базового контракта. Тогда, если умножить каждое возможное значение цены на соответствующую вероятность, результат можно использовать для расчета теоретической стоимости опциона. Проблема в том, что работать с бесконечным множеством значений цены и вероятностей очень трудно. К счастью, характеристики нормального распределения изучены настолько полно, что существуют формулы, облегчающие расчет и вероятностей, связанных с каждой точкой на кривой нормального распределения, и площади под любой частью кривой. Если исходить из того, что цены базового контракта имеют нормальное распределение, то эти формулы составляют инструментарий, позволяющий определять теоретическую стоимость опционов. Это одна из причин, по которым Блэк и Шоулз сделали в своей модели допущение о нормальном распределении.
К счастью, кривую нормального распределения можно охарактеризовать с помощью двух параметров – математического ожидания и стандартного отклонения. Если мы знаем, что распределение нормально, и нам известны оба этих параметра, то мы знаем все характеристики данного распределения.
Графически математическое ожидание соответствует точке расположения пика кривой, а стандартное отклонение показывает, насколько быстро или медленно убывают ее хвосты. У кривых, хвосты которых убывают медленно (илл. 4.4), стандартное отклонение больше, чем у кривых, хвосты которых убывают быстро (илл. 4.3).
Математическое ожидание – это не что иное, как средний результат, и потому знакомо многим трейдерам, а вот понятие стандартного отклонения менее известно. На самом деле, чтобы успешно торговать опционами, совершенно не обязательно знать, как рассчитываются эти параметры (для интересующихся детальный расчет представлен в приложении B). Что имеет значение для опционного трейдера, так это интерпретация параметров, особенно с точки зрения возможного изменения цены.
Вернемся к илл. 4.2 и рассмотрим находящиеся внизу игрового поля лунки с номерами от 0 до 15. В нашем варианте они показывают, сколько раз выпала решка при подбрасывании монетки 15 раз. С равным успехом они могут показывать, сколько раз шарик отклонился вправо, наткнувшись на очередной штырек при движении по игровому полю. Первой лунке присваивается нулевое значение, поскольку любой попавший в нее шарик должен был все время отклоняться влево. Последней лунке присваивается значение 15, поскольку попавший в нее шарик должен был все время отклоняться вправо.
Доустим, нам говорят, что математическое ожидание и стандартное отклонение на илл. 4.2 составляют соответственно 7,50 и 3,00. Как это характеризует распределение? (На самом деле эти параметры составляют 7,51 и 2,99, как показано в приложении B, но мы для простоты округлили их до 7,50 и 3,00.) Математическое ожидание показывает средний результат. Если мы сложим все результаты и разделим их на количество попыток, то получим 7,50. Если говорить о лунках, то средний результат окажется где-то посредине между 7-й и 8-й лунками (на самом деле это невозможно; как отмечалось в главе 3, средний результат не обязательно является реально возможным).
Стандартное отклонение характеризует не только степень пологости кривой, но и вероятность того, что шарик окажется в той или иной лунке или группе лунок. В частности, стандартное отклонение говорит о вероятности попадания шарика в лунку на определенном расстоянии от среднего. Например, мы можем узнать вероятность того, что шарик окажется в лунке с номером от 0 до 4 или от 11 до 15. Для получения ответа нужно узнать, на сколько стандарт ных отклонений шарик должен отклониться от среднего, а затем определить вероятность, соответствующую этому числу стандартных отклонений.
Вероятность, соответствующую любому числу стандартных отклонений, определяют по таблицам, которые приводятся в большинстве книг по статистике. Или же ее рассчитывают по соответствующим формулам (см. приложение B). Опционным трейдерам полезно знать, что:
• отклонения на ±1 стандартное отклонение наблюдаются примерно в 68,3 % (около 2/3) всех случаев;
• отклонения на ±2 стандартных отклонения наблюдаются примерно в 95,4 % (около 19/20) всех случаев;
• отклонения на ±3 стандартных отклонения наблюдаются примерно в 99,7 % (около 369/370) всех случаев.
Обратите внимание, что число стандартных отклонений указывается со знаком «плюс» или «минус». Поскольку нормальные распределения симметричны, вероятность повышательного и понижательного изменения одинакова.
Попробуем теперь ответить на вопрос о вероятности попадания шарика в лунки с номерами от 0 до 4 или от 11 до 15. Поместим перегородку между лунками 7 и 8, чтобы обозначить среднее значение 7½. Если стандартное отклонение – 3, то какие лунки находятся в пределах одного стандартного отклонения от среднего значения? Одно стандартное отклонение от среднего – это 7½ ±3, т. е. 4½ и 10½. Если представить ½ как перегородку между лунками, то мы увидим, что лунки с пятой по десятую находятся в пределах одного стандартного отклонения от среднего. Мы знаем, что на одно стандартное отклонение приходится 2/3 всех случаев, т. е. из каждых трех брошенных шариков два попадут в лунки с пятой по десятую. Остальные попадут в лунки с номерами 0–4 и 11–15. Таким образом, в ответ на исходный вопрос можно сказать, что вероятность попадания шарика в лунки с номерами от 0 до 4 или от 11 до 15 составляет один к трем или около 30 % (точный ответ: 100 % – 68,3 % = 31,7 %). Именно это показано на илл. 4.6.
Возможен и другой метод расчета. Представим себе, что держим пари. Допустим, кто-то считает, что вероятность непопадания шарика в лунку 14 или 15 составляет тридцать к одному. Стоит ли нам с ним спорить? Одна из особенностей стандартных отклонений заключается в том, что их можно просто складывать. В нашем примере, если одно стандартное отклонение – 3, то два стандартных отклонения – 6. Поэтому два стандартных отклонения от математического ожидания – это 7,5 ± 6 = 1,5 или 13,5. На илл. 4.6 видно, что лунки 14 и 15 лежат за пределами двух стандартных отклонений. Поскольку вероятность получения результата в пределах двух стандартных отклонений примерно равна 19 из 20, то вероятность получения результата за пределами двух стандартных отклонений – 1 к 20. Предложенные условия пари могут показаться весьма благо приятными, однако не следует забывать, что за пределами двух стандартных отклонений находятся также лунки 0 и 1. Поскольку нормальное распределение симметрично, вероятность попадания шарика в лунки 14 или 15 должна составлять половину от вероятности 1 к 20, т. е. 1 к 40. Таким образом, ставка 30 к 1 нам не подходит, поскольку риск в данном случае не оправдан.
Илл. 4.6. Вероятность, соответствующая 1, 2 и 3 стандартным отклонениям
Математическое ожидание – 7,50
Стандартное отклонение – 3,00
±1 стандартное отклонение – 68,3 % (2/3)
±2 стандартных отклонения – 95,4 % (19/20)
±3 стандартных отклонения – 99,7 % (369/370)

В главе 3 мы говорили, что один из логичных подходов к оценке опциона состоит в присвоении вероятностей бесконечному числу возможных значений цены базового контракта. Тогда, если умножить каждое возможное значение цены на соответствующую вероятность, результат можно использовать для расчета теоретической стоимости опциона. Проблема в том, что работать с бесконечным множеством значений цены и вероятностей очень трудно. К счастью, характеристики нормального распределения изучены настолько полно, что существуют формулы, облегчающие расчет и вероятностей, связанных с каждой точкой на кривой нормального распределения, и площади под любой частью кривой. Если исходить из того, что цены базового контракта имеют нормальное распределение, то эти формулы составляют инструментарий, позволяющий определять теоретическую стоимость опционов. Это одна из причин, по которым Блэк и Шоулз сделали в своей модели допущение о нормальном распределении.
Цена базового контракта как математическое ожидание распределения
Теперь, когда мы решили описывать цены через нормальное распределение, как отразить наше решение в модели, используемой для определения теоретической стоимости? Поскольку нормальное распределение характеризуется математическим ожиданием и стандартным отклонением, именно эти параметры следует вводить в модель. (Подразумевается, что речь идет о предполагаемом распределении цены базового контракта на дату экспирации опциона. – Прим. науч. ред.)
Вводя текущую цену базового контракта, мы фактически вводим математическое ожидание нормального распределения этой цены. Принципиальное допущение модели Блэка – Шоулза состоит в том, что в случае бесконечного числа повторений сделка с базовым контрактом становится безубыточной: трейдер ничего не зарабатывает и ничего не теряет. При таком допущении математическим ожиданием нормального распределения, принятого в модели, должна быть цена, при которой сделка с базовым инструментом, будь то покупка или продажа, окажется безубыточной. Что это за цена? Ответ зависит от вида базового инструмента.
Предположим, что трейдер покупает фьючерсный контракт по 100 долл. и сохраняет позицию в течение трех месяцев. Какой должна быть цена на этот фьючерсный контракт на конец трехмесячного периода, чтобы операция оказалась безубыточной? Поскольку фьючерсный контракт не предполагает затрат на поддержание позиции и по фьючерсам не выплачиваются дивиденды, цена безубыточности через три месяца после покупки точно равна первоначальной цене сделки, т. е. 100 долл.
Предположим теперь, что трейдер покупает акции по 100 долл. и держит их три месяца. Какой должна быть цена акций на конец периода владения, чтобы инвестиции оказались безубыточными? Поскольку покупка акций требует немедленных денежных расходов, цена безубыточности будет включать затраты на поддержание позиции в течение трех месяцев. Если годовая процентная ставка 8 %, то затраты на поддержание позиции составят 100 долл. × 8 % × 3/12 = 2 долл. Чтобы сделка оказалась безубыточной, через три месяца акции должны стоить 102 долл. Если в течение периода владения по акциям выплачиваются дивиденды в размере 1 долл., то для безубыточности сделки акции должны стоить 101 долл.
Заметим, что именно так рассчитывалась форвардная цена контракта в главе 3. Именно этот подход используется во всех модификациях формулы Блэка – Шоулза. Когда мы вводим цену базового инструмента, процентные ставки и дивиденды в модификацию формулы Блэка – Шоулза, соответствующую типу базового инструмента, на их основе рассчитывается форвардная цена базового инструмента, а результат становится математическим ожиданием нормального распределения.
Вводя текущую цену базового контракта, мы фактически вводим математическое ожидание нормального распределения этой цены. Принципиальное допущение модели Блэка – Шоулза состоит в том, что в случае бесконечного числа повторений сделка с базовым контрактом становится безубыточной: трейдер ничего не зарабатывает и ничего не теряет. При таком допущении математическим ожиданием нормального распределения, принятого в модели, должна быть цена, при которой сделка с базовым инструментом, будь то покупка или продажа, окажется безубыточной. Что это за цена? Ответ зависит от вида базового инструмента.
Предположим, что трейдер покупает фьючерсный контракт по 100 долл. и сохраняет позицию в течение трех месяцев. Какой должна быть цена на этот фьючерсный контракт на конец трехмесячного периода, чтобы операция оказалась безубыточной? Поскольку фьючерсный контракт не предполагает затрат на поддержание позиции и по фьючерсам не выплачиваются дивиденды, цена безубыточности через три месяца после покупки точно равна первоначальной цене сделки, т. е. 100 долл.
Предположим теперь, что трейдер покупает акции по 100 долл. и держит их три месяца. Какой должна быть цена акций на конец периода владения, чтобы инвестиции оказались безубыточными? Поскольку покупка акций требует немедленных денежных расходов, цена безубыточности будет включать затраты на поддержание позиции в течение трех месяцев. Если годовая процентная ставка 8 %, то затраты на поддержание позиции составят 100 долл. × 8 % × 3/12 = 2 долл. Чтобы сделка оказалась безубыточной, через три месяца акции должны стоить 102 долл. Если в течение периода владения по акциям выплачиваются дивиденды в размере 1 долл., то для безубыточности сделки акции должны стоить 101 долл.
Заметим, что именно так рассчитывалась форвардная цена контракта в главе 3. Именно этот подход используется во всех модификациях формулы Блэка – Шоулза. Когда мы вводим цену базового инструмента, процентные ставки и дивиденды в модификацию формулы Блэка – Шоулза, соответствующую типу базового инструмента, на их основе рассчитывается форвардная цена базового инструмента, а результат становится математическим ожиданием нормального распределения.
Волатильность как стандартное отклонение
Для полного описания кривой нормального распределения помимо математического ожидания нужно знать стандартное отклонение. Оно вводится в модель в виде волатильности. С незначительными вариациями, которые мы вскоре обсудим, значение волатильности базового инструмента определяется как одно стандартное отклонение изменения его цены, выраженное в процентах, на конец однолетнего периода.
Предположим, что в настоящее время базовый фьючерсный контракт стоит 100 долл., а его волатильность – 20 %. Поскольку 20 % – это одно стандартное отклонение изменения цены, мы ожидаем, что через год цена фьючерсного контракта будет находиться в интервале 80–120 долл. (100 долл. ± 20 %) с вероятностью приблизительно 68 %, в интервале 60–140 долл. (100 долл. ± 2 × 20 %) с вероятностью около 95 % и в интервале 40–160 долл. (100 долл. ± 3 × 20 %) с вероятностью 99,7 %.
Если базовый контракт – это акции, которые в настоящее время стоят 100 долл., то 20 %-ная волатильность должна рассчитываться на основе форвардной цены акции через год. Если процентная ставка – 8 %, и по акциям не выплачиваются дивиденды, то форвардная цена через год должна составить 108 долл. Тогда для стандартного отклонения изменения цены получаем 108 долл. × 20 % = 21,60 долл. Поэтому через год цена тех же акций будет лежать в интервале 86,40–129,60 долл. (108 долл. ± 21,60 долл.) с вероятностью приблизительно 68 %, в интервале 64,80–151,20 долл. (108 долл. ± 21,60 долл. ×2) с вероятностью 95 % и в интервале 43,20–172,80 долл. (108 долл. ± 21,60 долл. × 3) – с вероятностью 99,7 %.
Допустим, в конце года оказалось, что наш фьючерсный контракт, волатильность которого мы оценивали в 20 %, стоит 35 долл. Означает ли это ошибку в оценке волатильности? Изменение цены более чем на три стандартных отклонения маловероятно, но не нужно путать маловероятное с невозможным. Если 15 раз подбросить идеально сбалансированную монетку, то решка может выпасть 15 раз, хотя вероятность этого и составляет 1 к 32 000. Если волатильность действительно составляла 20 %, то вероятность того, что цена фьючерса через год упадет со 100 до 35 долл., всего 1 к 1500. Однако она не является нулевой, и, возможно, мы столкнулись как раз с тем случаем, когда цена упала до 35 долл. Конечно, мы вполне могли выбрать не ту волатильность. Но этого нельзя узнать без анализа динамики цены фьючерсного контракта за многие годы и без получения репрезентативного распределения значений цены.
Предположим, что в настоящее время базовый фьючерсный контракт стоит 100 долл., а его волатильность – 20 %. Поскольку 20 % – это одно стандартное отклонение изменения цены, мы ожидаем, что через год цена фьючерсного контракта будет находиться в интервале 80–120 долл. (100 долл. ± 20 %) с вероятностью приблизительно 68 %, в интервале 60–140 долл. (100 долл. ± 2 × 20 %) с вероятностью около 95 % и в интервале 40–160 долл. (100 долл. ± 3 × 20 %) с вероятностью 99,7 %.
Если базовый контракт – это акции, которые в настоящее время стоят 100 долл., то 20 %-ная волатильность должна рассчитываться на основе форвардной цены акции через год. Если процентная ставка – 8 %, и по акциям не выплачиваются дивиденды, то форвардная цена через год должна составить 108 долл. Тогда для стандартного отклонения изменения цены получаем 108 долл. × 20 % = 21,60 долл. Поэтому через год цена тех же акций будет лежать в интервале 86,40–129,60 долл. (108 долл. ± 21,60 долл.) с вероятностью приблизительно 68 %, в интервале 64,80–151,20 долл. (108 долл. ± 21,60 долл. ×2) с вероятностью 95 % и в интервале 43,20–172,80 долл. (108 долл. ± 21,60 долл. × 3) – с вероятностью 99,7 %.
Допустим, в конце года оказалось, что наш фьючерсный контракт, волатильность которого мы оценивали в 20 %, стоит 35 долл. Означает ли это ошибку в оценке волатильности? Изменение цены более чем на три стандартных отклонения маловероятно, но не нужно путать маловероятное с невозможным. Если 15 раз подбросить идеально сбалансированную монетку, то решка может выпасть 15 раз, хотя вероятность этого и составляет 1 к 32 000. Если волатильность действительно составляла 20 %, то вероятность того, что цена фьючерса через год упадет со 100 до 35 долл., всего 1 к 1500. Однако она не является нулевой, и, возможно, мы столкнулись как раз с тем случаем, когда цена упала до 35 долл. Конечно, мы вполне могли выбрать не ту волатильность. Но этого нельзя узнать без анализа динамики цены фьючерсного контракта за многие годы и без получения репрезентативного распределения значений цены.
Логнормальное распределение
Насколько обосновано наше предположение, что цены базового контракта распределены нормально? Даже если не касаться самой возможности существования какого-либо строгого распределения цен в реальной жизни, то можно утверждать, что у допущения о нормальном распределении есть один серьезный недостаток. Кривая нормального распределения симметрична. Если принимается допущение о нормальном распределении, то мы, предположив возможность повышательного изменения цены базового контракта, обязаны предположить возможность такого же понижательного изменения. Если мы допускаем возможность повышения цены 50-долларового базового инструмента на 75 долл. до 125 долл., то должны допустить и возможность ее падения на 75 долл. до –25 долл. Поскольку цены на традиционные товары и ценные бумаги не могут быть отрицательными, ясно, что допущение о нормальном распределении не вполне корректно. Как устранить этот недостаток?
До сих пор мы определяли волатильность как процентное изменение цены базового контракта. В этом смысле процентная ставка и волатильность схожи, поскольку и то и другое дает представление о доходности. Основное различие между ними заключается в том, что процентный доход положителен, в то время как волатильность отражает как положительные, так и отрицательные доходности. Если вкложить деньги под фиксированную ставку, то сумма всегда увеличивается. Но если вложить их в базовый контракт с волатильностью, отличной от нуля, то цена этого инструмента может как повыситься, так и понизиться. Волатильность, определяемая как стандартное отклонение процентных (или относительных) изменений цены базового контракта, ничего не говорит о направлении изменения цены.
Поскольку волатильность отражает доходность, большое значение имеет порядок расчета доходности. Предположим, что мы инвестировали 1000 долл. на год под 12 % годовых. Сколько мы получим в конце года? Ответ зависит от того, как будут выплачиваться проценты по инвестициям.
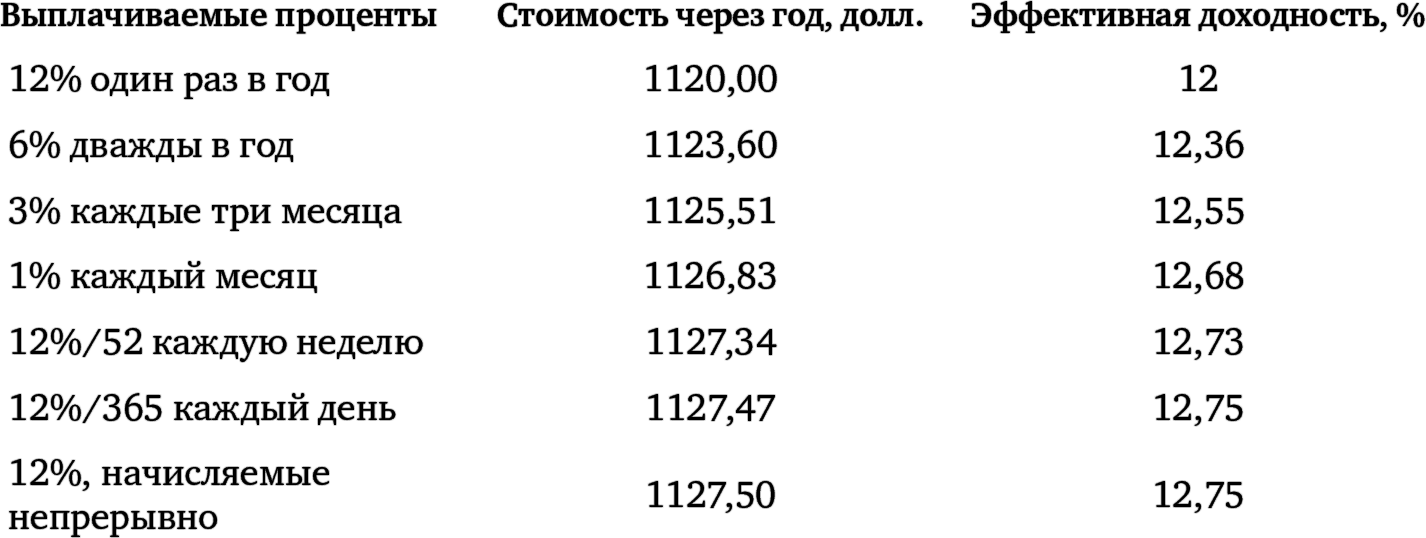
Когда проценты выплачиваются чаще, даже если годовая ставка не меняется, общая доходность инвестиций увеличивается. В случае непрерывной выплаты процентов доходность будет максимальной. (Предполагается, что процентные поступления реинвестируются на тех же условиях, в результате чего каждая следующая выплата рассчитывается относительно общей суммы, уже имеющейся к данному моменту, т. е. используется формула сложных процентов. Непрерывное начисление процентов означает, что интервал между выплатами становится все меньше и меньше, в предельном случае – бесконечно малым. При этом рост суммы описывается функцией exp(r*t), где r – процентная ставка, t – время в долях года. – Прим. науч. ред.)
Проделаем те же расчеты для отрицательной процентной ставки, хотя она встречается реже. Предположим, что мы ежегодно теряем 12 % инвестиций в размере 1000 долл. (процентная ставка –12 %). Сколько у нас останется в конце года? Ответ зависит от того, как часто начисляются убытки.

В случае отрицательной процентной ставки убытки, как и отрицательная доходность, меньше, если убытки начисляются чаще, хотя годовая ставка остается неизменной.
Точно так же, как процентные выплаты могут начисляться с разными интервалами и давать различные эффективные доходности, так и волатильность может рассчитываться с разными интервалами. Для целей оценки опциона делается допущение, что цена базового контракта меняется непрерывно (как вверх, так и вниз), а волатильность «накапливается» непрерывно со скоростью, соответствующей годовой волатильности данного базового инструмента. (Точнее, с постоянной скоростью накапливается не стандартное отклонение, а квадрат стандартного отклонения – дисперсия, поэтому сама волатильность увеличивается пропорционально корню квадратному из времени. – Прим. науч. ред.)
Что произойдет, если в каждый момент времени цена базового контракта будет повышаться или понижаться на заданный процент, а распределение этих движений будет нормальным? Если исходить из нормального распределения относительных изменений цены (доходности), то в результате непрерывного накопления этих изменений мы получим к дате экспирации логнормальное распределение цен. Такое распределение смещено из-за того, что движения цены вверх в абсолютном выражении больше движений цены вниз (илл. 4.7). В нашем примере с 12 %-ной ставкой непрерывное начисление положительного процента дает через год прибыль в размере 127,50 долл., в то время как непрерывное начисление отрицательного процента приводит к убытку всего в 113,08 долл. Если бы эти 12 % были волатильностью, то одно стандартное отклонение повышательного изменения цены составило бы на конец года +127,50 долл., а одно стандартное отклонение понижательного изменения цены –113,08 долл. Хотя в среднем относительные колебания цены (доходности), взятые по абсолютной величине, и сохраняются на уровне 12 %, непрерывное 12 %-ное нарастание и снижение приводит к различным повышательным и понижательным изменениям цены.
Модель Блэка – Шоулза – это модель непрерывного времени. Она исходит из того, что волатильность базового контракта в течение всего срока действия опциона постоянна, но эта волатильность рассчитывается по методу непрерывного начисления. Эти два допущения означают, что возможные цены базового контракта распределяются логнормально. Это также объясняет, почему у опционов с более высокой ценой исполнения стоимость больше, чем у опционов с более низкой ценой исполнения, когда обе цены как будто одинаково далеки от цены базового контракта. Предположим, что цена базового контракта составляет ровно 100 долл. Если не нужно учитывать проценты, и мы принимаем нормальное распределение возможных цен, то 110 колл и 90 пут, которые оба вне денег на 10 %, должны иметь одинаковую теоретическую стоимость. Но если мы допускаем в модели Блэка – Шоулза логнормальное распределение, то стоимость 110 колла всегда будет выше стоимости 90 пута. Логнормальное распределение предполагает более значительное в абсолютном выражении повышательное изменение цены. Таким образом, для 110 колла характерна более высокая вероятность роста цены, чем для 90 пута[14].
Илл. 4.7. Логнормальное распределение
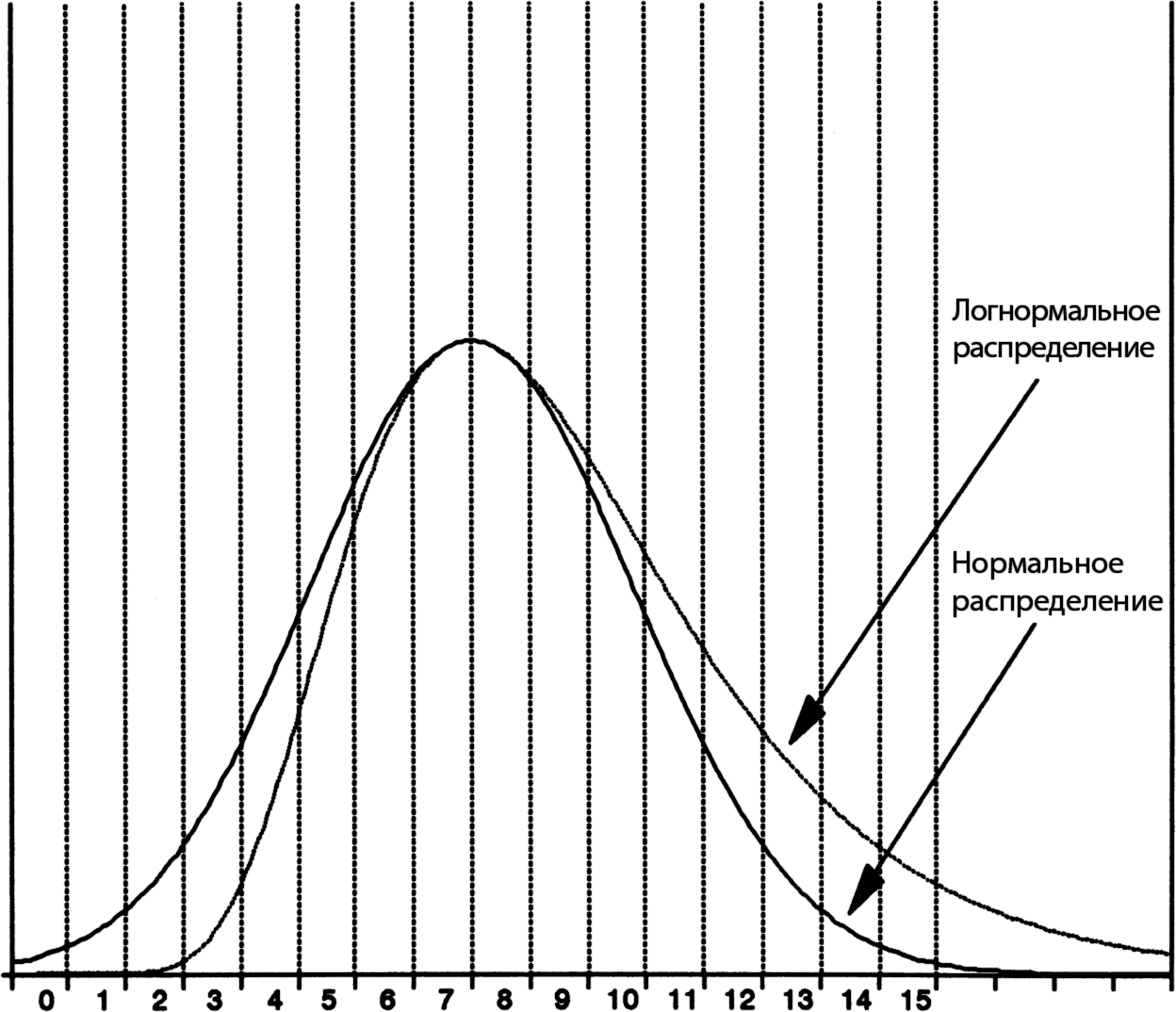
Наконец, встроенное в модель Блэка – Шоулза допущение о логнормальном распределении устраняет сформулированную ранее логическую проблему. Если мы допустим возможность неограниченного повышения цены базового контракта, то в случае нормального распределения придется допустить ее неограниченное понижательное изменение. Это приводит к появлению отрицательных цен базового контракта, что исключено для большинства рассматриваемых нами инструментов. Логнормальное распределение допускает возможность неограниченного роста цены (логарифм +∞ равен +∞), но исключает возможность ее падения ниже нуля (логарифм —∞ равен нулю). Это более точное представление распределения цен в реальной жизни.
Более детально расчет логарифмических изменений цены и вероятности рассматривается в приложении B.
Подведем итог и перечислим важнейшие допущения в отношении изменения цены, встроенные в модель Блэка – Шоулза.
1. Изменение цены базового инструмента носит случайный характер, и на него невозможно воздействовать, как невозможно предсказать заранее направление этого изменения.
2. Процентные или относительные изменения цены базового инструмента имеют нормальное распределение.
3. Поскольку мы принимаем, что процентные изменения цены базового контракта накапливаются непрерывно, цены базового контракта при экспирации распределяются логнормально.
4. Математическое ожидание данного логнормального распределения – это форвардная цена базового контракта.
Первое из допущений может вызвать у некоторых трейдеров возражения. Технические аналитики полагают, что, анализируя прошлую динамику цен, можно предсказать направление их будущего изменения. Можно выделить на графике точки поддержки и сопротивления, двойные максимумы и минимумы, «головы и плечи» и другие фигуры, которые, как считается, позволяют предсказать тенденции изменения цен. Не будем здесь дискутировать по этому поводу. В нашем случае важно то, что модель Блэка – Шоулза исходит из случайного изменения цен и невозможности предсказания направления их изменения. Это не означает, что использование модели Блэка – Шоулза не требует прогнозирования. Однако главная задача такого прогнозирования – предсказать величину изменения цены, а не направление изменения.
Как мы увидим дальше, есть основания сомневаться и в правомерности третьего допущения о логнормальном распределении цен при экспирации. Для одних рынков оно правомерно, а для других нет. Здесь опять-таки важно, чтобы использующий модель трейдер знал, какие допущения принимаются при расчете теоретической стоимости опциона. Тогда он сможет, опираясь на знание конкретного рынка, решить, насколько точны эти допущения, а следовательно, и полученные значения теоретической стоимости.
До сих пор мы определяли волатильность как процентное изменение цены базового контракта. В этом смысле процентная ставка и волатильность схожи, поскольку и то и другое дает представление о доходности. Основное различие между ними заключается в том, что процентный доход положителен, в то время как волатильность отражает как положительные, так и отрицательные доходности. Если вкложить деньги под фиксированную ставку, то сумма всегда увеличивается. Но если вложить их в базовый контракт с волатильностью, отличной от нуля, то цена этого инструмента может как повыситься, так и понизиться. Волатильность, определяемая как стандартное отклонение процентных (или относительных) изменений цены базового контракта, ничего не говорит о направлении изменения цены.
Поскольку волатильность отражает доходность, большое значение имеет порядок расчета доходности. Предположим, что мы инвестировали 1000 долл. на год под 12 % годовых. Сколько мы получим в конце года? Ответ зависит от того, как будут выплачиваться проценты по инвестициям.
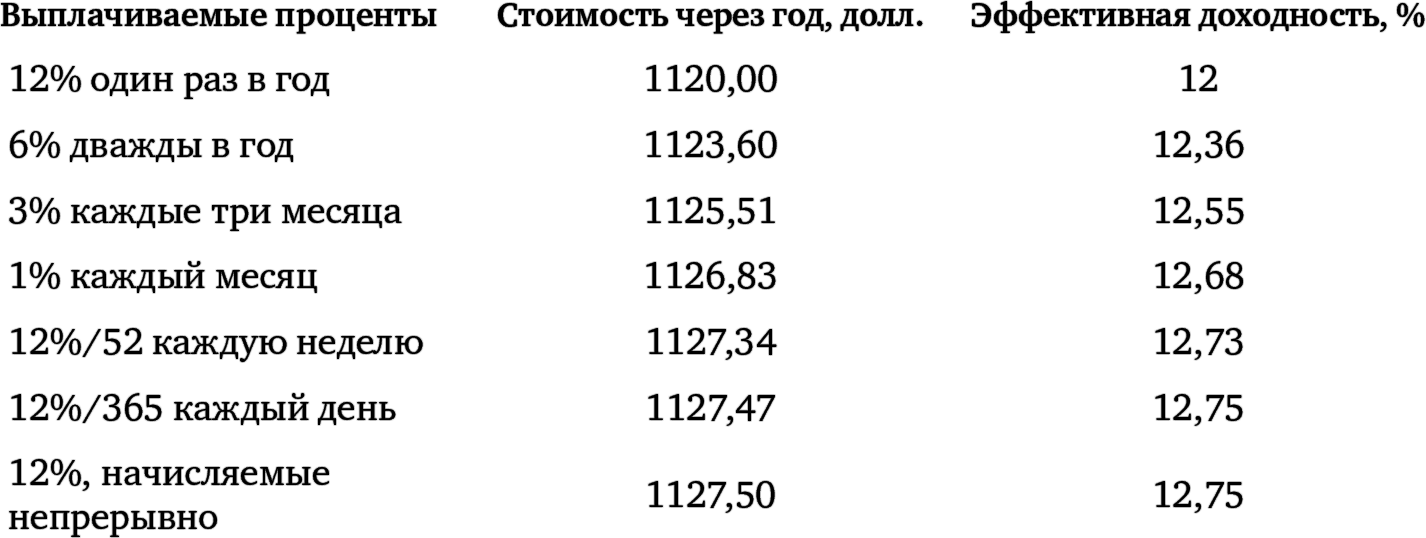
Когда проценты выплачиваются чаще, даже если годовая ставка не меняется, общая доходность инвестиций увеличивается. В случае непрерывной выплаты процентов доходность будет максимальной. (Предполагается, что процентные поступления реинвестируются на тех же условиях, в результате чего каждая следующая выплата рассчитывается относительно общей суммы, уже имеющейся к данному моменту, т. е. используется формула сложных процентов. Непрерывное начисление процентов означает, что интервал между выплатами становится все меньше и меньше, в предельном случае – бесконечно малым. При этом рост суммы описывается функцией exp(r*t), где r – процентная ставка, t – время в долях года. – Прим. науч. ред.)
Проделаем те же расчеты для отрицательной процентной ставки, хотя она встречается реже. Предположим, что мы ежегодно теряем 12 % инвестиций в размере 1000 долл. (процентная ставка –12 %). Сколько у нас останется в конце года? Ответ зависит от того, как часто начисляются убытки.

В случае отрицательной процентной ставки убытки, как и отрицательная доходность, меньше, если убытки начисляются чаще, хотя годовая ставка остается неизменной.
Точно так же, как процентные выплаты могут начисляться с разными интервалами и давать различные эффективные доходности, так и волатильность может рассчитываться с разными интервалами. Для целей оценки опциона делается допущение, что цена базового контракта меняется непрерывно (как вверх, так и вниз), а волатильность «накапливается» непрерывно со скоростью, соответствующей годовой волатильности данного базового инструмента. (Точнее, с постоянной скоростью накапливается не стандартное отклонение, а квадрат стандартного отклонения – дисперсия, поэтому сама волатильность увеличивается пропорционально корню квадратному из времени. – Прим. науч. ред.)
Что произойдет, если в каждый момент времени цена базового контракта будет повышаться или понижаться на заданный процент, а распределение этих движений будет нормальным? Если исходить из нормального распределения относительных изменений цены (доходности), то в результате непрерывного накопления этих изменений мы получим к дате экспирации логнормальное распределение цен. Такое распределение смещено из-за того, что движения цены вверх в абсолютном выражении больше движений цены вниз (илл. 4.7). В нашем примере с 12 %-ной ставкой непрерывное начисление положительного процента дает через год прибыль в размере 127,50 долл., в то время как непрерывное начисление отрицательного процента приводит к убытку всего в 113,08 долл. Если бы эти 12 % были волатильностью, то одно стандартное отклонение повышательного изменения цены составило бы на конец года +127,50 долл., а одно стандартное отклонение понижательного изменения цены –113,08 долл. Хотя в среднем относительные колебания цены (доходности), взятые по абсолютной величине, и сохраняются на уровне 12 %, непрерывное 12 %-ное нарастание и снижение приводит к различным повышательным и понижательным изменениям цены.
Модель Блэка – Шоулза – это модель непрерывного времени. Она исходит из того, что волатильность базового контракта в течение всего срока действия опциона постоянна, но эта волатильность рассчитывается по методу непрерывного начисления. Эти два допущения означают, что возможные цены базового контракта распределяются логнормально. Это также объясняет, почему у опционов с более высокой ценой исполнения стоимость больше, чем у опционов с более низкой ценой исполнения, когда обе цены как будто одинаково далеки от цены базового контракта. Предположим, что цена базового контракта составляет ровно 100 долл. Если не нужно учитывать проценты, и мы принимаем нормальное распределение возможных цен, то 110 колл и 90 пут, которые оба вне денег на 10 %, должны иметь одинаковую теоретическую стоимость. Но если мы допускаем в модели Блэка – Шоулза логнормальное распределение, то стоимость 110 колла всегда будет выше стоимости 90 пута. Логнормальное распределение предполагает более значительное в абсолютном выражении повышательное изменение цены. Таким образом, для 110 колла характерна более высокая вероятность роста цены, чем для 90 пута[14].
Илл. 4.7. Логнормальное распределение

Наконец, встроенное в модель Блэка – Шоулза допущение о логнормальном распределении устраняет сформулированную ранее логическую проблему. Если мы допустим возможность неограниченного повышения цены базового контракта, то в случае нормального распределения придется допустить ее неограниченное понижательное изменение. Это приводит к появлению отрицательных цен базового контракта, что исключено для большинства рассматриваемых нами инструментов. Логнормальное распределение допускает возможность неограниченного роста цены (логарифм +∞ равен +∞), но исключает возможность ее падения ниже нуля (логарифм —∞ равен нулю). Это более точное представление распределения цен в реальной жизни.
Более детально расчет логарифмических изменений цены и вероятности рассматривается в приложении B.
Подведем итог и перечислим важнейшие допущения в отношении изменения цены, встроенные в модель Блэка – Шоулза.
1. Изменение цены базового инструмента носит случайный характер, и на него невозможно воздействовать, как невозможно предсказать заранее направление этого изменения.
2. Процентные или относительные изменения цены базового инструмента имеют нормальное распределение.
3. Поскольку мы принимаем, что процентные изменения цены базового контракта накапливаются непрерывно, цены базового контракта при экспирации распределяются логнормально.
4. Математическое ожидание данного логнормального распределения – это форвардная цена базового контракта.
Первое из допущений может вызвать у некоторых трейдеров возражения. Технические аналитики полагают, что, анализируя прошлую динамику цен, можно предсказать направление их будущего изменения. Можно выделить на графике точки поддержки и сопротивления, двойные максимумы и минимумы, «головы и плечи» и другие фигуры, которые, как считается, позволяют предсказать тенденции изменения цен. Не будем здесь дискутировать по этому поводу. В нашем случае важно то, что модель Блэка – Шоулза исходит из случайного изменения цен и невозможности предсказания направления их изменения. Это не означает, что использование модели Блэка – Шоулза не требует прогнозирования. Однако главная задача такого прогнозирования – предсказать величину изменения цены, а не направление изменения.
Как мы увидим дальше, есть основания сомневаться и в правомерности третьего допущения о логнормальном распределении цен при экспирации. Для одних рынков оно правомерно, а для других нет. Здесь опять-таки важно, чтобы использующий модель трейдер знал, какие допущения принимаются при расчете теоретической стоимости опциона. Тогда он сможет, опираясь на знание конкретного рынка, решить, насколько точны эти допущения, а следовательно, и полученные значения теоретической стоимости.
Дневные и недельные стандартные отклонения
Мы знаем, что волатильность, как годовое стандартное отклонение, характеризует вероятное изменение цены контракта за период в один год. Однако этот период превышает срок существования большинства биржевых опционов. Нам можем потребоваться информация об изменении цены за более короткий период времени, например за месяц, неделю или день.
Важная особенность волатильности – ее пропорциональность квадратному корню из продолжительности периода. Это позволяет получить волатильность для более короткого, чем год, периода путем деления годовой волатильности на квадратный корень из количества этих периодов в году.
Допустим, нас интересует дневное изменение цены. Чтобы точно оценить его вероятностные характеристики с учетом логнормальности распределения, необходимо использовать в расчетах логарифмы и экспоненты, но сравнительно небольшое отличие логнормального распределения от нормального в связи с очень коротким промежутком времени позволяет оценить дневные колебания цены приблизительно. Прежде всего определим количество периодов в году. Если нам нужны цены на конец каждого дня, то сколько раз в году они могут измениться? Ограничимся биржевыми опционами. Хотя в году 365 дней, по выходным и праздникам цены на эти опционы меняться не могут. В результате остается примерно 256 торговых дней в году[15]. Поскольку квадратный корень из 256 равен 16, чтобы рассчитать дневную волатильность, разделим годовую волатильность на 16.
Возвращаясь к нашим фьючерсным контрактам, торгуемым по 100 долл. с волатильностью 20 %, определим величину стандартного отклонения процент ных изменений цены за день: 20/16 = 1¼ %. Таким образом, без учета эффекта логнормальности для стандартного отклонения дневного изменения цены приблизительно получаем 1¼ % × 100 = 1,25 долл. Мы ожидаем, что два торговых дня из трех цена будет меняться не более чем на 1,25 долл., а 19 торговых дней из 20 – не более чем на 2,50 долл. Только в один день из двадцати она изменится более чем на 2,50 долл.
Таким же образом определяется недельное стандартное отклонение. Только теперь нужно дать ответ на вопрос, сколько раз в году могут измениться цены, если фиксировать их раз в неделю. Поскольку выходных недель, в отличие от дней, у нас нет, в расчетах следует исходить из того, что в году 52 торговые недели. Разделив годовую 20 %-ную волатильность на квадратный корень из 52, или примерно на 7,2, получим 20 % / 7,2 ≈ 2¾. Следовательно, можно ожидать, что две недели из трех цена нашего фьючерсного контракта, первоначально составлявшая 100 долл., будет меняться не более чем на 2,75 долл., 19 недель из 20 – не более чем на 5,50 долл. и только одну неделю из двадцати – более чем на 5,50 долл.
Важная особенность волатильности – ее пропорциональность квадратному корню из продолжительности периода. Это позволяет получить волатильность для более короткого, чем год, периода путем деления годовой волатильности на квадратный корень из количества этих периодов в году.
Допустим, нас интересует дневное изменение цены. Чтобы точно оценить его вероятностные характеристики с учетом логнормальности распределения, необходимо использовать в расчетах логарифмы и экспоненты, но сравнительно небольшое отличие логнормального распределения от нормального в связи с очень коротким промежутком времени позволяет оценить дневные колебания цены приблизительно. Прежде всего определим количество периодов в году. Если нам нужны цены на конец каждого дня, то сколько раз в году они могут измениться? Ограничимся биржевыми опционами. Хотя в году 365 дней, по выходным и праздникам цены на эти опционы меняться не могут. В результате остается примерно 256 торговых дней в году[15]. Поскольку квадратный корень из 256 равен 16, чтобы рассчитать дневную волатильность, разделим годовую волатильность на 16.
Возвращаясь к нашим фьючерсным контрактам, торгуемым по 100 долл. с волатильностью 20 %, определим величину стандартного отклонения процент ных изменений цены за день: 20/16 = 1¼ %. Таким образом, без учета эффекта логнормальности для стандартного отклонения дневного изменения цены приблизительно получаем 1¼ % × 100 = 1,25 долл. Мы ожидаем, что два торговых дня из трех цена будет меняться не более чем на 1,25 долл., а 19 торговых дней из 20 – не более чем на 2,50 долл. Только в один день из двадцати она изменится более чем на 2,50 долл.
Таким же образом определяется недельное стандартное отклонение. Только теперь нужно дать ответ на вопрос, сколько раз в году могут измениться цены, если фиксировать их раз в неделю. Поскольку выходных недель, в отличие от дней, у нас нет, в расчетах следует исходить из того, что в году 52 торговые недели. Разделив годовую 20 %-ную волатильность на квадратный корень из 52, или примерно на 7,2, получим 20 % / 7,2 ≈ 2¾. Следовательно, можно ожидать, что две недели из трех цена нашего фьючерсного контракта, первоначально составлявшая 100 долл., будет меняться не более чем на 2,75 долл., 19 недель из 20 – не более чем на 5,50 долл. и только одну неделю из двадцати – более чем на 5,50 долл.
