Страница:
Поскольку для достижения безубыточности цена акций должна вырасти на сумму затрат на поддержание позиции, может показаться, что рассмотренный метод (деление на 16 в случае дневной волатильности или на 7,2 в случае недельной волатильности) не подходит для примерной оценки ожидаемого изменения цены базовых акций. Однако на коротком отрезке времени влияние затрат на поддержание позиции, как и отличие логнормального распределения от нормального, не так велико, а значит, метод позволяет достаточно точно оценивать дневные и недельные колебания цены. Предположим, что цена акций составляет 45 долл., а годовая волатильность – 28 %. Чему примерно равно одно стандартное отклонение колебаний цены за день или за неделю?
Дневное стандартное отклонение составит:
Говоря о волатильности, мы пользовались выражением «изменение цены». Но о какой цене шла речь? О максимальной/минимальной цене за какой-либо период, о цене открытия/закрытия или о какой-то другой цене? Хотя существует целый ряд методов оценки волатильности[16], обычно оперируют изменениями расчетной цены. При таком подходе одно стандартное отклонение дневного изменения цены в ¾ пункта означает, что расчетная цена одного дня отличается от расчетной цены следующего дня на ¾ пункта. Изменение максимальной/минимальной цены или цены открытия/закрытия может быть как больше, так и меньше, но нас интересует изменение именно расчетной цены.
Волатильность и наблюдаемые изменения цены
Кое-что о процентных фьючерсах и опционах
Виды волатильности
Будущая волатильность
Историческая волатильность
Прогнозируемая волатильность
Рыночная волатильность
Дневное стандартное отклонение составит:
Недельное стандартное отклонение составит:45 долл. × 28 % / 16 = 45 долл. × 1,75 % = 0,79 долл.
Следует ожидать, что два дня из трех цена будет меняться не более чем на ¾ пункта, 19 дней из 20 – не более чем на 1½, и только раз в 20 дней она изменится более чем на 1½ пункта. Если говорить о недельных показателях, то две недели из трех цена будет меняться не более чем на 1¾ пункта, 19 недель из 20 – не более чем на 3½ пункта и только в одну неделю из 20 она изменится более чем на 3½ пункта.45 долл. × 28 % / 7,2 = 45 долл. × 3,89 % = 1,75 долл.
Говоря о волатильности, мы пользовались выражением «изменение цены». Но о какой цене шла речь? О максимальной/минимальной цене за какой-либо период, о цене открытия/закрытия или о какой-то другой цене? Хотя существует целый ряд методов оценки волатильности[16], обычно оперируют изменениями расчетной цены. При таком подходе одно стандартное отклонение дневного изменения цены в ¾ пункта означает, что расчетная цена одного дня отличается от расчетной цены следующего дня на ¾ пункта. Изменение максимальной/минимальной цены или цены открытия/закрытия может быть как больше, так и меньше, но нас интересует изменение именно расчетной цены.
Волатильность и наблюдаемые изменения цены
Почему для трейдера так важно умение рассчитывать дневные или недельные изменения цены на основе годовой волатильности? Волатильность – такой входной параметр формул теоретической стоимости опциона, который невозможно наблюдать непосредственно. Однако без ее точной оценки немыслимо успешное применение многих опционных стратегий. Именно поэтому опционному трейдеру необходимо знать, насколько правильны его ожидания в отношении волатильности рынка. Если об успехе или провале стратегий, требующих прогнозирования направления изменения цены, немедленно сигнализируют объявленные цены, то волатильность нигде не публикуется. Трейдеру приходится самостоятельно определять, правильно ли он выбрал показатель волатильности для своей модели.
Предположим, что цена базового контракта составляет 40 долл., а трейдер в расчетах теоретической стоимости принял, что волатильность равна 30 %. Одно стандартное отклонение дневного изменения цены в этом случае примерно составляет 40 долл. × 30 %/16 = 0,75. За пять дней торгов наблюдались следующие изменения цены:
Трейдер полагал, что цена будет меняться более чем на 0,75 долл. (одно стандартное отклонение) примерно раз в три дня или 1–2 раза за пятидневный период. Однако за пять дней подобного изменения цены не произошло ни разу. Какой из этого следует вывод[17]? Ясно одно: перечисленные изменения цены не соответствуют 30 %-ной волатильности. Это может быть связано с двумя причинами. С одной стороны, выбранная неделя могла оказаться необычно спокойной (возможно, на нее пришлись праздники), а на следующей неделе жизнь войдет в обычную колею, и изменения цены будут более соответствовать 30 %-ной волатильности. Если так, то трейдеру следует и в дальнейшем использовать этот показатель в расчетах. С другой стороны, трейдер мог ошибочно взять не ту волатильность. В этом случае ему следует выбрать новый показатель, более соответствующий наблюдаемым изменениям цены. Если и далее использовать 30 %-ную волатильность в условиях более низкого изменения цен, возможным значениям цены базового контракта будут присвоены не те вероятности. Результат – неправильная теоретическая стоимость и потеря смысла применения теории.
Так какая же волатильность соответствует пяти изменениям цены в приведенном выше примере? Без расчета сказать довольно трудно (на самом деле ответ – 18,8 %). Однако если у трейдера есть представление о возможных изменениях цены, он вполне может увидеть, что изменения за пятидневный период не соответствуют 30 %-ной волатильности.
Возьмем другой пример. Теперь цена базового контракта – 333½ долл., а трейдер наблюдает следующие пять дневных изменений цены:
Предположим, что цена базового контракта составляет 40 долл., а трейдер в расчетах теоретической стоимости принял, что волатильность равна 30 %. Одно стандартное отклонение дневного изменения цены в этом случае примерно составляет 40 долл. × 30 %/16 = 0,75. За пять дней торгов наблюдались следующие изменения цены:
Соответствуют ли эти пять изменений цены 30 %-ному уровню волатильности?+0,43, –0,6, –0,61, +0,50, –0,28.
Трейдер полагал, что цена будет меняться более чем на 0,75 долл. (одно стандартное отклонение) примерно раз в три дня или 1–2 раза за пятидневный период. Однако за пять дней подобного изменения цены не произошло ни разу. Какой из этого следует вывод[17]? Ясно одно: перечисленные изменения цены не соответствуют 30 %-ной волатильности. Это может быть связано с двумя причинами. С одной стороны, выбранная неделя могла оказаться необычно спокойной (возможно, на нее пришлись праздники), а на следующей неделе жизнь войдет в обычную колею, и изменения цены будут более соответствовать 30 %-ной волатильности. Если так, то трейдеру следует и в дальнейшем использовать этот показатель в расчетах. С другой стороны, трейдер мог ошибочно взять не ту волатильность. В этом случае ему следует выбрать новый показатель, более соответствующий наблюдаемым изменениям цены. Если и далее использовать 30 %-ную волатильность в условиях более низкого изменения цен, возможным значениям цены базового контракта будут присвоены не те вероятности. Результат – неправильная теоретическая стоимость и потеря смысла применения теории.
Так какая же волатильность соответствует пяти изменениям цены в приведенном выше примере? Без расчета сказать довольно трудно (на самом деле ответ – 18,8 %). Однако если у трейдера есть представление о возможных изменениях цены, он вполне может увидеть, что изменения за пятидневный период не соответствуют 30 %-ной волатильности.
Возьмем другой пример. Теперь цена базового контракта – 333½ долл., а трейдер наблюдает следующие пять дневных изменений цены:
Соответствуют ли эти изменения цены 18 %-ной волатильности? При 18 % одно стандартное отклонение изменения цены составляет примерно 3¾ (333¾ долл. × 18 % / 16). За пять дней цена должна была один-два раза измениться более чем на 3¾ долл. Но здесь три дня из пяти цена менялась более чем на 3¾ долл., а однажды даже на 7¾ долл. (т. е. более чем на два стандартных отклонения), чего следовало ожидать не чаще раза в 20 дней. И снова, если трейдер не считает эту неделю необычной, он должен скорректировать показатель волатильности и привести его в соответствие с наблюдающимися изменениями цены.– 5, +2½, +1, –7¾, –4¼.
Кое-что о процентных фьючерсах и опционах
Допустим, цена фьючерсного контракта на ставку 3-месячных евродолларовых депозитов (ставку LIBOR) – 93,00, а волатильность равна 16 %. Описанный выше метод позволяет приблизительно определить одно стандартное отклонение дневного изменения цены фьючерса: 93,00 × 16 %/16 = 0,93. Однако любой трейдер, знакомый с данным рынком, скажет, что дневное изменение цены на 0,93 крайне маловероятно. Чем объясняется этот будто бы неверный результат? Можно предположить, что мы взяли слишком высокую волатильность. Однако на самом деле 16 %-ная волатильность для 3-месячной ставки LIBOR вовсе не редкость, поэтому следует искать какое-то другое объяснение.
Цены контрактов на евродоллар, как и многих других контрактов на процентную ставку (евромарки, евроиены, ставки краткосрочных стерлинговых депозитов, а также на американские казначейские краткосрочные бескупонные облигации) принято указывать как 100 минус процентная ставка. Это означает, что ставка, соответствующая цене фьючерсного контракта, равна 100 минус стоимость контракта. Также это означает, что, исключая маловероятный сценарий отрицательных процентных ставок, стоимость контракта не может превысить 100. В связи с этим 100 – это максимальная стоимость евродолларового контракта, точно так же, как нуль – минимальная стоимость традиционных базовых активов, таких как акции и товары. Мы можем учесть эту особенность в расчетах, сделав допущение, что стоимость евродолларового фьючерсного контракта на самом деле равна 100 минус его цена. При биржевой цене 93,00 для определения теоретической стоимости мы должны использовать в своей модели значение 100 – 93,00, т. е. 7,00. Если мы считаем, что стоимость контракта 7,00, то одно стандартное отклонение изменения цены – 7,00 × 16 %/16 = 0,07. Это, конечно, более реалистичный результат, чем 0,93.
Будем последовательными, и раз уж мы стали отсчитывать цены фьючерсных контрактов на евродоллар от 100, то пересчитаем и цены исполнения опционов. Поэтому цена исполнения, равная 93,50, в нашей модели на самом деле составляет 6,50 (100 – 93,50 = 6,50). Также нам необходимо изменить на противоположный тип опциона, т. е. колл поменять на пут, а пут – на колл. Для пояснения рассмотрим колл с ценой исполнения 93,50. Чтобы этот колл оказался в деньгах, базовый контракт должен вырасти в цене до 93,50. Но для этого процентные ставки должны упасть ниже 6,50 %. Поэтому колл с ценой исполнения 93,50, как он определен биржей, – это то же, что пут с ценой исполнения 6,50, если под 6,50 понимается собственно процентная ставка (6,50 %). Программы расчета стоимости для опционов на евродоллар или другие виды контрактов на отсчитываемую от 100 процентную ставку выполняют это преобразование автоматически. Цена базового контракта и цена исполнения вычитаются из 100, котируемые коллы рассматриваются как путы, а путы – как коллы.
Заметим, что для большинства облигаций подобные преобразования не требуются. В зависимости от купонной ставки цены этих инструментов могут свободно колебаться без каких-либо ограничений сверху и нередко превышают 100. Поэтому чаще всего их оценивают с помощью традиционных методов, хотя у процентных инструментов существуют другие особенности, требующие использования специальных подходов.
Для такого инструмента, как облигация, можно рассчитать текущую доходность на основе рыночной цены. Если взять несколько значений цены и рассчитать по ним несколько показателей доходности, то можно определить и волатильность доходности. Этот показатель можно использовать для оценки теоретической стоимости опциона на облигацию, хотя, чтобы быть последовательными, нам придется представить как доходность и цену исполнения опциона. Поскольку волатильность процентного инструмента можно рассчитать двумя методами, трейдеры процентными инструментами иногда вместо волатильности цены используют волатильность доходности.
Цены контрактов на евродоллар, как и многих других контрактов на процентную ставку (евромарки, евроиены, ставки краткосрочных стерлинговых депозитов, а также на американские казначейские краткосрочные бескупонные облигации) принято указывать как 100 минус процентная ставка. Это означает, что ставка, соответствующая цене фьючерсного контракта, равна 100 минус стоимость контракта. Также это означает, что, исключая маловероятный сценарий отрицательных процентных ставок, стоимость контракта не может превысить 100. В связи с этим 100 – это максимальная стоимость евродолларового контракта, точно так же, как нуль – минимальная стоимость традиционных базовых активов, таких как акции и товары. Мы можем учесть эту особенность в расчетах, сделав допущение, что стоимость евродолларового фьючерсного контракта на самом деле равна 100 минус его цена. При биржевой цене 93,00 для определения теоретической стоимости мы должны использовать в своей модели значение 100 – 93,00, т. е. 7,00. Если мы считаем, что стоимость контракта 7,00, то одно стандартное отклонение изменения цены – 7,00 × 16 %/16 = 0,07. Это, конечно, более реалистичный результат, чем 0,93.
Будем последовательными, и раз уж мы стали отсчитывать цены фьючерсных контрактов на евродоллар от 100, то пересчитаем и цены исполнения опционов. Поэтому цена исполнения, равная 93,50, в нашей модели на самом деле составляет 6,50 (100 – 93,50 = 6,50). Также нам необходимо изменить на противоположный тип опциона, т. е. колл поменять на пут, а пут – на колл. Для пояснения рассмотрим колл с ценой исполнения 93,50. Чтобы этот колл оказался в деньгах, базовый контракт должен вырасти в цене до 93,50. Но для этого процентные ставки должны упасть ниже 6,50 %. Поэтому колл с ценой исполнения 93,50, как он определен биржей, – это то же, что пут с ценой исполнения 6,50, если под 6,50 понимается собственно процентная ставка (6,50 %). Программы расчета стоимости для опционов на евродоллар или другие виды контрактов на отсчитываемую от 100 процентную ставку выполняют это преобразование автоматически. Цена базового контракта и цена исполнения вычитаются из 100, котируемые коллы рассматриваются как путы, а путы – как коллы.
Заметим, что для большинства облигаций подобные преобразования не требуются. В зависимости от купонной ставки цены этих инструментов могут свободно колебаться без каких-либо ограничений сверху и нередко превышают 100. Поэтому чаще всего их оценивают с помощью традиционных методов, хотя у процентных инструментов существуют другие особенности, требующие использования специальных подходов.
Для такого инструмента, как облигация, можно рассчитать текущую доходность на основе рыночной цены. Если взять несколько значений цены и рассчитать по ним несколько показателей доходности, то можно определить и волатильность доходности. Этот показатель можно использовать для оценки теоретической стоимости опциона на облигацию, хотя, чтобы быть последовательными, нам придется представить как доходность и цену исполнения опциона. Поскольку волатильность процентного инструмента можно рассчитать двумя методами, трейдеры процентными инструментами иногда вместо волатильности цены используют волатильность доходности.
Виды волатильности
Обсуждая друг с другом волатильность, даже опытные трейдеры могут говорить о разных вещах. Утверждение, что волатильность XYZ составляет 25 %, может иметь разный смысл. Во избежание путаницы для начала выясним, какая бывает волатильность.
Будущая волатильность
Именно будущую волатильность хотел бы знать каждый трейдер. Она лучше всего характеризует будущее распределение цен базового контракта. Как раз ее мы имеем в виду, когда говорим о волатильности в формуле оценки опциона. Будущая волатильность показывает трейдеру, какие у него шансы. Если он введет ее в формулу оценки опциона, то получит точную теоретиче скую стоимость, поскольку значения вероятности будут правильными. Как и казино, трейдер может иногда проигрывать из-за краткосрочного невезения. Но в долгосрочной перспективе шансы на его стороне, и он почти наверняка сумеет заработать.
Конечно, трейдеры редко говорят о будущей волатильности, поскольку угадать, что ожидает нас в будущем, невозможно.
Конечно, трейдеры редко говорят о будущей волатильности, поскольку угадать, что ожидает нас в будущем, невозможно.
Историческая волатильность
Хотя будущее предсказать невозможно, если трейдер хочет использовать формулу оценки опциона, он должен попытаться угадать будущую волатильность. В оценке опционов, как и в других дисциплинах, хорошим отправным пунктом может стать анализ исторических данных. Какой была волатильность данного контракта в том или ином периоде в прошлом? Если за последние 10 лет волатильность контракта не опускалась ниже 10 % и не превышала 30 %, то вряд ли стоит ожидать, что в будущем она составит 5 или 40 %. Это не означает, что крайние значения невозможны (в опционной торговле, похоже, невозможное рано или поздно случается), но с учетом прошлой динамики и в отсутствие экстраординарных событий прогноз 10–30 % будет реалистичнее любого другого. Конечно, 10–30 % – это большой диапазон, но он, по крайней мере, дает точку отсчета. Получив дополнительную информацию, мы сможем его сузить.
Заметим, что существует множество способов расчета исторической волатильности, но большинство из них предполагает выбор двух параметров: прошлого периода и временного интервала между последовательными изменениями цены. Прошлым периодом могут быть десять дней, шесть месяцев, пять лет или любой другой отрезок времени по усмотрению трейдера. Более длительные периоды позволяют определить среднюю или характерную волатильность, а более короткие – обнаружить необычные колебания волатильности. Чтобы полнее изучить историческую волатильность контракта, трейдер может взять не один, а несколько прошлых периодов.
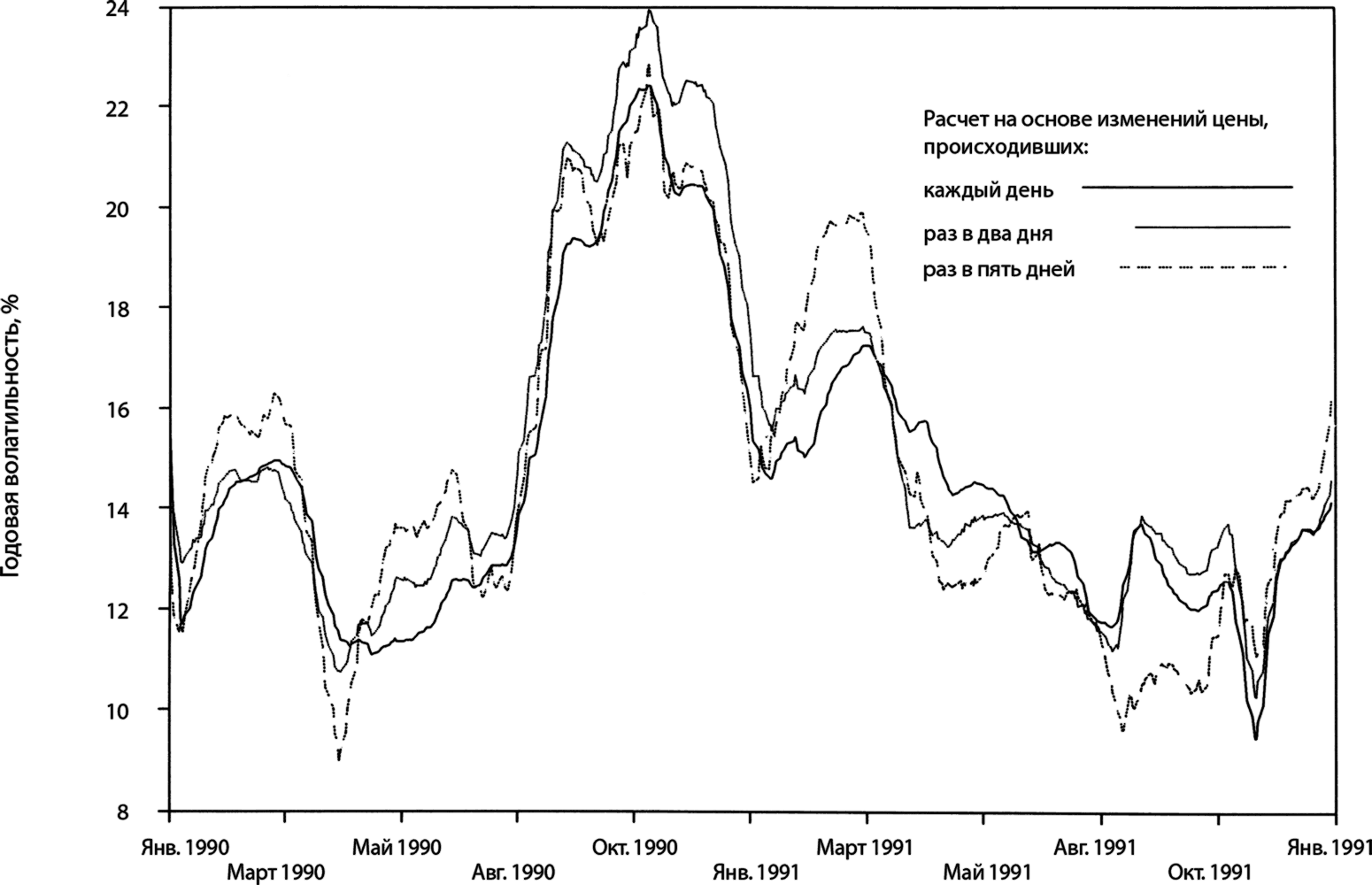
Затем необходимо решить, какие интервалы между изменениями цены использовать. Что лучше взять – дневные, недельные, месячные изменения цены или изменения, происходящие с каким-то необычным интервалом, скажем два дня или полторы недели? Как ни странно, но выбранный интервал не особенно влияет на результат. Контракт, цена которого сильно колеблется в течение дня, а за неделю практически не меняется, – исключение. Если контракт волатилен в течение дня, он волатилен и в течение недели, и в течение месяца. Об этом свидетельствуют графики на илл. 4.8. Они представляют волатильность индекса S&P 500 за последовательные 50-дневные периоды. Сплошная линия отражает динамику волатильности дневных изменений цены, точечная – изменений, происходивших каждые два дня, пунктирная – происходивших каждые пять дней. Хотя эти графики местами расходятся, по большей части они показывают одни и те же уровни и тенденции изменения волатильности.
Как правило, информационно-аналитические службы, которые предоставляют информацию об исторической волатильности, используют дневные изменения расчетной цены. В противном случае они сопровождают информацию пояснениями. Если, например, волатильность контракта в августе оценивают в 21,6 %, то можно считать, что были учтены дневные изменения расчетной цены за все рабочие дни этого месяца.
Историческую и будущую волатильность иногда называют реализованной волатильностью.
Илл. 4.8. Историческая 50-дневная волатильность индекса S&P 500
Заметим, что существует множество способов расчета исторической волатильности, но большинство из них предполагает выбор двух параметров: прошлого периода и временного интервала между последовательными изменениями цены. Прошлым периодом могут быть десять дней, шесть месяцев, пять лет или любой другой отрезок времени по усмотрению трейдера. Более длительные периоды позволяют определить среднюю или характерную волатильность, а более короткие – обнаружить необычные колебания волатильности. Чтобы полнее изучить историческую волатильность контракта, трейдер может взять не один, а несколько прошлых периодов.
Затем необходимо решить, какие интервалы между изменениями цены использовать. Что лучше взять – дневные, недельные, месячные изменения цены или изменения, происходящие с каким-то необычным интервалом, скажем два дня или полторы недели? Как ни странно, но выбранный интервал не особенно влияет на результат. Контракт, цена которого сильно колеблется в течение дня, а за неделю практически не меняется, – исключение. Если контракт волатилен в течение дня, он волатилен и в течение недели, и в течение месяца. Об этом свидетельствуют графики на илл. 4.8. Они представляют волатильность индекса S&P 500 за последовательные 50-дневные периоды. Сплошная линия отражает динамику волатильности дневных изменений цены, точечная – изменений, происходивших каждые два дня, пунктирная – происходивших каждые пять дней. Хотя эти графики местами расходятся, по большей части они показывают одни и те же уровни и тенденции изменения волатильности.
Как правило, информационно-аналитические службы, которые предоставляют информацию об исторической волатильности, используют дневные изменения расчетной цены. В противном случае они сопровождают информацию пояснениями. Если, например, волатильность контракта в августе оценивают в 21,6 %, то можно считать, что были учтены дневные изменения расчетной цены за все рабочие дни этого месяца.
Историческую и будущую волатильность иногда называют реализованной волатильностью.
Илл. 4.8. Историческая 50-дневная волатильность индекса S&P 500

Прогнозируемая волатильность
По аналогии со службами, занимающимися прогнозированием направления изменения цены контракта, существуют и службы, пытающиеся прогнозировать будущую волатильность контракта. Прогнозы составляются на любой период, но чаще всего на периоды, соответствующие оставшемуся сроку дей ствия опционов на базовый контракт. Для базового контракта, до экспирации которого осталось три месяца, такая служба может предсказать волатильность на следующие 3, 6 и 9 месяцев. Для базового контракта, срок действия которого истекает каждый месяц, эта служба может предсказать волатильность на следующие 1, 2 и 3 месяца. Из-за того, что опционы появились сравнительно недавно, прогнозирование волатильности находится еще в зачаточном состоянии и в лучшем случае может считаться неточной наукой. Тем не менее при оценке будущей волатильности контракта трейдер может опираться на любой прогноз волатильности, который ему только удастся найти.
Рыночная волатильность
Вообще говоря, любая волатильность, будущая, историческая или прогнозируемая, – это волатильность базового контракта. Когда мы говорим о будущей волатильности индекса S&P 500, исторической волатильности американских краткосрочных бескупонных казначейских облигаций или прогнозируемой волатильности акций IBM, речь идет о волатильности базового контракта. Однако существует и другая волатильность, ассоциируемая не с базовым контрактом, а с опционами на него.
Предположим, что цена фьючерсного контракта – 98,50, а процентная ставка – 8 %. Предположим также, что на этот контракт имеется колл с ценой исполнения 105, срок действия которого истекает через три месяца, и, по нашему мнению, в следующие три месяца волатильность составит 16 %. Чтобы узнать теоретическую стоимость 105 колла, нужно ввести эти данные в формулу. С помощью формулы Блэка – Шоулза мы получим, что теоретическая стоимость этого опциона – 0,96. Теперь можно сравнить теоретическую стоимость опциона с его рыночной ценой. К нашему удивлению, цена опциона равна 1,34. Чем объяснить, что опцион, оцененный нами в 0,96, стоит на рынке 1,34?
Если исходить из того, что все участники рынка пользуются той же формулой Блэка – Шоулза, то расхождение между нашей стоимостью и оценкой рынка должно объясняться разницей во мнениях относительно одного или нескольких использованных в формуле показателей. Можно пройтись по списку этих показателей и попытаться найти сомнительные.
Сразу исключим время до даты экспирации и цену исполнения, поскольку эти показатели зафиксированы в опционном контракте. А что можно сказать о цене базового актива в 98,50? Возможно, она только в нашем представлении составляет 98,50, а на самом деле базовый актив продается по более высокой цене, скажем по 99,00. В таких обстоятельствах полезно еще раз проверить исходные данные. Но предположим, что цена базового контракта все же 98,50. Даже если цена предложения отличается от цены спроса, в условиях ликвидного рынка широкий спред слишком маловероятен, чтобы объяснить расхождение в 0,38 между нашей и рыночной оценкой стоимости опциона. Может быть, все дело в 8 %-ной ставке? Но, как мы отмечали в предыдущей главе, процентная ставка обычно наименее важный из всех вводимых в формулу показателей. А в случае фьючерсных опционов этот показатель вообще несущественен. В результате остается только один возможный показатель – волатильность. Должно быть, рынок использует для оценки 105 колла значение волатильности, отличное от 16 %.
Какую именно волатильность он использует? Чтобы это выяснить, зададим следующий вопрос: в случае постоянства всех прочих показателей (время до даты экспирации, цена исполнения, цена базового контракта, процентная ставка), какое значение волатильности нужно ввести в формулу, чтобы получить теоретическую стоимость, равную рыночной цене опциона? В нашем примере нужно узнать, при какой волатильности стоимость 105 колла составит 1,34. Ясно, что она должна быть выше 16 %, поэтому сядем за компьютер с соответствующим программным обеспечением и поэкспериментируем с более высокими значениями волатильности. Нетрудно обнаружить, что тео ретическая стоимость 105 колла составляет 1,34 при волатильности 18,5 %. Такую волатильность называют рыночной волатильностью (implied volatility). Это волатильность, которую необходимо ввести в модель, чтобы получить теоретическую стоимость, равную рыночной цене опциона. Ее можно также представить как волатильность базового контракта, «подразумеваемую» ценами опциона на рынке.
При определении рыночной волатильности опциона мы делаем допущение, что теоретическая стоимость (цена опциона) известна, но неизвестна волатильность. По сути, мы заставляем формулу работать в обратном порядке, чтобы найти неизвестную (см. илл. 4.9). Это легче сказать, чем сделать, поскольку большинство формул стоимости опционов не позволяет получить решение обратной задачи в явном виде. Однако существует ряд компьютерных программ, которые рассчитывают рыночную волатильность при наличии всех остальных показателей.
Илл. 4.9. Порядок определения теоретической стоимости и рыночной волатильности

Заметим, что рыночная волатильность зависит от используемой формулы стоимости опциона. Для некоторых опционов разные формулы дают существенно различающиеся рыночные волатильности. Точность этого показателя также зависит от точности исходных данных, в число которых входит не только цена опциона. В частности, могут возникнуть проблемы, если какое-то время сделки с данным опционом не заключались, а рыночные условия серьезно изменились. Предположим, что в нашем примере цена 1,34 – это цена последней сделки, заключенной 2 часа назад, когда базовый фьючерсный контракт стоил 99,25. Если цена базового контракта 99,25, то рыночная волатильность опциона с ценой 1,34–17,3 %. Как видим, разница довольно велика, что подчеркивает значение точных и свежих данных при расчете рыночной волатильности.
Службы, занимающиеся теоретическим анализом опционов, обычно предоставляют информацию и о рыночной волатильности. Это может быть индивидуальный показатель для каждого опциона на некоторый базовый контракт или единый показатель для всех опционов на один и тот же базовый контракт. В последнем случае показатель представляет собой среднюю из всех индивидуальных значений волатильности. С этой целью отдельные значения рыночной волатильности взвешиваются по какому-нибудь критерию, например по объему сделки, количеству открытых позиций. Чаще всего наибольший вес присваивается опционам на деньгах.
Рыночная волатильность постоянно меняется, поскольку постоянно меняются цены опционов, а также другие рыночные условия. Рынок словно непрерывно опрашивает всех участников и формирует согласованное мнение относительно волатильности базового контракта. Это не опрос в традиционном смысле, поскольку трейдеры не собираются вместе и не решают вопрос голосованием, однако они делают предложения о покупке и продаже, и цена опциона отражает равновесие спроса и предложения. Это равновесие можно перевести на язык рыночной волатильности.
Хотя премией обычно называют цену опциона, нередко трейдеры называют рыночную волатильность премией или уровнем премии. Если текущая рыночная волатильность высока по историческим меркам или по сравнению с недавней волатильностью базового контракта, то трейдер может сказать, что уровни премии высоки; если рыночная волатильность необычно низка, то он может сказать, что уровни премии невысоки.
Имей трейдер надежную формулу цены опциона и возможность видеть через магический кристалл будущую волатильность базового контракта, то он смог бы точно оценивать опционы на этот контракт. Он мог бы оценить разницу между теоретической стоимостью каждого опциона и его рыночной ценой, продать опционы, оцененные выше теоретической стоимости, и купить недооцененные опционы. Если бы ему пришлось выбирать, какой из двух пере оцененных опционов продать, то он просто продал бы тот, что переоценен больше. Однако трейдер, имеющий информацию о рыночной волатильности, получает другой ориентир для сравнения. Он может сравнивать рыночную волатильность опциона либо с прогнозируемой волатильностью, либо с рыночной волатильностью других опционов на тот же базовый контракт. Возвращаясь к нашему примеру со 105 коллом, можно сказать, что при теоретической стоимости 0,96 и цене 1,34 этот колл переоценен на 0,38. Но с точки зрения волатильности он переоценен на 2,5 %, поскольку теоретическая стоимость рассчитана на основе 16 %-ной волатильности (принятой трейдером), а цена – на основе 18,5 %-ной (рыночной) волатильности. Из-за необычных характеристик опционов серьезному трейдеру полезнее анализировать цену опциона с точки зрения рыночной волатильности, а не абсолютного значения в долларах.
Предположим, что 98 колл на казначейские облигации продается по 3-32 (3500 долл.), а соответствующая рыночная волатильность – 10,5 %. Предположим также, что 102 колл с той же датой экспирации продается за 1-16 (1250 долл.), его рыночная волатильность – 11,5 %. В долларовом выражении 102 колл дешевле 98 колла на 2250 долл. Однако опытный трейдер может прийти к выводу, что 98 колл на самом деле дешевле 102 колла, поскольку его рыночная волатильность на целый процентный пункт меньше. Означает ли это, что следует купить 98 колл и продать 102 колл? Совсем не обязательно. Если будущая волатильность казначейских облигаций окажется равной 8 %, то оба опциона переоценены, а если 14 %, то недооценены. Кроме того, чувствительность этих опционов к изменению рыночных условий может быть разной, и поэтому покупка нескольких 102 коллов может быть более желательной, чем покупка одного 98 колла. Если мы проигнорируем эти соображения, то 98 колл будет выглядеть лучше относительно 102 колла, поскольку его рыночная волатильность ниже.
Хотя опционные трейдеры и пользуются всеми четырьмя показателями волатильности, самые важные из них – будущая и рыночная. Будущая волатильность базового контракта определяет стоимость опционов на этот контракт. Рыночная волатильность отражает цену каждого опциона. Стоимость и цена – два показателя, которые интересуют всех трейдеров, а не только опционных. Если у контракта высокая стоимость и низкая цена, то трейдер предпочитает быть покупателем, если у контракта низкая стоимость и высокая цена, то трейдер предпочитает быть продавцом. Опционный трейдер обычно сравнивает будущую волатильность с рыночной. Если по сравнению с будущей волатильностью рыночная волатильность невысока, он покупает опцион, а если высока – продает. Однако будущая волатильность неизвестна, поэтому, чтобы оценить ее, мы интересуемся исторической и прогнозируемой волатильностью. Но в конечном счете стоимость опциона определяет именно будущая волатильность.
Чтобы начинающему трейдеру было легче разобраться в видах волатильности, рассмотрим следующую аналогию с прогнозом погоды. Предположим, что одним июльским утром проживающий в Чикаго трейдер просыпается и размышляет, в чем идти на работу. Может ли он выбрать теплую куртку? Вряд ли, поскольку исторически известно, что июль в Чикаго не бывает настолько холодным, чтобы потребовалась зимняя одежда. Затем трейдер включает радио или телевизор и узнает прогноз погоды. Обещают ясную и жаркую погоду – около 32 °С. Исходя из этого, наш трейдер принимает решение: он пойдет в рубашке с короткими рукавами, без свитера или пиджака, а зонтик брать ни к чему. Однако на всякий случай он выглядывает в окно, чтобы узнать, как одеты люди. К его удивлению, все идут в пальто и с зонтиками. Одежда тех, кто уже вышел на улицу, подразумевает совершенно иную погоду. Так что теперь должен выбрать трейдер? Ему нужно принять какое-то решение, но чему верить – прогнозу погоды или людям на улице? Ответа на этот вопрос нет, потому что будущая погода будет известна только в конце дня.
Предположим, что цена фьючерсного контракта – 98,50, а процентная ставка – 8 %. Предположим также, что на этот контракт имеется колл с ценой исполнения 105, срок действия которого истекает через три месяца, и, по нашему мнению, в следующие три месяца волатильность составит 16 %. Чтобы узнать теоретическую стоимость 105 колла, нужно ввести эти данные в формулу. С помощью формулы Блэка – Шоулза мы получим, что теоретическая стоимость этого опциона – 0,96. Теперь можно сравнить теоретическую стоимость опциона с его рыночной ценой. К нашему удивлению, цена опциона равна 1,34. Чем объяснить, что опцион, оцененный нами в 0,96, стоит на рынке 1,34?
Если исходить из того, что все участники рынка пользуются той же формулой Блэка – Шоулза, то расхождение между нашей стоимостью и оценкой рынка должно объясняться разницей во мнениях относительно одного или нескольких использованных в формуле показателей. Можно пройтись по списку этих показателей и попытаться найти сомнительные.
Сразу исключим время до даты экспирации и цену исполнения, поскольку эти показатели зафиксированы в опционном контракте. А что можно сказать о цене базового актива в 98,50? Возможно, она только в нашем представлении составляет 98,50, а на самом деле базовый актив продается по более высокой цене, скажем по 99,00. В таких обстоятельствах полезно еще раз проверить исходные данные. Но предположим, что цена базового контракта все же 98,50. Даже если цена предложения отличается от цены спроса, в условиях ликвидного рынка широкий спред слишком маловероятен, чтобы объяснить расхождение в 0,38 между нашей и рыночной оценкой стоимости опциона. Может быть, все дело в 8 %-ной ставке? Но, как мы отмечали в предыдущей главе, процентная ставка обычно наименее важный из всех вводимых в формулу показателей. А в случае фьючерсных опционов этот показатель вообще несущественен. В результате остается только один возможный показатель – волатильность. Должно быть, рынок использует для оценки 105 колла значение волатильности, отличное от 16 %.
Какую именно волатильность он использует? Чтобы это выяснить, зададим следующий вопрос: в случае постоянства всех прочих показателей (время до даты экспирации, цена исполнения, цена базового контракта, процентная ставка), какое значение волатильности нужно ввести в формулу, чтобы получить теоретическую стоимость, равную рыночной цене опциона? В нашем примере нужно узнать, при какой волатильности стоимость 105 колла составит 1,34. Ясно, что она должна быть выше 16 %, поэтому сядем за компьютер с соответствующим программным обеспечением и поэкспериментируем с более высокими значениями волатильности. Нетрудно обнаружить, что тео ретическая стоимость 105 колла составляет 1,34 при волатильности 18,5 %. Такую волатильность называют рыночной волатильностью (implied volatility). Это волатильность, которую необходимо ввести в модель, чтобы получить теоретическую стоимость, равную рыночной цене опциона. Ее можно также представить как волатильность базового контракта, «подразумеваемую» ценами опциона на рынке.
При определении рыночной волатильности опциона мы делаем допущение, что теоретическая стоимость (цена опциона) известна, но неизвестна волатильность. По сути, мы заставляем формулу работать в обратном порядке, чтобы найти неизвестную (см. илл. 4.9). Это легче сказать, чем сделать, поскольку большинство формул стоимости опционов не позволяет получить решение обратной задачи в явном виде. Однако существует ряд компьютерных программ, которые рассчитывают рыночную волатильность при наличии всех остальных показателей.
Илл. 4.9. Порядок определения теоретической стоимости и рыночной волатильности

Заметим, что рыночная волатильность зависит от используемой формулы стоимости опциона. Для некоторых опционов разные формулы дают существенно различающиеся рыночные волатильности. Точность этого показателя также зависит от точности исходных данных, в число которых входит не только цена опциона. В частности, могут возникнуть проблемы, если какое-то время сделки с данным опционом не заключались, а рыночные условия серьезно изменились. Предположим, что в нашем примере цена 1,34 – это цена последней сделки, заключенной 2 часа назад, когда базовый фьючерсный контракт стоил 99,25. Если цена базового контракта 99,25, то рыночная волатильность опциона с ценой 1,34–17,3 %. Как видим, разница довольно велика, что подчеркивает значение точных и свежих данных при расчете рыночной волатильности.
Службы, занимающиеся теоретическим анализом опционов, обычно предоставляют информацию и о рыночной волатильности. Это может быть индивидуальный показатель для каждого опциона на некоторый базовый контракт или единый показатель для всех опционов на один и тот же базовый контракт. В последнем случае показатель представляет собой среднюю из всех индивидуальных значений волатильности. С этой целью отдельные значения рыночной волатильности взвешиваются по какому-нибудь критерию, например по объему сделки, количеству открытых позиций. Чаще всего наибольший вес присваивается опционам на деньгах.
Рыночная волатильность постоянно меняется, поскольку постоянно меняются цены опционов, а также другие рыночные условия. Рынок словно непрерывно опрашивает всех участников и формирует согласованное мнение относительно волатильности базового контракта. Это не опрос в традиционном смысле, поскольку трейдеры не собираются вместе и не решают вопрос голосованием, однако они делают предложения о покупке и продаже, и цена опциона отражает равновесие спроса и предложения. Это равновесие можно перевести на язык рыночной волатильности.
Хотя премией обычно называют цену опциона, нередко трейдеры называют рыночную волатильность премией или уровнем премии. Если текущая рыночная волатильность высока по историческим меркам или по сравнению с недавней волатильностью базового контракта, то трейдер может сказать, что уровни премии высоки; если рыночная волатильность необычно низка, то он может сказать, что уровни премии невысоки.
Имей трейдер надежную формулу цены опциона и возможность видеть через магический кристалл будущую волатильность базового контракта, то он смог бы точно оценивать опционы на этот контракт. Он мог бы оценить разницу между теоретической стоимостью каждого опциона и его рыночной ценой, продать опционы, оцененные выше теоретической стоимости, и купить недооцененные опционы. Если бы ему пришлось выбирать, какой из двух пере оцененных опционов продать, то он просто продал бы тот, что переоценен больше. Однако трейдер, имеющий информацию о рыночной волатильности, получает другой ориентир для сравнения. Он может сравнивать рыночную волатильность опциона либо с прогнозируемой волатильностью, либо с рыночной волатильностью других опционов на тот же базовый контракт. Возвращаясь к нашему примеру со 105 коллом, можно сказать, что при теоретической стоимости 0,96 и цене 1,34 этот колл переоценен на 0,38. Но с точки зрения волатильности он переоценен на 2,5 %, поскольку теоретическая стоимость рассчитана на основе 16 %-ной волатильности (принятой трейдером), а цена – на основе 18,5 %-ной (рыночной) волатильности. Из-за необычных характеристик опционов серьезному трейдеру полезнее анализировать цену опциона с точки зрения рыночной волатильности, а не абсолютного значения в долларах.
Предположим, что 98 колл на казначейские облигации продается по 3-32 (3500 долл.), а соответствующая рыночная волатильность – 10,5 %. Предположим также, что 102 колл с той же датой экспирации продается за 1-16 (1250 долл.), его рыночная волатильность – 11,5 %. В долларовом выражении 102 колл дешевле 98 колла на 2250 долл. Однако опытный трейдер может прийти к выводу, что 98 колл на самом деле дешевле 102 колла, поскольку его рыночная волатильность на целый процентный пункт меньше. Означает ли это, что следует купить 98 колл и продать 102 колл? Совсем не обязательно. Если будущая волатильность казначейских облигаций окажется равной 8 %, то оба опциона переоценены, а если 14 %, то недооценены. Кроме того, чувствительность этих опционов к изменению рыночных условий может быть разной, и поэтому покупка нескольких 102 коллов может быть более желательной, чем покупка одного 98 колла. Если мы проигнорируем эти соображения, то 98 колл будет выглядеть лучше относительно 102 колла, поскольку его рыночная волатильность ниже.
Хотя опционные трейдеры и пользуются всеми четырьмя показателями волатильности, самые важные из них – будущая и рыночная. Будущая волатильность базового контракта определяет стоимость опционов на этот контракт. Рыночная волатильность отражает цену каждого опциона. Стоимость и цена – два показателя, которые интересуют всех трейдеров, а не только опционных. Если у контракта высокая стоимость и низкая цена, то трейдер предпочитает быть покупателем, если у контракта низкая стоимость и высокая цена, то трейдер предпочитает быть продавцом. Опционный трейдер обычно сравнивает будущую волатильность с рыночной. Если по сравнению с будущей волатильностью рыночная волатильность невысока, он покупает опцион, а если высока – продает. Однако будущая волатильность неизвестна, поэтому, чтобы оценить ее, мы интересуемся исторической и прогнозируемой волатильностью. Но в конечном счете стоимость опциона определяет именно будущая волатильность.
Чтобы начинающему трейдеру было легче разобраться в видах волатильности, рассмотрим следующую аналогию с прогнозом погоды. Предположим, что одним июльским утром проживающий в Чикаго трейдер просыпается и размышляет, в чем идти на работу. Может ли он выбрать теплую куртку? Вряд ли, поскольку исторически известно, что июль в Чикаго не бывает настолько холодным, чтобы потребовалась зимняя одежда. Затем трейдер включает радио или телевизор и узнает прогноз погоды. Обещают ясную и жаркую погоду – около 32 °С. Исходя из этого, наш трейдер принимает решение: он пойдет в рубашке с короткими рукавами, без свитера или пиджака, а зонтик брать ни к чему. Однако на всякий случай он выглядывает в окно, чтобы узнать, как одеты люди. К его удивлению, все идут в пальто и с зонтиками. Одежда тех, кто уже вышел на улицу, подразумевает совершенно иную погоду. Так что теперь должен выбрать трейдер? Ему нужно принять какое-то решение, но чему верить – прогнозу погоды или людям на улице? Ответа на этот вопрос нет, потому что будущая погода будет известна только в конце дня.
