Лит.:Corin F., Paul Fourmarier (25. XII.1877 — 1940), Obitnary notice, «Geological Newsletter», 1970, v. 3, p. 289—90.
шанкр мягкий
— различные венерические заболевания. Последующие труды Ф. посвящены ряду аспектов учения о сифилисе (морфология сифилидов кожи; бытовой и врождённый сифилис; сифилис внутренних органов и нервной системы; лечение). Рассматривал сифилис как заболевание всего организма; указал, в частности, на сифилитическую природу
прогрессивного паралича
. Основатель (1901) французского общества санитарной и моральной профилактики венерических болезней. Именем Ф. названы проявления сифилиса (например, т. н. третичная розеола) и некоторые кожные заболевания.
Соч. в рус. пер.: Сифилис мозга, СПБ, 1881; Сифилис и брак, Тверь, 1882; Учение о сифилисе, в. 1—2, М., 1899; Уклонение в развитии при наследственном сифилисе, СПБ, 1899; Руководство к патологии и терапии сифилиса, в. 4 — Третичный период, СПБ, 1903; Поздний вторичный сифилис, СПБ, 1908.
А. С. Рабен.
Геда
. Играл видную роль на Марсельском конгрессе 1879, принявшем решение об основании
Рабочей партии
, в дальнейшем примкнул к
поссибилистам
. Сотрудничал в ряде социалистических газет. Участвовал в 1885 в основании «Ревю сосиалист» («Revue socialiste»). В конце 80-х гг. выступал как теоретик мелкобуржуазного реформистского социализма. В 1898—1902 депутат парламента (мильеранист). Автор многих научно-популярных работ по истории социализма и ряда художественных произведений.
Соч.: L'idйalisme social, P., 1898; Les thйories socialistes au XIX siиcle de Babeuf а Proudhon, P., 1904; La crise socialiste, P., 1908.
Зондербунд
). Один из авторов конституции Швейцарии 1848. В 1848—61 член Федерального совета (правительства) Швейцарии (возглавлял ведомство юстиции и иностранных дел). В 1848—49 первый президент Швейцарской конфедерации.


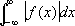 ,
,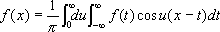 . (1)
. (1)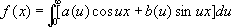 , (2)
, (2)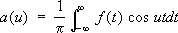 ;
;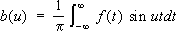 .
.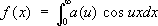 ,
,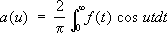 .
.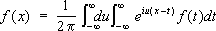 .
.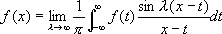 (3)
(3)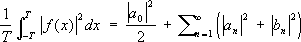
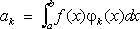 .
.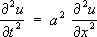 при краевых условиях
u(0,
t) =
u(
l,
t) = 0 и начальных условиях
u(
x,0) =
f(
x);
u'
t
(
x, 0) =
F(
x); 0 Ј
xЈ
l. Решения этого уравнения, имеющие вид
X(
x)
T(
t) и удовлетворяющие краевым условиям, выражаются формулой:
при краевых условиях
u(0,
t) =
u(
l,
t) = 0 и начальных условиях
u(
x,0) =
f(
x);
u'
t
(
x, 0) =
F(
x); 0 Ј
xЈ
l. Решения этого уравнения, имеющие вид
X(
x)
T(
t) и удовлетворяющие краевым условиям, выражаются формулой: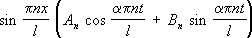 .
.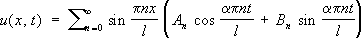
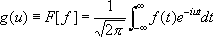 , (1)
, (1)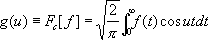 (2)
(2)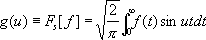 (3)
(3)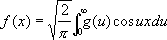 , (4)
, (4)