Рис
изучил пространства
l
pи
L
p(
a,
b), а С.
Банах
в 1922 выделил полные линейные нормированные пространства (банаховы пространства). В 1930—40-х гг. в работах Т.
Карлемана
, Ф. Риса, американских математиков М. Стоуна и Дж.
Неймана
была построена абстрактная теория самосопряжённых операторов в гильбертовом пространстве.
В СССР первые исследования по Ф. а. появились в 30-х гг.: работы
А. Н. Колмогорова (1934) по теории линейных топологических пространств;
Н. Н. Боголюбова (1936) по инвариантным мерам в динамических системах;
Л. В. Канторовича (1937) и его учеников по теории полуупорядоченных пространств, применениям Ф. а. к вычислительной математике и др.; М. Г. Крейна и его учеников (1938) по углублённому изучению геометрии банаховых пространств, выпуклых множеств и конусов в них, теории операторов и связей с различными проблемами классического математического анализа и др.; И. М. Гельфанда и его учеников (1940) по теории нормированных колец (банаховых алгебр) и др.
Для современного этапа развития Ф. а. характерно усиление связей с теоретической физикой, а также с различными разделами классического анализа и алгебры, например теорией функций многих комплексных переменных, теорией дифференциальных уравнений с частными производными и т.п.
2. Понятие пространства.Наиболее общими пространствами, фигурирующими в Ф. а., являются линейные (векторные) топологические пространства, т. е. линейные пространства Хнад полем комплексных чисел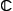 (или действительных чисел
(или действительных чисел
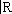 ), которые одновременно и топологические, причём линейные операции непрерывны в рассматриваемой топологии. Более частная, но очень важная ситуация возникает, когда в линейном пространстве
Хможно ввести норму (длину) векторов, свойства которой являются обобщением свойств длины векторов в обычном евклидовом пространстве. Именно, нормой элемента
xО
Хназывается действительное число ||
x|| такое, что всегда ||
x|| ³ 0 и ||
x|| = 0 тогда и только тогда, когда
x= 0;
), которые одновременно и топологические, причём линейные операции непрерывны в рассматриваемой топологии. Более частная, но очень важная ситуация возникает, когда в линейном пространстве
Хможно ввести норму (длину) векторов, свойства которой являются обобщением свойств длины векторов в обычном евклидовом пространстве. Именно, нормой элемента
xО
Хназывается действительное число ||
x|| такое, что всегда ||
x|| ³ 0 и ||
x|| = 0 тогда и только тогда, когда
x= 0;
||l x|| = |l| || x||, l О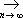 x, если ||
x
n—
x||
x, если ||
x
n—
x||
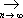 0.
0.
В большом числе задач возникает ещё более частная ситуация, когда в линейном пространстве Хможно ввести скалярное произведение — обобщение обычного скалярного произведения в евклидовом пространстве. Именно, скалярным произведением элементов x, уО Хназывается комплексное число ( x, у) такое, что всегда ( x, x) ³ 0 и ( x, x) = 0 тогда и только тогда, когда x= 0;
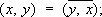
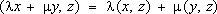 , l, m О
, l, m О
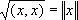 является нормой элемента
x. Такое пространство называется предгильбертовым. Для конструкций Ф. а. важно, чтобы рассматриваемые пространства были полными (т. е. из того, что
является нормой элемента
x. Такое пространство называется предгильбертовым. Для конструкций Ф. а. важно, чтобы рассматриваемые пространства были полными (т. е. из того, что
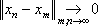 для
x
m,
x
nО
X,следует существование предела
для
x
m,
x
nО
X,следует существование предела
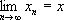 , также являющегося элементом
Х). Полное линейное нормированное и полное предгильбертово пространства называются, соответственно, банаховым и гильбертовым. При этом известная процедура пополнения метрического пространства (аналогичная переходу от рациональных чисел к действительным) в случае линейного нормированного (предгильбертова) пространства приводит к банахову (гильбертову) пространству.
, также являющегося элементом
Х). Полное линейное нормированное и полное предгильбертово пространства называются, соответственно, банаховым и гильбертовым. При этом известная процедура пополнения метрического пространства (аналогичная переходу от рациональных чисел к действительным) в случае линейного нормированного (предгильбертова) пространства приводит к банахову (гильбертову) пространству.
Обычное евклидово пространство является одним из простейших примеров (действительного) гильбертова пространства . Однако в Ф. а. играют основную роль бесконечномерные пространства, т. е. такие, в которых существует бесконечное число линейно независимых векторов. Вот примеры таких пространств, элементами которых являются классы комплекснозначных (т. е. со значениями в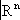 , норма ||
x|| =
, норма ||
x|| =
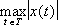 ; банахово пространство
L
p(
T) всех суммируемых с
р-й (
p³ 1) степенью функций на
Т, норма
; банахово пространство
L
p(
T) всех суммируемых с
р-й (
p³ 1) степенью функций на
Т, норма
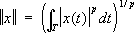 ; банахово пространство
l
pвсех последовательностей таких, что
; банахово пространство
l
pвсех последовательностей таких, что
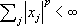 , здесь
, здесь
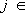
 (множеству целых чисел), норма ||
x|| =(е
(множеству целых чисел), норма ||
x|| =(е
 |
x
j|
p
)
1/
p; в случае
p= 2 пространства
l
2и
L
2(
T) гильбертовы, при этом, например, в
L
2(
T) скалярное произведение
|
x
j|
p
)
1/
p; в случае
p= 2 пространства
l
2и
L
2(
T) гильбертовы, при этом, например, в
L
2(
T) скалярное произведение
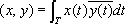 ; линейное топологическое пространство
D(
; линейное топологическое пространство
D(
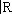 ), состоящее из бесконечно дифференцируемых функций на
), состоящее из бесконечно дифференцируемых функций на
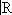 , каждая из которых финитна [т. е. равна нулю вне некоторого интервала (
а,
b)]; при этом
x
n
, каждая из которых финитна [т. е. равна нулю вне некоторого интервала (
а,
b)]; при этом
x
n
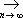 x,если
x
n(
t) равномерно финитны [т. е. (
а,
b) не зависит от
n] и сходятся равномерно со всеми своими производными к соответствующим производным
x(
t).
x,если
x
n(
t) равномерно финитны [т. е. (
а,
b) не зависит от
n] и сходятся равномерно со всеми своими производными к соответствующим производным
x(
t).
Все эти пространства бесконечномерны, проще всего это видно для l 2: векторы e j= {0,..., 0, 1, 0,...} линейно независимы.
С геометрической точки зрения наиболее простыми являются гильбертовы пространства Н, свойства которых больше всего напоминают свойства конечномерных евклидовых пространств. В частности, два вектора x, уО Нназываются ортогональными ( x^ y), если ( x, у) = 0. Для любого xО Нсуществует его проекция на произвольное подпространство F— линейное замкнутое подмножество Н, т. е. такой вектор x F, что x— x F^ fдля любого fО F. Благодаря этому факту большое количество геометрических конструкций, имеющих место в евклидовом пространстве, переносится на Н, где они часто приобретают аналитический характер. Так, например, обычная процедура ортогонализации приводит к существованию в Нортонормированного базиса — последовательности векторов e j, jО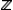 , из
Нтаких, что ||
e
j|| = 1,
e
j^
e
kпри
j¹
k, и для любого
xО
Hсправедливо «покоординатное» разложение
, из
Нтаких, что ||
e
j|| = 1,
e
j^
e
kпри
j¹
k, и для любого
xО
Hсправедливо «покоординатное» разложение
x= е x
je
j(1)
x
je
j(1)
где x j= ( x, e j), || x|| = е |
x
j|
2(для простоты
Нпредполагается сепарабельным, т. е. в нём существует счётное всюду плотное множество). Если в качестве
Нвзять
L
2(0, 2p) и положить
|
x
j|
2(для простоты
Нпредполагается сепарабельным, т. е. в нём существует счётное всюду плотное множество). Если в качестве
Нвзять
L
2(0, 2p) и положить
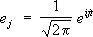 ,
j=...,—1, 0, 1..., то (1) даст разложение функции
x(
t) О
L
2(0, 2p) в ряд Фурье, сходящийся в среднем квадратичном. Кроме того, соотношение (1) показывает, что соответствие между
Ни
l
2'
{xj},
jО
,
j=...,—1, 0, 1..., то (1) даст разложение функции
x(
t) О
L
2(0, 2p) в ряд Фурье, сходящийся в среднем квадратичном. Кроме того, соотношение (1) показывает, что соответствие между
Ни
l
2'
{xj},
jО
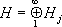 гильбертовых пространств
H
j— конструкция, подобная образованию
Нодномерными подпространствами, описываемому формулой (1); факторизация и пополнение: на исходном линейном пространстве
Хзадаётся квазискалярное произведение [т. е. возможно равенство (
x,
x) = 0 для
x¹ 0], часто весьма экзотического характера, и
Нстроится процедурой пополнения
Хотносительно (.,.) после предварительного отождествления с 0 векторов
x, для которых (
x,
x) = 0; тензорное произведение
гильбертовых пространств
H
j— конструкция, подобная образованию
Нодномерными подпространствами, описываемому формулой (1); факторизация и пополнение: на исходном линейном пространстве
Хзадаётся квазискалярное произведение [т. е. возможно равенство (
x,
x) = 0 для
x¹ 0], часто весьма экзотического характера, и
Нстроится процедурой пополнения
Хотносительно (.,.) после предварительного отождествления с 0 векторов
x, для которых (
x,
x) = 0; тензорное произведение
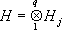 — образование его аналогично переходу от функций одной переменной
f(
x
1) к функциям многих переменных
f(
x
1,...,
x
q); проективный предел
— образование его аналогично переходу от функций одной переменной
f(
x
1) к функциям многих переменных
f(
x
1,...,
x
q); проективный предел
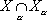 банаховых пространств — здесь
банаховых пространств — здесь
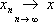 (грубо говоря), если
(грубо говоря), если
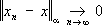 для каждого a; индуктивный предел
для каждого a; индуктивный предел
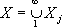 банаховых пространств
X
1М
X
2М..., здесь
банаховых пространств
X
1М
X
2М..., здесь
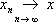 , если все
x
j, начиная с некоторого
j
0, лежат в одном
X
j0, и в нём
, если все
x
j, начиная с некоторого
j
0, лежат в одном
X
j0, и в нём
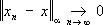 . Две последние процедуры обычно применяются для построения линейных топологических пространств. Таковы, например, ядерные пространства — проективный предел гильбертовых пространств
Н
a, обладающих тем свойством, что для каждого a найдётся b такое, что
h
bМ
Н
a, и это — т. н. вложение Гильберта — Шмидта [D (
. Две последние процедуры обычно применяются для построения линейных топологических пространств. Таковы, например, ядерные пространства — проективный предел гильбертовых пространств
Н
a, обладающих тем свойством, что для каждого a найдётся b такое, что
h
bМ
Н
a, и это — т. н. вложение Гильберта — Шмидта [D (
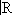 ) — пример ядерного пространства].
) — пример ядерного пространства].
Разработан важный раздел Ф, а., в котором изучаются пространства с конической структурой «x 0» (полуупорядоченностью). Пример такого пространства — действительное
С(
Т), в нём считается
x
0» (полуупорядоченностью). Пример такого пространства — действительное
С(
Т), в нём считается
x
 0, если
x(
t³)0 для всех
tО
T.
0, если
x(
t³)0 для всех
tО
T.
3. Операторы (общие понятия). Функционалы.Пусть X, Y— линейные пространства; отображение A: X® Yназывается линейным, если для x, уО X, l, m О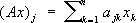 ,
,
где x 1,..., x nи ( Ax) 1,..., ( Ax) n — координаты векторов xи Axсоответственно. При переходе к бесконечномерным линейным топологическим пространствам положение значительно усложняется. Здесь прежде всего необходимо различать непрерывные и разрывные линейные операторы (для конечномерных пространств они всегда непрерывны). Так, действующий из пространства L 2( а, b) в него же оператор
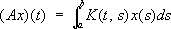 (2)
(2)
(где K( t, s) — ограниченная функция — ядро А) — непрерывен, в то время как определённый на подпространстве C 1( a, b) М L 2( a, b) оператор дифференцирования
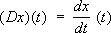 (3)
(3)
является разрывным (вообще, характерной особенностью разрывных операторов является то, что они не определены на всём пространстве).
Непрерывный оператор A: X® Y, где X, Y— банаховы пространства, характеризуется тем, что
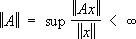 ,
,
поэтому его называют также ограниченным. Совокупность всех ограниченных операторов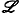 (
X,
Y) относительно обычных алгебраических операций образует банахово пространство с нормой ||
A||. Свойства
(
X,
Y) относительно обычных алгебраических операций образует банахово пространство с нормой ||
A||. Свойства
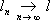 , если
, если
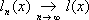 для каждого
xО
X], относительно которой шар, т. е. множество точек
xО
Хтаких, что ||
x|| Ј
r, уже будет компактным (такого эффекта никогда не будет в бесконечномерном пространстве относительно топологии, порождаемой нормой). Это позволяет более детально изучить ряд геометрических вопросов для множеств из
X', например установить структуру произвольного компактного выпуклого множества как замкнутой оболочки своих крайних точек (теорема Крейна — Мильмана).
для каждого
xО
X], относительно которой шар, т. е. множество точек
xО
Хтаких, что ||
x|| Ј
r, уже будет компактным (такого эффекта никогда не будет в бесконечномерном пространстве относительно топологии, порождаемой нормой). Это позволяет более детально изучить ряд геометрических вопросов для множеств из
X', например установить структуру произвольного компактного выпуклого множества как замкнутой оболочки своих крайних точек (теорема Крейна — Мильмана).
Важной задачей Ф. а. является отыскание общего вида функционалов для конкретных пространств. В ряде случаев (помимо гильбертова пространства) это удаётся сделать, например ( l p)ў, p> 1, состоит из функций вида е x
je
j, где
x
je
j, где
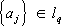 ,
,
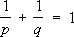 . Однако для большинства банаховых (и в особенности линейных топологических) пространств функционалы будут элементами новой природы, не конструирующимися просто средствами классического анализа. Так, например, при фиксированных
t
0и
mна пространстве
D(
. Однако для большинства банаховых (и в особенности линейных топологических) пространств функционалы будут элементами новой природы, не конструирующимися просто средствами классического анализа. Так, например, при фиксированных
t
0и
mна пространстве
D(
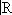 ) определён функционал
) определён функционал
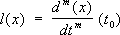 . В случае
m= 0 его ещё можно записать «классическим» образом — при помощи интеграла, однако при
m³ 1 это уже невозможно. Элементы из (
D(
. В случае
m= 0 его ещё можно записать «классическим» образом — при помощи интеграла, однако при
m³ 1 это уже невозможно. Элементы из (
D(
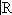 ))ў называются
обобщёнными функциями
(распределениями). Обобщённые функции как элементы сопряжённого пространства можно строить и тогда, когда
D(
))ў называются
обобщёнными функциями
(распределениями). Обобщённые функции как элементы сопряжённого пространства можно строить и тогда, когда
D(
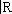 ) заменено другим пространством Ф, состоящим как из бесконечно, так и конечное число раз дифференцируемых функций; при этом существенную роль играют тройки пространств Ф' Й
НЙ Ф, где
Н— исходное гильбертово пространство, а Ф — линейное топологическое (в частности, гильбертово с др. скалярным произведением) пространство, например
) заменено другим пространством Ф, состоящим как из бесконечно, так и конечное число раз дифференцируемых функций; при этом существенную роль играют тройки пространств Ф' Й
НЙ Ф, где
Н— исходное гильбертово пространство, а Ф — линейное топологическое (в частности, гильбертово с др. скалярным произведением) пространство, например
Ф = W l 2( T).
Дифференциальный оператор D, фигурирующий в (3), будет непрерывным, если его понимать действующим в L 2[ a, b] из пространства C 1[ a, b], снабженного нормой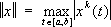 ,
,
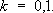 Однако для многих задач, и прежде всего для спектральной теории, такие дифференциальные операторы необходимо интерпретировать как действующие в одном и том же пространстве. Эти и другие близкие задачи привели к построению общей теории неограниченных, в частности неограниченных самосопряжённых, и эрмитовых операторов.
Однако для многих задач, и прежде всего для спектральной теории, такие дифференциальные операторы необходимо интерпретировать как действующие в одном и том же пространстве. Эти и другие близкие задачи привели к построению общей теории неограниченных, в частности неограниченных самосопряжённых, и эрмитовых операторов.
4. Специальные классы операторов. Спектральная теория.Многие задачи приводят к необходимости изучать разрешимость уравнения вида Cx= y, где С— некоторый оператор, уО Y— заданный, а xО Х— искомый векторы. Например, если Х= Y= L 2( а, b), С= Е— А, где А— оператор из (2), а Е— тождественный оператор, то получается интегральное уравнение Фредгольма 2-го рода; если С— дифференциальный оператор, то получается дифференциальное уравнение, и т.п. Однако здесь нельзя рассчитывать на достаточно полную аналогию с линейной алгеброй, не ограничивая класс рассматриваемых операторов. Одним из важнейших классов операторов, наиболее близких к конечномерному случаю, являются компактные (вполне непрерывные) операторы, характеризующиеся тем, что переводят каждое ограниченное множество из Хв множество из Y, замыкание которого компактно [таков, например, оператор Аиз (2)]. Для компактных операторов построена теория разрешимости уравнения x— Ax= у, вполне аналогичная конечномерному случаю (и содержащая, в частности, теорию упомянутых интегральных уравнений) (Ф. Рис).
В разнообразных задачах математической физики возникает т. н. задача на собственные значения : для некоторого оператора А: Х® Хтребуется выяснить возможность нахождения решения j ¹ 0 ( собственного вектора ) уравнения Аj = lj при некотором l О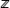 l
jx
je
j, (4)
l
jx
je
j, (4)
где l j , — собственное значение, отвечающее e j. Для конечномерного Хвопрос о таком представлении полностью выяснен, при этом в случае кратных собственных значений для получения базиса в Хнужно, вообще говоря, добавить к собственным т. н. присоединённые векторы. Набор SpA собственных значений в этом случае называется спектром А.
Первое перенесение этой картины на бесконечномерный случай было дано для интегральных операторов типа Аиз (2) с симметричным ядром [т. е. K( t, s) = K( s, t) и действительно] (Д. Гильберт). Затем подобная теория была развита для общих компактных самосопряжённых операторов в гильбертовом пространстве. Однако при переходе к простейшим некомпактным операторам возникли трудности, связанные с. самим определением спектра. Так, ограниченный оператор в L 2[ a, b]
( Tx)( t) = tx( t) (5)
не имеет собственных значений. Поэтому определение спектра было пересмотрено, обобщено и выглядит сейчас следующим образом.
Пусть Х— банахово пространство, АО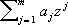 — многочлен, то
f(
A) =
— многочлен, то
f(
A) =
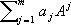 (степень оператора понимается как последовательное его применение). Однако если
f(
z) — аналитическая функция, то так прямо понимать
f(
A) уже не всегда возможно; в этом случае
f(
A) определяется следующей формулой, если
f(
z) аналитична в окрестности SpA, а Г — контур, охватывающий SpA и лежащий в области аналитичности
f(
z):
(степень оператора понимается как последовательное его применение). Однако если
f(
z) — аналитическая функция, то так прямо понимать
f(
A) уже не всегда возможно; в этом случае
f(
A) определяется следующей формулой, если
f(
z) аналитична в окрестности SpA, а Г — контур, охватывающий SpA и лежащий в области аналитичности
f(
z):
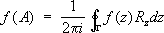 . (6)
. (6)
При этом алгебраические операции над функциями переходят в аналогичные операции над операторами [т. е. отображение f( z) ® f( A) — гомоморфизм]. Эти конструкции не дают возможности выяснить, например, вопросы полноты собственных и присоединённых векторов для общих операторов, однако для самосопряжённых операторов, представляющих основной интерес, например, для квантовой механики, подобная теория полностью разработана.
Пусть Н— гильбертово пространство. Ограниченный оператор А: Н® Нназывается самосопряжённым, если ( Ax, у) = ( x, Ау) (в случае неограниченного Аопределение более сложно). Если Н n-мерно, то в нём существует ортонормированный базис собственных векторов самосопряжённого оператора А; другими словами, имеют место разложения:
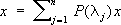 ,
,
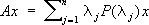 , (7)
, (7)
где P(l j ) — оператор проектирования (проектор) на подпространство, натянутое на все собственные векторы оператора А, отвечающие одному и тому же собственному значению l j .
Оказывается, что эти формулы могут быть обобщены на произвольный самосопряжённый оператор из Н, только сами проекторы P(l j ) могут не существовать, поскольку могут отсутствовать и собственные векторы [таков, например, оператор Тв (5)]. В формулах (7) суммы заменяются теперь интегралами Стилтьеса по неубывающей операторнозначной функции Е(l) [которая в конечномерном случае равна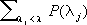 ], называется разложением единицы, или спектральной (проекторной) мерой, точки роста которой совпадают со спектром Sp
А. Если привлечь обобщённые функции, то формулы типа (7) сохраняются. Именно, если имеется тройка Ф' Й
НЙ
Ф, где Ф, например, ядерно, причём
Апереводит Ф в Фў и непрерывно, то соотношения (7) имеют место, только суммы переходят в интегралы по некоторой скалярной мере, а
Е(l) теперь «проектирует» Ф в Фў, давая векторы из Фў, которые будут собственными в обобщённом смысле для
Ас собственным значением l. Аналогичные результаты справедливы для т. н. нормальных операторов (т. е. коммутирующих со своими сопряжёнными). Например, они верны для
унитарных операторов
U— таких ограниченных операторов, которые отображают всё
Нна всё
Ни сохраняют при этом скалярное произведение. Для них спектр Sp
Uрасположен на окружности |
z| = 1, вдоль которой и производится интегрирование в аналогах формул (6). См. также
Спектральный анализ
линейных операторов.
], называется разложением единицы, или спектральной (проекторной) мерой, точки роста которой совпадают со спектром Sp
А. Если привлечь обобщённые функции, то формулы типа (7) сохраняются. Именно, если имеется тройка Ф' Й
НЙ
Ф, где Ф, например, ядерно, причём
Апереводит Ф в Фў и непрерывно, то соотношения (7) имеют место, только суммы переходят в интегралы по некоторой скалярной мере, а
Е(l) теперь «проектирует» Ф в Фў, давая векторы из Фў, которые будут собственными в обобщённом смысле для
Ас собственным значением l. Аналогичные результаты справедливы для т. н. нормальных операторов (т. е. коммутирующих со своими сопряжёнными). Например, они верны для
унитарных операторов
U— таких ограниченных операторов, которые отображают всё
Нна всё
Ни сохраняют при этом скалярное произведение. Для них спектр Sp
Uрасположен на окружности |
z| = 1, вдоль которой и производится интегрирование в аналогах формул (6). См. также
Спектральный анализ
линейных операторов.
5. Нелинейный функциональный анализ.Одновременно с развитием и углублением понятия пространства шло развитие и обобщение понятия функции. В конечном счёте оказалось необходимым рассматривать отображения (не обязательно линейные) одного пространства в другое (часто — в исходное). Одной из центральных задач нелинейного Ф. а. является изучение таких отображений. Как и в линейном случае, отображение пространства в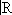 ) называется функционалом. Для нелинейных отображений (в частности, нелинейных функционалов) можно различными способами определить дифференциал, производную по направлению и т.д. аналогично соответствующим понятиям классического анализа. Выделение из отображения квадратичного и т.д. членов приводит к формуле, аналогичной формуле Тейлора.
) называется функционалом. Для нелинейных отображений (в частности, нелинейных функционалов) можно различными способами определить дифференциал, производную по направлению и т.д. аналогично соответствующим понятиям классического анализа. Выделение из отображения квадратичного и т.д. членов приводит к формуле, аналогичной формуле Тейлора.
Важной задачей нелинейного Ф. а. является задача отыскания неподвижных точек отображения (точка xназывается неподвижной для отображения F, если Fx= x). К отысканию неподвижных точек сводятся многие задачи о разрешимости операторных уравнений, а также задачи отыскания собственных значений и собственных векторов нелинейных операторов. При решении уравнений с нелинейными операторами, содержащими параметр, возникает существенное для нелинейного Ф. а. явление — т. н. точки ветвления (решений).
При исследовании неподвижных точек и точек ветвления используются топологические методы: обобщения на бесконечномерные пространства теоремы Брауэра о существовании неподвижных точек отображений конечномерных пространств, степени отображений и т.п. Топологические методы Ф. а. развивались польским математиком Ю. Шаудером, французским математиком Ж. Лере, советскими математиками М. А. Красносельским, Л. А. Люстерником и др.
6. Банаховы алгебры. Теория представлений.На ранних этапах развития Ф. а. изучались задачи, для постановки и решения которых необходимы были лишь линейные операции над элементами пространства. Исключение составляют, пожалуй, только теория колец операторов (факторов) (Дж. Нейман, 1929) и теория абсолютно сходящихся рядов Фурье (Н. Винер , 1936). В конце 30-x гг. в работах японского математика М. Нагумо, советских математиков И. М, Гельфанда, Г. Е. Шилова, М. А. Наймарка и др. стала развиваться теория т. н. нормированных колец (современное название — банаховы алгебры), в которой, кроме операций линейного пространства, аксиоматизируется операция умножения (причём || xy|| Ј || x|| || y||). Типичными представителями банаховых алгебр являются кольца ограниченных операторов, действующих в банаховом пространстве Х(умножение в нём — последовательное применение операторов — необходимо с учётом порядка), различного рода функциональные пространства, например C( T) с обычным умножением, L 1(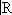 ) со свёрткой в качестве произведения, и широкое обобщение их — класс т. н. групповых алгебр (топологические группы
G), состоящих из комплекснозначных функций или мер, определённых на
Gсо свёрткой (в различных, не обязательно эквивалентных вариантах) в качестве умножения.
) со свёрткой в качестве произведения, и широкое обобщение их — класс т. н. групповых алгебр (топологические группы
G), состоящих из комплекснозначных функций или мер, определённых на
Gсо свёрткой (в различных, не обязательно эквивалентных вариантах) в качестве умножения.
Пусть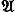 — коммутативная (т. е.
xy=
ухдля любых
x,
уО
— коммутативная (т. е.
xy=
ухдля любых
x,
уО
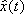 на
М, причём сумме
x+
yи произведению
xyсоответствуют сумма и произведение функций. Другими словами, существует гомоморфизм
на
М, причём сумме
x+
yи произведению
xyсоответствуют сумма и произведение функций. Другими словами, существует гомоморфизм
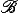 борелевских подмножеств
G, инвариантная справа: для любых
ВО
борелевских подмножеств
G, инвариантная справа: для любых
ВО
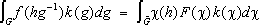 , где c(
h) — характер группы
G: непрерывная функция на
Gтакая, что |c(
h)| = 1 и c(
h
1h
2) = c(
h
1)c(
h
2),
dc — мера Хаара на группе характеров
, где c(
h) — характер группы
G: непрерывная функция на
Gтакая, что |c(
h)| = 1 и c(
h
1h
2) = c(
h
1)c(
h
2),
dc — мера Хаара на группе характеров
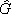 , а
, а
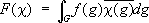 ,
,
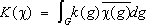
— обобщённое преобразование Фурье функций f( g) и k( g), которое продолжается до изоморфизма L 2( G, dg) в L 2( , dc). Для некоммутативных групп ситуация во многом усложняется. Если
Gкомпактна, то представление группы операторов сдвига (или, короче, группы сдвигов) удаётся хорошо описать; в этом случае
L
2(
G,
dg) распадается в прямую сумму конечномерных инвариантных относительно сдвигов подпространств. Если
Gнекомпактна, то также получается разложение
L
2(
G,
dg) на более простые инвариантные части, но уже не в прямую сумму, а в прямой интеграл.
, dc). Для некоммутативных групп ситуация во многом усложняется. Если
Gкомпактна, то представление группы операторов сдвига (или, короче, группы сдвигов) удаётся хорошо описать; в этом случае
L
2(
G,
dg) распадается в прямую сумму конечномерных инвариантных относительно сдвигов подпространств. Если
Gнекомпактна, то также получается разложение
L
2(
G,
dg) на более простые инвариантные части, но уже не в прямую сумму, а в прямой интеграл.
Если G=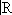 , то теория унитарных представлений может быть сведена к теории самосопряжённых операторов. Именно, однопараметрическая группа унитарных операторов
Т
l, l О
, то теория унитарных представлений может быть сведена к теории самосопряжённых операторов. Именно, однопараметрическая группа унитарных операторов
Т
l, l О
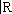 в гильбертовом пространстве
Ндопускает представление
Т
l= exp
il
A, где
А— самосопряжённый оператор (теорема Стоун а); оператор
Аназывается инфинитезимальным оператором (генератором) группы {
Т'
l}. Этот результат находит важные применения в изучении преобразований фазового пространства классической механики. Эта связь, а также приложения в статистической физике лежат в основе обширной ветви Ф. а. —
эргодической теории
. Связь между однопараметрическими группами преобразований и их генераторами допускает значительные обобщения: операторы
T
lне обязаны быть унитарными, могут действовать в банаховых и более общих пространствах и даже быть определёнными лишь для l ³ 0 (т. н. теория полугрупп операторов). Этот раздел Ф. а. имеет приложения в теории дифференциальных уравнений с частными производными и теории случайных (именно марковских) процессов.
в гильбертовом пространстве
Ндопускает представление
Т
l= exp
il
A, где
А— самосопряжённый оператор (теорема Стоун а); оператор
Аназывается инфинитезимальным оператором (генератором) группы {
Т'
l}. Этот результат находит важные применения в изучении преобразований фазового пространства классической механики. Эта связь, а также приложения в статистической физике лежат в основе обширной ветви Ф. а. —
эргодической теории
. Связь между однопараметрическими группами преобразований и их генераторами допускает значительные обобщения: операторы
T
lне обязаны быть унитарными, могут действовать в банаховых и более общих пространствах и даже быть определёнными лишь для l ³ 0 (т. н. теория полугрупп операторов). Этот раздел Ф. а. имеет приложения в теории дифференциальных уравнений с частными производными и теории случайных (именно марковских) процессов.
Лит.:Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа 4 изд., М., 1976; Ахиезер Н. И., Глазман И. М., Теория линейных операторов в гильбертовом пространстве, 2 изд., М., 1966; Вулих Б. З., Введение в теорию полуупорядоченных пространств, М., 1961; Банах С. С., Курс функцioнального аналiзу Кипв, 1948; Рисс Ф., Секефальви-Надь Б., Лекции по функциональному анализу, пер. с франц., М., 1954; Соболев С. Л., Некоторые применения функционального анализа в математической физике, Л., 1950; Канторович Л. В., Акилов Г. П., Функциональный анализ в нормированных пространствах, М., 1959; Красносельский М. А., Забрейко П. П., Геометрические методы нелинейного анализа, М., 1975; Наймарк М. А., Нормированные кольца, 2 изд., М., 1968; Рудин У., Функциональный анализ, пер. с англ., М., 1975; Иосида К., Функциональный анализ, пер, с англ., М., 1967; Данфорд Н., Шварц Дж., Линейные операторы, пер. с англ., ч. 1—3, М., 1962—74; Хилле Э., Филлипс Р., Функциональный анализ и полугруппы, пер. с англ., 2 изд., М., 1962; Эдвардс Р. Э., Функциональный анализ. Теория и приложения пер с англ., М., 1969.
Ю. М. Березанский, Б. М. Левитан.
Функциональный анализ (хим.)
В СССР первые исследования по Ф. а. появились в 30-х гг.: работы
А. Н. Колмогорова (1934) по теории линейных топологических пространств;
Н. Н. Боголюбова (1936) по инвариантным мерам в динамических системах;
Л. В. Канторовича (1937) и его учеников по теории полуупорядоченных пространств, применениям Ф. а. к вычислительной математике и др.; М. Г. Крейна и его учеников (1938) по углублённому изучению геометрии банаховых пространств, выпуклых множеств и конусов в них, теории операторов и связей с различными проблемами классического математического анализа и др.; И. М. Гельфанда и его учеников (1940) по теории нормированных колец (банаховых алгебр) и др.
Для современного этапа развития Ф. а. характерно усиление связей с теоретической физикой, а также с различными разделами классического анализа и алгебры, например теорией функций многих комплексных переменных, теорией дифференциальных уравнений с частными производными и т.п.
2. Понятие пространства.Наиболее общими пространствами, фигурирующими в Ф. а., являются линейные (векторные) топологические пространства, т. е. линейные пространства Хнад полем комплексных чисел
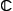 (или действительных чисел
(или действительных чисел
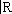 ), которые одновременно и топологические, причём линейные операции непрерывны в рассматриваемой топологии. Более частная, но очень важная ситуация возникает, когда в линейном пространстве
Хможно ввести норму (длину) векторов, свойства которой являются обобщением свойств длины векторов в обычном евклидовом пространстве. Именно, нормой элемента
xО
Хназывается действительное число ||
x|| такое, что всегда ||
x|| ³ 0 и ||
x|| = 0 тогда и только тогда, когда
x= 0;
), которые одновременно и топологические, причём линейные операции непрерывны в рассматриваемой топологии. Более частная, но очень важная ситуация возникает, когда в линейном пространстве
Хможно ввести норму (длину) векторов, свойства которой являются обобщением свойств длины векторов в обычном евклидовом пространстве. Именно, нормой элемента
xО
Хназывается действительное число ||
x|| такое, что всегда ||
x|| ³ 0 и ||
x|| = 0 тогда и только тогда, когда
x= 0;||l x|| = |l| || x||, l О
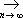 x, если ||
x
n—
x||
x, если ||
x
n—
x||
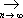 0.
0.В большом числе задач возникает ещё более частная ситуация, когда в линейном пространстве Хможно ввести скалярное произведение — обобщение обычного скалярного произведения в евклидовом пространстве. Именно, скалярным произведением элементов x, уО Хназывается комплексное число ( x, у) такое, что всегда ( x, x) ³ 0 и ( x, x) = 0 тогда и только тогда, когда x= 0;
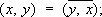
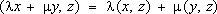 , l, m О
, l, m О
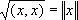 является нормой элемента
x. Такое пространство называется предгильбертовым. Для конструкций Ф. а. важно, чтобы рассматриваемые пространства были полными (т. е. из того, что
является нормой элемента
x. Такое пространство называется предгильбертовым. Для конструкций Ф. а. важно, чтобы рассматриваемые пространства были полными (т. е. из того, что
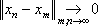 для
x
m,
x
nО
X,следует существование предела
для
x
m,
x
nО
X,следует существование предела
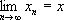 , также являющегося элементом
Х). Полное линейное нормированное и полное предгильбертово пространства называются, соответственно, банаховым и гильбертовым. При этом известная процедура пополнения метрического пространства (аналогичная переходу от рациональных чисел к действительным) в случае линейного нормированного (предгильбертова) пространства приводит к банахову (гильбертову) пространству.
, также являющегося элементом
Х). Полное линейное нормированное и полное предгильбертово пространства называются, соответственно, банаховым и гильбертовым. При этом известная процедура пополнения метрического пространства (аналогичная переходу от рациональных чисел к действительным) в случае линейного нормированного (предгильбертова) пространства приводит к банахову (гильбертову) пространству.Обычное евклидово пространство является одним из простейших примеров (действительного) гильбертова пространства . Однако в Ф. а. играют основную роль бесконечномерные пространства, т. е. такие, в которых существует бесконечное число линейно независимых векторов. Вот примеры таких пространств, элементами которых являются классы комплекснозначных (т. е. со значениями в
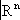 , норма ||
x|| =
, норма ||
x|| =
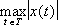 ; банахово пространство
L
p(
T) всех суммируемых с
р-й (
p³ 1) степенью функций на
Т, норма
; банахово пространство
L
p(
T) всех суммируемых с
р-й (
p³ 1) степенью функций на
Т, норма
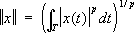 ; банахово пространство
l
pвсех последовательностей таких, что
; банахово пространство
l
pвсех последовательностей таких, что
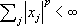 , здесь
, здесь
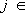
 (множеству целых чисел), норма ||
x|| =(е
(множеству целых чисел), норма ||
x|| =(е
 |
x
j|
p
)
1/
p; в случае
p= 2 пространства
l
2и
L
2(
T) гильбертовы, при этом, например, в
L
2(
T) скалярное произведение
|
x
j|
p
)
1/
p; в случае
p= 2 пространства
l
2и
L
2(
T) гильбертовы, при этом, например, в
L
2(
T) скалярное произведение
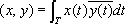 ; линейное топологическое пространство
D(
; линейное топологическое пространство
D(
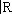 ), состоящее из бесконечно дифференцируемых функций на
), состоящее из бесконечно дифференцируемых функций на
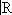 , каждая из которых финитна [т. е. равна нулю вне некоторого интервала (
а,
b)]; при этом
x
n
, каждая из которых финитна [т. е. равна нулю вне некоторого интервала (
а,
b)]; при этом
x
n
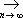 x,если
x
n(
t) равномерно финитны [т. е. (
а,
b) не зависит от
n] и сходятся равномерно со всеми своими производными к соответствующим производным
x(
t).
x,если
x
n(
t) равномерно финитны [т. е. (
а,
b) не зависит от
n] и сходятся равномерно со всеми своими производными к соответствующим производным
x(
t).Все эти пространства бесконечномерны, проще всего это видно для l 2: векторы e j= {0,..., 0, 1, 0,...} линейно независимы.
С геометрической точки зрения наиболее простыми являются гильбертовы пространства Н, свойства которых больше всего напоминают свойства конечномерных евклидовых пространств. В частности, два вектора x, уО Нназываются ортогональными ( x^ y), если ( x, у) = 0. Для любого xО Нсуществует его проекция на произвольное подпространство F— линейное замкнутое подмножество Н, т. е. такой вектор x F, что x— x F^ fдля любого fО F. Благодаря этому факту большое количество геометрических конструкций, имеющих место в евклидовом пространстве, переносится на Н, где они часто приобретают аналитический характер. Так, например, обычная процедура ортогонализации приводит к существованию в Нортонормированного базиса — последовательности векторов e j, jО
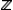 , из
Нтаких, что ||
e
j|| = 1,
e
j^
e
kпри
j¹
k, и для любого
xО
Hсправедливо «покоординатное» разложение
, из
Нтаких, что ||
e
j|| = 1,
e
j^
e
kпри
j¹
k, и для любого
xО
Hсправедливо «покоординатное» разложениеx= е
 x
je
j(1)
x
je
j(1)где x j= ( x, e j), || x|| = е
 |
x
j|
2(для простоты
Нпредполагается сепарабельным, т. е. в нём существует счётное всюду плотное множество). Если в качестве
Нвзять
L
2(0, 2p) и положить
|
x
j|
2(для простоты
Нпредполагается сепарабельным, т. е. в нём существует счётное всюду плотное множество). Если в качестве
Нвзять
L
2(0, 2p) и положить
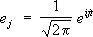 ,
j=...,—1, 0, 1..., то (1) даст разложение функции
x(
t) О
L
2(0, 2p) в ряд Фурье, сходящийся в среднем квадратичном. Кроме того, соотношение (1) показывает, что соответствие между
Ни
l
2'
{xj},
jО
,
j=...,—1, 0, 1..., то (1) даст разложение функции
x(
t) О
L
2(0, 2p) в ряд Фурье, сходящийся в среднем квадратичном. Кроме того, соотношение (1) показывает, что соответствие между
Ни
l
2'
{xj},
jО
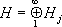 гильбертовых пространств
H
j— конструкция, подобная образованию
Нодномерными подпространствами, описываемому формулой (1); факторизация и пополнение: на исходном линейном пространстве
Хзадаётся квазискалярное произведение [т. е. возможно равенство (
x,
x) = 0 для
x¹ 0], часто весьма экзотического характера, и
Нстроится процедурой пополнения
Хотносительно (.,.) после предварительного отождествления с 0 векторов
x, для которых (
x,
x) = 0; тензорное произведение
гильбертовых пространств
H
j— конструкция, подобная образованию
Нодномерными подпространствами, описываемому формулой (1); факторизация и пополнение: на исходном линейном пространстве
Хзадаётся квазискалярное произведение [т. е. возможно равенство (
x,
x) = 0 для
x¹ 0], часто весьма экзотического характера, и
Нстроится процедурой пополнения
Хотносительно (.,.) после предварительного отождествления с 0 векторов
x, для которых (
x,
x) = 0; тензорное произведение
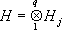 — образование его аналогично переходу от функций одной переменной
f(
x
1) к функциям многих переменных
f(
x
1,...,
x
q); проективный предел
— образование его аналогично переходу от функций одной переменной
f(
x
1) к функциям многих переменных
f(
x
1,...,
x
q); проективный предел
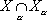 банаховых пространств — здесь
банаховых пространств — здесь
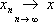 (грубо говоря), если
(грубо говоря), если
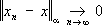 для каждого a; индуктивный предел
для каждого a; индуктивный предел
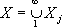 банаховых пространств
X
1М
X
2М..., здесь
банаховых пространств
X
1М
X
2М..., здесь
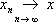 , если все
x
j, начиная с некоторого
j
0, лежат в одном
X
j0, и в нём
, если все
x
j, начиная с некоторого
j
0, лежат в одном
X
j0, и в нём
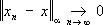 . Две последние процедуры обычно применяются для построения линейных топологических пространств. Таковы, например, ядерные пространства — проективный предел гильбертовых пространств
Н
a, обладающих тем свойством, что для каждого a найдётся b такое, что
h
bМ
Н
a, и это — т. н. вложение Гильберта — Шмидта [D (
. Две последние процедуры обычно применяются для построения линейных топологических пространств. Таковы, например, ядерные пространства — проективный предел гильбертовых пространств
Н
a, обладающих тем свойством, что для каждого a найдётся b такое, что
h
bМ
Н
a, и это — т. н. вложение Гильберта — Шмидта [D (
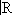 ) — пример ядерного пространства].
) — пример ядерного пространства].Разработан важный раздел Ф, а., в котором изучаются пространства с конической структурой «x
 0» (полуупорядоченностью). Пример такого пространства — действительное
С(
Т), в нём считается
x
0» (полуупорядоченностью). Пример такого пространства — действительное
С(
Т), в нём считается
x
 0, если
x(
t³)0 для всех
tО
T.
0, если
x(
t³)0 для всех
tО
T.3. Операторы (общие понятия). Функционалы.Пусть X, Y— линейные пространства; отображение A: X® Yназывается линейным, если для x, уО X, l, m О
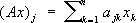 ,
,где x 1,..., x nи ( Ax) 1,..., ( Ax) n — координаты векторов xи Axсоответственно. При переходе к бесконечномерным линейным топологическим пространствам положение значительно усложняется. Здесь прежде всего необходимо различать непрерывные и разрывные линейные операторы (для конечномерных пространств они всегда непрерывны). Так, действующий из пространства L 2( а, b) в него же оператор
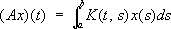 (2)
(2)(где K( t, s) — ограниченная функция — ядро А) — непрерывен, в то время как определённый на подпространстве C 1( a, b) М L 2( a, b) оператор дифференцирования
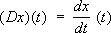 (3)
(3)является разрывным (вообще, характерной особенностью разрывных операторов является то, что они не определены на всём пространстве).
Непрерывный оператор A: X® Y, где X, Y— банаховы пространства, характеризуется тем, что
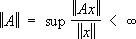 ,
,поэтому его называют также ограниченным. Совокупность всех ограниченных операторов
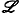 (
X,
Y) относительно обычных алгебраических операций образует банахово пространство с нормой ||
A||. Свойства
(
X,
Y) относительно обычных алгебраических операций образует банахово пространство с нормой ||
A||. Свойства
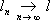 , если
, если
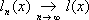 для каждого
xО
X], относительно которой шар, т. е. множество точек
xО
Хтаких, что ||
x|| Ј
r, уже будет компактным (такого эффекта никогда не будет в бесконечномерном пространстве относительно топологии, порождаемой нормой). Это позволяет более детально изучить ряд геометрических вопросов для множеств из
X', например установить структуру произвольного компактного выпуклого множества как замкнутой оболочки своих крайних точек (теорема Крейна — Мильмана).
для каждого
xО
X], относительно которой шар, т. е. множество точек
xО
Хтаких, что ||
x|| Ј
r, уже будет компактным (такого эффекта никогда не будет в бесконечномерном пространстве относительно топологии, порождаемой нормой). Это позволяет более детально изучить ряд геометрических вопросов для множеств из
X', например установить структуру произвольного компактного выпуклого множества как замкнутой оболочки своих крайних точек (теорема Крейна — Мильмана).Важной задачей Ф. а. является отыскание общего вида функционалов для конкретных пространств. В ряде случаев (помимо гильбертова пространства) это удаётся сделать, например ( l p)ў, p> 1, состоит из функций вида е
 x
je
j, где
x
je
j, где
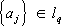 ,
,
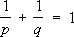 . Однако для большинства банаховых (и в особенности линейных топологических) пространств функционалы будут элементами новой природы, не конструирующимися просто средствами классического анализа. Так, например, при фиксированных
t
0и
mна пространстве
D(
. Однако для большинства банаховых (и в особенности линейных топологических) пространств функционалы будут элементами новой природы, не конструирующимися просто средствами классического анализа. Так, например, при фиксированных
t
0и
mна пространстве
D(
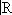 ) определён функционал
) определён функционал
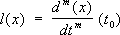 . В случае
m= 0 его ещё можно записать «классическим» образом — при помощи интеграла, однако при
m³ 1 это уже невозможно. Элементы из (
D(
. В случае
m= 0 его ещё можно записать «классическим» образом — при помощи интеграла, однако при
m³ 1 это уже невозможно. Элементы из (
D(
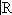 ))ў называются
обобщёнными функциями
(распределениями). Обобщённые функции как элементы сопряжённого пространства можно строить и тогда, когда
D(
))ў называются
обобщёнными функциями
(распределениями). Обобщённые функции как элементы сопряжённого пространства можно строить и тогда, когда
D(
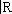 ) заменено другим пространством Ф, состоящим как из бесконечно, так и конечное число раз дифференцируемых функций; при этом существенную роль играют тройки пространств Ф' Й
НЙ Ф, где
Н— исходное гильбертово пространство, а Ф — линейное топологическое (в частности, гильбертово с др. скалярным произведением) пространство, например
) заменено другим пространством Ф, состоящим как из бесконечно, так и конечное число раз дифференцируемых функций; при этом существенную роль играют тройки пространств Ф' Й
НЙ Ф, где
Н— исходное гильбертово пространство, а Ф — линейное топологическое (в частности, гильбертово с др. скалярным произведением) пространство, напримерФ = W l 2( T).
Дифференциальный оператор D, фигурирующий в (3), будет непрерывным, если его понимать действующим в L 2[ a, b] из пространства C 1[ a, b], снабженного нормой
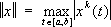 ,
,
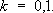 Однако для многих задач, и прежде всего для спектральной теории, такие дифференциальные операторы необходимо интерпретировать как действующие в одном и том же пространстве. Эти и другие близкие задачи привели к построению общей теории неограниченных, в частности неограниченных самосопряжённых, и эрмитовых операторов.
Однако для многих задач, и прежде всего для спектральной теории, такие дифференциальные операторы необходимо интерпретировать как действующие в одном и том же пространстве. Эти и другие близкие задачи привели к построению общей теории неограниченных, в частности неограниченных самосопряжённых, и эрмитовых операторов.4. Специальные классы операторов. Спектральная теория.Многие задачи приводят к необходимости изучать разрешимость уравнения вида Cx= y, где С— некоторый оператор, уО Y— заданный, а xО Х— искомый векторы. Например, если Х= Y= L 2( а, b), С= Е— А, где А— оператор из (2), а Е— тождественный оператор, то получается интегральное уравнение Фредгольма 2-го рода; если С— дифференциальный оператор, то получается дифференциальное уравнение, и т.п. Однако здесь нельзя рассчитывать на достаточно полную аналогию с линейной алгеброй, не ограничивая класс рассматриваемых операторов. Одним из важнейших классов операторов, наиболее близких к конечномерному случаю, являются компактные (вполне непрерывные) операторы, характеризующиеся тем, что переводят каждое ограниченное множество из Хв множество из Y, замыкание которого компактно [таков, например, оператор Аиз (2)]. Для компактных операторов построена теория разрешимости уравнения x— Ax= у, вполне аналогичная конечномерному случаю (и содержащая, в частности, теорию упомянутых интегральных уравнений) (Ф. Рис).
В разнообразных задачах математической физики возникает т. н. задача на собственные значения : для некоторого оператора А: Х® Хтребуется выяснить возможность нахождения решения j ¹ 0 ( собственного вектора ) уравнения Аj = lj при некотором l О
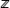 l
jx
je
j, (4)
l
jx
je
j, (4)где l j , — собственное значение, отвечающее e j. Для конечномерного Хвопрос о таком представлении полностью выяснен, при этом в случае кратных собственных значений для получения базиса в Хнужно, вообще говоря, добавить к собственным т. н. присоединённые векторы. Набор SpA собственных значений в этом случае называется спектром А.
Первое перенесение этой картины на бесконечномерный случай было дано для интегральных операторов типа Аиз (2) с симметричным ядром [т. е. K( t, s) = K( s, t) и действительно] (Д. Гильберт). Затем подобная теория была развита для общих компактных самосопряжённых операторов в гильбертовом пространстве. Однако при переходе к простейшим некомпактным операторам возникли трудности, связанные с. самим определением спектра. Так, ограниченный оператор в L 2[ a, b]
( Tx)( t) = tx( t) (5)
не имеет собственных значений. Поэтому определение спектра было пересмотрено, обобщено и выглядит сейчас следующим образом.
Пусть Х— банахово пространство, АО
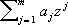 — многочлен, то
f(
A) =
— многочлен, то
f(
A) =
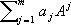 (степень оператора понимается как последовательное его применение). Однако если
f(
z) — аналитическая функция, то так прямо понимать
f(
A) уже не всегда возможно; в этом случае
f(
A) определяется следующей формулой, если
f(
z) аналитична в окрестности SpA, а Г — контур, охватывающий SpA и лежащий в области аналитичности
f(
z):
(степень оператора понимается как последовательное его применение). Однако если
f(
z) — аналитическая функция, то так прямо понимать
f(
A) уже не всегда возможно; в этом случае
f(
A) определяется следующей формулой, если
f(
z) аналитична в окрестности SpA, а Г — контур, охватывающий SpA и лежащий в области аналитичности
f(
z):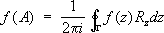 . (6)
. (6)При этом алгебраические операции над функциями переходят в аналогичные операции над операторами [т. е. отображение f( z) ® f( A) — гомоморфизм]. Эти конструкции не дают возможности выяснить, например, вопросы полноты собственных и присоединённых векторов для общих операторов, однако для самосопряжённых операторов, представляющих основной интерес, например, для квантовой механики, подобная теория полностью разработана.
Пусть Н— гильбертово пространство. Ограниченный оператор А: Н® Нназывается самосопряжённым, если ( Ax, у) = ( x, Ау) (в случае неограниченного Аопределение более сложно). Если Н n-мерно, то в нём существует ортонормированный базис собственных векторов самосопряжённого оператора А; другими словами, имеют место разложения:
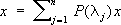 ,
,
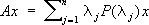 , (7)
, (7)где P(l j ) — оператор проектирования (проектор) на подпространство, натянутое на все собственные векторы оператора А, отвечающие одному и тому же собственному значению l j .
Оказывается, что эти формулы могут быть обобщены на произвольный самосопряжённый оператор из Н, только сами проекторы P(l j ) могут не существовать, поскольку могут отсутствовать и собственные векторы [таков, например, оператор Тв (5)]. В формулах (7) суммы заменяются теперь интегралами Стилтьеса по неубывающей операторнозначной функции Е(l) [которая в конечномерном случае равна
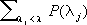 ], называется разложением единицы, или спектральной (проекторной) мерой, точки роста которой совпадают со спектром Sp
А. Если привлечь обобщённые функции, то формулы типа (7) сохраняются. Именно, если имеется тройка Ф' Й
НЙ
Ф, где Ф, например, ядерно, причём
Апереводит Ф в Фў и непрерывно, то соотношения (7) имеют место, только суммы переходят в интегралы по некоторой скалярной мере, а
Е(l) теперь «проектирует» Ф в Фў, давая векторы из Фў, которые будут собственными в обобщённом смысле для
Ас собственным значением l. Аналогичные результаты справедливы для т. н. нормальных операторов (т. е. коммутирующих со своими сопряжёнными). Например, они верны для
унитарных операторов
U— таких ограниченных операторов, которые отображают всё
Нна всё
Ни сохраняют при этом скалярное произведение. Для них спектр Sp
Uрасположен на окружности |
z| = 1, вдоль которой и производится интегрирование в аналогах формул (6). См. также
Спектральный анализ
линейных операторов.
], называется разложением единицы, или спектральной (проекторной) мерой, точки роста которой совпадают со спектром Sp
А. Если привлечь обобщённые функции, то формулы типа (7) сохраняются. Именно, если имеется тройка Ф' Й
НЙ
Ф, где Ф, например, ядерно, причём
Апереводит Ф в Фў и непрерывно, то соотношения (7) имеют место, только суммы переходят в интегралы по некоторой скалярной мере, а
Е(l) теперь «проектирует» Ф в Фў, давая векторы из Фў, которые будут собственными в обобщённом смысле для
Ас собственным значением l. Аналогичные результаты справедливы для т. н. нормальных операторов (т. е. коммутирующих со своими сопряжёнными). Например, они верны для
унитарных операторов
U— таких ограниченных операторов, которые отображают всё
Нна всё
Ни сохраняют при этом скалярное произведение. Для них спектр Sp
Uрасположен на окружности |
z| = 1, вдоль которой и производится интегрирование в аналогах формул (6). См. также
Спектральный анализ
линейных операторов.5. Нелинейный функциональный анализ.Одновременно с развитием и углублением понятия пространства шло развитие и обобщение понятия функции. В конечном счёте оказалось необходимым рассматривать отображения (не обязательно линейные) одного пространства в другое (часто — в исходное). Одной из центральных задач нелинейного Ф. а. является изучение таких отображений. Как и в линейном случае, отображение пространства в
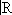 ) называется функционалом. Для нелинейных отображений (в частности, нелинейных функционалов) можно различными способами определить дифференциал, производную по направлению и т.д. аналогично соответствующим понятиям классического анализа. Выделение из отображения квадратичного и т.д. членов приводит к формуле, аналогичной формуле Тейлора.
) называется функционалом. Для нелинейных отображений (в частности, нелинейных функционалов) можно различными способами определить дифференциал, производную по направлению и т.д. аналогично соответствующим понятиям классического анализа. Выделение из отображения квадратичного и т.д. членов приводит к формуле, аналогичной формуле Тейлора.Важной задачей нелинейного Ф. а. является задача отыскания неподвижных точек отображения (точка xназывается неподвижной для отображения F, если Fx= x). К отысканию неподвижных точек сводятся многие задачи о разрешимости операторных уравнений, а также задачи отыскания собственных значений и собственных векторов нелинейных операторов. При решении уравнений с нелинейными операторами, содержащими параметр, возникает существенное для нелинейного Ф. а. явление — т. н. точки ветвления (решений).
При исследовании неподвижных точек и точек ветвления используются топологические методы: обобщения на бесконечномерные пространства теоремы Брауэра о существовании неподвижных точек отображений конечномерных пространств, степени отображений и т.п. Топологические методы Ф. а. развивались польским математиком Ю. Шаудером, французским математиком Ж. Лере, советскими математиками М. А. Красносельским, Л. А. Люстерником и др.
6. Банаховы алгебры. Теория представлений.На ранних этапах развития Ф. а. изучались задачи, для постановки и решения которых необходимы были лишь линейные операции над элементами пространства. Исключение составляют, пожалуй, только теория колец операторов (факторов) (Дж. Нейман, 1929) и теория абсолютно сходящихся рядов Фурье (Н. Винер , 1936). В конце 30-x гг. в работах японского математика М. Нагумо, советских математиков И. М, Гельфанда, Г. Е. Шилова, М. А. Наймарка и др. стала развиваться теория т. н. нормированных колец (современное название — банаховы алгебры), в которой, кроме операций линейного пространства, аксиоматизируется операция умножения (причём || xy|| Ј || x|| || y||). Типичными представителями банаховых алгебр являются кольца ограниченных операторов, действующих в банаховом пространстве Х(умножение в нём — последовательное применение операторов — необходимо с учётом порядка), различного рода функциональные пространства, например C( T) с обычным умножением, L 1(
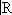 ) со свёрткой в качестве произведения, и широкое обобщение их — класс т. н. групповых алгебр (топологические группы
G), состоящих из комплекснозначных функций или мер, определённых на
Gсо свёрткой (в различных, не обязательно эквивалентных вариантах) в качестве умножения.
) со свёрткой в качестве произведения, и широкое обобщение их — класс т. н. групповых алгебр (топологические группы
G), состоящих из комплекснозначных функций или мер, определённых на
Gсо свёрткой (в различных, не обязательно эквивалентных вариантах) в качестве умножения.Пусть
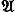 — коммутативная (т. е.
xy=
ухдля любых
x,
уО
— коммутативная (т. е.
xy=
ухдля любых
x,
уО
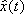 на
М, причём сумме
x+
yи произведению
xyсоответствуют сумма и произведение функций. Другими словами, существует гомоморфизм
на
М, причём сумме
x+
yи произведению
xyсоответствуют сумма и произведение функций. Другими словами, существует гомоморфизм
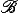 борелевских подмножеств
G, инвариантная справа: для любых
ВО
борелевских подмножеств
G, инвариантная справа: для любых
ВО
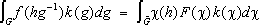 , где c(
h) — характер группы
G: непрерывная функция на
Gтакая, что |c(
h)| = 1 и c(
h
1h
2) = c(
h
1)c(
h
2),
dc — мера Хаара на группе характеров
, где c(
h) — характер группы
G: непрерывная функция на
Gтакая, что |c(
h)| = 1 и c(
h
1h
2) = c(
h
1)c(
h
2),
dc — мера Хаара на группе характеров
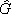 , а
, а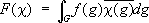 ,
,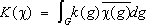
— обобщённое преобразование Фурье функций f( g) и k( g), которое продолжается до изоморфизма L 2( G, dg) в L 2(
 , dc). Для некоммутативных групп ситуация во многом усложняется. Если
Gкомпактна, то представление группы операторов сдвига (или, короче, группы сдвигов) удаётся хорошо описать; в этом случае
L
2(
G,
dg) распадается в прямую сумму конечномерных инвариантных относительно сдвигов подпространств. Если
Gнекомпактна, то также получается разложение
L
2(
G,
dg) на более простые инвариантные части, но уже не в прямую сумму, а в прямой интеграл.
, dc). Для некоммутативных групп ситуация во многом усложняется. Если
Gкомпактна, то представление группы операторов сдвига (или, короче, группы сдвигов) удаётся хорошо описать; в этом случае
L
2(
G,
dg) распадается в прямую сумму конечномерных инвариантных относительно сдвигов подпространств. Если
Gнекомпактна, то также получается разложение
L
2(
G,
dg) на более простые инвариантные части, но уже не в прямую сумму, а в прямой интеграл.Если G=
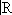 , то теория унитарных представлений может быть сведена к теории самосопряжённых операторов. Именно, однопараметрическая группа унитарных операторов
Т
l, l О
, то теория унитарных представлений может быть сведена к теории самосопряжённых операторов. Именно, однопараметрическая группа унитарных операторов
Т
l, l О
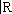 в гильбертовом пространстве
Ндопускает представление
Т
l= exp
il
A, где
А— самосопряжённый оператор (теорема Стоун а); оператор
Аназывается инфинитезимальным оператором (генератором) группы {
Т'
l}. Этот результат находит важные применения в изучении преобразований фазового пространства классической механики. Эта связь, а также приложения в статистической физике лежат в основе обширной ветви Ф. а. —
эргодической теории
. Связь между однопараметрическими группами преобразований и их генераторами допускает значительные обобщения: операторы
T
lне обязаны быть унитарными, могут действовать в банаховых и более общих пространствах и даже быть определёнными лишь для l ³ 0 (т. н. теория полугрупп операторов). Этот раздел Ф. а. имеет приложения в теории дифференциальных уравнений с частными производными и теории случайных (именно марковских) процессов.
в гильбертовом пространстве
Ндопускает представление
Т
l= exp
il
A, где
А— самосопряжённый оператор (теорема Стоун а); оператор
Аназывается инфинитезимальным оператором (генератором) группы {
Т'
l}. Этот результат находит важные применения в изучении преобразований фазового пространства классической механики. Эта связь, а также приложения в статистической физике лежат в основе обширной ветви Ф. а. —
эргодической теории
. Связь между однопараметрическими группами преобразований и их генераторами допускает значительные обобщения: операторы
T
lне обязаны быть унитарными, могут действовать в банаховых и более общих пространствах и даже быть определёнными лишь для l ³ 0 (т. н. теория полугрупп операторов). Этот раздел Ф. а. имеет приложения в теории дифференциальных уравнений с частными производными и теории случайных (именно марковских) процессов.Лит.:Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа 4 изд., М., 1976; Ахиезер Н. И., Глазман И. М., Теория линейных операторов в гильбертовом пространстве, 2 изд., М., 1966; Вулих Б. З., Введение в теорию полуупорядоченных пространств, М., 1961; Банах С. С., Курс функцioнального аналiзу Кипв, 1948; Рисс Ф., Секефальви-Надь Б., Лекции по функциональному анализу, пер. с франц., М., 1954; Соболев С. Л., Некоторые применения функционального анализа в математической физике, Л., 1950; Канторович Л. В., Акилов Г. П., Функциональный анализ в нормированных пространствах, М., 1959; Красносельский М. А., Забрейко П. П., Геометрические методы нелинейного анализа, М., 1975; Наймарк М. А., Нормированные кольца, 2 изд., М., 1968; Рудин У., Функциональный анализ, пер. с англ., М., 1975; Иосида К., Функциональный анализ, пер, с англ., М., 1967; Данфорд Н., Шварц Дж., Линейные операторы, пер. с англ., ч. 1—3, М., 1962—74; Хилле Э., Филлипс Р., Функциональный анализ и полугруппы, пер. с англ., 2 изд., М., 1962; Эдвардс Р. Э., Функциональный анализ. Теория и приложения пер с англ., М., 1969.
Ю. М. Березанский, Б. М. Левитан.
Функциональный анализ (хим.)
Функциона'льный ана'лиз(химический), совокупность химических и физических методов анализа (главным образом органических веществ), основанных на определении в молекулах реакционно-способных групп атомов (отдельных атомов) — т. н. функциональных групп. Такими группами являются, например, гидроксильная (—ОН), карбоксильная (
