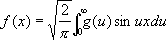.     (5)
     В общем случае имеет место формула
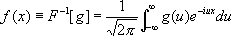    .     (6)
     Каждой операции над функциями соответствует операция над их Ф. п., которая во многих случаях проще соответствующей операции над f( x). Например, Ф. п. f'( x) является iug( u). Если
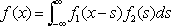    ,     (7)
   то g( u) = g ₁( u) g ₂( u). Для f( x+ а) Ф. п. является e ^iuag( u), а для c ₁f ₁( x) + c ₂f ₂( x) —функция c ₁g ₁( u) + c ₂g ₂( u).
     Если существует 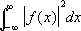, то интегралы в формулах (1) и (6) сходятся в среднем (см. Сходимость ), причём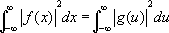
         (8)
   (теорема Планшереля). Формула (8) является обобщением на Ф. п. формулы Парсеваля (см. Парсеваля равенство ) для рядов Фурье (см. Фурье ряд ). Физический смысл формулы (8) заключается в равенстве энергии некоторого колебания сумме энергий его гармонических компонент. Отображение F: f( x) ® g( u) является унитарным оператором в гильбертовом пространстве функций f( x), — Ґ < x< Ґ, с интегрируемым квадратом. Этот оператор может быть представлен также в виде
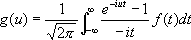    .     (9)
     При некоторых условиях на f( x) справедлива формула Пуассона
    ,
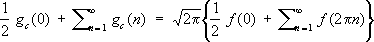   находящая применение в теории тэта-функций .
     Если функция f( x) достаточно быстро убывает, то её Ф. п. можно определить и при некоторых комплексных значениях u = v+ iw. Например, если существует 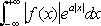, а> 0, то Ф. п. определено при | w| < а. Ф. п. при комплексных значениях тесно связано с двусторонним преобразованием Лапласа (см. Лапласа преобразование )
      .
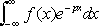
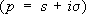     Оператор Ф. п. может быть расширен на более обширные классы функций, нежели совокупность суммируемых функций [например, для функций f( x) таких, что (1 + | x|) ^–1 f( x) суммируема, Ф. п. определяется формулой (9)], и даже на некоторые классы обобщённых функций (т. н. медленного роста).
     Имеются обобщения Ф. п. Одно из них использует различного рода специальные функции, например Бесселя функции , это направление получает завершение в теории представлений непрерывных групп . Другим является т. н. преобразование Фурье — Стилтьеса, широко применяемое, например, в теории вероятностей; оно определяется для произвольной ограниченной неубывающей функции j( x) Стилтьеса интегралом
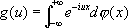         (10)
   и называется характеристической функцией распределения j. Для представимости функции g( u) в виде (10) необходимо и достаточно, чтобы при любых u ₁,..., u _n, x ₁,...,x _n было
   
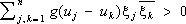
   (теорема Бохнера — Хинчина).
     Ф. п., первоначально возникшее в теории теплопроводности, имеет многочисленные применения как в самой математике (например, при решении дифференциальных, разностных и интегральных уравнений, в теории специальных функций и т.д.), так и в различных разделах теоретической физики. Например, Ф. п. стало стандартным аппаратом квантовой теории поля , широко используется в методе функций Грина для неравновесных задач квантовой механики и термодинамики, в теории рассеяния и т.д.
     Лит.:Снеддон И., Преобразование Фурье, пер. с англ., М., 1955; Владимиров В. С., Обобщенные функции в математической физике, М., 1976.

тригонометрический ряд , служащий для разложения периодической функции на гармонические компоненты. Если функция f( x) имеет период 2 T, то её Ф. р. имеет вид
    ,
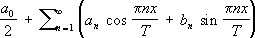   где a ₀, a _n, b _n( n&sup3; 1) — Фурье коэффициенты . В зависимости от того, в каком смысле понимаются интегралы в формулах для коэффициентов, говорят о рядах Фурье — Римана, Фурье — Лебега и т.д. Обычно рассматривают 2p-периодические функции (общий случай сводится к ним преобразованием независимого переменного).
     Ф. р. представляют собой простейший класс разложений по ортогональной системе функций , а именно — по тригонометрической системе 1, cos x, sin x, cos 2 x, sin 2 x,..., cos nx, sin nx,..., которая обладает двумя важными свойствами: замкнутостью и полнотой. Частичные суммы Ф. р. (суммы Фурье)
   
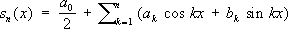
   обращают в минимум интеграл
    ,
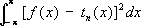   где t _n( x) — произвольный тригонометрический полином порядка Ј n, а функция f( x) интегрируема с квадратом. При этом
      ,
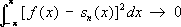
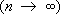   так что функции f( x), имеющие интегрируемый квадрат, сколь угодно хорошо аппроксимируются своими суммами Фурье в смысле среднего квадратичного уклонения (см. Приближение и интерполирование функций ).
     Для любой интегрируемой функции f( x) коэффициенты Фурье a _n, b _nпри n® Ґ стремятся к нулю (Б. Риман, А. Лебег). Если же функция f( x) несобственно интегрируема по Риману, то коэффициенты Фурье могут и не стремиться к нулю (Риман). В случае, если квадрат функции f( x) интегрируем, то ряд 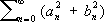 сходится и имеет место равенство Парсеваля
    .
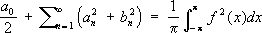     Один из вариантов этой формулы был впервые указан французским математиком М. Парсевалем (1799), а общая формула (где интеграл понимается в смысле Лебега) доказана Лебегом. Обратно, для любой последовательности действительных чисел a _n, b _nсо сходящимся рядом 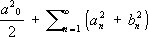 существует функция с интегрируемым по Лебегу квадратом, имеющая эти числа своими коэффициентами Фурье (немецкий математик Э. Фишер, венгерский математик Ф. Рис). Для интегралов в смысле Римана эта теорема неверна.
     Известно большое число признаков сходимости Ф. р., т. е. достаточных условий, гарантирующих сходимость ряда. Например, если функция f( x) имеет на периоде конечное число максимумов и минимумов, то её Ф. р. сходится в каждой точке (П. Дирихле ). Более общо, если f( x) имеет ограниченное изменение (см. Изменение функции ), то её Ф. р. сходится в каждой точке и притом равномерно на каждом отрезке, внутреннем к отрезку, на котором f( x) непрерывна (К. Жордан ). Если f( x) непрерывна и её модуль непрерывности w(d, f) удовлетворяет условию 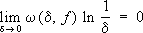, то её Ф. р. равномерно сходится (итальянский математик У. Дини, 1880).
     Проблема полного исследования условий сходимости Ф. р. оказалась весьма трудной, и в этом направлении до сих пор нет окончательных результатов. Как показал Риман, сходимость или расходимость Ф. р. в некоторой точке x ₀зависит от поведения функции f( x) лишь в сколь угодно малой окрестности этой точки (т. н. принцип локализации для Ф. р.). Если в точке x ₀функция f( x) имеет разрыв первого рода, т. с. существуют различные пределы f( x ₀— 0) и f( x ₀+ 0), и Ф. р. этой функции сходится в точке x ₀, то он сходится к значению ¹/ ₂{ f( x ₀— 0) + f( x ₀+ 0)}. В частности, если Ф. р. непрерывной периодической функции f( x) сходится в каждой точке, то его сумма равна f( x).
     Известно, что существуют непрерывные функции, Ф. р. которых расходятся в бесконечном числе точек (немецкий математик П. дю Буа-Реймон, 1875), и интегрируемые в смысле Лебега функции, Ф. р. которых расходятся в каждой точке (А. Н. Колмогоров , 1926). Однако Ф. р. всякой интегрируемой с квадратом функции сходится почти всюду (Л. Карлесон, 1966). Этот результат верен и для функций из любого пространства L ^p(—p, p) с p< 1 (Р. Хант, 1968). Упомянутые «дефекты сходимости» породили методы суммирования Ф. р. Вместо того чтобы исследовать поведение сумм Фурье, исследуют средние, образованные из этих сумм, поведение которых в ряде случаев оказывается значительно более правильным. Например, для любой непрерывной периодической функции f( x) сумма Фейера
   
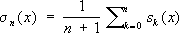
   при n® Ґ равномерно сходятся к f( x) (Л. Фейер , 1904).
     Лит.:Толстов Г. П., Ряды Фурье, 2 изд., М., 1960; Бари Н. К., Тригонометрические ряды, М., 1961; Зигмунд А., Тригонометрические ряды, пер. с англ., т. 1—2, М., 1965.

Просвещения , считая, что они противоречат опыту и оправдывают негодный общественный строй. Вместе с тем Ф. воспринял и развил ряд идей материалистов 18 в.: признание единства мироздания как извечно существующей и закономерно движущейся материи во всём многообразии её форм и видов движения; определение исторического процесса как движения, направленного на обеспечение всеобщего благополучия, и др. Задачу своей жизни Ф. видел в разработке «социальной науки» как части «теории всемирного единства», основанной на принципе «притяжения по страсти», всеобщей закономерности, обусловливающей природную склонность человека к какому-либо виду коллективного труда. Ф. разработал оригинальную схему истории человечества. Общество последовательно проходит периоды эдемизма («райской» первобытности), дикости, варварства и цивилизации. Особое внимание Ф. уделил анализу и критике современного периода («периода цивилизации»); он вскрыл его внутренние противоречия (кризисы от избытка, бедность, порождаемую изобилием, и др.). На смену строю цивилизации, по Ф., должен прийти высший общественный строй — строй гармонии, который не только соответствует предначертаниям бога-природы, но представляется как историческая необходимость.
     В системе Ф. сохранялись частная собственность, классы и нетрудовой доход. Для успеха нового общества, считал Ф., необходим рост производительности труда, обеспечивающий богатство для всех, для чего общественный доход должен распределяться соответственно: капиталу ( ⁴/ ₁₂), труду ( ⁵/ ₁₂) и таланту ³/ ₁₂). С укреплением и развитием строя ассоциации эти пропорции, как предполагал Ф., будут изменяться в пользу труда. Строй ассоциации создаёт, по Ф., крупное коллективизированное и механизированное сельское хозяйство, соединённое с промышленным производством. Это соединение произойдёт в первичных ячейках общества — «фалангах», располагающихся в огромных дворцах — «фаланстерах». Такая организация общества приведёт к ликвидации разрыва между городом и деревней, к созданию поселений нового типа, где объединятся все виды человеческой деятельности и преимущества городской и сельской жизни.
     Согласно Ф., естественные страсти человека, подавляемые и искажаемые при строе цивилизации, будут направлены на творческий труд, полный разнообразия и радостного соревнования. Разумно организованные могучие трудовые армии — региональные, национальные и международные — преобразуют лик Земли. В новых условиях общественной жизни будет формироваться и новый человек как целостная, всесторонне развитая личность.
     В учении Ф. было немало идей и концепций, которые позднее получили развитие не только в философии, социологии и экономической науке, но и в таких специальных отраслях, как социальная психология, психология труда, педагогика. Для учения Ф. характерны элементы материализма и диалектики. Вместе с тем его учению свойственны идеалистическое понимание истории, методологическая непоследовательность, беспочвенные мечтания. Мировоззрение Ф. несёт на себе отпечаток мелкобуржуазности: идеальный «строй гармонии» был далёк от экономических требований крупного общественного производства.
     По определению К. Маркса и Ф. Энгельса, «Фурье исходит непосредственно из учения французских материалистов» (Соч., 2 изд., т. 2, с. 146) и «... так же мастерски владеет диалектикой, как и его современник Гегель» (Энгельс Ф., там же, т. 19, с. 197). Маркс и Энгельс, указывая, что Ф. блестяще разработал ряд проблем будущего общества, вместе с тем критиковали его за отказ от классовой, революционной и всякой вообще политической борьбы, за сохранение в строе ассоциации основных элементов капиталистических общественных отношений, надежду на содействие лучших представителей господствующих классов делу разумного переустройства общества. Маркс и Энгельс признавали Ф. наряду с К. А. Сен-Симоном и Р. Оуэном одним из тех мыслителей, которые «... гениально предвосхитили бесчисленное множество таких истин, правильность которых мы доказываем теперь научно...» (Энгельс Ф., там же, т. 18, с. 499).
     Учение Ф. оказало значительное влияние на социальную и философскую мысль ряда стран. Во Франции учение Ф. развивали «социетарная школа» В. Консидерана и группа др. фурьеристов. Фурьеристы пытались создать опытный фаланстер и «социальную партию», но на практике неизменно оказывались бессильными и потерпели крах в ходе Революции 1848. Идеи Ф. получили отражение во французской художественной литературе (Э. Сю, Ф. Пиа, П. Ж. Беранже, Э. Потье и др.) и оказали воздействие на развитие французского утопического социализма (К. Пеккёр, Ф. Видаль, П. А. Леру, П. Ж. Прудон). В 30—40-х гг. влияние идей Ф. испытала ранняя социалистическая мысль в Англии (Хью Дохерти и др.), Германии (В. Вейтлинг, М. Гесс и др.), Италии (Б. Дж. Муре, С. Савини), Испании, где фурьеристы были также первыми проводниками социалистических идей (Х. С. Абреу и др.), и в др. странах Европы. В Северной Америке влияние Ф. на развитие прогрессивных социальных идей было столь значительным, что 30—40-е гг. 19 в. называют «фурьеристским периодом» истории социализма в Америке (А. Брисбен, П. Годвин, Х. Грили и др.). Было создано более 40 фурьеристских колоний (Брукфарм и др.).
     В России идеи Ф. уже в 1-й четверти 19 в. стали известны некоторым из декабристов и близким к ним представителям интеллигенции. В 30—40-х гг. учением Ф. интересовались А. И. Герцен, Н. П. Огарев. Выдающимися приверженцами Ф. были М. В. Петрашевский и петрашевцы . Идеи Ф. отразились в произведениях Ф. М. Достоевского, М. Е. Салтыкова-Щедрина, Н. Г. Чернышевского и др. (см. также ст. Утопический социализм ).
     Соч.: CEuvres complиtes, v. 1—6, P., 1841—1870; CEuvres complиtes, v. 1—11, P., 1966—67; в рус. пер. — Избр. соч., т. 1—4, М. — Л., 1951—54.
     Лит.:Бебель А., Ш. Фурье, пер. с нем., М., 1923; Дворцов А. Т., Шарль Фурье. Его жизнь и учение, М., 1938; Иоаннисян А. Р., Шарль Фурье, М., 1958; Зильберфарб И. И., Социальная философия Шарля Фурье и её место в истории социалистической мысли первой половины XIX в., М., 1964 (лит.); Armand F., Fourier, v. 1—2, P., 1937.
      И. И. Зильберфарб.

   Ш. Фурье.