TheLib.Ru » Энциклопедии » БСЭ » Большая Советская Энциклопедия (ФУ) » онлайн-чтение (стр. 7)

 

 

Обобщённые функции ) и дают ответ на исходную физическую задачу. Эти и аналогичные им обстоятельства стимулировали создание Ф. т. действительного переменного.
     Отдельные частные факты Ф. т. действительного переменного были открыты ещё в 19 в. (существование рядов непрерывных функций с разрывной суммой, примеры нигде не дифференцируемых непрерывных функций, не интегрируемых функций и т.п.). Однако эти факты воспринимались обычно как «исключения из правил» и не объединялись никакими общими схемами. Лишь в начале 20 в., когда в основу изучения функций были положены методы множеств теории , стала развиваться систематически современная Ф. т. действительного переменного.
     Можно различить три направления в Ф. т. действительного переменного.
     1) Метрическая Ф. т., где свойства функций изучаются при помощи меры (см. Мера множества ) тех множеств, на которых эти свойства имеют место. В метрической Ф. т. с общих точек зрения изучаются интегрирование и дифференцирование функций (см. Интеграл , Дифференциал , Производная ), различными способами обобщается понятие сходимости функциональных последовательностей, исследуется строение разрывных функций весьма широкого типа и т.п. Важнейшим классом функций, изучаемым в метрической Ф. т., являются измеримые функции .
     2) Дескриптивная Ф. т., в которой основным объектом изучения является операция предельного перехода (см. Бэра классификация ).
     3) Конструктивная Ф. т., изучающая вопросы изображения произвольных функций при помощи надлежащих аналитических средств (см. Приближение и интерполирование функций ).
     О Ф. т. комплексного переменного см. Аналитические функции .
     Лит.:Александров П. С., Введение в общую теорию множеств и функций, М. — Л., 1948; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 4 изд., М., 1976.

вариационном исчислении и означающее там переменную величину, зависящую от функции (линии) или от нескольких функций. Примерами Ф. являются площадь, ограниченная замкнутой кривой заданной длины, работа силового поля вдоль того или иного пути и т.д. С развитием функционального анализа термин «Ф.» стал пониматься в более широком смысле, а именно: как числовая функция, определённая на некотором линейном пространстве. См. Функциональный анализ .

эклектизму , выявившему характерное для буржуазной культуры расщепление эстетического и утилитарного начал (на что указывали, в частности, английский критик Дж. Рескин и английский писатель, теоретик и дизайнер У. Моррис). Идеи целесообразной архитектуры развивались под влиянием теорий естественных наук (прежде всего эволюционной теории Ч. Дарвина). Природа стала рассматриваться как источник образцов совершенного приспособления формы к её назначению (американский скульптор и теоретик искусства Х. Гриноу и др.).
     Систему идей американского «протофункционализма» конца 19 в. завершил архитектор Л. Г. Салливен . В США эти идеи не получили непосредственные продолжения; лишь Ф. Л. Райт развивал на их основе теорию органической архитектуры .
     Выдвинутая Салливеном формула «форму определяет функция» в середине 1920-х гг. была подхвачена западно-европейскими архитекторами, сторонниками рационализма , полемически упростившими её содержание, сведя его к первичности утилитарного по отношению к эстетическому. Основанные на этой формуле принципы функциональности разрабатывались и пропагандировались Ле Корбюзье во Франции, а наиболее последовательно — архитекторами, связанными с «Баухаузом» в Германии (В. Гропиус, Л. Мис ван дер Роэ, Х. Мейер и др.). Идеи целесообразного конструирования жизненной среды связывались с социальной утопией «жизнестроительства», создания материальных форм, которые могли бы способствовать «разумному преобразованию» капиталистического общества.
     На структуру построек переносился принцип построения механизма; здания расчленялись в точном соответствии с последовательностью функциональных процессов, для которых они предназначались. Функции при этом анализировались на основе методов научной организации труда, в духе тейлоризма . Принцип зонирования территории с выделением особого пространства для каждой из главных жизненных функций (их определяли так: «жить, работать, отдыхать, передвигаться») был перенесён и в область градостроительства. Рассудочные методы архитектурного творчества были доведены до крайней механистичности немецкими архитекторами, работавшими в конце 1920-х гг. в области муниципального жилищного строительства (Э. Май, Б. Таут, М. Вагнер).
     Под влиянием конструктивизма , представители которого решали задачи, во многом родственные поискам ведущих мастеров Ф., в творчестве западно-европейских архитекторов, связанных с Ф., во 2-й половине 1920-х гг. развивались демократические тенденции и элементы трезвого социального анализа. В условиях экономических трудностей конца 1920-х гг. идеи Ф. получили популярность у предпринимателей, их утопические идеи использовались социал-реформистскими политиками, но элементы социальной прогрессивности выхолащивались. Ф. утвердился во всех странах Западной Европы, а также в США и Японии. Однако наряду с распространением вширь он терял черты творческого метода, преобразуясь в некий «международный стиль», оперировавший внешними атрибутами целесообразной формы. Стремясь укрепить веру в трезвую целеустремлённость направления, приверженцы и стали называть его «Ф.» (швейцарский теоретик архитектуры З. Гидион внедрил этот термин как характеризующий всё «нетрадиционное» зодчество 1920—30-х гг.).
     Повсеместное, не зависящее от условий среды и климата насаждение форм и приёмов, возникших в конкретных условиях Германии и Франции, вело к противоречиям с самим принципом рационального подхода к архитектуре. Архитекторы Финляндии (А. Аалто и др.), Швеции (С. Маркелиус и др.) уже в 1930-е гг., опираясь на метод Ф., стали разрабатывать приёмы, отвечающие национальной специфике своих стран. Это положило начало развитию региональных архитектурных школ, развивавшихся в рамках Ф., «международный стиль» стал распадаться. Разочаровавшись в иллюзиях «великой социальной миссии архитектуры», объединявших зачинателей Ф., его приверженцы стали отходить от анализа социальных проблем, что ещё более подрывало позиции Ф.
     После 2-й мировой войны 1939—45 влияние архитектуры Ф. возродилось при восстановлении разрушенных городов, однако единство «международного стиля» распалось окончательно. Против основной доктрины Ф. выступил один из прежних его лидеров Л. Мис ван дер Роэ , а также приверженцы брутализма , возродившегося неоклассицизма и возврата к историческим традициям.
     В современной сов. архитектурной теории преобладает тенденция к внимательному изучению творческого наследия мастеров Ф. (в особенности тех концепций, которые были связаны с проблематикой советского зодчества 1920-х гг.); вместе с тем подвергаются критике социально-утопические воззрения представителей Ф., многие из которых надеялись преобразовать капиталистическое общество с помощью архитектуры.
     Лит.:Всеобщая история архитектуры, т. 11, М., 1973; Мастера архитектуры об архитектуре, М., 1972; Гропиус В., Границы архитектуры (пер. с нем.), М., 1971; Sfaellos C. A., Le fonctionnalisme dans l'architecture contemporaine, P., 1952; Zurko E. R. de, Origins of functionalist theory, N. Y., 1957.
      А. В. Иконников.

эволюционного учения , способствовавшего переходу от поэлементного анализа сознания в структурной психологии В. Вундта — Э. Титченера к изучению роли сознания при решении индивидом различных задач. В Ф. п. имелось несколько течений. В европейских странах естественнонаучной трактовки психических функций придерживались Т. Рибо (Франция), Н. Н. Ланге (Россия), Э. Клапаред (Швейцария), идеалистической трактовки — К. Штумпф и представители т. н. Вюрцбургской школы (Германия). В США сложился другой вариант Ф. п., восходящий к У. Джемсу и представленный двумя школами: чикагской (Дж. Дьюи , Дж. Энджелл, Г. Карр) и колумбийской (Р. Вудвортс ). Психология понималась как наука о функциях (или «деятельностях») сознания в процессе адаптации организма к изменяющемуся природному и социальному окружению. Область исследований психологии охватила не только сознание, но и поведение (приспособительные действия), его мотивы, механизмы научения и др. Сторонники этого направления внесли существенный вклад в экспериментальную психологию. Однако дуализм в понимании отношений между телесными и психическими функциями, телеологический взгляд на сознание как целенаправленно действующую сущность привели к тому, что это направление утратило научное влияние. В 20-х гг. американская Ф. п. была оттеснена бихевиоризмом .
     Лит.:Ярошевский М. Г., История психологии, М., 1966; Wood worth R. S., Dynamic psychology, N. Y., 1918; Carr Н. A., Psychology. A study of mental activity, N. Y., 1927; Boring E. G., A history of experimental psychology, 2 ed., N. Y., 1950; Misiak Н., Sexton U., History of psychology, 2 ed., N. Y. — L., 1968.
      М. Г. Ярошевский.

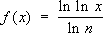многозначные логики , алгебры автоматов, алгебры рекурсивных функций и др. Ф. с. обладает определённой спецификой, состоящей в рассмотрении задач и подходов, возникающих при исследовании Ф. с. с позиций математической кибернетики, математической логики и алгебры. Так, с позиций математической кибернетики Ф. с. рассматриваются как языки, описывающие функционирование сложных систем. С позиций математической логики Ф. с. рассматриваются как модели логик, т. е. как системы высказываний с логическими операциями над ними. С точки зрения алгебры Ф. с. представляют собой т. н. алгебраические системы. Важной особенностью Ф. с., выделяющей их из общего класса алгебраических систем, является их содержательная связь с реальными кибернетическими моделями управляющих систем. Эта связь, с одной стороны, определяет гамму существенных требований, которые накладываются на Ф. с., а с другой стороны, порождает серию важных задач, имеющих как теоретическое, так и прикладное значение. Первоначально изучение Ф. с. началось с конкретных моделей логики, одной из первых среди которых была двузначная логика. Затем был изучен целый ряд конкретных Ф. с., многообразие которых и составляет содержание понятия Ф. с. Проблематика Ф. с. обширна и имеет много общего с проблематикой многозначных логик. К числу важнейших задач для Ф. с. относятся т. н. задачи о полноте, о сложности, выражения одних функций через другие, о тождественных преобразованиях, о синтезе и анализе и др., решение которых достаточно продвинуто применительно к целому ряду конкретных Ф. с.
     Лит.:Яблонский С. В., Функциональные построения в к-значной логике, «Труды Матем. института АН СССР», 1958, т. 51, с. 5—142; его же, Обзор некоторых результатов в области дискретной математики, «Информационные материалы», 1970, № 5 (42), с. 5—15; Проблемы кибернетики, в. 1, М., 1958.
      В. Б. Кудрявцев.

Музыковедение .

Малиновский и А. Р. Радклифф-Браун . В отличие от эволюционной школы и диффузионизма Малиновский и представители Ф. ш. (Р. Фёрт, Э. Эванс-Притчард и др.) рассматривали культуру каждого народа не как механическое сочетание пережитков и заимствований, а как систему «институтов» (норм, обычаев, верований), призванных выполнить необходимые общественные «функции» (отсюда название школы). Нарушение какой-либо функции приводит к разрушению социального организма в целом. Теоретические исследования функционалисты сочетали со сбором этнографических материалов. Метод последователей Ф. ш. был односторонним: они учитывали лишь «синхронное» функционирование культуры, игнорируя необходимость исторического подхода к проблемам общественного развития. Исследования Ф. ш. были использованы брит. колониальной администрацией («косвенное управление» через местных вождей, консервация архаических черт культуры). Метод и теоретические построения Ф. ш. в социологии развиты и частично пересмотрены сторонниками структурно-функционального анализа , в этнографии — структуралистами (Э. Лич, В. Тернер).
     Лит.:Этнологические исследования за рубежом, М., 1973; Malinowski В., А scientific theory of culture and other essays N. Y., 1960; Radcliffe-Brown A. R., Structure and function in primitive society, L., 1952; его же. Method in social anthropology, Chi., 1958.
      С. А. Токарев.

микроэлектроники . Ф. э. охватывает вопросы получения континуальных (непрерывных) комбинированных сред с наперёд заданными свойствами и создания различных электронных устройств методом физической интеграции, т. е. использования таких физических принципов и явлений, реализация которых позволяет получить компоненты со сложным схемотехническим или системотехническим функциональным назначением (в отличие от технологической интеграции — конструирования интегральных схем на основе функционально простых элементов типа транзисторов, диодов, резисторов и т.д.).

линейные пространства , рассматриваемые в функциональном анализе , являются Ф. п.

дифференциальные уравнения , интегральные уравнения , уравнения в конечных разностях (см. Конечных разностей исчисление ); следует, однако, отметить, что название «Ф. у.» обычно не относят к уравнениям этих типов. Под Ф. у. в узком смысле слова понимают уравнения, в которых искомые функции связаны с известными функциями одного или нескольких переменных при помощи операции образования сложной функции. Ф. у. можно также рассматривать как выражение свойства, характеризующего тот или иной класс функций [например, Ф. у. ( x) = f(— x) характеризует класс чётных функций, Ф. у. f( x+ 1) = f( x) — класс функций, имеющих период 1, и т.д.].
     Одним из простейших Ф. у. является уравнение f( x+ у) = f( x) + f( y). Непрерывные решения этого Ф. у. имеют вид f( x) = Cx. Однако в классе разрывных функций это Ф. у. имеет и иные решения. С рассмотренным Ф. у. связаны
    f( x+ у) = f( x) f( y), f( xy) — f( x) + f( y),
    f( xy) = f( x) f( y),
   непрерывные решения которых имеют соответственно вид e Cx, Cln x, x a( x> 0). Т. о., эти Ф. у. могут служить для определения показательной, логарифмической и степенной функций.
     В теории аналитических функций Ф. у. часто применяются для введения новых классов функций. Например, двоякопериодические функции характеризуются Ф. у. f( z+ а) = f( z) и f( z+ b) = f( z), автоморфные функции — Ф. у. f( s a z) = f( z), где { s a} — некоторая группа дробно-линейных преобразований. Если функция известна в некоторой области, то знание для неё Ф. у. позволяет расширить область определения этой функции. Например, Ф. у. f( x+ 1) = f( x) для периодических функций позволяет определить их значение в любой точке по значениям на отрезке [0, 1]. Этим часто пользуются для аналитического продолжения функций комплексного переменного. Например, пользуясь Ф. у. Г ( z+ 1) = zГ ( z) и зная значения функции Г ( z) (см. Гамма-функция ) в полосе 0 Ј Re zЈ 1, можно продолжить её на всю плоскость z.
     Условия симметрии, имеющиеся в какой-либо физической задаче, обусловливают определённые законы преобразования решений этой задачи при тех или иных преобразованиях координат. Этим определяются Ф. у., которым должно удовлетворять решение данной задачи. Значение соответствующих Ф. у. во многих случаях облегчает нахождение решений.
     Решения Ф. у. могут быть как конкретными функциями, так и классами функций, зависящими от произвольных параметров или произвольных функций. Для некоторых Ф. у. общее решение может быть найдено, если известны одно или несколько его частных решений. Например, общее решение Ф. у. f( x) = f( ax) имеет вид j[w( x)], где j( x) — произвольная функция, а w( x) — частное решение этого Ф. у. Для решения Ф. у. их во многих случаях сводят к дифференциальным уравнениям. Этот метод даёт лишь решения, принадлежащие классу дифференцируемых функций.
     Другим методом решения Ф. у. является метод итераций . Этот метод даёт, например, решение уравнения Абеля f[a( x)] = f( x) + 1 [где a( x) — заданная функция] и связанного с ним уравнения Шрёдера f[a( x)] = cf( x). А. Н. Коркин доказал, что если a( х) — аналитическая функция, то уравнение Абеля имеет аналитическое решение. Эти результаты, нашедшие применение в теории групп Ли (см. Непрерывные группы ), привели в дальнейшем к созданию теории итераций аналитических функций. В некоторых случаях уравнение Абеля решается в конечном виде. Например, Ф. у. f( x n) = f( x) + 1 имеет частное решение .
     Лит.:Ацель Я., Некоторые общие методы в теории функциональных уравнений одной переменной. Новые применения функциональных уравнений, «Успехи математических наук», 1956, т. 11, в. 3, с. 3—68.

Кантором теория множеств. Развитие этой теории, а также аксиоматической геометрии привело к возникновению в работах М. Фреше и Ф. Хаусдорфа метрической и более общей т. н. теоретико-множественной топологии, изучающей абстрактные пространства, т. е. множества произвольных элементов, для которых установлено тем или иным способом понятие близости.
     Среди абстрактных пространств для математического анализа и Ф. а. оказались важными функциональные пространства (т. е. пространства, элементами которых являются функции — откуда и название «Ф. а.»). В работах Д. Гильберта по углублению теории интегральных уравнений возникли пространства l 2 и L 2( a, b) (см. ниже). Обобщая эти пространства, Ф.