Страница:
Плюккера;доктор философии Боннского университета (1868). С 1872 профессор математики в Эрлангене, с 1875 в Мюнхенской Высшей технической школе, а с 1880 в Лейпцигском университете. В 1886 К. переехал в Геттинген, где оставался до конца жизни. Основные работы К. по неевклидовой геометрии, теории непрерывных групп, теории алгебраических уравнений, теории эллиптических функций, теории атоморфных функций. Свои геометрические идеи К. изложил в работе «Сравнительное рассмотрение новых геометрических исследований» (1872), известной под название
эрлангенской программы
. К. стремился раскрыть внутренние связи между отдельными ветвями математики и между математикой, с одной стороны, физикой и техникой — с другой. К. в сотрудничестве с немецким учёным А. Зоммерфельдом написал 4—томное сочинение «Теория волчка» (1910—23). Большой труд был вложен К. в создание «Энциклопедии математических наук» («Enzikiopдdie der mathematischen Wissenschaften»). В течение почти 40 лет (с 1876) К. был главным редактором журнала «Mathematische Annalen». Много занимался вопросами математического образования; перед 1-й мировой войной организовал международную комиссию по реорганизации преподавания математики.
Соч.: Gesammelte mathematische Abhandlungen, Bd 1—3, В., 1921—23; в рус. пер. — Высшая геометрия, М. — Л., 1939; Элементарная математика с точки зрения высшей, т. 1, 3 изд., т. 2, 2 изд., М. — Л., 1934—35; Неевклидова геометрия, М. — Л., 1936; Лекции о развитии математики в 19 столетии ч. 1, М. — Л., 1937.
относительности теории
) уравнение для частиц со спином нуль. Исторически К. — Г. у. было первым релятивистским уравнением
квантовой механики
для волновой функции частицы y; оно было предложено в 1926 Э.
Шрёдингером
(как релятивистское обобщение
Шрёдингера уравнения
) и независимо от него шведским физиком О. Клейном (О. Klein), советским физиком В. А.
Фоком,немецким физиком В. Гордоном (W. Gordon) и др.
Соч.: Gesammelte mathematische Abhandlungen, Bd 1—3, В., 1921—23; в рус. пер. — Высшая геометрия, М. — Л., 1939; Элементарная математика с точки зрения высшей, т. 1, 3 изд., т. 2, 2 изд., М. — Л., 1934—35; Неевклидова геометрия, М. — Л., 1936; Лекции о развитии математики в 19 столетии ч. 1, М. — Л., 1937.
относительности теории
) уравнение для частиц со спином нуль. Исторически К. — Г. у. было первым релятивистским уравнением
квантовой механики
для волновой функции частицы y; оно было предложено в 1926 Э.
Шрёдингером
(как релятивистское обобщение
Шрёдингера уравнения
) и независимо от него шведским физиком О. Клейном (О. Klein), советским физиком В. А.
Фоком,немецким физиком В. Гордоном (W. Gordon) и др.
Для свободной частицы К. — Г. у. записывается в виде:
.
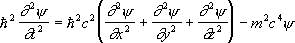Ему соответствует релятивистское соотношение между энергией
Eи импульсом
рчастицы:
(
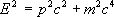m —масса частицы,
с —скорость света).
Решением уравнения является функция y (
х, у, z, t), зависящая только от координат (
х, у, z) и времени (
t)
.Следовательно, частицы, описываемые этой функцией, не обладают никакими дополнительными внутренними степенями свободы, т. е. действительно являются бесспиновыми (к таким частицам относятся, например, p
-и К-мезоны). Однако анализ уравнения показал, что его решение y принципиально отличается по своему физическому смыслу от обычной волновой функции как амплитуды вероятности обнаружить частицу в заданном месте пространства в заданный момент времени: y (
х, у, z, t)
неопределяется однозначно значением y в начальный момент времени (такая однозначная зависимость постулируется в квантовой механике), и, более того, выражение для вероятности данного состояния наряду с положительными значениями может принимать также и лишенные физического смысла отрицательные значения. Поэтому сначала от К. — Г. у. отказались. Однако в 1934 В.
Паули
и В.
Вайскопф
нашли правильную интерпретацию этого уравнения в рамках квантовой теории поля (они рассмотрели его как уравнение поля, аналогичное
Максвелла уравнениям
для электромагнитного поля, и проквантовали его; при этом y стало оператором).
М. А. Либерман.
односторонняя поверхность,введённая в рассмотрение Ф.
Клейном
(1874). К. п. может быть получена из трубы (
рис.
, а), открытой с обеих сторон, если, изогнув трубу, пропустить более узкий её конец через стенку и «склеить» (идентифицировать) оба граничных круга, изгибая внешний, широкий круг внутрь, а внутренний, узкий круг наружу. Т. о., получается поверхность (
рис.
, б), имеющая линию самопересечения. К. п. без самопересечения может быть реализована лишь в четырёхмерном пространстве.
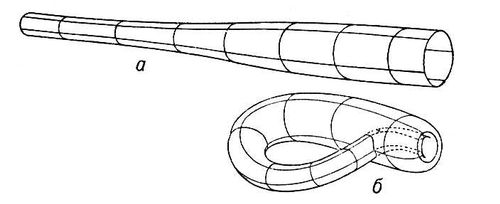Рис. к ст. Клейна поверхность.
