Страница:
счисления
и квадратные уравнения. Вавилонские математики пользовались шестидесятеричной системой счисления, в которой единицы обозначались
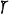 ,а десятки
,а десятки
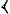 ; эти знаки употреблялись также для обозначения единиц и десятков следующих разрядов; например, число
; эти знаки употреблялись также для обозначения единиц и десятков следующих разрядов; например, число
153 = 2Ч60 + 33
изображалось так:
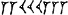
Особенностью вавилонской системы письменного счисления было то, что абсолютная величина чисел оставалась неопределённой. Так, вышеупомянутое число можно было прочесть как 2·60 2+33·60 = 9180 и как 2+ 33·60 -1=2 33/ 60; кроме того, в текстах классической эпохи (2-е тыс. до н. э.) отсутствовал знак, соответствующий нашему нулю. Если учесть, что в К. м. т. отсутствуют записи промежуточных вычислений, то указанное явление проще всего объяснить тем, что промежуточные вычисления производились на счётной доске (типа наших счётов или абака). Тем же самым можно объяснить отсутствие нуля, который при вычислениях на абаке не нужен (столбец, соответствующий отсутствующему разряду, оставлялся пустым). Можно предполагать, что и появление позиционного принципа связано с употреблением счётной доски.
Квадратные уравнения появились у вавилонян в связи с землемерной практикой; эта связь отразилась на терминологии: неизвестные назывались «длина» и «ширина». В дальнейшем неизвестные понимались более абстрактно, так что у вавилонян можно отметить начатки алгебраического мышления.
Лит.:Выгодский М. Я., Арифметика и алгебра в древнем мире, 2 изд., М., 1967; Нейгебауер О., Лекции по истории античных математических наук, пер. с нем., т. 1, М.—Л., 1937; Mathematische Keilschrift-Texte, hrsg. von О. Neugebauer, Tl 1, B., 1935; Mathematical cuneiform texts, ed. by О. Neugebauer and A. Sachs, New Haven, 1945.
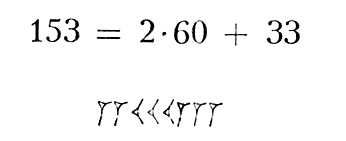 Илл. к ст. Клинописные математические тексты.
Илл. к ст. Клинописные математические тексты.
Шумере
. Около 3000 до н. э. шумерийцы начали передавать изображениями названия отдельных конкретных предметов и общих понятий (см.
Идеографическое письмо
). Так, рисунок ноги стал передавать понятия «ходить» (шумерийское du-, rб-), «стоять» (gub-), «приносить» (tum-) и т. п. Число знаков было порядка тысячи. Знаки являлись лишь вехами для памяти, закреплявшими важнейшие моменты передаваемой мысли, а не связную речь, но так как читающие говорили на шумерском языке, то знаки связывались с определенными словами, что позволило использовать знаки для обозначения звуковых комбинаций уже и независимо от их значения; так, знак ноги мог употребляться не только для передачи упомянутых глаголов, но также для слогов du, rб и т. д.; знак звезды мог обозначать и имена dingir — «бог» и an — «небо», и слог an и т. д. Словесно-слоговая письменность складывается в систему к середине 3-го тысячелетия до н. э. Основа имени или глагола выражалась в ней идеограммой (знаком для понятия), а грамматические показатели и служебные слова — знаками в их слоговом значении. Одинаково звучавшие основы различного значения выражались разными знаками (омофония). Каждый знак мог иметь несколько значений, как слоговых, так и связанных с понятиями (полифония). Для выделения слов, выражавших понятия некоторых определённых категорий (например, птицы, рыбы, профессии и т. д.), применялось небольшое число детерминативов — непроизносимых показателей. Число знаков сократилось до 600, не считая комбинированных. С ускорением письма рисунки упрощались. Черточки знаков вдавливались прямоугольной палочкой, входящей в глину под углом и потому создававшей клиновидное углубление. Направление письма: вначале вертикальными столбцами справа налево, позже — построчное, слева направо. Аккадцы (вавилоняне и ассирийцы) приспособили К. для своего семитского флективного языка в середине 3-го тысячелетия до н. э., сократив число ходовых знаков до 300 и создав новые слоговые значения, соответствующие аккадской фонетической системе; стали употребляться чисто фонетические (силлабические) записи слов; однако шумерские идеограммы и написание отдельных слов и выражений (в аккадском чтении) также продолжали применяться. Аккадская система К. распространилась за пределы Двуречья, приспособившись также к языкам эламскому, хурритскому, хетто-лувийским, урартскому. Начиная со 2-й половины 1-го тысячелетия до н. э. К. использовалась в религиозных и юридических целях лишь в отдельных городах Южного Двуречья (для уже мёртвых шумерского и аккадского языков).
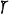 ,а десятки
,а десятки
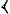 ; эти знаки употреблялись также для обозначения единиц и десятков следующих разрядов; например, число
; эти знаки употреблялись также для обозначения единиц и десятков следующих разрядов; например, число153 = 2Ч60 + 33
изображалось так:
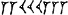
Особенностью вавилонской системы письменного счисления было то, что абсолютная величина чисел оставалась неопределённой. Так, вышеупомянутое число можно было прочесть как 2·60 2+33·60 = 9180 и как 2+ 33·60 -1=2 33/ 60; кроме того, в текстах классической эпохи (2-е тыс. до н. э.) отсутствовал знак, соответствующий нашему нулю. Если учесть, что в К. м. т. отсутствуют записи промежуточных вычислений, то указанное явление проще всего объяснить тем, что промежуточные вычисления производились на счётной доске (типа наших счётов или абака). Тем же самым можно объяснить отсутствие нуля, который при вычислениях на абаке не нужен (столбец, соответствующий отсутствующему разряду, оставлялся пустым). Можно предполагать, что и появление позиционного принципа связано с употреблением счётной доски.
Квадратные уравнения появились у вавилонян в связи с землемерной практикой; эта связь отразилась на терминологии: неизвестные назывались «длина» и «ширина». В дальнейшем неизвестные понимались более абстрактно, так что у вавилонян можно отметить начатки алгебраического мышления.
Лит.:Выгодский М. Я., Арифметика и алгебра в древнем мире, 2 изд., М., 1967; Нейгебауер О., Лекции по истории античных математических наук, пер. с нем., т. 1, М.—Л., 1937; Mathematische Keilschrift-Texte, hrsg. von О. Neugebauer, Tl 1, B., 1935; Mathematical cuneiform texts, ed. by О. Neugebauer and A. Sachs, New Haven, 1945.
Шумере
. Около 3000 до н. э. шумерийцы начали передавать изображениями названия отдельных конкретных предметов и общих понятий (см.
Идеографическое письмо
). Так, рисунок ноги стал передавать понятия «ходить» (шумерийское du-, rб-), «стоять» (gub-), «приносить» (tum-) и т. п. Число знаков было порядка тысячи. Знаки являлись лишь вехами для памяти, закреплявшими важнейшие моменты передаваемой мысли, а не связную речь, но так как читающие говорили на шумерском языке, то знаки связывались с определенными словами, что позволило использовать знаки для обозначения звуковых комбинаций уже и независимо от их значения; так, знак ноги мог употребляться не только для передачи упомянутых глаголов, но также для слогов du, rб и т. д.; знак звезды мог обозначать и имена dingir — «бог» и an — «небо», и слог an и т. д. Словесно-слоговая письменность складывается в систему к середине 3-го тысячелетия до н. э. Основа имени или глагола выражалась в ней идеограммой (знаком для понятия), а грамматические показатели и служебные слова — знаками в их слоговом значении. Одинаково звучавшие основы различного значения выражались разными знаками (омофония). Каждый знак мог иметь несколько значений, как слоговых, так и связанных с понятиями (полифония). Для выделения слов, выражавших понятия некоторых определённых категорий (например, птицы, рыбы, профессии и т. д.), применялось небольшое число детерминативов — непроизносимых показателей. Число знаков сократилось до 600, не считая комбинированных. С ускорением письма рисунки упрощались. Черточки знаков вдавливались прямоугольной палочкой, входящей в глину под углом и потому создававшей клиновидное углубление. Направление письма: вначале вертикальными столбцами справа налево, позже — построчное, слева направо. Аккадцы (вавилоняне и ассирийцы) приспособили К. для своего семитского флективного языка в середине 3-го тысячелетия до н. э., сократив число ходовых знаков до 300 и создав новые слоговые значения, соответствующие аккадской фонетической системе; стали употребляться чисто фонетические (силлабические) записи слов; однако шумерские идеограммы и написание отдельных слов и выражений (в аккадском чтении) также продолжали применяться. Аккадская система К. распространилась за пределы Двуречья, приспособившись также к языкам эламскому, хурритскому, хетто-лувийским, урартскому. Начиная со 2-й половины 1-го тысячелетия до н. э. К. использовалась в религиозных и юридических целях лишь в отдельных городах Южного Двуречья (для уже мёртвых шумерского и аккадского языков).
Формы памятников К. разнообразны (призмы, цилиндры, конусы, каменные плиты); наиболее распространены плитки из глины. До нас дошло огромное количество текстов, написанных К.: деловые документы, исторические надписи, эпос, словари, математические и другие научные сочинения, религиозно-магические тексты.
Особо выделяются: 1) угаритская алфавитная К. из г. Угарита (Рас-Шамры) 2-го тысячелетия до н. э. — приспособление древнесемитского алфавита к письму на глине; с аккадской К. сходна лишь способом нанесения знаков; 2) иранская (древнеперсидская) слоговая К. 6—4 вв. до н. э.; расшифровка её начата немецким учёным Г. Гротефендом в 1802; наличие трёхъязычных персидско-эламско-аккадских надписей позволило в 50-х гг. 19 в. расшифровать и аккадскую К. (английский учёный Г. Роулинсон, ирландский учёный Э. Хинкс, французский учёный Ж. Опперт и др.). Шумерская система К. была расшифрована рядом учёных в конце 19—начале 20 вв., угаритская — в 1930—32 французским учёным Ш. Виролло, немецким учёным Х. Бауэром и др. Начало расшифровке архаического шумерского рисуночного письма положено советским учёным А. А. Вайманом. Хеттская и урартская К., относящиеся к аккадской системе, не нуждались в расшифровке в собственном смысле.
Лит.:Фридрих И., Дешифровка забытых письменностей и языков, пер. с нем., М., 1961; Вайман А. А., К расшифровке протошумерской письменности, в кн.: Переднеазиатский сборник, в. 2, М., 1966; Дьяконов И. М., Языки древней Передней Азии, М., 1967.
И. М. Дьяконов.
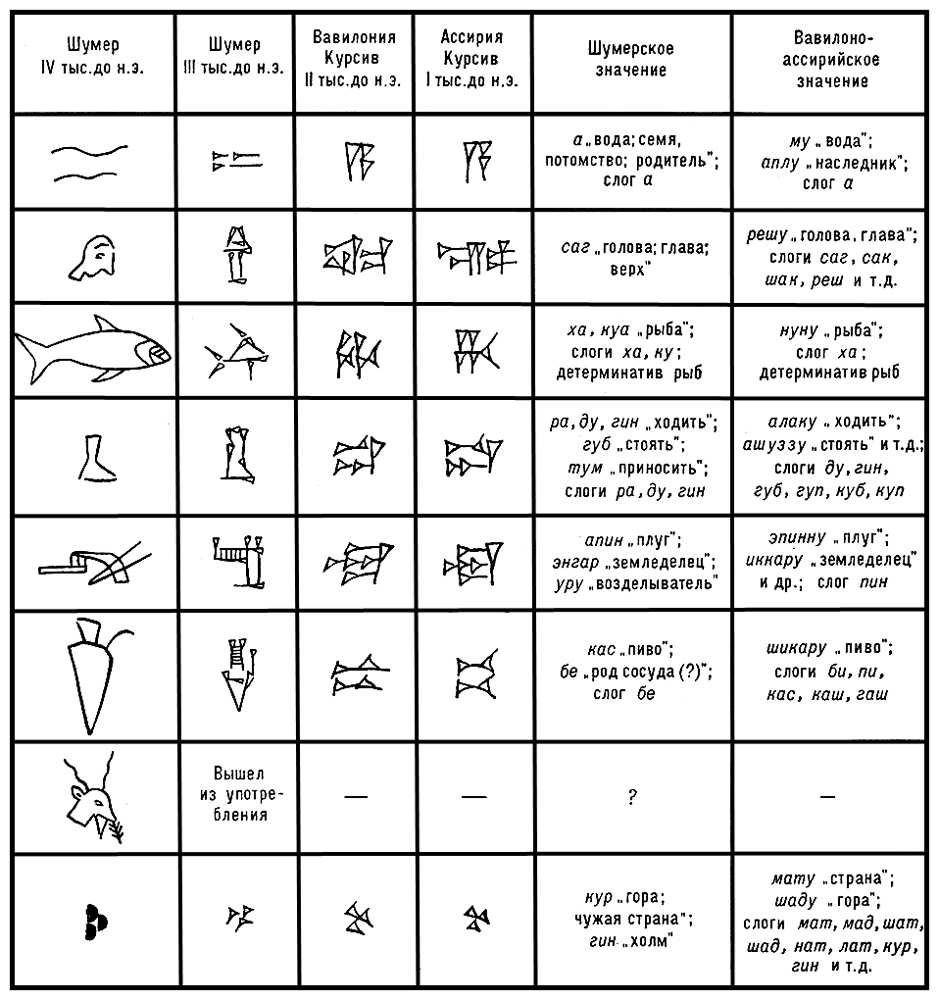 Развитие клинописных знаков.
Развитие клинописных знаков.

