Лит.:Видаль А., А. Барбюс — солдат мира, пер. с французского. Предисловие Ж. Дюкло. [Послесловие Ф. С. Наркирьера], М., 1962; Наркирьер Ф., Французская революционная литература (1914—1924), М., 1965; Brett V., H. Barbusse. Sa marche vers la clartй, son mouvement Clartй, Prague, 1963.
В. С. Лозовецкий.
отряды
(животных) или
порядки
(растений). Например, отряды грызунов, насекомоядных, хищных и др. объединяют в К. млекопитающих. В свою очередь, К., представители которых сходны по общему плану строения и происходят от общих предков, объединяют в
типы
(животных) или
отделы
(растений). Например, К. рыб, земноводных, пресмыкающихся, млекопитающих и др. составляют тип хордовых животных; К. однодольных и двудольных растений — отдел покрытосеменных (цветковых) растений. Понятие «К.» введено в систематику французским ботаником Ж. Турнефором и впоследствии принято К. Линнеем в его «Системе природы» (1735).
множеств теории
)
;про такие предметы говорят, что они являются элементами (данного) К. (отношение принадлежности элемента классу обозначается обычно знаком О; запись
аО
Ачитается: «
аесть элемент класса
А»)
.Предполагается, что в связи с каждым свойством (
понятием
о свойстве) можно рассматривать К. предметов, имеющих это свойство (например, свойству быть чётным числом соответствует К. всех чётных чисел). К. соответствующий некоторому свойству, может состоять из любого конечного числа предметов (конечные К. часто задаются перечнем своих элементов — списком их названий); он может быть бесконечным (например, упомянутый К. всех чётных чисел) или пустым (т. е. вовсе не содержать элементов; пустой К. обычно обозначается О или Ж). К., состоящий только из одного элемента, называется единичным, или сингулярным (сингулярные и пустые К. Аристотель не вводил при построении своей силлогики; см.
Силлогизм
). Пустому К. противополагается универсальный К. (обозначается V), уточняющий круг исследуемых предметов и состоящий из всех объектов подлежащей рассмотрению предметной области. Геометрический К. изображаются обычно фигурами, ограниченными простыми замкнутыми кривыми (например, окружностями на плоскости). Рассматриваются операции над К. и отношения между К. Операции над К.: пересечение классов
Аи
В— класс (обычное обозначение: АЗВ), состоящий из всех тех, и только тех элементов, которые содержатся в обоих классах
Аи
В;объединение классов
Аи
В— класс (AИ
В)
,состоящий из всех тех, и только тех элементов, которые содержатся хотя бы в одном из классов
Аили
В;дополнение класса
А—
класс
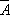 ,состоящий из всех тех, и только тех предметов универсального К., которые не входят в класс
А.Отношения между (двумя произвольными) К.: тождественности (совпадения); включения — один К. является частью (подклассом) другого; частичного совпадения (когда К. имеют хотя бы один общий элемент) и исключения (когда они не имеют общих элементов). Изучение свойств операций над К. и отношений между К. проводится в
логике классов.
,состоящий из всех тех, и только тех предметов универсального К., которые не входят в класс
А.Отношения между (двумя произвольными) К.: тождественности (совпадения); включения — один К. является частью (подклассом) другого; частичного совпадения (когда К. имеют хотя бы один общий элемент) и исключения (когда они не имеют общих элементов). Изучение свойств операций над К. и отношений между К. проводится в
логике классов.
Лит.:Гильберт Д., Аккерман В., Основы теоретической логики, пер. с нем., М., 1947; Тарский А., Введение в логику и методологию дедуктивных наук, пер. с англ., М., 1948; Яновская С. А., Логика классов, в кн.: Философская энциклопедия, т. 3, М., 1964; Кузичев А. С., Диаграммы Венна, М., 1968; Мендельсон Э., Введение в математическую логику, пер. с англ., М., 1971.
А. С. Кузичев.
Классы.

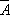 ,состоящий из всех тех, и только тех предметов универсального К., которые не входят в класс
А.Отношения между (двумя произвольными) К.: тождественности (совпадения); включения — один К. является частью (подклассом) другого; частичного совпадения (когда К. имеют хотя бы один общий элемент) и исключения (когда они не имеют общих элементов). Изучение свойств операций над К. и отношений между К. проводится в
логике классов.
,состоящий из всех тех, и только тех предметов универсального К., которые не входят в класс
А.Отношения между (двумя произвольными) К.: тождественности (совпадения); включения — один К. является частью (подклассом) другого; частичного совпадения (когда К. имеют хотя бы один общий элемент) и исключения (когда они не имеют общих элементов). Изучение свойств операций над К. и отношений между К. проводится в
логике классов.