Страница:
Эти два закона вполне определили истинный характер движения планет и, устранив из небесного пространства «совершенное» круговое движение, сделали мировоззрение Коперника ближе отвечающим как об'ективной истине, так и здравому смыслу и практическим запросам жизни.
В поисках правильных числовых соотношений между размерами орбит, по которым несутся в пространстве планеты, и временами (периодами) их обращения около Солнца Кеплер открыл свой третий закон; квадраты времен обращения планет около Солнца относятся как кубы их средних расстояний от Солнца. Этим законом была окончательно установлена истинная закономерность движений планет. Вместе с тем, третий закон Кеплера позволяет, определив из наблюдений период обращения планеты около. Солнца, сразу высчитать ее расстояние от него. Заметим, что средним расстоянием планеты от Солнца является большая полуось описываемой ею эллиптической орбиты (ОА на рис. 1).
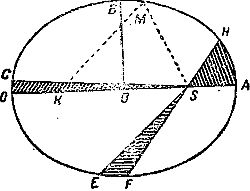 Рис. 1.
Рис. 1.
Для полной характеристики орбиты данной планеты потребовалось ввести понятие о шести величинах, так называемых элементах орбиты. Одним из них является большая полуось орбиты, выражаемая в единицах большой полуоси земной орбиты. Последнюю поэтому называют «астрономической единицей» Второй элемент определяет степень вытянутости эллипса и измеряется величиной его эксцентриситета.
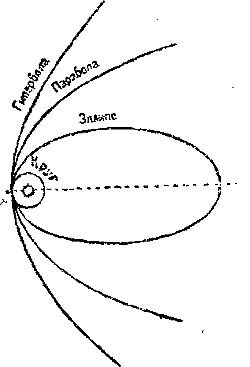
Рис. 2. Конические сечения.
Для круговой орбиты эксцентриситет равен нулю и растет с увеличением вытянутости эллипса. При эксцентриситете, равном единице, эллипс становится бесконечно вытянутым, так что если один из его фокусов остается на месте, то другой отодвигается в бесконечность, и две ветви этого эллипса в пределе становятся параллельными друг другу: они никогда больше фактически не соединяются. Такая, уже разомкнутая кривая называется параболой и изображена на рис. 2. Третий элемент определяет угол i, под которым плоскость планетного эллипса наклонена к плоскости земной орбиты (плоскость эклиптики), и называется наклонением.
Четвертый элемент определяет положение в пространстве той линии, по которой пересекаются плоскости планетной и земной орбит. Он измеряется углом ?, который отсчитывают от некоторого неизменного направления, идущего от Солнца в мировое пространство. Этот элемент называют долготой восходящего узла.
Пятый элемент указывает угол ? который с упомянутой линией пересечения плоскостей, называемой линией узлов, образует направление от Солнца на перигелий планетной орбиты. Этот элемент называют расстоянием перигелия от узла и выражают его в градусах.
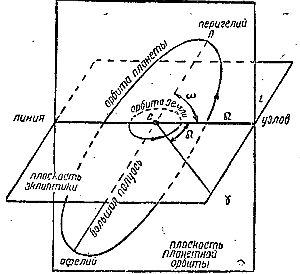
Рис. 3. Элементы планетных орбит.
Шестой элемент представляет один из моментов времени, когда планета при своем движении проходит через точку перигелия.
Зная шесть элементов орбиты, которые вначале считали совершенно постоянными, легко представить себе мысленно, как расположена орбита данной планеты по отношению к Солнцу и к орбите Земли. Знание шести элементов орбиты позволяет, как доказал сам Кеплер, всегда строго рассчитать, в какой точке своего пути находится планета в любой момент будущего или прошедшего времени. Зная, где в то же время находится на своей орбите Земля, легко рассчитать, как должна быть видна планета с нее в этот момент, в каком созвездии и на каком расстоянии от Земли. Когда впоследствии были открыты спутники, обращающиеся вокруг своих планет подобно тому, как Луна обращается вокруг Земли, то оказалось, что их движение также подчиняется законам Кеплера, если только в них слово Солнце заменить словами «своя планета». Например, системы девяти спутников Юпитера и девяти спутников Сатурна являются как бы уменьшенными копиями системы Солнца и планет. Луна тоже движется по законам Кеплера, и в фокусе ее эллиптической орбиты находится Земля. Когда в почти бесконечной дали от солнечной системы были открыты двойные звезды, из которых меньшая обращается около большей, то и тут оказались в силе законы Кеплера. Очевидно, движения небесных тел, происходящие везде по законам Кеплера, всеобщи и обусловлены одной причиной.
От Кеплера до Ньютона
Всемирное тяготение
Успехи ньютонианства
В поисках правильных числовых соотношений между размерами орбит, по которым несутся в пространстве планеты, и временами (периодами) их обращения около Солнца Кеплер открыл свой третий закон; квадраты времен обращения планет около Солнца относятся как кубы их средних расстояний от Солнца. Этим законом была окончательно установлена истинная закономерность движений планет. Вместе с тем, третий закон Кеплера позволяет, определив из наблюдений период обращения планеты около. Солнца, сразу высчитать ее расстояние от него. Заметим, что средним расстоянием планеты от Солнца является большая полуось описываемой ею эллиптической орбиты (ОА на рис. 1).

Для полной характеристики орбиты данной планеты потребовалось ввести понятие о шести величинах, так называемых элементах орбиты. Одним из них является большая полуось орбиты, выражаемая в единицах большой полуоси земной орбиты. Последнюю поэтому называют «астрономической единицей» Второй элемент определяет степень вытянутости эллипса и измеряется величиной его эксцентриситета.

Рис. 2. Конические сечения.
Для круговой орбиты эксцентриситет равен нулю и растет с увеличением вытянутости эллипса. При эксцентриситете, равном единице, эллипс становится бесконечно вытянутым, так что если один из его фокусов остается на месте, то другой отодвигается в бесконечность, и две ветви этого эллипса в пределе становятся параллельными друг другу: они никогда больше фактически не соединяются. Такая, уже разомкнутая кривая называется параболой и изображена на рис. 2. Третий элемент определяет угол i, под которым плоскость планетного эллипса наклонена к плоскости земной орбиты (плоскость эклиптики), и называется наклонением.
Четвертый элемент определяет положение в пространстве той линии, по которой пересекаются плоскости планетной и земной орбит. Он измеряется углом ?, который отсчитывают от некоторого неизменного направления, идущего от Солнца в мировое пространство. Этот элемент называют долготой восходящего узла.
Пятый элемент указывает угол ? который с упомянутой линией пересечения плоскостей, называемой линией узлов, образует направление от Солнца на перигелий планетной орбиты. Этот элемент называют расстоянием перигелия от узла и выражают его в градусах.

Рис. 3. Элементы планетных орбит.
Шестой элемент представляет один из моментов времени, когда планета при своем движении проходит через точку перигелия.
Зная шесть элементов орбиты, которые вначале считали совершенно постоянными, легко представить себе мысленно, как расположена орбита данной планеты по отношению к Солнцу и к орбите Земли. Знание шести элементов орбиты позволяет, как доказал сам Кеплер, всегда строго рассчитать, в какой точке своего пути находится планета в любой момент будущего или прошедшего времени. Зная, где в то же время находится на своей орбите Земля, легко рассчитать, как должна быть видна планета с нее в этот момент, в каком созвездии и на каком расстоянии от Земли. Когда впоследствии были открыты спутники, обращающиеся вокруг своих планет подобно тому, как Луна обращается вокруг Земли, то оказалось, что их движение также подчиняется законам Кеплера, если только в них слово Солнце заменить словами «своя планета». Например, системы девяти спутников Юпитера и девяти спутников Сатурна являются как бы уменьшенными копиями системы Солнца и планет. Луна тоже движется по законам Кеплера, и в фокусе ее эллиптической орбиты находится Земля. Когда в почти бесконечной дали от солнечной системы были открыты двойные звезды, из которых меньшая обращается около большей, то и тут оказались в силе законы Кеплера. Очевидно, движения небесных тел, происходящие везде по законам Кеплера, всеобщи и обусловлены одной причиной.
От Кеплера до Ньютона
Кеплер открыл законы движения планет, но он еще не об'яснил их причины. Почему, например, именно Солнце находится в фокусе всех планетных орбит? Кеплер сравнивал Солнце с магнитом по его Действию на планеты и полагал, что вращающееся Солнце своими лучами увлекает планеты в движение по орбитам. Правда, он понимал, что тут кроется какая-то иная причина, но не мог даже выразиться ясно о ней – четкое понятие силы и взаимодействия было лишь позднее введено Ньютоном. Кеплер писал: «Физики, навострите ваши уши, ведь здесь предпринимается замысел насчет вторжения в вашу область». Но вторгнуться в эту область никто не мог, потому что из всех понятий механики были сколько-нибудь разработаны только простейшие понятия статики (учения о равновесии) и кинематики (науки о движении). Понятия динамики – учения о силах и их взаимодействии, четкие понятия массы и ускорения создал лишь гений Ньютона.
В таких условиях большое впечатление произвела на современников теория вихрей, выдвинутая во Франции Декартом в 1644 году.
По мнению Декарта, к которому нам придется еще не раз возвращаться, мировое пространство заполнено особым, легко подвижным веществом, образующим гигантские вихри. В центральной части каждого такого вихря сгущается светоносное вещество, образующее небесные светила. Вихри Декарта, которые он называет небесами, окружают все небесные тела, причем каждое из них окружено одним таким вихрем. Эти вихревые потоки увлекают и приводят в движение все тела, попадающие в сферу вихря. Так, солнечный вихрь увлекает в своем движении все планеты с их спутниками, а вихрь, окружающий Землю, увлекает круговым движением около Земли ее спутника Луну. Так же двигаются вокруг своих планет и другие спутники, причем в каждом вихре тело, находящееся ближе к центру, вращается вокруг него быстрее, чем более далекое – точно так же, как речные водовороты крутят соломинки, захваченные течением воды. Этим Декарт об'яснил в глазах своих современников тот поражавший их факт, что, чем ближе планеты к Солнцу, тем короче периоды их обращения – всего 88 дней для Меркурия, 225 дней для Венеры, год для Земли и т. д. вплоть до долгих тридцати лет, в течение которых Сатурн только один раз завершает свой путь вокруг центрального светила.
Конечно, такие взгляды являлись огромным шагом вперед по сравнению с средневековыми воззрениями, так выпукло обрисованными в строфах «Божественной Комедии» Данте и позднее в поэме Торквато Тассо «Освобожденный Иерусалим».
Система философских и научных взглядов Декарта получила название картезианства: Декарт подписывал свои сочинения фамилией Картезиус. Картезианское мировоззрение быстро получило широкое распространение, особенно во Франции, и еще в первой половине XVIII века, непосредственно перед выступлением Лапласа на научной арене, картезианство имело там своих ярых последователей.
В идеях Декарта не допускается мысль о дальнодействии, и само пространство, по его понятиям, является материальным в физическом смысле этого слова. Взаимодействие тел, в частности приведение их в состояние движения, может произойти только при непосредственном их соприкосновении. Такое соприкосновение может осуществляться и посредством промежуточной среды, роль которой у Декарта выполняли вихри. Дальнодействие – действие на расстоянии в пустоте, отвергалось его философией и всей его физической теорией мироздания. Таким образом, еще примитивная материалистическая точка зрения на взаимодействие небесных тел выражена в мировоззрении Декарта наиболее четко.
Французская Академия наук во второй половине XVII века и даже в начале XVIII века являлась оплотом картезианских идей.
В таких условиях большое впечатление произвела на современников теория вихрей, выдвинутая во Франции Декартом в 1644 году.
По мнению Декарта, к которому нам придется еще не раз возвращаться, мировое пространство заполнено особым, легко подвижным веществом, образующим гигантские вихри. В центральной части каждого такого вихря сгущается светоносное вещество, образующее небесные светила. Вихри Декарта, которые он называет небесами, окружают все небесные тела, причем каждое из них окружено одним таким вихрем. Эти вихревые потоки увлекают и приводят в движение все тела, попадающие в сферу вихря. Так, солнечный вихрь увлекает в своем движении все планеты с их спутниками, а вихрь, окружающий Землю, увлекает круговым движением около Земли ее спутника Луну. Так же двигаются вокруг своих планет и другие спутники, причем в каждом вихре тело, находящееся ближе к центру, вращается вокруг него быстрее, чем более далекое – точно так же, как речные водовороты крутят соломинки, захваченные течением воды. Этим Декарт об'яснил в глазах своих современников тот поражавший их факт, что, чем ближе планеты к Солнцу, тем короче периоды их обращения – всего 88 дней для Меркурия, 225 дней для Венеры, год для Земли и т. д. вплоть до долгих тридцати лет, в течение которых Сатурн только один раз завершает свой путь вокруг центрального светила.
Конечно, такие взгляды являлись огромным шагом вперед по сравнению с средневековыми воззрениями, так выпукло обрисованными в строфах «Божественной Комедии» Данте и позднее в поэме Торквато Тассо «Освобожденный Иерусалим».
Эллиптическое движение планет по известным уже тогда законам Кеплера Декарт мог об'яснить лишь очень неясно, говоря, что под действием давления соседних вихрей и от других причин вихри могут принимать сплюснутую или эллиптическую форму. Проще говоря, теория вихрей Декарта совершенно не могла об'яснить движения планет по законам Кеплера.
«… Планеты ниже стройные вертятся,
Что ангелами в ход приведены.
Так что в пути не могут заблуждаться…»
Система философских и научных взглядов Декарта получила название картезианства: Декарт подписывал свои сочинения фамилией Картезиус. Картезианское мировоззрение быстро получило широкое распространение, особенно во Франции, и еще в первой половине XVIII века, непосредственно перед выступлением Лапласа на научной арене, картезианство имело там своих ярых последователей.
В идеях Декарта не допускается мысль о дальнодействии, и само пространство, по его понятиям, является материальным в физическом смысле этого слова. Взаимодействие тел, в частности приведение их в состояние движения, может произойти только при непосредственном их соприкосновении. Такое соприкосновение может осуществляться и посредством промежуточной среды, роль которой у Декарта выполняли вихри. Дальнодействие – действие на расстоянии в пустоте, отвергалось его философией и всей его физической теорией мироздания. Таким образом, еще примитивная материалистическая точка зрения на взаимодействие небесных тел выражена в мировоззрении Декарта наиболее четко.
Французская Академия наук во второй половине XVII века и даже в начале XVIII века являлась оплотом картезианских идей.
Всемирное тяготение
В Англии, где идеи француза Декарта не оставили столь же сильных следов, как на родине философа, развитие научного мышления шло более самостоятельным путем и увенчалось гениальными работами Ньютона. В 1687 году появилось его сочинение «Математические начала натуральной философии», которое с небывалой дотоле ясностью и четкостью определило новое научное мировоззрение. Здесь давалось исчерпывающее, на первый взгляд, об'яснение величайшего множества явлений природы, исходя из немногих четких принципов. Кроме того, тут же давался и новый метод научного исследования природы, метод индукции.
[3]Этой работой Ньютона были предопределены, как известно, основные линии дальнейшего развития всей астрономии и физики вплоть до начала XX века и отчасти даже позднее. Понятие причинности всех явлений природы стало после этого на твердую почву и вдохновило исследователей на дальнейшее углубление полученных результатов. Успехи Ньютона в значительной мере определялись тем что ему, независимо от Лейбница и почти одновременно с ним, удалось изобрести могущественное средство математического анализа – исчисление бесконечно малых. Другими словами, Ньютон изобрел высшую математику – основы дифференциального и интегрального исчислений. Только при посредстве этого метода Ньютон мог шагнуть гораздо дальше, чем его предшественники. С тех пор дифференциальное и интегральное исчисления являются незаменимым способом математической трактовки различных явлений природы.
Анализируя законы, найденные Кеплером непосредственно из наблюдений, как говорят, эмпирически, учитывая эллиптичность планетных орбит, Ньютон доказал, что планеты испытывают ускорение, всегда направленное к Солнцу и изменяющееся обратно пропорционально квадрату расстояния планет от Солнца. Так же изменяется ускорение и в движении одной и той же планеты, когда при движении по эллипсу меняется ее расстояние от Солнца. Пользуясь сформулированными им понятиями массы и силы, Ньютон доказал, что сила взаимного тяготения между планетой и Солнцем пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.
Ньютон доказал также – и это чрезвычайно важно, – что если между двумя телами действует сила тяготения, то тело с меньшей массой должно двигаться около тела с большей массой именно по законам Кеплера, а не как-либо иначе. Мало того, выведенные им законы движения под действием тяготения получили очень общий характер: те законы, которые открыл сам Кеплер, оказались лишь частным случаем этих, более общих законов.
Таким образом, Ньютон установил законы:
1. Всякое тело под действием тяготения к другому (большей массы) должно описывать около него одно из конических сечений (рис. 2). Коническими сечениями являются кривые, получаемые от – пересечения поверхности конуса с плоскостью. В число их входят: круг, эллипс, парабола и гипербола (рис. 2), из которых две последние кривые не замкнуты.
2. Закон, устанавливающий, что площади, описываемые радиусом-вектором, пропорциональны времени, оказался справедливым при движении по любой из перечисленных кривых.
3. Выражение третьего закона Кеплера, связывающее размеры орбит и периоды обращения, должно быть более сложным, в него должны войти массы Солнца и планет. Вследствие того, что масса Солнца гораздо больше массы всех планет, вместе взятых, различие между выражением третьего закона, установленным Кеплером, и выражением того же закона, найденным Ньютоном, очень незначительно. Однако именно это различие позволяет на основании наблюдаемого движения тел вычислить их массу.
Ньютон развил также способы вычислить орбиту планеты по наблюденным положениям ее на небе среди звезд, т. е. способы определения элементов орбиты. Зная элементы орбиты, можно наперед вычислить, в какой точке неба планета будет видна с Земли в тот или другой момент.
Далее, Ньютон сделал еще одно замечательное открытие: он доказал, что тяготение Луны к Земле имеет ту же природу, что и тяготение к ней обычных предметов, находящихся у ее поверхности. Другими словами, он доказал, что сила тяготения – та же сила, которую до тех пор называли тяжестью и наблюдали ее проявление в падении предметов на Землю. Так, большинство движений, наблюдаемых на Земле, связывалось воедино с разнообразнейшими движениями всех тел солнечной системы и находило себе общую причину: свойство взаимного притяжения, действующее во всех случаях по одному и тому же закону.
Обнаружилось, что движение спутников вокруг своих планет происходит в согласии с тем же законом тяготения. Во второй половине XIX века было строго доказано, что и за пределами солнечной системы, в движении далеких двойных звезд друг около друга, закон тяготения действует так же, как на Земле. Недаром поэтому закон тяготения получил название всемирного. Рассматриваемый как причина, он об'яснил не только качественно, но и количественно все основные движения планет и их спутников в солнечной системе. С этих пор картина мироздания получила законченную ясность. В науке не осталось больше места для астрологии – лжеучения о мнимом влиянии небесных светил на судьбу людей и народов и о возможности, якобы, предсказать эту судьбу на основе астрономических данных.
Тем же законом тяготения Ньютон удачно об'яснил основные черты двух явлений, стоящих на первый взгляд совсем особняком.
Периодическое возникновение приливов и отливов в земных океанах оказалось естественным следствием различия в величине силы, с которой Луна притягивает к себе ближайшие и далекие части Земли и ее океанов.
С давних пор было известно открытое еще Гиппархом (II в. до нашей эры) систематическое перемещение среди звезд полюса мира – точки, вокруг которой кажется происходящим суточное вращение небосвода, обусловливающее восход и заход светил (рис. 4). Благодаря этому явлению, с течением времени некоторые созвездия перестают быть видимыми в данной местности, и на смену им появляются другие. Так, рассчитано, что через несколько тысячелетий в Европе станет видимо созвездие Южного Креста, которым сейчас могут любоваться только жители Южного полушария Земли и жители тропических стран.
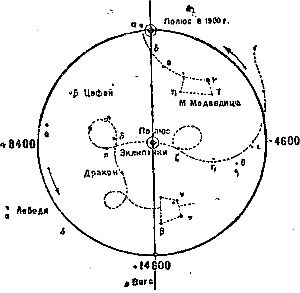
Рис. 4.
Вместе с перемещением полюса мира перемещается перпендикулярная к ней плоскость небесного экватора и точка ее пересечения с небесной эклиптикой – линией кажущегося годичного перемещения Солнца среди созвездий. Эта точка, называемая точкой весеннего равноденствия, медленно и равномерно смещается по направлению к западу. Солнце, перемещаясь по эклиптике, попадает каждый год в эту точку раньше, и весна на Земле ежегодно наступает раньше, чем через один полный оборот Земли вокруг Солнца. Поэтому описанное явление назвали предварением равноденствий (21 марта день равен ночи на всей Земле) или прецессией.
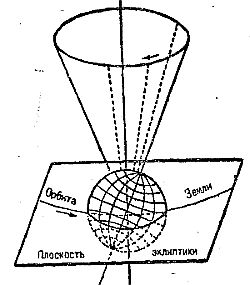
Рис. 5.
Коперник, создав свою систему мира, правильно об'яснил явление прецессии тем, что ось вращения Земли медленно поворачивается в пространстве. Она описывает при этом конус (рис. 5) с периодом в 26 тысяч лет. Каждые 26 тысяч лет весна начинается в тот момент, когда Земля находится в одной и той же точке пространства. Причина прецессии, т. е. движения земной оси по конусу, однако, оставалась загадочной. Ньютон, применив свои законы механики к вращающейся Земле, пришел к убеждению, что вследствие развивающейся при вращении центробежной силы Земля должна быть сплющена у полюсов, имея вдоль своего экватора как бы выступ.
Между прочим, это теоретическое заключение Ньютона горячо оспаривалось французскими учеными, определявшими в 1718 году размеры и форму Земли.
Впоследствии оказалось, что результат французских ученых был вызван неточностью их измерений. Новые измерения, произведенные в середине XVIII века, подтвердили правильность вывода Ньютона.
Ньютон, решившись раскрыть тайну прецессии, доказал, что прецессия вызвана этой сплюснутостью Земли. Луна и Солнце, находясь обычно не в плоскости земного экватора и действуя на избыток массы, расположенной вдоль него (благодаря упомянутому сжатию), стремятся повернуть ось Земли. Но Земля вращается вокруг своей оси, и, сопротивляясь этому насилию со стороны Луны и Солнца, земная ось, в согласии с законами механики, описывает при этом конус. Общеизвестно, что Землю можно сравнить с вращающимся волчком. Если надавить на ось волчка, она станет описывать в пространстве конус, подобный тому, какой описывает ось Земли.
Открыв закон тяготения и об'яснив им количественно почти все движения, известные астрономам, Ньютон не стремился выяснить природу этого тяготения и глубже проникнуть в его сущность. Вскоре стало принято считать, что тяготение может молниеносно передаваться через пустоту, действовать на огромных расстояниях без посредства какой-либо вещественной среды. Сам Ньютон сказал знаменитую фразу о природе тяготения: «Гипотез я не строю, ибо все то, что не может быть выведено из явлений, должно быть названо гипотезой».
Понять закон тяготения современникам Ньютона было не легко, особенно тем из них, которые находились под влиянием философии Декарта. Многие крупнейшие ученые, даже позднейшей эпохи, не могли понять тяготения и признать его существование. Например, Лейбниц, соперник Ньютона в области изобретения дифференциального и интегрального исчислений, писал Гюйгенсу: «Я не понимаю, как Ньютон представляет себе тяжесть или притяжение. По его мнению, повидимому, это не что иное, как некое необ'яснимое нематериальное качество». Гюйгенс, тогда уже широко известный своими работами по математике, физике и астрономии, отвечал Лейбницу: «Что касается причины приливов, которую дает Ньютон, то она меня не удовлетворяет нисколько, как и все другие его теории, которые он строит на своем принципе притяжения, который мне кажется нелепым».
Еще в 1730 году Иоганн Бернулли получил премию от парижской Академии наук за попытку выяснить причину эллиптичности орбит планет, совершенно игнорируя закон тяготения. Оппозиция, с которой теория Ньютона была принята на континенте, стала ослабевать, когда расширенная парижская Академия приняла в свой состав много молодежи, более восприимчивой к новым идеям.
В 1727 году молодой Вольтер, вернувшись из Англии на континент, со свойственным ему остроумным сарказмом так описал антагонизм научных взглядов, разделивших передовые страны его времени на два лагеря. «Если француз приедет в Лондон, он найдет здесь большое различие в философии, а также во многих других вопросах. В Париже он оставил мир, полным вещества, здесь он находит его пустым. В Париже вселенная наполнена эфирными вихрями, тогда как тут в том же пространстве действуют невидимые силы. В Париже давление Луны на море вызывает отлив и прилив, – в Англии же, наоборот, море тяготеет к Луне. У картезианцев все достигается давлением, что, по правде говоря, не вполне ясно, у ньютонианцев все об'ясняется притяжением, что, однако, немногим яснее. Наконец, в Париже Землю считают вытянутой у полюсов, как яйцо, а в Лондоне она сжата, как тыква…»
Анализируя законы, найденные Кеплером непосредственно из наблюдений, как говорят, эмпирически, учитывая эллиптичность планетных орбит, Ньютон доказал, что планеты испытывают ускорение, всегда направленное к Солнцу и изменяющееся обратно пропорционально квадрату расстояния планет от Солнца. Так же изменяется ускорение и в движении одной и той же планеты, когда при движении по эллипсу меняется ее расстояние от Солнца. Пользуясь сформулированными им понятиями массы и силы, Ньютон доказал, что сила взаимного тяготения между планетой и Солнцем пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.
Ньютон доказал также – и это чрезвычайно важно, – что если между двумя телами действует сила тяготения, то тело с меньшей массой должно двигаться около тела с большей массой именно по законам Кеплера, а не как-либо иначе. Мало того, выведенные им законы движения под действием тяготения получили очень общий характер: те законы, которые открыл сам Кеплер, оказались лишь частным случаем этих, более общих законов.
Таким образом, Ньютон установил законы:
1. Всякое тело под действием тяготения к другому (большей массы) должно описывать около него одно из конических сечений (рис. 2). Коническими сечениями являются кривые, получаемые от – пересечения поверхности конуса с плоскостью. В число их входят: круг, эллипс, парабола и гипербола (рис. 2), из которых две последние кривые не замкнуты.
2. Закон, устанавливающий, что площади, описываемые радиусом-вектором, пропорциональны времени, оказался справедливым при движении по любой из перечисленных кривых.
3. Выражение третьего закона Кеплера, связывающее размеры орбит и периоды обращения, должно быть более сложным, в него должны войти массы Солнца и планет. Вследствие того, что масса Солнца гораздо больше массы всех планет, вместе взятых, различие между выражением третьего закона, установленным Кеплером, и выражением того же закона, найденным Ньютоном, очень незначительно. Однако именно это различие позволяет на основании наблюдаемого движения тел вычислить их массу.
Ньютон развил также способы вычислить орбиту планеты по наблюденным положениям ее на небе среди звезд, т. е. способы определения элементов орбиты. Зная элементы орбиты, можно наперед вычислить, в какой точке неба планета будет видна с Земли в тот или другой момент.
Далее, Ньютон сделал еще одно замечательное открытие: он доказал, что тяготение Луны к Земле имеет ту же природу, что и тяготение к ней обычных предметов, находящихся у ее поверхности. Другими словами, он доказал, что сила тяготения – та же сила, которую до тех пор называли тяжестью и наблюдали ее проявление в падении предметов на Землю. Так, большинство движений, наблюдаемых на Земле, связывалось воедино с разнообразнейшими движениями всех тел солнечной системы и находило себе общую причину: свойство взаимного притяжения, действующее во всех случаях по одному и тому же закону.
Обнаружилось, что движение спутников вокруг своих планет происходит в согласии с тем же законом тяготения. Во второй половине XIX века было строго доказано, что и за пределами солнечной системы, в движении далеких двойных звезд друг около друга, закон тяготения действует так же, как на Земле. Недаром поэтому закон тяготения получил название всемирного. Рассматриваемый как причина, он об'яснил не только качественно, но и количественно все основные движения планет и их спутников в солнечной системе. С этих пор картина мироздания получила законченную ясность. В науке не осталось больше места для астрологии – лжеучения о мнимом влиянии небесных светил на судьбу людей и народов и о возможности, якобы, предсказать эту судьбу на основе астрономических данных.
Тем же законом тяготения Ньютон удачно об'яснил основные черты двух явлений, стоящих на первый взгляд совсем особняком.
Периодическое возникновение приливов и отливов в земных океанах оказалось естественным следствием различия в величине силы, с которой Луна притягивает к себе ближайшие и далекие части Земли и ее океанов.
С давних пор было известно открытое еще Гиппархом (II в. до нашей эры) систематическое перемещение среди звезд полюса мира – точки, вокруг которой кажется происходящим суточное вращение небосвода, обусловливающее восход и заход светил (рис. 4). Благодаря этому явлению, с течением времени некоторые созвездия перестают быть видимыми в данной местности, и на смену им появляются другие. Так, рассчитано, что через несколько тысячелетий в Европе станет видимо созвездие Южного Креста, которым сейчас могут любоваться только жители Южного полушария Земли и жители тропических стран.

Рис. 4.
Вместе с перемещением полюса мира перемещается перпендикулярная к ней плоскость небесного экватора и точка ее пересечения с небесной эклиптикой – линией кажущегося годичного перемещения Солнца среди созвездий. Эта точка, называемая точкой весеннего равноденствия, медленно и равномерно смещается по направлению к западу. Солнце, перемещаясь по эклиптике, попадает каждый год в эту точку раньше, и весна на Земле ежегодно наступает раньше, чем через один полный оборот Земли вокруг Солнца. Поэтому описанное явление назвали предварением равноденствий (21 марта день равен ночи на всей Земле) или прецессией.

Рис. 5.
Коперник, создав свою систему мира, правильно об'яснил явление прецессии тем, что ось вращения Земли медленно поворачивается в пространстве. Она описывает при этом конус (рис. 5) с периодом в 26 тысяч лет. Каждые 26 тысяч лет весна начинается в тот момент, когда Земля находится в одной и той же точке пространства. Причина прецессии, т. е. движения земной оси по конусу, однако, оставалась загадочной. Ньютон, применив свои законы механики к вращающейся Земле, пришел к убеждению, что вследствие развивающейся при вращении центробежной силы Земля должна быть сплющена у полюсов, имея вдоль своего экватора как бы выступ.
Между прочим, это теоретическое заключение Ньютона горячо оспаривалось французскими учеными, определявшими в 1718 году размеры и форму Земли.
Впоследствии оказалось, что результат французских ученых был вызван неточностью их измерений. Новые измерения, произведенные в середине XVIII века, подтвердили правильность вывода Ньютона.
Ньютон, решившись раскрыть тайну прецессии, доказал, что прецессия вызвана этой сплюснутостью Земли. Луна и Солнце, находясь обычно не в плоскости земного экватора и действуя на избыток массы, расположенной вдоль него (благодаря упомянутому сжатию), стремятся повернуть ось Земли. Но Земля вращается вокруг своей оси, и, сопротивляясь этому насилию со стороны Луны и Солнца, земная ось, в согласии с законами механики, описывает при этом конус. Общеизвестно, что Землю можно сравнить с вращающимся волчком. Если надавить на ось волчка, она станет описывать в пространстве конус, подобный тому, какой описывает ось Земли.
Открыв закон тяготения и об'яснив им количественно почти все движения, известные астрономам, Ньютон не стремился выяснить природу этого тяготения и глубже проникнуть в его сущность. Вскоре стало принято считать, что тяготение может молниеносно передаваться через пустоту, действовать на огромных расстояниях без посредства какой-либо вещественной среды. Сам Ньютон сказал знаменитую фразу о природе тяготения: «Гипотез я не строю, ибо все то, что не может быть выведено из явлений, должно быть названо гипотезой».
Понять закон тяготения современникам Ньютона было не легко, особенно тем из них, которые находились под влиянием философии Декарта. Многие крупнейшие ученые, даже позднейшей эпохи, не могли понять тяготения и признать его существование. Например, Лейбниц, соперник Ньютона в области изобретения дифференциального и интегрального исчислений, писал Гюйгенсу: «Я не понимаю, как Ньютон представляет себе тяжесть или притяжение. По его мнению, повидимому, это не что иное, как некое необ'яснимое нематериальное качество». Гюйгенс, тогда уже широко известный своими работами по математике, физике и астрономии, отвечал Лейбницу: «Что касается причины приливов, которую дает Ньютон, то она меня не удовлетворяет нисколько, как и все другие его теории, которые он строит на своем принципе притяжения, который мне кажется нелепым».
Еще в 1730 году Иоганн Бернулли получил премию от парижской Академии наук за попытку выяснить причину эллиптичности орбит планет, совершенно игнорируя закон тяготения. Оппозиция, с которой теория Ньютона была принята на континенте, стала ослабевать, когда расширенная парижская Академия приняла в свой состав много молодежи, более восприимчивой к новым идеям.
В 1727 году молодой Вольтер, вернувшись из Англии на континент, со свойственным ему остроумным сарказмом так описал антагонизм научных взглядов, разделивших передовые страны его времени на два лагеря. «Если француз приедет в Лондон, он найдет здесь большое различие в философии, а также во многих других вопросах. В Париже он оставил мир, полным вещества, здесь он находит его пустым. В Париже вселенная наполнена эфирными вихрями, тогда как тут в том же пространстве действуют невидимые силы. В Париже давление Луны на море вызывает отлив и прилив, – в Англии же, наоборот, море тяготеет к Луне. У картезианцев все достигается давлением, что, по правде говоря, не вполне ясно, у ньютонианцев все об'ясняется притяжением, что, однако, немногим яснее. Наконец, в Париже Землю считают вытянутой у полюсов, как яйцо, а в Лондоне она сжата, как тыква…»
Успехи ньютонианства
Ньютон вполне строго разрешил проблему двух тел, т. е. вопрос о том, каково должно быть относительное движение двух тел под действием взаимного тяготения. Такой случай является идеализацией условий, имеющихся в солнечной системе. Какая-нибудь планета притягивается в действительности не только Солнцем, но и остальными планетами. В реальном мире мы имеем проблему не двух, а большего числа тел. Наиболее простым будет случай проблемы трех тел, но и эта проблема настолько сложна, что Ньютон не мог ее решить даже в самом общем виде. Однако все, сделанное им, было так грандиозно, потребовало такой затраты времени и сил, что ждать большего было невозможно. Вскоре выяснилось, что определение условия движения нескольких тел под действием взаимного тяготения требует несравненно более совершенного математического аппарата, чем тот, которым располагал Ньютон.
Основную задачу небесной механики – изучение движения нескольких тел – можно разделить на две: одну, имеющую самый общий характер, и другую – непосредственно относящуюся к частному случаю солнечной системы. Первая значительно труднее, чем вторая. В солнечной системе масса Солнца в 770 раз больше массы всех планет вместе взятых, и потому движение их происходит в первом приближении, как говорят, в соответствии с решением проблемы двух тел, т. е. по законам Кеплера. Притяжение данной планеты остальными лишь немного расстраивает это движение. Движение немного отклоняется от законов Кеплера; например, орбита оказывается не эллипсом, а более сложной кривой, притом не лежащей строго в одной плоскости. Точно также скорость движения планеты по своей орбите в сравнении с требованиями второго закона Кеплера бывает то больше, то меньше. Эти отклонения от кеплеровского движения называются возмущениями. Они невелики и потому не помешали Кеплеру и Ньютону открыть свои законы. Тем не менее, накапливаясь с течением времени, действие возмущений заметным образом меняет элементы орбиты планеты. Если возмущения не учитывать теоретически заранее, то вычисленные наперед положения светил на небе разойдутся с наблюдениями, и астрономическая теория не ответит тем требованиям, которые пред'являют к ней техника и астрономы-наблюдатели.
Было бы долго перечислять все области науки, техники и промышленности, которые так или иначе связаны с теорией движения небесных тел, т. е. с небесной механикой. Например, мореплавание, аэронавигация, картография и нахождение залежей подземных ископаемых нуждаются в точном теоретическом предвычислении положений небесных светил. Стоит вспомнить, например, как широко пользовались астрономическими методами ориентировки летчики Герои Советского Союза при организации плавучей полярной станции, при перелете через Северный полюс, при перелетах вдоль всего СССР и т. п. Кроме того, необходимо доказать, что если взаимное притяжение планет и расстраивает их движение по сравнению с элементарной теорией движения двух тел, то теория тяготения все же способна предусмотреть их количественно. При этом результат подсчета должен в точности совпадать с фактическими данными. Без подобного доказательства абсолютная истинность теории тяготения все же может быть подвергнута сомнению.
Ньютон вполне отдавал себе отчет в существовании всех этих осложнений, он отметил их, но успел коснуться их математически лишь вскользь, хотя главнейшие неправильности в движении Луны, установленные наблюдателями еще до изобретения телескопа, он смог об'яснить.
На долю последователей Ньютона – Эйлера, Клеро, Даламбера, Лагранжа и Лапласа выпало завершить! грандиозное здание, заложенное Ньютоном, и довести его до полного совершенства. Лаплас застал Эйлера и Даламбера еще в расцвете их творческих способностей. Воинствующим оплотом защитников Ньютона явилась не Англия, а Франция, так долго вначале не принимавшая ньютонианства. Лаплас был младшим в этой плеяде великих умов, и он в значительной степени закончил то, что не вполне удалось его предшественникам и старшим товарищам.
После Ньютона Эйлер и Клеро первыми принялись за разработку небесной механики. В 1747 году Эйлер закончил работу о возмущениях в движении планет Юпитера и Сатурна. Следующие работы Эйлер посвятил исследованию движения Луны. Огромные услуги дальнейшему развитию небесной механики принесла разработка Эйлером методов дифференциального и в особенности интегрального исчислений, которые в его руках (по сравнению с тем, чем располагал Ньютон) выросли необычайно. Недаром Лаплас часто говаривал постоянно окружавшей его молодежи: «Читайте, читайте Эйлера, он наш общий учитель».
Так же велики были и заслуги Даламбера, которого можно считать воспреемником Лапласа во французской Академии наук. В один день с Клеро он представил в Академию попытку решения проблемы трех тел и ее применения к теории движения Луны. Стало уже выясняться, что решение общей задачи о трех телах вообще не может быть получено вполне точно. Можно написать уравнения, соответствующие этой проблеме, но затем встает задача их интегрирования. Она оказалась столь трудной, по крайней мере при тогдашнем состоянии математики, что Клеро махнул на эти уравнения рукой, сказав: «Пусть интегрирует, кто сможет».
Основную задачу небесной механики – изучение движения нескольких тел – можно разделить на две: одну, имеющую самый общий характер, и другую – непосредственно относящуюся к частному случаю солнечной системы. Первая значительно труднее, чем вторая. В солнечной системе масса Солнца в 770 раз больше массы всех планет вместе взятых, и потому движение их происходит в первом приближении, как говорят, в соответствии с решением проблемы двух тел, т. е. по законам Кеплера. Притяжение данной планеты остальными лишь немного расстраивает это движение. Движение немного отклоняется от законов Кеплера; например, орбита оказывается не эллипсом, а более сложной кривой, притом не лежащей строго в одной плоскости. Точно также скорость движения планеты по своей орбите в сравнении с требованиями второго закона Кеплера бывает то больше, то меньше. Эти отклонения от кеплеровского движения называются возмущениями. Они невелики и потому не помешали Кеплеру и Ньютону открыть свои законы. Тем не менее, накапливаясь с течением времени, действие возмущений заметным образом меняет элементы орбиты планеты. Если возмущения не учитывать теоретически заранее, то вычисленные наперед положения светил на небе разойдутся с наблюдениями, и астрономическая теория не ответит тем требованиям, которые пред'являют к ней техника и астрономы-наблюдатели.
Было бы долго перечислять все области науки, техники и промышленности, которые так или иначе связаны с теорией движения небесных тел, т. е. с небесной механикой. Например, мореплавание, аэронавигация, картография и нахождение залежей подземных ископаемых нуждаются в точном теоретическом предвычислении положений небесных светил. Стоит вспомнить, например, как широко пользовались астрономическими методами ориентировки летчики Герои Советского Союза при организации плавучей полярной станции, при перелете через Северный полюс, при перелетах вдоль всего СССР и т. п. Кроме того, необходимо доказать, что если взаимное притяжение планет и расстраивает их движение по сравнению с элементарной теорией движения двух тел, то теория тяготения все же способна предусмотреть их количественно. При этом результат подсчета должен в точности совпадать с фактическими данными. Без подобного доказательства абсолютная истинность теории тяготения все же может быть подвергнута сомнению.
Ньютон вполне отдавал себе отчет в существовании всех этих осложнений, он отметил их, но успел коснуться их математически лишь вскользь, хотя главнейшие неправильности в движении Луны, установленные наблюдателями еще до изобретения телескопа, он смог об'яснить.
На долю последователей Ньютона – Эйлера, Клеро, Даламбера, Лагранжа и Лапласа выпало завершить! грандиозное здание, заложенное Ньютоном, и довести его до полного совершенства. Лаплас застал Эйлера и Даламбера еще в расцвете их творческих способностей. Воинствующим оплотом защитников Ньютона явилась не Англия, а Франция, так долго вначале не принимавшая ньютонианства. Лаплас был младшим в этой плеяде великих умов, и он в значительной степени закончил то, что не вполне удалось его предшественникам и старшим товарищам.
После Ньютона Эйлер и Клеро первыми принялись за разработку небесной механики. В 1747 году Эйлер закончил работу о возмущениях в движении планет Юпитера и Сатурна. Следующие работы Эйлер посвятил исследованию движения Луны. Огромные услуги дальнейшему развитию небесной механики принесла разработка Эйлером методов дифференциального и в особенности интегрального исчислений, которые в его руках (по сравнению с тем, чем располагал Ньютон) выросли необычайно. Недаром Лаплас часто говаривал постоянно окружавшей его молодежи: «Читайте, читайте Эйлера, он наш общий учитель».
Так же велики были и заслуги Даламбера, которого можно считать воспреемником Лапласа во французской Академии наук. В один день с Клеро он представил в Академию попытку решения проблемы трех тел и ее применения к теории движения Луны. Стало уже выясняться, что решение общей задачи о трех телах вообще не может быть получено вполне точно. Можно написать уравнения, соответствующие этой проблеме, но затем встает задача их интегрирования. Она оказалась столь трудной, по крайней мере при тогдашнем состоянии математики, что Клеро махнул на эти уравнения рукой, сказав: «Пусть интегрирует, кто сможет».
