Страница:
Если не иметь точной теории движения Луны, нельзя заранее вычислить видимое с Земли положение Луны на фоне звездного неба. Такое положение дела представляется нетерпимым не только с точки зрения науки, стремящейся не оставить необ'ясненных явлений в природе, но и для повседневной человеческой практики. Из наблюдения над положением Луны среди звезд и сравнения его с вычисленным наперед положением, данным по определенному, например, Гринвичскому времени, сухопутные путешественники и моряки могли определять свою географическую долготу. Этим способом, более надежным, чем наблюдения спутников Юпитера, очень широко пользовались в течение нескольких столетий, а иногда пользуются еще и сейчас.
Однако для успеха применения наблюдений Луны к определению долготы нужны достаточно точные предвычисления ее положения, а при отсутствии точной теории движения нашего спутника сделать это невозможно.
В XVII и XVIII столетиях британское правительство, обладавшее наиболее мощным флотом, усиленно захватывавшее новые колонии за океанами, терпело большие убытки от несовершенства морских методов определения долгот. В 1713 году английское правительство об'явило премию в 20 тысяч фунтов стерлингов (120 тысяч рублей по тогдашнему курсу) за способ, позволяющий определять долготу с точностью хотя бы до полуградуса, и меньшие премии – за менее точные методы.
В поисках новых методов и в попытках улучшения старых приняли участие лучшие астрономы XVIII столетия. Но их поиски не скоро увенчались успехом. Главные усилия направились на составление улучшенных таблиц движения Луны.
Эйлер, Клеро и Даламбер почти одновременно и независимо друг от друга получили приближенные решения проблемы трех тел, которую каждый из них пытался применить к движению Луны под действием тяготения к Земле и Солнцу.
Эйлер дважды обращался к теории Луны и достиг того, что основанные на его теории таблицы Майера оказались в относительном согласии с наблюдениями. По этим таблицам долгота получалась с точностью около одного градуса. Работа Эйлера была премирована британским правительством (частью суммы). 18 тысяч рублей получила и вдова Майера.
Несмотря на этот успех теории, и Эйлер, и Клеро, и Даламбер оказались бессильными об'яснить загадочное ускорение в движении Луны, замеченное Галлеем еще в 1693 году из сравнения древних наблюдений над затмениями с современными. Вековое ускорение в среднем движении Луны, необ'яснимое в течение целого столетия, сделалось одним из наиболее интересных, грозивших к тому же подорвать доверие к точности закона Ньютона. Попытка Лагранжа, предпринятая в 1774 году, потерпела полнейшую неудачу, и он стал даже сомневаться в подлинности древних наблюдений.
Лапласу пришлось много потрудиться над решением загадки, и по временам даже он сбивался с истинного пути, допуская, например, что тяготение распространяется не мгновенно, а подобно свету, с некоторой конечной скоростью.
В 1787 году Лаплас нашел окончательное и верное решение вопроса, так долго мучившего теоретиков и практиков. Лаплас указал на причину векового ускорения в движении Луны и теоретически вычислил его величину.
Под действием возмущения от планет земная орбита непрерывно меняется; колеблется и ее размер (большая полуось) и степень вытянутости (эксцентриситет). Лаплас еще раньше доказал, что земная орбита делается то более круглой (когда эксцентриситет уменьшается), то более вытянутой, и эти изменения происходят периодически, хотя и очень медленно.
Лаплас убедился, что средняя скорость движения Луны около Земли зависит от эксцентриситета земной орбиты. Движение Луны, ускоряется, когда форма орбиты Земли приближается к кругу, и наоборот. Таким образом, «вековое» ускорение в движении Луны, как и для Юпитера, является не вечным, а периодическим, и настанет время, когда Луна станет двигаться с замедлением.
Разрешением лунной загадки Лаплас устранил последнее важное в его время разногласие между теорией тяготения и наблюдениями. Это был полный и окончательный триумф ньютонианства и небесной механики, заставивший представителей других менее точных наук с завистью посматривать на астрономов.
В третьем томе «Небесной механики» Лаплас дал полное и совершенно новое изложение теории Луны, пользуясь которым Бюрг (в Вене), а затем Бургардт (немец, поселившийся в Париже) составили и издали новые таблицы движения Луны. Эти таблицы вытеснили менее точные таблицы Майера и надолго явились надежным пособием для отважных мореплавателей и исследователей новооткрытых стран.
Чрезвычайно трудно описать или хотя бы перечислить все усовершенствования теории движения тел солнечной системы и практики их вычисления, которые ввел Лаплас и изложил на страницах своей «Небесной механики». В 1780 году им был, например, разработан совершенно новый способ определения орбит новооткрытых планет и комет, послуживший основанием для большей части позднейших работ, например, для недавней работы Лейшнера. Способом Лапласа, хотя и в измененном виде, пользуются современные вычислители планетных путей.
Методы учета возмущений в движении небесных тел, как методы классической небесной механики, разработанные Лапласом и Лагранжем, до сих пор сохраняют большое значение и применяются не только в астрономии, но и в теоретической физике, например, при изучении движения электронов в недрах модели атомов, созданной Бором.
Основываясь на формулах Лапласа, его современники и последователи составили столь важные для практической астрономии таблицы движения планет. В 1845 году сравнение наблюдений с таблицами Бувара, представляющими Лапласову теорию движения планет, привело Леверрье к предсказанию (путем вычислений) существования новой планеты – Нептуна.
Лаплас деятельно интересовался практическими применениями своих теорий. Многие из вычислений он проверял лично, по поводу других вел оживленную переписку.
Устойчивость солнечной системы
Расстояние от Луны до Солнца
Форма и вращение Земли
Теория приливов
Однако для успеха применения наблюдений Луны к определению долготы нужны достаточно точные предвычисления ее положения, а при отсутствии точной теории движения нашего спутника сделать это невозможно.
В XVII и XVIII столетиях британское правительство, обладавшее наиболее мощным флотом, усиленно захватывавшее новые колонии за океанами, терпело большие убытки от несовершенства морских методов определения долгот. В 1713 году английское правительство об'явило премию в 20 тысяч фунтов стерлингов (120 тысяч рублей по тогдашнему курсу) за способ, позволяющий определять долготу с точностью хотя бы до полуградуса, и меньшие премии – за менее точные методы.
В поисках новых методов и в попытках улучшения старых приняли участие лучшие астрономы XVIII столетия. Но их поиски не скоро увенчались успехом. Главные усилия направились на составление улучшенных таблиц движения Луны.
Эйлер, Клеро и Даламбер почти одновременно и независимо друг от друга получили приближенные решения проблемы трех тел, которую каждый из них пытался применить к движению Луны под действием тяготения к Земле и Солнцу.
Эйлер дважды обращался к теории Луны и достиг того, что основанные на его теории таблицы Майера оказались в относительном согласии с наблюдениями. По этим таблицам долгота получалась с точностью около одного градуса. Работа Эйлера была премирована британским правительством (частью суммы). 18 тысяч рублей получила и вдова Майера.
Несмотря на этот успех теории, и Эйлер, и Клеро, и Даламбер оказались бессильными об'яснить загадочное ускорение в движении Луны, замеченное Галлеем еще в 1693 году из сравнения древних наблюдений над затмениями с современными. Вековое ускорение в среднем движении Луны, необ'яснимое в течение целого столетия, сделалось одним из наиболее интересных, грозивших к тому же подорвать доверие к точности закона Ньютона. Попытка Лагранжа, предпринятая в 1774 году, потерпела полнейшую неудачу, и он стал даже сомневаться в подлинности древних наблюдений.
Лапласу пришлось много потрудиться над решением загадки, и по временам даже он сбивался с истинного пути, допуская, например, что тяготение распространяется не мгновенно, а подобно свету, с некоторой конечной скоростью.
В 1787 году Лаплас нашел окончательное и верное решение вопроса, так долго мучившего теоретиков и практиков. Лаплас указал на причину векового ускорения в движении Луны и теоретически вычислил его величину.
Под действием возмущения от планет земная орбита непрерывно меняется; колеблется и ее размер (большая полуось) и степень вытянутости (эксцентриситет). Лаплас еще раньше доказал, что земная орбита делается то более круглой (когда эксцентриситет уменьшается), то более вытянутой, и эти изменения происходят периодически, хотя и очень медленно.
Лаплас убедился, что средняя скорость движения Луны около Земли зависит от эксцентриситета земной орбиты. Движение Луны, ускоряется, когда форма орбиты Земли приближается к кругу, и наоборот. Таким образом, «вековое» ускорение в движении Луны, как и для Юпитера, является не вечным, а периодическим, и настанет время, когда Луна станет двигаться с замедлением.
Разрешением лунной загадки Лаплас устранил последнее важное в его время разногласие между теорией тяготения и наблюдениями. Это был полный и окончательный триумф ньютонианства и небесной механики, заставивший представителей других менее точных наук с завистью посматривать на астрономов.
В третьем томе «Небесной механики» Лаплас дал полное и совершенно новое изложение теории Луны, пользуясь которым Бюрг (в Вене), а затем Бургардт (немец, поселившийся в Париже) составили и издали новые таблицы движения Луны. Эти таблицы вытеснили менее точные таблицы Майера и надолго явились надежным пособием для отважных мореплавателей и исследователей новооткрытых стран.
Чрезвычайно трудно описать или хотя бы перечислить все усовершенствования теории движения тел солнечной системы и практики их вычисления, которые ввел Лаплас и изложил на страницах своей «Небесной механики». В 1780 году им был, например, разработан совершенно новый способ определения орбит новооткрытых планет и комет, послуживший основанием для большей части позднейших работ, например, для недавней работы Лейшнера. Способом Лапласа, хотя и в измененном виде, пользуются современные вычислители планетных путей.
Методы учета возмущений в движении небесных тел, как методы классической небесной механики, разработанные Лапласом и Лагранжем, до сих пор сохраняют большое значение и применяются не только в астрономии, но и в теоретической физике, например, при изучении движения электронов в недрах модели атомов, созданной Бором.
Основываясь на формулах Лапласа, его современники и последователи составили столь важные для практической астрономии таблицы движения планет. В 1845 году сравнение наблюдений с таблицами Бувара, представляющими Лапласову теорию движения планет, привело Леверрье к предсказанию (путем вычислений) существования новой планеты – Нептуна.
Лаплас деятельно интересовался практическими применениями своих теорий. Многие из вычислений он проверял лично, по поводу других вел оживленную переписку.
Устойчивость солнечной системы
Показав, что в движении Юпитера и Сатурна нет вековых неравенств, Лаплас еще в своей первой работе по этому вопросу (в 1773 г.) поставил и более общий вопрос: устойчива ли солнечная система вообще? Если в движении какой-нибудь планеты, например, Земли, наблюдается вековое замедление, то это означает, это среднее расстояние этой планеты от Солнца увеличивается, В результате Земля может так отдалиться от Солнца, что вследствие недостаточного тепла жизнь на ней станет невозможной.
Если наклонность орбиты какой-нибудь планеты будет неограниченно расти, то эта планета станет двигаться в плоскости, перпендикулярной к той, в которой она движется сейчас, и солнечная система придет в полное расстройство.
При беспредельных увеличениях больших полуосей орбит, планеты, например, Земля или Сатурну могут совсем оторваться от Солнца и унестись в морозные и темные дали межзвездных пространств или могут столкнуться с другими планетами, что поведет к грандиозной катастрофе. При таком же уменьшении больших полуосей орбит или увеличении их эксцентриситетов планеты обрушатся на раскаленную поверхность Солнца и, воспламенясь, кончат свое существование.
Наличие трудно учитываемых возмущений не давало уверенности в устойчивости движения тел солнечной системы и смущало всех предшественников Лапласа. Ньютон настолько безнадежно смотрел на возможность предсказать будущее солнечной системы, вследствие наличия возмущений, что писал следующее: «…едва заметные неравенства, могущие происходить от взаимодействия планет и комет… вероятно, будут увеличиваться в течение весьма долгого времени, до тех пор, пока, наконец, систему не будет нуждаться в приведении ее в порядок руками творца». На эти слова трудно ответить остроумнее, чем ответил Лейбниц: «Ньютон и его приверженцы имеют чрезвычайно забавное представление о божественном творении. С их точки зрения бог должен время от времени заводить свои мировые часы… Бог создал такую несовершенную машину, что он должен по временам очищать ее от грязи и даже чинить, как часовщик исправляет свою работу».
Во времена Лапласа мнения об устойчивости солнечной системы, подверженной действию одних лишь внутренних для нее сил, разделились. Эйлер, например, разделял точку зрения Ньютона, а Лагранж склонялся к мысли об устойчивости системы.
Установив неизменность средних расстояний от Солнца, Юпитера и Сатурна (если не говорить об их небольших периодических возмущениях), Лаплас рассмотрел общий случай и открыл, что в пределах той точности, с которой он вел вычисление рядов, заключение, сделанное относительно Юпитера и Сатурна, остается верным и для других планет, в том числе и для Земли.
Последующая разработка проблемы велась им то попеременно, то одновременно с Лагранжем; каждый из ученых возвращался к ней неоднократно, как к наиболее трудному вопросу.
В 1774 году Лагранж доказал иным методом то, что до него сделал Лаплас, произведя к тому же более точные вычисления. Лаплас в следующем же году применил восхищавший его метод Лагранжа к изучению формы (эксцентриситетов) орбит и нашел их изменения также периодическими. За ним Лагранж снова продвинул дело несколько вперед, а в период с 1781 по 1784 год дал еще пять замечательных работ на эту тему.
Лаплас позднее установил, что два элемента планетных орбит – эксцентриситеты и наклонности – связаны простым математическим соотношением, устанавливающим тесные пределы для их изменений. Знаменитые теоремы Лапласа, устанавливающие свойства солнечной системы, явились, таким образом, доказательством ее устойчивости. Однако это доказательство не является вполне строгим ввиду особой сложности бесконечных рядов, которыми пользовались Лаплас и Лагранж. Они не могли при вычислениях строго учесть влияние всех бесконечных членов рядов и совершенно строго установить, что оставленные ими без внимания члены не скажутся на движении планет по прошествии бесконечно долгого времени. Во всяком случае, Лапласу и Лагранж у мы обязаны знанием того, что не только в ближайшем будущем, но и на протяжении многих миллионов лет в будущем ни Земле, ни другим планетам вообще не угрожает ни гибель в раскаленных вихрях Солнца, ни медленная агония в леденящих безднах межзвездной дали. Их исследования (в той плоскости, как поставила задачу классическая небесная механика) были подтверждены последующими изысканиями учеников Лапласа – Пуансо, Пуассона и других ученых.
Если наклонность орбиты какой-нибудь планеты будет неограниченно расти, то эта планета станет двигаться в плоскости, перпендикулярной к той, в которой она движется сейчас, и солнечная система придет в полное расстройство.
При беспредельных увеличениях больших полуосей орбит, планеты, например, Земля или Сатурну могут совсем оторваться от Солнца и унестись в морозные и темные дали межзвездных пространств или могут столкнуться с другими планетами, что поведет к грандиозной катастрофе. При таком же уменьшении больших полуосей орбит или увеличении их эксцентриситетов планеты обрушатся на раскаленную поверхность Солнца и, воспламенясь, кончат свое существование.
Наличие трудно учитываемых возмущений не давало уверенности в устойчивости движения тел солнечной системы и смущало всех предшественников Лапласа. Ньютон настолько безнадежно смотрел на возможность предсказать будущее солнечной системы, вследствие наличия возмущений, что писал следующее: «…едва заметные неравенства, могущие происходить от взаимодействия планет и комет… вероятно, будут увеличиваться в течение весьма долгого времени, до тех пор, пока, наконец, систему не будет нуждаться в приведении ее в порядок руками творца». На эти слова трудно ответить остроумнее, чем ответил Лейбниц: «Ньютон и его приверженцы имеют чрезвычайно забавное представление о божественном творении. С их точки зрения бог должен время от времени заводить свои мировые часы… Бог создал такую несовершенную машину, что он должен по временам очищать ее от грязи и даже чинить, как часовщик исправляет свою работу».
Во времена Лапласа мнения об устойчивости солнечной системы, подверженной действию одних лишь внутренних для нее сил, разделились. Эйлер, например, разделял точку зрения Ньютона, а Лагранж склонялся к мысли об устойчивости системы.
Установив неизменность средних расстояний от Солнца, Юпитера и Сатурна (если не говорить об их небольших периодических возмущениях), Лаплас рассмотрел общий случай и открыл, что в пределах той точности, с которой он вел вычисление рядов, заключение, сделанное относительно Юпитера и Сатурна, остается верным и для других планет, в том числе и для Земли.
Последующая разработка проблемы велась им то попеременно, то одновременно с Лагранжем; каждый из ученых возвращался к ней неоднократно, как к наиболее трудному вопросу.
В 1774 году Лагранж доказал иным методом то, что до него сделал Лаплас, произведя к тому же более точные вычисления. Лаплас в следующем же году применил восхищавший его метод Лагранжа к изучению формы (эксцентриситетов) орбит и нашел их изменения также периодическими. За ним Лагранж снова продвинул дело несколько вперед, а в период с 1781 по 1784 год дал еще пять замечательных работ на эту тему.
Лаплас позднее установил, что два элемента планетных орбит – эксцентриситеты и наклонности – связаны простым математическим соотношением, устанавливающим тесные пределы для их изменений. Знаменитые теоремы Лапласа, устанавливающие свойства солнечной системы, явились, таким образом, доказательством ее устойчивости. Однако это доказательство не является вполне строгим ввиду особой сложности бесконечных рядов, которыми пользовались Лаплас и Лагранж. Они не могли при вычислениях строго учесть влияние всех бесконечных членов рядов и совершенно строго установить, что оставленные ими без внимания члены не скажутся на движении планет по прошествии бесконечно долгого времени. Во всяком случае, Лапласу и Лагранж у мы обязаны знанием того, что не только в ближайшем будущем, но и на протяжении многих миллионов лет в будущем ни Земле, ни другим планетам вообще не угрожает ни гибель в раскаленных вихрях Солнца, ни медленная агония в леденящих безднах межзвездной дали. Их исследования (в той плоскости, как поставила задачу классическая небесная механика) были подтверждены последующими изысканиями учеников Лапласа – Пуансо, Пуассона и других ученых.
Расстояние от Луны до Солнца
Движение Луны, блестяще исследованное Лапласом, явилось неисчерпаемым источником для извлечения самых неожиданных результатов, касавшихся не только других небесных тел, но и самой Земли. Выводы Лапласа, даже при кратком знакомстве, представляют прекрасный пример плодовитости и поразительной интуиции их автора.
Каково расстояние от Земли до Солнца – вот вопрос, которым задавалось человечество уже с первых шагов своей сознательной жизни. Знание этого расстояния играет особенно важную роль, потому что при помощи третьего закона Кеплера все расстояния в солнечной системе можно выразить через расстояние Земли от Солнца. Мала того, этой же единицей пользуются и при выражении расстояний до далеких звезд.

Рис. 6. Сравнительные размеры Солнца и планет.
До Лапласа наиболее точным методом определения расстояния до Солнца считались наблюдения над прохождением Венеры по диску Солнца. Этот метод был предложен Галлеем и заключается в следующем. Путь Венеры около Солнца целиком расположен внутри земной орбиты, и потому эта планета по временам, оказываясь как раз между Солнцем и Землей, проектируется на солнечный диск в виде маленького черного кружка. Когда она проходит между нами и Солнцем, то видно, как этот кружок пересекает солнечный диск. Такие прохождения Венеры по диску Солнца не из всех мест Земли видны одинаково хорошо, но и тот путь, по которому кружок Венеры проходит по солнечному диску, виден различно, если наблюдать явление с разных точек Земли. Расстояние между двумя наблюдателями на Земле называется в этом случае базисом, и чем он больше, тем больше кажущееся смещение пути Венеры перед Солнцем. Его называют параллактическим смещением. Зная длину базиса и величину кажущегося смещения линии, которой путь Венеры пректируется на Солнце, можно вычислить расстояние Земли от Венеры, а затем по третьему закону Кеплера найти и расстояние Земли от Солнца.
К сожалению, прохождения Венеры по диску Солнца случаются очень редко. Например, они наблюдались в 1631 и 1639 годах, а следующий раз лишь в 1761 и 1769 годах – в годы ранней молодости Лапласа. Следующие прохождения должны были случиться лишь в 1874 и 1882 годах. В нашем столетии это явление не будет наблюдаться.
Понятное дело, астрономы всячески готовились к наблюдениям Венеры по методу, на который Галлей возлагал большие надежды. Так как определение расстояния Земли от Солнца лежит в основе ряда практических применений астрономии, то правительства не жалели денег на организацию далеких и трудных экспедиций. В 1761 году для наблюдения явления с концов возможно большого базиса экспедиции ученых отправились с большим риском и затратами в Тобольск, на остров св. Елены, на мыс Доброй Надежды, в Индию; кроме того, повсеместно производились наблюдения на станциях Европы. Физические явления при этом прохождении наблюдал, между прочим, и Ломоносов (в Петербурге), впервые доказавший при этом, что Венера, подобно Земле, окружена атмосферой. Результаты наблюдений оказались недостаточно схожими друг с другом. Прохождение 1769 года наблюдалось в еще более грандиозном масштабе. Тогда, по просьбе петербургской Академии наук, обращенной в Париж к Лаланду, ей были присланы в помощь два швейцарских астронома. Ученые раз'ехались по всей России: в Оренбург, Орск, Якутск, Умбу, Колу и т. д.
Некоторое представление о трудностях, с которыми были сопряжены эти экспедиции, дают следующие примеры.
Верона, посланный в Индию для первого наблюдения, умер по дороге, не доехав до места назначения. Война, расстроив правильные пути сообщения, помешала Лежантилю и Мазону добраться до Индии вовремя. Лежантиль опоздал и высадился на сушу, когда явление уже закончилось. Путешествия были так трудны, что, по рассказу Лапласа, Лежантиль остался в Индии готовиться к наблюдениям следующего прохождения Венеры, до которого оставалось восемь лет. Желанный день настал, погода радовала наблюдателя, но в самый момент начала прохождения случайное облачко закрыло Солнце, и плоды многолетней подготовки пропали даром. Пропавшего без вести ученого считали во Франции уже мертвецом и справили по нем гражданские панихиды. С похоронами поторопились, хотя и не намного. Совершенно расстроенный своим неуспехом и измученный трудной дорогой, Лежантиль умер вскоре после возвращения на родину.
Лаплас подошел к проблеме с совершенно неожиданного конца и определил расстояние от Земли до Солнца без всяких экспедиций, не выходя из своего кабинета.
Знаток лунного движения, он понял, что обычные наблюдения над движением Луны определяют величину возмущений, которым оно подвержено. Небесная механика дает теоретическую связь этих возмущений, главной причиной которых является Солнце, с расстоянием Луны от этого светила. Таким образом, расстояние системы Земля—Луна от Солнца, от которого зависит величина возмущений, может быть вычислено теоретически. Лаплас его и вычислил. Его результат был не хуже, чем результаты, полученные ценой дорогих экспедиций и многолетней кропотливой обработки наблюдений.
Впоследствии, пользуясь открытием новых небесных тел, [4]подходящих к Земле ближе, чем Венера, астрономы нашли и другие точные способы определения расстояния до Солнца.
Усовершенствование метода Лапласа в XIX и XX веках обеспечивает ему почетное место среди чисто наблюдательных методов, тем более, что нарастание возмущений с течением времени повышает точность, которую дает его способ.
Каково расстояние от Земли до Солнца – вот вопрос, которым задавалось человечество уже с первых шагов своей сознательной жизни. Знание этого расстояния играет особенно важную роль, потому что при помощи третьего закона Кеплера все расстояния в солнечной системе можно выразить через расстояние Земли от Солнца. Мала того, этой же единицей пользуются и при выражении расстояний до далеких звезд.

Рис. 6. Сравнительные размеры Солнца и планет.
До Лапласа наиболее точным методом определения расстояния до Солнца считались наблюдения над прохождением Венеры по диску Солнца. Этот метод был предложен Галлеем и заключается в следующем. Путь Венеры около Солнца целиком расположен внутри земной орбиты, и потому эта планета по временам, оказываясь как раз между Солнцем и Землей, проектируется на солнечный диск в виде маленького черного кружка. Когда она проходит между нами и Солнцем, то видно, как этот кружок пересекает солнечный диск. Такие прохождения Венеры по диску Солнца не из всех мест Земли видны одинаково хорошо, но и тот путь, по которому кружок Венеры проходит по солнечному диску, виден различно, если наблюдать явление с разных точек Земли. Расстояние между двумя наблюдателями на Земле называется в этом случае базисом, и чем он больше, тем больше кажущееся смещение пути Венеры перед Солнцем. Его называют параллактическим смещением. Зная длину базиса и величину кажущегося смещения линии, которой путь Венеры пректируется на Солнце, можно вычислить расстояние Земли от Венеры, а затем по третьему закону Кеплера найти и расстояние Земли от Солнца.
К сожалению, прохождения Венеры по диску Солнца случаются очень редко. Например, они наблюдались в 1631 и 1639 годах, а следующий раз лишь в 1761 и 1769 годах – в годы ранней молодости Лапласа. Следующие прохождения должны были случиться лишь в 1874 и 1882 годах. В нашем столетии это явление не будет наблюдаться.
Понятное дело, астрономы всячески готовились к наблюдениям Венеры по методу, на который Галлей возлагал большие надежды. Так как определение расстояния Земли от Солнца лежит в основе ряда практических применений астрономии, то правительства не жалели денег на организацию далеких и трудных экспедиций. В 1761 году для наблюдения явления с концов возможно большого базиса экспедиции ученых отправились с большим риском и затратами в Тобольск, на остров св. Елены, на мыс Доброй Надежды, в Индию; кроме того, повсеместно производились наблюдения на станциях Европы. Физические явления при этом прохождении наблюдал, между прочим, и Ломоносов (в Петербурге), впервые доказавший при этом, что Венера, подобно Земле, окружена атмосферой. Результаты наблюдений оказались недостаточно схожими друг с другом. Прохождение 1769 года наблюдалось в еще более грандиозном масштабе. Тогда, по просьбе петербургской Академии наук, обращенной в Париж к Лаланду, ей были присланы в помощь два швейцарских астронома. Ученые раз'ехались по всей России: в Оренбург, Орск, Якутск, Умбу, Колу и т. д.
Некоторое представление о трудностях, с которыми были сопряжены эти экспедиции, дают следующие примеры.
Верона, посланный в Индию для первого наблюдения, умер по дороге, не доехав до места назначения. Война, расстроив правильные пути сообщения, помешала Лежантилю и Мазону добраться до Индии вовремя. Лежантиль опоздал и высадился на сушу, когда явление уже закончилось. Путешествия были так трудны, что, по рассказу Лапласа, Лежантиль остался в Индии готовиться к наблюдениям следующего прохождения Венеры, до которого оставалось восемь лет. Желанный день настал, погода радовала наблюдателя, но в самый момент начала прохождения случайное облачко закрыло Солнце, и плоды многолетней подготовки пропали даром. Пропавшего без вести ученого считали во Франции уже мертвецом и справили по нем гражданские панихиды. С похоронами поторопились, хотя и не намного. Совершенно расстроенный своим неуспехом и измученный трудной дорогой, Лежантиль умер вскоре после возвращения на родину.
Лаплас подошел к проблеме с совершенно неожиданного конца и определил расстояние от Земли до Солнца без всяких экспедиций, не выходя из своего кабинета.
Знаток лунного движения, он понял, что обычные наблюдения над движением Луны определяют величину возмущений, которым оно подвержено. Небесная механика дает теоретическую связь этих возмущений, главной причиной которых является Солнце, с расстоянием Луны от этого светила. Таким образом, расстояние системы Земля—Луна от Солнца, от которого зависит величина возмущений, может быть вычислено теоретически. Лаплас его и вычислил. Его результат был не хуже, чем результаты, полученные ценой дорогих экспедиций и многолетней кропотливой обработки наблюдений.
Впоследствии, пользуясь открытием новых небесных тел, [4]подходящих к Земле ближе, чем Венера, астрономы нашли и другие точные способы определения расстояния до Солнца.
Усовершенствование метода Лапласа в XIX и XX веках обеспечивает ему почетное место среди чисто наблюдательных методов, тем более, что нарастание возмущений с течением времени повышает точность, которую дает его способ.
Форма и вращение Земли
Другой результат, еще ближе касающийся Земли – вопрос о ее форме – Лаплас также сумел получить, исходя из наблюдений Луны.
Предсказанный Ньютоном факт сжатия Земли у полюсов был подтвержден точными геодезическими измерениями французских астрономов. Для этой цели измерения приходится делать в самых разнообразных местах земного шара, у экватора и у полюсов, опять-таки при помощи специальных экспедиций. Результаты длительных и трудных наблюдений в поле подлежат после этого еще многолетней обработке. Без знаний точной фигуры Земли нельзя построить точную географическую карту, столь нужную для транспорта, промышленности и в военном деле.
Лаплас и тут нашел теоретическое решение задачи, затратив несравненно меньше времени и труда, чем геодезисты. Он рассудил, что планета притягивает другие тела как материальная точка, помещенная в центре этой планеты, лишь в том случае, если она состоит из шаровых концентрических слоев однородной плотности. Если Земля сжата у полюсов, то вдоль ее экватора должен существовать избыток вещества, как бы твердый пояс, окружающий планету. Ближайшая к Луне часть этого пояса должна притягивать нашего спутника сильнее, чем более далекая, и притяжение Луны Землей нельзя заменить притяжением материальной точкой, так как расстояние от Земли до Луны не слишком велико в сравнении с размерами этого экваториального пояса. В результате в теоретические формулы, представляющие движение Луны, должны войти члены, зависящие от величины земного сжатия. Сжатие Земли Лаплас вычислил из этих формул, сравнивая свою теорию с наблюдениями. Луны, произведенными в одном месте. Найденная им величина сжатия 1/306 очень близка к величине 1/297, принимаемой для Земли в настоящее время.
По величине сжатия Земли, зная скорость ее вращения вокруг оси, можно вычислить упругость земных недр и можно догадываться о ее внутреннем строении.
Клеро впервые вывел замечательную теорему (носящую его имя), позволяющую определить сжатие Земли из известного распределения силы тяжести на ее поверхности, независимо от распределения плотностей внутри Земли. Для определения самой силы тяжести астрономические экспедиции определяли период колебания маятников, зависящий, как известно, от величины этой силы тяжести. На полюсах она должна быть больше, на экваторе меньше. Практическое использование метода Клеро, контролирующее собственный результат, полученный другим методом, впервые было сделано Лапласом. Вообще фигурой Земли Лаплас занимался очень много. Он изучал в связи с этим фигуру равновесия вращающейся жидкой массы, развивая исследования Ньютона, Мак Лорена, Клеро и Даламбера. В связи с этим Лаплас ввел в науку чрезвычайно плодотворное понятие о так называемом потенциале (или силовой функции), немедленно использованное Лежандром и другими учеными.
Выяснилось, что степень сжатия Земли меньше, чем должно быть в случае однородного жидкого тела, вращающегося со скоростью Земли. Отсюда следовало, что внутри Земля плотнее, чем у поверхности. Закон нарастания плотности по мере погружения в Землю Лаплас мог вычислить на основании своей теории и сравнения ее с уже известным сжатием Земли. Так было найдено, что удельный вес вещества, составляющего недра Земли, равен 11-ти, т. е. больше удельного веса железа.
Вместе с тем Лаплас гораздо подробнее, чем Даламбер, рассмотрел явления прецессии и нутации, заставляющие земную ось странствовать в мировом пространстве. Явление прецессии тесно связано с формой, которую имеет Земля, Лаплас учел упущенные Даламбером и Эйлером физические факторы – наличие океанов и атмосферы. Он доказал, что океаны и атмосферу, несмотря на их подвижность, в данном случае можно рассматривать как твердые Тела, слитые со всей Землей в одно целое.
Не влияют ли внутренние причины – вулканические извержения и землетрясения – на равномерность звездных суток, т. е. на время вращения Земли вокруг своей оси, которое является в сущности основной единицей для нашего измерения времени? Этот вопрос был впервые затронут Лапласом. Результат оказался вполне успокоительным: эти причины не могут изменять продолжительность суток.
Наконец, Лаплас поинтересовался тем, не может ли ось Земли менять свое положение внутри самого тела планеты. В результате этого со временем изменились бы географические широты местностей, отчего в лучшем случае пришлось бы постоянно переделывать географические карты. В худшем случае это повело бы к изменению климатических областей. Земной полюс, попав в Европу, сковал бы ее в своих ледяных об'ятиях, холодная необитаемая Антарктика могла бы стать жаркой экваториальной страной. В XVIII веке не было надежных наблюдательных данных, чтобы ответить на этот вопрос.
Лаплас рассмотрел проблему теоретически и убедился, что нет никакой причины, которая могла бы вызвать такие большие последствия. Ось Земли, как и продолжительность суток, Должны быть неизменны при всех мыслимых перемещениях масс у поверхности Земли или в ее глубине.
Недавно наблюдения обнаружили систематическое колебание широт, для изучения которого советское правительство содержит одну из международных «широтных станций» (в Китабе, около Самарканда). Найденные перемещения полюса по земной поверхности происходят приблизительно по спирали и не выходят из пределов круга радиусом около десятка метров, с периодом несколько больше года. Эти незначительные колебания земной оси не противоречат выводам Лапласа и не являются серьезной угрозой для изменения климатов.
Фигура Луны, сопровождающей нас в беге Земли вокруг Солнца, должна быть еще сложнее, чем фигура Земли. Лаплас занимался и ею, в частности вопросом, который всегда так интересует школьников: почему Луна повернута к Земле одной и той же стороной? Работа Лагранжа недостаточно осветила это явление, и Лаплас нашел, что Луна должна быть слегка вытянута по направлению к Земле. Эта особенность вызывает во вращении Луны вокруг оси возмущения, обусловленные Землей и не позволяющие Луне покачнуться так, чтобы стала видна большая часть той отвернутой от нас ее половины, про которую Уэльс и другие писатели-фантасты написали увлекательные романы.
Предсказанный Ньютоном факт сжатия Земли у полюсов был подтвержден точными геодезическими измерениями французских астрономов. Для этой цели измерения приходится делать в самых разнообразных местах земного шара, у экватора и у полюсов, опять-таки при помощи специальных экспедиций. Результаты длительных и трудных наблюдений в поле подлежат после этого еще многолетней обработке. Без знаний точной фигуры Земли нельзя построить точную географическую карту, столь нужную для транспорта, промышленности и в военном деле.
Лаплас и тут нашел теоретическое решение задачи, затратив несравненно меньше времени и труда, чем геодезисты. Он рассудил, что планета притягивает другие тела как материальная точка, помещенная в центре этой планеты, лишь в том случае, если она состоит из шаровых концентрических слоев однородной плотности. Если Земля сжата у полюсов, то вдоль ее экватора должен существовать избыток вещества, как бы твердый пояс, окружающий планету. Ближайшая к Луне часть этого пояса должна притягивать нашего спутника сильнее, чем более далекая, и притяжение Луны Землей нельзя заменить притяжением материальной точкой, так как расстояние от Земли до Луны не слишком велико в сравнении с размерами этого экваториального пояса. В результате в теоретические формулы, представляющие движение Луны, должны войти члены, зависящие от величины земного сжатия. Сжатие Земли Лаплас вычислил из этих формул, сравнивая свою теорию с наблюдениями. Луны, произведенными в одном месте. Найденная им величина сжатия 1/306 очень близка к величине 1/297, принимаемой для Земли в настоящее время.
По величине сжатия Земли, зная скорость ее вращения вокруг оси, можно вычислить упругость земных недр и можно догадываться о ее внутреннем строении.
Клеро впервые вывел замечательную теорему (носящую его имя), позволяющую определить сжатие Земли из известного распределения силы тяжести на ее поверхности, независимо от распределения плотностей внутри Земли. Для определения самой силы тяжести астрономические экспедиции определяли период колебания маятников, зависящий, как известно, от величины этой силы тяжести. На полюсах она должна быть больше, на экваторе меньше. Практическое использование метода Клеро, контролирующее собственный результат, полученный другим методом, впервые было сделано Лапласом. Вообще фигурой Земли Лаплас занимался очень много. Он изучал в связи с этим фигуру равновесия вращающейся жидкой массы, развивая исследования Ньютона, Мак Лорена, Клеро и Даламбера. В связи с этим Лаплас ввел в науку чрезвычайно плодотворное понятие о так называемом потенциале (или силовой функции), немедленно использованное Лежандром и другими учеными.
Выяснилось, что степень сжатия Земли меньше, чем должно быть в случае однородного жидкого тела, вращающегося со скоростью Земли. Отсюда следовало, что внутри Земля плотнее, чем у поверхности. Закон нарастания плотности по мере погружения в Землю Лаплас мог вычислить на основании своей теории и сравнения ее с уже известным сжатием Земли. Так было найдено, что удельный вес вещества, составляющего недра Земли, равен 11-ти, т. е. больше удельного веса железа.
Вместе с тем Лаплас гораздо подробнее, чем Даламбер, рассмотрел явления прецессии и нутации, заставляющие земную ось странствовать в мировом пространстве. Явление прецессии тесно связано с формой, которую имеет Земля, Лаплас учел упущенные Даламбером и Эйлером физические факторы – наличие океанов и атмосферы. Он доказал, что океаны и атмосферу, несмотря на их подвижность, в данном случае можно рассматривать как твердые Тела, слитые со всей Землей в одно целое.
Не влияют ли внутренние причины – вулканические извержения и землетрясения – на равномерность звездных суток, т. е. на время вращения Земли вокруг своей оси, которое является в сущности основной единицей для нашего измерения времени? Этот вопрос был впервые затронут Лапласом. Результат оказался вполне успокоительным: эти причины не могут изменять продолжительность суток.
Наконец, Лаплас поинтересовался тем, не может ли ось Земли менять свое положение внутри самого тела планеты. В результате этого со временем изменились бы географические широты местностей, отчего в лучшем случае пришлось бы постоянно переделывать географические карты. В худшем случае это повело бы к изменению климатических областей. Земной полюс, попав в Европу, сковал бы ее в своих ледяных об'ятиях, холодная необитаемая Антарктика могла бы стать жаркой экваториальной страной. В XVIII веке не было надежных наблюдательных данных, чтобы ответить на этот вопрос.
Лаплас рассмотрел проблему теоретически и убедился, что нет никакой причины, которая могла бы вызвать такие большие последствия. Ось Земли, как и продолжительность суток, Должны быть неизменны при всех мыслимых перемещениях масс у поверхности Земли или в ее глубине.
Недавно наблюдения обнаружили систематическое колебание широт, для изучения которого советское правительство содержит одну из международных «широтных станций» (в Китабе, около Самарканда). Найденные перемещения полюса по земной поверхности происходят приблизительно по спирали и не выходят из пределов круга радиусом около десятка метров, с периодом несколько больше года. Эти незначительные колебания земной оси не противоречат выводам Лапласа и не являются серьезной угрозой для изменения климатов.
Фигура Луны, сопровождающей нас в беге Земли вокруг Солнца, должна быть еще сложнее, чем фигура Земли. Лаплас занимался и ею, в частности вопросом, который всегда так интересует школьников: почему Луна повернута к Земле одной и той же стороной? Работа Лагранжа недостаточно осветила это явление, и Лаплас нашел, что Луна должна быть слегка вытянута по направлению к Земле. Эта особенность вызывает во вращении Луны вокруг оси возмущения, обусловленные Землей и не позволяющие Луне покачнуться так, чтобы стала видна большая часть той отвернутой от нас ее половины, про которую Уэльс и другие писатели-фантасты написали увлекательные романы.
Теория приливов
Последнее явление, связанной с Луной и отраженное в трудах Лапласа, океанские приливы и отливы. Приливная волна дважды в сутки поднимается и затопляет берега прибрежных местностей. Во внутренних морях эта волна невелика, но в устьях рек, впадающих в обширный океан, она позволяет даже глубоко сидящим судам заходить далеко вверх по течению. Дважды же в сутки волна прилива спадает и уступает место отливу, когда корабли должны спешно выходить из реки обратно в море, чтобы не сесть на мель. Все чаще и чаще говорят о необходимости и даже пробуют использовать технически (для гидроэлектростанций) колоссальную энергию приливов. Все это требует возможности предсказывать время наступления приливов и их высоту.
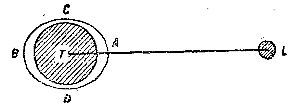
Рис. 7. Схема смены приливов.
Но приливы изменчивы и капризны. Высота их на берегах открытого океана в зависимости от разных условий колеблется от 50 сантиметров до 21 метра, да и время их наступления чередуется по сложному закону. Даже в одной и той же местности высота и время приливов сильно меняются.
Ньютон указал, что приливы и отливы вызваны различием в притяжении Луной и Солнцем близких к ним и более далеких частей водной оболочки Земли. Все же Ньютон был очень далек от придания теории приливов формы, способной удовлетворить запросы мореплавания.
Луна, находясь на одной прямой с Солнцем и Землей (в новолунии и полнолунии), увеличивает высоту приливов, действуя совместно с Солнцем. Во время первой и последней четверти Луны, когда она видна с Земли под прямым углом к Солнцу, притяжение Солнца уменьшает прилив, вызванный Луной. Лунный прилив стремится быть наибольшим в той точке Земли и в то время, где и когда Луна видна в зените, т. е. прямо над головой. Однако из-за сложности лунного движения положение этой точки на Земле все время меняется. Если еще вспомнить о непрерывных изменениях расстояния между Землей, Луной и Солнцем и о многочисленных возможных комбинациях в их взаимном расположении, то получится некоторое представление о трудностях, с которыми сталкивается даже чисто астрономическая теория приливов.
Бернулли, Эйлер и Маклорен тщетно пытались создать теорию, сколько-нибудь годную для практических нужд. Они создали так называемую статическую теорию приливов, допуская для простоты расчетов, что поверхность воды в каждый данный момент мгновенно принимает фигуру равновесия под действием приложенных к ней приливных сил. При этом они считали, что земной шар целиком окружает океан одинаковой глубины и что вода идеально подвижна… Конечно, эти предположения не соответствуют действительности.
Лаплас повернул дело совсем по-новому и создал динамическую теорию приливов. Из всех сил, действующих на воду по направлению к Луне, Лаплас принял во внимание только силы, касательные к поверхности воды, так как лишь они играют в явлении приливов серьезную роль. Эти силы на рис. 8 изображены стрелками и заставляют воду образовывать выпуклость, направленную к Луне и от нее. (Солнце действует точно так же, но вызываемые им приливные силы вдвое меньше, чем в случае Луны). В полосе этих выпуклостей (А и В на рис. 7) и находятся приливы, которых, как мы видим, одновременно бывает два на противоположных сторонах земного шара. В остальных частях Земли (Д и С на рис. 7) происходит отлив. Положение Луны на рисунках отмечено буквой L.

Рис. 7. Схема смены приливов.
Но приливы изменчивы и капризны. Высота их на берегах открытого океана в зависимости от разных условий колеблется от 50 сантиметров до 21 метра, да и время их наступления чередуется по сложному закону. Даже в одной и той же местности высота и время приливов сильно меняются.
Ньютон указал, что приливы и отливы вызваны различием в притяжении Луной и Солнцем близких к ним и более далеких частей водной оболочки Земли. Все же Ньютон был очень далек от придания теории приливов формы, способной удовлетворить запросы мореплавания.
Луна, находясь на одной прямой с Солнцем и Землей (в новолунии и полнолунии), увеличивает высоту приливов, действуя совместно с Солнцем. Во время первой и последней четверти Луны, когда она видна с Земли под прямым углом к Солнцу, притяжение Солнца уменьшает прилив, вызванный Луной. Лунный прилив стремится быть наибольшим в той точке Земли и в то время, где и когда Луна видна в зените, т. е. прямо над головой. Однако из-за сложности лунного движения положение этой точки на Земле все время меняется. Если еще вспомнить о непрерывных изменениях расстояния между Землей, Луной и Солнцем и о многочисленных возможных комбинациях в их взаимном расположении, то получится некоторое представление о трудностях, с которыми сталкивается даже чисто астрономическая теория приливов.
Бернулли, Эйлер и Маклорен тщетно пытались создать теорию, сколько-нибудь годную для практических нужд. Они создали так называемую статическую теорию приливов, допуская для простоты расчетов, что поверхность воды в каждый данный момент мгновенно принимает фигуру равновесия под действием приложенных к ней приливных сил. При этом они считали, что земной шар целиком окружает океан одинаковой глубины и что вода идеально подвижна… Конечно, эти предположения не соответствуют действительности.
Лаплас повернул дело совсем по-новому и создал динамическую теорию приливов. Из всех сил, действующих на воду по направлению к Луне, Лаплас принял во внимание только силы, касательные к поверхности воды, так как лишь они играют в явлении приливов серьезную роль. Эти силы на рис. 8 изображены стрелками и заставляют воду образовывать выпуклость, направленную к Луне и от нее. (Солнце действует точно так же, но вызываемые им приливные силы вдвое меньше, чем в случае Луны). В полосе этих выпуклостей (А и В на рис. 7) и находятся приливы, которых, как мы видим, одновременно бывает два на противоположных сторонах земного шара. В остальных частях Земли (Д и С на рис. 7) происходит отлив. Положение Луны на рисунках отмечено буквой L.
