Страница:
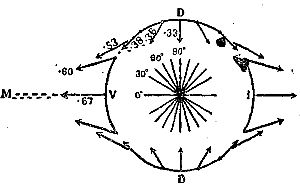
Рис. 8.
Лаплас вынужден был также допустить для упрощения теории, что океан равномерно окружает всю Землю и имеет постоянную глубину. Поэтому можно было ожидать, что его теория будет применима лишь к островам, но не к берегам материков. Новизна исследований Лапласа заключалась, главным образом, в том, что он изучал, какую форму должна принять водная поверхность под действием так называемых вынужденных колебаний, т. е. колебаний всей водной массы под действием приливных сил.
Очень подробные изыскания проделаны Лапласом для различных глубин океана и сравнены с многолетними наблюдениями приливов в Брестском порту.
Результаты, полученные Лапласом, не дали практикам того удовлетворения, которого они домогались, но и сейчас нельзя еще предсказывать приливы на основе одной лишь чисто астрономической теории. Однако теоретическое значение работы Лапласа огромно и гораздо шире, чем задача предсказания приливов. Будущая теория, окончательно разрешая этот вопрос, не обойдется без упоминания имени Лапласа. Вот что сказал о нем на рубеже XX столетия лучший знаток теории приливов Джордж Дарвин: «Именно он (Лаплас) впервые выяснил всю трудность вопроса и показал, что вращение Земли является важнейшим фактором в решении задачи. Современная постановка вопроса о явлении приливов всецело дана Лапласом… Среди всех великих ученых работ, трактовавших этот вопрос, выделяется, во-первых, работа Ньютона, а за ним мы должны сейчас же поставить Лапласа. Какие бы оригинальные и важные труды по теории приливай в будущем ни появлялись, все они неизбежно должны основываться на выводах этих великих людей».
Лаплас сам прекрасно знал, в чем состоит основная трудность практических применений теории приливов.
Океаны не покрывают Землю сплошь. Берега материков препятствуют движению воды по направлению движения Луны. Глубина моря различна, и дно очень неровно. Это создает трение, тормозящее движение воды и даже вращение Земли в целом. Учесть все эти влияния, даже если бы был точно известен рельеф океанского дна и его геологический состав, – дело непосильное и для современной науки. Тем не менее, теория приливов и приливного трения, которому большое внимание уделил Энгельс в «Диалектике природы», была применена к об'яснению того, как родились Луна и двойные звезды, каково далекое будущее их и нашей Земли.
Вместе с тем Лаплас был первым, рассмотревшим приливы в земной атмосфере. Он рассеял своими исследованиями убеждение, что Луна влияет своим притяжением на показания барометра.
Природа тяготения
Занимаясь приложением теории тяготения к разнообразнейшим явлениям, Лаплас не прошел мимо проверки основных принципов тяготения.
Размышляя о принципах тяготения, Лаплас говорит: «Является ли этот закон первичным законом природы? Не есть ли это лишь общее следствие некоторой неизвестной причины? Здесь наше незнание внутренних свойств материи ставит нам преграду и отнимает у нас всякую надежду удовлетворительно ответить на эти вопросы. Вместо того, чтобы создавать для этого гипотезы, ограничимся непосредственным изучением того, как принципы тяготения применяются геометрами».
Далее Лаплас очень кратко касается проверки свойств, приписываемых этими «геометрами» тяготению.
Как известно, среди физических явлений тяготение стоит совсем особо, и для выяснения его природы было бы крайне существенно знать, существует ли экран для тяготения, т. е. можно ли чем-нибудь загородиться от действия тяготения. Многочисленные наблюдения заставляют признать, что тяготение проникает сквозь небесные тела так же свободно, как если бы этих тел не существовало. От тяготения ничем загородиться нельзя, для него не существует экрана, подобного тому, который существует для света или электричества.
Другая величина, также не установленная Ньютоном, – скорость распространения тяготения. Бесконечно ли она велика или конечна, и если конечна, то какова именно? В «Изложении системы Мира» Лаплас говорит: «Сообщается ли притяжение от одного тела к другому мгновенно? Время передачи, если бы оно было для нас заметно, обнаружилось бы преимущественно вековым ускорением в движении Луны. Я предлагал это средство для об'яснения ускорения, замеченного в упомянутом движении, и нашел, что для удовлетворения наблюдениям должно приписать притягательной силе скорость в семь миллионов раз большую, чем скорость светового луча. А так как ныне причина векового уравнения – Луны хорошо известна, то мы можем утверждать, что притяжение передается со скоростью, по крайней мере в пятьдесят миллионов раз превосходящей скорость света. Поэтому, не опасаясь какой-либо заметной погрешности, мы можем принимать передачу тяготения за мгновенную».
Так как скорость света составляет 300000 километров в секунду, то отсюда получается минимальная скорость тяготения около 15000 миллиардов километров в секунду. Хотя впоследствии и оказалось, что истинная теоретическая величина векового ускорения Луны вдвое меньше, чем ее нашел Лаплас, к его словам о скорости распространения тяготения нельзя прибавить ничего более определенного. До настоящего времени классическая механика (физика или астрономия) не может установить с определенностью, близка ли скорость тяготения к скорости света или же она бесконечно велика – мгновенна.
Помимо указанных выше вопросов, Лаплас в «Изложении системы Мира» рассматривает, насколько справедливы основные положения теории тяготения: 1) тяготение действует между наиболее мелкими частицами тела; 2) оно пропорционально массам; 3) оно обратно пропорционально квадратам расстояния; 4) оно одинаковым образом действует на движущееся и на покоящееся тело. Лаплас приводит факты и соображения, на его взгляд бесспорно подтверждающие правильность этих основных положений.
К сказанному им современная наука ничего принципиально нового добавить не может. До наших дней физическая сторона природы тяготения в классической физике осталось столь же неясной как была. Только теория относительности Эйнштейна, подходящая к физике с принципиально новой точки зрения, дала возможность рассматривать природу тяготения в совершенно новом свете.
Размышляя о принципах тяготения, Лаплас говорит: «Является ли этот закон первичным законом природы? Не есть ли это лишь общее следствие некоторой неизвестной причины? Здесь наше незнание внутренних свойств материи ставит нам преграду и отнимает у нас всякую надежду удовлетворительно ответить на эти вопросы. Вместо того, чтобы создавать для этого гипотезы, ограничимся непосредственным изучением того, как принципы тяготения применяются геометрами».
Далее Лаплас очень кратко касается проверки свойств, приписываемых этими «геометрами» тяготению.
Как известно, среди физических явлений тяготение стоит совсем особо, и для выяснения его природы было бы крайне существенно знать, существует ли экран для тяготения, т. е. можно ли чем-нибудь загородиться от действия тяготения. Многочисленные наблюдения заставляют признать, что тяготение проникает сквозь небесные тела так же свободно, как если бы этих тел не существовало. От тяготения ничем загородиться нельзя, для него не существует экрана, подобного тому, который существует для света или электричества.
Другая величина, также не установленная Ньютоном, – скорость распространения тяготения. Бесконечно ли она велика или конечна, и если конечна, то какова именно? В «Изложении системы Мира» Лаплас говорит: «Сообщается ли притяжение от одного тела к другому мгновенно? Время передачи, если бы оно было для нас заметно, обнаружилось бы преимущественно вековым ускорением в движении Луны. Я предлагал это средство для об'яснения ускорения, замеченного в упомянутом движении, и нашел, что для удовлетворения наблюдениям должно приписать притягательной силе скорость в семь миллионов раз большую, чем скорость светового луча. А так как ныне причина векового уравнения – Луны хорошо известна, то мы можем утверждать, что притяжение передается со скоростью, по крайней мере в пятьдесят миллионов раз превосходящей скорость света. Поэтому, не опасаясь какой-либо заметной погрешности, мы можем принимать передачу тяготения за мгновенную».
Так как скорость света составляет 300000 километров в секунду, то отсюда получается минимальная скорость тяготения около 15000 миллиардов километров в секунду. Хотя впоследствии и оказалось, что истинная теоретическая величина векового ускорения Луны вдвое меньше, чем ее нашел Лаплас, к его словам о скорости распространения тяготения нельзя прибавить ничего более определенного. До настоящего времени классическая механика (физика или астрономия) не может установить с определенностью, близка ли скорость тяготения к скорости света или же она бесконечно велика – мгновенна.
Помимо указанных выше вопросов, Лаплас в «Изложении системы Мира» рассматривает, насколько справедливы основные положения теории тяготения: 1) тяготение действует между наиболее мелкими частицами тела; 2) оно пропорционально массам; 3) оно обратно пропорционально квадратам расстояния; 4) оно одинаковым образом действует на движущееся и на покоящееся тело. Лаплас приводит факты и соображения, на его взгляд бесспорно подтверждающие правильность этих основных положений.
К сказанному им современная наука ничего принципиально нового добавить не может. До наших дней физическая сторона природы тяготения в классической физике осталось столь же неясной как была. Только теория относительности Эйнштейна, подходящая к физике с принципиально новой точки зрения, дала возможность рассматривать природу тяготения в совершенно новом свете.
НАУКА, МЕТОДЫ И ЛЮДИ
ЕСЛИ сам Лаплас и его современники оставили очень мало сведений о личной и общественной жизни замечательного ученого, то в переписке и трудах Лапласа мы, как в зеркале, видим все его мировоззрение, те внутренние двигатели, которые побуждали его без устали всю жизнь служить науке.
Понять и оценить творчество великого геометра, как принято называть Лапласа, нужно не только потому, что тогда перед нами полнее выступит его личность, но еще более потому, что эта оценка является характеристикой одного из основных направлений науки XVIII и XIX веков. Стиль работ Лапласа передался многим его ученикам. В работах Лапласа находит свое лучшее выражение заключительный период эпохи Просвещения и французского материализма XVIII века.
Чтобы верно оценить истинное значение работ, рожденных в прошлые века, мало еще определить их современный вес в сокровищнице человеческого знания. Необходимо мысленно перенестись в ту среду, в которой идеи эти возникли.
Наука побеждает не только гениальными взлетами мысли отдельных личностей, но и совокупными усилиями целых поколений ученых. Эту особенность сам Лаплас выразил так: «Наука развивается не так, Как литература. У последней есть пределы, которые ей ставит не только гениальность писателя, но совершенство языка и стиля и уменье их использовать. Во все века мы с одинаковым интересом прочитаем его произведения, и слава писателя, не ослабевающая с течением времени, увеличивается благодаря неустанным попыткам пытающихся ему подражать. Наука же, наоборот, безгранична, как природа, разрастается до бесконечности, благодаря трудам последующих поколений. Наиболее совершенные труды поднимают науку на высоту, с которой она уже не имеет права спуститься, и рождают новые открытия, подготовляя этим самым труды, которым суждено затмить их самих».
В этой оценке Лаплас ошибочно отвергает роль и влияние предшествующих писателей на последующих и забывает об эволюции в литературе, однако это высказывание прекрасно характеризует самого Лапласа.
Понять и оценить творчество великого геометра, как принято называть Лапласа, нужно не только потому, что тогда перед нами полнее выступит его личность, но еще более потому, что эта оценка является характеристикой одного из основных направлений науки XVIII и XIX веков. Стиль работ Лапласа передался многим его ученикам. В работах Лапласа находит свое лучшее выражение заключительный период эпохи Просвещения и французского материализма XVIII века.
Чтобы верно оценить истинное значение работ, рожденных в прошлые века, мало еще определить их современный вес в сокровищнице человеческого знания. Необходимо мысленно перенестись в ту среду, в которой идеи эти возникли.
Наука побеждает не только гениальными взлетами мысли отдельных личностей, но и совокупными усилиями целых поколений ученых. Эту особенность сам Лаплас выразил так: «Наука развивается не так, Как литература. У последней есть пределы, которые ей ставит не только гениальность писателя, но совершенство языка и стиля и уменье их использовать. Во все века мы с одинаковым интересом прочитаем его произведения, и слава писателя, не ослабевающая с течением времени, увеличивается благодаря неустанным попыткам пытающихся ему подражать. Наука же, наоборот, безгранична, как природа, разрастается до бесконечности, благодаря трудам последующих поколений. Наиболее совершенные труды поднимают науку на высоту, с которой она уже не имеет права спуститься, и рождают новые открытия, подготовляя этим самым труды, которым суждено затмить их самих».
В этой оценке Лаплас ошибочно отвергает роль и влияние предшествующих писателей на последующих и забывает об эволюции в литературе, однако это высказывание прекрасно характеризует самого Лапласа.
Незаконченные открытия
Лаплас уже в возрасте двадцати лет овладел всем, что можно было тогда изучить, и с первых же шагов своей научной работы оказался в ряду передовых ученых своей эпохи.
Ньютон установил основы теории тяготения и в общих чертах об'яснил явления движения планет и их спутников, комет, форму Земли, колебания ее оси, приливы и отливы. Но создание и разработка теории тяготения этим не были закончены. Современное Ньютону состояние математического анализа ставило предел, и он мог положить лишь скромное начало механике небес.
Достаточно ли теории тяготения, чтобы вполне точно представить себе все эти явления?
Ответить на это было трудно из-за огромного количества взаимных влияний (притяжений) многочисленных членов солнечной системы.
Ньютон полагал, что солнечная система не обладает достаточной устойчивостью, что тяготение планет не только к Солнцу, но и друг к другу, постепенно расстраивает солнечную систему. Отдавая еще дань теологии, он допускал, что по временам творец (бог) должен вмешиваться, снова и снова водворять заблудшие светила на уготовленные им заранее места.
После смерти Ньютона успехи математики позволили приступить к углубленному изучению следствий теории всемирного тяготения и тщательному сравнению ее выводов с данными наблюдений.
Французская Академия наук стимулировала такие исследования, предлагая темы и об'являя премии за их выполнение. Параллельно росла и практика наблюдений, позволившая точно установить форму Земли и такие подробности движения небесных тел, которые не были известны Ньютону.
В области теорий подвизались крупнейшие имена. Эйлер, братья Бернулли, Клеро, Даламбер и Лагранж решили часть стоявших перед ними проблем. Бывало, однако, что у них опускались руки, и иногда, может быть, даже мелькало сомнение во всеобщности самого принципа тяготения.
Целый ряд таких не разгаданных до конца явлений встал перед молодым Лапласом; возникал вопрос, не действуют ли в природе посторонние, еще неизвестные, влияния или силы, если усилия его предшественников не увенчались успехом.
Не удивительно ли, что юноша, вопреки обычаям, сразу взялся за скрупулезное исследование этих проблем заново, с колоссальным упорством и настойчивостью изучая их одну за другой. Он преследовал свою цель до тех пор, пока не доводил дело до победного конца. Эта кропотливая и трудная область – небесная механика – сразу стала предметом его любимых занятий. С полным правом мог он сказать по поводу теории тяготения: такова была природа этого поразительного открытия, что каждое возникшее перед ним затруднение становилось для него новым об'ектом триумфа.
Другой областью, которой Лаплас также уделил много времени и внимания, была математическая теория вероятностей или теория случайностей, как называли ее в то время. В течение XVIII столетия значение этой теории неуклонно возрастало.
Основы теории вероятностей были заложены Паскалем и Ферма, а затем развиты Яковом Бернулли, Моавром и Байесом. Эта теория родилась из стремления анализировать законы азартных игр, выяснить шансы на выигрыш у участников игры или лотереи. После того, как астроном Галлей положил основание статистике, теория вероятностей постепенно получила широчайшее применение. Ею стали пользоваться в финансовых, экономических и даже в исторических науках.
Аналитически строгий ум Лапласа не мог не увлечься выяснением законов в той сфере, которую принято было считать игрой слепого случая. Овладеть этими случаями, подчинить их расчету, раскрыть тайну случайных событий, введя их в рамки закономерности так, как это сделано для движений небесных тел, – вот что поставил себе задачей Лаплас. Заслуги его в этой области также чрезвычайно велики и носят принципиальный характер.
Третья, меньшая по значению область работ Лапласа – разработка им различных вопросов физики. В жизни Лапласа было два таких периода, когда его внимание сосредоточивалось на этих проблемах, и всегда это было связано с общением его с современными выдающимися физиками и химиками.
Сперва – близость и совместная работа с основателем химии Лавуазье, позднее, уже в старческие годы, тесная дружба с химиком Бертолле. Работая в области физики, Лаплас находит и там новое и плодотворное применение теории сил отталкивания и притяжения.
Сначала он вместе с Лавуазье занялся опытами по теплоте, здесь его, повидимому, увлекла та широта размаха, с которой Лавуазье ставил свои опыты. 21 августа 1783 года Лаплас пишет Лагранжу: «Я, право, не знаю, каким образом я дал себя увлечь в работу по физике, и вы найдете, быть может, что я лучше бы сделал, если бы воздержался от этого; но я не мог устоять против настояний моего друга Лавуазье, который вкладывает в эту совместную работу столько приятности и ума, сколько лишь я мог бы пожелать. Кроме того, так как он очень богат, он не жалеет ничего, чтобы придать опытам точность, необходимую при таких тонких исследованиях».
Наконец, немало сделал Лаплас в первые же годы его научной карьеры и в области чистой математики. Он дополнил и развил ряд теорий, созданных его предшественниками и современниками: Эйлером, Даламбером, Кондорсе и Лагранжем. В письме к Даламберу (15 ноября 1777 г.) молодой Лаплас пишет: «Я всегда изучал математику скорее для собственного удовольствия, чем из пустого тщеславия, которого я всегда избегаю. Для меня составляет наибольшее удовольствие следовать по тому пути, по которому идут исследователи, видеть борьбу их гения со встречающимися препятствиями и победу над этими препятствиями. Я мысленно ставлю себя на их место и задаюсь вопросом, как бы поступил я сам, встретив такие препятствия, и, хотя это доставляет по большей части лишь унижение моему самолюбию, удовольствие от использования их успехов все же вполне возмещает мне это маленькое унижение. Если я оказываюсь достаточно счастливым, чтобы добавить что-либо к их работам, я вполне оцениваю их пионерские усилия, хорошо представляя себе, что в моем положении они пошли бы еще дальше. Из этого вы видите, что никто не читает ваших трудов с большим вниманием, чем я, никто полнее меня их не использует».
Ньютон установил основы теории тяготения и в общих чертах об'яснил явления движения планет и их спутников, комет, форму Земли, колебания ее оси, приливы и отливы. Но создание и разработка теории тяготения этим не были закончены. Современное Ньютону состояние математического анализа ставило предел, и он мог положить лишь скромное начало механике небес.
Достаточно ли теории тяготения, чтобы вполне точно представить себе все эти явления?
Ответить на это было трудно из-за огромного количества взаимных влияний (притяжений) многочисленных членов солнечной системы.
Ньютон полагал, что солнечная система не обладает достаточной устойчивостью, что тяготение планет не только к Солнцу, но и друг к другу, постепенно расстраивает солнечную систему. Отдавая еще дань теологии, он допускал, что по временам творец (бог) должен вмешиваться, снова и снова водворять заблудшие светила на уготовленные им заранее места.
После смерти Ньютона успехи математики позволили приступить к углубленному изучению следствий теории всемирного тяготения и тщательному сравнению ее выводов с данными наблюдений.
Французская Академия наук стимулировала такие исследования, предлагая темы и об'являя премии за их выполнение. Параллельно росла и практика наблюдений, позволившая точно установить форму Земли и такие подробности движения небесных тел, которые не были известны Ньютону.
В области теорий подвизались крупнейшие имена. Эйлер, братья Бернулли, Клеро, Даламбер и Лагранж решили часть стоявших перед ними проблем. Бывало, однако, что у них опускались руки, и иногда, может быть, даже мелькало сомнение во всеобщности самого принципа тяготения.
Целый ряд таких не разгаданных до конца явлений встал перед молодым Лапласом; возникал вопрос, не действуют ли в природе посторонние, еще неизвестные, влияния или силы, если усилия его предшественников не увенчались успехом.
Не удивительно ли, что юноша, вопреки обычаям, сразу взялся за скрупулезное исследование этих проблем заново, с колоссальным упорством и настойчивостью изучая их одну за другой. Он преследовал свою цель до тех пор, пока не доводил дело до победного конца. Эта кропотливая и трудная область – небесная механика – сразу стала предметом его любимых занятий. С полным правом мог он сказать по поводу теории тяготения: такова была природа этого поразительного открытия, что каждое возникшее перед ним затруднение становилось для него новым об'ектом триумфа.
Другой областью, которой Лаплас также уделил много времени и внимания, была математическая теория вероятностей или теория случайностей, как называли ее в то время. В течение XVIII столетия значение этой теории неуклонно возрастало.
Основы теории вероятностей были заложены Паскалем и Ферма, а затем развиты Яковом Бернулли, Моавром и Байесом. Эта теория родилась из стремления анализировать законы азартных игр, выяснить шансы на выигрыш у участников игры или лотереи. После того, как астроном Галлей положил основание статистике, теория вероятностей постепенно получила широчайшее применение. Ею стали пользоваться в финансовых, экономических и даже в исторических науках.
Аналитически строгий ум Лапласа не мог не увлечься выяснением законов в той сфере, которую принято было считать игрой слепого случая. Овладеть этими случаями, подчинить их расчету, раскрыть тайну случайных событий, введя их в рамки закономерности так, как это сделано для движений небесных тел, – вот что поставил себе задачей Лаплас. Заслуги его в этой области также чрезвычайно велики и носят принципиальный характер.
Третья, меньшая по значению область работ Лапласа – разработка им различных вопросов физики. В жизни Лапласа было два таких периода, когда его внимание сосредоточивалось на этих проблемах, и всегда это было связано с общением его с современными выдающимися физиками и химиками.
Сперва – близость и совместная работа с основателем химии Лавуазье, позднее, уже в старческие годы, тесная дружба с химиком Бертолле. Работая в области физики, Лаплас находит и там новое и плодотворное применение теории сил отталкивания и притяжения.
Сначала он вместе с Лавуазье занялся опытами по теплоте, здесь его, повидимому, увлекла та широта размаха, с которой Лавуазье ставил свои опыты. 21 августа 1783 года Лаплас пишет Лагранжу: «Я, право, не знаю, каким образом я дал себя увлечь в работу по физике, и вы найдете, быть может, что я лучше бы сделал, если бы воздержался от этого; но я не мог устоять против настояний моего друга Лавуазье, который вкладывает в эту совместную работу столько приятности и ума, сколько лишь я мог бы пожелать. Кроме того, так как он очень богат, он не жалеет ничего, чтобы придать опытам точность, необходимую при таких тонких исследованиях».
Наконец, немало сделал Лаплас в первые же годы его научной карьеры и в области чистой математики. Он дополнил и развил ряд теорий, созданных его предшественниками и современниками: Эйлером, Даламбером, Кондорсе и Лагранжем. В письме к Даламберу (15 ноября 1777 г.) молодой Лаплас пишет: «Я всегда изучал математику скорее для собственного удовольствия, чем из пустого тщеславия, которого я всегда избегаю. Для меня составляет наибольшее удовольствие следовать по тому пути, по которому идут исследователи, видеть борьбу их гения со встречающимися препятствиями и победу над этими препятствиями. Я мысленно ставлю себя на их место и задаюсь вопросом, как бы поступил я сам, встретив такие препятствия, и, хотя это доставляет по большей части лишь унижение моему самолюбию, удовольствие от использования их успехов все же вполне возмещает мне это маленькое унижение. Если я оказываюсь достаточно счастливым, чтобы добавить что-либо к их работам, я вполне оцениваю их пионерские усилия, хорошо представляя себе, что в моем положении они пошли бы еще дальше. Из этого вы видите, что никто не читает ваших трудов с большим вниманием, чем я, никто полнее меня их не использует».
Великое и мелочное
Если оставить в стороне некоторую излишнюю и условную скромность автора приведенных строк, форму вежливости «галантного века», отчасти продиктованную обстоятельствами, при которых письмо было написано, мы увидим в нем очень точно один из методов работы, распространенный среди ученых XVIII века. Эта черта ясно выражается и в строках Лагранжа: «Вы хорошо понимаете, что – я не мог прочитать эти исследования, не сделав многочисленных замечаний, клонящихся к их обобщению и упрощению».
В таких условиях иногда очень трудно достоверно установить, кто является истинным автором той или другой блестящей теории, той или иной трактовки вопроса. Каждый ученый, прочитавший только-что вышедший мемуар или прослушавший сообщение о нем на заседании академии, стремится прибавить к ним что-нибудь свое, развить или пополнить их труды. Такая живость мысли крайне способствовала быстрому развитию науки, и иногда значение нового метода становилось совершенно очевидным уже в самое короткое время.
Однако из-за этого же некоторые авторы-пионеры чувствовали себя обиженными и стремились доказать, что именно их работы вызвали дальнейшее развитие и улучшение, внесенные в теорию другими.
Поэтому между учеными наступало нередко взаимное охлаждение и возникала полемика о приоритете, так часто встречающаяся в XVIII и в начале XIX столетия. Время не всегда могло уничтожить трещины в их личных отношениях. Эта страстность часто проглядывает сквозь маску утонченной вежливости и академической сдержанности.
Много копий было, например, сломано в спорах о том, кто был истинным изобретателем дифференциального исчисления – Лейбниц или Ньютон. Между тем эту честь, может быть, следует приписать Ферма, как утверждали Лагранж и Лаплас, а до них еще Даламбер.
Лапласу чаще, чем другим, ставили в вину некоторое тщеславие, мешавшее ему отдавать должное работам своих предшественников и в особенности современников.
Мнение об исключительном тщеславии и зависти Лапласа подтверждают, в частности, рассказы Апаго и механика Пуансо.
Вот история, рассказанная Пуансо.
В своей работе, представленной в Академию и переданной Лагранжу для отзыва, Пуансо, якобы, написал: «Лагранж и Лаплас впервые…» Лагранж удивился, что в статье упоминается Лаплас, не имевший работ в этой области, и спросил Пуансо, зачем он цитирует Лапласа. Пуансо ответил: «Сначала я цитировал только ваше имя, но я показал первую редакцию своей статьи одному своему другу. – Ты хочешь представить Академии, – сказал он мне, – мемуар по механике, не упоминая имени Лапласа? Твоя работа не будет оценена».
Апаго – отчасти ученик Лапласа – очень уважал его как ученого, но невысоко ставил его как человека. В биографии Лапласа он избегает давать ему характеристику, выходящую за рамки чисто научных заслуг. Апаго часто бывал дома, в семье Лапласа, и в одном месте своей автобиографии описывает следующий эпизод.
Когда сын Лапласа готовился сдавать приемные экзамены для поступления в знаменитую Политехническую школу (при поступлении пред'являли очень высокие требования), Апаго помогал ему готовиться по математике. Апаго был тогда сотрудником парижской Астрономической обсерватории, куда к нему для занятий иногда приходил юный Шарль Лаплас. В одно из посещений Апаго об'яснил ему метод непрерывных дробей, при помощи которого Лагранж определяет корни числовых уравнений. Шарлю этот метод очень понравился, и со всей непосредственностью юности он рассказал об этом отцу. «Я никогда не забуду гнева отца при этих словах сына, – говорит Апаго. – Лаплас осыпал упреками меня и его. Никогда еще зависть не высказывалась так обнаженно и в таком отвратительном виде. – Ах, – сказал я самому себе, – древние справедливо приписывали слабости даже тому, кто движением бровей колебал Олимп».
Мы уже приводили письма Лагранжа и Кондорсе, в которых они на второй год после вступления Лапласа в Академию отмечают у Лапласа некоторое «головокружение от успехов», хотя и приписывают это молодости нормандца. Повидимому, Кондорсе и Лагранж находили, что Лаплас ожидал слишком быстрого эффекта от тех многочисленных научных записок, которыми он тогда заваливал Академию.
Судя по первым письмам Лагранжа к Лапласу, он тоже не оставался безучастным как к появлению на сцене молодого геометра, начинавшего обращать на себя внимание ученого мира, так и к тем проявлениям невнимательности к коллегам, которые допускал Лаплас. «Я не знаю, читали ли вы то, что я иногда публиковал по этому вопросу. Тогда я лишь коснулся вопроса и всегда предлагал в дальнейшем заняться его углублением. Однако вы исчерпали проблему, и я был очарован тем, как вы хорошо выполнили обязательства, взятые мною по этому поводу перед другими геометрами… Что касается моей теории Юпитера и Сатурна, то я поздравляю себя с тем, что вы превзошли меня и что ваши исследования уже лишают меня возможности сделать что-либо еще в этом направлении».
Не лишена интереса история открытия так называемых вековых или долгопериодических неравенств в движении планет.
Первенство в этом вопросе бесспорно принадлежит Лагранжу, отправившему свою научную работу из Берлина вс французскую Академию наук. Однако Лагранж ограничился рассмотрением наклона планетных орбит к орбите Земли и положения линии пересечения плоскостей этих орбит. Работа сделалась известной Лапласу, который немедленно распространил метод Лагранжа на изучение размеров и форм планетных орбит и поторопился опубликовать свои результаты в приложении к своему сочинению, посвященному совершенно другому вопросу. Он сделал это быстрее, чем труд Лагранжа мог появиться в печати.
Говоря об уравнениях, представляющих вековые неравенства в движении планет, Лаплас выражается так: «Уже в течение долгого времени я предполагал их проинтегрировать. В этом намерении мне помешала малая польза, которую эти вычисления принесли бы астрономии, а также и те трудности, с которыми они были связаны. Я и не взялся бы за это дело, если бы не прочитал превосходную работу г. Лагранжа, присланную в академию и имеющую появиться в следующих томах».
В примечании Лаплас добавляет: «Конечно, прежде, чем сдавать в печать свой труд, я должен был бы подождать, пока исследования г. Лагранжа будут опубликованы. Однако, допуская появление своего сочинения на эту тему, я думал, что смогу сообщить в нем геометрам в форме дополнения то, чего труду г. Лагранжа нехватало до полноты. Я отдаю, конечно, должную честь работе г. Лагранжа. Я надеялся, что они меня поблагодарят „за то, что я дал им возможность заранее познакомиться с замечательным произведением г. Лагранжа в моем изложении“».
Получив сочинение Лапласа, Лагранж ответил очень просто (10 апреля 1775 года): «Поскольку я вижу, что Вы сами уже раньше предпринимали это исследование, я охотно отказываюсь от него, и я Вам даже очень признателен за устранение меня от этого труда, будучи уверен, что от этого науки смогут лишь много выиграть».
Но через полтора месяца после этого Лагранж пишет Даламберу: «Я сейчас почти готов дать полную теорию изменения элементов планет под влиянием взаимодействия. Мне очень понравилось то, что г. Лаплас сделал по этому поводу, и я льщу себя надеждой на то, что он не будет на меня в претензии, если я не выполнил данное ему обещание отказаться от этой области в его пользу. Я не мог сопротивляться желанию снова ею заняться, но я, как и раньше, очарован тем, что он со своей стороны разрабатывает ту же тему».
Оценка Лапласа Лагранжем вполне искренна. Например, в письме к Даламберу 10 июля 1778 года он пишет о двадцатилетнем Лапласе: «Новые шаги, сделанные г. Лапласом в теории приливов и отливов, достойны и его и того ранга, который он занимает как ваш первый последователь во Франции. Если он и дальше будет продолжать так, то Вашей родине не придется опасаться судьбы, постигшей Англию после смерти Ньютона».
С течением времени переписка Лапласа с Лагранжем принимает характер все большей сердечности.
Полезное для науки соревнование двух величайших умов своей эпохи продолжалось до конца их жизни. По разным поводам Лаплас вспоминает, например, многочисленные обстоятельства знаменательного заседания в Бюро долгот, происходившего 17 августа 1808 года. На заседании Лаплас и Лагранж представили доклады на одну и ту же тему – об изменении элементов планетных орбит, но каждый ученый подошел к решению, так сказать, с противоположного конца.
Лаплас говорит: «Эта работа последних лет жизни – одно из его лучших произведений, она показывает, что годы не ослабили его гения».
Есть свидетельства, что Даламбер частенько и с некоторой горечью жаловался, что Лаплас заимствует у него его идеи. Между тем Даламбер сам предоставил это право другим ученым словами, которые заканчивают одно из его сочинений:
«Я не сомневаюсь, что это новое исследование вызовет ряд оригинальных замечаний, но я их предоставляю другим геометрам, поскольку вопрос теперь уже не встречает затруднений».
Поэтому Лаплас мог писать Даламберу (10 марта 1782 г.): «Вы не должны находить плохим то, что ваши вычисления продолжены теперь так далеко, как вы сначала и не подозревали».
Сам Даламбер вызвал как-то у Aраго, знаменитого биографа плеяды французских ученых, следующее замечание: «Даламбер, сам того не ведая, руководимый необ'яснимым чувством ревности, не вполне отдавал должное заслугам Клеро».
Можно подумать, что отчасти те же мотивы руководили великим энциклопедистом и в отношении Лапласа. По крайней мерс, в связи со своим первым докладом в Академии о приливах и отливах (15 ноября 1777 г.) Лаплас писал: «В сущности говоря, первые точные исследования, появившиеся по этому поводу, принадлежат Даламберу. Этот известный автор в своем замечательном сочинении, озаглавленном „Размышления о причине ветров“… пользуется анализом не только научным, но и искусно применяющим правильные уравнения этой проблемы; однако трудность интегрирования этих уравнений вынудила его прибегнуть к допущениям, сделавшим решение неуверенным».
Повидимому, Даламбер не удовлетворился этим знаком внимания, потребовав большего удовлетворения, и вечером того же дня Лаплас должен был писать ему: «Вместо того, чтобы докучать вам завтра, как я первоначально предполагал, я предпочел послать вам дополнение, о котором мы договорились… Я приписал следующее: В заключение я должен отметить для справедливости, что если мне удалось добавить кое-что к его
В таких условиях иногда очень трудно достоверно установить, кто является истинным автором той или другой блестящей теории, той или иной трактовки вопроса. Каждый ученый, прочитавший только-что вышедший мемуар или прослушавший сообщение о нем на заседании академии, стремится прибавить к ним что-нибудь свое, развить или пополнить их труды. Такая живость мысли крайне способствовала быстрому развитию науки, и иногда значение нового метода становилось совершенно очевидным уже в самое короткое время.
Однако из-за этого же некоторые авторы-пионеры чувствовали себя обиженными и стремились доказать, что именно их работы вызвали дальнейшее развитие и улучшение, внесенные в теорию другими.
Поэтому между учеными наступало нередко взаимное охлаждение и возникала полемика о приоритете, так часто встречающаяся в XVIII и в начале XIX столетия. Время не всегда могло уничтожить трещины в их личных отношениях. Эта страстность часто проглядывает сквозь маску утонченной вежливости и академической сдержанности.
Много копий было, например, сломано в спорах о том, кто был истинным изобретателем дифференциального исчисления – Лейбниц или Ньютон. Между тем эту честь, может быть, следует приписать Ферма, как утверждали Лагранж и Лаплас, а до них еще Даламбер.
Лапласу чаще, чем другим, ставили в вину некоторое тщеславие, мешавшее ему отдавать должное работам своих предшественников и в особенности современников.
Мнение об исключительном тщеславии и зависти Лапласа подтверждают, в частности, рассказы Апаго и механика Пуансо.
Вот история, рассказанная Пуансо.
В своей работе, представленной в Академию и переданной Лагранжу для отзыва, Пуансо, якобы, написал: «Лагранж и Лаплас впервые…» Лагранж удивился, что в статье упоминается Лаплас, не имевший работ в этой области, и спросил Пуансо, зачем он цитирует Лапласа. Пуансо ответил: «Сначала я цитировал только ваше имя, но я показал первую редакцию своей статьи одному своему другу. – Ты хочешь представить Академии, – сказал он мне, – мемуар по механике, не упоминая имени Лапласа? Твоя работа не будет оценена».
Апаго – отчасти ученик Лапласа – очень уважал его как ученого, но невысоко ставил его как человека. В биографии Лапласа он избегает давать ему характеристику, выходящую за рамки чисто научных заслуг. Апаго часто бывал дома, в семье Лапласа, и в одном месте своей автобиографии описывает следующий эпизод.
Когда сын Лапласа готовился сдавать приемные экзамены для поступления в знаменитую Политехническую школу (при поступлении пред'являли очень высокие требования), Апаго помогал ему готовиться по математике. Апаго был тогда сотрудником парижской Астрономической обсерватории, куда к нему для занятий иногда приходил юный Шарль Лаплас. В одно из посещений Апаго об'яснил ему метод непрерывных дробей, при помощи которого Лагранж определяет корни числовых уравнений. Шарлю этот метод очень понравился, и со всей непосредственностью юности он рассказал об этом отцу. «Я никогда не забуду гнева отца при этих словах сына, – говорит Апаго. – Лаплас осыпал упреками меня и его. Никогда еще зависть не высказывалась так обнаженно и в таком отвратительном виде. – Ах, – сказал я самому себе, – древние справедливо приписывали слабости даже тому, кто движением бровей колебал Олимп».
Мы уже приводили письма Лагранжа и Кондорсе, в которых они на второй год после вступления Лапласа в Академию отмечают у Лапласа некоторое «головокружение от успехов», хотя и приписывают это молодости нормандца. Повидимому, Кондорсе и Лагранж находили, что Лаплас ожидал слишком быстрого эффекта от тех многочисленных научных записок, которыми он тогда заваливал Академию.
Судя по первым письмам Лагранжа к Лапласу, он тоже не оставался безучастным как к появлению на сцене молодого геометра, начинавшего обращать на себя внимание ученого мира, так и к тем проявлениям невнимательности к коллегам, которые допускал Лаплас. «Я не знаю, читали ли вы то, что я иногда публиковал по этому вопросу. Тогда я лишь коснулся вопроса и всегда предлагал в дальнейшем заняться его углублением. Однако вы исчерпали проблему, и я был очарован тем, как вы хорошо выполнили обязательства, взятые мною по этому поводу перед другими геометрами… Что касается моей теории Юпитера и Сатурна, то я поздравляю себя с тем, что вы превзошли меня и что ваши исследования уже лишают меня возможности сделать что-либо еще в этом направлении».
Не лишена интереса история открытия так называемых вековых или долгопериодических неравенств в движении планет.
Первенство в этом вопросе бесспорно принадлежит Лагранжу, отправившему свою научную работу из Берлина вс французскую Академию наук. Однако Лагранж ограничился рассмотрением наклона планетных орбит к орбите Земли и положения линии пересечения плоскостей этих орбит. Работа сделалась известной Лапласу, который немедленно распространил метод Лагранжа на изучение размеров и форм планетных орбит и поторопился опубликовать свои результаты в приложении к своему сочинению, посвященному совершенно другому вопросу. Он сделал это быстрее, чем труд Лагранжа мог появиться в печати.
Говоря об уравнениях, представляющих вековые неравенства в движении планет, Лаплас выражается так: «Уже в течение долгого времени я предполагал их проинтегрировать. В этом намерении мне помешала малая польза, которую эти вычисления принесли бы астрономии, а также и те трудности, с которыми они были связаны. Я и не взялся бы за это дело, если бы не прочитал превосходную работу г. Лагранжа, присланную в академию и имеющую появиться в следующих томах».
В примечании Лаплас добавляет: «Конечно, прежде, чем сдавать в печать свой труд, я должен был бы подождать, пока исследования г. Лагранжа будут опубликованы. Однако, допуская появление своего сочинения на эту тему, я думал, что смогу сообщить в нем геометрам в форме дополнения то, чего труду г. Лагранжа нехватало до полноты. Я отдаю, конечно, должную честь работе г. Лагранжа. Я надеялся, что они меня поблагодарят „за то, что я дал им возможность заранее познакомиться с замечательным произведением г. Лагранжа в моем изложении“».
Получив сочинение Лапласа, Лагранж ответил очень просто (10 апреля 1775 года): «Поскольку я вижу, что Вы сами уже раньше предпринимали это исследование, я охотно отказываюсь от него, и я Вам даже очень признателен за устранение меня от этого труда, будучи уверен, что от этого науки смогут лишь много выиграть».
Но через полтора месяца после этого Лагранж пишет Даламберу: «Я сейчас почти готов дать полную теорию изменения элементов планет под влиянием взаимодействия. Мне очень понравилось то, что г. Лаплас сделал по этому поводу, и я льщу себя надеждой на то, что он не будет на меня в претензии, если я не выполнил данное ему обещание отказаться от этой области в его пользу. Я не мог сопротивляться желанию снова ею заняться, но я, как и раньше, очарован тем, что он со своей стороны разрабатывает ту же тему».
Оценка Лапласа Лагранжем вполне искренна. Например, в письме к Даламберу 10 июля 1778 года он пишет о двадцатилетнем Лапласе: «Новые шаги, сделанные г. Лапласом в теории приливов и отливов, достойны и его и того ранга, который он занимает как ваш первый последователь во Франции. Если он и дальше будет продолжать так, то Вашей родине не придется опасаться судьбы, постигшей Англию после смерти Ньютона».
С течением времени переписка Лапласа с Лагранжем принимает характер все большей сердечности.
Полезное для науки соревнование двух величайших умов своей эпохи продолжалось до конца их жизни. По разным поводам Лаплас вспоминает, например, многочисленные обстоятельства знаменательного заседания в Бюро долгот, происходившего 17 августа 1808 года. На заседании Лаплас и Лагранж представили доклады на одну и ту же тему – об изменении элементов планетных орбит, но каждый ученый подошел к решению, так сказать, с противоположного конца.
Лаплас говорит: «Эта работа последних лет жизни – одно из его лучших произведений, она показывает, что годы не ослабили его гения».
Есть свидетельства, что Даламбер частенько и с некоторой горечью жаловался, что Лаплас заимствует у него его идеи. Между тем Даламбер сам предоставил это право другим ученым словами, которые заканчивают одно из его сочинений:
«Я не сомневаюсь, что это новое исследование вызовет ряд оригинальных замечаний, но я их предоставляю другим геометрам, поскольку вопрос теперь уже не встречает затруднений».
Поэтому Лаплас мог писать Даламберу (10 марта 1782 г.): «Вы не должны находить плохим то, что ваши вычисления продолжены теперь так далеко, как вы сначала и не подозревали».
Сам Даламбер вызвал как-то у Aраго, знаменитого биографа плеяды французских ученых, следующее замечание: «Даламбер, сам того не ведая, руководимый необ'яснимым чувством ревности, не вполне отдавал должное заслугам Клеро».
Можно подумать, что отчасти те же мотивы руководили великим энциклопедистом и в отношении Лапласа. По крайней мерс, в связи со своим первым докладом в Академии о приливах и отливах (15 ноября 1777 г.) Лаплас писал: «В сущности говоря, первые точные исследования, появившиеся по этому поводу, принадлежат Даламберу. Этот известный автор в своем замечательном сочинении, озаглавленном „Размышления о причине ветров“… пользуется анализом не только научным, но и искусно применяющим правильные уравнения этой проблемы; однако трудность интегрирования этих уравнений вынудила его прибегнуть к допущениям, сделавшим решение неуверенным».
Повидимому, Даламбер не удовлетворился этим знаком внимания, потребовав большего удовлетворения, и вечером того же дня Лаплас должен был писать ему: «Вместо того, чтобы докучать вам завтра, как я первоначально предполагал, я предпочел послать вам дополнение, о котором мы договорились… Я приписал следующее: В заключение я должен отметить для справедливости, что если мне удалось добавить кое-что к его
