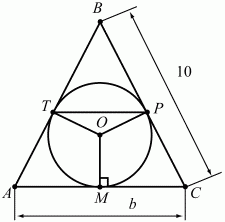
Решение. Пусть О – центр вписанной в треугольник окружности; ОМ, ОТ, ОР – радиусы, проведённые к точкам касания. Так как АС = 6, то МС = PC = 3, ВР = ВТ = 10 – 3 = 7. ?ТВР подобен ?ABC и TP/AC = BP/BC; TP/6 = 7/10; TP = 42/10 = 4,2.
Ответ: 4,2 см.
Задача 89 (рис. 265)
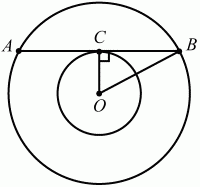
Решение. Пусть радиус большого круга равен R, радиус малого круга r (см. рис.) ОС = r; OB = R.
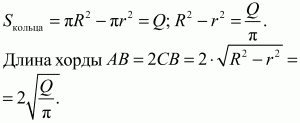
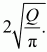
Задача 90 (рис. 266)
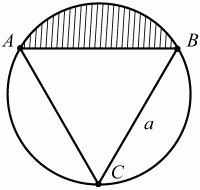
Решение. Т. к. ?ABC – равносторонний, то
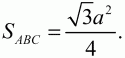
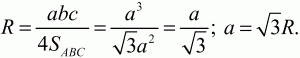
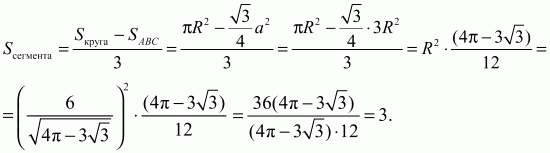
Задача 91 (рис. 267)
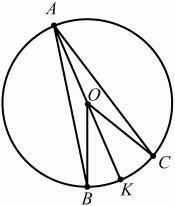
Решение. Пусть точка О – центр окружности и r – её радиус. Соединим точки В и С с центром О и проведём диаметр АК. Так как вписанный угол ВАС опирается на дугу ВКС и его величина равна ?/6, то центральный угол ВОС, опирающийся на ту же дугу, имеет величину, равную ?/3. Так как хорды АВ и АС имеют одинаковые длины, то ?BOA = ?АОС. Поскольку ?BOA + ?АОС = 2? – ?/3, то отсюда получаем, что ?BOA = ?АОС = 5?/6. Теперь подсчитаем площадь SABKC той части круга, которая заключена в угле ВАС. Она равна сумме площадей сектора ОВКС и треугольников АОВ и АОС (заметим, что у этих треугольников ОА = ОВ = ОС = r):
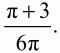
§ 2. Решения и ответы к задачам § 2 главы 2
Задача 94 (рис. 268)
Решение. Решение задачи непосредственно видно из чертежа. Соединив центр окружности с вершинами треугольника и с точками касания, получим три пары равных треугольников. Периметр Р = 7 + 7 + 6 = 20.
Ответ: Р = 20 см.
Задача 95 (рис. 269, 270)
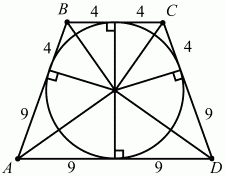
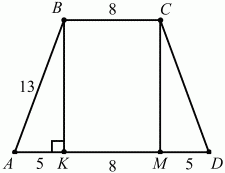
Решение. Опять соединим центр окружности с вершинами трапеции и с точками касания; получим четыре пары равных треугольников. Из рис. 269 легко видеть, что АВ = CD = 13; ВС = 8; AD = 18.
Теперь мы знаем все стороны трапеции. Осталось найти её высоту. Для этого исходный рисунок представим ниже в следующем виде. Проведём высоты ВК и СМ. Тогда КМ = ВС = 8, АК = MD = (18 – 8)/2 = 5 (рис. 270).
Из прямоугольного треугольника АВК по теореме Пифагора:
Задача 96 (рис. 271)
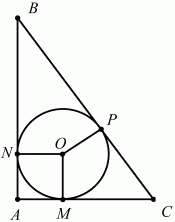
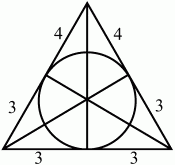
Решение. Обозначим через А вершину прямого угла данного треугольника, через АВ и АС – катеты треугольника, причем так, что АВ > АС, через О – центр вписанной окружности, через r – ее радиус. Пусть M, N и P– точки касания этой окружности соответственно со сторонами АС, АВ, ВС. Так как длины отрезков касательных, проведённых к окружности из одной точки, равны, то BN = ВР, СМ = СР, AN = AM. Так как АВ > АС, то из этих равенств следует, что ВР > СР и, значит, СР: ВР = 2:3. Пусть СР = 2х; тогда ВР = Зх и ВС = 5х.
Радиус, проведённый в точку касания, перпендикулярен касательной, поэтому ОМ ? AC, ON ? АВ. Так как угол А – прямой, то ANOM – прямоугольник, и AM = ON = r, AN = ОМ = r. Теперь находим, что АВ = r + Зх, АС = r + 2х. Периметр треугольника равен 36 см, поэтому:
5х + (r + 2х) + (r + 3х) = 36; (1)
С другой стороны, по теореме Пифагора:
(r + 2х)2+ (r + 3х)2= 25х2(2)
Из уравнения (1) следует, что r = 18 – 5х; подставив полученное выражение для r в уравнение (2), после упрощений получаем уравнение х2– 15х – 54 = 0, имеющее единственный положительный корень х = 3. Тогда r = 3 см и АВ = 12 см, АС = 9 см, ВС = 15 см.
Ответ: стороны треугольника равны 9 см, 12 см, 15 см.
Задача 99 (рис. 272)
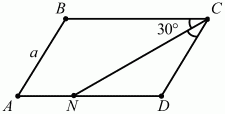
Решение. Так как ?BCD = 60°, то ?D = 120°. ?CND = ?BCN = ?NCD = 30°. Значит, ?NCD – равнобедренный и ND = CD = а.
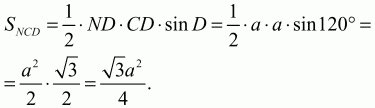
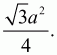
Задача 100 (рис. 273)
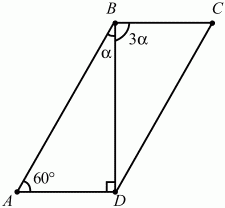
Решение. Так как ?А = 60°, то ?ABC = 120°. Из чертежа видно, что ? + 3? = 120°; ? = 30°, тогда ?BDA = 90°. AD = АВ ? sin 30° = AB/2. Пусть AD = a; тогда АВ = 2а. Из условия следует, что а + 2а + а + 2а = 90; 6а = 90; а = 15. Следовательно AD = BC = 15 см, AB = CD = 30 см.
Ответ: 15 см, 30 см, 15 см, 30 см.
Задача 101 (рис. 274)
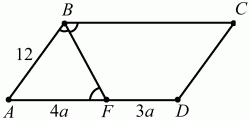
Решение. ?AFB = ?FBC, как внутренние накрест лежащие углы при параллельных прямых. Но ?FBC = ?ABF по условию, значит, ?ABF – равнобедренный и AF = АВ = 12. Пусть AF = 4а, тогда по условию FD = За; 4а = 12; а = 3; AD = 7 ? а = 21. Искомый периметр PABCD = (12 + 21) ? 2 = 66.
Ответ: 66.
Задача 105 (рис. 275)
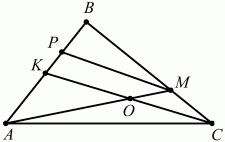
Решение. Проведём MP||СК, тогда по теореме о пропорциональных отрезках ВР: РК = ВМ: МС = 3; значит, КР = 1/4 КВ = 1/4 АК и КР: АК = ОМ: АО = 1:4 и АО = 4OМ = 4/5 AM. По условию АК = КВ = 1/2 АВ.
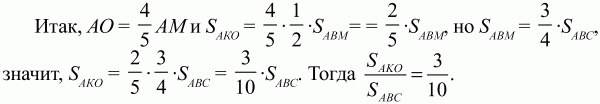
Задача 106 (рис. 276)
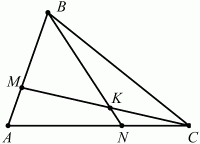
Решение. Чтобы найти отношение СК/КМ, применим теорему Менелая к треугольнику АСМ и секущей BN. Получим: CK/KM ? MB/BA ? AN/NC = 1. Так как MB/BA = 2/3, AN/NC = 2, то CK/KM = 3/4.
Аналогично, применив теорему Менелая к треугольнику ABN и секущей СМ, находим BK/KN ? CN/AC ? AM/MB = BK/KN ? 1/3 ? 1/2 = 1, откуда BK/KN = 6.
Ответ: 6; 3/4.
Задача 109 (рис. 277)
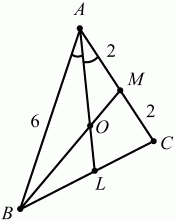
Решение. Так как АМ = 2, то по свойству биссектрисы в треугольнике АВМ ВО/OM = АВ/AM = 6/2 = 3.
Ответ: 3.
Задача 110 (рис. 278)
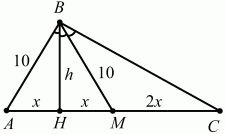
Решение. Пусть ВМ – медиана, а ВН – высота в треугольнике. Обозначим ВН через h, МС через 2х. Так как ВН – одновременно биссектриса и высота в треугольнике АВМ, то данный треугольник – равнобедренный и АН = НМ = х, AB = BM = 10. Так как ВМ – биссектриса ?НВС, то BH/BC = HM/MC; h/BC = x/2x; BC = 2h.
Из ?НВМ и ?НВС по теореме Пифагора:
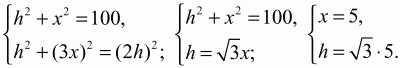
Ответ: 10 см; 20 см; 10?3 см.
Задача 118 (рис. 279)
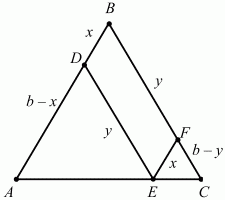
Решение. Пусть АС = а; АВ = ВС = b, BF = y, EF = x. ?ADE ~ ?EFC, поэтому FC/DE = FE/DA; (b – y)/y = x/(b – x); b2= by – bx + xy = xy. Отсюда x + у = b; PDBFE = 2(x + y) = 2b, т. е. периметр параллелограмма не зависит от х и y, а зависит только от длины боковой стороны треугольника, другими словами, для данного треугольника периметр вписанного в него параллелограмма есть величина постоянная.
Задача 119 (рис. 280)
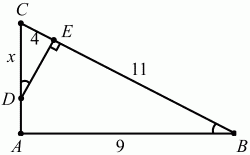
Решение. Так как СЕ = 4, то BE = 11. Из ?ABC по теореме Пифагора:
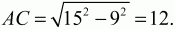
Ответ: 5.
Задача 120 (рис. 281)
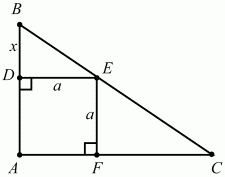
Решение. Пусть BD = х, DE = а. Из подобия ?BDE и ?ВАС BD/BE = BA/BC; x/30 = (x + a)/70; 7х = 3х + 3a; x = 3/4a. Заметим, что ADEF – квадрат, т. е. DE = EF = AF = DA = a.
Из ?DBE по теореме Пифагора BD2+ DE2= BE2; х2+ а2= 900; 9а2/16 + a2 = 900; 25а2/16 = 900; а = 24; х = 3/4 ? 24 = 18.
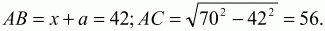
Задача 121 (рис. 282)
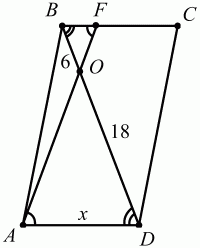
Решение. Пусть AD = х. ?BOF ~ ?AOD по равенству трёх углов, поэтому AD/BF = OD/OB; AD/4 = 18/6; AD = 12.
Ответ: 12.
Задача 122 (рис. 283)
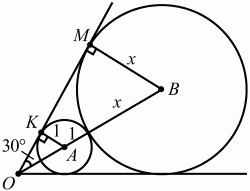
Решение. Обозначим радиус большей окружности через х. Из рисунка видно, что из прямоугольного треугольника ОКА ОА = AK/sin 30° = 1/(1/2) = 2. Треугольники OAK и ОВМ подобны, поэтому ОА/OB = АК/BM; 2/(3 + x) = 1/x; 2х = 3 + х; х = 3.
Ответ: 3.
Задача 123 (рис. 284)
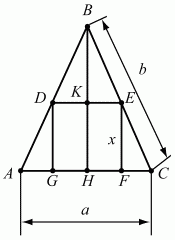
Решение. Обозначим сторону квадрата GDEF через х и проведем высоту ВН. ?ВКЕ подобен ?ВНС (см. рис.), значит, BK/KE = BH/HC; (BH – x)/(x/2) = BH/(a/2);
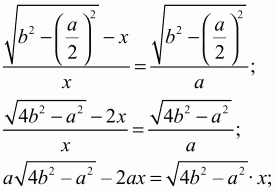
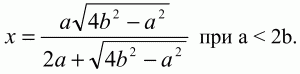
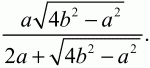
Задача 124 (рис. 285)
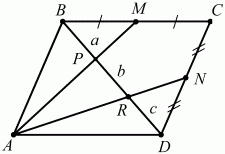
Решение. Пусть ВР = a; PR = b; RD = с. ?ВРМ ~ ?APD, значит, ВР/PD = ВМ/AD = 1/2; отсюда b + с = 2а. Аналогично ?RND ~ ?BRA; RD/BR = ND/AB = 1/2; a + b = 2c.
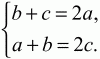
Ответ: а = b = с, что и требовалось доказать.
Задача 125
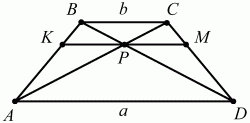
Решение. ?РВС подобен ?PAD, поэтому РВ/PD = BC/AD = b/a, PB = PD ? b/a. ?PMD подобен ?BCD, значит РМ/BC = PD/BD;
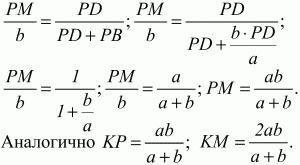
Задача 126 (рис. 287)
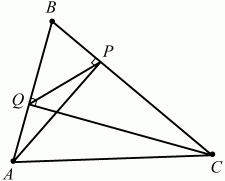
Решение. Из прямоугольных треугольников АВР, BCQ находим ВР/AB = cos В, BQ/BC = cos В. Из этих равенств следует, что треугольники BPQ и ABC подобны (по двум сторонам и углу между ними), причём коэффициент подобия равен cos В. Так как отношение площадей подобных многоугольников равно квадрату коэффициента подобия, то
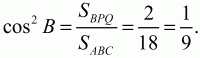
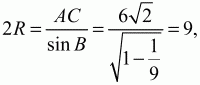
Ответ: R = 9/2.
Задача 129 (рис. 288)
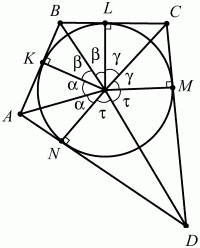
Решение. Соединим центр окружности О с вершинами четырёхугольника и точками касания. Перед нами четыре пары равных треугольников: ?АОК = ?AON. ?ВОК = ?BOL, ?COL = ?COM, ?DOM = ?DON. Тогда ?АОК = ?AON, ?ВОК = ?BOL, ?COL = ?COM, ?DOM = ?DON. Из рисунка видно, что 2? + 2? + 2? + 2? = 360°, ? + ? + ? + ? = 180°. ?АОВ + ?COD = ? + ? + ? + ? = 180°.
Ответ: 180°.
Задача 130 (рис. 289)
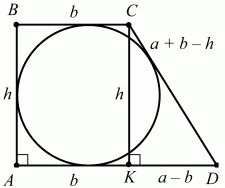
Решение. Так как в трапецию можно вписать окружность, то АВ + CD = AD + ВС. Если АВ = h; AD = a; BC = b, то CD = a + b – h, KD = а – b. Из треугольника KCD следует, что KD2+ CK2= CD2; (а – b2) + h2= (a + b – h2). Имеем: a2 – 2ab + b2+ h2= a2+ b2+ h2+ 2ab – 2ah – 2bh; -2ab = 2ab – 2ah – 2bh; ah + bh = 2ab; h = 2ab/(a + b). h – диаметр окружности.
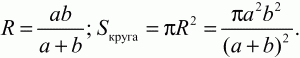
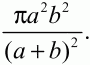
Задача 131 (рис. 290)
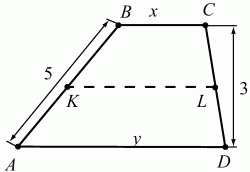
Решение. Пусть ABCD – данная трапеция, АВ = 5, CD = 3, KL – средняя линия. Обозначим величины отрезков ВС и AD через х и у соответственно. Так как в четырёхугольник ABCD можно вписать окружность, то х + у = ВС + AD = АВ + CD = 8. Поскольку KL – средняя линия трапеции, то KL = (BC + AD)/2 = 4. Если h – высота трапеции ABCD, то из теоремы о пропорциональных отрезках, отсекаемых параллельными прямыми, следует, что высоты трапеций KBCL и AKLD равны h/2. Для площадей этих трапеций имеем
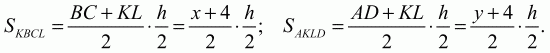
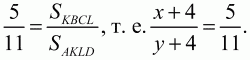
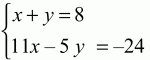
Ответ: BC = 1, AD = 7.
Задача 135 (рис. 291)
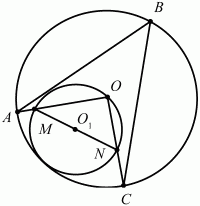
Решение. По теореме о величине вписанного в окружность угла ?ABC = 1/2 ?АОС. Заметим, что ?АОС = ?MON, a yroл ?МОN опирается на диаметр MN окружности с центром О1. ?АОС = 90°, и значит 1/2 ?АОС = 1/2 90° = 45°.
Ответ: 45°
Задача 136 (рис. 292)
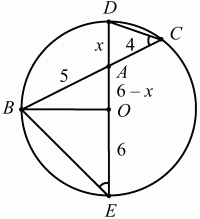
Решение. Пусть точка А делит хорду ВС на отрезки 5 и 4. Проведём через точки А и О (центр окружности) диаметр ED, причём ED = 2R = 12. Обозначим AD через х, тогда ОА = 6 – х (см. рис.). ?DCA = ?АЕВ (опираются на одну и ту же дугу BD), ?ADC подобен ?BEА (по двум углам), значит, AD/AB = AC/AE; x/5 = 4/(12 – x); 12х – х2= 20; х2 – 12х + 20 = 0; х = 10 или 2. Учитывая, что х ? R, получим x = AD = 2.
Ответ: 2.
Задача 137
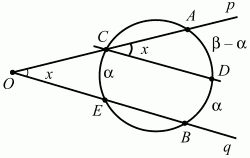
Решение I (рис. 293). Обозначим точки пересечения окружности лучами р и q соответственно через С, А и Е, В. Проведём CD||ЕВ. Получим угол ?ACD = х. Угол ?ACD является вписанным в окружность и по определению равен половине дуги AD. По условию задачи дуга СЕ = ?, а дуга АВ равна ?. Тогда дуга AD = ? – ?. В таком случае х = 1/2 (? – ?).
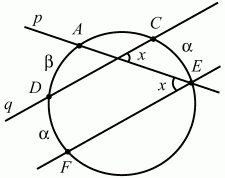
Решение II (рис. 294). Обозначим точки пересечения окружности прямыми р и q соответственно через А, Е и D, С. Проведём EF||CD. Угол AEF будет равен х (как внутренние накрест лежащие углы при параллельных CD, FE и секушей АЕ). ?AEF является вписанным в окружность и равен половине дуги AF. Из условия задачи и построений следует, что дуга AF = ? + ?.
Следовательно,
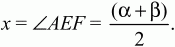
Задача 138 (рис. 295)
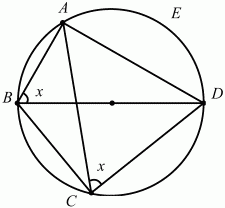
Решение. Так как BD – диаметр окружности, то ?BAD = ?BCD = ?/2. Обозначим ?ABD через х, тогда из прямоугольного треугольника ABD получаем, что cos х = AB/BD. По условию BD = 2, АВ = 1, значит, cos х = 1/2, и так как х – внутренний угол прямоугольного треугольника ABD, то х = ?/3. Тогда ?DBC = 3/4 (?ABD) = 3/4 ? ?/3 = ?/4. Вписанные углы ACD и ABD опираются на одну и ту же дугу AED, значит, ?ACD = ?ABD = ?/3. Из треугольника ADC по теореме синусов получаем, что
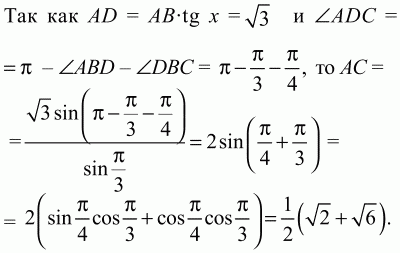
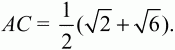
Задача 141
Решение. OB = 4; ВС = 3, значит ОС = 7. OB ? ОС = ОА2; 4 ? 7 = OA2; OA = 2?7.
Ответ: 2?7.
Ответ: 2?7.
Задача 146 (рис. 296)
Решение. Достроим ?ABD до параллелограмма. Тогда АС < АВ + ВС, но АС = 2AM, 2AM < АВ + ВС = АВ + AD, что и требовалось доказать. Заметим, что AM является медианой ?ABD.
Задача 147 (рис. 297)
Решение. Достаточно построить симметричные точки относительно берегов и длина полученной ломаной равна длине прямолинейного отрезка А'В', т. е. минимальна.
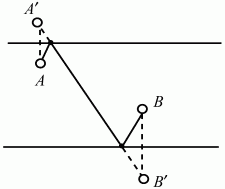
Задача 148 (рис. 298)
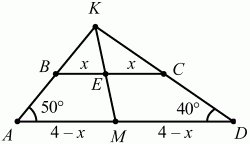
Решение. Так как средняя линия трапеции ABCD равна 4, то сумма оснований равна 8. Воспользуемся тем, что середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой КМ. Из ?AKD ?AKD = 90°. Заметим, что ?AKD – прямоугольный, причем AD – гипотенуза и точкой М делится пополам. Но тогда AM = MD = КМ = 4 – х (радиусы описанной около ?AKD окружности), КЕ = 3 – х, где х – это длина отрезков BE и ЕС. Из подобия ?АКМ и ?ВКЕ следует: (4 – х)/x = (4 – х)/(3 – x); x = 3/2; BC = 3, AD = 5.
Ответ: 5 и 3.
Задача 154 (рис. 299)
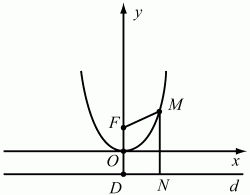
Решение. Пусть D – проекция точки F на прямую d. Середину О отрезка DF примем за начало прямоугольной системы координат, а прямую OF – за ось ординат. Точке F отнесём координаты (0; 1). Прямая d будет иметь уравнение у = -1. Пусть М(х; y) – произвольная точка плоскости. Тогда
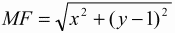
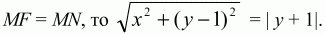
Обратно, если координаты точки М удовлетворяют этому уравнению, то х2= 4у и, следовательно,
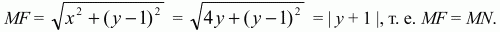
Из школьного курса алгебры известно, что линия, определяемая уравнением у = ах2, называется параболой.
Задача 155 (рис. 300)
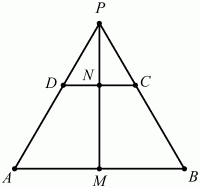
Решение. Переведём условие задачи на векторный язык. Поскольку точки Р, A, D так же, как и точки Р, В, С, лежат на одной прямой, то PD = аРА, PC = bРВ, где а и b – коэффициенты пропорциональности, а > 0; b > 0. Точки М и N – середины отрезков АВ и CD. Следовательно,
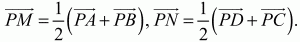
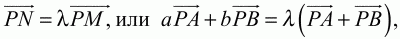
Задача 156 (рис. 301)
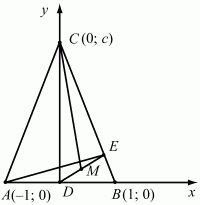
Решение. Высота равнобедренного треугольника является его осью симметрии. Поэтому середину D основания АВ треугольника ABC удобно принять за начало прямоугольной системы координат, а направленные прямые АВ и DC – за оси координат. Тогда вершинам треугольника можно отнести координаты: А(-1; 0), B(1; 0), С(0; с).
Вычислим угловые коэффициенты прямых АЕ и СМ. Для этого сначала найдём координаты точек Е и М. Запишем уравнение прямой ВС: х + у/с = 1 или у = – сх + с.
Так как DE ? ВС, то угловой коэффициент прямой DE равен 1/с, а её уравнение есть у = (1/c)x. Решая систему уравнений
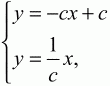
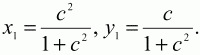
Угловые коэффициенты прямых АЕ и СМ равны соответственно
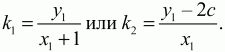
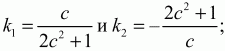
Задача 157
Решение. Имеем (PA + РВ + PC)2? 0, причем равенство достигается только тогда, когда Р – центроид треугольника ABC. Отсюда
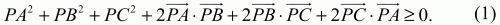Но
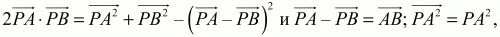
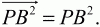Тогда
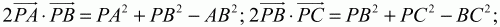
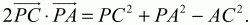Подставив эти значения скалярных произведений в неравенство (1), получим:
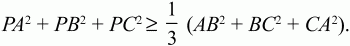
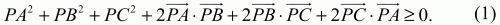
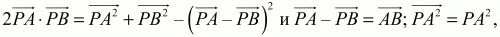
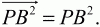
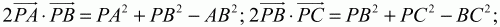
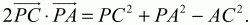
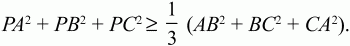
Задача 163 (рис. 302)
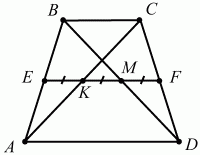
Решение. Пусть ЕК = КМ = MF = а. ЕК – средняя линия в ?ABC, значит, ВС = 2а. ЕМ – средняя линия в ?ABD, поэтому AD = 2ЕМ = 2 ? 2а = 4а; AD/BC = 4а/2а =2.
Ответ: 2:1.
Задача 164 (рис. 303)
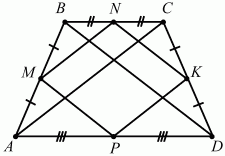
Решение. NK и MP – средние линии в ?BCD и ?ABD, поэтому NK||BD и MP||BD; MP = 1/2 BD и NK = 1/2 BD. Значит, MP||NK и MP = NK. Аналогично MN||PK (||AC) и MN = PK = 1/2 AC. Так как трапеция равнобедренная, то АС = BD, значит MN = NK = КР = РМ. Параллелограмм MNKP – ромб.
Задача 165 (рис. 304)
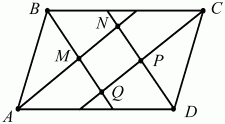
Решение. Очевидно, что MNPQ – параллелограмм. ?BAD + ?ABC = 180°. Так как AM и ВМ – биссектрисы, то ?ВАМ + ?АВМ = 90°, значит, ?АМВ = 90° и ?NMQ = 90°. Таким образом, MNPQ – прямоугольник.
Задача 166 (рис. 305)
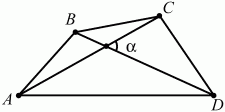
Решение. SABCD = 1/2 BD ? AC ? sin ? = S. Sпараллелограмма = ab sin ? = BD ? AC ? sin ? = 2S.
Ответ: 2S.
Задача 167 (рис. 306)
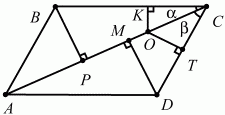
Решение. Обозначим точку на диагонали, о которой идет речь в условии задачи, через О. Так как ?ABC = ?ACD, то равны и высоты ВР и DM этих треугольников. ОК = ОС ? sin ?; ОТ = ОС ? sin ? (см. рис).
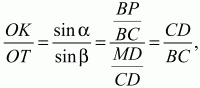
Задача 168 (рис. 307)
Решение. Пусть ABCD – данный в условии задачи четырёхугольник. Обозначим через Е, К, F, N середины сторон АВ, ВС, CD и AD соответственно. Тогда EN – средняя линия треугольника ABD, и, значит, EN||BD. Аналогично доказывается, что KF||BD, ЕК||АС и NF||АС. Это означает, что EN||KF и ЕК||NF, т. е. четырёхугольник NEKF – параллелограмм. По свойству параллелограмма ЕК = NF. EN = KF, и по условию EF = NK. Отсюда следует, что четырёхугольник NEFK – прямоугольник. Ранее доказано, что EN|| BD и ЕК||АС, поэтому BD ? AC. SABCD = 1/2 ? AC ? BD ? sin90° = 1/2 ? 2 ? 1 ? 1 = 1.
Ответ: 1 м2.
§ 3. Ответы к задачам экзаменационных комплектов
Ответы и указания к задачам экзаменационного комплекта № 1
Билет № 1
3) 74°.4) ?1/?2 = R2/R1.
Билет № 2
3) 94 см.4) AB + BD + DC = 14 см.
Билет № 3
3) 12? см2.4) Воспользоваться тем, что две крайние части средней линии трапеции равны половине верхнего основания.
Билет № 4
3) 4 и 6 см.4) Если В1К1С – точки касания (К – точка касания окружностей), О1, О2 – центры окружностей, то сначала доказываем, что ?АО1К = ?АКO2, а затем, что ?ВАО1 = ?АO2С.
Билет № 5
3) 5 см (воспользоваться подобием ?DCE и ?АСЕ).4) Воспользоваться теоремой Фалеса.
Билет № 6
3) Воспользуйтесь свойством параллельных прямых.4) Учесть то, что треугольник разбивается на прямоугольник и два равнобедренных треугольника (значит, сторона прямоугольника равна катету малого треугольника). Периметр равен сумме катетов.
Билет № 7
3) 12 см (?BOF ~ ?AOD).4) Докажите, что расстояния от точки пересечения диагоналей до сторон ромба равны.
Билет № 8
3) Докажите равенство углов DBA и ACF и воспользуйтесь признаком параллельности прямых.4) Выразите по теореме Пифагора квадрат каждой стороны четырёхугольника через соответствующие отрезки диагоналей.
Билет № 9
3) 68°, 68° и 44°.4) 4?3 см и 6?2 см.
Билет № 10
3) 4 (т. к. 180° (n – 2) = 360°).4) Если АС = а, то AD = a/2, АВ = 2а, DB = 3a/2.
Билет № 11
3) 56 см.4) В равностороннем треугольнике биссектрисы и медианы совпадают; воспользуйтесь свойством точки пересечения медиан.
Билет № 12
3) 66° и 66°.4) По 60°.
Билет № 13
3) 8, 6 и 6 см.4) 60° (угол DOG, больший 180°, равен 2 ? 150° = 300°).
Билет № 14
3) 13 см.4) Стороны равностороннего треугольника – по 12 см, а равнобедренного – 12, 14 и 14 см.
Билет № 15
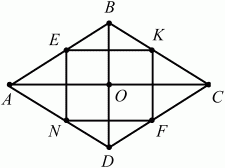
3) Треугольники равны по двум сторонам и углу между ними.4)
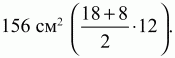
Билет № 16
3) Треугольники равны по двум сторонам и углу между ними.4) 1:1:?3.
Билет № 17
3) 5 см (обозначьте АВ = ВС = a; AD = DC = в, BD = х и запишите систему уравнений).4) 12 и 8 см (докажите равенство ?AMP и ?PNC, из которого следует, что АР = 12).
Билет № 18
3) 67°.4) Воспользуйтесь тем, что внешний угол треугольника равен сумме двух внутренних, с ним не смежных.
Билет № 19
3) 25/2 см2.4) 5 (т. к. сумма внешних углов равна 360°, то угол в правильном многоугольнике равен 468° – 360° = 108°. Далее: 180°(n – 2)/n = 108°; n = 5).
Билет № 20
3) Пусть АВ – общая хорда двух окружностей с центрами О1 и O2, ?О1АO2 = ?О1BO2 (по трем сторонам), значит, углы АO2О1 и O1O2B равны, а биссектриса в равнобедренном треугольнике является и высотой.4) 16 (т. к. в трапецию вписана окружность, то сумма оснований – а она равна 8 – равна сумме боковых сторон).
Билет № 21
3) Увеличивается на 20? см.4) Проведите диагонали в трапеции, рассмотрите средние линии полученных треугольников и учтите равенство боковых сторон трапеции.
Билет № 22
3) С(0; -6).4) 20 см.
Билет № 23
3) Медиана в равнобедренном треугольнике является и серединным перпендикуляром.4) Окружность (середины равных хорд окружности равноудалены от центра окружности).
Ответы и указания к задачам экзаменационного комплекта № 2
Билет № 1
3) 37,9 дм.4)
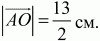
Билет № 2
3) 12 и 8 см.4) а) 6 см; б) 8 см; нет.
5) К (18, 12).
Билет № 3
3)
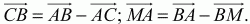
5) Докажите равенство ?AFC и ?АМС.
Билет № 4
3) 41° и 49°.4) а) угол D = 30°, угол CAD = 15°; б)
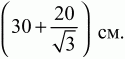
Билет № 5
3) 4 и 3 см (воспользуйтесь свойством биссектрисы).4) 6 см.
5) Уменьшится в 21 раз.
Билет № 6
3) Получится равная трапеция.4) 25?2 см2.
5) Докажите равенство ?АОВ и ?EOD.
Билет № 7
3) 53° (ВС параллельна AD).4) x = 2; y = -0,5;z = -1.
5)
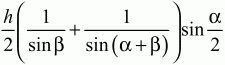
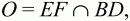
Билет № 8
3)
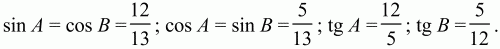
5) 15° (?АВР – равнобедренный, а т. к. угол В равен 50°, то угол PAC = 65° – 50° = 15°).
Билет № 9
3) Да.4) (9 + 3?3) см.
5) 60° (угол ВАО равен углу СВО и пусть он равен ?;
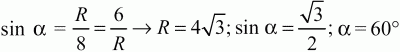
Билет № 10
з) ?3.4) ?7 см.
5) 10/?7 = (по теореме косинусов третья сторона равна ?21, значит
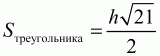
Билет № 11
3) 32° (СО – часть высоты).4) 15 и 24 м.
5) Докажите, что ?MDP = ?NBK, ?ANM = ?КСР и воспользуйтесь признаком параллелограмма).
Билет № 12
3) 73°.4) 30?2 см2.
5)
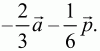
Билет № 13
3) 40?3 см2.4) Нет, т. к. треугольника со сторонами 1, 4 и 5 не существует (сумма двух любых сторон треугольника всегда больше третьей стороны).
5) 5 см (достройте трапецию до правильного шестиугольника).
Билет № 14
3) Да (k = 2).4) 4?3 + 6.
5) 62°, 49°, 69°.
Билет № 15
3) 43°.4) DE = 96/5 м (проще всего заметить, что ?ADE ~ ?ABC).
5) 22 см.
Билет № 16
3) 12; 12?3; 24 см.4) а) равенство следует из подобия треугольников ВНС и DCP.
б) 4/5.
5) Проведите из центра квадрата прямые, параллельные сторонам квадрата и найдите равные треугольники.
Билет № 17
3)
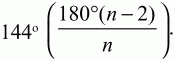
5) 110° и 70°.
Билет № 18
3) Угол DBC равен 17°, угол ABC равен 34°, АС = 18 см.4) а) 0; б) – 2 (угол между векторами 120°).
5) 2, 3, 4, 5 или 6 см.
Ответы к задачам экзаменационного комплекта № 3
Билет № 1
3) ?3a2/4 (задача 99; см. решение на стр. 155).4) 84° (задача 133).
Билет № 2
3) 3(?2–1) (задача 72; см. решение на стр. 149).4) 100 (задача 48; см. решение на стр. 144).
Билет № 3
3) 5 (задача 75).4) (задача 167; см. решение на стр.167).
Билет № 4
3)
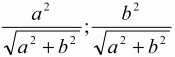
4) 6 (задача 103).
Билет № 5
3) 12 и 4 (задача 53; см. решение на стр. 145).4) 2 (задача 136; см. решение на стр.162).
Билет № 6
3) 3/2 (задача 81).4)
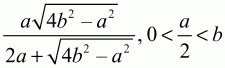
Билет № 7
3) 12 (задача 45; см. решение на стр. 142).4) 16 см (задача 68).
Билет № 8
3) 6 (задача 20).4) 2:3 (задача 151).
Билет № 9
3) 5 (задача 119; см. решение на стр. 157).4)
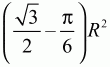
Билет № 10
3) 1 (задача 12; см. решение на стр. 133).4) 85?/4 (задача 20).
Билет № 11
3) 15/2 см (задача 87; см. решение на стр. 151).4) 150 (задача 57).
Билет № 12
3) 13, 14 и 15 (задача 93).4) 96; 156 (задача 55; см. решение на стр. 145).
Билет № 13
3) (задача 164; см. решение на стр. 166).4) 10; 20; 10?3 см.
Билет № 14
3) 9 см (задача 116).4) 30°, 60° (задача 33; см. решение на стр.139).
Билет № 15
3) 20/3 см (задача 21).4) 3 (задача 82).
Билет № 16
3)
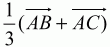
4) 4?3 (задача 52).
Билет № 17
3) 15 и 5 (задача 39).4) cos В (задача 114).
Билет № 18
3) 24 (задача 127).4) 6?3 (задача 115).
Билет № 19
3) 7 (задача 54; см. решение на стр. 145).4) 25? см2(задача 28).
Билет № 20
3) 8 и 15 см (задача 92).4) 156 см2(задача 95; см. решение на стр. 153).
Ответы к задачам экзаменационного комплекта № 4
Билет № 1
4) R = 9/2 (задача 126; см. решение на стр. 159).5) 3/4 аb (задача 144).
Билет № 2
4)
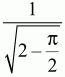
5) 13/4 (задача 153).
Билет № 3
4)
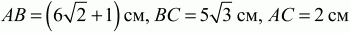
5)
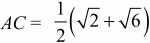
Билет № 4
4) 1/2 b2cos2? ctg ? (задача 29).5) 1 м2(задача 168; см. решение на стр. 167).
Билет № 5
4) ВС = 1, AD = 7 (задача 131; см. решение на стр.161).5) 2/3?145 см (задача 14).
Билет № 6
4) 4?5 (задача 78; см. решение на стр.135).5) 7/4 (задача 104).
Билет № 7
4) 2?13 м (задача 41).5) 15 (задача 15; см. решение на стр. 135).
Билет № 8
4)
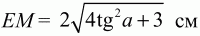
5) Длина BL больше длины BG (задача 35; см. решение на стр. 140).
Билет № 9
4) 147/8 (задача 117).5) (задача 155; см. решение на стр. 164).
Билет № 10
4)
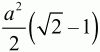
5) 27/8 см2(задача 98).
Билет № 11
4) 10 см (задача 84).5) (задача 156; см. решение на стр. 165).
Билет № 12
4) отношение длины АВ к длине АС равно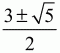
5) 72/5 (задача 49; см. решение на стр. 144).
Билет № 13
4) 10?З см2(задача 42).5) 9 см, 12 см, 15 см (задача 96; см. решение на стр. 154).
Билет № 14
4)
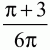
5) ?7 (задача 145).
Билет № 15
4) (задача 154; см. решение на стр. 164).5) Длина стороны квадрата равна 17; точка О лежит внутри квадрата (задача 69).
Билет № 16
4) (задача 16; см. решение на стр. 136).5)
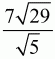
Билет № 17
4)
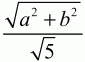
5) Парабола (задача 154; см. решение на стр. 164).
Билет № 18
4) (задача 63).5) 6; 3/4 (задача 106; см. решение на стр. 156).
Билет № 19
4)
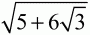
5) 30 см2, 90° (задача 143).
Билет № 20
4) (задача 162).5) 5 и 3 (задача 148; см. решение на стр. 164).