Павлов Андрей. Геометрия: Планиметрия в тезисах и решениях. 9 класс

   5. На рис. 219 ABCD – прямоугольник, AM = BN = СК = DP. Докажите, что MNKP – параллелограмм.

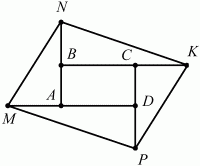   Рис. 219.

Билет № 12

   1. Теорема о величине вписанного в окружность угла (с доказательством).
   2. Аксиомы, теоремы, определения. Пример аксиом.
   3. В треугольнике ABC проведена биссектриса AK. Найдите угол В, если угол С = 33°, угол АКС = 110°.
   4. В треугольнике две стороны равны 10 и 12 см, а угол между ними 45°. Найдите площадь треугольника.
   5. Точка М лежит на диагонали АС параллелограмма ABCD, а точка Н – на его стороне AD, причем AM: МС = 2:1, АН = HD. Выразите вектор MN через векторы а и р где вектор а равен вектору АВ и вектор p равен вектору AD.

Билет № 13

   1. Теорема косинусов (с выводом).
   2. Виды движений на плоскости.
   3. Стороны параллелограмма равны 8 и 10 см, угол между ними 60°. Найдите площадь параллелограмма.
   4. Длина одного отрезка на 1 см больше второго и на 4 см больше третьего. Могут ли эти отрезки быть сторонами треугольника, периметр которого равен 10 см?
   5. Каждая из боковых сторон и меньшее основание трапеции равны 5 см, а один из его углов равен 60°. Найдите радиус окружности, описанной около нее.

Билет № 14

   1. Теорема синусов (с выводом).
   2. Признаки параллельных прямых (без доказательства).
   3. Подобны ли два треугольника ABC и А1В1С1, если АС = 14 см, А1В1 = 22 см, В1С1 = 26 см, А1C1 = 28 см, АВ = 11 см, ВС = 13 см.
   4. Сторона описанного правильного четырёхугольника на ?3 больше стороны правильного треугольника, вписанного в ту же окружность. Найдите сторону четырёхугольника.
   5. Окружность с центром О касается сторон МК, КТ и ТМ треугольника МКТ в точках А, В и С соответственно. Найдите углы треугольника ABC, если угол МКТ = 42°, угол КМТ = 82°.

Билет № 15

   1. Многоугольники. Правильные многоугольники. Основные формулы для правильных n-угольников (с выводом).
   2. Формула Герона (без вывода).
   3. Через вершину А треугольника ABC с прямым углом С проведена прямая AD, параллельная стороне ВС. Найдите угол В треугольника, если угол DAB = 43°.
   4. В треугольнике АВС АВ = 15 м, АС = 20 м, ВС = 32 м. На стороне АВ отложен отрезок AD = 9 м, а на стороне АС – отрезок АЕ = 12 м. Найдите DE.
   5. Каким должен быть радиус окружности, чтобы ее длина была равна разности длин двух окружностей с радиусами 37 и 15 см?

Билет № 16

   1. Касательная к окружности, ее свойство (с доказательством).
   2. Формулы площади треугольника и трапеции (без вывода).
   3. Один из углов прямоугольного треугольника равен 30°, а сумма гипотенузы и меньшего катета равна 36 см. Найдите стороны треугольника.
   4. Через вершину С параллелограмма ABCD проведена прямая HP так, что точка С лежит между точками Н и Р, которые принадлежат прямым АВ и AD соответственно:
   а) докажите, что BH ? DP = ВС ? CD;
   б) найдите косинус угла CDP, если синус угла НВС = 3/5.
   5. Через центр квадрата ABCD проведены две взаимно перпендикулярные прямые, каждая из которых пересекает противоположные стороны квадрата. Докажите, что отрезки этих прямых, заключенные внутри квадрата, равны между собой.

Билет № 17

   1. Свойство биссектрисы треугольника (с доказательством).
   2. Прямая, обратная, противоположная и обратная к противоположной теоремы. Сущность метода доказательства от противного.
   3. Найдите углы правильного десятиугольника.
   4. Даны точки М(0; 4), Р (2; 1), К (2; -2), Т (0; -5):
   а) докажите, что четырёхугольник МРКТ – трапеция;
   б) равны ли углы МРК и РКT?
   5. Из вершины М тупого угла параллелограмма MNKP проведены перпендикуляры МН1 и МН2 к прямым NK и КР. Найдите углы параллелограмма, если угол Н1МН2 = 70°.

Билет № 18

   1. Свойство точки пересечения медиан (с доказательством).
   2. Теорема о пропорциональных отрезках (без доказательства).
   3. BD является высотой равнобедренного треугольника ABC (АВ = ВС); угол ABD = 17°, AD = 9 см. Найдите углы DВС, ABC и основание АС.
   4. В прямоугольнике МНРК диагонали пересекаются в точке О, РК = 2, угол МОК = 120°. Вычислите скалярное произведение векторов.
   5. В треугольнике ABC АВ = 4,2 см, АС = 2,7 см, длина ВС выражается целым числом. Найдите её.

§ 3. Экзаменационный комплект № 3 (углубленный уровень)

Билет № 1

   1. Признаки равенства треугольников.
   2. Соотношение между вписанным и центральным углами в окружности, опирающимися на одну дугу.
   3. В параллелограмме ABCD угол BCD равен 60°, длина стороны АВ равна а. Биссектриса угла BCD пересекает сторону AD в точке N. Найдите площадь треугольника NCD.
   4. Дан правильный 30-угольник A1A2...A30 с центром О. Найдите угол между прямыми ОА3 и А1А4.

Билет № 2

   1. Свойства равнобедренного треугольника.
   2. Докажите, что если через произвольную точку S провести две прямые, пересекающие окружность в точках А, В и С, D соответственно, то AS ? BS = CS ? DS.
   3. Квадрат со стороной 3 см срезан по углам так, что образовался правильный восьмиугольник. Найдите сторону восьмиугольника.
   4. Найдите площадь равнобедренной трапеции, у которой высота равна 10, а диагонали взаимно перпендикулярны.

Билет № 3

   1. Признаки равенства прямоугольных треугольников.
   2. Окружность и круг. Длина окружности и площадь круга. Площадь кругового сектора и сегмента.
   3. Сколько сторон имеет выпуклый многоугольник, у которого все углы равны, если сумма его внешних углов с одним из внутренних равна 468°?
   4. Докажите, что в параллелограмме ABCD расстояния от любой точки диагонали АС до прямых ВС и CD обратно пропорциональны длинам этих сторон.

Билет № 4

   1. Геометрическое место центра описанной около треугольника окружности.
   2. Сумма углов выпуклого n-угольника.
   3. Стороны прямоугольника равны а и b. На стороне а, как на диаметре, построена окружность. На какие отрезки окружность делит диагональ прямоугольника?
   4. В треугольнике ABC на стороне ВС взята точка М так, что MB = МС, а на стороне АС взята точка К так, что АК = 3 ? КС. Отрезки ВК и AM пересекаются в точке О. Найдите AO/AM.

Билет № 5

   1. Признаки подобия треугольников.
   2. Многоугольники. Правильные многоугольники. Величина угла в правильном n-угольнике.
   3. В параллелограмме с периметром 32 см проведены диагонали. Разность между периметрами двух смежных треугольников равна 8 см. Найдите длины сторон параллелограмма.
   4. Точка находится внутри круга радиуса 6 и делит проходящую через неё хорду на отрезки длиной 5 и 4. Найдите расстояние от точки до окружности.

Билет № 6

   1. Признаки параллельности прямых.
   2. Теорема Пифагора.
   3. Две окружности с радиусами R = 3 и r = 1 касаются внешним образом. Найдите расстояния от точки касания окружностей до их общих касательных.
   4. Найдите длину стороны квадрата, вписанного в равнобедренный треугольник с основанием а и боковой стороной b так, что две его вершины лежат на основании, а две другие вершины – на боковых сторонах.

Билет № 7

   1. Докажите, что если параллельные прямые пересечены третьей прямой, то образовавшиеся внутренние накрест лежащие углы равны.
   2. Выведите формулу R = abc/4S, где R – радиус описанной около треугольника окружности; а, b, с – длины его сторон, S – площадь треугольника.
   3. Длины параллельных сторон трапеции равны 25 и 4, а длины боковых сторон равны 20 и 13. Найдите высоту трапеции.
   4. Сторона квадрата, вписанного в окружность, отсекает сегмент, площадь которого (2? – 4) см2. Найдите периметр квадрата.

Билет № 8

   1. Касательная к окружности и её свойство. Виды касания окружностей.
   2. Формула Герона.
   3. Основание равнобедренного треугольника равно 4?2, медиана боковой стороны равна 5. Найдите длину боковой стороны.
   4. В прямоугольнике ABCD точки М и N – середины сторон АВ и ВС. Точка О – точка пересечения AN и DM. Найдите AO/ON.

Билет № 9

   1. Свойства параллелограмма.
   2. Свойство биссектрисы треугольника; длина биссектрисы.
   3. Из точки D, лежащей на катете АС прямоугольного треугольника ABC, на гипотенузу СВ опущен перпендикуляр DE. Найдите длину CD, если СВ = 15, АВ = 9, СЕ = 4.
   4. Диаметр окружности радиуса R является основанием правильного треугольника. Вычислите площадь той части треугольника, которая лежит вне данного круга.

Билет № 10

   1. Свойства и признаки ромба, прямоугольника, квадрата.
   2. Теорема синусов. Докажите, что отношение сторон треугольника к синусам противолежащих углов равно диаметру описанной окружности.
   3. Основание треугольника равно ?2. Найдите длину отрезка прямой, параллельной основанию и делящей площадь треугольника пополам.
   4. В равнобедренной трапеции даны основания а = 21, b = 9 и высота h = 8. Найдите длину описанной окружности.

Билет № 11

   1. Теорема Фалеса и её обобщение (теорема о пропорциональных отрезках).
   2. Геометрическое введение синуса, косинуса, тангенса и котангенса угла. Решение прямоугольных треугольников.
   3. В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6 см. Найдите радиус окружностей.
   4. Высота ромба равна 12, а одна из его диагоналей равна 15. Найдите площадь ромба.

Билет № 12

   1. Свойство средней линии трапеции.
   2. Основные тригонометрические тождества.
   3. В треугольник вписана окружность с радиусом 4. Одна из сторон треугольника разделена точкой касания на отрезки, длины которых 6 и 8. Найдите длины сторон треугольника.
   4. Параллелограмм ABCD, у которого АВ = 153, AD = 180, BE = 135 (BE – высота), разделён на три одинаковые по площади фигуры прямыми, перпендикулярными AD. На каком расстоянии от точки А находятся точки пересечения этих перпендикуляров с AD?

Билет № 13

   1. Уравнение прямой и окружности. Геометрический смысл коэффициентов k и b в уравнении y = kx + b. Взаимное расположение прямой и окружности.
   2. Площадь четырёхугольника.
   3. Докажите, что середины сторон равнобокой трапеции являются вершинами ромба.
   4. Определите стороны треугольника, если медиана и высота, проведённые из вершины одного угла, делят этот угол на три равные части, а сама медиана равна 10 см.

Билет № 14

   1. Векторы; действия с векторами. Скалярное произведение векторов.
   2. Свойство медиан треугольника. Длина медианы.
   3. Из одной точки проведены к окружности две касательные, каждая длиной 12 см. Расстояние между точками касания 14,4 см. Определите радиус окружности.
   4. Площадь равностороннего треугольника, построенного на гипотенузе прямоугольного треугольника, вдвое больше площади последнего. Определите углы прямоугольного треугольника.

Билет № 15

   1. Признаки параллелограмма.
   2. Теорема косинусов.
   3. На основании равнобедренного треугольника, равном 8 см, как на хорде, построена окружность, касающаяся боковых сторон треугольника. Найдите радиус окружности, если длина высоты, опущенной на основание треугольника, равна 3 см.
   4. В сектор с центральным углом в 60° вписан круг. При каком радиусе сектора площадь круга равна ??

Билет № 16

   1. Критерий описанного около окружности четырёхугольника.
   2. Значения синуса, косинуса, тангенса и котангенса углов I четверти.
   3. В треугольнике ABC точка М – точка пересечения медиан. Выразите вектор AM через вектора АВ и АС.
   4. Найдите площадь параллелограмма, если его диагонали равны 3 и 5, а острый угол параллелограмма – 60°.

Билет № 17

   1. Геометрическое место центра вписанной в треугольник окружности.
   2. Площадь параллелограмма.
   3. Средняя линия трапеции равна 10 и делит площадь трапеции в отношении 3:5. Найдите длины оснований этой трапеции.
   4. В треугольнике ABC проведены высоты AD и СЕ. Докажите, что треугольники ABC и DBE подобны. Чему равен коэффициент подобия?

Билет № 18

   1. Теорема о разложении вектора по базису.
   2. Докажите, что S = рr, где S– площадь треугольника, p – полупериметр треугольника, r – радиус вписанной окружности.
   3. Известно, что в трапецию ABCD с основаниями AD и ВС можно вписать окружность и около неё можно описать окружность, EF – её средняя линия. Известно, что АВ + CD + EF = 18. Найдите периметр трапеции.
   4. В равносторонний треугольник вписана окружность. Этой окружности и сторон треугольника касаются три малые окружности. Найдите сторону треугольника, если радиус малой окружности равен 1.

Билет № 19

   1. Критерий вписанного в окружность четырёхугольника.
   2. Площадь треугольника.
   3. В параллелограмме ABCD длина диагонали BD, перпендикулярной стороне АВ, равна 6. Длина диагонали АС равна 2?22. Найдите длину стороны AD.
   4. Периметр прямоугольного треугольника равен 24 см, а его площадь равна 24 см2. Найдите площадь описанного круга.

Билет № 20

   1. Свойство средней линии треугольника.
   2. Формулы радиусов вписанной и описанной окружностей для правильного n-угольника. Площадь правильного многоугольника.
   3. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5 и 12 см. Найдите катеты треугольника.
   4. Около окружности описана равнобокая трапеция, у которой боковая сторона точкой касания делится на отрезки 4 и 9 см. Найдите площадь трапеции.

§ 4. Экзаменационный комплект № 4 (элективный уровень)

Билет № 1

   1. Аксиомы и теоремы. Определения. Аксиомы планиметрии.
   2. Критерий вписанной в четырехугольник окружности.
   3. Формула угла между прямыми a1x + BLy + c1 = 0 и а2х + b2у + с2 = 0.
   4. В остроугольном треугольнике ABC из вершине и С на стороны ВС и АВ опущены высоты АР и CQ. Известно, что площадь треугольника ABC равна 18, площадь треугольника BPQ равна 2, а длина отрезка PQ равна 2?2. Вычислите радиус окружности, описанной около треугольника ABC.
   5. Основание АВ трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Длина диагонали АС равна а, а длина боковой стороны ВС равна b. Найти площадь трапеции.

Билет № 2

   1. Признаки и свойства фигур. Характеристическое свойство геометрической фигуры. Примеры.
   2. Критерий описанной около четырёхугольника окружности.
   3. Координатные формулы деления отрезка в данном отношении.
   4. В треугольнике, один из углов которого равен разности двух других, длина меньшей стороны равна 1, а сумма площадей квадратов, построенных на двух других сторонах, в два раза больше площади описанного около треугольника круга. Найти длину большей стороны треугольника.
   5. В выпуклом четырёхугольнике ABCD диагонали АС и BD пересекаются в точке F. Известно, что AF = CF = 2, BF = 1, DF = 4, ?BFC = ?/3. Найти косинус угла между векторами АВ и DC.

Билет № 3

   1. Прямая, обратная, противоположная и обратная к противоположной теоремы. Закон контрапозиции. Метод доказательства от противного.
   2. Формула Герона площади треугольника.
   3. Смешанное произведение векторов, его геометрический смысл.
   4. В треугольнике ABC величина угла ВАС равна ?/3, длина высоты, опущенной из вершины С на сторону АВ, равна – ?3 см, а радиус окружности, описанной около треугольника ABC, равен 5 см. Найти длины сторон треугольника ABC.
   5. Диагональ BD четырёхугольника ABCD является диаметром окружности, описанной около этого четырёхугольника. Вычислить длину диагонали АС, если BD = 2, АВ = 1, ?ABD: ?ВВС = 4:3.

Билет № 4

   1. Геометрическое место точек. Основные геометрические места точек на плоскости. Метод геометрических мест.
   2. Признаки подобия треугольников.
   3. Формула расстояния между параллельными прямыми ах + by + с1 = 0 и ах + by + с2 = 0.
   4. На катете АС прямоугольного треугольника ABC как на диаметре построена окружность, которая пересекает гипотенузу АВ в точке К. Найти площадь треугольника СКВ, если длина катета AС равна b и величина угла ABC равна ?.
   5. В выпуклом четырёхугольнике длины диагоналей равны одному и двум метрам. Найти площадь четырёхугольника, зная, что длины отрезков, соединяющих середины его противоположных сторон, равны.

Билет № 5

   1. Вектор. Координаты вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число.
   2. Признаки параллельности прямых.
   3. Зависимость между высотами треугольника и радиусом вписанной в него окружности.
   4. Длины боковых сторон трапеции равны 3 и 5. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит её на две части, отношение площадей которых равно 5/11. Найти длины оснований трапеции.
   5. В треугольнике ABC длина высоты BD равна 6 см, длина медианы СЕ равна 5 см, расстояние от точки пересечения отрезков BD и СЕ до стороны АС равно 1 см. Найти длину стороны АВ.

Билет № 6

   1. Движения на плоскости, их виды. Композиция движений.
   2. Свойство биссектрисы треугольника.
   3. Взаимное расположение прямой ах + by + с = 0 и вектора n = (а; b).
   4. Выпуклый четырёхугольник ABCD описан вокруг окружности с центром в точке О, при этом АО = ОС = 1, ВО = OD = 2. Найти периметр четырёхугольника ABCD.
   5. В треугольнике ABC на стороне АВ взята точка К так, что АК: ВК = 2:1, а на стороне ВС взята точка L так, что CL: BL = 2:1. Пусть Q – точка пересечения прямых AL и СК. Найти площадь треугольника ABC, если дано, что площадь треугольника BQC равна 1.

Билет № 7

   1. Преобразования плоскости. Преобразование подобия. Гомотетия.
   2. Докажите, что точка пересечения боковых сторон трапеции, точка пересечения диагоналей и середины оснований трапеции лежат на одной прямой.
   3. Свойство точки пересечения медиан.
   4. В выпуклом четырёхугольнике MNLQ углы при вершинах N и L – прямые, а величина угла при вершине М равна arctg2/3. Найти длину диагонали NQ, если известно, что длина стороны LQ вдвое меньше длины стороны MN и на 2 м больше длины стороны LN.
   5. В треугольнике ABC высота BD равна 11,2, а высота АЕ равна 12. Точка Е лежит на стороне ВС и BE: ЕС – 5:9. Найти длину стороны АС.

Билет № 8

   1. Равенство фигур. Признаки равенства треугольников.
   2. Уравнение прямой. Геометрический смысл числа k в уравнении у = kx + b.
   3. Число ? и методы его вычисления. Длина окружности.
   4. В окружность вписан четырёхугольник ABCD, диагонали которого взаимно перпендикулярны и пересекаются в точке Е. Прямая, проходящая через точку Е и перпендикулярная к АВ, пересекает сторону CD в точке М. Доказать, что ЕМ – медиана треугольника CED, и найти её длину, если AD = 8 см, АВ = 4 см и ?CDB = ?.
   5. В треугольнике ABC угол ВАС прямой, длины сторон АВ и ВС равны соответственно 1 и 2. Биссектриса угла ABC пересекает сторону АС в точке L, G – точка пересечения медиан треугольника ABC. Что больше, длина BL или длина BG?

Билет № 9

   1. Свойства параллельных прямых. Сумма углов треугольника и выпуклого n-угольника.
   2. Формулы приведения.
   3. Теорема Менелая и обратная к ней.
   4. Центр О окружности радиуса 3 лежит на гипотенузе АС прямоугольного треугольника ABC. Катеты треугольника касаются окружности. Найти площадь треугольника ABC, если известно, что длина отрезка ОС равна 5.
   5. Продолжения сторон AD и ВС четырёхугольника ABCD пересекаются в точке Р. Точки M и N – середины сторон АВ и CD. Доказать, что если прямая MN проходит через точку Р, то ABCD – трапеция.

Билет № 10

   1. Геометрическое место центров вписанной в треугольник и описанной около треугольника окружностей.
   2. Теорема Чевы и обратная к ней.
   3. Многоугольники. Правильные многоугольники. Формулы R и r для правильного n-угольника со стороной а.
   4. На плоскости лежит равнобедренный прямоугольный треугольник, у которого катеты имеют длину а. Поворотом в этой плоскости данного треугольника вокруг вершины его прямого угла на угол 45° получается другой равнобедренный прямоугольный треугольник. Найти площадь четырёхугольника, являющегося общей частью этих двух треугольников.
   5. В параллелограмме ABCD сторона АВ равна 6 см, а высота, проведенная к основанию AD, равна 3 см. Биссектриса угла BAD пересекает сторону ВС в точке М так, что МС = 4 см. N – точка пересечения биссектрисы AM и диагонали BD. Вычислить площадь треугольника BNM.

Билет № 11

   1. Векторное произведение векторов, его геометрический смысл.
   2. Использование теорем синусов и косинусов для решения треугольников.
   3. Свойства ромба, прямоугольника, квадрата.
   4. На плоскости даны две окружности радиусов 12 см и 7 см с центрами в точках О1 и O2, касающиеся некоторой прямой в точках М1 и М2 и лежащие по одну сторону от этой прямой. Отношение длины отрезка M1M2 к длине отрезка О1O2 равно

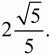   Вычислить длину отрезка М1М2.
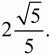
   5. Дан равнобедренный треугольник ABC, в котором проведены высота CD и перпендикуляр DE к боковой стороне ВС. Точка М – середина отрезка DE. Доказать, что отрезки АЕ и СМ перпендикулярны.

Билет № 12

   1. Признаки и свойства параллелограмма.
   2. Формула Эйлера о расстоянии между центрами вписанной в треугольник и описанной около треугольника окружностей.
   3. Геометрическое введение синуса, косинуса, тангенса, котангенса. Основные тригонометрические тождества.
   4. В треугольниках ABC и А1В1С1 длина стороны АВ равна длине стороны А1В1, длина стороны АС равна длине стороны А1С1, величина угла ВАС равна 60° и величина угла В1А1С1 равна 120°. Известно, что отношение длины В1С1 к длине ВС равно ?n (где n – целое число). Найти отношение длины АВ к длине АС. При каких значениях n задача имеет хотя бы одно решение?
   5. В трапецию ABCD с основаниями AD и ВС и с боковыми сторонами АВ и CD вписана окружность с центром О. Найти площадь трапеции, если угол DAB прямой, ОС = 2 и OD = 4.

Билет № 13

   1. Аксиоматический подход в геометрии. Требования к системе аксиом. Аксиоматическая теория.
   2. Теорема синусов. Формула 2R = a/sin ?.
   3. Вписанные в окружность углы. Соотношение между вписанным и центральным углами, опирающимися на одну дугу.
   4. В трапеции ABCD отрезки АВ и DC являются основаниями. Диагонали трапеции пересекаются в точке Е. Найти площадь треугольника ВСЕ, если АВ = 30 см, DC = 24 см, AD = 3 см и ?DAB = ?/3.
   5. В прямоугольный треугольник, периметр которого равен 36 см, вписана окружность. Гипотенуза делится точкой касания в отношении 2:3. Найти длины сторон треугольника.

Билет № 14

   1. Теорема Фалеса. Теорема о пропорциональных отрезках.
   2. Длина медианы треугольника.
   3. Скалярное произведение векторов. Угол между векторами. Угол между прямыми.
   4. Хорды АВ и АС имеют одинаковую длину. Величина образованного ими вписанного в окружность угла равна ?/6. Найти отношение площади той части круга, которая заключена в этом угле, к площади всего круга.
   5. Внутри равностороннего треугольника ABC дана точка М, такая, что AM = 1, ВМ = ?3 и СМ = 2. Найти АВ, ?АМВ и ?ВМС.

Билет № 15

   1. Теорема Пифагора. Египетский треугольник.
   2. Длина биссектрисы треугольника.
   3. Понятие площади фигуры. Площадь прямоугольника, параллелограмма, треугольника, трапеции.
   4. Доказать, что для треугольника ABC и любой точки Р выполняется неравенство: РА2+ РВ2+ PC2? 1/3(АВ2+ ВС2+ СА2).
   5. В плоскости дан квадрат с последовательно расположенными вершинами А, В, С, D и точка О. Известно, что OB = OD = 13, ОС = 5?2 и что площадь квадрата больше 225. Найти длину стороны квадрата и выяснить, где расположена точка О – вне или внутри квадрата.

Билет № 16

   1. Формула расстояния от точки А(х0, у0) до прямой ах + by + с = 0.
   2. Значения sin, cos, tg, ctg от углов 30°, 45° и 60°.
   3. Докажите, что если треугольники подобны, то с тем же коэффициентом пропорциональны произвольные соответствующие линейные элементы этих треугольников.
   4. В треугольнике ABC длина стороны АС равна 3, ?ВАС = ?/6 и радиус описанной окружности равен 2. Доказать, что площадь треугольника ABC меньше 3.
   5. Площадь прямоугольника ABCD равна 48, а длина диагонали равна 10. На плоскости, в которой расположен прямоугольник, выбрана точка О так, что OB = OD = 13. Найти расстояние от точки О до наиболее удалённой от нее вершины прямоугольника.