Страница:
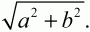
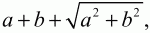
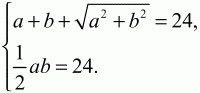
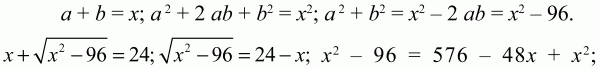
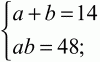
Так как центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, то радиус окружности
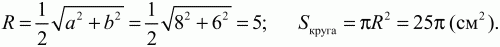
29. На катете АС прямоугольного треугольника ABC как на диаметре построена окружность, которая пересекает гипотенузу АВ в точке К. Найти площадь треугольника СКВ, если длина катета AС равна b и величина угла ABC равна ? (рис. 141). (3)
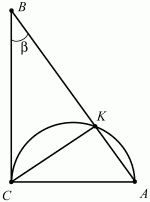
Решение. Пусть ABC – данный в условии задачи треугольник. Так как АС – диаметр окружности, то угол СКА прямой и треугольник СКА прямоугольный. Поскольку величина угла САК равна 90° – ?, то величина угла КСА равна ?. Из прямоугольного треугольника СКА имеем, что СК = bcos ?. Из прямоугольного треугольника СКВ находим ВК = СК ctg? = bcos ? ctg?. Но тогда площадь треугольника СКВ равна
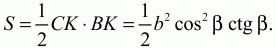
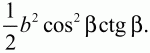
30. В треугольнике ABC угол А прямой, величина угла В равна 30°. В треугольник вписана окружность, радиус которой равен ?3. Найти расстояние от вершины С до точки N касания этой окружности с катетом АВ (рис. 142). (3)
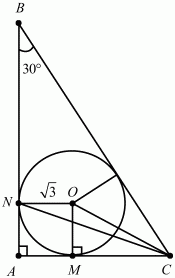
Решение. Пусть ABC – прямоугольный треугольник, удовлетворяющий условию задачи. Обозначим через О центр окружности, вписанной в этот треугольник, а через M и N – точки касания этой окружности соответственно с катетами AС и АВ. Поскольку радиус, проведенный в точку касания, перпендикулярен касательной, то ОМ ? АС и ON ? АВ. Так как угол А прямой, то четырёхугольник AMON – прямоугольник. Отсюда следует, что AM = ON = ?3 и AN = OM = ?3. Рассмотрим треугольник ОМС. Это прямоугольный треугольник, у которого ?ОСМ = 1/2 (?АСВ) = ?/6. Так как ОМ = ?3 то МС = QM ? ctg ?/6 = 3. Но тогда AC = AM + МС = ?3 + 3. Из прямоугольного треугольника ANC находим, что
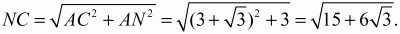
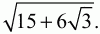
Задачи для самостоятельного решения
31. В прямоугольном равнобедренном треугольнике гипотенуза равна 12 см. Определите высоту треугольника, опущенную из прямого угла. (1)32. В прямоугольном треугольнике ABC даны: длина катета ВС, равная 36, и косинус угла ВАС, равный 8/17. Найдите длину другого катета АС и площадь треугольника. (1)
33. Площадь равностороннего треугольника, построенного на гипотенузе прямоугольного треугольника, вдвое больше площади последнего. Определите углы прямоугольного треугольника. (2)
34. В прямоугольном треугольнике высота, опущенная из вершины прямого угла, делит гипотенузу на отрезки длиной 9 и 16. Найдите радиус вписанной в треугольник окружности. (2)
35. В треугольнике ABC угол ВАС прямой, длины сторон АВ и ВС равны соответственно 1 и 2. Биссектриса угла ABC пересекает сторону АС в точке L, G – точка пересечения медиан треугольника ABC. Что больше, длина BL или длина BG? (2)
36. На плоскости лежит равнобедренный прямоугольный треугольник, у которого катеты имеют длину. Поворотом в этой плоскости данного треугольника вокруг вершины его прямого угла на угол 45° получается другой равнобедренный прямоугольный треугольник. Найти площадь четырехугольника, являющегося общей частью этих двух треугольников. (3)
1.4. Задачи на трапецию
При решении задач на трапецию нужно помнить следующие положения:
1)
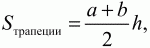где а, b – длины оснований, h – высота трапеции;
2) Если около трапеции ABCD можно описать окружность, то она равнобокая. Если при этом требуется найти радиус этой окружности, то он совпадает с радиусом окружности, описанной около любого из треугольников: ABC, ABD, ACD, BCD.
3) Если в трапецию ABCD вписана окружность, то AB + CD = BC + AD.
4) Трапецию принято изображать как на рис. 143.
Рис. 143.
При нижнем основании оба угла – острые, но она может выглядеть и как на рис. 144.
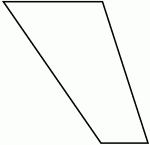Рис. 144.
Поэтому, например, задача «Одно из оснований трапеции равно 6, боковые стороны трапеции равны ?5 и ?13. Высота трапеции равна 2. Найдите площадь трапеции» имеет 4 решения:16, 14, 10 и 8.
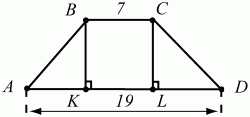Рис. 145.
Решение. Так как трапеция равнобокая, то треугольники АВК и CLD равны. В самом деле, АВ = CD по условию, ВК = CL как высоты трапеции. Значит, прямоугольные треугольники АВК и CLD равны по гипотенузе и катету. Так как KBCL – прямоугольник, то KL = ВС = 7; АК + LD = AD – KL = 19 – 7 = 12; AK = LD = 6.
Ответ: 6; 6.
38. Углы при основании трапеции равны 60° и 45°, высота трапеции равна 6 см. Найдите боковые стороны трапеции (рис. 146). (1)
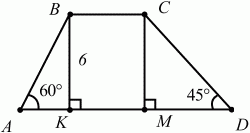Рис. 146.
Решение. Построим трапецию ABCD и проведём высоты ВК и СМ. Из прямоугольного ?АВК находим:
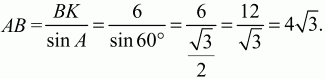Из прямоугольного ?CMD получаем:
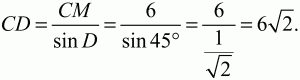Ответ: 4?3 см; 6?2 см.
39. Средняя линия трапеции равна 10 и делит площадь трапеции в отношении 3:5. Найдите длины оснований этой трапеции. (2)
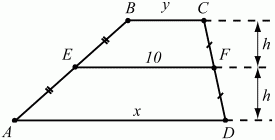Рис. 147.
Решение. Рассмотрим трапеции EBCF и AEFD (рис. 147). Введем обозначения: AD = х, ВС = у; высоты трапеций EBCF и AEFD обозначим через h. Так как площадь трапеции равна произведению полусуммы оснований на высоту трапеции, то
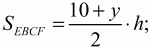
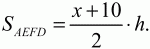Отсюда
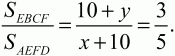Из свойства средней линии трапеции:
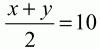Таким образом, получаем систему уравнений:
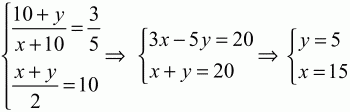Ответ: 5; 15.
40. В равнобедренной трапеции даны основания а = 21, b = 9 и высота h = 8. Найдите длину описанной около трапеции окружности (рис. 148; окружность на рисунке не показана). (2)
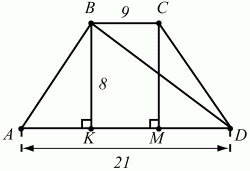Рис. 148.
Решение. Проведём высоты трапеции ВК и СМ. Так как АВ = CD, то
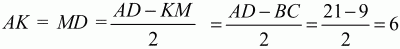Из ?АВК по теореме Пифагора получаем:
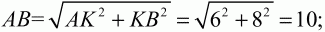тогда
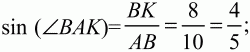KD = KM + MD = 9 + 6 = 15. Так как окружность, описанная около трапеции, совпадает с окружностью, описанной около треугольника ABD, то по теореме синусов имеем:
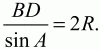Отсюда
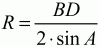или
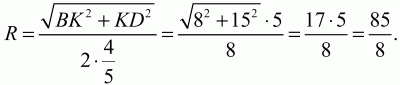Длина окружности
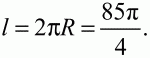Ответ: 85?/4.
41. В выпуклом четырёхугольнике MNLQ углы при вершинах N и L – прямые, а величина угла при вершине М равна arctg2/3. Найти длину диагонали NQ, если известно, что длина стороны LQ вдвое меньше длины стороны MN и на 2 м больше длины стороны LN (рис. 149). (2)
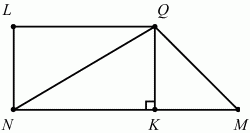Рис. 149.
Решение: Из условия задачи следует, что угол NMQ острый. Пусть QK – высота треугольника MNQ. По условию LN ? MN и LN ? LQ, следовательно, MN||LQ и LN||QK, т. е. четырёхугольник KNLQ – параллелограмм. Тогда QK = LN и NK = LQ. Имеем, пользуясь условием задачи: QK = LN = LQ – 2, КМ = NM – NK = 2LQ – LQ = LQ. В прямоугольном треугольнике QKM отрезки QK и КМ являются катетами, следовательно,
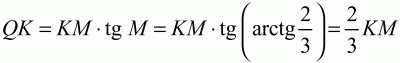и, значит, LQ – 2 = 2/3 LQ, откуда LQ = 6 и LN = 4. Из прямоугольного треугольника NLQ, наконец, по теореме Пифагора находим:
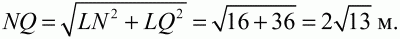Ответ:
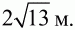
42. В трапеции ABCD отрезки АВ и DC являются основаниями. Диагонали трапеции пересекаются в точке Е. Найти площадь треугольника, ВСЕ, если АВ = 30 см, DC = 24 см, AD = 3 см и ?DAB = ?/3. (рис. 150). (3)
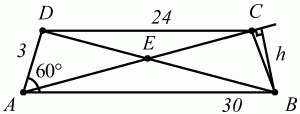Рис. 150.
Решение. Обозначим через h длину высоты треугольника ABC, опущенной из вершины В на продолжение стороны АС. Так как этот отрезок одновременно является и высотой в треугольнике ВСЕ, то имеем:
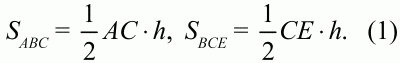Из полученных равенств находим:
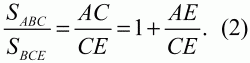В треугольниках ABE и CED равны величины соответствующих углов (?АЕВ = ?CED, ?ABE = ?CDE). Значит, эти треугольники подобны и
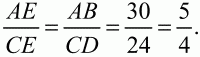Теперь из (1) и (2) находим, что
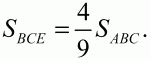Треугольники ABC и ABD имеют общее основание АВ. Поскольку АВ||CD, то их высоты, опущенные соответственно из вершин С и D, имеют равную величину. Поэтому
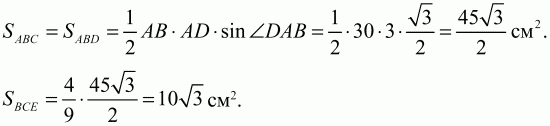Ответ:
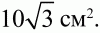
44. Меньшее основание равнобедренной трапеции равно высоте и равно h. Острый угол трапеции равен 30°. Найдите периметр трапеции. (1)
45. Длины параллельных сторон трапеции равны 25 и 4, а длины боковых сторон равны 20 и 13. Найдите высоту трапеции. (2)
46. Основания трапеции равны а и b, боковые стороны равны с. Найдите длину диагонали трапеции. (2)
47. Определите длину высоты трапеции, если её основания равны 28 и 16 см, а боковые стороны равны 25 и 17 см. (2)
48. Найдите площадь равнобедренной трапеции, у которой высота равна 10, а диагонали взаимно перпендикулярны. (2)
49. В трапецию ABCD с основаниями AD и ВС и с боковыми сторонами АВ и CD вписана окружность с центром О. Найти площадь трапеции, если угол DAB прямой, ОС = 2 и OD = 4. (3)
1)
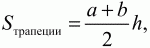
2) Если около трапеции ABCD можно описать окружность, то она равнобокая. Если при этом требуется найти радиус этой окружности, то он совпадает с радиусом окружности, описанной около любого из треугольников: ABC, ABD, ACD, BCD.
3) Если в трапецию ABCD вписана окружность, то AB + CD = BC + AD.
4) Трапецию принято изображать как на рис. 143.
При нижнем основании оба угла – острые, но она может выглядеть и как на рис. 144.
Поэтому, например, задача «Одно из оснований трапеции равно 6, боковые стороны трапеции равны ?5 и ?13. Высота трапеции равна 2. Найдите площадь трапеции» имеет 4 решения:16, 14, 10 и 8.
Примеры решения задач
37. В равнобокой трапеции ABCD высоты ВК и CL отсекают на основании AD отрезки АК и LD. Найдите длины этих отрезков, если AD = 19, ВС = 7 (рис. 145). (1)Решение. Так как трапеция равнобокая, то треугольники АВК и CLD равны. В самом деле, АВ = CD по условию, ВК = CL как высоты трапеции. Значит, прямоугольные треугольники АВК и CLD равны по гипотенузе и катету. Так как KBCL – прямоугольник, то KL = ВС = 7; АК + LD = AD – KL = 19 – 7 = 12; AK = LD = 6.
Ответ: 6; 6.
38. Углы при основании трапеции равны 60° и 45°, высота трапеции равна 6 см. Найдите боковые стороны трапеции (рис. 146). (1)
Решение. Построим трапецию ABCD и проведём высоты ВК и СМ. Из прямоугольного ?АВК находим:
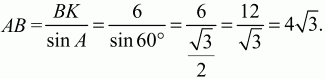
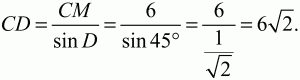
39. Средняя линия трапеции равна 10 и делит площадь трапеции в отношении 3:5. Найдите длины оснований этой трапеции. (2)
Решение. Рассмотрим трапеции EBCF и AEFD (рис. 147). Введем обозначения: AD = х, ВС = у; высоты трапеций EBCF и AEFD обозначим через h. Так как площадь трапеции равна произведению полусуммы оснований на высоту трапеции, то
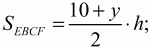
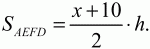
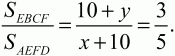
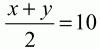
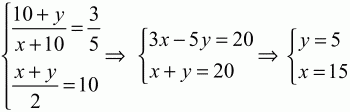
40. В равнобедренной трапеции даны основания а = 21, b = 9 и высота h = 8. Найдите длину описанной около трапеции окружности (рис. 148; окружность на рисунке не показана). (2)
Решение. Проведём высоты трапеции ВК и СМ. Так как АВ = CD, то
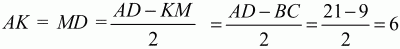
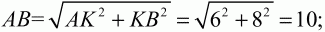
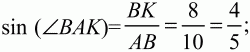
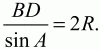
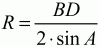
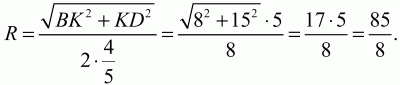
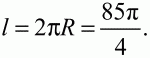
41. В выпуклом четырёхугольнике MNLQ углы при вершинах N и L – прямые, а величина угла при вершине М равна arctg2/3. Найти длину диагонали NQ, если известно, что длина стороны LQ вдвое меньше длины стороны MN и на 2 м больше длины стороны LN (рис. 149). (2)
Решение: Из условия задачи следует, что угол NMQ острый. Пусть QK – высота треугольника MNQ. По условию LN ? MN и LN ? LQ, следовательно, MN||LQ и LN||QK, т. е. четырёхугольник KNLQ – параллелограмм. Тогда QK = LN и NK = LQ. Имеем, пользуясь условием задачи: QK = LN = LQ – 2, КМ = NM – NK = 2LQ – LQ = LQ. В прямоугольном треугольнике QKM отрезки QK и КМ являются катетами, следовательно,
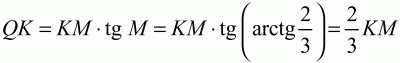
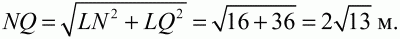
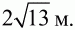
42. В трапеции ABCD отрезки АВ и DC являются основаниями. Диагонали трапеции пересекаются в точке Е. Найти площадь треугольника, ВСЕ, если АВ = 30 см, DC = 24 см, AD = 3 см и ?DAB = ?/3. (рис. 150). (3)
Решение. Обозначим через h длину высоты треугольника ABC, опущенной из вершины В на продолжение стороны АС. Так как этот отрезок одновременно является и высотой в треугольнике ВСЕ, то имеем:
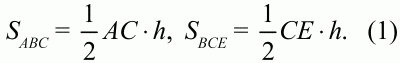
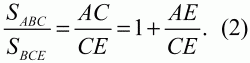
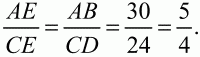
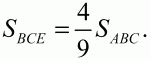
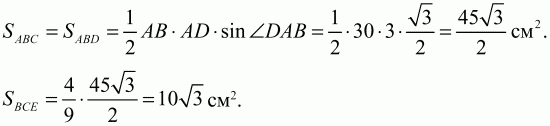
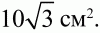
Задачи для самостоятельного решения
43. Найдите площадь равнобокой трапеции, если ее основания равны 12 и 4 см, а боковая сторона образует с одним из оснований угол в 45°. (1)44. Меньшее основание равнобедренной трапеции равно высоте и равно h. Острый угол трапеции равен 30°. Найдите периметр трапеции. (1)
45. Длины параллельных сторон трапеции равны 25 и 4, а длины боковых сторон равны 20 и 13. Найдите высоту трапеции. (2)
46. Основания трапеции равны а и b, боковые стороны равны с. Найдите длину диагонали трапеции. (2)
47. Определите длину высоты трапеции, если её основания равны 28 и 16 см, а боковые стороны равны 25 и 17 см. (2)
48. Найдите площадь равнобедренной трапеции, у которой высота равна 10, а диагонали взаимно перпендикулярны. (2)
49. В трапецию ABCD с основаниями AD и ВС и с боковыми сторонами АВ и CD вписана окружность с центром О. Найти площадь трапеции, если угол DAB прямой, ОС = 2 и OD = 4. (3)
1.5. Задачи на параллелограмм
Площадь параллелограмма со сторонами а, b и углом ? между ними вычисляется по формуле S = absin ?. Можно также воспользоваться формулой S = 1/2 d1d2 sin? где d1, d2 – длины диагоналей, ? – угол между ними (или S = aha, где ha – высота). Если в параллелограмм можно вписать окружность, то это ромб. Если около параллелограмма можно описать окружность, то это прямоугольник.
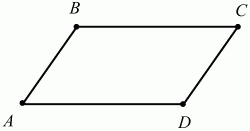Рис. 151.
Решение. По условию задачи ?А + ?С = 132°. Но, так как в параллелограмме противоположные углы равны, то ?А = ?С = 132°/2 = 66°. Учтём также, что ?А + ?В = ?С + ?D = 180°. Имеем:?В = ?D = 180° – 66° = 114°.
Ответ: 66°, 114°, 66°, 114°.
51. Одна из диагоналей параллелограмма разбивает его на два равносторонних треугольника со стороной а. Найдите длину другой диагонали (рис. 152). (1)
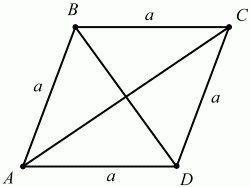Рис. 152.
Решение. Раз ?ABD и ?BCD – равносторонние, то углы ?BAD = ?BCD = 60°, тогда ?ABC = 120°.
По теореме косинусов из треугольника ABC получаем:
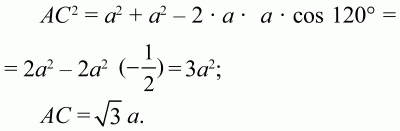Ответ:
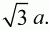
52. Найдите площадь параллелограмма, если его диагонали 3 и 5, а острый угол параллелограмма 60° (рис. 153). (2)
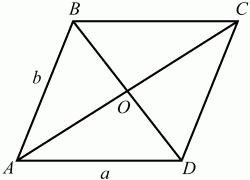Рис. 153.
Решение. Обозначим стороны параллелограмма: AD = а, АВ = b, ?BAD = 60°. BD = 3; АС = 5. Очевидно, что ?ABC = 120°. По теореме косинусов из треугольников ABD и АСВ имеем:
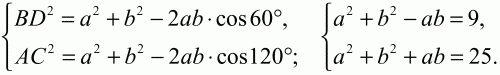Вычитая первое уравнение из второго, получим 2ab = 16. Тогда площадь будет равна:
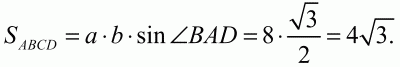Ответ:
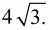
54. В параллелограмме ABCD длина диагонали BD, перпендикулярной стороне АВ, равна 6. Длина диагонали АС равна 2?22. Найдите длину стороны AD. (1)
55. Параллелограмм ABCD, у которого АВ = 153, AD = 180, BE = 135 (BE – высота), разделен на три одинаковые по площади фигуры прямыми, перпендикулярными AD. На каком расстоянии от точки А находятся точки пересечения этих перпендикуляров с AD? (2)
Примеры решения задач
50. В параллелограмме сумма двух противолежащих углов равна 132°. Найдите градусную меру каждого из углов параллелограмма (рис. 151). (1)Решение. По условию задачи ?А + ?С = 132°. Но, так как в параллелограмме противоположные углы равны, то ?А = ?С = 132°/2 = 66°. Учтём также, что ?А + ?В = ?С + ?D = 180°. Имеем:?В = ?D = 180° – 66° = 114°.
Ответ: 66°, 114°, 66°, 114°.
51. Одна из диагоналей параллелограмма разбивает его на два равносторонних треугольника со стороной а. Найдите длину другой диагонали (рис. 152). (1)
Решение. Раз ?ABD и ?BCD – равносторонние, то углы ?BAD = ?BCD = 60°, тогда ?ABC = 120°.
По теореме косинусов из треугольника ABC получаем:
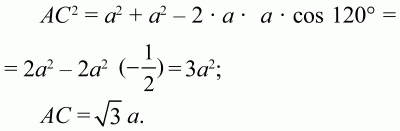
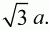
52. Найдите площадь параллелограмма, если его диагонали 3 и 5, а острый угол параллелограмма 60° (рис. 153). (2)
Решение. Обозначим стороны параллелограмма: AD = а, АВ = b, ?BAD = 60°. BD = 3; АС = 5. Очевидно, что ?ABC = 120°. По теореме косинусов из треугольников ABD и АСВ имеем:
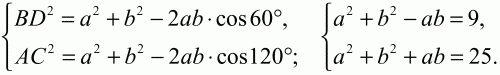
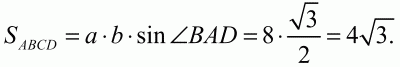
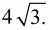
Задачи для самостоятельного решения
53. В параллелограмме с периметром 32 см проведены диагонали. Разность между периметрами двух смежных треугольников равна 8 см. Найдите длины сторон параллелограмма. (1)54. В параллелограмме ABCD длина диагонали BD, перпендикулярной стороне АВ, равна 6. Длина диагонали АС равна 2?22. Найдите длину стороны AD. (1)
55. Параллелограмм ABCD, у которого АВ = 153, AD = 180, BE = 135 (BE – высота), разделен на три одинаковые по площади фигуры прямыми, перпендикулярными AD. На каком расстоянии от точки А находятся точки пересечения этих перпендикуляров с AD? (2)
1.6. Задачи на ромб
Для ромба характерны все формулы для параллелограмма, только а = b.
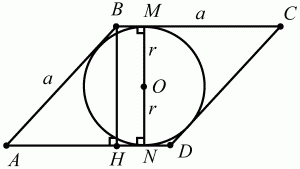Рис. 154.
Решение. Пусть сторона ромба равна а. В ромбе, как и во всяком параллелограмме, сумма внутренних односторонних углов BAD (обозначим этот угол ?А) и ABC (обозначим его ?В) равна 180°. Получаем систему уравнений:
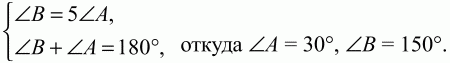Радиус r вписанной окружности, как видно из рисунка, равен половине высоты ВН ромба (2r = MN = ВН). Но из ?АВН следует, что
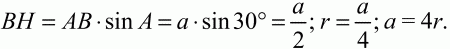Ответ: в 4 раза.
57. Высота ромба равна 12, а одна из его диагоналей равна 15. Найдите площадь ромба (рис. 155). (2)
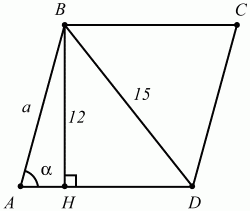Рис. 155.
Решение. Для нахождения площади ромба нам нужно знать длину стороны ромба и хотя бы один из его углов. Пусть АВ = а; ?А = ?. Проведём высоту ВН. Из ?АВН находим, что ВН = AB ? sin ?; 12 = asin ?. Из ?ABD по теореме косинусов BD2= АВ2+ AD2– 2AB ? AD ? cos ?; 152= а2 + а2– 2 ? a ? acos ?; 225 = 2а2(1 – cos ?). Получаем систему уравнений:
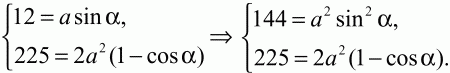Делим первое уравнение на второе:
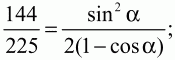
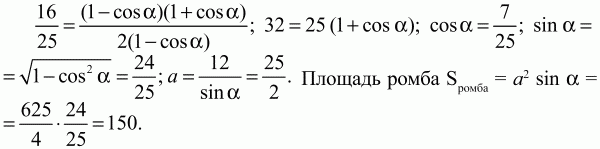Ответ: 150.
59. В ромб, сторона которого 20 см, вписан круг. Найти площадь круга, если одна диагональ ромба больше другой в 4/3 раза. (2)
60. В ромб с острым углом 30° вписан круг, площадь которого равна Q. Найдите площадь ромба. (2)
Примеры решения задач
56. Тупой угол ромба в 5 раз больше его острого угла. Во сколько раз сторона ромба больше радиуса вписанной в него окружности (рис. 154)? (1)Решение. Пусть сторона ромба равна а. В ромбе, как и во всяком параллелограмме, сумма внутренних односторонних углов BAD (обозначим этот угол ?А) и ABC (обозначим его ?В) равна 180°. Получаем систему уравнений:
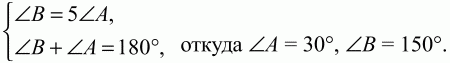
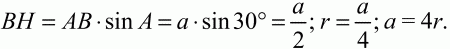
57. Высота ромба равна 12, а одна из его диагоналей равна 15. Найдите площадь ромба (рис. 155). (2)
Решение. Для нахождения площади ромба нам нужно знать длину стороны ромба и хотя бы один из его углов. Пусть АВ = а; ?А = ?. Проведём высоту ВН. Из ?АВН находим, что ВН = AB ? sin ?; 12 = asin ?. Из ?ABD по теореме косинусов BD2= АВ2+ AD2– 2AB ? AD ? cos ?; 152= а2 + а2– 2 ? a ? acos ?; 225 = 2а2(1 – cos ?). Получаем систему уравнений:
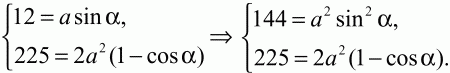
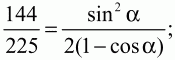
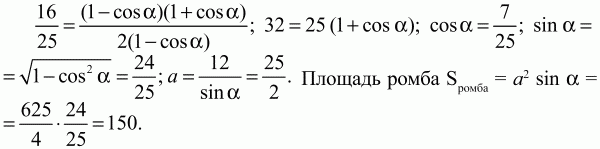
Задачи для самостоятельного решения
58. Диагональ ромба равна его стороне, ее длина 10 см. Найдите вторую диагональ и углы ромба. (1)59. В ромб, сторона которого 20 см, вписан круг. Найти площадь круга, если одна диагональ ромба больше другой в 4/3 раза. (2)
60. В ромб с острым углом 30° вписан круг, площадь которого равна Q. Найдите площадь ромба. (2)
1.7. Задачи на прямоугольник
Для прямоугольника справедливы все формулы для параллелограмма, только угол между сторонами равен 90°. Поэтому S = ab = 1/2d2d2 sin?.
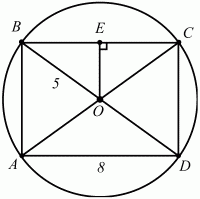Рис. 156.
Решение. Очевидно, что центр описанной около прямоугольника окружности является точкой пересечения диагоналей прямоугольника. Из рисунка видно, что ОВ = 5, BE = BC/2 = 8/2 = 4.
Тогда по теореме Пифагора находим:
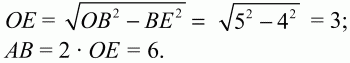Ответ: 6 см; 8 см; 6 см.
62. Стороны прямоугольника 5 и 4 см. Биссектрисы углов, прилежащих к большей стороне, делят противолежащую сторону на 3 части. Найдите длины этих частей (рис. 157). (2)
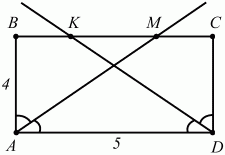Рис. 157.
Решение. Проведем в прямоугольнике ABCD биссектрисы AM и DK (см. рис. 157). Получим:?ВАМ = 1/2 ?BAD = 1/2 ?90° = 45°. Отсюда следует, что ?АВМ – равнобедренный (?ВMA = 45°) и, значит, ВМ = АВ = 4. МС = ВС – ВМ = 5–4 = 1.
Очевидно, что ВК = МС = 1;
КМ = ВС – ВК – МС = 5–1 – 1 = 3.
Ответ: 1; 3; 1.
63. Из всех прямоугольников, вписанных в полукруг, найти прямоугольник наибольшей площади (рис. 158). (3)
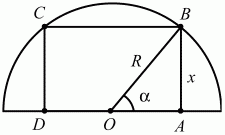Рис. 158.
Решение. Обозначив ?АОВ =?, получим: АВ = R sin ?, АО = R cos ?, S = AB ? AD = AB ? 2AO = 2R2sin ? ? cos ?, 0° < ? < 90°.
Воспользуемся формулой синуса двойного аргумента и будем иметь:
S = R2sin2?. Так как sin2? ? 1, то S максимальна при условии sin2? = 1, т. е. когда 2? = 90°, ? = 45°. При этом S = R2. Стороны прямоугольника при этом будут равны
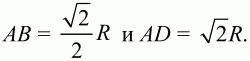Ответ:
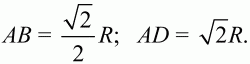
65. Площадь прямоугольника равна 9?3 см2, а величина одного из углов, образованного диагоналями, равна 120°. Найдите стороны прямоугольника. (2)
66. Площадь прямоугольника ABCD равна 48, а длина диагонали равна 10. На плоскости, в которой расположен прямоугольник, выбрана точка О так, что OB = OD = 13. Найти расстояние от точки О до наиболее удаленной от нее вершины прямоугольника. (3)
Примеры решения задач
61. Прямоугольник вписан в окружность радиуса 5 см. Одна из сторон равна 8 см. Найдите другие стороны прямоугольника (рис. 156). (1)Решение. Очевидно, что центр описанной около прямоугольника окружности является точкой пересечения диагоналей прямоугольника. Из рисунка видно, что ОВ = 5, BE = BC/2 = 8/2 = 4.
Тогда по теореме Пифагора находим:
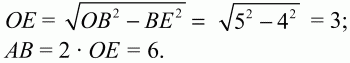
62. Стороны прямоугольника 5 и 4 см. Биссектрисы углов, прилежащих к большей стороне, делят противолежащую сторону на 3 части. Найдите длины этих частей (рис. 157). (2)
Решение. Проведем в прямоугольнике ABCD биссектрисы AM и DK (см. рис. 157). Получим:?ВАМ = 1/2 ?BAD = 1/2 ?90° = 45°. Отсюда следует, что ?АВМ – равнобедренный (?ВMA = 45°) и, значит, ВМ = АВ = 4. МС = ВС – ВМ = 5–4 = 1.
Очевидно, что ВК = МС = 1;
КМ = ВС – ВК – МС = 5–1 – 1 = 3.
Ответ: 1; 3; 1.
63. Из всех прямоугольников, вписанных в полукруг, найти прямоугольник наибольшей площади (рис. 158). (3)
Решение. Обозначив ?АОВ =?, получим: АВ = R sin ?, АО = R cos ?, S = AB ? AD = AB ? 2AO = 2R2sin ? ? cos ?, 0° < ? < 90°.
Воспользуемся формулой синуса двойного аргумента и будем иметь:
S = R2sin2?. Так как sin2? ? 1, то S максимальна при условии sin2? = 1, т. е. когда 2? = 90°, ? = 45°. При этом S = R2. Стороны прямоугольника при этом будут равны
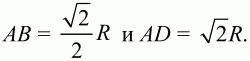
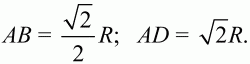
Задачи для самостоятельного решения
64. Диагональ прямоугольника делит угол в отношении 2:1. Найдите отношение сторон прямоугольника. (1)65. Площадь прямоугольника равна 9?3 см2, а величина одного из углов, образованного диагоналями, равна 120°. Найдите стороны прямоугольника. (2)
66. Площадь прямоугольника ABCD равна 48, а длина диагонали равна 10. На плоскости, в которой расположен прямоугольник, выбрана точка О так, что OB = OD = 13. Найти расстояние от точки О до наиболее удаленной от нее вершины прямоугольника. (3)
1.8. Задачи на квадрат
Если а – сторона квадрата, d – его диагональ, то S = a2= d2/2.
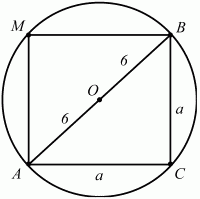Рис. 159.
Решение. Очевидно, что центр описанной около квадрата окружности есть точка пересечения его диагоналей. Это означает, что ОВ – радиус окружности и ОВ = 6. Тогда АВ = 12 и по теореме Пифагора AC2+ ВС2= AB2. Обозначив длину стороны квадрата через а, получим: а2+ а2= 122; 2 ? а2= 144; а2 = 72. Sквадрата = a2= 72.
Ответ: 72.
68. Сторона квадрата, вписанного в окружность, отсекает сегмент, площадь которого (2? – 4) см2. Найдите периметр квадрата (рис. 160). (2)
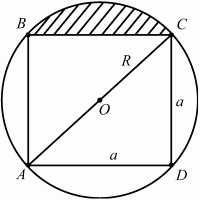Рис. 160.
Решение. Площадь заштрихованного сегмента, как видно из рисунка, можно вычислить по формуле:
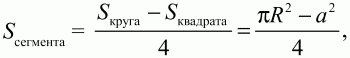где а – длина стороны квадрата, R – радиус описанной окружности. Выразим R через а.
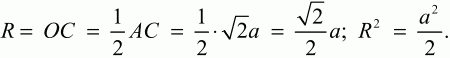Таким образом,
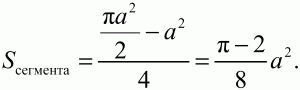С учётом условия получаем уравнение:
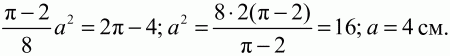Рквадрата = 4a = 4 ? 4 = 16 см.
Ответ: 16 см.
69. В плоскости дан квадрат с последовательно расположенными вершинами А, В, С, D и точка О. Известно, что OB = OD = 13, ОС = 5?2 и что площадь квадрата больше 225. Найти длину стороны квадрата и выяснить, где расположена точка О – вне или внутри квадрата (рис. 161). (3)
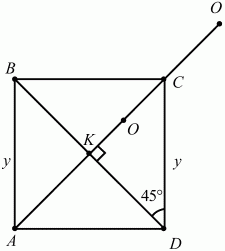Рис. 161.
Решение. Так как OB = OD, то точка О лежит на перпендикуляре к середине отрезка BD, т. е. на прямой АС. Обозначим через К точку пересечения диагоналей квадрата. Из условия следует, что ОВ > ОС; значит, точка О лежит по одну сторону с точкой С относительно перпендикуляра к середине отрезка ВС. Отсюда следует, что точка О лежит на луче КС.
Обозначим КО через х и АВ = CD через y. Так как
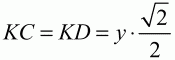и
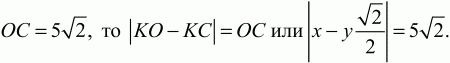Применяя к прямоугольному треугольнику KOD теорему Пифагора, получаем: OD2= КО2+ KD2или 169 = х2+ 1/2 у2.
Предположим, что КО ? КС или
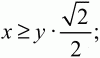тогда х2 ? 1/2 у2(заметим, что числа x и y неотрицательны) и
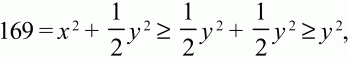т. е. площадь квадрата не превосходит 169, что противоречит условию. Следовательно,
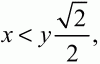т. е. КО < КС, и точка О лежит внутри квадрата. Теперь получаем
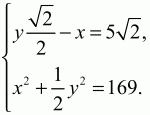Из первого уравнения
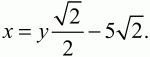Подставляя
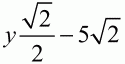вместо х во второе уравнение, после арифметических преобразований получаем уравнение у2– 10у – 119 = 0. Это квадратное уравнение имеет корни у1 = -7 и у2 = 17. Так как у есть длина отрезка, то у > 0 и, значит, y = 17.
Ответ: длина стороны квадрата равна 17; точка О лежит внутри квадрата.
71. В квадрат вписан круг, а в полученный круг вписан квадрат. Найдите отношение площадей квадратов. (1)
72. Квадрат со стороной 3 см срезан по углам так, что образовался правильный восьмиугольник. Найдите сторону восьмиугольника. (2)
73. Дан квадрат ABCD. На его сторонах вовне построены равносторонние треугольники ABM, BCN, CDK, DAL. Найдите площадь четырёхугольника MNKL, если АВ = 1. (2)
Примеры решения задач
67. Радиус окружности, в которую вписали квадрат, равен 6. Найдите площадь квадрата (рис. 159). (1)Решение. Очевидно, что центр описанной около квадрата окружности есть точка пересечения его диагоналей. Это означает, что ОВ – радиус окружности и ОВ = 6. Тогда АВ = 12 и по теореме Пифагора AC2+ ВС2= AB2. Обозначив длину стороны квадрата через а, получим: а2+ а2= 122; 2 ? а2= 144; а2 = 72. Sквадрата = a2= 72.
Ответ: 72.
68. Сторона квадрата, вписанного в окружность, отсекает сегмент, площадь которого (2? – 4) см2. Найдите периметр квадрата (рис. 160). (2)
Решение. Площадь заштрихованного сегмента, как видно из рисунка, можно вычислить по формуле:
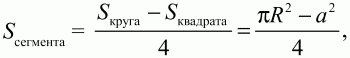
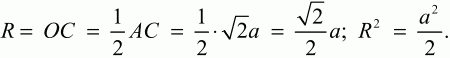
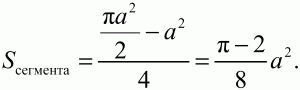
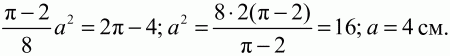
Ответ: 16 см.
69. В плоскости дан квадрат с последовательно расположенными вершинами А, В, С, D и точка О. Известно, что OB = OD = 13, ОС = 5?2 и что площадь квадрата больше 225. Найти длину стороны квадрата и выяснить, где расположена точка О – вне или внутри квадрата (рис. 161). (3)
Решение. Так как OB = OD, то точка О лежит на перпендикуляре к середине отрезка BD, т. е. на прямой АС. Обозначим через К точку пересечения диагоналей квадрата. Из условия следует, что ОВ > ОС; значит, точка О лежит по одну сторону с точкой С относительно перпендикуляра к середине отрезка ВС. Отсюда следует, что точка О лежит на луче КС.
Обозначим КО через х и АВ = CD через y. Так как
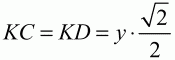
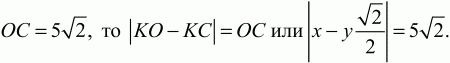
Предположим, что КО ? КС или
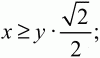
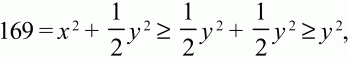
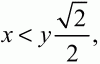
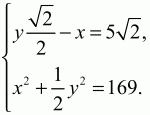
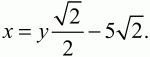
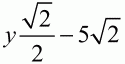
Ответ: длина стороны квадрата равна 17; точка О лежит внутри квадрата.
Задачи для самостоятельного решения
70. Сторона квадрата равна 7 см. Определите диаметр окружности, описанной около квадрата. (1)71. В квадрат вписан круг, а в полученный круг вписан квадрат. Найдите отношение площадей квадратов. (1)
72. Квадрат со стороной 3 см срезан по углам так, что образовался правильный восьмиугольник. Найдите сторону восьмиугольника. (2)
73. Дан квадрат ABCD. На его сторонах вовне построены равносторонние треугольники ABM, BCN, CDK, DAL. Найдите площадь четырёхугольника MNKL, если АВ = 1. (2)
1.9. Задачи на n-угольник (n > 3)
Для произвольного выпуклого четырёхугольника S = 1/2 d1d2 sin?. Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны, a S = рr, где р – полупериметр, r – радиус вписанной окружности.
Если около четырёхугольника можно описать окружность, то суммы противоположных углов равны по 180°.
Для правильного n-угольника:
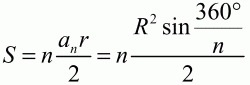(R и r – радиусы описанной и вписанной окружностей, а – длина стороны правильного n-угольника).
Полезно также помнить, что в правильном шестиугольнике a6 = R.
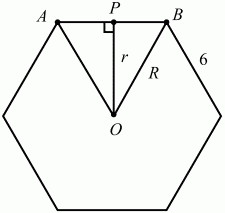Рис. 162.
Решение. В правильном шестиугольнике сторона равна радиусу описанной окружности. Значит, треугольник АВО – правильный, угол АВО составляет 60°, a OB = R = 6. Радиусы вписанной в правильный шестиугольник окружности перпендикулярны его сторонам. В частности на рис. показано, что r ? АВ, где r = ОР. Тогда из прямоугольного треугольника ОРВ имеем:
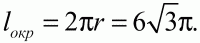Ответ:
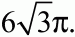
75. Сколько сторон имеет выпуклый многоугольник, у которого все углы равны, если сумма его внешних углов с одним из внутренних равна 468°? (2)
Решение. Сумма внешних углов выпуклого многоугольника равна 360°, сумма внутренних углов равна 180°(n – 2). Величина угла в правильном n-угольнике равна
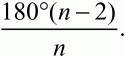Получаем уравнение:
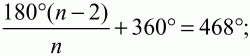180°(n – 2) = 108°n;
72°n = 360°; n = 5.
Ответ: 5.
77. В правильный треугольник вписана окружность, а в неё – правильный шестиугольник. Найдите отношение площадей треугольника и шестиугольника. (2)
78. Выпуклый четырёхугольник ABCD описан вокруг окружности с центром в точке О, при этом АО = ОС = 1, ВО = OD = 2. Найти периметр четырёхугольника ABCD. (3)
Если около четырёхугольника можно описать окружность, то суммы противоположных углов равны по 180°.
Для правильного n-угольника:
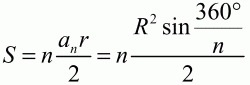
Полезно также помнить, что в правильном шестиугольнике a6 = R.
Примеры решения задач
74. Сторона правильного шестиугольника равна 6. Найдите длину вписанной в него окружности (рис. 162). (1)Решение. В правильном шестиугольнике сторона равна радиусу описанной окружности. Значит, треугольник АВО – правильный, угол АВО составляет 60°, a OB = R = 6. Радиусы вписанной в правильный шестиугольник окружности перпендикулярны его сторонам. В частности на рис. показано, что r ? АВ, где r = ОР. Тогда из прямоугольного треугольника ОРВ имеем:
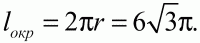
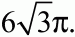
75. Сколько сторон имеет выпуклый многоугольник, у которого все углы равны, если сумма его внешних углов с одним из внутренних равна 468°? (2)
Решение. Сумма внешних углов выпуклого многоугольника равна 360°, сумма внутренних углов равна 180°(n – 2). Величина угла в правильном n-угольнике равна
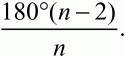
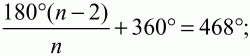
72°n = 360°; n = 5.
Ответ: 5.
Задачи для самостоятельного решения
76. Сторона правильного шестиугольника равна 14. Найдите сторону равновеликого ему правильного треугольника. (1)77. В правильный треугольник вписана окружность, а в неё – правильный шестиугольник. Найдите отношение площадей треугольника и шестиугольника. (2)
78. Выпуклый четырёхугольник ABCD описан вокруг окружности с центром в точке О, при этом АО = ОС = 1, ВО = OD = 2. Найти периметр четырёхугольника ABCD. (3)
1.10. Задачи на окружность и круг
При решении задач на окружность и круг применяются следующие формулы:
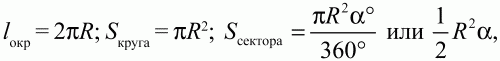если ? выражена в радианах. Sсегмента = Sсектора – Sтреугольника.
Вписанный в окружность угол равен половине центрального угла, опирающегося на ту же дугу.
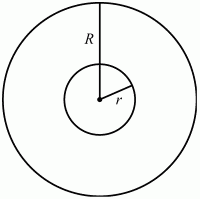Рис. 163.
Решение. Очевидно, что ширина кольца hкольца = R – r (см. рис). Зная длины окружностей, найдём их радиусы.
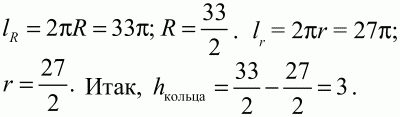Ответ: 3.
80. Найдите площадь сектора круга с радиусом R = 4 и центральным углом в 30°. (1)
Решение. Площадь сектора с углом в 30° в 36°/3° = 12 раз меньше площади всего круга. Значит, площадь сектора
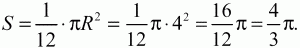Ответ: 4/3?.
81. Две окружности с радиусами R = 3 и r = 1 касаются внешним образом. Найдите расстояния от точки касания окружностей до их общих касательных (рис. 164, а; б). (2)
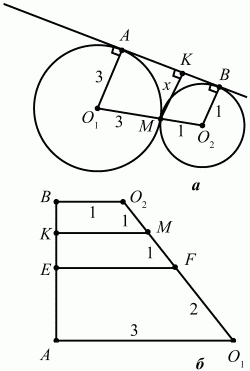Рис. 164.
Решение. Из рисунка видно, что четырёхугольник АВ02О1 – трапеция. В самом деле, радиусы О1А и О2В перпендикулярны общей касательной АВ, а значит, параллельны друг другу. Проведём среднюю линию EF трапеции АВO2О1. По свойству средней линии трапеции находим
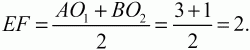Легко видеть, что КМ – средняя линия трапеции EВО2F(см. рис. 164, б).
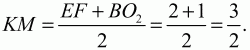Ответ: 3/2.
82. В сектор с центральным углом в 60° вписан круг. При каком радиусе сектора площадь круга равна ? (рис. 165)? (2)
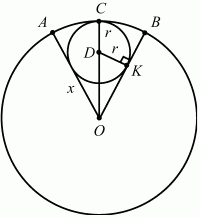Рис. 165.
Решение. Пусть АО = ОВ = ОС = х (см. рис). D – центр вписанного в сектор круга. Тогда ОС – биссектриса ?АОВ и ?СОВ = 1/2 ?АОВ = 1/2 ? 60° = 30°. Из прямоугольного треугольника ODK:
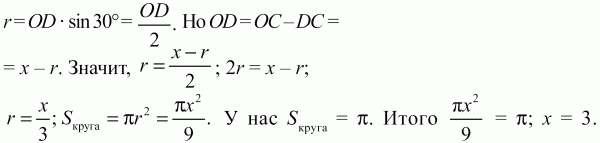Ответ: 3.
83. Диаметр окружности радиуса R является основанием правильного треугольника. Вычислите площадь той части треугольника, которая лежит вне данного круга (рис. 166). (2)
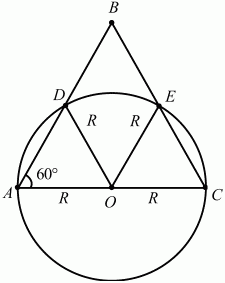Рис. 166.
Решение. Как видно из рисунка, треугольники ADO и ОЕС – равносторонние (например, у ?ADO ?А = 60°; АО = OD, значит, ?ADO = 60°).
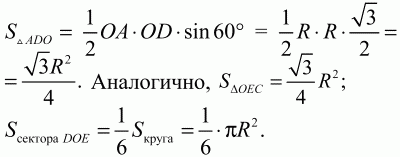Искомая площадь:
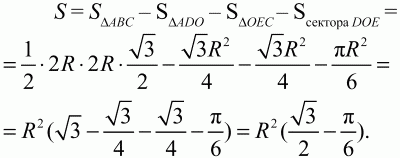Ответ:
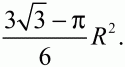
84. На плоскости даны две окружности с радиусами 12 см и 7 см и центрами в точках О1 и О2 касающиеся некоторой прямой в точках М1 и М2 и лежащие по одну сторону от этой прямой. Отношение длины отрезка М1М2 к длине отрезка О1O2 равно
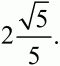Вычислить длину отрезка М1М2 (рис. 167). (3)
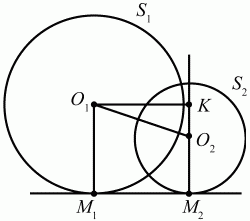Рис. 167.
Решение. Пусть S1 и S2 – две окружности, удовлетворяющие условию задачи. Поскольку точки М1 и М2 являются точками касания окружностей S1 и S2 с прямой М1М2, то О1М1 ? М1М2 и O2М2 ? М1М2. Соединим центры О1 и O2 этих окружностей и проведём через точку О1 прямую, параллельную прямой М1М2. Пусть точка К будет точкой пересечения прямых O2М2 и прямой, проведённой параллельно прямой М1М2 через точку О1. Получим прямоугольный треугольник O1O2K с гипотенузой O1O2. Применяя к прямоугольному треугольнику О1КO2 теорему Пифагора, имеем:
О1О22= O1K2+ KO22(1)
Поскольку
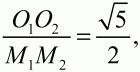то
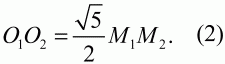Поскольку КМ2 = О1М1 и КO2 = КМ2 – М2O2, то КO2 = 5 см. Наконец,
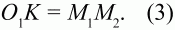Теперь из равенства (1) с учётом (2) и (3), а также КO2 = 5 см, следует, что 5/4 М1М22= М1М22+ 25, откуда
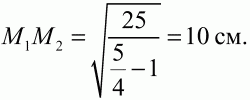Ответ: 10 см.
86. Точка лежит вне круга на расстоянии диаметра от центра круга. Найдите угол между касательными, проведенными из данной точки к данному кругу. (1)
87. В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6 см. Найдите радиус окружностей. (2)
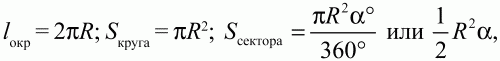
Вписанный в окружность угол равен половине центрального угла, опирающегося на ту же дугу.
Примеры решения задач
79. Даны две концентрические окружности. Длина одной из них равна 33?, другой 27?. Найдите ширину кольца (рис. 163). (1)Решение. Очевидно, что ширина кольца hкольца = R – r (см. рис). Зная длины окружностей, найдём их радиусы.
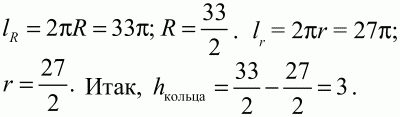
80. Найдите площадь сектора круга с радиусом R = 4 и центральным углом в 30°. (1)
Решение. Площадь сектора с углом в 30° в 36°/3° = 12 раз меньше площади всего круга. Значит, площадь сектора
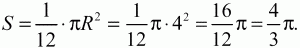
81. Две окружности с радиусами R = 3 и r = 1 касаются внешним образом. Найдите расстояния от точки касания окружностей до их общих касательных (рис. 164, а; б). (2)
Решение. Из рисунка видно, что четырёхугольник АВ02О1 – трапеция. В самом деле, радиусы О1А и О2В перпендикулярны общей касательной АВ, а значит, параллельны друг другу. Проведём среднюю линию EF трапеции АВO2О1. По свойству средней линии трапеции находим
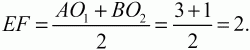
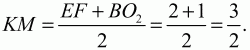
82. В сектор с центральным углом в 60° вписан круг. При каком радиусе сектора площадь круга равна ? (рис. 165)? (2)
Решение. Пусть АО = ОВ = ОС = х (см. рис). D – центр вписанного в сектор круга. Тогда ОС – биссектриса ?АОВ и ?СОВ = 1/2 ?АОВ = 1/2 ? 60° = 30°. Из прямоугольного треугольника ODK:
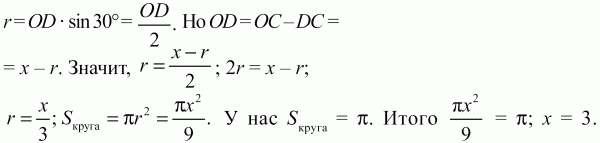
83. Диаметр окружности радиуса R является основанием правильного треугольника. Вычислите площадь той части треугольника, которая лежит вне данного круга (рис. 166). (2)
Решение. Как видно из рисунка, треугольники ADO и ОЕС – равносторонние (например, у ?ADO ?А = 60°; АО = OD, значит, ?ADO = 60°).
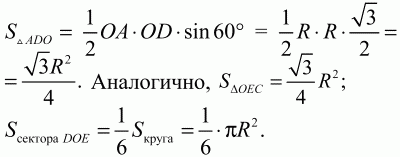
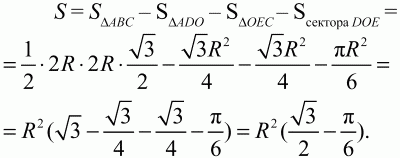
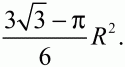
84. На плоскости даны две окружности с радиусами 12 см и 7 см и центрами в точках О1 и О2 касающиеся некоторой прямой в точках М1 и М2 и лежащие по одну сторону от этой прямой. Отношение длины отрезка М1М2 к длине отрезка О1O2 равно
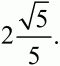
Решение. Пусть S1 и S2 – две окружности, удовлетворяющие условию задачи. Поскольку точки М1 и М2 являются точками касания окружностей S1 и S2 с прямой М1М2, то О1М1 ? М1М2 и O2М2 ? М1М2. Соединим центры О1 и O2 этих окружностей и проведём через точку О1 прямую, параллельную прямой М1М2. Пусть точка К будет точкой пересечения прямых O2М2 и прямой, проведённой параллельно прямой М1М2 через точку О1. Получим прямоугольный треугольник O1O2K с гипотенузой O1O2. Применяя к прямоугольному треугольнику О1КO2 теорему Пифагора, имеем:
О1О22= O1K2+ KO22(1)
Поскольку
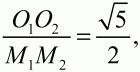
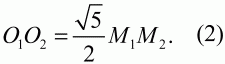
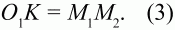
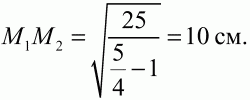
Задачи для самостоятельного решения
85. Дуги А1В1 и А2В2 равной длины 1 принадлежат разным окружностям с радиусами R1 и R2. Найдите отношение градусных мер центральных углов, соответствующих этим дугам. (1)86. Точка лежит вне круга на расстоянии диаметра от центра круга. Найдите угол между касательными, проведенными из данной точки к данному кругу. (1)
87. В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6 см. Найдите радиус окружностей. (2)