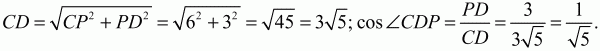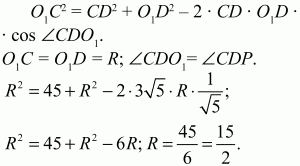Страница:
Билет № 17
1. Координаты на плоскости. Расстояние между точками.
2. Теорема косинусов. Связь теоремы косинусов и теоремы Пифагора.
3. Площадь четырёхугольника, правильного n-угольника.
4. В треугольнике ABC медианы, проведенные к сторонам АС и ВС, пересекаются под прямым углом. Длина стороны АС равна b, длина стороны ВС равна а. Найти длину стороны АВ.
5. Найдите геометрическое место точек, равноудалённых от данной прямой и данной точки.
2. Теорема косинусов. Связь теоремы косинусов и теоремы Пифагора.
3. Площадь четырёхугольника, правильного n-угольника.
4. В треугольнике ABC медианы, проведенные к сторонам АС и ВС, пересекаются под прямым углом. Длина стороны АС равна b, длина стороны ВС равна а. Найти длину стороны АВ.
5. Найдите геометрическое место точек, равноудалённых от данной прямой и данной точки.
Билет № 18
1. Уравнение фигуры. Уравнение окружности.
2. Базис на плоскости. Теорема о разложении вектора по базису.
3. Формула S = рr для треугольника.
4. Из всех прямоугольников, вписанных в полукруг, найти прямоугольник наибольшей площади.
5. На сторонах АВ и АС треугольника ABC взяты точки М и Т, такие, что AM/MB = CN/NA = 1/2. Отрезки BN и СМ пересекаются в точке К. Найти отношения отрезков BK/KN и CK/KM.
2. Базис на плоскости. Теорема о разложении вектора по базису.
3. Формула S = рr для треугольника.
4. Из всех прямоугольников, вписанных в полукруг, найти прямоугольник наибольшей площади.
5. На сторонах АВ и АС треугольника ABC взяты точки М и Т, такие, что AM/MB = CN/NA = 1/2. Отрезки BN и СМ пересекаются в точке К. Найти отношения отрезков BK/KN и CK/KM.
Билет № 19
1. Касательная к окружности, её свойство. Виды касания окружностей.
2. Координатные формулы движений.
3. Формула S = abc/4R для треугольника.
4. В треугольнике ABC угол А прямой, величина угла В равна 30°. В треугольник вписана окружность, радиус которой равен ?3. Найти расстояние от вершины С до точки касания этой окружности с катетом АВ.
5. Основания трапеции равны 4 см и 9 см, а диагонали равны 5 см и 12 см. Найти площадь трапеции и угол между её диагоналями.
2. Координатные формулы движений.
3. Формула S = abc/4R для треугольника.
4. В треугольнике ABC угол А прямой, величина угла В равна 30°. В треугольник вписана окружность, радиус которой равен ?3. Найти расстояние от вершины С до точки касания этой окружности с катетом АВ.
5. Основания трапеции равны 4 см и 9 см, а диагонали равны 5 см и 12 см. Найти площадь трапеции и угол между её диагоналями.
Билет № 20
1. Пропорциональность отрезков хорд и секущих окружности.
2. Первая теорема косинусов для четырёхугольника.
3. Свойство средней линии треугольника и трапеции.
4. Стороны треугольника образуют арифметическую прогрессию. Доказать, что радиус окружности, вписанной в треугольник, равен 1/3 высоты, проведённой к средней по величине стороне треугольника.
5. Средняя линия трапеции равна 4, отрезок, соединяющий середины оснований, равен 1, углы при основании трапеции равны 40° и 50°. Найдите длины оснований трапеции.
2. Первая теорема косинусов для четырёхугольника.
3. Свойство средней линии треугольника и трапеции.
4. Стороны треугольника образуют арифметическую прогрессию. Доказать, что радиус окружности, вписанной в треугольник, равен 1/3 высоты, проведённой к средней по величине стороне треугольника.
5. Средняя линия трапеции равна 4, отрезок, соединяющий середины оснований, равен 1, углы при основании трапеции равны 40° и 50°. Найдите длины оснований трапеции.
Глава 4
Решения и ответы к задачам
§ 1. Решения и ответы к задачам § 1 главы 2
Задача 10 (рис. 220)
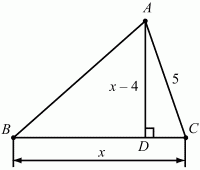
Решение. Пусть ВС = х, тогда AD = х – 4. Площадь треугольника ABC равна 1/2 ? ВС ? AD = 1/2 ? х ? (х – 4). По условию площадь равна 16. Значит, 1/2 ? х ? (х – 4) = 16, откуда х = 8. BС = 8, AD = BС – 4 = 4. По теореме Пифагора
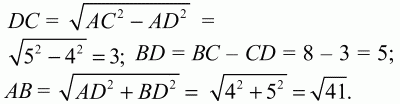
Ответ: 13 + ?41 см.
Задача 11
Решение. Запишем площадь треугольника тремя способами:
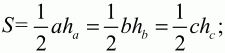 c другой стороны,
c другой стороны,
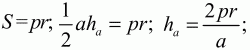
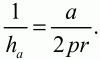 Аналогично
Аналогично
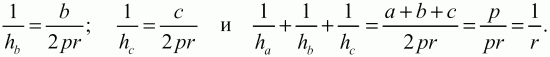
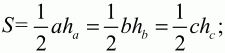
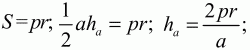
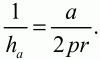
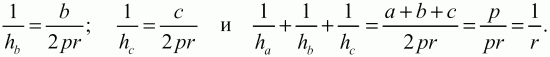
Задача 12 (рис. 221)
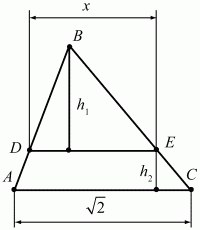
Решение. Пусть в треугольнике ABC АС = ?2. Проведем отрезок DE так, что площадь треугольника DBE равна площади трапеции ADEC. Так как нам нужно найти длину отрезка DE, обозначим ее через х. Введем еще обозначения: высоту треугольника DBE обозначим через h1 высоту трапеции ADEC через h2 Составим систему уравнений:
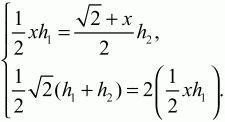
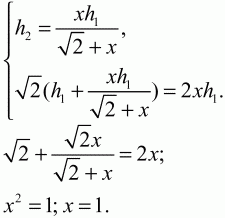
Задача 13 (рис. 222)
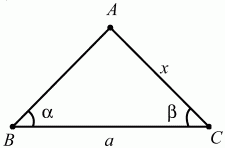
Решение. Пусть в треугольнике ABC ВС = а, ?АВС = ?, ?АСВ = ?, длину АС обозначим через х. По теореме синусов:
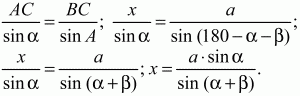
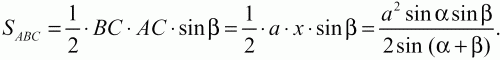
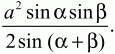
Задача 14 (рис. 223)
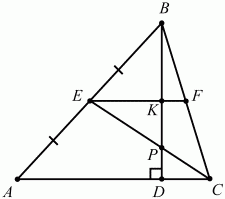
Решение. Пусть ABC – данный в условии задачи треугольник. Так как медиана треугольника ABC – отрезок СЕ – всегда лежит внутри треугольника, то, чтобы точка пересечения отрезков СЕ и BD также лежала внутри треугольника ABC, необходимо, чтобы угол С был меньшим 90°. Обозначим через Р точку пересечения прямых BD и СЕ. Так как PD перпендикулярна АС, то расстояние от точки Р до стороны АС равно длине отрезка PD, т. е. равно 1 см. Проведём через точку Е прямую, параллельную основанию АС треугольника ABC. Пусть эта прямая пересекает высоту BD в точке К, а сторону ВС в точке F. Так как СЕ – медиана и прямая EF параллельна АС, то EF – средняя линяя треугольника ABC. Поэтому, в частности, прямая EF делит пополам высоту BD, т. е. KD = 1/2BD = 3 см. Теперь находим, что КР = KD – PD = 2 см. Треугольники ЕРК и DPC подобны, так как у них ?ЕРК = ?DPC, как величины вертикальных углов, ?РКЕ = ?PDC = 90°. Из подобия этих треугольников следует, что KP/PD = EP/PC. Так как PC = ЕС – ЕР, то это равенство можно записать в виде 2/1 = EP/(5 – EP), откуда получаем, что ЕР = 10/3 см. Из прямоугольного треугольника ЕКР находим, что
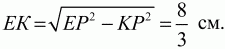
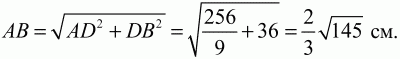
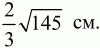
Задача 15 (рис. 224)
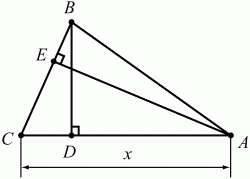
Решение. Обозначим длину отрезка АС через х. Из прямоугольного треугольника АЕС по теореме Пифагора находим

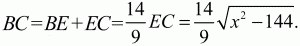
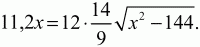
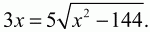
Ответ: 15.
Задача 16 (рис. 225)
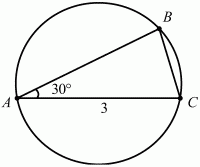
Решение. По теореме синусов ВС = 2Rsin ?ВАС = 2 ? 2 ? 1/2 = 2, где R – радиус описанной окружности. Так как АВ – хорда, то её длина не больше диаметра, т. е. АВ ? 2R = 4. Покажем, что АВ < 4. Если АВ = 4, то ?АСВ = ?/2 и должно выполняться равенство АВ2= АС2+ ВС2. Но оно не выполняется, так как 42? З2+ 22. Значит, АВ < 4. Тогда
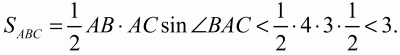
Задача 17 (рис. 226)
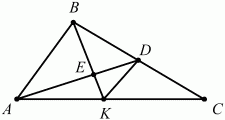
Решение. Пусть ВК и AD – медианы, проведенные соответственно к сторонам АС и ВС. Обозначим через Е точку их пересечения. Так как точка К – середина стороны АС и точка D – середина стороны ВС, то отрезок KD – средняя линия треугольника ABC. Следовательно, АВ = 2 ? KD. Так как по условию задачи ВК и AD перпендикулярны, то треугольники АЕК, KED, BED, АЕВ прямоугольные. Применяя теорему Пифагора к этим треугольникам, имеем:
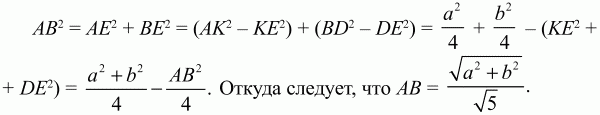
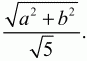
Задача 22 (рис. 227)
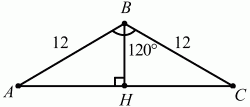
Решение. Пусть в треугольнике ABC АВ = ВС = 12, ?ABC = 120°. Так как в треугольнике сумма углов равна 180°, то ?А + ?С = 180° – 120° = 60°. Учитывая, что в равнобедренном треугольнике углы при основании равны, получаем: ?А = 30°. Рассмотрим треугольник ВНА, где ВН – высота треугольника. ВН – катет в этом треугольнике, лежащий напротив угла в 30°.
Тогда ВН = 1/2 ? АВ = 6.
Ответ: 6.
Задача 23 (рис. 228)
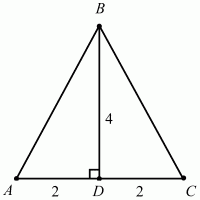
Решение. Поскольку высота в равнобедренном треугольнике, проведённая к основанию, является и медианой треугольника, то AD = DC = 2. Тогда по теореме Пифагора имеем:
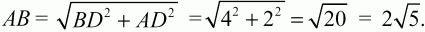
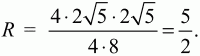
Ответ: 25?/4.
Задача 24 (рис. 229)
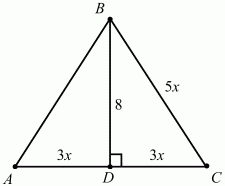
Решение. Так как BD – высота в равнобедренном треугольнике ABC, то она является и медианой, т. е. AD = DC. Так как AC/BC = 6/5, то можно обозначить DC = Зх; ВС = 5х (см. рис.). Из ?BCD по теореме Пифагора DB2+ DC2= ВС2. Или 82+ (Зх)2= (5х)2; х = 2. Радиус вписанной окружности r = S/P; площадь треугольника S = 1/2 АС ? BD = 1/2 ? 6х ? 8 = 48; полупериметр р = (5x + 5x + 6x)/2 = 16; r = 48/16 =3.
Ответ: 3.
Задача 25
Решение. Sзаштрихованного сектора = 1/3(Sкруга – Sтреугольника). Длина окружности l = 2?R. По условию l = 4?; 2?R = 4?; R = 2. Sкpyгa = ?R2= 4?. Длину стороны треугольника найдём по теореме синусов:
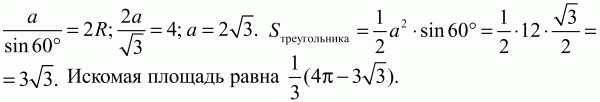 Ответ:
Ответ:
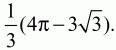
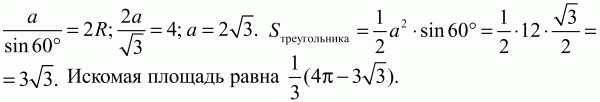
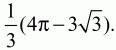
Задача 26 (рис. 230)
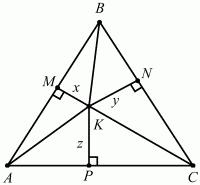
Решение. Пусть К – произвольная точка внутри равностороннего треугольника ABC со стороной а. Опустим перпендикуляры KM, KN, КР на стороны треугольника. Обозначим эти перпендикуляры следующим образом: КМ = х, KN = у, КР = z. Тогда SABC = SABK + SBKC + SAKC. Получаем равенство:
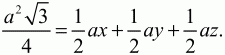
Задача 31 (рис. 231)
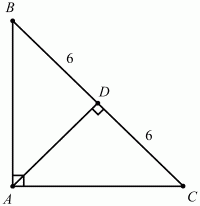
Решение. Так как AD – высота в равнобедренном треугольнике ABC, то она является и медианой. Значит, BD = DC = 6. Тогда AD = BD = 6, так как ?ABD = ?BAD = 45°.
Можно было увидеть и другую закономерность. Так как D – середина гипотенузы, то D – центр описанной около треугольника ABC окружности. Значит. DA = DB = DC = 6.
Ответ: 6 см.
Задача 32 (рис. 232)
Решение. Обозначим угол ВАС через ?. Тогда AC = BC ? ctg?. Последовательно находим:
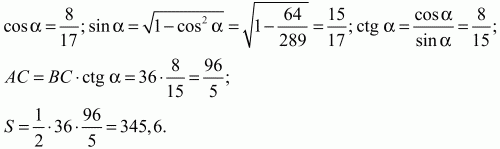
Задача 33 (рис. 233)
Решение. Обозначим катеты прямоугольного треугольника ABC с гипотенузой ВС через а и b (см. рис). Тогда
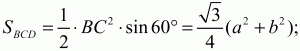
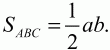
По условию SBCD = 2SABC. Значит,
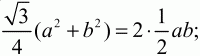
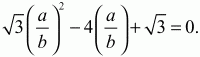
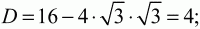
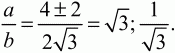
Ответ: 60°; 30°.
Задача 34 (рис. 234)
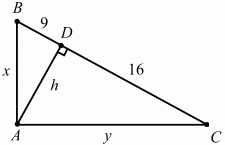
Решение. Пусть ABC – заданный треугольник, AD – высота, опущенная на гипотенузу. Тогда по условию BD = 9, DC = 16. Обозначим АВ через х, АС через у, высоту AD через h. По теореме Пифагора: BD2+ AD2= АВ2; DC2+ AD2= АС2; АВ2+ AC2= ВС2. Получаем систему уравнений:
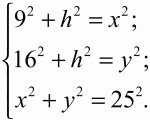
81 + 256 + 2h2+ х2+ у2= х2+ у2+ 625;
2h2= 228; h = 12; х2= 81 + 144 = 225; x = 15;
у2= 256 + 144 = 400; y = 20.
Далее воспользуемся формулой r = S/p.
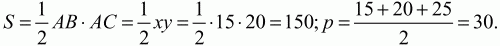
Ответ: 5.
Задача 35 (рис. 235)
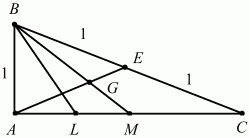
Решение. Пусть ABC – данный в условии задачи треугольник. По теореме Пифагора находим, что AC = ?3. Поскольку sin ?ABC = ?3/2, то, учитывая, что угол ?ABC – угол прямоугольного треугольника, находим, что ?ABC = ?/3. Следовательно, ?АСВ = ?/6. Так как BL – биссектриса угла ABC, то ?ABL = ?/6. Из прямоугольного треугольника ABL находим
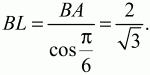
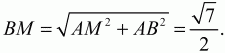
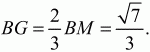
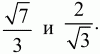
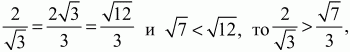
Ответ: длина BL больше длины BG.
Задача 36 (рис. 236)
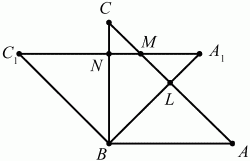
Решение. Пусть ABC – данный в условии задачи прямоугольный треугольник, А1ВС1 – прямоугольный треугольник, полученный поворотом треугольника ABC вокруг вершины его прямого угла В на угол 45°. Из условия задачи следует, что величины углов CBC1, CBA1, ABA1, ВСА, ВА1C1 равны 45°. Прямые АВ и А1C1 параллельны, т. к. при их пересечении прямой ВА1 равны накрест лежащие углы АВА1 и ВА1С1. Но тогда, поскольку треугольник ABC прямоугольный и, значит, АВ ? ВС, получаем, что прямая С1А1 перпендикулярна прямой ВС. Обозначим через N точку пересечения прямых С1А1 и СВ. Поскольку
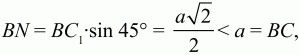

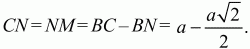
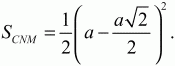
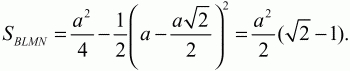
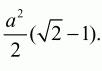
Задача 43 (рис. 237)
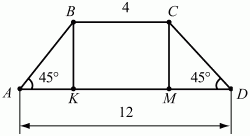
Решение. Проведём высоты трапеции ВК и СМ. Очевидно, что КМ = 4; AK = MD = (12 – 4)/2 = 4. Так как треугольник АВК – равнобедренный (?АВК = ?ВАК = 45°). то ВК = АК = 4.
SABCD = (AD + BC)/2 ? BK = (12 + 4)/2 ? 4 = 32.
Ответ: 32 см2.
Задача 44 (рис. 238)
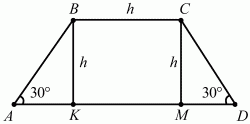
Решение. Проведём высоты трапеции ВК и СМ. Мы получили два прямоугольных треугольника АВК и CMD, в которых ?ВАК и ?CDM равны 30°; так как напротив угла в 30° лежит катет (ВК), равный половине гипотенузы (АВ), то АВ = 2h (ВК = h).
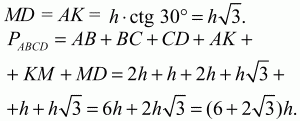
Задача 45 (рис. 239)
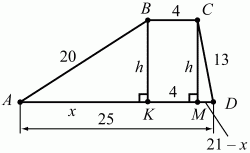
Решение. Пусть АК = х, высоты ВК и СМ равны h, тогда, так как КМ = ВС = 4, MD = 21 – х.
Из ?АВК и ?MCD по теореме Пифагора получим:
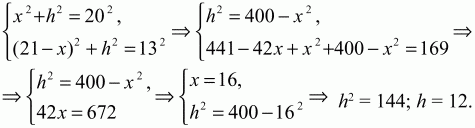
Ответ: 12.
Задача 46 (рис. 240)
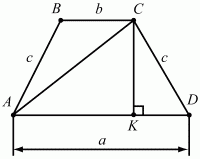
Решение. Проведем высоту трапеции СК (см. рис.). Тогда, KD = (a – b)/2; cos D = (a – b)/2c. Из ?ACD по теореме косинусов AC2= AD2+ CD2– 2AD ? CD ? cos D = a2+ с2– 2 ? а ? с ? (a – b)/2c = a2+ с2– a2+ аb = c2+ ab.
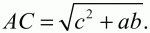
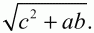
Задача 47 (рис. 241)
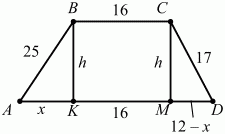
Решение. По содержанию задача идентична задаче 45. Однако, если мы начертим аналогичную трапецию и введем 25 соответствующие обозначения, то из чертежа получится система:
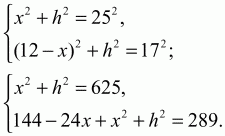
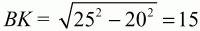
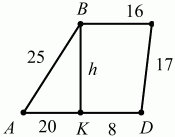
Ответ: 15 см.
Задача 48 (рис. 243)
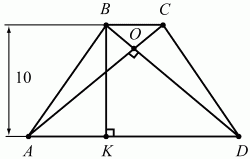
Решение. Так как ABCD – равнобедренная трапеция, то АО = OD и ?OAD = ?ODA = 45°. Проведём высоту BK (см. рис.). Раз ?ODA = 45°, то ?KBD – равнобедренный и KD = BK = 10.
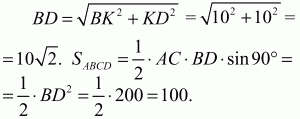
Задача 49 (рис. 244)
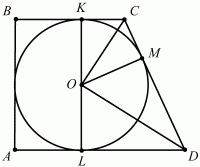
Решение. Пусть ABCD – данная в условиях задачи трапеция. Обозначим через точку М точку касания окружности со стороной CD трапеции ABCD. Соединив точки С и D с центром окружности, получим треугольник COD. Так как точка О равноудалена от прямых ВС и CD, то СО – биссектриса угла BCD и ?OCD = 1/2 ?BCD. Аналогично, ?ODC = 1/2 ?ADC. Поскольку BC||AD, то ?BCD + ?ADC = ?, следовательно, ?OCD + ?ODC = ?/2. Тогда ?COD = ?/2, т. е. треугольник COD – прямоугольный. По теореме Пифагора
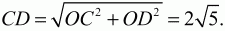
Отсюда
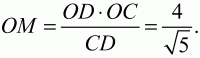
Ответ: 72/5.
Задача 53 (рис. 245)
Решение. Исходя из условия задачи, получим систему:
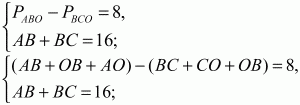
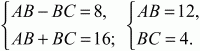
Задача 54 (рис. 246)
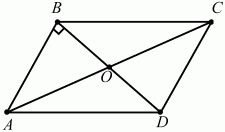
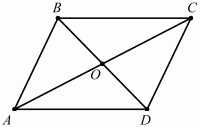
Решение. Так как по условию BD = 6, АС = 2?22, то, учитывая, что диагонали параллелограмма точкой пересечения делятся пополам, получим: АО = ?22, ВО = 3. Из прямоугольного треугольника АВО по теореме Пифагора
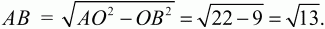
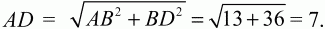
Задача 55 (рис. 247)
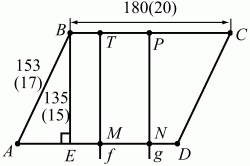
Решение. С целью упрощения арифметических вычислений уменьшим все линейные размеры в 9 раз. Тогда АВ = 17; ВС = 20; BE = 15. Линии f и g делят площадь трапеции на три равные по площади части (см. рис.). Проведем высоту BE. Последовательно находим: SABCD = AD ? BE = 20 ? 15 = 300 (в «новом формате»).
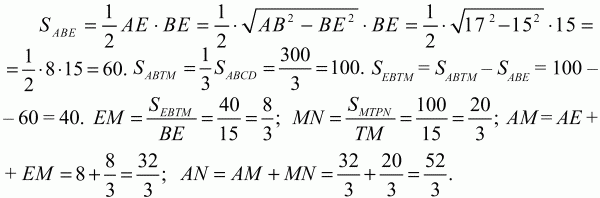
Ответ: 96; 156.
Задача 58 (рис. 248)
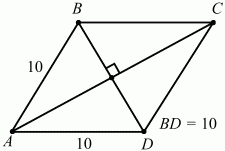
Решение. Пусть в ромбе ABCD BD = АВ = AD. Тогда ?ABD – равносторонний и АВ = ВС = 10, ?BAD = 60°, ?АВС = 120°. По теореме косинусов из треугольника ABC
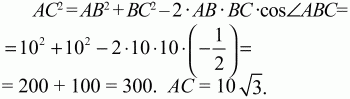
Задача 59 (рис. 249)
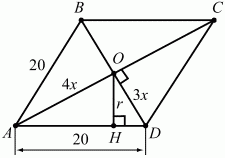
Решение. Начертим ромб ABCD. По условию
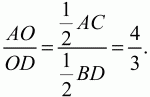
(4х)2+ (Зх)2= 202; 25х2= 400; х2= 16; х = 4. АО = 16; OD = 12. Осталось найти высоту ОН в ?AOD, которая и является радиусом вписанного круга. Из рисунка
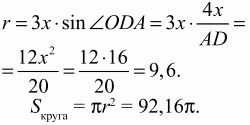
Задача 60 (рис. 250)
Решение. Во-первых, раз
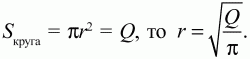
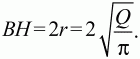
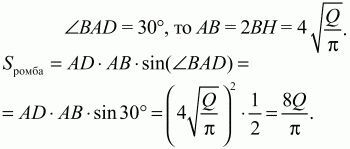
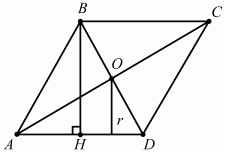
Задача 64 (рис. 251)
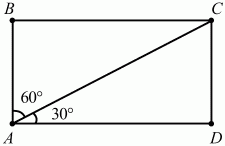
Решение. Так как ?BAC/?CAD = 1/2, а ?ВАС + ?CAD = 90°, то ?ВАС = 60°, ?CAD = 30°. Из ?ACD CD = AD ? tg 30° = AD/?3. Тогда CD: AD = 1:?3.
Ответ: 1:?3.
Задача 65 (рис. 252)
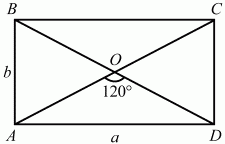
Решение. Пусть AD = а, АВ = b. По условию SABCD = а ? b = 9?3.
Так как ?AOD = 120°, то ?BOA = 60°. Значит, ?АОВ – равносторонний и OB = b; BD = 2b. Из ?ABD а2+ b2= (2b)2; а = ?3b. ?3b ? b = 9?3; b = 3; а = 3?3.
Ответ: 3 см; 3?3 см.
Задача 66 (рис. 253)
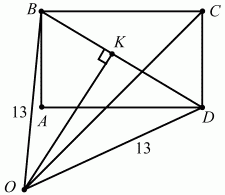
Решение. Для определённости будем считать, что АВ < AD. Так как AB ? AD = 48 и АВ2+ AD2= BD2= 100, то AD = 8, АВ = 6. Поскольку OB = OD = 13 > BD, то точка О лежит вне круга с диаметром BD и потому вне прямоугольника. Пусть она находится по ту же сторону от диагонали BD, что и точка А. Тогда требуется найти ОС. Обозначим ?OBD через ? и ?DВС через ?. Чтобы найти угол ?, опустим из точки О на диагональ BD перпендикуляр ОК. Получим ВК = KD = 1/2BD. Из прямоугольного ?ОВК следует:
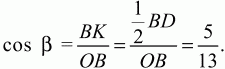
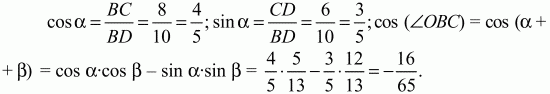

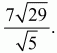
Задача 70 (рис. 254)
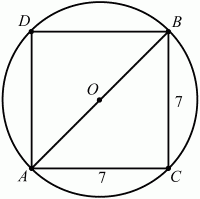
Решение. Как видно из рисунка, диаметр окружности d совпадает с диагональю квадрата АВ. По теореме Пифагора
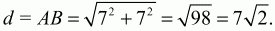
Задача 71 (рис. 255)
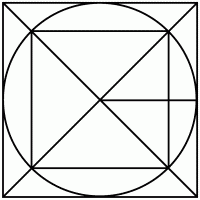
Решение. Пусть сторона малого квадрата а, тогда диаметр d = 2Rкруга круга равен диагонали малого квадрата, т. е.
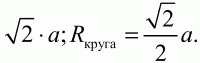

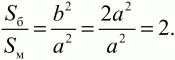
Задача 72 (рис. 256)
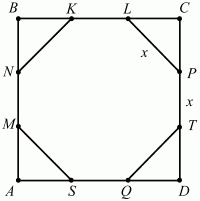
Решение. MNKLPTQS – правильный восьмиугольник (см. рис.). Пусть РТ = х, тогда
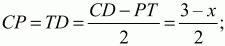
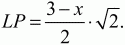
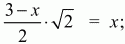
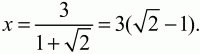
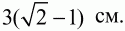
Задача 73 (рис. 257)
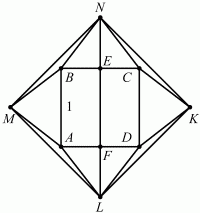
Решение. Очевидно, что MNKL – квадрат. Его диагональ NL = NE + FL + EF = 2NE + EF = 2NE + 1 (см. рис.). Так как NE – высота в равностороннем треугольнике BNC, то
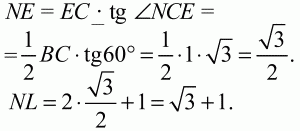
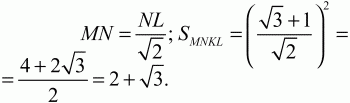
Задача 76 (рис. 258)
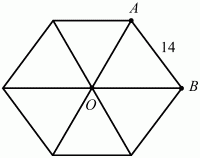
Решение. Можно, конечно, пуститься в достаточно длинные арифметические вычисления, но мы покажем самое простое и красивое решение. Раз площадь большого треугольника равна площади шестиугольника, то площадь этого треугольника в 6 раз больше площади треугольника ОАВ. А поскольку площадь правильного треугольника пропорциональна квадрату стороны, то его сторона в ?6 раз больше стороны АВ, т. е. сторона его будет равна 14?6.
Ответ: 14?6.
Задача 77 (рис. 259)
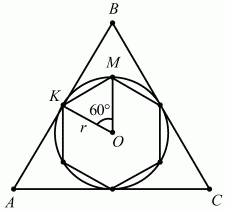
Решение. Пусть сторона равностороннего треугольника АВ = a;
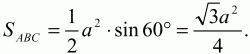
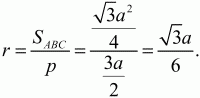
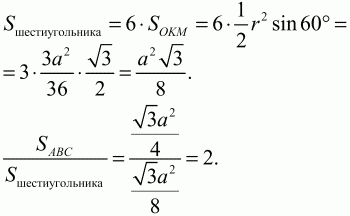
Задача 78 (рис. 260)
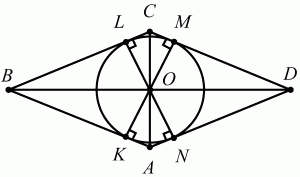
Решение. Пусть ABCD – данный четырёхугольник. Обозначим К, L, М, N – точки касания окружности соответственно со сторонами АВ, ВС, CD, AD четырёхугольника ABCD. Соединим эти точки с центром О. Треугольники АОК, AON, CLO, СМО – равны, как имеющие равные гипотенузы и катеты: у них АО = ОС по условию и КО = OL = ОМ = ON = r, где r – радиус окружности, вписанной в четырёхугольник ABCD. Аналогично доказывается, что равны треугольники КОВ, BOL, DON и DOM. Из равенства треугольников имеем, что ?КОВ = ?BOL = ?NOD = ?DOM, а также ?АОК = ?LOC = ?AON = ?СОМ. Значит, ?AON + ?NOD = ?АОК + ?КОВ = ?BOL + ?LOC = ?СОМ + ?MOD. Так как ?АОВ = ?АОК + ?КОВ, ?ВОС = ?BOL + ?LOC, ?COD = ?СОМ + ?MOD, ?AOD = ?AON + ?NOD, то ?АОВ = ?ВОС = ?COD = ?AOD, и поскольку в сумме они составляют 360°, то каждый из них равен 90°. По теореме Пифагора из треугольника АОВ находим, что
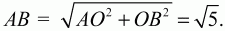
Ответ: 4?5.
Задача 85 (рис. 261)
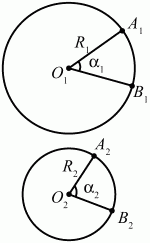
Решение. Составим пропорции: ?10? длина дуги А1В1 = 1.
360° ? длина окружности 2?R1. Отсюда
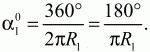
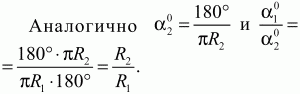
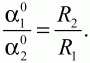
Задача 86 (рис. 262)
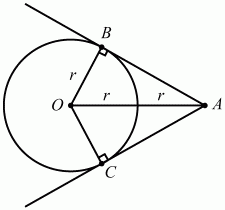
Решение. Так как ОА = 2r, то из прямоугольного треугольника ОBА имеем: ?ВАО = 30° (гипотенуза ОА в 2 раза больше катета OB) и ?ВАС = 60°.
Ответ: 60°
Задача 87 (рис. 263)
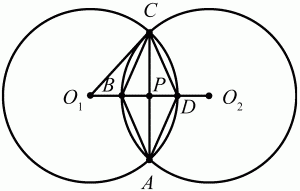
Решение. Так как BD = 6, АС = 12, то PD = 3; CP = 6 (см. рис.).