Страница:
Решение. Повернём треугольник АСМ вокруг точки С на 60°. Тогда точка А перейдёт в точку В, точка М – в некоторую точку D, треугольник АСМ – в треугольник BCD. При этом CD = СМ и ?MCD = 60°, следовательно, треугольник CDM – равносторонний, а значит, и ?CDM = ?DMC = 60°. С помощью поворота получен вспомогательный треугольник BDM. Заметим, что BD = AM = 1, ВМ = ?3, DM = CM = 2. Значит, треугольник BDM прямоугольный (ведь BM2+ BD2= (?3)2+ 12= DM2), ?DBM = 90° и ?BMD = 30° (противолежащий катет BD равен половине гипотенузы MD). Далее вычислим угол ВМС. ?ВМС = ?BMD + ?DMC = 30° + 60° = 90°. Применив теорему Пифагора к треугольнику ВСМ, найдём, что
Задачи для самостоятельного решения
146. Доказать, что медиана треугольника меньше полусуммы заключающих ее сторон. (1)147. Туристы находятся на острове «А». Им надо прибыть на остров «В», – при этом сначала побывав на обоих берегах реки. Каков будет их кратчайший маршрут (рис. 204)? (2)
148. Средняя линия трапеции равна 4; отрезок, соединяющий середины оснований, равен 1; углы при основании трапеции равны 40° и 50°. Найдите длины оснований трапеции. (3)
2.10. Задачи, решаемые координатным и векторным методами
Вообще говоря, в данном случае речь идет не о частных идеях решения определенного класса задач, а об универсальных методах решения самых разнообразных геометрических проблем.
Суть метода состоит в том, что для решения задач вводится система координат (прямоугольная или аффинная), пишутся необходимые уравнения прямых, других фигур, по известным формулам находятся длины и углы.
Решение. АВ = (3; 4); CD = (3; 4). Противоположные стороны четырёхугольника, таким образом, равны и параллельны. Значит, ABCD – параллелограмм.
Ответ: ABCD – параллелограмм.
150. В треугольнике ABC точка М – точка пересечения медиан. Выразите вектор AM через вектора АВ и АС (рис. 205). (2)
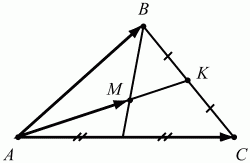Рис. 205.
Решение. Медианы точкой пересечения делятся в отношении 2:1, считая от вершины, поэтому
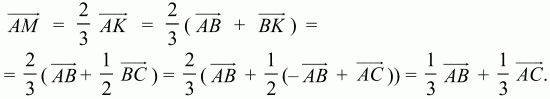Задачу можно решить проще, если достроить треугольник ABC до параллелограмма ABDC, тогда AM = 2/3 АК, но АК = 1/2 AD = 1/2 (АВ + АС). Отсюда сразу получаем, что AM = 1/3(АВ + АС).
Ответ: 1/3(АВ + АС).
151. В прямоугольнике ABCD точки М и N – середины сторон АВ и ВС. Точка О – точка пересечения AN и DM. Найдите AO/ON (рис. 206). (2)
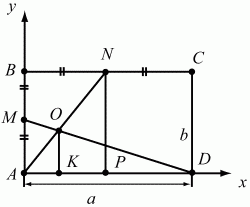Рис. 206.
Решение. Решим задачу аналитическим путём. Пусть А(0; 0); D (a; 0); B(0; b), тогда M(0; b/2); N(a/2; b). Напишем уравнения прямых AN и MD.
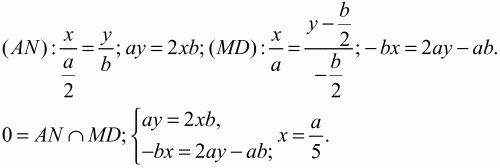Точка О будет иметь координаты:
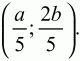
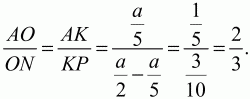Ответ: 2:3.
152. ВМ: МС = 3:1, АК = КВ. Найдите: SAKO/SABC (рис. 207). (3)
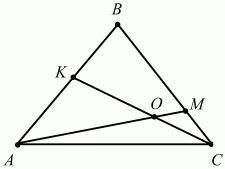Рис. 207.
Решение. См. задачу 105 (с. 88). Тогда мы решили её, применив теорему о пропорциональных отрезках. Здесь мы применим векторный подход и метод неопределенных коэффициентов.
Пусть ВА = а, ВС = b, АО = х ? AM, КО = у ? КС, тогда АО + ОК = АК, х ? АМ + (-у ? КС) = -1/2а.
Так как AM = AB + ВМ = – ВА + 3/4ВС = – а + 3/4b и КС = KB + ВС = -1/2ВА + ВС = -1/2а + b, то с учётом этого получаем уравнение: хAM + (-уКС) = -1/2а или х(-а + 3/4b) – у(-1/2а + b) = -1/2а. Приравнивая к нулю коэффициенты при векторах а и b, стоящих в левой и правой частях уравнения, получим систему:
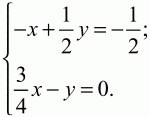х = 4/5, у = 3/5;
Итак,
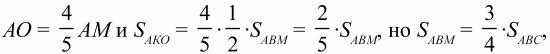значит,
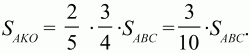Ответ: 3/10.
153. В выпуклом четырёхугольнике ABCD диагонали АС и BD пересекаются в точке F. Известно, что AF = CF = 2, BF = 1, DF = 4, ?BFC = ?/3.
Найти косинус угла между векторами АВ и DC (рис. 208). (3)
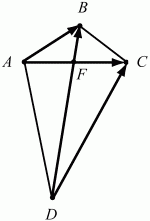Рис. 208.
Решение:
Пусть ? – искомый угол между векторами АВ и DC тогда
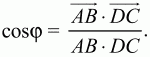Пользуясь свойствами скалярного произведения векторов и условиями задачи, вычислим АВ, DC и АВ ? DC. Так как
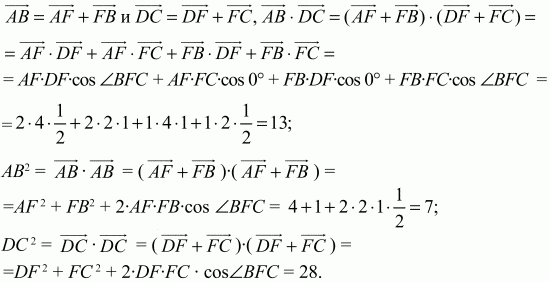Теперь получаем, что
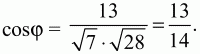Ответ: 13/14.
155. Продолжения сторон AD и ВС четырёхугольника ABCD пересекаются в точке Р. Точки М и N – середины сторон АВ и CD. Доказать, что если прямая MN проходит через точку Р, то ABCD – трапеция. (3)
156. Дан равнобедренный треугольник ABC, в котором проведены высота CD и перпендикуляр DE к боковой стороне ВС. Точка M – середина отрезка DE. Доказать, что отрезки АЕ и СМ перпендикулярны. (3)
157. Доказать, что для треугольника ABC и любой точки Р выполняется неравенство:
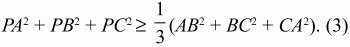
Суть метода состоит в том, что для решения задач вводится система координат (прямоугольная или аффинная), пишутся необходимые уравнения прямых, других фигур, по известным формулам находятся длины и углы.
Примеры решения задач
149. Даны точки А(-2; 1); В(1; 5); С(3; -2); D(6; 2). Является ли четырёхугольник ABCD параллелограммом? Ответ: обоснуйте. (1)Решение. АВ = (3; 4); CD = (3; 4). Противоположные стороны четырёхугольника, таким образом, равны и параллельны. Значит, ABCD – параллелограмм.
Ответ: ABCD – параллелограмм.
150. В треугольнике ABC точка М – точка пересечения медиан. Выразите вектор AM через вектора АВ и АС (рис. 205). (2)
Решение. Медианы точкой пересечения делятся в отношении 2:1, считая от вершины, поэтому
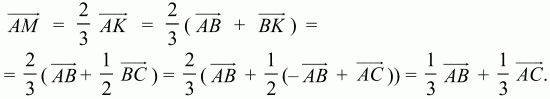
Ответ: 1/3(АВ + АС).
151. В прямоугольнике ABCD точки М и N – середины сторон АВ и ВС. Точка О – точка пересечения AN и DM. Найдите AO/ON (рис. 206). (2)
Решение. Решим задачу аналитическим путём. Пусть А(0; 0); D (a; 0); B(0; b), тогда M(0; b/2); N(a/2; b). Напишем уравнения прямых AN и MD.
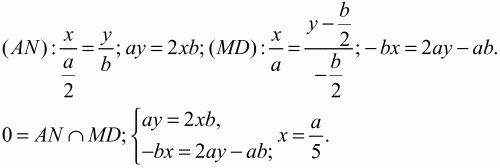
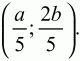
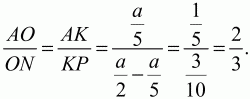
152. ВМ: МС = 3:1, АК = КВ. Найдите: SAKO/SABC (рис. 207). (3)
Решение. См. задачу 105 (с. 88). Тогда мы решили её, применив теорему о пропорциональных отрезках. Здесь мы применим векторный подход и метод неопределенных коэффициентов.
Пусть ВА = а, ВС = b, АО = х ? AM, КО = у ? КС, тогда АО + ОК = АК, х ? АМ + (-у ? КС) = -1/2а.
Так как AM = AB + ВМ = – ВА + 3/4ВС = – а + 3/4b и КС = KB + ВС = -1/2ВА + ВС = -1/2а + b, то с учётом этого получаем уравнение: хAM + (-уКС) = -1/2а или х(-а + 3/4b) – у(-1/2а + b) = -1/2а. Приравнивая к нулю коэффициенты при векторах а и b, стоящих в левой и правой частях уравнения, получим систему:
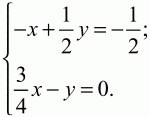
Итак,
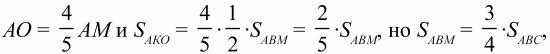
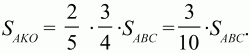
153. В выпуклом четырёхугольнике ABCD диагонали АС и BD пересекаются в точке F. Известно, что AF = CF = 2, BF = 1, DF = 4, ?BFC = ?/3.
Найти косинус угла между векторами АВ и DC (рис. 208). (3)
Решение:
Пусть ? – искомый угол между векторами АВ и DC тогда
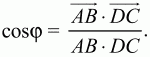
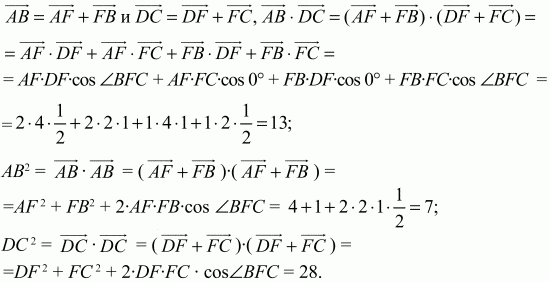
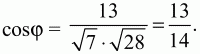
Задачи для самостоятельного решения
154. Найдите геометрическое место точек, равноудалённых от данной прямой и данной точки. (2)155. Продолжения сторон AD и ВС четырёхугольника ABCD пересекаются в точке Р. Точки М и N – середины сторон АВ и CD. Доказать, что если прямая MN проходит через точку Р, то ABCD – трапеция. (3)
156. Дан равнобедренный треугольник ABC, в котором проведены высота CD и перпендикуляр DE к боковой стороне ВС. Точка M – середина отрезка DE. Доказать, что отрезки АЕ и СМ перпендикулярны. (3)
157. Доказать, что для треугольника ABC и любой точки Р выполняется неравенство:
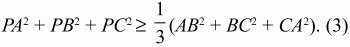
2.11. Разные задачи
Примеры решения задач
158. Можно ли утверждать, что треугольники равны по двум сторонам и медиане, проведенной к одной из этих сторон? Ответ: обоснуйте (рис. 209). (1)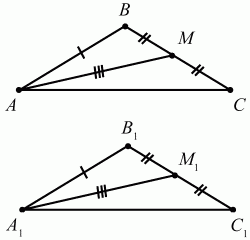
Решение. Рассмотрим треугольники ABC и А1В1C1. Пусть AB = A1B1, BC = B1C1,AM = A1M1 (см. рис). Так как ВС = В1С1, то ВМ = В1М1 ?АВМ = ?A1B1M1 (по трём сторонам), значит, ?В = ?B1. В этом случае ?ABC = ?A1B1C1 по двум сторонам и углу между ними.
Ответ: да.
159. Определите острые углы прямоугольного треугольника, если медиана, проведённая к его гипотенузе, делит прямой угол в отношении 2:1 (рис. 210). (1)
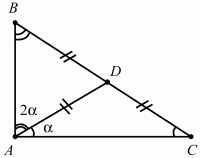
Решение. Нарисуем треугольник ABC, где ?ВАС = 3? = 90°. Медиана AD равна длинам BD и CD, так как D – середина гипотенузы, а, значит, является центром описанной около треугольника окружности. Пусть для определённости ?BAD = 2?, ?DAC =?. Очевидно, что 2? + ? = 90°, ? = 30°. Учитывая, что треугольники BDA и DAC – равнобедренные, получаем:?В = 2? = 60°, ?С = ? = 30°.
Ответ: 60°, 30°.
160. Дан произвольный четырёхугольник ABCD. Точки М, N, Р, Q – середины его сторон. Докажите, что MNPQ – параллелограмм (рис. 211). (1)
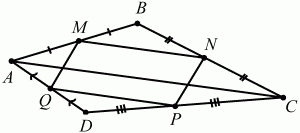
Решение. Из условия задачи и чертежа видно, что MN – средняя средняя линия ?ABC и QP средняя линия ?ACD. Поэтому MN = 1/2АС и MN||AC; QP = 1/2АС и QP||АС. В итоге получаем, что MN = QP и MN||QP. Поэтому, по признаку параллелограмма четырёхугольник MNPQ – параллелограмм.
161. Диагонали АС и BD трапеции ABCD пересекаются в точке О. Докажите, что треугольник АОВ и COD имеют одинаковые площади (рис. 212). (2)
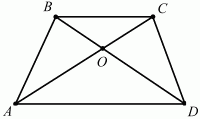
Решение. Обозначим через h высоту трапеции. Запишем равенства:
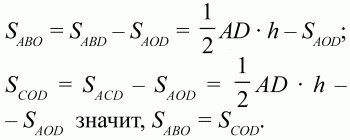
162. Стороны треугольника образуют арифметическую прогрессию. Доказать, что радиус окружности, вписанной в треугольник, равен 1/3 высоты, проведённой к средней по величине стороне треугольника. (3)
Решение. Пусть стороны а, b, с треугольника ABC образуют арифметическую прогрессию с разностью d. Будем считать, что а ? b ? с. тогда a = b – d, c = b + d, периметр Р = 2р = 3b.
Воспользуемся формулой r = S/P, получим r = 2S/3b. А так как S = 1/2bhb, то r = 1/3hb.
Задачи для самостоятельного решения
163. Диагонали трапеции делят её среднюю линию на три равные части. Как относятся основания этой трапеции? (1)164. Докажите, что середины сторон равнобокой трапеции являются вершинами ромба. (1)
165. В параллелограмме, смежные стороны которого не равны, проведены биссектрисы четырех углов. Докажите, что при их пересечении образуется прямоугольник. (2)
166. Площадь четырёхугольника равна S. Найдите площадь параллелограмма, стороны которого равны и параллельны диагоналям четырёхугольника. (2)
167. Докажите, что в параллелограмме ABCD расстояния от любой точки диагонали АС до прямых ВС и CD обратно пропорциональны длинам этих сторон. (2)
168. В выпуклом четырёхугольнике длины диагоналей равны одному и двум метрам. Найти площадь четырёхугольника, зная, что длины отрезков, соединяющих середины его противоположных сторон, равны. (1)
Глава 3
Билеты по геометрии
§ 1. Экзаменационный комплект № 1 (зачётная работа)
Билет № 1
1. Признаки параллельности прямых (формулировки и примеры).
2. Решение треугольника по стороне и двум углам.
3. Углы ADC и ABC вписаны в окружность, ?ABC = 74°. Найдите градусную меру ?ADC (рис. 213).
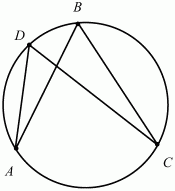Рис. 213.
4. Дуги А1В1 и А2В2 равной длины 1 принадлежат разным окружностям с радиусами R1 и R2. Найдите отношение градусных мер центральных углов, соответствующих этим дугам.
2. Решение треугольника по стороне и двум углам.
3. Углы ADC и ABC вписаны в окружность, ?ABC = 74°. Найдите градусную меру ?ADC (рис. 213).
4. Дуги А1В1 и А2В2 равной длины 1 принадлежат разным окружностям с радиусами R1 и R2. Найдите отношение градусных мер центральных углов, соответствующих этим дугам.
Билет № 2
1. Свойство углов, образованных при пересечении двух параллельных прямых третьей прямой (формулировки и примеры).
2. Решение треугольника по двум сторонам и углу между ними.
3. В треугольнике ABC отмечены точки D и Е, которые являются серединами сторон АВ и ВС соответственно. Найдите периметр четырёхугольника ADEC, если АВ = 24 см, ВС = 32 см и АС = 44 см.
4. Расстояние от точки А до точек В и С равны 3 см и 14 см соответственно, а расстояния от точки D до точек В и С равны 5 см и 6 см соответственно. Докажите, что точки А, В, С и D лежат на одной прямой.
2. Решение треугольника по двум сторонам и углу между ними.
3. В треугольнике ABC отмечены точки D и Е, которые являются серединами сторон АВ и ВС соответственно. Найдите периметр четырёхугольника ADEC, если АВ = 24 см, ВС = 32 см и АС = 44 см.
4. Расстояние от точки А до точек В и С равны 3 см и 14 см соответственно, а расстояния от точки D до точек В и С равны 5 см и 6 см соответственно. Докажите, что точки А, В, С и D лежат на одной прямой.
Билет № 3
1. Третий признак равенства треугольников (формулировки и пример).
2. Теорема об углах, вписанных в окружность.
3. Найдите площадь круга, вписанного в правильный шестиугольник, сторона которого равна 4 см.
4. Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям трапеции и равен полуразности оснований.
2. Теорема об углах, вписанных в окружность.
3. Найдите площадь круга, вписанного в правильный шестиугольник, сторона которого равна 4 см.
4. Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям трапеции и равен полуразности оснований.
Билет № 4
1. Теорема о сумме углов треугольника (формулировка и пример).
2. Решение треугольника по трём сторонам.
3. В трапеции ABCD с основаниями AD = 12 см и ВС = 8 см проведена средняя линия ML, которая пересекает диагональ АС в точке К. Чему равны отрезки МК и KL?
4. Из одной точки к двум касающимися внешним образом окружностям проведены три касательные, причем одна из них проходит через точку касания окружностей. Докажите, что касательные равны.
2. Решение треугольника по трём сторонам.
3. В трапеции ABCD с основаниями AD = 12 см и ВС = 8 см проведена средняя линия ML, которая пересекает диагональ АС в точке К. Чему равны отрезки МК и KL?
4. Из одной точки к двум касающимися внешним образом окружностям проведены три касательные, причем одна из них проходит через точку касания окружностей. Докажите, что касательные равны.
Билет № 5
1. Определение синуса острого угла прямоугольного треугольника. Пример его применения для решения прямоугольных треугольников.
2. Свойство углов равнобедренного треугольника.
3. Из точки D, лежащей на катете АС прямоугольного треугольника ABC, опущен на гипотенузу СВ перпендикуляр DE. Найдите отрезок CD, если СВ = 15 см, АВ = 9 см и СЕ = 4 см.
4. Точки К и L – середины сторон AD и ВС параллелограмма ABCD. Докажите, что прямые AL и СК делят диагональ BD на три равные части.
2. Свойство углов равнобедренного треугольника.
3. Из точки D, лежащей на катете АС прямоугольного треугольника ABC, опущен на гипотенузу СВ перпендикуляр DE. Найдите отрезок CD, если СВ = 15 см, АВ = 9 см и СЕ = 4 см.
4. Точки К и L – середины сторон AD и ВС параллелограмма ABCD. Докажите, что прямые AL и СК делят диагональ BD на три равные части.
Билет № 6
1. Определение косинуса острого угла прямоугольного треугольника. Пример его применения для решения прямоугольных треугольников.
2. Признак равнобедренного треугольника.
3. Прямая, параллельная основанию равнобедренного треугольника ABC, пересекает боковые стороны АВ и АС в точках М и N. Докажите, что треугольник MAN – равнобедренный.
4. В прямоугольный равнобедренный треугольник вписан прямоугольник так, что угол прямоугольника совпадает с углом при вершине треугольника, а вершина противолежащего угла лежит на гипотенузе. Докажите, что периметр прямоугольника есть величина постоянная для данного треугольника.
2. Признак равнобедренного треугольника.
3. Прямая, параллельная основанию равнобедренного треугольника ABC, пересекает боковые стороны АВ и АС в точках М и N. Докажите, что треугольник MAN – равнобедренный.
4. В прямоугольный равнобедренный треугольник вписан прямоугольник так, что угол прямоугольника совпадает с углом при вершине треугольника, а вершина противолежащего угла лежит на гипотенузе. Докажите, что периметр прямоугольника есть величина постоянная для данного треугольника.
Билет № 7
1. Определение тангенса острого угла прямоугольного треугольника. Пример его применения для решения прямоугольных треугольников.
2. Свойство медианы равнобедренного треугольника.
3. В параллелограмме ABCD проведена диагональ BD и отрезок
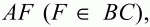пересекающий BD в точке О. Известно, что ВО = 6 см, OD = 18 см. Определите сторону параллелограмма AD, если FB = 4 см.
4. Докажите, что в ромб можно вписать окружность.
2. Свойство медианы равнобедренного треугольника.
3. В параллелограмме ABCD проведена диагональ BD и отрезок
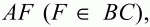
4. Докажите, что в ромб можно вписать окружность.
Билет № 8
1. Теорема косинусов. Пример ее применения для решения треугольников.
2. Окружность, вписанная в треугольник. Теорема о центре окружности, вписанной в треугольник.
3. В треугольниках ADB и AFC: AD = DB, AF = FC. Докажите, что DB||FC (рис. 214).
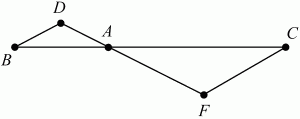Рис. 214.
4. Докажите, что если диагонали четырёхугольника ABCD взаимно перпендикулярны, то AB2+ CD2= BС2+ AD 2.
2. Окружность, вписанная в треугольник. Теорема о центре окружности, вписанной в треугольник.
3. В треугольниках ADB и AFC: AD = DB, AF = FC. Докажите, что DB||FC (рис. 214).
4. Докажите, что если диагонали четырёхугольника ABCD взаимно перпендикулярны, то AB2+ CD2= BС2+ AD 2.
Билет № 9
1. Теорема синусов. Пример её применения для решения треугольников.
2. Окружность, описанная около треугольника. Теорема о центре окружности, описанной около треугольника.
3. Найдите углы равнобедренного треугольника, если внешний угол при основании равен 112°.
4. Углы при основании трапеции равны 60° и 45°, высота трапеции равна 6 см. Найдите боковые стороны трапеции.
2. Окружность, описанная около треугольника. Теорема о центре окружности, описанной около треугольника.
3. Найдите углы равнобедренного треугольника, если внешний угол при основании равен 112°.
4. Углы при основании трапеции равны 60° и 45°, высота трапеции равна 6 см. Найдите боковые стороны трапеции.
Билет № 10
1. Построение с помощью циркуля и линейки треугольника по трем сторонам.
2. Сложение векторов. Свойства сложения векторов.
3. Сумма углов выпуклого многоугольника равна сумме его внешних углов, взятых по одному при каждой вершине. Найдите число сторон этого многоугольника.
4. В прямоугольном треугольнике ABC (?С – прямой) проведена высота CD. Докажите, что если ?СВА = 30°, то АВ: BD = 4:3.
2. Сложение векторов. Свойства сложения векторов.
3. Сумма углов выпуклого многоугольника равна сумме его внешних углов, взятых по одному при каждой вершине. Найдите число сторон этого многоугольника.
4. В прямоугольном треугольнике ABC (?С – прямой) проведена высота CD. Докажите, что если ?СВА = 30°, то АВ: BD = 4:3.
Билет № 11
1. Построение с помощью циркуля и линейки угла, равного данному.
2. Умножение вектора на число. Свойства произведения вектора на число.
3. Радиус окружности равен 7 см. Найдите периметр описанного около нее правильного четырёхугольника.
4. Докажите, что в равностороннем треугольнике расстояние от точки пересечения двух биссектрис до стороны в два раза меньше расстояния от этой же точки до вершины.
2. Умножение вектора на число. Свойства произведения вектора на число.
3. Радиус окружности равен 7 см. Найдите периметр описанного около нее правильного четырёхугольника.
4. Докажите, что в равностороннем треугольнике расстояние от точки пересечения двух биссектрис до стороны в два раза меньше расстояния от этой же точки до вершины.
Билет № 12
1. Построение с помощью циркуля и линейки биссектрисы угла.
2. Неравенство треугольника.
3. В параллелограмме сумма двух противолежащих углов равна 132°. Найдите градусную меру каждого из этих углов.
4. На диаметре окружности построен равносторонний треугольник. Определите градусную меру дуг, на которые стороны треугольника делят полуокружность.
2. Неравенство треугольника.
3. В параллелограмме сумма двух противолежащих углов равна 132°. Найдите градусную меру каждого из этих углов.
4. На диаметре окружности построен равносторонний треугольник. Определите градусную меру дуг, на которые стороны треугольника делят полуокружность.
Билет № 13
1. Построение с помощью циркуля и линейки перпендикулярной прямой.
2. Признаки подобия треугольников (доказательство одного из них).
3. Прямоугольник вписан в окружность радиуса 5 см. Одна из его сторон равна 8 см. Найдите другие стороны прямоугольника.
4. Угол DFG вписан в окружность с центром в точке О. Найдите градусную меру ?DOG, если ?DFG = 150° (рис. 215).
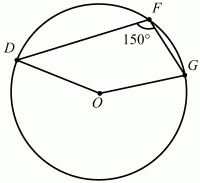Рис. 215.
2. Признаки подобия треугольников (доказательство одного из них).
3. Прямоугольник вписан в окружность радиуса 5 см. Одна из его сторон равна 8 см. Найдите другие стороны прямоугольника.
4. Угол DFG вписан в окружность с центром в точке О. Найдите градусную меру ?DOG, если ?DFG = 150° (рис. 215).
Билет № 14
1. Деление отрезка пополам с помощью циркуля и линейки.
2. Теорема о средней линии треугольника.
3. Диагонали ромба равны 10 см и 24 см. Найдите стороны ромба.
4. Периметр равностороннего треугольника равен 36 см, а периметр равнобедренного – 40 см. Найдите стороны данных треугольников, если они имеют общее основание.
2. Теорема о средней линии треугольника.
3. Диагонали ромба равны 10 см и 24 см. Найдите стороны ромба.
4. Периметр равностороннего треугольника равен 36 см, а периметр равнобедренного – 40 см. Найдите стороны данных треугольников, если они имеют общее основание.
Билет № 15
1. Свойства параллелограмма (формулировки и примеры).
2. Теорема о внешнем угле треугольника.
3. В треугольнике AEF проведена биссектриса AD угла А, на сторонах угла от его вершины отложены равные отрезки АВ и АС. Докажите равенство треугольников BAD и CAD.
4. Около окружности описана равнобокая трапеция, у которой боковая сторона точкой касания делится на отрезки 4 см и 9 см. Найдите площадь трапеции.
2. Теорема о внешнем угле треугольника.
3. В треугольнике AEF проведена биссектриса AD угла А, на сторонах угла от его вершины отложены равные отрезки АВ и АС. Докажите равенство треугольников BAD и CAD.
4. Около окружности описана равнобокая трапеция, у которой боковая сторона точкой касания делится на отрезки 4 см и 9 см. Найдите площадь трапеции.
Билет № 16
1. Теорема о средней линии трапеции (формулировка и пример).
2. Теорема о сумме углов выпуклого многоугольника.
3. Даны две концентрические окружности с центром в точке О. АС и BD – диаметры этих окружностей. Докажите, что ?АВО = ?CDO.
4. Один из углов равнобедренного треугольника 120°. Найдите отношение сторон этого треугольника.
2. Теорема о сумме углов выпуклого многоугольника.
3. Даны две концентрические окружности с центром в точке О. АС и BD – диаметры этих окружностей. Докажите, что ?АВО = ?CDO.
4. Один из углов равнобедренного треугольника 120°. Найдите отношение сторон этого треугольника.
Билет № 17
1. Формулы для радиусов вписанных и описанных окружностей правильного n-угольника (формулы и примеры).
2. Свойство диагоналей ромба.
3. BD – медиана равнобедренного треугольника ABC (АВ = ВС). Найдите ее длину, если периметр треугольника ABC равен 50 см, а периметр ?ABD равен 30 см.
4. Точки М, N и P лежат соответственно на сторонах АВ, ВС и АС треугольника ABC, причем MN||AC, NP||АВ. Найдите стороны четырёхугольника AMNP, если АВ = 16 см, АС = 24 см, PN: MN = 2:3.
2. Свойство диагоналей ромба.
3. BD – медиана равнобедренного треугольника ABC (АВ = ВС). Найдите ее длину, если периметр треугольника ABC равен 50 см, а периметр ?ABD равен 30 см.
4. Точки М, N и P лежат соответственно на сторонах АВ, ВС и АС треугольника ABC, причем MN||AC, NP||АВ. Найдите стороны четырёхугольника AMNP, если АВ = 16 см, АС = 24 см, PN: MN = 2:3.
Билет № 18
1. Формулы для радиусов вписанных и описанных окружностей правильного треугольника, правильного четырёхугольника, правильного шестиугольника (формулы и примеры).
2. Свойство диагоналей прямоугольника.
3. На сторонах угла Q отложены равные отрезки QR и QP. Через точки R и P проведена прямая. Определите ?QRP, если ?RPQ = 67°.
4. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна его основанию.
2. Свойство диагоналей прямоугольника.
3. На сторонах угла Q отложены равные отрезки QR и QP. Через точки R и P проведена прямая. Определите ?QRP, если ?RPQ = 67°.
4. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна его основанию.
Билет № 19
1. Формула длины окружности (формула и пример).
2. Первый признак равенства треугольников.
3. Найдите площадь квадрата, если его диагональ равна 5 см.
4. Сколько сторон имеет выпуклый многоугольник, у которого все углы равны, если сумма его внешних углов с одним из внутренних равна 468°?
2. Первый признак равенства треугольников.
3. Найдите площадь квадрата, если его диагональ равна 5 см.
4. Сколько сторон имеет выпуклый многоугольник, у которого все углы равны, если сумма его внешних углов с одним из внутренних равна 468°?
Билет № 20
1. Формулы площади треугольника (формулы и примеры).
2. Признаки параллелограмма.
3. Докажите, что общая хорда двух пересекающихся окружностей перпендикулярна линии центров.
4. Средняя линия описанной около окружности трапеции равна 4. Найдите периметр трапеции.
2. Признаки параллелограмма.
3. Докажите, что общая хорда двух пересекающихся окружностей перпендикулярна линии центров.
4. Средняя линия описанной около окружности трапеции равна 4. Найдите периметр трапеции.
Билет № 21
1. Формулы площади прямоугольника и параллелограмма (формулы и примеры).
2. Второй признак равенства треугольников.
3. На сколько увеличится или уменьшится длина окружности, если ее радиус увеличить на 10 см.
4. Докажите, что середины сторон равнобокой трапеции являются вершинами ромба.
2. Второй признак равенства треугольников.
3. На сколько увеличится или уменьшится длина окружности, если ее радиус увеличить на 10 см.
4. Докажите, что середины сторон равнобокой трапеции являются вершинами ромба.
Билет № 22
1. Формула площади трапеции (формула и пример).
2. Признаки равенства прямоугольных треугольников.
3. Даны точки А (1, -3) и В (2, 0). Найдите такую точку С (х, у), чтобы векторы АВ и СА были равны.
4. Точка касания окружности, вписанной в равнобедренный треугольник, делит боковую сторону на отрезки, равные 3 см и 4 см, считая от основания. Найдите периметр треугольника.
2. Признаки равенства прямоугольных треугольников.
3. Даны точки А (1, -3) и В (2, 0). Найдите такую точку С (х, у), чтобы векторы АВ и СА были равны.
4. Точка касания окружности, вписанной в равнобедренный треугольник, делит боковую сторону на отрезки, равные 3 см и 4 см, считая от основания. Найдите периметр треугольника.
Билет № 23
1. Формула площади круга (формула и пример).
2. Теорема Пифагора.
3. Докажите, что центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к основанию.
4. Найдите геометрическое место середин равных хорд окружности.
2. Теорема Пифагора.
3. Докажите, что центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к основанию.
4. Найдите геометрическое место середин равных хорд окружности.
§ 2. Экзаменационный комплект № 2 (базовый уровень)
Билет № 1
1. Равенство фигур. Признаки равенства треугольников (доказательство одного из них).
2. Критерий описанного около окружности четырёхугольника (без доказательства).
3. Точка С – середина отрезка АВ. Найдите длину отрезка АС в дециметрах, если АВ = 7 м 58 см.
4. В прямоугольнике ABCD AD = 12 см, CD = 5 см, О – точка пересечения диагоналей. Найдите
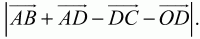5. В треугольнике ABC угол А = углу В = 75°. Найдите ВС, если площадь треугольника равна 36 см2.
2. Критерий описанного около окружности четырёхугольника (без доказательства).
3. Точка С – середина отрезка АВ. Найдите длину отрезка АС в дециметрах, если АВ = 7 м 58 см.
4. В прямоугольнике ABCD AD = 12 см, CD = 5 см, О – точка пересечения диагоналей. Найдите
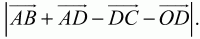
Билет № 2
1. Сумма углов треугольника (с доказательством). Вывод формулы суммы углов выпуклого n-угольника.
2. Критерий вписанного в окружность четырёхугольника (без доказательства).
3. Основания трапеции относятся как 2:3, а высота равна 6 см. площадь трапеции 60 см2. Найдите основания трапеции.
4. В прямоугольном треугольнике ABC АВ = 6 см, АС = 8 см. ВС = 10 см. Найдите расстояние:
а) от точки В до прямой АС;
б) от точки С до прямой АВ.
Может ли расстояние от точки А до прямой СВ быть равным 7 см?
5. Точка М принадлежит отрезку РК, причем РМ: МК = 2:1. Найдите координаты точки К, если координаты точек Р и М равны (6; 3) и (14; 9) соответственно.
2. Критерий вписанного в окружность четырёхугольника (без доказательства).
3. Основания трапеции относятся как 2:3, а высота равна 6 см. площадь трапеции 60 см2. Найдите основания трапеции.
4. В прямоугольном треугольнике ABC АВ = 6 см, АС = 8 см. ВС = 10 см. Найдите расстояние:
а) от точки В до прямой АС;
б) от точки С до прямой АВ.
Может ли расстояние от точки А до прямой СВ быть равным 7 см?
5. Точка М принадлежит отрезку РК, причем РМ: МК = 2:1. Найдите координаты точки К, если координаты точек Р и М равны (6; 3) и (14; 9) соответственно.
Билет № 3
1. Геометрическое место центров описанной около треугольника и вписанной в треугольник окружностей (с доказательством).
2. Площадь четырёхугольника (без вывода).
3. Даны треугольник ABC и точка М на отрезке ВС. Выразите:
а) вектор СВ через векторы АС и АВ;
б) вектор МА через векторы ВА и ВМ.
4. В ромбе ABCD, где угол А острый, BE и BF – высоты. Угол между диагональю BD и высотой BF равен 40°:
а) докажите, что BE = BF.
б) найдите углы ромба.
5. В треугольнике ABC точки F и М лежат соответственно на сторонах АВ и ВС, причем CF = AM, а угол MAC = углу FCA. Докажите, что треугольник ABC равнобедренный.
2. Площадь четырёхугольника (без вывода).
3. Даны треугольник ABC и точка М на отрезке ВС. Выразите:
а) вектор СВ через векторы АС и АВ;
б) вектор МА через векторы ВА и ВМ.
4. В ромбе ABCD, где угол А острый, BE и BF – высоты. Угол между диагональю BD и высотой BF равен 40°:
а) докажите, что BE = BF.
б) найдите углы ромба.
5. В треугольнике ABC точки F и М лежат соответственно на сторонах АВ и ВС, причем CF = AM, а угол MAC = углу FCA. Докажите, что треугольник ABC равнобедренный.
Билет № 4
1. Свойства параллелограмма (с доказательством).
2. Геометрическое введение синуса, косинуса, тангенса котангенса. Значения sin, cos, tg, ctg от углов 30°, 45°, 60°.
3. Прямой угол ADB разделен лучом DC на два угла, из которых один больше другого на 8°. Найдите градусные меры этих углов.
4. В равнобедренной трапеции ABCD угол А = 30°, угол ACD = 135°, AD = 20 см, ВС = 10 см:
а) докажите, что АС – биссектриса угла ВАС;
б) найдите периметр трапеции.
5. В треугольнике ABC АВ = 17 см, ВС = 25 см. Высота BD равна 15 см. Найдите площадь треугольника.
2. Геометрическое введение синуса, косинуса, тангенса котангенса. Значения sin, cos, tg, ctg от углов 30°, 45°, 60°.
3. Прямой угол ADB разделен лучом DC на два угла, из которых один больше другого на 8°. Найдите градусные меры этих углов.
4. В равнобедренной трапеции ABCD угол А = 30°, угол ACD = 135°, AD = 20 см, ВС = 10 см:
а) докажите, что АС – биссектриса угла ВАС;
б) найдите периметр трапеции.
5. В треугольнике ABC АВ = 17 см, ВС = 25 см. Высота BD равна 15 см. Найдите площадь треугольника.
Билет № 5
1. Свойства ромба, прямоугольника, квадрата (с доказательством).
2. Уравнение прямой (без вывода). Смысл коэффициента k в уравнении у = kx + b (без обоснования).
3. Периметр треугольника равен 35 см. Найдите отрезки, на которые биссектриса треугольника делит противоположную сторону, если две другие стороны треугольника равны 12 и 16 см.
4. Найдите радиус окружности, вписанной в треугольник со сторонами 20, 20 и 24 см.
5. Как изменится длина окружности, если площадь соответствующего ей круга уменьшится в 441 раз?
2. Уравнение прямой (без вывода). Смысл коэффициента k в уравнении у = kx + b (без обоснования).
3. Периметр треугольника равен 35 см. Найдите отрезки, на которые биссектриса треугольника делит противоположную сторону, если две другие стороны треугольника равны 12 и 16 см.
4. Найдите радиус окружности, вписанной в треугольник со сторонами 20, 20 и 24 см.
5. Как изменится длина окружности, если площадь соответствующего ей круга уменьшится в 441 раз?
Билет № 6
1. Теорема Фалеса (с доказательством).
2. Вектор. Действия над векторами. Базис на плоскости. Теорема о разложении вектора по базису (без доказательства).
3. Дана трапеция ABCD. Постройте фигуру, на которую отображается данная трапеция при центральной симметрии с центром А.
4. В треугольнике ABC CD – медиана. Найдите площадь треугольника BDC, если АС = 10 см, ВС = 20 см и угол АСВ = 135°.
5. На рисунке изображена окружность с центром О, АВ = DE. Докажите, что угол АОЕ равен углу BOD (рис. 216).
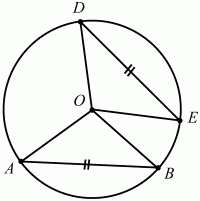Рис. 216.
2. Вектор. Действия над векторами. Базис на плоскости. Теорема о разложении вектора по базису (без доказательства).
3. Дана трапеция ABCD. Постройте фигуру, на которую отображается данная трапеция при центральной симметрии с центром А.
4. В треугольнике ABC CD – медиана. Найдите площадь треугольника BDC, если АС = 10 см, ВС = 20 см и угол АСВ = 135°.
5. На рисунке изображена окружность с центром О, АВ = DE. Докажите, что угол АОЕ равен углу BOD (рис. 216).
Билет № 7
1. Свойство средней линии треугольника и трапеции (с доказательством).
2. Длина окружности и площадь круга (без вывода).
3. На рис. 217 угол 1 = 67°, угол 2 = 127°, угол 4 = 67°. Найдите угол 3 (рис. 217).
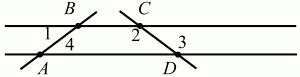Рис. 217.
4. Диагонали параллелограмма ABCD пересекаются в точке О. Найдите х, у, z, если:
а) АС = х ? АО; б) ВО = у ? DB; в) АВ = z ? CD.
5. В треугольнике ABC АВ = ВС, BD – высота. Через середину высоты проведена прямая, пересекающая стороны АВ и ВС в точках Е и F соответственно. Найдите EF, если BD = h, угол ABC = ?, угол BEF = ?.
2. Длина окружности и площадь круга (без вывода).
3. На рис. 217 угол 1 = 67°, угол 2 = 127°, угол 4 = 67°. Найдите угол 3 (рис. 217).
4. Диагонали параллелограмма ABCD пересекаются в точке О. Найдите х, у, z, если:
а) АС = х ? АО; б) ВО = у ? DB; в) АВ = z ? CD.
5. В треугольнике ABC АВ = ВС, BD – высота. Через середину высоты проведена прямая, пересекающая стороны АВ и ВС в точках Е и F соответственно. Найдите EF, если BD = h, угол ABC = ?, угол BEF = ?.
Билет № 8
1. Теорема Пифагора (с доказательством).
2. Пропорциональность отрезков хорд и секущих окружности (без вывода).
3. Найдите синус, косинус и тангенс острых углов А и В прямоугольного треугольника ABC, если АВ = 13 см, ВС = 12 см.
4. В прямоугольнике ABCD сторона AD равна 10 см. Расстояние от точки пересечения диагоналей до этой стороны равно 3 см. Найдите площадь прямоугольника.
5. В равнобедренном треугольнике ABC с основанием АС серединный перпендикуляр стороны АВ пересекает сторону ВС в точке Р. Найдите угол РАС, если угол ВСА = 65°.
2. Пропорциональность отрезков хорд и секущих окружности (без вывода).
3. Найдите синус, косинус и тангенс острых углов А и В прямоугольного треугольника ABC, если АВ = 13 см, ВС = 12 см.
4. В прямоугольнике ABCD сторона AD равна 10 см. Расстояние от точки пересечения диагоналей до этой стороны равно 3 см. Найдите площадь прямоугольника.
5. В равнобедренном треугольнике ABC с основанием АС серединный перпендикуляр стороны АВ пересекает сторону ВС в точке Р. Найдите угол РАС, если угол ВСА = 65°.
Билет № 9
1. Координаты на плоскости. Расстояние между точками (с выводом).
2. Признаки подобия треугольников (без доказательств).
3. Параллельны ли прямые a и b, изображенные на рисунке (рис. 218).
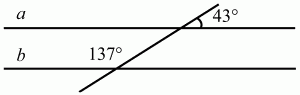Рис. 218.
4. В прямоугольном треугольнике с углом 30° и меньшим катетом – 6 см проведены средние линии. Найдите периметр треугольника, образованного средними линиями.
5. АВ и АС – касательные к окружности с центром О (С и В – точки касания). Найдите градусную меру меньшей из дуг ВС, если расстояние от центра окружности до точки А равно 8 см, а до хорды ВС – 6 см.
2. Признаки подобия треугольников (без доказательств).
3. Параллельны ли прямые a и b, изображенные на рисунке (рис. 218).
4. В прямоугольном треугольнике с углом 30° и меньшим катетом – 6 см проведены средние линии. Найдите периметр треугольника, образованного средними линиями.
5. АВ и АС – касательные к окружности с центром О (С и В – точки касания). Найдите градусную меру меньшей из дуг ВС, если расстояние от центра окружности до точки А равно 8 см, а до хорды ВС – 6 см.
Билет № 10
1. Уравнение фигуры. Уравнение окружности (с выводом).
2. Формула для радиуса вписанной в треугольник окружности (без вывода).
3. Найдите площадь равностороннего треугольника со стороной а = 2.
4. В параллелограмме две стороны равны 2 и 3 см, а один из углов 120°. Найдите длину меньшей диагонали параллелограмма.
5. Стороны треугольника равны 4 и 5, а угол между ними 60°. Найдите высоту h, опущенную на третью сторону треугольника.
2. Формула для радиуса вписанной в треугольник окружности (без вывода).
3. Найдите площадь равностороннего треугольника со стороной а = 2.
4. В параллелограмме две стороны равны 2 и 3 см, а один из углов 120°. Найдите длину меньшей диагонали параллелограмма.
5. Стороны треугольника равны 4 и 5, а угол между ними 60°. Найдите высоту h, опущенную на третью сторону треугольника.
Билет № 11
1. Скалярное произведение векторов. Угол между векторами (с выводом).
2. Формулы для радиуса описанной около треугольника окружности (без вывода).
3. В остроугольном треугольнике ABC высоты АА1 и ВВ1 пересекаются в точке О. Найдите угол ОСА, если угол BAС = 58°.
4. Длина стороны многоугольника равна 3 м, а длина сходственной стороны подобного ему многоугольника равна 48 дм. Найдите периметры этих многоугольников, если их разность составляет 9 м.
2. Формулы для радиуса описанной около треугольника окружности (без вывода).
3. В остроугольном треугольнике ABC высоты АА1 и ВВ1 пересекаются в точке О. Найдите угол ОСА, если угол BAС = 58°.
4. Длина стороны многоугольника равна 3 м, а длина сходственной стороны подобного ему многоугольника равна 48 дм. Найдите периметры этих многоугольников, если их разность составляет 9 м.