Страница:
Оценка спреда дефолта
Самый простой способ оценки спреда дефолта для каждого рейтингового класса – это нахождение выборки облигаций в пределах данного рейтингового класса и выяснение текущей рыночной процентной ставки по этим облигациям. Почему необходимо использовать выборку, а не просто одну облигацию? Облигация может быть ошибочно оценена или отнесена к ошибочной рейтинговой группе. Использование выборки уменьшает или даже полностью устраняет данную проблему. При составлении данной выборки следует пытаться сосредоточить внимание на наиболее ликвидных облигациях, обладающих как можно меньшим числом особых характеристик. Корпоративные облигации часто отличаются неликвидностью, а процентные ставки по ним могут не отражать текущие рыночные ставки. Присутствие особых характеристик у облигаций, таких как конвертируемость, может повлиять на ценообразование этих облигаций и, следовательно, на оценку процентных ставок по ним.
Как только определена выборка облигаций в пределах каждого рейтингового класса, необходимо оценить процентные ставки по этим облигациям. Существуют два широко используемых подхода. Первый заключается в оценке доходности облигации, т. е. представляет из себя купонную ставку, деленную на рыночную цену. Второй оценивает выплаты к истечению срока облигации, определяя приведенную стоимость купонов, а также номинальную стоимость облигации по рыночной цене. Как правило, выплаты к дате погашения оказываются наилучшей мерой рыночной процентной ставки по облигации.
Выяснив процентную ставку, соответствующую выборке облигаций, следует принять два решения. Первое относится к взвешиванию. Можно вычислить простую среднюю величину из процентных ставок по облигациям, входящим в выборку, или же взвешенную среднюю величину, связывая при этом веса с объемом торговли: более ликвидные облигации получают большие веса, чем менее ликвидные облигации. Второе решение относится к индексу казначейской ставки, поскольку средняя процентная ставка для определенного рейтингового класса сравнивается с этой ставкой для выяснения спреда дефолта. Как правило, срок истечения действия казначейской ценной бумаги должен соответствовать среднему сроку истечения корпоративной ценной бумаги, выбранной для оценки средней процентной ставки. Таким образом, для получения спреда по облигациям с рейтингом ВВВ средняя процентная ставка для пятилетних корпоративных облигаций с рейтингом ВВВ должна сравниваться со средней процентной ставкой для пятилетних казначейских бумаг.
Хотя такие издания, как Barron’s, исторически предоставляли процентные ставки по облигациям с наивысшими рейтингами (ВВВ или выше), сегодня ту же информацию по всем облигациям, имеющим рейтинги, дает все большее количество сетевых служб. Данные по 10-летним облигациям для таблицы 7.6 получены в одной из таких служб, работающей в режиме он-лайн, в начале 2001 г.
Детерминанты спреда дефолта
В таблице 7.6 представлена информация о спреде дефолта в определенный момент времени, причем спред различается в зависимости не только от времени, но и от облигаций, имеющих одинаковый рейтинг, но разные сроки погашения. В данном разделе обсуждается, как спред дефолта изменяется со временем и различается для облигаций с разными сроками погашения.
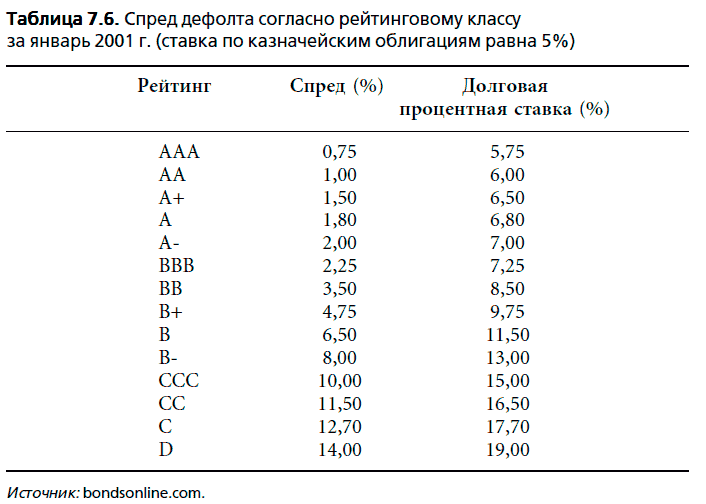Спред дефолта и срок погашения облигации. С эмпирической точки зрения спред дефолта для корпоративных облигаций, принадлежащих к определенному рейтинговому классу, как правило, повышается с увеличением срока до погашения облигации. На рисунке 7.2 представлены спреды дефолта, оцененные для облигаций с рейтингами ААА, ВВВ и ССС и сроками погашения от 1 до 10 лет в январе 2001 г.
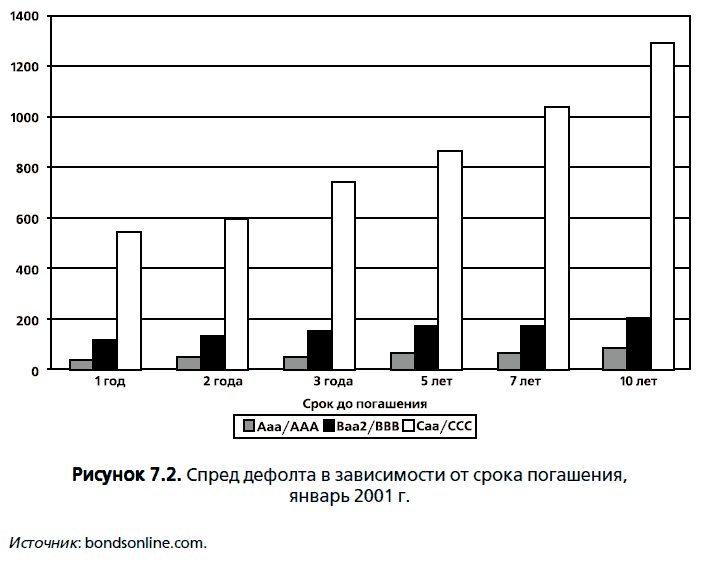
Для каждого рейтингового класса спред дефолта обычно расширяется с ростом сроков погашения, и подобная тенденция находит большее проявление для облигаций с низким рейтингом. С чем это связано? Вполне возможно, спред дефолта умножается, когда мы рассматриваем более длительные сроки погашения. Инвестор, покупающий 10-летнюю облигацию компании с рейтингом ССС, может чувствовать себя в большей степени подверженным риску дефолта, чем владелец облигации с более высоким рейтингом.
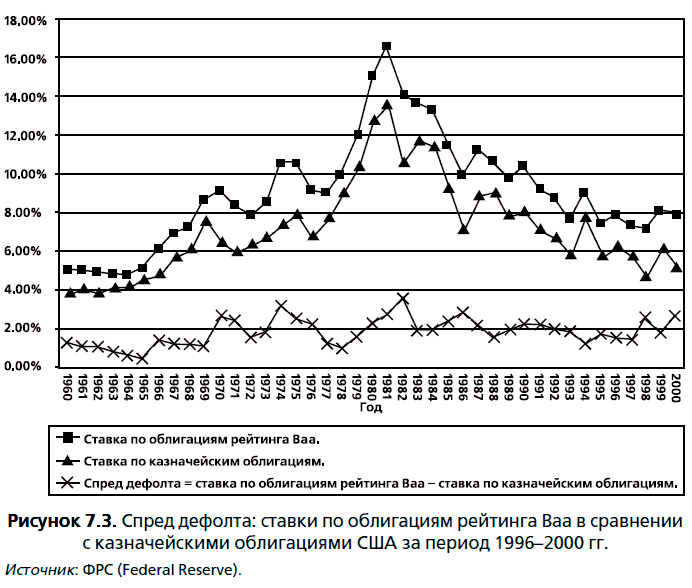
Изменения спреда дефолта со временем. Спреды дефолта, представленные в таблице 7.6, – после года спада на рынке и замедления темпов экономического роста – были существенно выше, чем спреды дефолта годом ранее. Этот феномен не нов. Исторически спреды дефолта для каждого рейтингового класса повышались во время спада и понижались в период экономического подъема. На рисунке 7.3 показан ежегодный график спреда между 10-летней облигацией с рейтингом Ваа (Moody’s) и 10-летней казначейской облигацией на протяжении 40 лет – за период 1960–2000 гг. Спред дефолта повышался в периоды низкого экономического роста. Обратите внимание на повышения, наблюдавшиеся в 1973–1974 гг. и в особенности в 1978–1981 гг. В действительности, регрессия ежегодного спреда дефолта по отношению к экономическому росту подтверждает этот вывод:
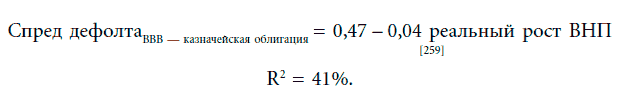После периода высокого реального роста спреды дефолта имеют тенденцию к сокращению.
Практическое использование данного явления состоит в том, что спреды дефолта для облигаций должны на регулярной основе повторно переоцениваться. Это особенно важно, если экономика движется от низких темпов роста к высоким, и наоборот.
ЗАКЛЮЧЕНИЕ
КОНТРОЛЬНЫЕ ВОПРОСЫ
Глава 8. ОЦЕНКА ПАРАМЕТРОВ РИСКА И СТОИМОСТИ ФИНАНСИРОВАНИЯ
СТОИМОСТЬ ПРИВЛЕЧЕНИЯ СОБСТВЕННОГО И ДОЛГОВОГО КАПИТАЛА
СТОИМОСТЬ ПРИВЛЕЧЕНИЯ СОБСТВЕННОГО КАПИТАЛА
Самый простой способ оценки спреда дефолта для каждого рейтингового класса – это нахождение выборки облигаций в пределах данного рейтингового класса и выяснение текущей рыночной процентной ставки по этим облигациям. Почему необходимо использовать выборку, а не просто одну облигацию? Облигация может быть ошибочно оценена или отнесена к ошибочной рейтинговой группе. Использование выборки уменьшает или даже полностью устраняет данную проблему. При составлении данной выборки следует пытаться сосредоточить внимание на наиболее ликвидных облигациях, обладающих как можно меньшим числом особых характеристик. Корпоративные облигации часто отличаются неликвидностью, а процентные ставки по ним могут не отражать текущие рыночные ставки. Присутствие особых характеристик у облигаций, таких как конвертируемость, может повлиять на ценообразование этих облигаций и, следовательно, на оценку процентных ставок по ним.
Как только определена выборка облигаций в пределах каждого рейтингового класса, необходимо оценить процентные ставки по этим облигациям. Существуют два широко используемых подхода. Первый заключается в оценке доходности облигации, т. е. представляет из себя купонную ставку, деленную на рыночную цену. Второй оценивает выплаты к истечению срока облигации, определяя приведенную стоимость купонов, а также номинальную стоимость облигации по рыночной цене. Как правило, выплаты к дате погашения оказываются наилучшей мерой рыночной процентной ставки по облигации.
Выяснив процентную ставку, соответствующую выборке облигаций, следует принять два решения. Первое относится к взвешиванию. Можно вычислить простую среднюю величину из процентных ставок по облигациям, входящим в выборку, или же взвешенную среднюю величину, связывая при этом веса с объемом торговли: более ликвидные облигации получают большие веса, чем менее ликвидные облигации. Второе решение относится к индексу казначейской ставки, поскольку средняя процентная ставка для определенного рейтингового класса сравнивается с этой ставкой для выяснения спреда дефолта. Как правило, срок истечения действия казначейской ценной бумаги должен соответствовать среднему сроку истечения корпоративной ценной бумаги, выбранной для оценки средней процентной ставки. Таким образом, для получения спреда по облигациям с рейтингом ВВВ средняя процентная ставка для пятилетних корпоративных облигаций с рейтингом ВВВ должна сравниваться со средней процентной ставкой для пятилетних казначейских бумаг.
Хотя такие издания, как Barron’s, исторически предоставляли процентные ставки по облигациям с наивысшими рейтингами (ВВВ или выше), сегодня ту же информацию по всем облигациям, имеющим рейтинги, дает все большее количество сетевых служб. Данные по 10-летним облигациям для таблицы 7.6 получены в одной из таких служб, работающей в режиме он-лайн, в начале 2001 г.
Детерминанты спреда дефолта
В таблице 7.6 представлена информация о спреде дефолта в определенный момент времени, причем спред различается в зависимости не только от времени, но и от облигаций, имеющих одинаковый рейтинг, но разные сроки погашения. В данном разделе обсуждается, как спред дефолта изменяется со временем и различается для облигаций с разными сроками погашения.
Изменения спреда дефолта со временем. Спреды дефолта, представленные в таблице 7.6, – после года спада на рынке и замедления темпов экономического роста – были существенно выше, чем спреды дефолта годом ранее. Этот феномен не нов. Исторически спреды дефолта для каждого рейтингового класса повышались во время спада и понижались в период экономического подъема. На рисунке 7.3 показан ежегодный график спреда между 10-летней облигацией с рейтингом Ваа (Moody’s) и 10-летней казначейской облигацией на протяжении 40 лет – за период 1960–2000 гг. Спред дефолта повышался в периоды низкого экономического роста. Обратите внимание на повышения, наблюдавшиеся в 1973–1974 гг. и в особенности в 1978–1981 гг. В действительности, регрессия ежегодного спреда дефолта по отношению к экономическому росту подтверждает этот вывод:
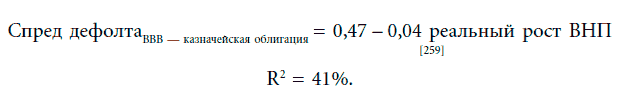
Практическое использование данного явления состоит в том, что спреды дефолта для облигаций должны на регулярной основе повторно переоцениваться. Это особенно важно, если экономика движется от низких темпов роста к высоким, и наоборот.
ЗАКЛЮЧЕНИЕ
Безрисковая ставка – это исходный пункт для всех моделей оценки ожидаемого дохода. Чтобы актив был безрисковым, он должен быть свободен от риска дефолта и риска реинвестиции. Если полагаться на эти критерии, то соответствующей безрисковой ставкой, используемой для получения ожидаемого дохода, должна служить безрисковая ставка облигаций (правительственных) с нулевым купоном, которая выясняется через дисконтирование денежных потоков. Однако обычно на практике целесообразно сопоставлять срок жизни безрискового актива с продолжительностью анализируемых денежных потоков. В задачах оценки это подведет нас к использованию ставок по долгосрочным правительственным облигациям в качестве безрисковых ставок. Важно также, чтобы безрисковая ставка согласовывалась с дисконтируемыми денежными потоками. В частности, валюта, в которой выражается безрисковая ставка, а также определение того, идет ли речь о номинальной или о реальной безрисковой ставке, должны зависеть от валюты, в которой оцениваются денежные потоки, а также от того, производится ли оценка в реальных или номинальных величинах.
Премия за риск – это фундаментальный и критически важный компонент в портфельном менеджменте, корпоративных финансах и оценке. Несмотря на ее важность, вызывает удивление, что не уделяется достаточного внимания вопросам оценки с практической точки зрения. В данной главе был рассмотрен стандартный подход к оценке премии за риск, т. е. использование исторической доходности акций и правительственных ценных бумаг, и были изучены его некоторые недостатки. Также исследовалось, как распространить этот подход на формирующиеся рынки, где исторические данные обычно ограничены и изменчивы. Альтернативой историческим премиям является оценка премии за риск инвестирования в акции, подразумеваемой ценами на собственный капитал. Данный подход требует, чтобы мы отталкивались от модели оценки для обыкновенных акций и совместно оценили ожидаемый рост и денежные потоки, возникающие в результате инвестиции в акции. Этот подход обладает тем преимуществом, что он не требует исторических данных и основывается на текущих показателях рынка.
Премия за риск – это фундаментальный и критически важный компонент в портфельном менеджменте, корпоративных финансах и оценке. Несмотря на ее важность, вызывает удивление, что не уделяется достаточного внимания вопросам оценки с практической точки зрения. В данной главе был рассмотрен стандартный подход к оценке премии за риск, т. е. использование исторической доходности акций и правительственных ценных бумаг, и были изучены его некоторые недостатки. Также исследовалось, как распространить этот подход на формирующиеся рынки, где исторические данные обычно ограничены и изменчивы. Альтернативой историческим премиям является оценка премии за риск инвестирования в акции, подразумеваемой ценами на собственный капитал. Данный подход требует, чтобы мы отталкивались от модели оценки для обыкновенных акций и совместно оценили ожидаемый рост и денежные потоки, возникающие в результате инвестиции в акции. Этот подход обладает тем преимуществом, что он не требует исторических данных и основывается на текущих показателях рынка.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Предположим, вы оцениваете индонезийскую фирму в долларах США. Что бы вы использовали в качестве безрисковой ставки?
2. Объясните, почему ставка по шестимесячному казначейскому векселю не может быть адекватно рассмотрена в качестве безрисковой ставки при дисконтировании пятилетних денежных потоков (за период пять лет).
3. Вам требуется оценить безрисковую ставку в индонезийских рупиях. Индонезийское правительство выпустило облигации, деноминированные в рупиях и с процентной ставкой 17 %. Агентство S&P определило рейтинг этих облигаций как ВВ, а типичный спред для страны с рейтингом ВВ составляет 5 % сверх безрисковой ставки. Оцените безрисковую ставку на основе рупий.
4. Вы оцениваете индийскую компанию в рупиях. Текущий обменный курс соответствует 70 рупиям за 1 доллар, и вы можете получить 10-летний форвардный курс 70 рупий за доллар. Если ставка по казначейским облигациям США равна 5 %, оцените безрисковую ставку на основе индийских рупий.
5. Вы пытаетесь произвести оценку чилийской компании в реальном выражении. Хотя вы не смогли получить реальную безрисковую ставку в Латинской Америке, вам известно, что казначейские облигации, индексируемые согласно уровню инфляции, в США приносят 3 %. Возможно ли использовать эту величину в качестве безрисковой ставки? Почему да или почему нет? Каковы альтернативы?
6. Предположим, вы оценили историческую премию за риск как 6 %, основываясь на данных за 50 лет. Оцените стандартную ошибку в оценке премии за риск при условии, что годовое стандартное отклонение цен акций равно 30 %.
7. Когда вы используете историческую премию за риск в качестве ожидаемой премии за будущий риск, какие предложения по поводу инвесторов и рынков вы сделаете? При этих условиях даст ли историческая премия за риск слишком высокую величину (при использовании в качестве ожидаемой премии)?
8. Вы пытаетесь оценить премию за суверенный риск инвестирования в акции для Польши. Вы знаете, что агентство S&P назначило ей рейтинг А, и Польша выпустила облигации, деноминированные в евро и приносящие в настоящий момент 7,6 % на рынке. (Германия, страна с рейтингом ААА, имеет обращающиеся на рынке облигации, приносящие 5,1 %.)
а) Оцените премию за риск по стране, используя спред дефолта по суверенной облигации в качестве приблизительной оценки.
б) Вы узнали, что стандартное отклонение на польском фондовом рынке составляло 25 %, а стандартное отклонение по польской еврооблигации – 15 %. Оцените премию за суверенный риск.
9. Стандартное отклонение мексиканского фондового индекса (Mexican Equity Index) равно 48 %, а стандартное отклонение индекса S&P 500 составляет 20 %. Вы используете премию за риск инвестирования в акции, равную 5,5 % для Соединенных Штатов.
а) Оцените премию за суверенный риск инвестирования в акции для Мексики, используя относительное стандартное отклонение по акциям.
б) Теперь предположите, что агентство Standard&Poor’s присвоило Мексике рейтинг ВВВ и страна выпустила облигации, выраженные в долларах, которые торгуются со спредом примерно 3 % сверх ставки по казначейским облигациям США. Предполагая, что стандартное отклонение по этим облигациям составляет 24 %, оцените премию за суверенный риск Мексики.
10. Индекс S&P 500 находится на уровне 1400. Предполагаемые дивиденды и денежные потоки, создаваемые акциями из индекса, в следующем году ожидаются на уровне 6 %, а безрисковая ставка – 5,5 %. Оцените подразумеваемую премию за риск инвестирования в акции.
11. Bovespa (бразильский фондовый индекс) находится на уровне 15 000. Дивиденды по индексу в прошлом году равнялись 5 % от стоимости индекса. Аналитики ожидают, что в реальном выражении они будут расти на 15 % ежегодно в течение последующих 5 лет. Через пять лет ожидается, что темпы снизятся до 5 % в реальном выражении и данные темпы будут сохраняться и далее в обозримом будущем. Оцените подразумеваемую премию за риск инвестирования в акции на этом рынке, если реальная безрисковая ставка равна 6 %.
12. По мере роста цен на акции подразумеваемые премии за риск инвестирования в акции будут снижаться. Всегда ли верно данное утверждение? Если не верно, то в каких случаях?
2. Объясните, почему ставка по шестимесячному казначейскому векселю не может быть адекватно рассмотрена в качестве безрисковой ставки при дисконтировании пятилетних денежных потоков (за период пять лет).
3. Вам требуется оценить безрисковую ставку в индонезийских рупиях. Индонезийское правительство выпустило облигации, деноминированные в рупиях и с процентной ставкой 17 %. Агентство S&P определило рейтинг этих облигаций как ВВ, а типичный спред для страны с рейтингом ВВ составляет 5 % сверх безрисковой ставки. Оцените безрисковую ставку на основе рупий.
4. Вы оцениваете индийскую компанию в рупиях. Текущий обменный курс соответствует 70 рупиям за 1 доллар, и вы можете получить 10-летний форвардный курс 70 рупий за доллар. Если ставка по казначейским облигациям США равна 5 %, оцените безрисковую ставку на основе индийских рупий.
5. Вы пытаетесь произвести оценку чилийской компании в реальном выражении. Хотя вы не смогли получить реальную безрисковую ставку в Латинской Америке, вам известно, что казначейские облигации, индексируемые согласно уровню инфляции, в США приносят 3 %. Возможно ли использовать эту величину в качестве безрисковой ставки? Почему да или почему нет? Каковы альтернативы?
6. Предположим, вы оценили историческую премию за риск как 6 %, основываясь на данных за 50 лет. Оцените стандартную ошибку в оценке премии за риск при условии, что годовое стандартное отклонение цен акций равно 30 %.
7. Когда вы используете историческую премию за риск в качестве ожидаемой премии за будущий риск, какие предложения по поводу инвесторов и рынков вы сделаете? При этих условиях даст ли историческая премия за риск слишком высокую величину (при использовании в качестве ожидаемой премии)?
8. Вы пытаетесь оценить премию за суверенный риск инвестирования в акции для Польши. Вы знаете, что агентство S&P назначило ей рейтинг А, и Польша выпустила облигации, деноминированные в евро и приносящие в настоящий момент 7,6 % на рынке. (Германия, страна с рейтингом ААА, имеет обращающиеся на рынке облигации, приносящие 5,1 %.)
а) Оцените премию за риск по стране, используя спред дефолта по суверенной облигации в качестве приблизительной оценки.
б) Вы узнали, что стандартное отклонение на польском фондовом рынке составляло 25 %, а стандартное отклонение по польской еврооблигации – 15 %. Оцените премию за суверенный риск.
9. Стандартное отклонение мексиканского фондового индекса (Mexican Equity Index) равно 48 %, а стандартное отклонение индекса S&P 500 составляет 20 %. Вы используете премию за риск инвестирования в акции, равную 5,5 % для Соединенных Штатов.
а) Оцените премию за суверенный риск инвестирования в акции для Мексики, используя относительное стандартное отклонение по акциям.
б) Теперь предположите, что агентство Standard&Poor’s присвоило Мексике рейтинг ВВВ и страна выпустила облигации, выраженные в долларах, которые торгуются со спредом примерно 3 % сверх ставки по казначейским облигациям США. Предполагая, что стандартное отклонение по этим облигациям составляет 24 %, оцените премию за суверенный риск Мексики.
10. Индекс S&P 500 находится на уровне 1400. Предполагаемые дивиденды и денежные потоки, создаваемые акциями из индекса, в следующем году ожидаются на уровне 6 %, а безрисковая ставка – 5,5 %. Оцените подразумеваемую премию за риск инвестирования в акции.
11. Bovespa (бразильский фондовый индекс) находится на уровне 15 000. Дивиденды по индексу в прошлом году равнялись 5 % от стоимости индекса. Аналитики ожидают, что в реальном выражении они будут расти на 15 % ежегодно в течение последующих 5 лет. Через пять лет ожидается, что темпы снизятся до 5 % в реальном выражении и данные темпы будут сохраняться и далее в обозримом будущем. Оцените подразумеваемую премию за риск инвестирования в акции на этом рынке, если реальная безрисковая ставка равна 6 %.
12. По мере роста цен на акции подразумеваемые премии за риск инвестирования в акции будут снижаться. Всегда ли верно данное утверждение? Если не верно, то в каких случаях?
Глава 8. ОЦЕНКА ПАРАМЕТРОВ РИСКА И СТОИМОСТИ ФИНАНСИРОВАНИЯ
В предыдущей главе были изложены основы оценки стоимости привлечения собственного и долгового капитала. Для этого мы рассмотрели оптимальные способы оценки безрисковой ставки, лежащей в основе определения любых издержек, премии за риск инвестирования в акции – для измерения стоимости привлечения собственного капитала, а также спреда дефолта – для оценки стоимости привлечения долгового капитала. Однако мы не коснулись вопроса о том, каким образом оценивать параметры риска для отдельных фирм. В данной главе будет обсуждаться процесс оценки параметров риска отдельных фирм с целью определения стоимости привлечения собственного и долгового капитала.
Касаясь стоимости привлечения собственного капитала, мы рассмотрим стандартный процесс оценки коэффициента бета для фирмы и обсудим альтернативные подходы. Обращаясь к стоимости привлечения долгового капитала, мы проанализируем рейтинги облигаций, используемые в качестве меры риска дефолта, а также детерминанты этих рейтингов.
Глава завершается сведением воедино оценок параметров риска отдельных фирм и общеэкономических оценок безрисковой ставки и премий за риск, чтобы оценить стоимость привлечения капитала для фирмы. Для этого источники капитала должны быть взвешены по их относительной рыночной стоимости.
Касаясь стоимости привлечения собственного капитала, мы рассмотрим стандартный процесс оценки коэффициента бета для фирмы и обсудим альтернативные подходы. Обращаясь к стоимости привлечения долгового капитала, мы проанализируем рейтинги облигаций, используемые в качестве меры риска дефолта, а также детерминанты этих рейтингов.
Глава завершается сведением воедино оценок параметров риска отдельных фирм и общеэкономических оценок безрисковой ставки и премий за риск, чтобы оценить стоимость привлечения капитала для фирмы. Для этого источники капитала должны быть взвешены по их относительной рыночной стоимости.
СТОИМОСТЬ ПРИВЛЕЧЕНИЯ СОБСТВЕННОГО И ДОЛГОВОГО КАПИТАЛА
В качестве источника средств для финансирования своих инвестиций фирмы используют инвесторов в акции, а также кредиторов. В главе 4 доказывается, что ожидаемая доходность для инвесторов в акции должна включать премию за риск инвестирования в акции, содержащийся в этой инвестиции. Мы называем эту ожидаемую доходность стоимостью привлечения собственного капитала. Аналогично этому, доход, который кредиторы ожидают получить на свои инвестиции, включает премию за риск дефолта. Мы называем эту ожидаемую доходность стоимостью привлечения долгового капитала. Если мы рассмотрим финансирование фирмы в целом, то общая стоимость финансирования окажется средневзвешенной величиной стоимости привлечения собственного и долгового капитала.
Данная глава начинается с оценки риска фирмы, связанного с акциями. При этом мы используем риск инвестирования в акции для оценки стоимости привлечения собственного капитала. Затем мы затронем измерение риска дефолта, которое необходимо для оценки стоимости привлечения долгового капитала. В завершение мы займемся определением весов – их следует приписать каждой из этих стоимостей для получения стоимости финансирования.
Данная глава начинается с оценки риска фирмы, связанного с акциями. При этом мы используем риск инвестирования в акции для оценки стоимости привлечения собственного капитала. Затем мы затронем измерение риска дефолта, которое необходимо для оценки стоимости привлечения долгового капитала. В завершение мы займемся определением весов – их следует приписать каждой из этих стоимостей для получения стоимости финансирования.
СТОИМОСТЬ ПРИВЛЕЧЕНИЯ СОБСТВЕННОГО КАПИТАЛА
Стоимость привлечения собственного капитала – это доходность, которую инвесторы ожидают от инвестиций в собственный капитал фирмы. Модели риска и доходности, описанные в главе 4, требовали безрисковых ставок и премии за риск (модель САРМ) или множества премий (модель АРМ и многофакторная модель), подход к определению которых был представлен в предыдущей главе. Кроме того, эти модели требуют знать меру подверженности фирмы рыночному риску, реализуемую в форме коэффициента бета. Эти входные данные используются для получения оценки ожидаемой доходности от инвестиции в акции:
Ожидаемая доходность = безрисковая ставка + коэфф. бета (премия за риск).
Эта ожидаемая доходность для инвесторов в акции включает компенсацию за рыночный риск, свойственный инвестиции, а также стоимость привлечения собственного капитала. В данном разделе основное внимание мы уделим оценке коэффициента бета фирмы. Хотя значительная часть этого обсуждения посвящена модели САРМ, его выводы можно распространить на арбитражную модель оценки и на многофакторную модель.
Коэффициенты бета
В модели САРМ коэффициент бета инвестиции – это риск, который инвестиция добавляет к рыночному портфелю. В модели АРМ и многофакторной модели коэффициенты бета инвестиции должны быть измерены относительно каждого фактора. Существуют подходы, предназначенные для оценки этих параметров. Один из таких подходов – это использование исторических данных о рыночных ценах для конкретной инвестиции. Второй подход связан с оценкой коэффициента бета на основе фундаментальных характеристик инвестиции. А третий подход использует данные отчетности фирмы.
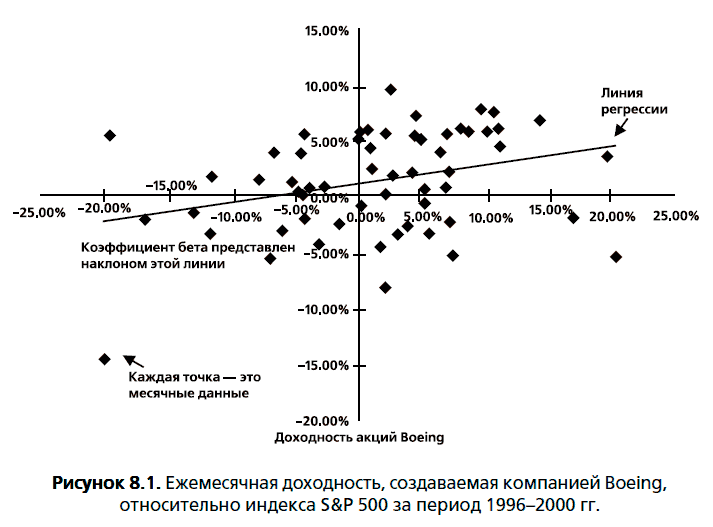
Исторические рыночные коэффициенты бета. Общепринятый подход к оценке коэффициента бета инвестиции основывается на регрессионном анализе доходности инвестиции относительно доходности рыночного индекса. Для фирмы, акции которой на протяжении длительного периода торгуются на открытом рынке, не представляет большого затруднения оценить доходы, которые инвестор получил бы от своей инвестиции в акции на различных интервалах (например, месячных или недельных) в течение периода. В теории для оценки коэффициентов бета активов эти показатели доходности вложений в акции должны быть соотнесены с доходностью рыночного портфеля (т. е. портфеля, который включает все торгуемые активы). На практике же мы обычно в качестве приблизительной оценки рыночного портфеля используем какой-нибудь фондовый индекс (например, S&P 500) и оцениваем коэффициенты бета для акций относительно индекса.
Оценки регрессии коэффициентов бета. Стандартная процедура для оценки коэффициентов бета предусматривает выяснение регрессии доходности акции (R.) относительно рыночной доходности (Rm):
Rj = a + b Rm
где a = точка пересечения на оси абсцисс;
b = наклон линии регрессии = ковариация (Rj, Rm)/σ2m.
Наклон линии регрессии соответствует коэффициенту бета акции и выражает рискованность этой акции.
Точка пересечения линии регрессии с осью ординат дает простую оценку эффективности инвестиции в течение периода регрессии, когда доходность измеряется в сравнении с ожидаемой доходностью, полученной по модели оценки финансовых активов. Чтобы понять почему, обсудим следующую запись модели оценки финансовых активов:
Rj = Rf + Β(Rm-Rf) = Rf (1 – Β) + ΒRm.
Сравните эту формулировку доходности инвестиции с уравнением доходности из регрессии:
Rj = a + b Rm.
Таким образом, сравнение точки пересечения с Rf (1 – Β) должно предоставить меру доходности акции, по крайней мере для случая модели оценки финансовых активов[65]. Суммируя, можно определить:
если a > Rf (1 – Β)… акция была более доходной, чем ожидалось в течение периода регрессии. a = Rf (1 – Β)… доходность акции в течение периода регрессии соответствовала ожиданиям. a < Rf (1 – Β). акция оказалась менее доходной, чем ожидалось в течение периода регрессии.
Разница между a и Rf (1 – Β) называется альфой Дженсена[66], которая предоставляет собой меру того, создает ли рассматриваемая инвестиция доход – больший или меньший, чем требуемый, с учетом рыночной доходности и риска. Например, фирма, заработавшая 15 % в течение периода, когда фирмы с аналогичными коэффициентами бета заработали 12 %, обеспечила себе избыточный доход в 3 %. Точка пересечения также превысит Rf (1 – Β) на 3 %.
Третьим показателем, который выводится на основе регрессионного анализа, является R-квадрат (R2) регрессии. Хотя с точки зрения статистики R-квадрат трактуется как «мера добротности построения регрессии», с позиции экономической теории данный показатель позволяет оценить долю риска фирмы, которую можно приписать рыночному риску. В этом случае остаток (1 – R2) можно отнести к специфическому риску фирмы.
Последний показатель, достойный упоминания, – это стандартная ошибка оценки коэффициента бета. Наклон линии регрессии, подобно любой статистической оценке, может отличаться от действительного значения, и стандартная ошибка показывает, насколько ошибочной может быть полученная оценка. Стандартную ошибку можно также использовать для получения доверительного интервала для «истинной» величины коэффициента бета, основываясь на оценке угла наклона.
Использование коэффициентов бета, полученных от специализированных фирм. Большинство из тех, кто использует коэффициенты бета, получает их от фирм, специализирующихся на оценке. Merrill Lynch, Barra, Value Line, Standard & Poor’s, Morningstar и Bloomberg – это лишь небольшой список наиболее известных служб подобного рода. Все они исходят из регрессионных (только что описанных) коэффициентов бета и корректируют их с целью отражения ими ожидаемого в будущем риска, полагаясь на собственное мнение по этому поводу. Многие из этих сервисных служб не раскрывают свои процедуры оценки, в то время как компания Bloomberg является исключением. На рисунке 8.2 представлен оригинальный лист с вычислениями коэффициента бета компании Boeing, выполненными Bloomberg в том же периоде, который был нами рассмотрен ранее (январь 1996 г. – декабрь 2000 г.).
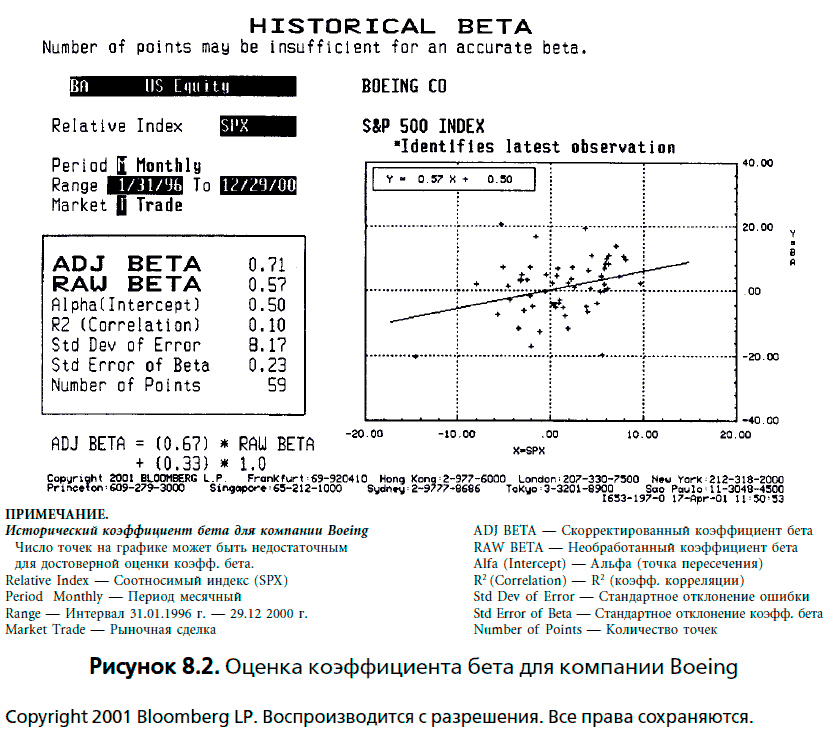Хотя временной период аналогичен периоду, использованному в нашем предыдущем регрессионном анализе, между данной регрессией и регрессией на рисунке 8.1 отмечаются небольшие различия. Во-первых, при оценке коэффициентов бета Bloomberg использует прирост стоимости акций и рыночный индекс, игнорируя при этом дивиденды[67]. Факт игнорирования дивидендов не играет столь уж большой роли для компании, подобной Boeing, но становится важным для акций компании, которая либо не выплачивает дивидендов, либо выплачивает их в значительно большем размере по сравнению с рынком. Это объясняет разницу между точкой пересечения (0,50 % против 0,54 %) и коэффициентом бета (0,57 против 0,56).
Во-вторых, служба Bloomberg вычисляет также показатель, который она называет скорректированным коэффициентом бета. Он записывается следующим образом:
Скорректирован. коэфф. бета = необработ. коэфф. бета (0,67) + 1,00 (0,33).
Использованные веса (0,67 и 0,33) для различных акций не отличаются, и данный процесс заставляет двигаться все коэффициенты бета к единице. Большинство служб использует аналогичные процедуры для корректировки коэффициентов бета в сторону единицы. Делая это, они прибегают к эмпирическим данным, свидетельствующим о том, что коэффициенты бета для большинства компаний обладают тенденцией со временем двигаться к среднему коэффициенту бета, равному единице. Это может быть объяснено тем фактом, что фирмы по мере своего роста становятся более диверсифицированными в своих продуктовой комбинации и клиентской базе. Хотя можно согласиться со стремлением коэффициента бета перемещаться к единице со временем, процесс взвешивания, используемый большинством служб, поражает своей произвольностью и относительной бесполезностью.
Выбор оценки для определения коэффициента бета. Возникает три вопроса, которые необходимо решить при проведении регрессионного анализа, описанного выше. Первый из них касается продолжительности периода оценки. Большинство оценок коэффициента бета, включая выводы Value Ьте и Standard & Poor’s, предполагают обращение к данным за пять лет, в то время как в оценках Bloomberg используются двухлетние данные. Компромисс прост: более длительный период обеспечивает больший объем данных, но характеристики специфического риска фирмы могли в течение этого периода измениться. Скажем, компания Boeing в течение рассматриваемого периода приобрела Rockwell и McDonnell Douglas, что изменило комбинацию бизнеса и базовые характеристики риска.
Второй вопрос относится к интервалу дохода. Данные о доходности акций доступны на недельной, дневной или даже внутридневной основе. Использование дневных или внутридневных доходов повышает количество наблюдений в регрессии, но подвергает процесс оценки коэффициента бета значительному воздействию необъективности, связанному с периодами отсутствия торговли[68]. Например, коэффициенты бета малых фирм, которые с большей вероятностью страдают вследствие отсутствия торгов, как правило, будут иметь заниженные величины при использовании дневной доходности. Использование недельной или месячной доходности может значительно сократить необъективность вследствие отсутствия торговли[69]. В этом случае использование недельной доходности за два года дает оценку коэффициента бета для компании Boeing, равную всего лишь 0,88, в то время как оценка коэффициента бета в месячном масштабе оказывается равной 0,96.
Ожидаемая доходность = безрисковая ставка + коэфф. бета (премия за риск).
Эта ожидаемая доходность для инвесторов в акции включает компенсацию за рыночный риск, свойственный инвестиции, а также стоимость привлечения собственного капитала. В данном разделе основное внимание мы уделим оценке коэффициента бета фирмы. Хотя значительная часть этого обсуждения посвящена модели САРМ, его выводы можно распространить на арбитражную модель оценки и на многофакторную модель.
Коэффициенты бета
В модели САРМ коэффициент бета инвестиции – это риск, который инвестиция добавляет к рыночному портфелю. В модели АРМ и многофакторной модели коэффициенты бета инвестиции должны быть измерены относительно каждого фактора. Существуют подходы, предназначенные для оценки этих параметров. Один из таких подходов – это использование исторических данных о рыночных ценах для конкретной инвестиции. Второй подход связан с оценкой коэффициента бета на основе фундаментальных характеристик инвестиции. А третий подход использует данные отчетности фирмы.
Исторические рыночные коэффициенты бета. Общепринятый подход к оценке коэффициента бета инвестиции основывается на регрессионном анализе доходности инвестиции относительно доходности рыночного индекса. Для фирмы, акции которой на протяжении длительного периода торгуются на открытом рынке, не представляет большого затруднения оценить доходы, которые инвестор получил бы от своей инвестиции в акции на различных интервалах (например, месячных или недельных) в течение периода. В теории для оценки коэффициентов бета активов эти показатели доходности вложений в акции должны быть соотнесены с доходностью рыночного портфеля (т. е. портфеля, который включает все торгуемые активы). На практике же мы обычно в качестве приблизительной оценки рыночного портфеля используем какой-нибудь фондовый индекс (например, S&P 500) и оцениваем коэффициенты бета для акций относительно индекса.
Оценки регрессии коэффициентов бета. Стандартная процедура для оценки коэффициентов бета предусматривает выяснение регрессии доходности акции (R.) относительно рыночной доходности (Rm):
Rj = a + b Rm
где a = точка пересечения на оси абсцисс;
b = наклон линии регрессии = ковариация (Rj, Rm)/σ2m.
Наклон линии регрессии соответствует коэффициенту бета акции и выражает рискованность этой акции.
Точка пересечения линии регрессии с осью ординат дает простую оценку эффективности инвестиции в течение периода регрессии, когда доходность измеряется в сравнении с ожидаемой доходностью, полученной по модели оценки финансовых активов. Чтобы понять почему, обсудим следующую запись модели оценки финансовых активов:
Rj = Rf + Β(Rm-Rf) = Rf (1 – Β) + ΒRm.
Сравните эту формулировку доходности инвестиции с уравнением доходности из регрессии:
Rj = a + b Rm.
Таким образом, сравнение точки пересечения с Rf (1 – Β) должно предоставить меру доходности акции, по крайней мере для случая модели оценки финансовых активов[65]. Суммируя, можно определить:
если a > Rf (1 – Β)… акция была более доходной, чем ожидалось в течение периода регрессии. a = Rf (1 – Β)… доходность акции в течение периода регрессии соответствовала ожиданиям. a < Rf (1 – Β). акция оказалась менее доходной, чем ожидалось в течение периода регрессии.
Разница между a и Rf (1 – Β) называется альфой Дженсена[66], которая предоставляет собой меру того, создает ли рассматриваемая инвестиция доход – больший или меньший, чем требуемый, с учетом рыночной доходности и риска. Например, фирма, заработавшая 15 % в течение периода, когда фирмы с аналогичными коэффициентами бета заработали 12 %, обеспечила себе избыточный доход в 3 %. Точка пересечения также превысит Rf (1 – Β) на 3 %.
Третьим показателем, который выводится на основе регрессионного анализа, является R-квадрат (R2) регрессии. Хотя с точки зрения статистики R-квадрат трактуется как «мера добротности построения регрессии», с позиции экономической теории данный показатель позволяет оценить долю риска фирмы, которую можно приписать рыночному риску. В этом случае остаток (1 – R2) можно отнести к специфическому риску фирмы.
Последний показатель, достойный упоминания, – это стандартная ошибка оценки коэффициента бета. Наклон линии регрессии, подобно любой статистической оценке, может отличаться от действительного значения, и стандартная ошибка показывает, насколько ошибочной может быть полученная оценка. Стандартную ошибку можно также использовать для получения доверительного интервала для «истинной» величины коэффициента бета, основываясь на оценке угла наклона.
Во-вторых, служба Bloomberg вычисляет также показатель, который она называет скорректированным коэффициентом бета. Он записывается следующим образом:
Скорректирован. коэфф. бета = необработ. коэфф. бета (0,67) + 1,00 (0,33).
Использованные веса (0,67 и 0,33) для различных акций не отличаются, и данный процесс заставляет двигаться все коэффициенты бета к единице. Большинство служб использует аналогичные процедуры для корректировки коэффициентов бета в сторону единицы. Делая это, они прибегают к эмпирическим данным, свидетельствующим о том, что коэффициенты бета для большинства компаний обладают тенденцией со временем двигаться к среднему коэффициенту бета, равному единице. Это может быть объяснено тем фактом, что фирмы по мере своего роста становятся более диверсифицированными в своих продуктовой комбинации и клиентской базе. Хотя можно согласиться со стремлением коэффициента бета перемещаться к единице со временем, процесс взвешивания, используемый большинством служб, поражает своей произвольностью и относительной бесполезностью.
Выбор оценки для определения коэффициента бета. Возникает три вопроса, которые необходимо решить при проведении регрессионного анализа, описанного выше. Первый из них касается продолжительности периода оценки. Большинство оценок коэффициента бета, включая выводы Value Ьте и Standard & Poor’s, предполагают обращение к данным за пять лет, в то время как в оценках Bloomberg используются двухлетние данные. Компромисс прост: более длительный период обеспечивает больший объем данных, но характеристики специфического риска фирмы могли в течение этого периода измениться. Скажем, компания Boeing в течение рассматриваемого периода приобрела Rockwell и McDonnell Douglas, что изменило комбинацию бизнеса и базовые характеристики риска.
Второй вопрос относится к интервалу дохода. Данные о доходности акций доступны на недельной, дневной или даже внутридневной основе. Использование дневных или внутридневных доходов повышает количество наблюдений в регрессии, но подвергает процесс оценки коэффициента бета значительному воздействию необъективности, связанному с периодами отсутствия торговли[68]. Например, коэффициенты бета малых фирм, которые с большей вероятностью страдают вследствие отсутствия торгов, как правило, будут иметь заниженные величины при использовании дневной доходности. Использование недельной или месячной доходности может значительно сократить необъективность вследствие отсутствия торговли[69]. В этом случае использование недельной доходности за два года дает оценку коэффициента бета для компании Boeing, равную всего лишь 0,88, в то время как оценка коэффициента бета в месячном масштабе оказывается равной 0,96.