Страница:
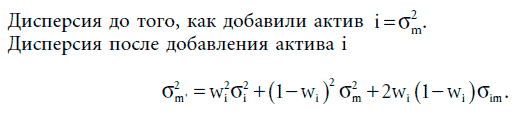
Стандартизация ковариации. Ковариация измеряется в процентах, поэтому трудно вынести решение по поводу относительного риска инвестиции, основываясь на ее значении. Другими словами, знание ковариации компании Boeing с рыночным портфелем (составляющей 55 %) не дает нам подсказки, в большей или в меньшей степени рискованна компания по сравнению со средним активом. По этой причине мы стандартизируем меру риска путем деления ковариации каждого актива с рыночным портфелем на дисперсию рыночного портфеля. Это позволяет получить показатель риска, который называется коэффициентом бета (beta) данного актива:
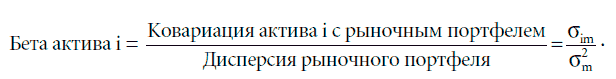
Получение ожидаемых доходов. Факт удержания каждым инвестором некоторой комбинации безрискового актива и рыночного портфеля приводит к заключению, что ожидаемый доход на актив линейно зависит от беты актива. В частности, ожидаемый доход на актив можно записать как функцию безрисковой ставки и беты этого актива:
E(Ri) = Rf + Pi [E(Rm)-Rf],
где E(Ri) = ожидаемая доходность актива i;
Rf = безрисковая ставка;
E(Rm) = ожидаемая доходность на рыночный портфель;
Pi = коэффициент бета актива i.
Для использования модели оценки финансовых активов нам необходимо иметь три входные величины. Следующая глава будет посвящена детальному разбору процесса оценки, поэтому пока только заметим, что каждая из этих входных величин оценивается следующим образом:
• Безрисковый актив определяется как актив, относительно которого инвестору с абсолютной определенностью известна ожидаемая доходность для временного горизонта анализа.
• Премия за риск является премией, запрашиваемой инвесторами за инвестирование в рыночный портфель, включающий все рисковые активы на рынке, вместо инвестирования в безрисковый актив.
• Коэффициент бета, который определяется как ковариация актива, поделенная на дисперсию рыночного портфеля, измеряет риск, добавляемый инвестицией к рыночному портфелю.
Таким образом, в модели оценки финансовых активов весь рыночный риск охватывается одним коэффициентом бета, измеренным по отношению к рыночному портфелю, который, хотя бы теоретически, должен содержать все обращающиеся на рынке активы пропорционально их рыночной стоимости.
Модель арбитражной оценки. Ограничивающие предположения, касающиеся транзакционных издержек и получения информации в модели оценки финансовых активов, а также зависимость модели от рыночного портфеля на протяжении длительного времени воспринимались академическими кругами и специалистами-практиками со скептицизмом. Росс (Ross, 1976) предложил альтернативную модель для измерения риска, которая называется моделью арбитражной оценки (arbitrage pricing model – APM).
Предположения. Если инвесторы могут инвестировать без риска и зарабатывать больше, чем по безрисковой ставке, то это означает, что они нашли возможность арбитража[25]. Предположение, лежащее в основе модели арбитражной оценки, заключается в том, что инвесторы пользуются выгодами возможности совершения арбитража и устраняют их в процессе торгов. Если два портфеля в одинаковой степени подвержены риску, но предлагают различный ожидаемый доход, то инвесторы приобретут портфель с более высоким ожидаемым доходом и продадут портфель с меньшим ожидаемым доходом. Заработанная разница будет безрисковой прибылью. Для предотвращения возможности арбитража два портфеля должны создавать одинаковые ожидаемые доходы.
Подобно модели оценки финансовых активов, модель арбитражной оценки начинает с разделения риска на специфический риск фирмы и рыночный риск. Как и в модели оценки финансовых активов, специфический риск фирмы охватывает информацию, которая влияет в основном на саму фирму. Рыночный риск касается многих или всех фирм и предполагает непредвиденные изменения в определенном числе экономических переменных, включая ВВП, инфляцию и процентные ставки. Включив оба типа риска в модель доходности, мы получаем:
R= E(R) + m + ε,
где R – фактическая доходность, E(R) – ожидаемая доходность, m – компонент непредвиденного риска в масштабе всего рынка, ε – компонент отдельной фирмы. Таким образом, фактический доход может отличаться от ожидаемого дохода либо по причине рыночного риска, либо вследствие специфического риска фирмы.
Источники рыночного риска. Хотя и модель оценки финансовых активов, и модель арбитражной оценки различают риск отдельной фирмы и рыночный риск, они измеряют рыночный риск по-разному. Модель САРМ предполагает, что рыночный риск полностью охватывается рыночным портфелем, в то время как модель арбитражной оценки допускает множество источников рыночного риска, измеряя чувствительность инвестиций к изменениям в каждом идентифицированном источнике. Вообще говоря, рыночный компонент непредвиденных доходов можно разложить на экономические факторы:
R = E(R) + m + ε = R + (Β1F1 + Β2F2 + … + ΒnFn) + ε,
где Βj = чувствительность инвестиции к непредвиденным изменениям в факторе j;
где Fj = чувствительность инвестиции к непредвиденным
Отметим, что измерение чувствительности инвестиции к любому макроэкономическому фактору принимает форму коэффициента бета, который называется фактором бета. В действительности, данный фактор бета во многом сходен с рыночным коэффициентом бета в модели САРМ.
Результаты диверсификации. Преимущества диверсификации обсуждались ранее в контексте разделения на рыночный и специфический риск фирмы. Основные положения этой дискуссии связаны с устранением этой диверсификации специфического риска фирмы. Модель арбитражной оценки привлекает ту же самую аргументацию и приводит к выводу, что доходность портфеля не будет содержать компонент непредвиденных доходов отдельной фирмы. Доход портфеля можно записать как сумму двух средневзвешенных – ожидаемого дохода портфеля и рыночных факторов:


Модель оценки финансовых активов можно рассматривать как особый случай модели арбитражной оценки, где присутствует только один экономический фактор, создающий доходы в масштабах всего рынка, и этим фактором является рыночный портфель.
E(R) = Rf + Βm[E(Rm)-Rf].
Модель арбитражной оценки на практике. Модель арбитражной оценки позволяет оценить коэффициенты бета для каждого фактора и премии за риск по факторам в дополнение к безрисковой ставке. На практике они обычно оцениваются при помощи исторических данных по доходам, приходящимся на актив, и факторного анализа. На интуитивном уровне понятно, что в факторном анализе мы изучаем исторические данные на основе исторических образов, характерных скорее для значительных групп активов (чем для одного сектора или нескольких активов). Факторный анализ дает два итоговых показателя:
1. Позволяет определить число общих факторов, влияющих на исторические данные по доходам.
2. Дает возможность измерить коэффициент бета каждой инвестиции относительно любого из общих факторов и обеспечивает оценку фактических премий за риск, заработанных каждым фактором.
Тем не менее факторный анализ не занимается идентификацией факторов с экономических позиций. Как правило, в модели арбитражной оценки рыночный риск измеряется по отношению к множеству не поддающихся спецификации макроэкономических переменных. При этом чувствительность инвестиции соотносится с каждым фактором, измеренным при помощи коэффициента бета. Количество факторов риска, коэффициенты бета для факторов, премии за факторы риска – все эти величины можно оценить при помощи факторного анализа.
Многофакторные модели для риска и доходности. Отказ от идентификации факторов в модели арбитражной оценки, по всей вероятности, можно оправдать, обращаясь к статистическим методам, но, вместе с тем, интуиция подсказывает, что это свидетельствует о слабости подобного подхода. Решение кажется простым: заменить неопределяемые статистические факторы специальными экономическими факторами, и результирующая модель будет обладать экономической основой, вместе с тем сохраняя в себе многие достоинства модели арбитражной оценки. Именно на это и нацелены многофакторные модели.
Создание многофакторной модели. Как правило, многофакторные модели основаны на исторических данных, а не на экономическом моделировании. Как только в модели арбитражной оценки выявлено определенное количество факторов, их поведение можно выяснить с помощью данных. Поведение неназванных факторов во времени можно сравнить с поведением макроэкономических переменных за тот же период с целью проверки, коррелируют ли во времени какие-либо из переменных с идентифицированными факторами.
Например, Чен, Ролл и Росс (Chen, Roll and Ross, 1986) предполагают, что с факторами, полученными при помощи факторного анализа, в значительной степени коррелируют следующие макроэкономические переменные: промышленная продукция, изменения размера премии за дефолт, сдвиги во временной структуре, непредвиденная инфляция и изменения в фактической доходности. Затем можно выяснить корреляцию этих переменных с доходами (что даст нам модель ожидаемых доходов), а также с коэффициентами бета отдельных фирм, рассчитанными по отношению к каждой переменной.

В конечном итоге, многофакторные модели, подобно моделям арбитражной оценки, предполагают, что рыночный риск может быть учтен лучше, если использовать множество экономических факторов и коэффициенты бета, соотнесенные с каждым из них. В отличие от модели арбитражной оценки, многофакторные модели нацелены на идентификацию макроэкономических факторов, определяющих рыночный риск.
Регрессия, или приближенные модели. Все описанные модели начинают с определения рыночного риска в широком смысле, а затем развивают модели, оценивающие этот рыночный риск наилучшим образом. Но все они извлекают свои показатели рыночного риска (бета) из анализа исторических данных. Существует целевой класс моделей риска и доходности, которые начинают с доходов и пытаются объяснить различия в этих доходах, приходящихся на разные акции, в течение длительного временного периода. Для этого используются такие характеристики, как рыночная стоимость фирмы или мультипликаторы, включающие в себя цену[26]. Сторонники этих моделей доказывают, что если доходность некоторых инвестиций выше, чем у других, то и рискованность их должна оказаться выше. Следовательно, мы можем взглянуть на характеристики, объединяющие эти высокодоходные инвестиции, и принять их в качестве косвенных или приближенных показателей рыночного риска.
Фама и Френч (Fama and French, 1992) в своем исследовании модели оценки финансовых активов, получившем широкое признание, отметили, что фактические доходы за период 1963–1990 гг. сильно коррелировали с мультипликаторами «балансовая стоимость/цена»[27] и размером. Высокодоходные инвестиции в этот период, как правило, были связаны с вложениями в компании с низкой рыночной капитализацией и высокими мультипликаторами «балансовая стоимость/цена». Фама и Френч предположили, что эти показатели можно использовать в качестве приближенных оценок риска, и вывели следующую регрессию для ежемесячных доходов на акции, обращающиеся на Нью-Йоркской фондовой бирже (New York Stock Exchange – NYSE):
где ln = натуральный логарифм;Rt = 1,77 % – 0,11ln (MV)+0,35ln (BV/MV),
MV = рыночная стоимость собственного капитала;
BV/MV = балансовая стоимость/рыночная стоимость собственного капитала.
Значения рыночной стоимости собственного капитала и мультипликатора «BV/MV» для отдельных фирм, принятые в качестве значений для регрессионных переменных, должны давать ожидаемый ежемесячный доход.
СРАВНИТЕЛЬНЫЙ АНАЛИЗ МОДЕЛЕЙ РИСКА И ДОХОДНОСТИ
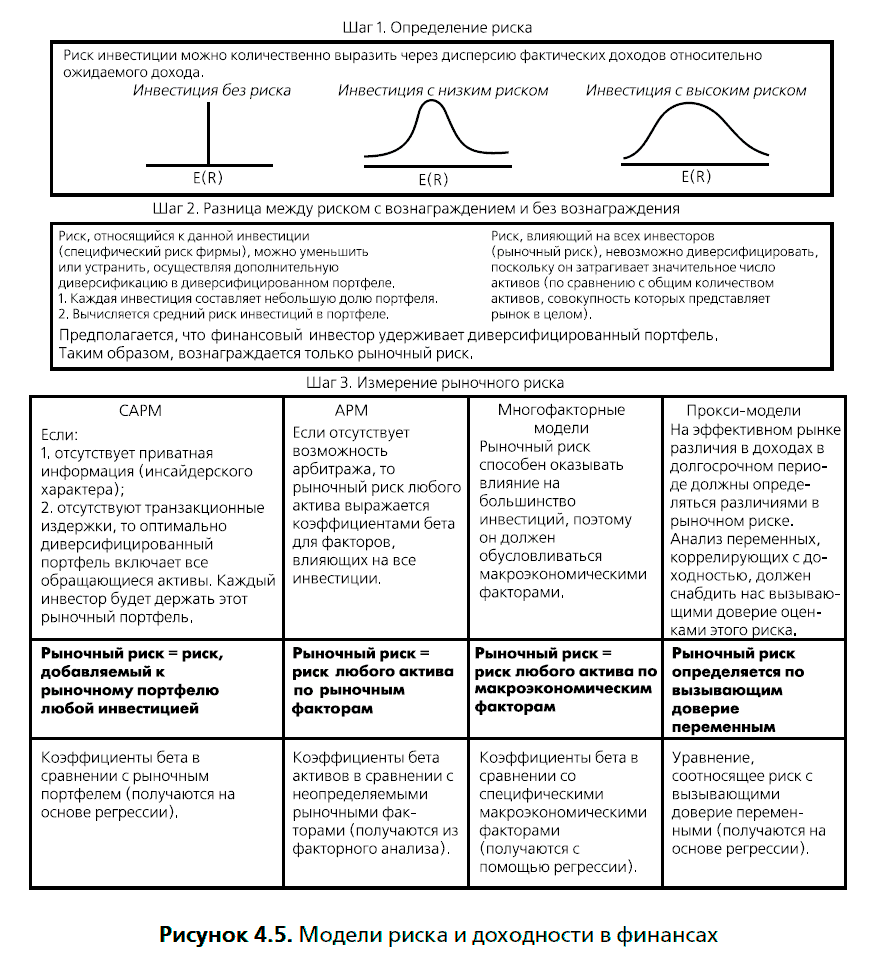
На рисунке 4.5 отображены все модели риска и доходности, применяемые в финансах. На первых двух шагах указаны их общие характеристики, а также различия в способе определения рыночного риска.
Как показано на этом рисунке, все модели риска и доходности, рассмотренные в этой главе, имеют некоторые общие предположения. Все они исходят из того, что только рыночный риск получает вознаграждение, а также выводят ожидаемый доход как функцию показателя этого риска. Модель оценки финансовых активов делает наиболее строгие предположения относительно того, как работает рынок, и все же оказывается самой простой моделью, где присутствует только один фактор, влияющий на риск и требующий оценки. Модель арбитражной оценки отличается меньшим числом предположений, но она оказывается и самой сложной моделью, по крайней мере с точки зрения требующих оценки параметров.
 Модель оценки финансовых активов можно рассматривать как особый случай модели арбитражной оценки, где есть только один базовый фактор, полностью выражаемый рыночным индексом. Как правило, преимущество модели САРМ заключается в простоте оценки и использования, однако она менее эффективна, чем более богатая модель АРМ, особенно когда инвестиции чувствительны к экономическим факторам, плохо представленным в рыночном индексе. Например, акции нефтяной компании, чей риск в основном связан с движением цен на нефть, как правило, имеют в модели CAPM низкие коэффициенты бета и низкие ожидаемые доходы. Использование модели арбитражной оценки, где один из факторов способен выразить движение цен на нефть и другие сырьевые товары, может дать лучшую оценку риска и более высокие ожидаемые доходы для этих фирм[28].
Модель оценки финансовых активов можно рассматривать как особый случай модели арбитражной оценки, где есть только один базовый фактор, полностью выражаемый рыночным индексом. Как правило, преимущество модели САРМ заключается в простоте оценки и использования, однако она менее эффективна, чем более богатая модель АРМ, особенно когда инвестиции чувствительны к экономическим факторам, плохо представленным в рыночном индексе. Например, акции нефтяной компании, чей риск в основном связан с движением цен на нефть, как правило, имеют в модели CAPM низкие коэффициенты бета и низкие ожидаемые доходы. Использование модели арбитражной оценки, где один из факторов способен выразить движение цен на нефть и другие сырьевые товары, может дать лучшую оценку риска и более высокие ожидаемые доходы для этих фирм[28].
Какая из этих моделей является наилучшей? Подходит ли коэффициент бета в качестве приблизительной оценки риска, и коррелирует ли этот показатель с ожидаемыми доходами? Эти вопросы широко обсуждались в течение двух последних десятилетий. Первые проверки модели САРМ показали, что коэффициенты бета и доходы имеют положительную корреляцию. В то же время и другие меры риска (например, дисперсия) продолжали объяснять различия в фактических доходах. Подобный разнобой был отнесен на счет ограничений в методах проверки. В 1977 г. Ролл в своей обширной критике тестов модели предположил, что поскольку рыночный портфель наблюдать невозможно, то модель САРМ соответственно протестирована быть не может, поэтому все тесты такого рода были совместными тестами – одновременно и для модели, и для рыночного портфеля, используемого в тестах. Другими словами, любой тест САРМ может показать только то, что данная модель работает (или нет) при конкретных предположениях, используемых применительно к рыночному портфелю. Следовательно, можно доказать, что в любом эмпирическом тесте, претендующем на критику САРМ, опровержение может касаться только аппроксимаций в отношении рыночного портфеля, а не самой модели. Ролл заметил, что такого способа, с помощью которого можно было бы доказать действенность модели САРМ, не существует, следовательно, отсутствует эмпирическая основа для использования этой модели.
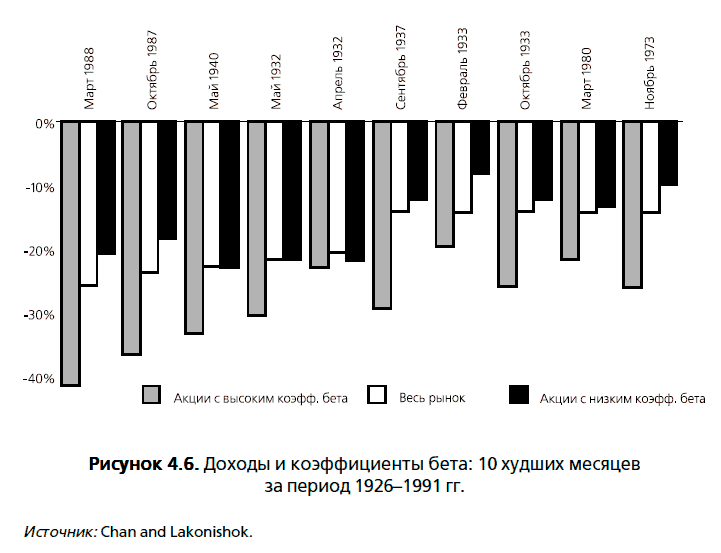
Фама и Френч (Fama and French, 1992) исследовали связь между коэффициентами бета и доходами за период 1963–1990 гг. и пришли к заключению, что корреляция между ними отсутствует. Эти результаты вызвали возражения по трем аспектам. Во-первых, Амихуд, Кристенсен и Мендельсон (Amihud, Christensen and Mendelson, 1992), которые использовали те же самые данные, но применяли другие статистические тесты, показали, что различия в коэффициентах бета фактически объясняют разницу в доходах за данный период. Во-вторых, Котари и Шанкен (Kothari and Shanken, 1995) оценили коэффициенты бета, используя при этом данные за год, а не за более короткие периоды времени, применяемые во многих тестах, и пришли к выводу, что коэффициенты бета объясняют в определенной пропорции различия между инвестициями. В-третьих, Чан и Лаконишок (Chan and Lakonishok, 1993) проанализировали временные ряды доходов за существенно более длительный период (1926–1991 гг.) и выявили положительную корреляцию между коэффициентами бета и доходами, которая была нарушена только в период после 1982 г. Они также обнаружили, что коэффициенты бета являются полезным инструментом для изучения риска в экстремальных рыночных условиях. При этом фирмы, связанные с наибольшим риском (10 % с наивысшим коэффициентом бета), функционируют куда менее эффективно, чем рынок в целом в течение 10 наихудших месяцев для рынка в период между 1926–1991 гг. (рисунок 4.6).
 Хотя первоначальные тесты APM обещали больший успех в объяснении различий в доходах, была проведена разделительная линия между использованием этих моделей для объяснения различий в доходах в прошлом и их применением для предсказания будущих доходов. Противники САРМ со всей очевидностью достигли более серьезного успеха в объяснении прошлых доходов, поскольку они не ограничивали себя одним фактором, как это делается в модели САРМ. Подобный учет значительного числа факторов становится более проблематичным, когда мы пытаемся планировать ожидаемые в будущем доходы, поскольку приходится оценивать коэффициенты бета и премии для каждого из этих факторов. Коэффициенты бета и премии для факторов сами по себе изменчивы, поэтому ошибка в оценке может уничтожить все преимущества, которые мы можем получить, переходя от модели САРМ к более сложным моделям. При использовании моделей регрессии, предлагаемых в качестве альтернативы, мы также сталкиваемся с трудностями при оценке, поскольку переменные, прекрасно работающие в качестве вызывающих доверие показателей риска в одном периоде (например, рыночная капитализация), могут оказаться неработоспособными в следующем периоде.
Хотя первоначальные тесты APM обещали больший успех в объяснении различий в доходах, была проведена разделительная линия между использованием этих моделей для объяснения различий в доходах в прошлом и их применением для предсказания будущих доходов. Противники САРМ со всей очевидностью достигли более серьезного успеха в объяснении прошлых доходов, поскольку они не ограничивали себя одним фактором, как это делается в модели САРМ. Подобный учет значительного числа факторов становится более проблематичным, когда мы пытаемся планировать ожидаемые в будущем доходы, поскольку приходится оценивать коэффициенты бета и премии для каждого из этих факторов. Коэффициенты бета и премии для факторов сами по себе изменчивы, поэтому ошибка в оценке может уничтожить все преимущества, которые мы можем получить, переходя от модели САРМ к более сложным моделям. При использовании моделей регрессии, предлагаемых в качестве альтернативы, мы также сталкиваемся с трудностями при оценке, поскольку переменные, прекрасно работающие в качестве вызывающих доверие показателей риска в одном периоде (например, рыночная капитализация), могут оказаться неработоспособными в следующем периоде.
В конечном итоге, живучесть модели оценки финансовых активов в качестве модели, используемой по умолчанию для оценки риска в условиях реального мира, оправдывается не только ее интуитивной привлекательностью, но и тем, что даже с помощью более сложных моделей не удалось внести существенный вклад в оценку ожидаемых доходов. По-видимому, наиболее эффективным способом обращения с риском в современных корпоративных финансах является рациональное использование модели оценки финансовых активов без чрезмерной опоры на исторические данные.
Как показано на этом рисунке, все модели риска и доходности, рассмотренные в этой главе, имеют некоторые общие предположения. Все они исходят из того, что только рыночный риск получает вознаграждение, а также выводят ожидаемый доход как функцию показателя этого риска. Модель оценки финансовых активов делает наиболее строгие предположения относительно того, как работает рынок, и все же оказывается самой простой моделью, где присутствует только один фактор, влияющий на риск и требующий оценки. Модель арбитражной оценки отличается меньшим числом предположений, но она оказывается и самой сложной моделью, по крайней мере с точки зрения требующих оценки параметров.

Какая из этих моделей является наилучшей? Подходит ли коэффициент бета в качестве приблизительной оценки риска, и коррелирует ли этот показатель с ожидаемыми доходами? Эти вопросы широко обсуждались в течение двух последних десятилетий. Первые проверки модели САРМ показали, что коэффициенты бета и доходы имеют положительную корреляцию. В то же время и другие меры риска (например, дисперсия) продолжали объяснять различия в фактических доходах. Подобный разнобой был отнесен на счет ограничений в методах проверки. В 1977 г. Ролл в своей обширной критике тестов модели предположил, что поскольку рыночный портфель наблюдать невозможно, то модель САРМ соответственно протестирована быть не может, поэтому все тесты такого рода были совместными тестами – одновременно и для модели, и для рыночного портфеля, используемого в тестах. Другими словами, любой тест САРМ может показать только то, что данная модель работает (или нет) при конкретных предположениях, используемых применительно к рыночному портфелю. Следовательно, можно доказать, что в любом эмпирическом тесте, претендующем на критику САРМ, опровержение может касаться только аппроксимаций в отношении рыночного портфеля, а не самой модели. Ролл заметил, что такого способа, с помощью которого можно было бы доказать действенность модели САРМ, не существует, следовательно, отсутствует эмпирическая основа для использования этой модели.
Фама и Френч (Fama and French, 1992) исследовали связь между коэффициентами бета и доходами за период 1963–1990 гг. и пришли к заключению, что корреляция между ними отсутствует. Эти результаты вызвали возражения по трем аспектам. Во-первых, Амихуд, Кристенсен и Мендельсон (Amihud, Christensen and Mendelson, 1992), которые использовали те же самые данные, но применяли другие статистические тесты, показали, что различия в коэффициентах бета фактически объясняют разницу в доходах за данный период. Во-вторых, Котари и Шанкен (Kothari and Shanken, 1995) оценили коэффициенты бета, используя при этом данные за год, а не за более короткие периоды времени, применяемые во многих тестах, и пришли к выводу, что коэффициенты бета объясняют в определенной пропорции различия между инвестициями. В-третьих, Чан и Лаконишок (Chan and Lakonishok, 1993) проанализировали временные ряды доходов за существенно более длительный период (1926–1991 гг.) и выявили положительную корреляцию между коэффициентами бета и доходами, которая была нарушена только в период после 1982 г. Они также обнаружили, что коэффициенты бета являются полезным инструментом для изучения риска в экстремальных рыночных условиях. При этом фирмы, связанные с наибольшим риском (10 % с наивысшим коэффициентом бета), функционируют куда менее эффективно, чем рынок в целом в течение 10 наихудших месяцев для рынка в период между 1926–1991 гг. (рисунок 4.6).

В конечном итоге, живучесть модели оценки финансовых активов в качестве модели, используемой по умолчанию для оценки риска в условиях реального мира, оправдывается не только ее интуитивной привлекательностью, но и тем, что даже с помощью более сложных моделей не удалось внести существенный вклад в оценку ожидаемых доходов. По-видимому, наиболее эффективным способом обращения с риском в современных корпоративных финансах является рациональное использование модели оценки финансовых активов без чрезмерной опоры на исторические данные.
МОДЕЛИ РИСКА ДЕФОЛТА
Пока в данной главе мы касались оценки риска, имеющего отношение к связанным с инвестициями денежным потокам, которые отличаются от ожидаемых. Однако есть определенные инвестиции, где денежные потоки обещаны в момент осуществления инвестиции. В качестве примера можно привести предоставление кредита какому-то предприятию или покупку корпоративной облигации. Заемщик может оказаться не в состоянии уплатить процентные или основные платежи по своему займу. Вообще говоря, заемщик с повышенным риском дефолта должен платить более высокий процент по займу, чем заемщик с меньшим риском дефолта. В этом разделе обсуждается измерение риска дефолта, а также связь между риском дефолта и процентными ставками по займам.
В отличие от общих моделей риска и доходности собственного капитала, оценивающих воздействие рыночного риска на ожидаемые доходы, модели риска дефолта измеряют последствия специфического (на уровне определенной фирмы) риска дефолта на обещанные доходы. Поскольку диверсификация способна объяснить, почему специфический риск фирмы не учитывается в ожидаемой доходности собственного капитала, то аналогичное обоснование можно применить к ценным бумагам, обладающим ограниченным потенциалом роста и значительно более существенным потенциалом снижения на основе событий, которые связаны с конкретной фирмой. Чтобы понять, что имеется в виду под ограниченным потенциалом роста, обсудим инвестирование в облигацию, выпущенную компанией. Купоны определяются в момент выпуска, и они представляют собой обещанные денежные потоки на облигацию. Лучший исход для инвестора – это получение обещанных денежных потоков. Инвестор не имеет права на получение большего, даже если компания оказывается более успешной. Все другие сценарии содержат только плохие новости, хотя и с разным уровнем последствий: поступающие денежные потоки оказываются меньше обещанных. Следовательно, ожидаемый доход по корпоративным облигациям, по всей вероятности, будет отражать специфический риск фирмы, выпускающей облигации.
Детерминанты риска дефолта
Риск дефолта фирмы является функцией двух переменных. Во-первых, определенную роль играет способность фирмы создавать денежные потоки благодаря своим основным операциям. Во-вторых, значение имеет финансовая задолженность фирмы, в том числе процентные и основные платежи[29]. Фирмы, создающие значительные по сравнению с финансовой задолженностью денежные потоки, должны обладать меньшим риском дефолта, чем фирмы, создающие денежные потоки, меньшие задолженности. Таким образом, фирмы с крупными инвестициями, производящие значительные денежные потоки, будут иметь меньший риск дефолта, чем фирмы, не обладающие подобным объемом инвестиций.
В отличие от общих моделей риска и доходности собственного капитала, оценивающих воздействие рыночного риска на ожидаемые доходы, модели риска дефолта измеряют последствия специфического (на уровне определенной фирмы) риска дефолта на обещанные доходы. Поскольку диверсификация способна объяснить, почему специфический риск фирмы не учитывается в ожидаемой доходности собственного капитала, то аналогичное обоснование можно применить к ценным бумагам, обладающим ограниченным потенциалом роста и значительно более существенным потенциалом снижения на основе событий, которые связаны с конкретной фирмой. Чтобы понять, что имеется в виду под ограниченным потенциалом роста, обсудим инвестирование в облигацию, выпущенную компанией. Купоны определяются в момент выпуска, и они представляют собой обещанные денежные потоки на облигацию. Лучший исход для инвестора – это получение обещанных денежных потоков. Инвестор не имеет права на получение большего, даже если компания оказывается более успешной. Все другие сценарии содержат только плохие новости, хотя и с разным уровнем последствий: поступающие денежные потоки оказываются меньше обещанных. Следовательно, ожидаемый доход по корпоративным облигациям, по всей вероятности, будет отражать специфический риск фирмы, выпускающей облигации.
Детерминанты риска дефолта
Риск дефолта фирмы является функцией двух переменных. Во-первых, определенную роль играет способность фирмы создавать денежные потоки благодаря своим основным операциям. Во-вторых, значение имеет финансовая задолженность фирмы, в том числе процентные и основные платежи[29]. Фирмы, создающие значительные по сравнению с финансовой задолженностью денежные потоки, должны обладать меньшим риском дефолта, чем фирмы, создающие денежные потоки, меньшие задолженности. Таким образом, фирмы с крупными инвестициями, производящие значительные денежные потоки, будут иметь меньший риск дефолта, чем фирмы, не обладающие подобным объемом инвестиций.
