Страница:
ВРЕМЕННАЯ СТРУКТУРА ПРОЦЕНТНЫХ СТАВОК
Временнáя структура процентных ставок – понятие, без которого невозможна оценка стоимости облигации. Именно поэтому в нашей книге ее описанию отведен пространный раздел.
Кривая доходности
Графическим изображением взаимосвязи между доходностями облигаций, имеющих одинаковое кредитное качество и разные сроки до погашения, служит кривая доходности. В прошлом инвесторы, как правило, строили кривую доходности на основании наблюдений над ценами и доходностями на рынке казначейских облигаций. Выбор рынка объясняется двояко. Во-первых, инвестиции в казначейские ценные бумаги не связаны с риском дефолта и разницы в кредитном качестве не влияют на доходности. Финансовые инструменты, таким образом, оказываются сравнимыми. Во-вторых, поскольку рынок казначейских ценных бумаг чрезвычайно обширен и активен, на нем с меньшей остротой стоят проблемы неликвидной или редкой торговли. Заметим, однако, что доходности казначейских ценных бумаг нередко могут быть занижены, поскольку значения доходностей могут отражать более выгодные возможности финансирования.
На рис. 5.1 представлены три наиболее типичные кривые доходности, наблюдающиеся на рынке.
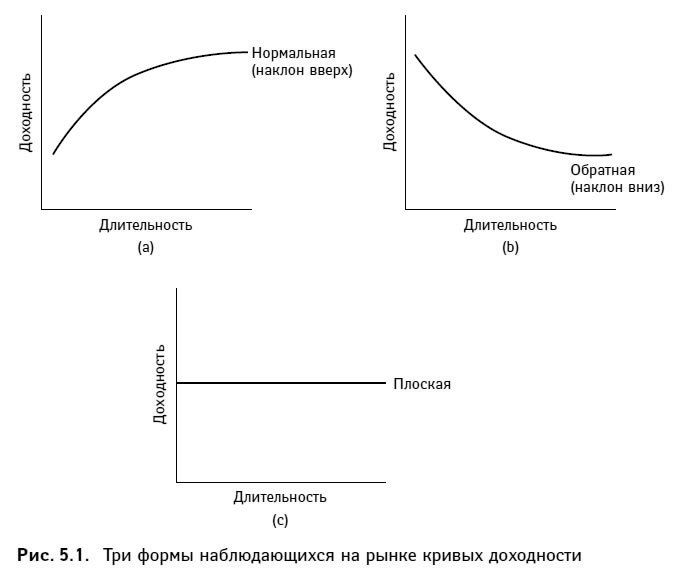С практической точки зрения ценность кривой доходности казначейских облигаций заключается в следующем: данная кривая служит эталоном при ценообразовании облигаций и определяет доходности в прочих секторах рынка долговых обязательств, т. е. на рынках банковских кредитов, ипотечного кредитования, корпоративного долга и международных облигаций. Между тем в настоящее время участники рынка склонны считать традиционно выстраиваемую кривую доходности казначейских ценных бумаг неудовлетворительным аналитическим инструментом для нахождения связи между требуемой доходностью и длительностью. Наиболее существенное из возражений против принятого метода связано с тем, что в реальной практике у ценных бумаг одинаковой длительности подчас бывает разная доходность. Далее мы покажем, что этот феномен отражает роль и влияние разницы в купонных ставках облигаций. Таким образом, мы оказываемся перед необходимостью разработать более точный и надежный способ построения кривой доходности казначейских ценных бумаг. В следующих разделах мы критически рассматриваем традиционную кривую доходности и предлагаем наиболее разумное решение проблемы построения такой кривой. Суть предлагаемого метода сводится к определению доходностей бескупонных облигаций: в этом случае влиянием купонной ставки на взаимосвязь доходность – длительность можно пренебречь.
На рис. 5.1 представлены три наиболее типичные кривые доходности, наблюдающиеся на рынке.
Почему при определении цены облигации не следует полагаться на кривую доходности
Цена облигации – это приведенная стоимость ее денежного потока. Напомним, что, обсуждая ценообразование облигаций в главе 2, мы исходили из того, что все денежные потоки облигации дисконтируются по одной процентной ставке. Процентная ставка вычислялась как сумма доходности казначейской ценной бумаги, длительность которой равна длительности облигации, и соответствующей премии за риск.
Между тем, как мы уже замечали, определение доходности, по которой дисконтируются денежные потоки облигации, через анализ кривой доходности казначейских ценных бумаг – занятие не всегда продуктивное. В качестве иллюстрации рассмотрим две гипотетические пятилетние казначейские облигации – облигацию А и облигацию В. Они отличаются только купонной ставкой: ставка на облигацию А составляет 12 %, а на облигацию В – 3 %. Денежный поток этих двух облигаций на $100 номинала для 10 полугодовых периодов (пять лет), оставшихся до погашения, равен:
Ввиду разной структуры денежных потоков было бы неправильным использовать одну и ту же процентную ставку для дисконтирования всех денежных потоков. Разумнее было бы дисконтировать каждый из денежных потоков по особой ставке, соответствующей периоду времени, в который данный поток поступит к инвестору. Остается выяснить, каким образом определить значения процентных ставок для каждого из периодов.
Попробуем представить себе, что ценные бумаги А и В – это не две облигации, а два «пакета» денежных потоков. Каждый из «пакетов» будет включать некоторое количество бескупонных инструментов. Заработанный инвестором процент по каждому из этих бескупонных инструментов будет равен разнице между номинальной стоимостью и ценой приобретения. Так, облигацию А можно рассматривать как 10 бескупонных инструментов: один имеет номинальную стоимость $6 и длительность полгода; второй – номинальную стоимость $6 и длительность год; третий – номинальную стоимость $6 и длительность полтора года и т. д. Последний бескупонный долговой инструмент имеет срок погашения, равный 10 полугодовым периодам, его номинальная стоимость составляет $106. Облигация В также может рассматриваться как 10 бескупонных инструментов: первые девять будут иметь номинальную стоимость $1,50; последний – номинальную стоимость $101,50. Очевидно, что стоимость, или цена, каждой из купонных облигаций (А и В) будет равна общей сумме стоимостей ее бескупонных компонентов.
В качестве набора бескупонных инструментов может рассматриваться любая облигация. Сроком погашения бескупонного инструмента, входящего в «пакет», будет считаться дата осуществления купонной выплаты или, если речь идет о номинале, дата погашения самой облигации. Стоимость облигации будет равна сумме стоимостей всех входящих в состав пакета бескупонных компонентов. Если же это равенство на практике не выполняется, то участнику рынка предоставляется возможность «расщепить» (strip) облигацию и через продажу стрипов на рынке получить безрисковую прибыль (подробнее см. главу 6).
Для того чтобы верно определить стоимость каждого из бескупонных инструментов, инвестору следует знать доходность бескупонной казначейской ценной бумаги той же длительности. Такая доходность носит название спот-ставки, а графическое изображение взаимосвязи между спот-ставкой и длительностью принято называть кривой спот-ставок. Поскольку наибольшая длительность бескупонных казначейских долговых обязательств – один год, такую кривую невозможно построить, исходя исключительно из наблюдений над реальной торговой активностью на рынке казначейских бумаг. Построение кривой спот-ставок основывается на теоретических выводах, сделанных на базе изучения доходностей реально торгующихся казначейских купонных долговых обязательств. Речь, таким образом, идет о кривой теоретических спот-ставок, являющейся наглядным отражением временной структуры процентных ставок.
Между тем, как мы уже замечали, определение доходности, по которой дисконтируются денежные потоки облигации, через анализ кривой доходности казначейских ценных бумаг – занятие не всегда продуктивное. В качестве иллюстрации рассмотрим две гипотетические пятилетние казначейские облигации – облигацию А и облигацию В. Они отличаются только купонной ставкой: ставка на облигацию А составляет 12 %, а на облигацию В – 3 %. Денежный поток этих двух облигаций на $100 номинала для 10 полугодовых периодов (пять лет), оставшихся до погашения, равен:
Попробуем представить себе, что ценные бумаги А и В – это не две облигации, а два «пакета» денежных потоков. Каждый из «пакетов» будет включать некоторое количество бескупонных инструментов. Заработанный инвестором процент по каждому из этих бескупонных инструментов будет равен разнице между номинальной стоимостью и ценой приобретения. Так, облигацию А можно рассматривать как 10 бескупонных инструментов: один имеет номинальную стоимость $6 и длительность полгода; второй – номинальную стоимость $6 и длительность год; третий – номинальную стоимость $6 и длительность полтора года и т. д. Последний бескупонный долговой инструмент имеет срок погашения, равный 10 полугодовым периодам, его номинальная стоимость составляет $106. Облигация В также может рассматриваться как 10 бескупонных инструментов: первые девять будут иметь номинальную стоимость $1,50; последний – номинальную стоимость $101,50. Очевидно, что стоимость, или цена, каждой из купонных облигаций (А и В) будет равна общей сумме стоимостей ее бескупонных компонентов.
В качестве набора бескупонных инструментов может рассматриваться любая облигация. Сроком погашения бескупонного инструмента, входящего в «пакет», будет считаться дата осуществления купонной выплаты или, если речь идет о номинале, дата погашения самой облигации. Стоимость облигации будет равна сумме стоимостей всех входящих в состав пакета бескупонных компонентов. Если же это равенство на практике не выполняется, то участнику рынка предоставляется возможность «расщепить» (strip) облигацию и через продажу стрипов на рынке получить безрисковую прибыль (подробнее см. главу 6).
Для того чтобы верно определить стоимость каждого из бескупонных инструментов, инвестору следует знать доходность бескупонной казначейской ценной бумаги той же длительности. Такая доходность носит название спот-ставки, а графическое изображение взаимосвязи между спот-ставкой и длительностью принято называть кривой спот-ставок. Поскольку наибольшая длительность бескупонных казначейских долговых обязательств – один год, такую кривую невозможно построить, исходя исключительно из наблюдений над реальной торговой активностью на рынке казначейских бумаг. Построение кривой спот-ставок основывается на теоретических выводах, сделанных на базе изучения доходностей реально торгующихся казначейских купонных долговых обязательств. Речь, таким образом, идет о кривой теоретических спот-ставок, являющейся наглядным отражением временной структуры процентных ставок.
Построение кривой теоретических спот-ставок казначейских ценных бумаг[32]
Идеальная кривая теоретических спот-ставок может быть получена на основе значений доходностей казначейских долговых обязательств. В качестве исходных данных выбираются данные о доходностях:
1) казначейских облигаций «в ходу»; либо
2) казначейских облигаций «в ходу» и избранных казначейских облигаций «не в ходу»; либо
3) всех казначейских купонных облигаций и векселей; либо
4) стрипов казначейских купонных ценных бумаг.
(Каждый из типов казначейских ценных бумаг подробно описан в следующей главе). После того как будут выбраны ценные бумаги, анализ которых даст возможность построить кривую теоретических спот-ставок, следует определить методологию построения кривой. Тип методологии зависит от вида ценных бумаг. Если в качестве материала используются стрипы купонных облигаций, процедура будет простой, поскольку наблюдаемые доходности равны спот-ставкам. Если кривая строится исходя из доходностей казначейских облигаций «в ходу» (вместе с ними могут рассматриваться избранные казначейские облигации «не в ходу»), применяется методология, известная как «бутстреппинг» (bootstrapping). Если рассматриваются сразу все купонные казначейские облигации и векселя, приходится прибегать к помощи сложных статистических методов.
Казначейские облигационные выпуски «в ходу». Казначейскимиоблигациями «в ходу» называют долговые обязательства данной длительности, размещенные на аукционе в самое последнее время. К этой категории относятся казначейские векселя сроком погашения 3 месяца, 6 месяцев и 1 год; казначейские ноты длительностью 2 года, 5 лет и 10 лет; а также казначейские облигации длительностью 30 лет. Казначейские векселя являются бескупонными инструментами, ноты и облигации – это ценные бумаги с купонными выплатами.
Для каждой из ценных бумаг «в ходу» известны значения наблюдаемых доходностей (см., например, табл. 5.1). (Напомним, что в настоящее время казначейские облигации длительностью 3 года больше не выпускаются.) Между тем при построении кривой данные значения (за исключением случаев, когда облигация торгуется по номиналу) не используются. Для каждой из купонных ценных бумаг «в ходу» находится значение доходности, необходимой для того, чтобы данная бумага торговалась по номиналу, – именно эти цифры становятся затем основой построения кривой. Полученная кривая доходности казначейских облигаций «в ходу» носит название номинальной купонной кривой.
Цель исследования – построение кривой теоретических спот-ставок с 60 полугодовыми спот-ставками: от полугодовой спот-ставки до ставки 30-летней. Казначейские облигационные выпуски «в ходу» предлагают нам всего шесть значений длительностей (трехмесячные векселя в расчет не принимаются). Недостающие 54 значения интерполируются из наиболее близких точек номинальной кривой доходности. Самый простой и наиболее часто употребляемый способ интерполяции – это линейная экстраполяция. Имея значения доходностей для двух длительностей на номинальной купонной кривой, мы можем провести следующие вычисления:
Доходности для всех промежуточных полугодовых точек на шкале длительности вычисляются путем прибавления к доходности для наименьшей из длительностей полученного согласно формуле результата.
Предположим, например, что на номинальной кривой доходности казначейских облигаций «в ходу» значения доходностей для длительностей два года и пять лет составляют соответственно 6 % и 6,6 %. Между этими двумя точками на шкале длительности умещается шесть полугодовых периодов. Экстраполированные доходности для длительностей 2; 2,5; 3; 3,5; 4; и 4,5 находятся следующим образом.
Сначала получим:
Затем:
Покажем теперь, каким образом с помощью метода бутстреппинга номинальная кривая доходности может быть превращена в кривую теоретических спот-ставок. Для упрощения процедуры мы будем строить кривую теоретических спот-ставок для временного промежутка, равного 10 годам. Нам предстоит, следовательно, подсчитать значения 20 полугодовых спот-ставок. За номинальную кривую возьмем кривую, представленную в табл. 5.3[33].
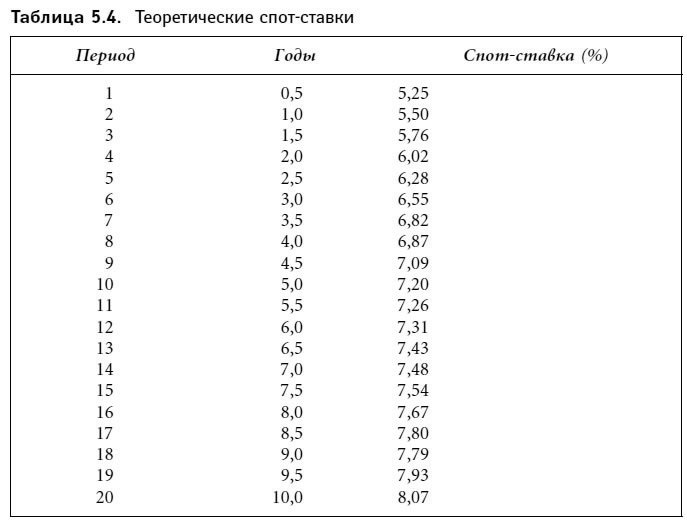
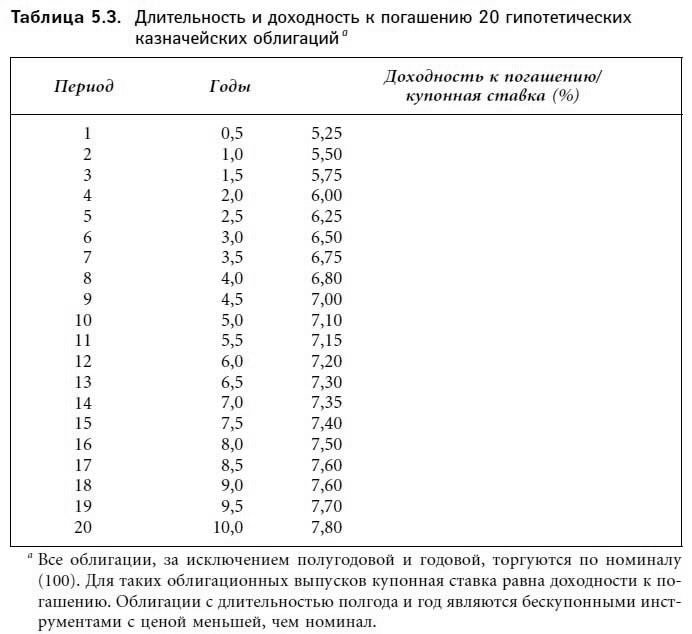Процедура построения кривой теоретических спот-ставок на основе наблюдаемых доходностей казначейских ценных бумаг иллюстрируется на примере данных о цене, годовой доходности (доходности к погашению) и длительности 20 гипотетических казначейских облигаций, представленных в табл. 5.4. Предполагается, что рыночная цена каждой из облигаций равна ее номинальной стоимости. Таким образом, доходность к погашению и купонная ставка совпадают.
В ходе дальнейших рассуждений мы будем опираться на высказанное ранее утверждение: стоимость купонной казначейской ценной бумаги равна стоимости «пакета» бескупонных казначейских ценных бумаг, денежные потоки по которым имеют размер денежных потоков, поступающих от купонных выплат.
Рассмотрим представленный в табл. 5.4 казначейский вексель со сроком погашения шесть месяцев. В главе 6 мы расскажем о том, что казначейские векселя являются бескупонными инструментами; таким образом, годовая доходность в 5,25 % равна в этом случае спот-ставке. Для казначейского векселя с длительностью один год доходность 5,5 % также равна годовой спот-ставке. На основании данных двух спот-ставок мы можем вычислить спот-ставку теоретической бескупонной казначейской облигации с длительностью 1,5 года. Цена теоретической бескупонной казначейской ценной бумаги со сроком погашения 1,5 года будет равна приведенной стоимости трех денежных потоков реальной купонной казначейской облигации с длительностью 1,5 года; доходность, используемая для дисконтирования в этом случае, и будет спот-ставкой, соответствующей данному денежному потоку. В табл. 5.4 приводится купонная ставка казначейской облигации с длительностью 1,5 года; она равна 5,75 %. При номинале в $100 денежный поток для этой казначейской ценной бумаги может быть вычислен как:
где:
z1 – половина шестимесячной теоретической спот-ставки, выраженной в процентах годовых;
z2 – половина годовой теоретической спот-ставки;
z3 – половина полуторагодовой теоретической спот-ставки, выраженной в процентах годовых.
Поскольку значения полугодовой и годовой спот-ставки составляют соответственно 5,25 % и 5,50 %, мы знаем, что:
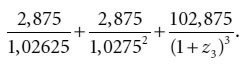Поскольку цена купонной казначейской облигации длительностью 1,5 года составляет $100, можно считать верным следующее равенство:
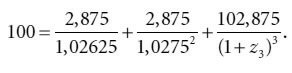Теоретическая полуторагодовая спот-ставка находится как:
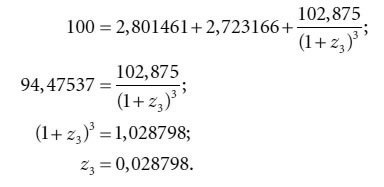Удвоив эту доходность, получим доходность, эквивалентную облигационной, в размере 0,0576, т. е. 5,76 %. Это и есть теоретическая спот-ставка для длительности полтора года, т. е. ставка, под которую торговались бы на рынке полуторагодовые бескупонные ценные бумаги, если бы они существовали в действительности.
Зная теоретическую спот-ставку для полутора лет, мы можем найти теоретическую спот-ставку для длительности 2 года. Денежный поток двухлетней купонной казначейской ценной бумаги, представленной в табл. 5.3, равен:
где z4 – половина теоретической спот-ставки для длительности два года. Поскольку полугодовая спот-ставка, годовая спот-ставка и полуторагодовая спот-ставка составляют соответственно 5,25 %, 5,50 % и 5,76 %, то:
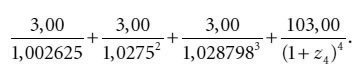Зная, что цена двухлетней купонной казначейской облигации составляет $100, мы можем записать следующее отношение:
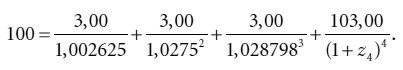Теоретическая спот-ставка для длительности два года вычисляется следующим образом:
Удвоив полученную доходность, мы найдем значение доходности, эквивалентной облигационной, – иными словами, значение теоретической двухлетней спот-ставки – оно равно 6,02 %.
Предлагаем читателю самостоятельно продолжить наши рассуждения и найти теоретическую спот-ставку для длительности 2,5 года. Напомним, что для этого понадобятся полученные выше величины z1, z2, z3, z4 (спот-ставки для длительностей 6 месяцев, год, полтора и два года), а также значение цены и купонов облигации со сроком погашения 2,5 года. Аналогичным образом могут быть получены теоретические спот-ставки для всех прочих 15 полугодовых промежутков.
Спот-ставки, вычисленные нами, собраны в табл. 5.4. Представленные здесь данные – это временная структура процентных ставок для длительностей до 10 лет в момент, соответствующий данным котировкам цены.
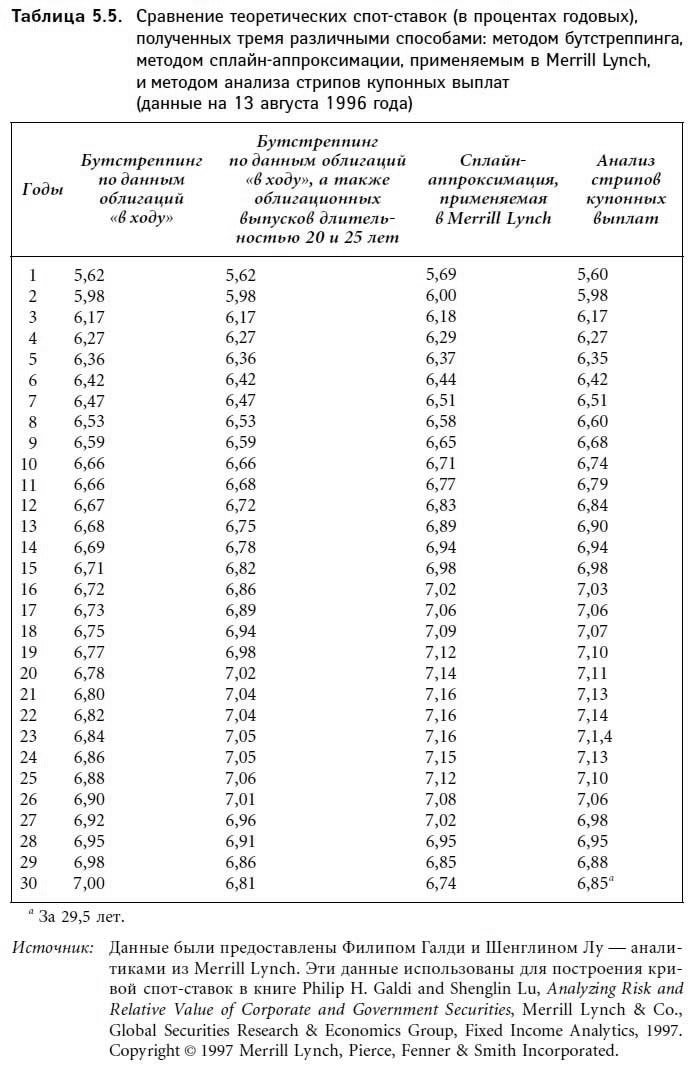
В табл. 5.5 собраны характеристики кривой теоретических спот-ставок, построенной 13 августа 1996 года методом бутстреппинга на материале облигаций «в ходу». Здесь же приводятся значения ставок, полученные в результате анализа купонных стрипов. Обратите внимание: после точки на шкале длительности, соответствующей шести годам, значения, полученные бутстреппингом, и значения, наблюдаемые на материале стрипов, существенно расходятся.
Казначейские облигации «в ходу» и избранные казначейские облигации «не в ходу». Как мы уже писали, один из недостатков использования исключительно казначейских облигаций «в ходу» обусловлен существованием больших «провалов» между датами погашения, в особенности после длительности пять лет. Для устранения неточностей, объясняемых этим обстоятельством, часть дилеров привлекает в качестве материала некоторые избранные казначейские облигации «не в ходу». Как правило, в этом случае используются облигации сроком погашения 20 и 25 лет. Для заполнения оставшихся «пустот» используется метод линейной экстраполяции. Напомним, что номинальная кривая включает на этот раз данные об избранных казначейских бумагах «не в ходу». Построение кривой теоретических спот-ставок проходит методом бутстреппинга.
В табл. 5.5 приводятся теоретические спот-ставки, полученные 13 августа 1996 года на данных: 1) исключительно облигаций «в ходу»; 2) облигаций «в ходу» плюс облигаций «не в ходу» длительностью 20 и 25 лет. Здесь же суммируются результаты вычислений, проделанных на основе анализа стрипов купонных выплат казначейских ценных бумаг. Заметим, что кривая теоретических спот-ставок в случае, когда облигации «в ходу» дополнены 20– и 25-летними облигационными выпусками «не в ходу», располагается намного ближе к кривой стрипов купонных облигаций.
Все казначейские купонные облигации и векселя. Используя в качестве материала для анализа только ценные бумаги «в ходу», дополненные или не дополненные избранными облигационными выпусками «не в ходу», инвестор оказывается не в состоянии учесть всю полноту информации о ценах на казначейские облигации. Часть исследователей полагает поэтому, что достоверная кривая теоретических спот-ставок может быть построена только исходя из данных обо всех казначейских облигациях и векселях. Заметим, что казначейские облигации со встроенным колл-опционом при этом, как правило, из материалов анализа исключаются[34].
Построение кривой теоретических спот-ставок на основании всех купонных казначейских облигаций и векселей проводится с помощью статистических методов: бутстреппинг не действует, поскольку для каждой длительности может существовать более одного значения доходности. Для построения кривой спот-ставок в разное время было предложено несколько различных статистических техник. Наиболее распространенной является сплайн-аппроксимация[35]. В статистическую модель могут быть включены также поправки на характерные для американских казначейских ценных бумаг эффекты налогообложения и возможного исполнения колл-опциона. Обсуждение достоинств и недостатков данного статистического метода не входит в настоящее время в рамки нашего обсуждения[36].
В табл. 5.5 приведены сравнительные результаты вычисления теоретических спот-ставок, полученных 13 августа 1996 года на основе метода сплайн-аппроксимации в том виде, в котором он был разработан в Merrill Lynch, и метода бутстреппинга. Обратите внимание на то, как близко к кривой стрипов купонных выплат подходит кривая спот-ставок, построенная с помощью метода сплайн-аппроксимации, – это особенно заметно на длительностях больше шести лет.
Стрипы купонных казначейских облигаций. Из текста следующей главы мы узнаем, что стрипы купонных казначейских облигаций – это бескупонные казначейские финансовые инструменты. Вместо того чтобы идти по длинному и трудоемкому пути, описанному нами выше, было бы логично строить кривую спот-ставок на основании реально наблюдаемых доходностей стрипов. Между тем исследователь, использующий в ходе анализа наблюдаемые доходности стрипов, сталкивается с тремя видами трудностей. Во-первых, ликвидность рынка стрипов не так высока, как ликвидность рынка казначейских купонных ценных бумаг. Наблюдаемые ставки, таким образом, отражают премию за ликвидность.
Во-вторых, налогообложение стрипов отличается от налогообложения казначейских купонных ценных бумаг. В частности, налогом облагается накопленный купонный доход от стрипов, даже если сам инвестор при этом денег наличными не получил. С точки зрения налогооблагаемых юридических лиц, эта ценная бумага дает отрицательный денежный поток – очевидно, что данное неудобство также отражается на значении ее доходности.
И наконец, стрипами некоторых длительностей активно торгуют некоторые неамериканские инвесторы, руководствующиеся в этом случае соображениями более выгодного налогообложения. Так, налоговые законодательства некоторых иностранных государств позволяют своим гражданам рассматривать разницу между номинальной стоимостью и ценой покупки как прирост капитала, который облагается налогом по щадящей ставке. Иногда такая льготная ставка применяется только для стрипов, созданных на основе номинала, а не купона. Именно поэтому для построения кривой спот-ставок используются только стрипы купонных казначейских бумаг.
1) казначейских облигаций «в ходу»; либо
2) казначейских облигаций «в ходу» и избранных казначейских облигаций «не в ходу»; либо
3) всех казначейских купонных облигаций и векселей; либо
4) стрипов казначейских купонных ценных бумаг.
(Каждый из типов казначейских ценных бумаг подробно описан в следующей главе). После того как будут выбраны ценные бумаги, анализ которых даст возможность построить кривую теоретических спот-ставок, следует определить методологию построения кривой. Тип методологии зависит от вида ценных бумаг. Если в качестве материала используются стрипы купонных облигаций, процедура будет простой, поскольку наблюдаемые доходности равны спот-ставкам. Если кривая строится исходя из доходностей казначейских облигаций «в ходу» (вместе с ними могут рассматриваться избранные казначейские облигации «не в ходу»), применяется методология, известная как «бутстреппинг» (bootstrapping). Если рассматриваются сразу все купонные казначейские облигации и векселя, приходится прибегать к помощи сложных статистических методов.
Казначейские облигационные выпуски «в ходу». Казначейскимиоблигациями «в ходу» называют долговые обязательства данной длительности, размещенные на аукционе в самое последнее время. К этой категории относятся казначейские векселя сроком погашения 3 месяца, 6 месяцев и 1 год; казначейские ноты длительностью 2 года, 5 лет и 10 лет; а также казначейские облигации длительностью 30 лет. Казначейские векселя являются бескупонными инструментами, ноты и облигации – это ценные бумаги с купонными выплатами.
Для каждой из ценных бумаг «в ходу» известны значения наблюдаемых доходностей (см., например, табл. 5.1). (Напомним, что в настоящее время казначейские облигации длительностью 3 года больше не выпускаются.) Между тем при построении кривой данные значения (за исключением случаев, когда облигация торгуется по номиналу) не используются. Для каждой из купонных ценных бумаг «в ходу» находится значение доходности, необходимой для того, чтобы данная бумага торговалась по номиналу, – именно эти цифры становятся затем основой построения кривой. Полученная кривая доходности казначейских облигаций «в ходу» носит название номинальной купонной кривой.
Цель исследования – построение кривой теоретических спот-ставок с 60 полугодовыми спот-ставками: от полугодовой спот-ставки до ставки 30-летней. Казначейские облигационные выпуски «в ходу» предлагают нам всего шесть значений длительностей (трехмесячные векселя в расчет не принимаются). Недостающие 54 значения интерполируются из наиболее близких точек номинальной кривой доходности. Самый простой и наиболее часто употребляемый способ интерполяции – это линейная экстраполяция. Имея значения доходностей для двух длительностей на номинальной купонной кривой, мы можем провести следующие вычисления:
Предположим, например, что на номинальной кривой доходности казначейских облигаций «в ходу» значения доходностей для длительностей два года и пять лет составляют соответственно 6 % и 6,6 %. Между этими двумя точками на шкале длительности умещается шесть полугодовых периодов. Экстраполированные доходности для длительностей 2; 2,5; 3; 3,5; 4; и 4,5 находятся следующим образом.
Сначала получим:
Вычисления, основанные исключительно на облигациях «в ходу», неудобны с двух точек зрения. Во-первых, две точки на шкале длительности могут быть разделены значительным расстоянием и метод линейной интерполяции, который будет применен для вычисления промежуточных доходностей, даст в этом случае весьма приблизительный результат. Данное замечание в первую очередь касается промежутков между длительностями 5 и 10 лет и 10 и 30 лет. Вторая сложность связана с анализом самих наблюдаемых доходностей облигаций «в ходу»: как мы знаем, большинство из них отражает благоприятные возможности финансирования, которые предоставляются таким ценным бумагам на рынке репо. Реальная доходность, таким образом, окажется выше котируемой (наблюдаемой).доходность для 2,5 лет = 6,00 % + 0,10 % = 6,10 %;
доходность для 3 лет = 6,10 % + 0,10 % = 6,20 %;
доходность для 3,5 лет = 6,20 % + 0,10 % = 6,30 %;
доходность для 4 лет = 6,30 % + 0,10 % = 6,40 %;
доходность для 4,5 лет = 6,40 % + 0,10 % = 6,50 %.
Покажем теперь, каким образом с помощью метода бутстреппинга номинальная кривая доходности может быть превращена в кривую теоретических спот-ставок. Для упрощения процедуры мы будем строить кривую теоретических спот-ставок для временного промежутка, равного 10 годам. Нам предстоит, следовательно, подсчитать значения 20 полугодовых спот-ставок. За номинальную кривую возьмем кривую, представленную в табл. 5.3[33].
В ходе дальнейших рассуждений мы будем опираться на высказанное ранее утверждение: стоимость купонной казначейской ценной бумаги равна стоимости «пакета» бескупонных казначейских ценных бумаг, денежные потоки по которым имеют размер денежных потоков, поступающих от купонных выплат.
Рассмотрим представленный в табл. 5.4 казначейский вексель со сроком погашения шесть месяцев. В главе 6 мы расскажем о том, что казначейские векселя являются бескупонными инструментами; таким образом, годовая доходность в 5,25 % равна в этом случае спот-ставке. Для казначейского векселя с длительностью один год доходность 5,5 % также равна годовой спот-ставке. На основании данных двух спот-ставок мы можем вычислить спот-ставку теоретической бескупонной казначейской облигации с длительностью 1,5 года. Цена теоретической бескупонной казначейской ценной бумаги со сроком погашения 1,5 года будет равна приведенной стоимости трех денежных потоков реальной купонной казначейской облигации с длительностью 1,5 года; доходность, используемая для дисконтирования в этом случае, и будет спот-ставкой, соответствующей данному денежному потоку. В табл. 5.4 приводится купонная ставка казначейской облигации с длительностью 1,5 года; она равна 5,75 %. При номинале в $100 денежный поток для этой казначейской ценной бумаги может быть вычислен как:
Тогда приведенная стоимость денежного потока будет равна:0,5 года: 0,0575 × $100 × 0,5 = $2,875;
1 год: 0,0575 × $100 × 0,5 = 2,875;
1,5 года: 0,0575 × $100 × 0,5 + 100 = 102,875.
z1 – половина шестимесячной теоретической спот-ставки, выраженной в процентах годовых;
z2 – половина годовой теоретической спот-ставки;
z3 – половина полуторагодовой теоретической спот-ставки, выраженной в процентах годовых.
Поскольку значения полугодовой и годовой спот-ставки составляют соответственно 5,25 % и 5,50 %, мы знаем, что:
Приведенная стоимость полуторагодовой купонной казначейской облигации может быть вычислена как:z1 = 0,02625, а z2 = 0,0275.
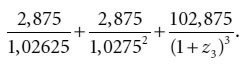
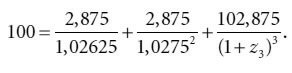
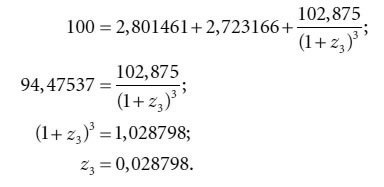
Зная теоретическую спот-ставку для полутора лет, мы можем найти теоретическую спот-ставку для длительности 2 года. Денежный поток двухлетней купонной казначейской ценной бумаги, представленной в табл. 5.3, равен:
Тогда приведенная стоимость денежного потока равна:0,5 лет: 0,060 × $100 × 0,5 = $3,00;
1 год: 0,060 × $100 × 0,5 = 3,00;
1,5 года: 0,060 × $100 × 0,5 = 3,00;
2 года: 0,060 × $100 × 0,5 + 100 = 103,00.
Таким образом, приведенная стоимость двухлетней купонной казначейской облигации будет равна:z 1 = 0,02625; z 2 = 0,0275; z 3 = 0,028798.
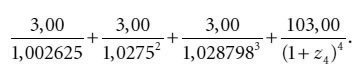
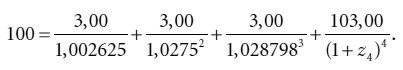
Предлагаем читателю самостоятельно продолжить наши рассуждения и найти теоретическую спот-ставку для длительности 2,5 года. Напомним, что для этого понадобятся полученные выше величины z1, z2, z3, z4 (спот-ставки для длительностей 6 месяцев, год, полтора и два года), а также значение цены и купонов облигации со сроком погашения 2,5 года. Аналогичным образом могут быть получены теоретические спот-ставки для всех прочих 15 полугодовых промежутков.
Спот-ставки, вычисленные нами, собраны в табл. 5.4. Представленные здесь данные – это временная структура процентных ставок для длительностей до 10 лет в момент, соответствующий данным котировкам цены.
В табл. 5.5 собраны характеристики кривой теоретических спот-ставок, построенной 13 августа 1996 года методом бутстреппинга на материале облигаций «в ходу». Здесь же приводятся значения ставок, полученные в результате анализа купонных стрипов. Обратите внимание: после точки на шкале длительности, соответствующей шести годам, значения, полученные бутстреппингом, и значения, наблюдаемые на материале стрипов, существенно расходятся.
В табл. 5.5 приводятся теоретические спот-ставки, полученные 13 августа 1996 года на данных: 1) исключительно облигаций «в ходу»; 2) облигаций «в ходу» плюс облигаций «не в ходу» длительностью 20 и 25 лет. Здесь же суммируются результаты вычислений, проделанных на основе анализа стрипов купонных выплат казначейских ценных бумаг. Заметим, что кривая теоретических спот-ставок в случае, когда облигации «в ходу» дополнены 20– и 25-летними облигационными выпусками «не в ходу», располагается намного ближе к кривой стрипов купонных облигаций.
Построение кривой теоретических спот-ставок на основании всех купонных казначейских облигаций и векселей проводится с помощью статистических методов: бутстреппинг не действует, поскольку для каждой длительности может существовать более одного значения доходности. Для построения кривой спот-ставок в разное время было предложено несколько различных статистических техник. Наиболее распространенной является сплайн-аппроксимация[35]. В статистическую модель могут быть включены также поправки на характерные для американских казначейских ценных бумаг эффекты налогообложения и возможного исполнения колл-опциона. Обсуждение достоинств и недостатков данного статистического метода не входит в настоящее время в рамки нашего обсуждения[36].
В табл. 5.5 приведены сравнительные результаты вычисления теоретических спот-ставок, полученных 13 августа 1996 года на основе метода сплайн-аппроксимации в том виде, в котором он был разработан в Merrill Lynch, и метода бутстреппинга. Обратите внимание на то, как близко к кривой стрипов купонных выплат подходит кривая спот-ставок, построенная с помощью метода сплайн-аппроксимации, – это особенно заметно на длительностях больше шести лет.
Стрипы купонных казначейских облигаций. Из текста следующей главы мы узнаем, что стрипы купонных казначейских облигаций – это бескупонные казначейские финансовые инструменты. Вместо того чтобы идти по длинному и трудоемкому пути, описанному нами выше, было бы логично строить кривую спот-ставок на основании реально наблюдаемых доходностей стрипов. Между тем исследователь, использующий в ходе анализа наблюдаемые доходности стрипов, сталкивается с тремя видами трудностей. Во-первых, ликвидность рынка стрипов не так высока, как ликвидность рынка казначейских купонных ценных бумаг. Наблюдаемые ставки, таким образом, отражают премию за ликвидность.
Во-вторых, налогообложение стрипов отличается от налогообложения казначейских купонных ценных бумаг. В частности, налогом облагается накопленный купонный доход от стрипов, даже если сам инвестор при этом денег наличными не получил. С точки зрения налогооблагаемых юридических лиц, эта ценная бумага дает отрицательный денежный поток – очевидно, что данное неудобство также отражается на значении ее доходности.
И наконец, стрипами некоторых длительностей активно торгуют некоторые неамериканские инвесторы, руководствующиеся в этом случае соображениями более выгодного налогообложения. Так, налоговые законодательства некоторых иностранных государств позволяют своим гражданам рассматривать разницу между номинальной стоимостью и ценой покупки как прирост капитала, который облагается налогом по щадящей ставке. Иногда такая льготная ставка применяется только для стрипов, созданных на основе номинала, а не купона. Именно поэтому для построения кривой спот-ставок используются только стрипы купонных казначейских бумаг.
Применение кривой теоретических спот-ставок
Покажем теперь, каким образом спот-ставки помогают оценить облигацию. В главе 2 мы описали процесс ценообразования, исходя из предположения о том, что все денежные потоки дисконтируются по единой дисконтной ставке. Таблица 5.6 демонстрирует, как можно оценить действительную стоимость казначейской облигации с помощью теоретических спот-ставок. Облигация, о которой идет речь, – гипотетическая десятилетняя казначейская ценная бумага с купонной ставкой 10 %.
Третья колонка таблицы дает представление о денежном потоке на $100 номинала в каждый из 20 полугодовых периодов. Четвертая колонка – теоретическая спот-ставка для каждой длительности, представленной в табл. 5.4. Пятая колонка демонстрирует дисконтированную по теоретической спот-ставке из четвертой колонки приведенную стоимость $1. Последняя колонка показывает приведенную стоимость денежного потока, найденную умножением значений третьей и пятой колонок. Теоретическая цена нашей облигации складывается из сумм приведенных стоимостей, стоящих в последней колонке; она равна $115,4206.
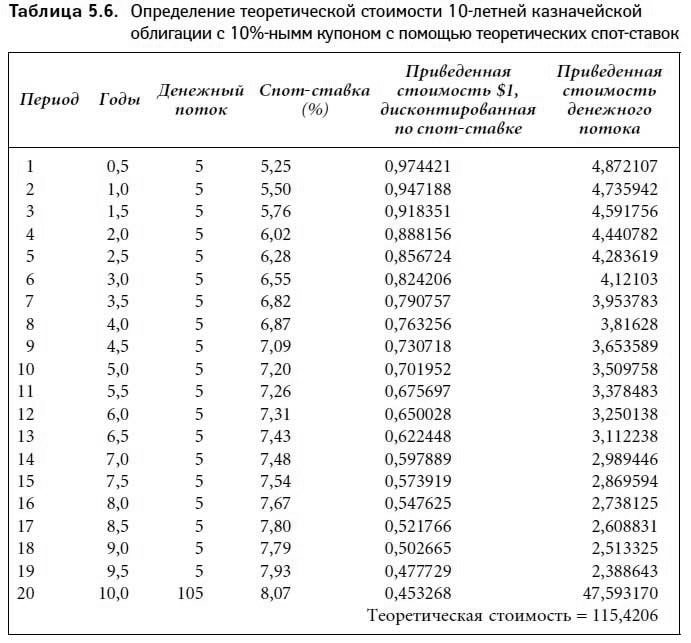Мы установили, что цена казначейской облигации должна быть равна приведенной стоимости ее денежного потока, причем каждая из составляющих общего денежного потока дисконтируется по особой теоретической спот-ставке. Возникает вопрос: что заставляет оценивать казначейскую облигацию в соответствии со спот-ставкой? Ответ прост: в качестве действующей силы здесь выступает арбитраж. Вспомним, что теоретическая цена $115,4206 может рассматриваться как стоимость «пакета» бескупонных инструментов: если наша 10-летняя казначейская ценная бумага с 10 %-ным купоном будет куплена, а затем расщеплена и продана, то выручка от продажи составит $115,4206. Полученные ценные бумаги – стрипы – будут подробно описаны в главе 6.
Третья колонка таблицы дает представление о денежном потоке на $100 номинала в каждый из 20 полугодовых периодов. Четвертая колонка – теоретическая спот-ставка для каждой длительности, представленной в табл. 5.4. Пятая колонка демонстрирует дисконтированную по теоретической спот-ставке из четвертой колонки приведенную стоимость $1. Последняя колонка показывает приведенную стоимость денежного потока, найденную умножением значений третьей и пятой колонок. Теоретическая цена нашей облигации складывается из сумм приведенных стоимостей, стоящих в последней колонке; она равна $115,4206.