Страница:
Предположим теперь, что рынок оценил 10-летнюю казначейскую облигацию с 10 %-ным купоном исходя из доходности к погашению 10-летних казначейских ценных бумаг, представленной на кривой доходности. Из табл. 5.3 видно, что доходность к погашению 10-летней казначейской ценной бумаги равна 7,8 %. Если 10-летняя казначейская ценная бумага с купоном 10 % оценивается с помощью дисконтной ставки 7,8 %, ее цена равна $115,0826 – числу, меньшему, чем ее теоретическая стоимость. Дилер рынка казначеских бумаг, имеющий возможность приобрести казначейскую облигацию по $115,0826, купит ее, затем расщепит и продаст полученные бескупонные инструменты. Как мы только что видели, выручка от продажи стрипов в этом случае составит $115,4206. Дилер, таким образом, заработает арбитражную прибыль в размере $0,338 на $100 номинала. Стремление дилеров получить такую арбитражную прибыль приведет к движению цен на данную казначейскую облигацию. Арбитраж перестанет существовать только в момент, когда цена достигнет значения $115,4206, т. е. сравняется с теоретической стоимостью, предполагающей, что денежные потоки дисконтированы по теоретическим спот-ставкам. Наш пример наглядно демонстрирует механизм ценообразования казначейских облигаций исходя из теоретических спот-ставок.
Спот-ставки и базовая процентная ставка
Форвардные ставки
Факторы, влияющие на графический тип временной структуры процентных ставок
Спот-ставки и базовая процентная ставка
Мы можем теперь вернуться к данному ранее определению базовой процентной ставки для данной длительности. Говоря о базовой ставке, мы будем отныне иметь в виду не просто доходность казначейской облигации «в ходу» данной длительности, но теоретическую спот-ставку для казначейских бумаг этой длительности. Определяя стоимость неказначейской ценной бумаги, величину премии за риск следует прибавлять именно к значению теоретической спот-ставки.
Форвардные ставки
Мы видели, что на основании кривой доходности может быть проведена экстраполяция теоретических спот-ставок. Между тем нам следовало бы экстраполировать и другое значение, которое нередко называют «мнением рынка относительно будущих процентных ставок». Для того чтобы представить себе, насколько важно знать мнение рынка о будущих процентных ставках, рассмотрим две возможности вложения капитала, которые предоставляются инвестору на инвестиционном горизонте в один год:
Возможность 1: купить финансовый инструмент со сроком погашения один год.
Возможность 2: купить инструмент с длительностью шесть месяцев, а после истечения срока до погашения купить другой инструмент с той же длительностью.
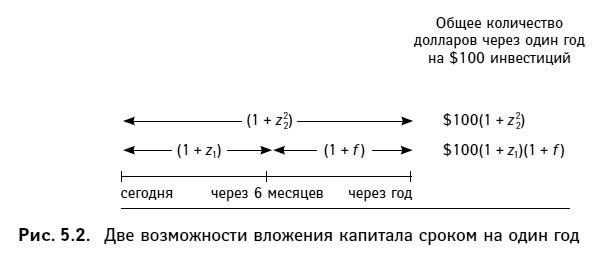
Выбрав возможность 1, инвестор совершит капиталовложение под годовую спот-ставку – эта ставка заранее точно известна. Выбирая возможность 2, инвестор точно знает свою первую полугодовую спот-ставку и не имеет представления о второй – той, которая будет установлена через шесть месяцев с настоящего времени. Таким образом, в варианте 2 доходность, которую можно получить, инвестировав средства на год, заранее не ясна. Это положение наглядно представлено на рис. 5.2.
Допустим, инвестор рассчитывает на то, что через шесть месяцев полугодовая ставка будет выше, чем в настоящее время. На первый взгляд, возможность 2 представляется в этой ситуации более привлекательной. Тем не менее такой вывод вполне может оказаться неверным. Почему? Продолжим наши рассуждения. Они приведут нас, в частности, к осознанию важности такого фактора, как мнение рынка о будущих процентных ставках.
Возможности 1 и 2 покажутся равно привлекательными инвестору, если по окончании временного горизонта в один год обе принесут одинаковое количество долларов. Допустим, что годовая спот-ставка известна; ставку на шестимесячный финансовый инструмент, приобретаемый через шесть месяцев с настоящего времени, которая позволит уравнять две возможности, обозначим как f.
Величину f можно без труда найти, зная теоретическую годовую спот-ставку и спот-ставку для полугода. Если инвестор вкладывает $100 в финансовый инструмент длительностью один год (возможность 1), общее количество долларов, которое он получит по окончании этого года, будет равно:
Инвестиция, осуществленная на полгода, по полугодовой спот-ставке через шесть месяцев принесет следующее количество долларов:
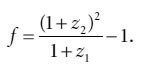(5.5)
Удваивая f, получаем эквивалентную облигационной доходность для полугодовой ставки, которая будет установлена на рынке через шесть месяцев.
Продемонстрируем применение формулы (5.5) на примере теоретических спот-ставок, представленных в табл. 5.5. Из таблицы известно, что:
полугодовая спот-ставка = 0,0525, т. е. z1 = 0,2625;
годовая спот-ставка = 0,0550, т. е. z2 = 0,2750.
Подставляем необходимые значения в формулу (5.5) и получаем:
Следовательно, годовая эквивалентная облигационной ставка для f составит 5,75 % (2,8752 % × 2).
Анализ данного значения проводится следующим образом. Если через полгода шестимесячная ставка будет меньше, чем 5,75 %, выгоднее совершить инвестицию в инструмент со сроком погашения один год (возможность 1). Если через полгода шестимесячная ставка будет больше, чем 5,75 %, выгоднее совершить инвестицию в инструмент длительностью полгода, а затем реинвестировать полученные деньги еще на полгода по установившейся новой полугодовой ставке (возможность 2). Очевидно, что, если через полгода полугодовая ставка составит 5,75 %, обе возможности через год принесут равное количество долларов.
Мы получили интересовавшее нас значение f и знаем, как его следует интерпретировать, – вернемся же к проблеме, поставленной в начале раздела. Из табл. 5.4 известно, что полугодовая спот-ставка равна 5,25 %. Допустим, инвестор предполагает, что через полгода полугодовая ставка составит 5,50 %. Иными словами, инвестор считает, что полугодовая ставка поднимется на более высокий уровень. Следует ли, исходя исключительно из этого предположения, выбирать инвестиционную возможность 2? Ответ на вопрос должен быть отрицательным. Мы уже видели, что при ставке меньшей, чем 5,75 %, лучшим вариантом является возможность 1. Наш инвестор ожидает, что размер ставки составит 5,60 % – это значит, что, несмотря на ожидаемое повышение полугодовой ставки, ему следует выбрать первую инвестиционную возможность.
Вывод может показаться неожиданным; однако читателю не следует забывать о том, что рынок учитывает предположения основной массы инвесторов относительно будущих процентных ставок, отражая их в текущих ставках на инвестиции с различными длительностями. Именно поэтому нам так важно бывает знать мнение участников рынка о будущих ставках. Ставка, обозначенная нами как f, – это ставка на шестимесячные финансовые инструменты, которая, по мнению большинства, будет наблюдаться на рынке через полгода. Будущая процентная ставка, вычисленная на основе значений спот-ставок либо кривой доходности, носит название форвардной ставки.
Соотношение форвардных ставок и спот-ставок. Отношение между спот-ставкой для t периодов, текущей полугодовой спот-ставкой и полугодовыми форвардными ставками можно выразить следующим образом:
Продемонстрируем использование формулы (5.6) на примере отношений пятилетней (10-периодной) спот-ставки и полугодовых форвардных ставок. Полугодовые форвардные ставки были рассчитаны исходя из спот-ставок, приведенных в табл. 5.4. Значения, обозначенные нами как f1 – f9, приводятся ниже:
Прочие форвардные ставки. Ход рассуждений может быть продолжен. Инвестору незачем ограничиваться вычислением полугодовой форвардной ставки. С помощью значений спот-ставок мы в состоянии подсчитать форвардную ставку на любой момент времени в будущем для любого инвестиционного горизонта. Мы без труда узнаем, например:
• форвардную ставку, которая через пять лет установится на срок два года;
• форвардную ставку, которая через 10 лет установится на срок шесть лет;
• форвардную ставку, которая через три года установится на срок семь лет.
Форвардная ставка как хеджируемая ставка. В разговоре о форвардной ставке неизбежно возникает вопрос: насколько хорошо она предсказывает процентную ставку, которая в будущем установится на данный финансовый инструмент? Исследования показали: форвардные ставки не в состоянии дать полноценную информацию о будущих процентных ставках[37]. Читатель вправе спросить: для чего тогда служит данная величина? Напомним приведенное выше описание двух инвестиционных возможностей: форвардные ставки помогают инвестору сравнить свои ожидания с ожиданиями большинства и таким образом принять верное решение относительно выбора типа капиталовложений.
Возможно, что полугодовая форвардная ставка, вычисленная в нашем примере, на рынке так и не установится. Для инвестора, однако, этот факт не имеет значения. Форвардная ставка служит своего рода знаком, указывающим верное направление движения: если вы ожидаете, что через полгода на рынке на полугодовой инструмент установится ставка меньшая, чем 5,75 %, выбирайте возможность 1.
Читатель поймет теперь, почему часть участников рынка, говоря о форвардных ставках, предпочитает делать акцент не на их соотнесении с мнением большинства, а на необходимости их хеджирования. Так, приобретая ценную бумагу длительностью один год, инвестор хеджирует ставки, которые через полгода установятся на полугодовые долговые инструменты.
Возможность 1: купить финансовый инструмент со сроком погашения один год.
Возможность 2: купить инструмент с длительностью шесть месяцев, а после истечения срока до погашения купить другой инструмент с той же длительностью.
Выбрав возможность 1, инвестор совершит капиталовложение под годовую спот-ставку – эта ставка заранее точно известна. Выбирая возможность 2, инвестор точно знает свою первую полугодовую спот-ставку и не имеет представления о второй – той, которая будет установлена через шесть месяцев с настоящего времени. Таким образом, в варианте 2 доходность, которую можно получить, инвестировав средства на год, заранее не ясна. Это положение наглядно представлено на рис. 5.2.
Возможности 1 и 2 покажутся равно привлекательными инвестору, если по окончании временного горизонта в один год обе принесут одинаковое количество долларов. Допустим, что годовая спот-ставка известна; ставку на шестимесячный финансовый инструмент, приобретаемый через шесть месяцев с настоящего времени, которая позволит уравнять две возможности, обозначим как f.
Величину f можно без труда найти, зная теоретическую годовую спот-ставку и спот-ставку для полугода. Если инвестор вкладывает $100 в финансовый инструмент длительностью один год (возможность 1), общее количество долларов, которое он получит по окончании этого года, будет равно:
где z2 – годовая спот-ставка (напомним, что мы работаем с полугодовыми периодами; индекс 2 обозначает здесь два периода, равных шести месяцам, или один год).общее количество долларов по окончании года в варианте 1 = $100(1 + z2)2, (5.1)
Инвестиция, осуществленная на полгода, по полугодовой спот-ставке через шесть месяцев принесет следующее количество долларов:
где z1 – полугодовая спот-ставка. Если сумма, вычисленная по формуле (5.2) будет через шесть месяцев реинвестирована под полугодовую ставку, которую мы обозначили как f, общее количество долларов через год составит:общее количество долларов по окончании полугода в варианте 2 = $100(1 + z1), (5.2)
Инвестору будет все равно, какую из возможностей выбрать, если количество долларов для обоих вариантов окажется равным, т. е. если можно будет поставить знак равенства между формулами (5.1) и (5.3). Приравняв два выражения, получим:общее количество долларов по окончании года в варианте 2 = $100(1 + z1)(1 + f). (5.3)
Из формулы (5.4) очевидно, что:$100(1 + z2)2 = $100(1 + z1)(1 + f). (5.4)
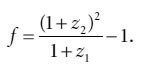(5.5)Удваивая f, получаем эквивалентную облигационной доходность для полугодовой ставки, которая будет установлена на рынке через шесть месяцев.
Продемонстрируем применение формулы (5.5) на примере теоретических спот-ставок, представленных в табл. 5.5. Из таблицы известно, что:
полугодовая спот-ставка = 0,0525, т. е. z1 = 0,2625;
годовая спот-ставка = 0,0550, т. е. z2 = 0,2750.
Подставляем необходимые значения в формулу (5.5) и получаем:
Анализ данного значения проводится следующим образом. Если через полгода шестимесячная ставка будет меньше, чем 5,75 %, выгоднее совершить инвестицию в инструмент со сроком погашения один год (возможность 1). Если через полгода шестимесячная ставка будет больше, чем 5,75 %, выгоднее совершить инвестицию в инструмент длительностью полгода, а затем реинвестировать полученные деньги еще на полгода по установившейся новой полугодовой ставке (возможность 2). Очевидно, что, если через полгода полугодовая ставка составит 5,75 %, обе возможности через год принесут равное количество долларов.
Мы получили интересовавшее нас значение f и знаем, как его следует интерпретировать, – вернемся же к проблеме, поставленной в начале раздела. Из табл. 5.4 известно, что полугодовая спот-ставка равна 5,25 %. Допустим, инвестор предполагает, что через полгода полугодовая ставка составит 5,50 %. Иными словами, инвестор считает, что полугодовая ставка поднимется на более высокий уровень. Следует ли, исходя исключительно из этого предположения, выбирать инвестиционную возможность 2? Ответ на вопрос должен быть отрицательным. Мы уже видели, что при ставке меньшей, чем 5,75 %, лучшим вариантом является возможность 1. Наш инвестор ожидает, что размер ставки составит 5,60 % – это значит, что, несмотря на ожидаемое повышение полугодовой ставки, ему следует выбрать первую инвестиционную возможность.
Вывод может показаться неожиданным; однако читателю не следует забывать о том, что рынок учитывает предположения основной массы инвесторов относительно будущих процентных ставок, отражая их в текущих ставках на инвестиции с различными длительностями. Именно поэтому нам так важно бывает знать мнение участников рынка о будущих ставках. Ставка, обозначенная нами как f, – это ставка на шестимесячные финансовые инструменты, которая, по мнению большинства, будет наблюдаться на рынке через полгода. Будущая процентная ставка, вычисленная на основе значений спот-ставок либо кривой доходности, носит название форвардной ставки.
Соотношение форвардных ставок и спот-ставок. Отношение между спот-ставкой для t периодов, текущей полугодовой спот-ставкой и полугодовыми форвардными ставками можно выразить следующим образом:
где ft – полугодовая форвардная ставка, которая установится на рынке через t полугодовых периодов с настоящего времени.z2 = [(1 + z1)(1 + f1)(1 + f2)(1 + f3)…(1 + ft —1)]1/t – 1, (5.6)
Продемонстрируем использование формулы (5.6) на примере отношений пятилетней (10-периодной) спот-ставки и полугодовых форвардных ставок. Полугодовые форвардные ставки были рассчитаны исходя из спот-ставок, приведенных в табл. 5.4. Значения, обозначенные нами как f1 – f9, приводятся ниже:
Полугодовая спот-ставка составляет 2,625 % (5,25 %, если говорить о доходности, эквивалентной облигационной). Подставив нужные значения в формулу (5.6), получим:f1 = 0,02875; f2 = 0,03140; f3 = 0,03670; f4 = 0,03945; f5 = 0,04320; f6 = 0,03605; f7 = 0,04455; f8 = 0,04100; f9 = 0,03885.
Заметим, что удвоение полученного результата дает значение пятилетней (10-периодной) спот-ставки, приведенное в табл. 5.4.z10 = (1,02875 × 1,02625 × 1,03140 × 1,03670 × 1,03945 × 1,04320 × 1,03605 × 1,04455 × 1,04100 × 1,03855)1/10 – 1 = 0,036 = 3,6 %.
Прочие форвардные ставки. Ход рассуждений может быть продолжен. Инвестору незачем ограничиваться вычислением полугодовой форвардной ставки. С помощью значений спот-ставок мы в состоянии подсчитать форвардную ставку на любой момент времени в будущем для любого инвестиционного горизонта. Мы без труда узнаем, например:
• форвардную ставку, которая через пять лет установится на срок два года;
• форвардную ставку, которая через 10 лет установится на срок шесть лет;
• форвардную ставку, которая через три года установится на срок семь лет.
Форвардная ставка как хеджируемая ставка. В разговоре о форвардной ставке неизбежно возникает вопрос: насколько хорошо она предсказывает процентную ставку, которая в будущем установится на данный финансовый инструмент? Исследования показали: форвардные ставки не в состоянии дать полноценную информацию о будущих процентных ставках[37]. Читатель вправе спросить: для чего тогда служит данная величина? Напомним приведенное выше описание двух инвестиционных возможностей: форвардные ставки помогают инвестору сравнить свои ожидания с ожиданиями большинства и таким образом принять верное решение относительно выбора типа капиталовложений.
Возможно, что полугодовая форвардная ставка, вычисленная в нашем примере, на рынке так и не установится. Для инвестора, однако, этот факт не имеет значения. Форвардная ставка служит своего рода знаком, указывающим верное направление движения: если вы ожидаете, что через полгода на рынке на полугодовой инструмент установится ставка меньшая, чем 5,75 %, выбирайте возможность 1.
Читатель поймет теперь, почему часть участников рынка, говоря о форвардных ставках, предпочитает делать акцент не на их соотнесении с мнением большинства, а на необходимости их хеджирования. Так, приобретая ценную бумагу длительностью один год, инвестор хеджирует ставки, которые через полгода установятся на полугодовые долговые инструменты.
Факторы, влияющие на графический тип временной структуры процентных ставок
Каким образом будет выглядеть графическое изображение временной структуры процентных ставок – доходностей к погашению или спот-ставок для последовательных значений длительности? На рис. 5.1 приведены три наиболее характерные кривые, наблюдавшиеся на рынках как американских, так и неамериканских ценных бумаг. График (а) – это растущая кривая: при увеличении длительности доходность неизменно растет. Такая кривая получила название нормальной, или положительной, кривой доходности. Изображение (b) – падающая, или обратная, кривая доходности: при увеличении длительности доходность падает. И наконец, рисунок (с) – плоская кривая доходности.
Интерпретацию наблюдаемых на рынке типов временных структур процентных ставок читатель найдет в работах исследователей, представляющих два основных теоретических направления: теорию ожиданий и теорию рыночной сегментации.
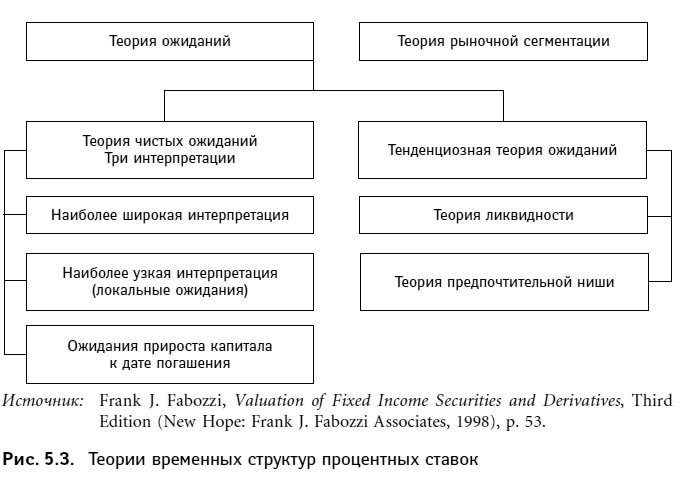
Теория ожиданий, в свою очередь, существует в нескольких формах: теория чистых ожиданий, теория ликвидности и теорияпредпочтительной ниши. Теория ожиданий строится на основании изучения поведения будущих краткосрочных ставок; предполагается также, что форвардные ставки на находящиеся в обращении долгосрочные облигации достаточно полно отражают мнение рынка относительно характера будущих краткосрочных ставок. Три подвида теории расходятся, однако, в вопросе о выборе факторов, влияние которых на форвардные ставки следует признавать существенным. Приверженцы теории чистых ожиданий заявляют, что на форвардные ставки не оказывают систематического влияния никакие факторы, кроме предположений участников рынка о будущих краткосрочных ставках. Теория ликвидности и теория предпочтительной ниши выделяют еще несколько значимых факторов, именно поэтому эти теории получили в ряде исследований название тенденциозных теорий ожидания. На рис. 5.3 наглядно представлена взаимосвязь всех теорий.
Теория чистых ожиданий. Согласно теории чистых ожиданий форвардные ставки представляют не что иное, как ожидаемые в будущем ставки на финансовые инструменты. Вся временная структура, таким образом, отражает ожидаемые рынком в каждый данный момент времени будущие краткосрочные ставки. С этой точки зрения растущая временная структура, изображенная на графике (а) рис. 5.1, указывает на то, что рынок в ближайшем будущем ожидает рост краткосрочных ставок. Плоская временная структура говорит о том, что по мнению рынка будущие краткосрочные ставки в целом не изменятся. Падающая кривая указывает на ожидаемое в будущем падение ставок.
Для иллюстрации этого теоретического положения рассмотрим следующую ситуацию: рынок ожидает, что краткосрочные ставки в будущем будут расти, мнение рынка определенным образом сказывается на поведении его участников, в результате кривая доходности растет. Допустим, что временная структура ставок изначально была плоской, а затем некие экономические новости позволили участникам рынка сделать предположение о будущем росте ставок.
1. Участники рынка, заинтересованные в долгосрочных инвестициях, не станут покупать долгосрочные облигации, поскольку, по их мнению, кривая доходности рано или поздно пойдет вверх, а значит, упадут цены на облигации и инвестиции окажутся убыточными. Они предпочтут инвестировать в краткосрочные долговые обязательства: рост доходности позволит им в будущем реинвестировать капитал под более высокие ставки.
2. Спекулянты, ожидающие роста ставок, предполагая, что цены на долгосрочные облигации упадут, захотят продать такие облигации и, возможно, «продать коротко», т. е. продать не только те бумаги, которые находятся в их распоряжении, но и те, что будут взяты взаймы. (Если процентные ставки действительно поднимутся, цены на долгосрочные облигации упадут. Спекулянты, открывшие короткие позиции, смогут покрыть их, купив облигации на рынке по более дешевой цене и тем самым обеспечив себе известную прибыль.)
3. Заемщики, желающие получить долгосрочные кредиты, будут более активны, поскольку промедление может стоить им денег.
Все три обстоятельства приведут к тому, что чистый спрос на облигации с большим сроком до погашения упадет (предложение вырастет); и наоборот, увеличится спрос на краткосрочные долговые обязательства. Доходности долгосрочных облигаций в такой ситуации вырастут относительно доходностей облигаций краткосрочных; совместные усилия инвесторов, спекулянтов и заемщиков будут толкать временную структуру вверх до тех пор, пока она не придет в соответствие с мнением о будущих более высоких ставках. Аналогичным образом неожиданное событие, указывающее на возможность падения ставок в будущем, приведет к падению кривой доходности.
К сожалению, теория чистых ожиданий страдает одним, но чрезвычайно серьезным недостатком. Она не учитывает риски, сопряженные с инвестициями в облигации и сходные с ними финансовые инструменты. Если бы форвардные ставки безошибочно предсказывали будущие процентные ставки, будущие цены на облигации были бы заранее известны. Прибыль на любом инвестиционном горизонте вычислялась бы заранее и не зависела ни от длительности приобретенного финансового инструмента, ни от момента времени, в который инвестор захочет ликвидировать позицию. Между тем, поскольку будущие процентные ставки, а значит, и цены точно неизвестны, облигации оказываются рискованными финансовыми инструментами, т. е. инструментами, прибыль от которых при покупке подсчитать невозможно.
Невозможность узнать точное значение прибыли на данном инвестиционном горизонте связана с двумя типами риска: ценовым риском и риском реинвестиций. Первый отражает невозможность предсказать точное значение цены облигации на момент окончания временного горизонта. Предположим, инвестор планирует совершить инвестицию на пять лет и рассматривает три возможных варианта: 1) инвестировать в пятилетние облигации и держать их пять лет; 2) инвестировать в 12-летние облигации и продать их через пять лет; 3) инвестировать в 30-летние облигации и продать их через пять лет. Прибыль, которая может быть получена от инвестиций 2) и 3), заранее неизвестна, поскольку неизвестно, какое именно значение цены установится на долгосрочную облигацию через пять лет. В случае 12-летних облигаций цена будет зависеть от доходности семилетних долговых обязательств через пять лет; в случае 30-летних облигаций – от доходности 25-летних долговых инструментов через пять лет. Поскольку форвардные ставки, принятые в текущей временной структуре для 12– и 25-летних облигаций, не могут точно предсказать реальных будущих ставок, цена обеих облигаций через пять лет остается неизвестной. Это значит, что существует ценовой риск: цена в момент окончания временного горизонта может оказаться ниже предполагаемого в настоящий момент уровня. Как явствует из материалов главы 4, важное свойство ценового риска – его увеличение с увеличением длительности облигации.
Второй тип риска связан с невозможностью заранее узнать процентные ставки, под которые в момент окончания временного горизонта будет реинвестирована прибыль от облигации. Этот тип риска получил название риска реинвестиций. Предположим, что инвестор, решивший совершить капиталовложение сроком на пять лет, рассматривает следующие три возможности: 1) инвестировать в пятилетние облигации и держать их пять лет; 2) инвестировать в инструмент с длительностью полгода, затем реинвестировать капитал еще на шесть месяцев и т. д. в течение всего пятилетнего срока; 3) инвестировать в облигацию со сроком погашения два года, а затем реинвестировать капитал в финансовый инструмент с длительностью три года. Риск во втором и третьем случае обусловлен неизвестным размером прибыли, которую можно получить через пять лет: ставки, под которые инвестор будет реинвестировать деньги, в настоящий момент неизвестны.
Экономистами было предложено несколько различных интерпретаций теории чистого ожидания. Эти интерпретации сильно разнятся и подчас противоречат друг другу. Частично такие несоответствия объясняются разными толкованиями двух типов риска, о которых мы писали выше[38].
Наиболее широкая интерпретация теории чистых ожиданий сводится к утверждению о том, что прибыль, которую ожидают получить инвесторы в момент окончания временного горизонта, не зависит от избранной ими стратегии сочетания длительностей финансовых инструментов[39]. Вспомним нашего инвестора с пятилетним временным горизонтом. Согласно теории, не имеет значения, какую именно облигацию – пятилетнюю, 12-летнюю или 30-летнюю – он купит и продержит пять лет: предполагаемая прибыль от всех трех инструментов одинакова. Основное возражение против такой интерпретации связано с существованием ценового риска: известно, что инвестировать в долговые обязательства с длительностью, превышающей инвестиционный горизонт, опасно, поэтому предполагаемая прибыль от трех инвестиций наверняка будет существенно разниться[40].
Вторая интерпретация получила название теории локальныхожиданий. Это разновидность теории ожиданий, предполагающая, что на краткосрочном инвестиционном горизонте прибыль от облигаций разной длительности будет одинаковой. Так, если инвестор с инвестиционным горизонтом в полгода купит 5-, 10– или 20-летнюю облигацию, по окончании шести месяцев он получит одну и ту же прибыль. Исследователи показали, что теория локальных ожиданий, будучи чрезвычайно узкой, – единственная достойная доверия интерпретация теории чистых ожиданий[41].
Третья и последняя интерпретация теории чистых ожиданий сводится, вкратце, к следующему утверждению: прибыль, которую по окончании установленного временного горизонта получит инвестор от переноса позиции из одних краткосрочных облигаций в другие, будет равна прибыли от держания бескупонной облигации с длительностью, совпадающей с протяженностью инвестиционного горизонта. (Бескупонная облигация не связана с риском реинвестиций, а это значит, что будущие процентные ставки не влияют на прибыль.) Этот вариант получил название ожиданий прибыли к погашению. Предположим, например, что инвестиционный горизонт составляет пять лет. Инвестор, купивший пятилетнюю бескупонную облигацию и продержавший ее до погашения, получит прибыль, равную отношению разности между номиналом и ценой облигации. Согласно теории ожиданий прибыли к погашению, ту же прибыль получит инвестор, в течение пяти лет переводивший свои инвестиции из одной шестимесячной облигации в другую. В настоящее время верность такой интерпретации ставится под сомнение многими исследователями.
Теория ликвидности. Мы писали о том, что основной недостаток теории чистых ожиданий – пренебрежение риском, связанным с инвестициями в облигации. Держание долгосрочной облигации в течение некоего периода сопряжено с риском, который растет с увеличением длительности, поскольку длительность и волатильность цены находятся в прямой зависимости друг от друга.
Итак, прибыль по окончании временного горизонта неизвестна, а инвесторы, как правило, не любят неизвестности. Исходя из этого построили свою теорию некоторые экономисты и финансовые аналитики. Эта теория утверждает: инвестор будет держать более «длинные» облигации, если долгосрочные ставки окажутся выше среднего значения ожидаемых форвардных ставок на величину премии за риск, напрямую связанную с размером длительности[42]. Иными словами, форвардные ставки отражают как величину ожидаемых процентных ставок, так и премию за «ликвидность» (в действительности, премию за риск), причем чем больше длительность, тем выше должна быть премия.
Согласно этой теории, названной теорией ликвидности, форвардные ставки не являются непредвзятым отражением мнения рынка о будущих процентных ставках: временная структура несет также информацию о премиях за ликвидность. Таким образом, растущая кривая доходности может говорить о том, что: 1) либо на рынке ожидается рост процентных ставок, 2) либо ставки, по мнению большинства, останутся прежними или даже упадут, но премия за ликвидность с увеличением длительности увеличивается настолько быстро, что кривая доходности получает восходящий наклон.
Теория предпочтительной ниши. Другая теория – теория предпочтительной ниши – также строится исходя из утверждения о том, что временная структура процентных ставок отражает ожидания рынка как относительно будущего изменения процентных ставок, так и относительно будущих премий за риск. В то же время сторонники этой теории не согласны с выводом о том, что премии за риск должны расти параллельно росту длительности[43].
Интерпретацию наблюдаемых на рынке типов временных структур процентных ставок читатель найдет в работах исследователей, представляющих два основных теоретических направления: теорию ожиданий и теорию рыночной сегментации.
Теория ожиданий, в свою очередь, существует в нескольких формах: теория чистых ожиданий, теория ликвидности и теорияпредпочтительной ниши. Теория ожиданий строится на основании изучения поведения будущих краткосрочных ставок; предполагается также, что форвардные ставки на находящиеся в обращении долгосрочные облигации достаточно полно отражают мнение рынка относительно характера будущих краткосрочных ставок. Три подвида теории расходятся, однако, в вопросе о выборе факторов, влияние которых на форвардные ставки следует признавать существенным. Приверженцы теории чистых ожиданий заявляют, что на форвардные ставки не оказывают систематического влияния никакие факторы, кроме предположений участников рынка о будущих краткосрочных ставках. Теория ликвидности и теория предпочтительной ниши выделяют еще несколько значимых факторов, именно поэтому эти теории получили в ряде исследований название тенденциозных теорий ожидания. На рис. 5.3 наглядно представлена взаимосвязь всех теорий.
Для иллюстрации этого теоретического положения рассмотрим следующую ситуацию: рынок ожидает, что краткосрочные ставки в будущем будут расти, мнение рынка определенным образом сказывается на поведении его участников, в результате кривая доходности растет. Допустим, что временная структура ставок изначально была плоской, а затем некие экономические новости позволили участникам рынка сделать предположение о будущем росте ставок.
1. Участники рынка, заинтересованные в долгосрочных инвестициях, не станут покупать долгосрочные облигации, поскольку, по их мнению, кривая доходности рано или поздно пойдет вверх, а значит, упадут цены на облигации и инвестиции окажутся убыточными. Они предпочтут инвестировать в краткосрочные долговые обязательства: рост доходности позволит им в будущем реинвестировать капитал под более высокие ставки.
2. Спекулянты, ожидающие роста ставок, предполагая, что цены на долгосрочные облигации упадут, захотят продать такие облигации и, возможно, «продать коротко», т. е. продать не только те бумаги, которые находятся в их распоряжении, но и те, что будут взяты взаймы. (Если процентные ставки действительно поднимутся, цены на долгосрочные облигации упадут. Спекулянты, открывшие короткие позиции, смогут покрыть их, купив облигации на рынке по более дешевой цене и тем самым обеспечив себе известную прибыль.)
3. Заемщики, желающие получить долгосрочные кредиты, будут более активны, поскольку промедление может стоить им денег.
Все три обстоятельства приведут к тому, что чистый спрос на облигации с большим сроком до погашения упадет (предложение вырастет); и наоборот, увеличится спрос на краткосрочные долговые обязательства. Доходности долгосрочных облигаций в такой ситуации вырастут относительно доходностей облигаций краткосрочных; совместные усилия инвесторов, спекулянтов и заемщиков будут толкать временную структуру вверх до тех пор, пока она не придет в соответствие с мнением о будущих более высоких ставках. Аналогичным образом неожиданное событие, указывающее на возможность падения ставок в будущем, приведет к падению кривой доходности.
К сожалению, теория чистых ожиданий страдает одним, но чрезвычайно серьезным недостатком. Она не учитывает риски, сопряженные с инвестициями в облигации и сходные с ними финансовые инструменты. Если бы форвардные ставки безошибочно предсказывали будущие процентные ставки, будущие цены на облигации были бы заранее известны. Прибыль на любом инвестиционном горизонте вычислялась бы заранее и не зависела ни от длительности приобретенного финансового инструмента, ни от момента времени, в который инвестор захочет ликвидировать позицию. Между тем, поскольку будущие процентные ставки, а значит, и цены точно неизвестны, облигации оказываются рискованными финансовыми инструментами, т. е. инструментами, прибыль от которых при покупке подсчитать невозможно.
Невозможность узнать точное значение прибыли на данном инвестиционном горизонте связана с двумя типами риска: ценовым риском и риском реинвестиций. Первый отражает невозможность предсказать точное значение цены облигации на момент окончания временного горизонта. Предположим, инвестор планирует совершить инвестицию на пять лет и рассматривает три возможных варианта: 1) инвестировать в пятилетние облигации и держать их пять лет; 2) инвестировать в 12-летние облигации и продать их через пять лет; 3) инвестировать в 30-летние облигации и продать их через пять лет. Прибыль, которая может быть получена от инвестиций 2) и 3), заранее неизвестна, поскольку неизвестно, какое именно значение цены установится на долгосрочную облигацию через пять лет. В случае 12-летних облигаций цена будет зависеть от доходности семилетних долговых обязательств через пять лет; в случае 30-летних облигаций – от доходности 25-летних долговых инструментов через пять лет. Поскольку форвардные ставки, принятые в текущей временной структуре для 12– и 25-летних облигаций, не могут точно предсказать реальных будущих ставок, цена обеих облигаций через пять лет остается неизвестной. Это значит, что существует ценовой риск: цена в момент окончания временного горизонта может оказаться ниже предполагаемого в настоящий момент уровня. Как явствует из материалов главы 4, важное свойство ценового риска – его увеличение с увеличением длительности облигации.
Второй тип риска связан с невозможностью заранее узнать процентные ставки, под которые в момент окончания временного горизонта будет реинвестирована прибыль от облигации. Этот тип риска получил название риска реинвестиций. Предположим, что инвестор, решивший совершить капиталовложение сроком на пять лет, рассматривает следующие три возможности: 1) инвестировать в пятилетние облигации и держать их пять лет; 2) инвестировать в инструмент с длительностью полгода, затем реинвестировать капитал еще на шесть месяцев и т. д. в течение всего пятилетнего срока; 3) инвестировать в облигацию со сроком погашения два года, а затем реинвестировать капитал в финансовый инструмент с длительностью три года. Риск во втором и третьем случае обусловлен неизвестным размером прибыли, которую можно получить через пять лет: ставки, под которые инвестор будет реинвестировать деньги, в настоящий момент неизвестны.
Экономистами было предложено несколько различных интерпретаций теории чистого ожидания. Эти интерпретации сильно разнятся и подчас противоречат друг другу. Частично такие несоответствия объясняются разными толкованиями двух типов риска, о которых мы писали выше[38].
Наиболее широкая интерпретация теории чистых ожиданий сводится к утверждению о том, что прибыль, которую ожидают получить инвесторы в момент окончания временного горизонта, не зависит от избранной ими стратегии сочетания длительностей финансовых инструментов[39]. Вспомним нашего инвестора с пятилетним временным горизонтом. Согласно теории, не имеет значения, какую именно облигацию – пятилетнюю, 12-летнюю или 30-летнюю – он купит и продержит пять лет: предполагаемая прибыль от всех трех инструментов одинакова. Основное возражение против такой интерпретации связано с существованием ценового риска: известно, что инвестировать в долговые обязательства с длительностью, превышающей инвестиционный горизонт, опасно, поэтому предполагаемая прибыль от трех инвестиций наверняка будет существенно разниться[40].
Вторая интерпретация получила название теории локальныхожиданий. Это разновидность теории ожиданий, предполагающая, что на краткосрочном инвестиционном горизонте прибыль от облигаций разной длительности будет одинаковой. Так, если инвестор с инвестиционным горизонтом в полгода купит 5-, 10– или 20-летнюю облигацию, по окончании шести месяцев он получит одну и ту же прибыль. Исследователи показали, что теория локальных ожиданий, будучи чрезвычайно узкой, – единственная достойная доверия интерпретация теории чистых ожиданий[41].
Третья и последняя интерпретация теории чистых ожиданий сводится, вкратце, к следующему утверждению: прибыль, которую по окончании установленного временного горизонта получит инвестор от переноса позиции из одних краткосрочных облигаций в другие, будет равна прибыли от держания бескупонной облигации с длительностью, совпадающей с протяженностью инвестиционного горизонта. (Бескупонная облигация не связана с риском реинвестиций, а это значит, что будущие процентные ставки не влияют на прибыль.) Этот вариант получил название ожиданий прибыли к погашению. Предположим, например, что инвестиционный горизонт составляет пять лет. Инвестор, купивший пятилетнюю бескупонную облигацию и продержавший ее до погашения, получит прибыль, равную отношению разности между номиналом и ценой облигации. Согласно теории ожиданий прибыли к погашению, ту же прибыль получит инвестор, в течение пяти лет переводивший свои инвестиции из одной шестимесячной облигации в другую. В настоящее время верность такой интерпретации ставится под сомнение многими исследователями.
Теория ликвидности. Мы писали о том, что основной недостаток теории чистых ожиданий – пренебрежение риском, связанным с инвестициями в облигации. Держание долгосрочной облигации в течение некоего периода сопряжено с риском, который растет с увеличением длительности, поскольку длительность и волатильность цены находятся в прямой зависимости друг от друга.
Итак, прибыль по окончании временного горизонта неизвестна, а инвесторы, как правило, не любят неизвестности. Исходя из этого построили свою теорию некоторые экономисты и финансовые аналитики. Эта теория утверждает: инвестор будет держать более «длинные» облигации, если долгосрочные ставки окажутся выше среднего значения ожидаемых форвардных ставок на величину премии за риск, напрямую связанную с размером длительности[42]. Иными словами, форвардные ставки отражают как величину ожидаемых процентных ставок, так и премию за «ликвидность» (в действительности, премию за риск), причем чем больше длительность, тем выше должна быть премия.
Согласно этой теории, названной теорией ликвидности, форвардные ставки не являются непредвзятым отражением мнения рынка о будущих процентных ставках: временная структура несет также информацию о премиях за ликвидность. Таким образом, растущая кривая доходности может говорить о том, что: 1) либо на рынке ожидается рост процентных ставок, 2) либо ставки, по мнению большинства, останутся прежними или даже упадут, но премия за ликвидность с увеличением длительности увеличивается настолько быстро, что кривая доходности получает восходящий наклон.
Теория предпочтительной ниши. Другая теория – теория предпочтительной ниши – также строится исходя из утверждения о том, что временная структура процентных ставок отражает ожидания рынка как относительно будущего изменения процентных ставок, так и относительно будущих премий за риск. В то же время сторонники этой теории не согласны с выводом о том, что премии за риск должны расти параллельно росту длительности[43].