Страница:
Выпуклость: характерные особенности
Для выпуклости всех облигаций без встроенных опционов характерны следующие три основных свойства:
Свойство 1: Если требуемая доходность растет (падает), выпуклость облигации падает (растет). Это свойство носит название положительной выпуклости.
На практике данный феномен выражается следующим образом: если рыночные ставки растут, цена облигации начинает падать. Падение цены замедляется уменьшением дюрации, связанным с ростом требуемой доходности. И наоборот: стоит рыночным ставкам упасть, дюрация возрастет, ускоряя процентное изменение цены. На рынке облигаций без встроенных опционов можно наблюдать оба описанных типа изменений дюрации.
Данное свойство мы графически изобразили на рис. 4.5. Угол наклона касательной уменьшается с ростом процентных ставок. Меньший наклон соответствует меньшей дюрации, характерной для ситуации увеличения требуемой доходности. И наоборот: при уменьшении процентных ставок наклон касательной растет, а значит, увеличивается и дюрация. Данное свойство характерно для всех без исключения облигаций, не имеющих встроенных опционов. Приведенный график позволяет также увидеть, что выпуклость действительно является мерой оценки скорости изменения долларовой дюрации, связанной с изменением рыночных ставок.
Свойство 2: При данных доходности и длительности облигации, более низкий купон обусловливает более высокую выпуклость облигации.
Подтверждением этому выводу могут служить значения выпуклости, полученные нами для шести гипотетических облигаций. Из трех пятилетних облигаций наибольшей выпуклостью обладает бескупонная, наименьшей – облигация с купоном, равным 9 %. Тот же результат получаем, анализируя 25-летние облигации.
Свойство 3: При данных доходности и модифицированной дюрации, чем ниже купон, тем меньше выпуклость.
В инвестиционной практике свойство 3 интерпретируется следующим образом: при данной модифицированной дюрации наименьшая выпуклость характерна для облигаций с нулевым купоном.
Свойство 1: Если требуемая доходность растет (падает), выпуклость облигации падает (растет). Это свойство носит название положительной выпуклости.
На практике данный феномен выражается следующим образом: если рыночные ставки растут, цена облигации начинает падать. Падение цены замедляется уменьшением дюрации, связанным с ростом требуемой доходности. И наоборот: стоит рыночным ставкам упасть, дюрация возрастет, ускоряя процентное изменение цены. На рынке облигаций без встроенных опционов можно наблюдать оба описанных типа изменений дюрации.
Данное свойство мы графически изобразили на рис. 4.5. Угол наклона касательной уменьшается с ростом процентных ставок. Меньший наклон соответствует меньшей дюрации, характерной для ситуации увеличения требуемой доходности. И наоборот: при уменьшении процентных ставок наклон касательной растет, а значит, увеличивается и дюрация. Данное свойство характерно для всех без исключения облигаций, не имеющих встроенных опционов. Приведенный график позволяет также увидеть, что выпуклость действительно является мерой оценки скорости изменения долларовой дюрации, связанной с изменением рыночных ставок.
Подтверждением этому выводу могут служить значения выпуклости, полученные нами для шести гипотетических облигаций. Из трех пятилетних облигаций наибольшей выпуклостью обладает бескупонная, наименьшей – облигация с купоном, равным 9 %. Тот же результат получаем, анализируя 25-летние облигации.
Свойство 3: При данных доходности и модифицированной дюрации, чем ниже купон, тем меньше выпуклость.
В инвестиционной практике свойство 3 интерпретируется следующим образом: при данной модифицированной дюрации наименьшая выпуклость характерна для облигаций с нулевым купоном.
ДРУГИЕ ПРОБЛЕМЫ, СВЯЗАННЫЕ С ПРИМЕНЕНИЕМ ДЮРАЦИИ
Мы уже писали о том, что применять дюрацию в качестве единственной меры волатильности цены облигации неразумно. Ниже мы обратимся к двум другим особенностям использования понятия дюрации в инвестиционной практике.
Напомним, что, выясняя характер зависимости между модифицированной дюрацией и волатильностью цены облигации, мы начали анализ с ценового уравнения (4.1). Данная формула предполагает, что все денежные потоки облигации дисконтированы по единой дисконтной ставке (целесообразность этого предположения мы обсуждаем в главе 5, говоря о кривой доходности). В целом, как формула (4.3), так и ее варианты строятся на основании утверждения о том, что кривая доходности является плоской и изменения доходности в любой ее части параллельны. В главе 19 мы доказываем, что применение дюрации в ситуации, когда изменения доходности в разных частях кривой не параллельны, дает не слишком надежный результат. Это особенно важно помнить инвесторам, пытающимся с помощью значения портфельной дюрации выяснить степень чувствительности стоимости портфеля к изменению процентных ставок. Если в портфель входят облигации с различными длительностями, дюрация, как правило, не учитывает неодинаковые изменения процентных ставок для различных длительностей. В конце этой главы мы предложим один из возможных способов измерения чувствительности портфеля в ситуации, когда процентные ставки для разных длительностей меняются на разное число базисных пунктов.
Второе положение, которое следует помнить инвесторам, работающим с понятием дюрации: все выводы, сделанные нами в этой главе, имеют отношение только к облигациям без встроенных опционов. Если изменение доходностей приводит к изменениям предполагаемых денежных потоков облигации (а именно так происходит с облигациями, имеющими встроенные опционы), меры дюрации и выпуклости применимы лишь в некоторых специфических случаях. Волатильность цен облигаций со встроенными опционами мы анализируем в главах 17 и 18.
Мера дюрации, о которой пойдет речь в этих главах, т. е. дюрация, принимающая в расчет встроенные опционы, получила название эффективной дюрации.
Напомним, что, выясняя характер зависимости между модифицированной дюрацией и волатильностью цены облигации, мы начали анализ с ценового уравнения (4.1). Данная формула предполагает, что все денежные потоки облигации дисконтированы по единой дисконтной ставке (целесообразность этого предположения мы обсуждаем в главе 5, говоря о кривой доходности). В целом, как формула (4.3), так и ее варианты строятся на основании утверждения о том, что кривая доходности является плоской и изменения доходности в любой ее части параллельны. В главе 19 мы доказываем, что применение дюрации в ситуации, когда изменения доходности в разных частях кривой не параллельны, дает не слишком надежный результат. Это особенно важно помнить инвесторам, пытающимся с помощью значения портфельной дюрации выяснить степень чувствительности стоимости портфеля к изменению процентных ставок. Если в портфель входят облигации с различными длительностями, дюрация, как правило, не учитывает неодинаковые изменения процентных ставок для различных длительностей. В конце этой главы мы предложим один из возможных способов измерения чувствительности портфеля в ситуации, когда процентные ставки для разных длительностей меняются на разное число базисных пунктов.
Второе положение, которое следует помнить инвесторам, работающим с понятием дюрации: все выводы, сделанные нами в этой главе, имеют отношение только к облигациям без встроенных опционов. Если изменение доходностей приводит к изменениям предполагаемых денежных потоков облигации (а именно так происходит с облигациями, имеющими встроенные опционы), меры дюрации и выпуклости применимы лишь в некоторых специфических случаях. Волатильность цен облигаций со встроенными опционами мы анализируем в главах 17 и 18.
Мера дюрации, о которой пойдет речь в этих главах, т. е. дюрация, принимающая в расчет встроенные опционы, получила название эффективной дюрации.
НЕ СЛЕДУЕТ СЧИТАТЬ ДЮРАЦИЮ МЕРОЙ ВРЕМЕНИ
Многие участники рынка, к сожалению, до сих пор не усвоили сути понятия дюрации, считая ее одной из мер взвешенной средней продолжительности жизни облигации. По-видимому, такая путаница происходит из-за первоначального использования термина самим Маколеем. Между тем данная интерпретация дюрации нередко приводит ее приверженцев в недоумение: действительно, как можно объяснить тот факт, что дюрация облигации с длительностью 20 лет превышает 20-летний срок? В главе 12, например, мы рассматриваем обеспеченные ипотеками облигации (collateralized mortgage obligation – СМО). У части СМО значение дюрации выше длительности соответствующих ипотек. Так, СМО может иметь дюрацию, равную 40, несмотря на то что соответствующие ипотеки, на основе которых данная облигация была создана, будут погашены через 30 лет. Кроме того, для некоторых СМО характерна отрицательная дюрация. Как объяснить этот феномен?
Ответ будет несложно найти, если вспомнить, что дюрация – это аппроксимированное процентное изменение цены при малом изменении процентных ставок. Напомним, что мы предлагали рассматривать дюрацию как приближенное процентное изменение цены при изменении процентных ставок на 100 базисных пунктов.
Дюрация, таким образом, говорит нам о чувствительности цены, в частности, о ценовой волатильности таких финансовых инструментов, использующих кредитное плечо, как СМО. СМО с дюрацией 40 – это не облигация, «средняя взвешенная продолжительность жизни» которой равна 40 лет. Смысл величины таков: при изменении доходности на 100 базисных пунктов цена этой облигации изменится приблизительно на 40 %.
Аналогичным образом должна интерпретироваться и дюрация опциона. Колл-опцион может иметь дюрацию 20 и истекать через год[24]. Интерпретируя дюрацию как меру продолжительности жизни опциона, инвесторы становятся в тупик перед этим странным несоответствием. В действительности, данное значение имеет следующий смысл: при изменении доходности соответствующей облигации на 100 базисных пунктов, стоимость опциона изменится примерно на 20 %.
Ответ будет несложно найти, если вспомнить, что дюрация – это аппроксимированное процентное изменение цены при малом изменении процентных ставок. Напомним, что мы предлагали рассматривать дюрацию как приближенное процентное изменение цены при изменении процентных ставок на 100 базисных пунктов.
Дюрация, таким образом, говорит нам о чувствительности цены, в частности, о ценовой волатильности таких финансовых инструментов, использующих кредитное плечо, как СМО. СМО с дюрацией 40 – это не облигация, «средняя взвешенная продолжительность жизни» которой равна 40 лет. Смысл величины таков: при изменении доходности на 100 базисных пунктов цена этой облигации изменится приблизительно на 40 %.
Аналогичным образом должна интерпретироваться и дюрация опциона. Колл-опцион может иметь дюрацию 20 и истекать через год[24]. Интерпретируя дюрацию как меру продолжительности жизни опциона, инвесторы становятся в тупик перед этим странным несоответствием. В действительности, данное значение имеет следующий смысл: при изменении доходности соответствующей облигации на 100 базисных пунктов, стоимость опциона изменится примерно на 20 %.
АППРОКСИМАЦИЯ ДЮРАЦИИ И МЕРЫ ВЫПУКЛОСТИ ОБЛИГАЦИИ
Инвестору, осознавшему, что значение дюрации связано с процентным изменением цены, будет несложно вычислить приближенное значение дюрации облигации, производного финансового инструмента или опциона. Напомним, что нам нужно всего-навсего определить процентное изменение цены на облигацию при изменении процентных ставок на небольшую величину. Процедура вычисления искомого значения предельно проста:
Этап 1. Увеличим доходность облигации на небольшое число базисных пунктов и определим новую цену, соответствующую этому новому уровню доходности. Новую цену обозначим как Р+.
Этап 2. Уменьшим доходность облигации на то же число базисных пунктов и определим новую цену. Новую цену обозначим как Р—.
Этап 3. Если исходная цена обозначена как Р0, дюрация может быть аппроксимирована по следующей формуле:
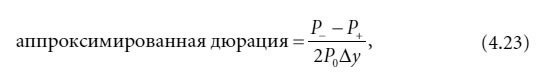где Dу – это изменение доходности, использовавшееся для вычисления новой цены (в десятичных дробях). Результатом является среднее процентное изменение цены (относительно начальной цены) при изменении доходности на 1 базисный пункт.
Для того чтобы выяснить, насколько хороша данная аппроксимация, проверим формулу на примере 25-летней облигации с купоном 6 %, торгующейся при доходности 9 %. Вся необходимая для вычислений информация представлена в табл. 4.2. Исходная цена Р0 равна 70,3570. Искомое значение определяется следующим образом:
Этап 1. Увеличим доходность облигации на 10 базисных пунктов, т. е. с 9 % до 9,1 %. Таким образом, Dу составит 0,001. Новая цена Р+ равна 69,6164.
Этап 2. Уменьшим доходность облигации на 10 базисных пунктов, т. е. с 9 % до 8,9 %. Новая цена Р– составит 71,1105.
Этап 3. При начальной цене Р0, равной 70,3570, аппроксимированная дюрация равна:
(4.23)
Насколько хороша такая аппроксимация? Модифицированная дюрация, которую можно подсчитать с помощью формул (4.5) и (4.7), равна 10,62.
Итак, инвестор, решивший определить дюрацию какого-либо финансового инструмента, может смело пользоваться формулой (4.23). Заметим, однако, что верный результат невозможен при отсутствии надежной модели ценообразования, позволяющей провести операции 1 и 2. Такие модели мы анализируем в следующих главах. Подчеркнем: дюрация – побочный продукт модели ценообразования. Если модель ценообразования работает плохо, полученное значение дюрации далеко от действительного.
Мера выпуклости облигации может быть аппроксимирована согласно следующей формуле:
(4.24)
В нашем случае аппроксимированная мера выпуклости составит:
Напомним, что мера выпуклости, найденная согласно точной формуле, равна 182,92. Выражение (4.24), таким образом, дает хорошую аппроксимацию.
Как уже было отмечено, мера выпуклости измеряется различными способами. Выражение (4.24) может быть видоизменено таким образом, чтобы в знаменателе стояло 2. Обратите внимание на то, что в этом случае при подсчете процентного изменения цены, связанного с выпуклостью, по формуле (4.20) коэффициент 1/2 не учитывается.
Этап 1. Увеличим доходность облигации на небольшое число базисных пунктов и определим новую цену, соответствующую этому новому уровню доходности. Новую цену обозначим как Р+.
Этап 2. Уменьшим доходность облигации на то же число базисных пунктов и определим новую цену. Новую цену обозначим как Р—.
Этап 3. Если исходная цена обозначена как Р0, дюрация может быть аппроксимирована по следующей формуле:
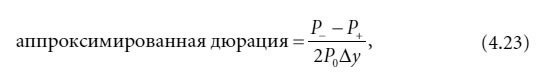
Для того чтобы выяснить, насколько хороша данная аппроксимация, проверим формулу на примере 25-летней облигации с купоном 6 %, торгующейся при доходности 9 %. Вся необходимая для вычислений информация представлена в табл. 4.2. Исходная цена Р0 равна 70,3570. Искомое значение определяется следующим образом:
Этап 1. Увеличим доходность облигации на 10 базисных пунктов, т. е. с 9 % до 9,1 %. Таким образом, Dу составит 0,001. Новая цена Р+ равна 69,6164.
Этап 2. Уменьшим доходность облигации на 10 базисных пунктов, т. е. с 9 % до 8,9 %. Новая цена Р– составит 71,1105.
Этап 3. При начальной цене Р0, равной 70,3570, аппроксимированная дюрация равна:
(4.23)Насколько хороша такая аппроксимация? Модифицированная дюрация, которую можно подсчитать с помощью формул (4.5) и (4.7), равна 10,62.
Итак, инвестор, решивший определить дюрацию какого-либо финансового инструмента, может смело пользоваться формулой (4.23). Заметим, однако, что верный результат невозможен при отсутствии надежной модели ценообразования, позволяющей провести операции 1 и 2. Такие модели мы анализируем в следующих главах. Подчеркнем: дюрация – побочный продукт модели ценообразования. Если модель ценообразования работает плохо, полученное значение дюрации далеко от действительного.
Мера выпуклости облигации может быть аппроксимирована согласно следующей формуле:
(4.24)В нашем случае аппроксимированная мера выпуклости составит:
Как уже было отмечено, мера выпуклости измеряется различными способами. Выражение (4.24) может быть видоизменено таким образом, чтобы в знаменателе стояло 2. Обратите внимание на то, что в этом случае при подсчете процентного изменения цены, связанного с выпуклостью, по формуле (4.20) коэффициент 1/2 не учитывается.
Дюрация облигации с обратной плавающей купонной ставкой
В главе 2 мы обсуждали процесс создания облигации с обратной плавающей купонной ставкой, а также основные особенности ее ценообразования. Данный раздел посвящен дюрации облигаций этого типа. Дюрация облигации с обратной плавающей ставкой обусловлена дюрацией обеспечения и дюрацией облигации с обычной плавающей купонной ставкой. Предположив, что дюрация облигации с плавающей ставкой близка к нулю, получим дюрацию облигации с обратной плавающей ставкой, равную[25]:
где L – отношение номинальной стоимости облигации с плавающей ставкой к номинальной стоимости облигации с обратной плавающей ставкой. Так, если для создания облигации с плавающей ставкой номиналом $80 млн и облигации с обратной плавающей ставкой номиналом $20 млн используется базовая облигация (обеспечение) номинальной стоимостью $100 млн, L равно 4 ($80 млн / $20 млн).
Нетрудно заметить, что дюрация облигации с обратной плавающей ставкой линейно зависит от дюрации базовой облигации. Предположим, что номинальная стоимость базовой облигации, равная $100 млн, распределена следующим образом: $80 млн – на облигацию с плавающей ставкой и $20 – на облигацию с обратной плавающей ставкой. Предположим также, что и базовая облигация, и облигация с обратной плавающей ставкой торгуются по номиналу, так что отношение цен равно 1, а дюрация базовой облигации равна 8. При изменении процентных ставок на 100 базисных пунктов цена базовой облигации упадет на 8 %, т. е. на $8 млн (8 % × $100 млн). При условии, что цена облигации с плавающей ставкой не меняется с ростом процентных ставок, падение на $8 млн должно обеспечиваться облигацией с обратной плавающей ставкой. Для того чтобы облигация с обратной плавающей ставкой стоимостью $20 млн могла упасть на $8 млн, ее дюрация должна быть равна 40: именно дюрация 40 приведет к изменению цены на 40 %, или на $8 млн. Таким образом, дюрация облигации с обратной плавающей ставкой – это произведение дюрации базовой облигации на коэффициент 5 (т. е. 8 × 5). Или же, поскольку L = 4, она равна (1 + 4), умноженному на дюрацию базовой облигации.
Заметьте: если длительность обеспечивающей облигации равняется 30, то дюрация облигации с обратной плавающей ставкой, равная 40, превысит длительность обеспечения. Инвестор, интерпретирующий дюрацию как средневзвешенную продолжительность жизни облигации, наверняка будет удивлен подобным фактом.
Нетрудно заметить, что дюрация облигации с обратной плавающей ставкой линейно зависит от дюрации базовой облигации. Предположим, что номинальная стоимость базовой облигации, равная $100 млн, распределена следующим образом: $80 млн – на облигацию с плавающей ставкой и $20 – на облигацию с обратной плавающей ставкой. Предположим также, что и базовая облигация, и облигация с обратной плавающей ставкой торгуются по номиналу, так что отношение цен равно 1, а дюрация базовой облигации равна 8. При изменении процентных ставок на 100 базисных пунктов цена базовой облигации упадет на 8 %, т. е. на $8 млн (8 % × $100 млн). При условии, что цена облигации с плавающей ставкой не меняется с ростом процентных ставок, падение на $8 млн должно обеспечиваться облигацией с обратной плавающей ставкой. Для того чтобы облигация с обратной плавающей ставкой стоимостью $20 млн могла упасть на $8 млн, ее дюрация должна быть равна 40: именно дюрация 40 приведет к изменению цены на 40 %, или на $8 млн. Таким образом, дюрация облигации с обратной плавающей ставкой – это произведение дюрации базовой облигации на коэффициент 5 (т. е. 8 × 5). Или же, поскольку L = 4, она равна (1 + 4), умноженному на дюрацию базовой облигации.
Заметьте: если длительность обеспечивающей облигации равняется 30, то дюрация облигации с обратной плавающей ставкой, равная 40, превысит длительность обеспечения. Инвестор, интерпретирующий дюрацию как средневзвешенную продолжительность жизни облигации, наверняка будет удивлен подобным фактом.
ОПРЕДЕЛЕНИЕ СТЕПЕНИ ЧУВСТВИТЕЛЬНОСТИ ПОРТФЕЛЯ К НЕПАРАЛЛЕЛЬНЫМ ИЗМЕНЕНИЯМ ПРОЦЕНТНЫХ СТАВОК
Говоря о сложностях использования понятия дюрации в реальной инвестиционной практике, мы отмечали, что данная мера может давать неверное представление об изменении цен на облигацию или на весь портфель в ситуации, когда процентные ставки меняются не параллельно (подробнее на описании кривой доходности мы остановимся в главе 5). Особенно неутешительные результаты связаны в этом случае с оценкой чувствительности портфеля в целом. Нам, таким образом, необходимо исследовать способ измерения реакции портфеля облигаций на непараллельные изменения кривой доходности. Для измерения данной величины было предложено несколько методик. Двумя основными методиками являются дюрация при изменении формы кривой доходности и дюрация ключевых процентных ставок. Ниже мы опишем каждую из этих методик[26].
Дюрация при изменении формы кривой доходности
Первая методика основывается на чувствительности портфеля к изменению наклона кривой доходности. Первый шаг в применении этой методики заключается в определение того, что подразумевается под наклоном кривой доходности. Участники рынка используют различные определения. Некоторые считают наклоном разницу в кривой доходности казначейских ценных бумаг на двух уровнях сроков погашения. Например, наклон кривой доходности можно определить как разницу между доходностью показателя для долгосрочных (30-летних казначейских облигаций) и двухлетних казначейских облигаций «в ходу». Некоторые считают коротким сроком погашения 6 месяцев.
Одна из первых мер по данной методике была представлена тремя исследователями из инвестиционной компании Salomon Brothers (теперь называемой Salomon Smith Barney): Клаффки, Ма и Нозари[27]. Они назвали ее дюрацией при изменении формы кривой доходности. Они выбрали три срока погашения: 2 года, 10 лет и 30 лет. Используя эти три срока, они рассчитали спред между доходностью десятилетних и двухлетних облигаций и назвали его спредом короткого конца кривой доходности (SEDUR), спред между доходностью тридцатилетних и десятилетних облигаций называется спредом длинного конца кривой доходности (LEDUR). Однако эти концепции применимы и к другим точкам на кривой доходности.
Чтобы рассчитать SEDUR портфеля, сначала рассчитывается изменение в цене каждой ценной бумаги для:
1. увеличения крутизны кривой доходности в коротком конце на х базисных пунктов
2. уменьшения крутизны кривой доходности в коротком конце на х базисных пунктов
Доходность портфеля для кривой доходности рассчитывается путем сложения доходности каждой ценной бумаги портфеля после увеличения крутизны. Обозначим эту доходность как VSE,S, где V означает доходность портфеля, SE короткий конец, а S – увеличение крутизны. Точно так же доходность портфеля после уменьшения крутизны рассчитывается путем сложения доходности каждой ценной бумаги портфеля, а получившаяся доходность обозначается как VSE,F, где F означает уменьшение крутизны. Тогда SEDUR рассчитывается следующим образом:
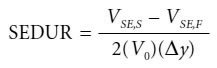где V0 является первоначальной доходностью портфеля (доходностью до увеличения или уменьшения крутизны), а ∆y – числом базисных пунктов, используемых для расчета увеличения или уменьшения крутизны кривой доходности (х).
Сравните приведенную выше формулу с формулой (4.23) для расчета аппроксимированной дюрации. Обратите внимание, что это та же самая формула, но вместо P используется V, и P— и P+ заменены на VSE,S и VSE,F соответственно.
Чтобы рассчитать LEDUR портфеля, сначала рассчитывается изменение в цене каждой ценной бумаги для:
1. уменьшения крутизны кривой доходности в длинном конце на х базисных пунктов
2. увеличения крутизны кривой доходности в длинном конце на х базисных пунктов
Доходность портфеля после каждого изменения обозначается как VLE,S и VLE,F, где LE обозначает длинный конец кривой доходности. Затем рассчитывается LEDUR по следующей формуле:
SEDUR и LEDUR интерпретируются следующим образом. SEDUR является приблизительным процентным изменением доходности портфеля для изменения наклона короткого конца кривой доходности на 100 базисных пунктов. LEDUR является приблизительным процентным изменением доходности портфеля для изменения наклона длинного конца кривой доходности на 100 базисных пунктов.
Одна из первых мер по данной методике была представлена тремя исследователями из инвестиционной компании Salomon Brothers (теперь называемой Salomon Smith Barney): Клаффки, Ма и Нозари[27]. Они назвали ее дюрацией при изменении формы кривой доходности. Они выбрали три срока погашения: 2 года, 10 лет и 30 лет. Используя эти три срока, они рассчитали спред между доходностью десятилетних и двухлетних облигаций и назвали его спредом короткого конца кривой доходности (SEDUR), спред между доходностью тридцатилетних и десятилетних облигаций называется спредом длинного конца кривой доходности (LEDUR). Однако эти концепции применимы и к другим точкам на кривой доходности.
Чтобы рассчитать SEDUR портфеля, сначала рассчитывается изменение в цене каждой ценной бумаги для:
1. увеличения крутизны кривой доходности в коротком конце на х базисных пунктов
2. уменьшения крутизны кривой доходности в коротком конце на х базисных пунктов
Доходность портфеля для кривой доходности рассчитывается путем сложения доходности каждой ценной бумаги портфеля после увеличения крутизны. Обозначим эту доходность как VSE,S, где V означает доходность портфеля, SE короткий конец, а S – увеличение крутизны. Точно так же доходность портфеля после уменьшения крутизны рассчитывается путем сложения доходности каждой ценной бумаги портфеля, а получившаяся доходность обозначается как VSE,F, где F означает уменьшение крутизны. Тогда SEDUR рассчитывается следующим образом:
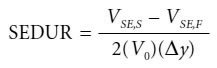
Сравните приведенную выше формулу с формулой (4.23) для расчета аппроксимированной дюрации. Обратите внимание, что это та же самая формула, но вместо P используется V, и P— и P+ заменены на VSE,S и VSE,F соответственно.
Чтобы рассчитать LEDUR портфеля, сначала рассчитывается изменение в цене каждой ценной бумаги для:
1. уменьшения крутизны кривой доходности в длинном конце на х базисных пунктов
2. увеличения крутизны кривой доходности в длинном конце на х базисных пунктов
Доходность портфеля после каждого изменения обозначается как VLE,S и VLE,F, где LE обозначает длинный конец кривой доходности. Затем рассчитывается LEDUR по следующей формуле:
Дюрация ключевых процентных ставок
Наиболее популярной мерой оценки чувствительности ценной бумаги или портфеля к изменениям кривой доходности является дюрация ключевых процентных ставок.
Вычисление значения дюрации ключевых процентных ставок в общем сводится к следующему: изменяется доходность для определенной даты погашения на кривой доходности, а затем при прочих равных определяется чувствительность ценной бумаги или портфеля к этому изменению. Чувствительность, выражающаяся в изменении стоимости портфеля при определенном изменении доходности, носит название дюрации процентной ставки. Для каждой точки кривой доходности существует своя дюрация процентной ставки. Таким образом, можно говорить не об одном значении дюрации процентной ставки, а о векторе дюраций, охватывающем все даты погашения на кривой доходности. Общее изменение стоимости облигации или портфеля при изменении всех процентных ставок на одинаковое число базисных пунктов – это то самое значение дюрации, о котором шла речь выше в этой главе.
Идея использования множественных дюраций была предложена Дональдом Чамберсом и Виллардом Карлтоном в 1988 году; исследователи назвали новую меру вектором дюраций[28]. Роберт Рейтано в нескольких статьях писал об аналогичных методиках; свою дюрацию он назвал частичной дюрацией[29]. Наибольшую популярность получило, однако, исследование Томаса Хоу 1992 года: здесь речь шла о дюрациях процентных ставок[30].
Хоу предложил обратить особое внимание на 11 ключевых сроков погашения, расположенных на кривой казначейских ценных бумаг, которые мы обсудим в главе 5. Специфическая кривая, использованная при анализе, получила название кривой казначейских спот-ставок: она показывает, как зависят от срока до погашения доходности бескупонных казначейских ценных бумаг (подробнее см. главу 5). Дюрации процентных ставок в этих точках были названы дюрациями ключевых процентных ставок. Длительности, для которых принято измерять значения дюрации ключевых процентных ставок, – 3 месяца, 1 год, 2 года, 3 года, 5 лет, 7, 10, 15, 20, 25 и 30 лет. Изменения ставок в промежутке между двумя ключевыми процентными ставками вычисляются с помощью линейной аппроксимации.
Дюрация ключевых процентных ставок для данного срока погашения интерпретируется следующим образом: при неизменной доходности для всех прочих сроков погашения, дюрация ключевой процентной ставки – это примерное процентное изменение стоимости портфеля (облигации) при изменении на 100 базисных пунктов доходности для определенного срока погашения. Дюрация ключевой процентной ставки, таким образом, находится через изменение доходности данного срока погашения и выяснение размера соответствующего изменения стоимости (цены). Иными словами, мы используем здесь формулу (4.23). Величины, обозначенные в ней как Р– и Р+, – это стоимости портфеля в случае измерения чувствительности портфеля в целом (доходность меняется только для срока погашения, для которого должна быть выяснена дюрация ключевой ставки; прочие процентные ставки оставляются без изменений).
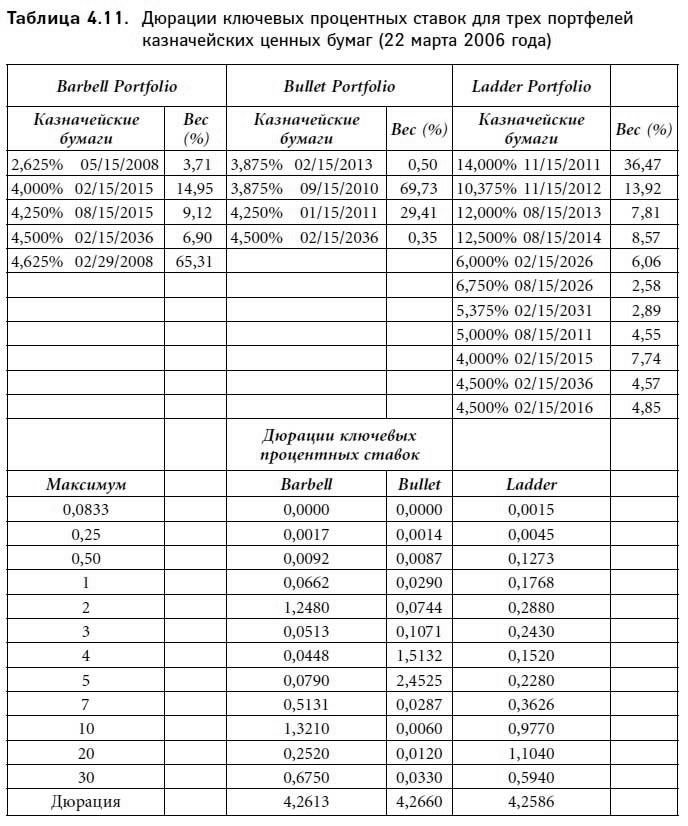
Для того чтобы понятие дюрации ключевых процентных ставок стало в полной мере ясно читателю, обратимся к анализу трех реальных портфелей. Таблица 4.11 демонстрирует данные, относящиеся к трем портфелям, состоящим из казначейских бумаг разной длительности (информация приводится на 22 марта 2006 года). У всех портфелей одинаковая дюрация: она равна 4,26[31].
В таблице приводятся дюрации ключевых процентных ставок для каждой ценной бумаги и для каждого портфеля. Выясняется, что дюрации ключевых процентных ставок для трех портфелей различны. Рассмотрим дюрации ключевой процентной ставки для срока погашения 30 лет во всех трех портфелях. В первом портфеле дюрация ключевой процентной ставки для длительности, равной 30 годам, составляет 0,675. Это значит, что при изменении спот-ставки на 30-летние казначейские бумаги на 100 базисных пунктов (при неизменности спот-ставок для прочих сроков погашения) стоимость портфеля изменится примерно на 0,675 %. Для второго портфеля дюрация ключевой процентной ставки для срока погашения 30 лет равна нулю. Таким образом, при изменении на 100 базисных пунктов спот-ставки на 30-летние казначейские бумаги (напомним, что спот-ставки для прочих длительностей остаются прежними) стоимость второго портфеля не претерпит никаких изменений. Дюрация ключевой процентной ставки третьего портфеля для срока погашения 30 лет составляет 0,594: при изменении на 100 базисных пунктов 30-летней спот-ставки (ставки для прочих длительностей не меняются) стоимость этого портфеля изменится на 0,594 %.
Вывод очевиден: несмотря на то что дюрации всех трех портфелей одинаковы (4, 26), портфели по-разному отреагируют на изменение 30-летних спот-ставок. Из материалов таблицы можно заключить, что реакция каждого из портфелей на изменения процентных ставок для той или иной длительности будет различна.
Резюме
Зависимость цена – доходность для всех облигаций без встроенных опционов является выпуклой функцией. Волатильность цен облигации, не имеющей встроенных опционов, характеризуется тремя признаками: 1) при малых изменениях доходности процентные изменения цены симметричны; 2) при существенных изменениях доходности процентные изменения цены асимметричны, и 3) в случае существенных изменений доходности рост цены больше, чем ее падение при изменении доходности на ту же абсолютную величину.
Волатильность цены облигации без встроенного опциона зависит от двух параметров облигации – ее длительности и купона, а также от уровня доходности, при котором торгуется данная ценная бумага. При данных длительности и доходности: чем ниже купонная ставка, тем выше волатильность цен. При данных купонной ставке и доходности: чем больше длительность, тем выше волатильность. При данной купонной ставке и длительности: чем ниже доходность, тем выше волатильность цен.
Существует две меры волатильности цены облигации: ценовая стоимость базисного пункта и дюрация. Мы рассмотрим различные меры дюрации – дюрацию Маколея, модифицированную дюрацию и долларовую дюрацию – и покажем отношения между волатильностью цены облигации и каждой из этих мер. Модифицированная дюрация является аппроксимированным процентным изменением цены для изменения доходности на 100 базисных пунктов. Долларовая дюрация является аппроксимированным изменением долларовой цены.
Дюрация – удобная мера определения процентного изменения цены при малых изменениях доходности. Между тем в ситуации существенного изменения доходности данная величина оказывается не столь надежной. Аппроксимированное изменение цены, вычисляемое на основе дюрации, может быть уточнено благодаря использованию понятия «выпуклость». Дюрация и выпуклость вместе взятые позволяют получить прекрасную аппроксимацию изменений цены при значительных изменениях доходности.
Дюрация – это аппроксимация ценовых изменений при условии параллельных смещений кривой доходности. Дюрацию не следует интерпретировать как средневзвешенный срок до погашения облигации. Для некоторых облигаций значение модифицированной дюрации может превышать срок до погашения. Дюрация и выпуклость могут быть вычислены путем изучения поведения цены облигации при росте и падении доходности на небольшое число базисных пунктов. Дюрация облигации с обратной плавающей ставкой линейно зависит от дюрации облигации, являющейся обеспечением.
Вычисление значения дюрации ключевых процентных ставок в общем сводится к следующему: изменяется доходность для определенной даты погашения на кривой доходности, а затем при прочих равных определяется чувствительность ценной бумаги или портфеля к этому изменению. Чувствительность, выражающаяся в изменении стоимости портфеля при определенном изменении доходности, носит название дюрации процентной ставки. Для каждой точки кривой доходности существует своя дюрация процентной ставки. Таким образом, можно говорить не об одном значении дюрации процентной ставки, а о векторе дюраций, охватывающем все даты погашения на кривой доходности. Общее изменение стоимости облигации или портфеля при изменении всех процентных ставок на одинаковое число базисных пунктов – это то самое значение дюрации, о котором шла речь выше в этой главе.
Идея использования множественных дюраций была предложена Дональдом Чамберсом и Виллардом Карлтоном в 1988 году; исследователи назвали новую меру вектором дюраций[28]. Роберт Рейтано в нескольких статьях писал об аналогичных методиках; свою дюрацию он назвал частичной дюрацией[29]. Наибольшую популярность получило, однако, исследование Томаса Хоу 1992 года: здесь речь шла о дюрациях процентных ставок[30].
Хоу предложил обратить особое внимание на 11 ключевых сроков погашения, расположенных на кривой казначейских ценных бумаг, которые мы обсудим в главе 5. Специфическая кривая, использованная при анализе, получила название кривой казначейских спот-ставок: она показывает, как зависят от срока до погашения доходности бескупонных казначейских ценных бумаг (подробнее см. главу 5). Дюрации процентных ставок в этих точках были названы дюрациями ключевых процентных ставок. Длительности, для которых принято измерять значения дюрации ключевых процентных ставок, – 3 месяца, 1 год, 2 года, 3 года, 5 лет, 7, 10, 15, 20, 25 и 30 лет. Изменения ставок в промежутке между двумя ключевыми процентными ставками вычисляются с помощью линейной аппроксимации.
Дюрация ключевых процентных ставок для данного срока погашения интерпретируется следующим образом: при неизменной доходности для всех прочих сроков погашения, дюрация ключевой процентной ставки – это примерное процентное изменение стоимости портфеля (облигации) при изменении на 100 базисных пунктов доходности для определенного срока погашения. Дюрация ключевой процентной ставки, таким образом, находится через изменение доходности данного срока погашения и выяснение размера соответствующего изменения стоимости (цены). Иными словами, мы используем здесь формулу (4.23). Величины, обозначенные в ней как Р– и Р+, – это стоимости портфеля в случае измерения чувствительности портфеля в целом (доходность меняется только для срока погашения, для которого должна быть выяснена дюрация ключевой ставки; прочие процентные ставки оставляются без изменений).
Для того чтобы понятие дюрации ключевых процентных ставок стало в полной мере ясно читателю, обратимся к анализу трех реальных портфелей. Таблица 4.11 демонстрирует данные, относящиеся к трем портфелям, состоящим из казначейских бумаг разной длительности (информация приводится на 22 марта 2006 года). У всех портфелей одинаковая дюрация: она равна 4,26[31].
В таблице приводятся дюрации ключевых процентных ставок для каждой ценной бумаги и для каждого портфеля. Выясняется, что дюрации ключевых процентных ставок для трех портфелей различны. Рассмотрим дюрации ключевой процентной ставки для срока погашения 30 лет во всех трех портфелях. В первом портфеле дюрация ключевой процентной ставки для длительности, равной 30 годам, составляет 0,675. Это значит, что при изменении спот-ставки на 30-летние казначейские бумаги на 100 базисных пунктов (при неизменности спот-ставок для прочих сроков погашения) стоимость портфеля изменится примерно на 0,675 %. Для второго портфеля дюрация ключевой процентной ставки для срока погашения 30 лет равна нулю. Таким образом, при изменении на 100 базисных пунктов спот-ставки на 30-летние казначейские бумаги (напомним, что спот-ставки для прочих длительностей остаются прежними) стоимость второго портфеля не претерпит никаких изменений. Дюрация ключевой процентной ставки третьего портфеля для срока погашения 30 лет составляет 0,594: при изменении на 100 базисных пунктов 30-летней спот-ставки (ставки для прочих длительностей не меняются) стоимость этого портфеля изменится на 0,594 %.
Вывод очевиден: несмотря на то что дюрации всех трех портфелей одинаковы (4, 26), портфели по-разному отреагируют на изменение 30-летних спот-ставок. Из материалов таблицы можно заключить, что реакция каждого из портфелей на изменения процентных ставок для той или иной длительности будет различна.
Резюме
Зависимость цена – доходность для всех облигаций без встроенных опционов является выпуклой функцией. Волатильность цен облигации, не имеющей встроенных опционов, характеризуется тремя признаками: 1) при малых изменениях доходности процентные изменения цены симметричны; 2) при существенных изменениях доходности процентные изменения цены асимметричны, и 3) в случае существенных изменений доходности рост цены больше, чем ее падение при изменении доходности на ту же абсолютную величину.
Волатильность цены облигации без встроенного опциона зависит от двух параметров облигации – ее длительности и купона, а также от уровня доходности, при котором торгуется данная ценная бумага. При данных длительности и доходности: чем ниже купонная ставка, тем выше волатильность цен. При данных купонной ставке и доходности: чем больше длительность, тем выше волатильность. При данной купонной ставке и длительности: чем ниже доходность, тем выше волатильность цен.
Дюрация – удобная мера определения процентного изменения цены при малых изменениях доходности. Между тем в ситуации существенного изменения доходности данная величина оказывается не столь надежной. Аппроксимированное изменение цены, вычисляемое на основе дюрации, может быть уточнено благодаря использованию понятия «выпуклость». Дюрация и выпуклость вместе взятые позволяют получить прекрасную аппроксимацию изменений цены при значительных изменениях доходности.
Дюрация – это аппроксимация ценовых изменений при условии параллельных смещений кривой доходности. Дюрацию не следует интерпретировать как средневзвешенный срок до погашения облигации. Для некоторых облигаций значение модифицированной дюрации может превышать срок до погашения. Дюрация и выпуклость могут быть вычислены путем изучения поведения цены облигации при росте и падении доходности на небольшое число базисных пунктов. Дюрация облигации с обратной плавающей ставкой линейно зависит от дюрации облигации, являющейся обеспечением.