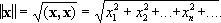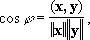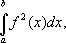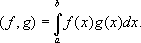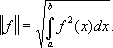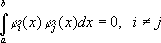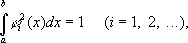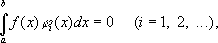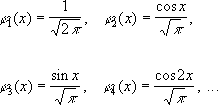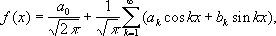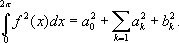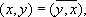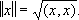Страница:
Соч.: Le chanson de ma vie. Mes mйmoires, Р., 1927; Autres temps, autres chants, 12 йd., [Р.], 1946.
Вейль
, Р.
Курант
) были написаны под руководством Г.
Вейль
, Р.
Курант
) были написаны под руководством Г.
Научная биография Г. резко распадается на периоды, посвященные работе в какой-либо одной области математики: а) теория инвариантов (1885—93), б) теория алгебраических чисел (1893—98), в) основания геометрии (1898—1902), г) принцип Дирихле и примыкающие к нему проблемы вариационного исчисления и дифференциальных уравнений (1900—06), д) теория интегральных уравнений (1900—10), е) решение проблемы Варинга в теории чисел (1908—09), ж) основы математической физики (1910—22), з) логической основы математики (1922—39).
В теории инвариантов исследования Г. явились завершением периода бурного развития этой области математики во 2-й половине 19 в. Им доказана основная теорема о существовании конечного базиса системы инвариантов. Работы Г. по теории алгебраических чисел преобразовали эту область математики и стали исходным пунктом её последующего развития. Данное Г. решение проблемы Дирихле положило начало разработке т. н. прямых методов в вариационном исчислении. Построенная Г. теория интегральных уравнений с симметричным ядром составила одну из основ современного функционального анализа (см.
Гильбертово пространство
) и особенно спектральной теории линейных операторов. Основания геометрии Г. (1899) стали образцом для дальнейших работ по аксиоматическому построению геометрии. К 1922 у Г. сложило значительно более обширный план обоснования всей математики путём её полной формализации с последующим «метаматематическим» доказательством непротиворечивости формализованной математики. Два тома «Оснований математики», написанных Г. совместно с П. Бернайсом, в которых эта концепция подробно развивается, вышли в 1934 и 1939. Первоначальные надежды Г. в этой области не оправдались: проблема непротиворечивости формализованных математических теорий оказалась глубже и труднее, чем Г. предполагал сначала. Но вся дальнейшая работа над логическими основами математики в большой мере идёт по путям, намеченным Г., и пользуется созданными им концепциями. Считая с логической точки зрения необходимой полную формализацию математики, Г. в то же время верил в силу творческой математической интуиции. Он был большим мастером в высшей степени наглядного изложения математических теорий. В этом отношении замечательна «Наглядная геометрия», написанная Г. совместно с С. Кон-Фоссеном. Для творчества Г. характерны уверенность в неограниченной силе человеческого разума, убеждение в единстве математической науки и единстве математики и естествознания. Собрание сочинений Г., изданное под его наблюдением (1932—35), кончается статьей «Познание природы», а эта статья лозунгом «Мы должны знать — мы будем знать».
Соч.: Gesammelte Abhandlungen, Bd 1—3, В., 1932—35; в рус. пер. — Основания геометрии, М. — Л., 1948; Основы теоретической логики, М., 1947 (совм. с В. Аккерманом); Наглядная геометрия, 2 изд., М. — Л., 1951 (совм. с С. Кон-Фоссеном).
Лит.:Проблемы Гильберта. Сборник, под ред. П. С. Александрова, М., 1969; Weyl Н., David Hilbert and his mathematical work, «Bulletin of the American Mathematical Society», 1944, t. 50, p. 612—54; Reid C., Hilbert, В., 1970.
А. Н. Колмогоров.
 Д. Гильберт.
Д. Гильберт.