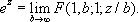).
Лит.:Страхов Н. М., Типы литогенеза и их эволюция в истории Земли, М., 1963; Перельман А. И., Геохимия эпигенетических процессов (Зона гипергенеза), 3 изд., М., 1968.
В. В. Щербина.
гипергеометрического ряда
. Название «Г. ф.» было дано Дж.
Валлисом
(1650). Г. ф. являются интегралами гипергеометрического уравнения
z(1—
z)
w»+ [
g—(1 + a+ bz]
w'—abw= 0.
Это уравнение имеет три регулярные особые точки 0, 1 и Ґ и является канонической формой уравнений гипергеометрического типа. Важнейшие специальные функции математического анализа являются интегралами уравнений гипергеометрического типа (например,
шаровые функции
) или уравнений, возникающих из гипергеометрических путём слияния их особых точек (например,
цилиндрические функции
). Теория уравнений гипергеометрического типа явилась основой для возникновения важной математической дисциплины — аналитической теории дифференциальных уравнений. Между различными Г. ф.
w =
F(a, b; g;
z)
имеется большое число соотношений, например:
F(a, 1;
g,
z) = (1—
z)
–1
F(1,
g —a; g; z/(z—1)).
Лит.:Уиттекер Э. Т. и Ватсон Дж. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963.
Эйлером
(1778). Разложение многих функций в бесконечные ряды представляет собой частные случаи Г. р. Например:
(1 + z)
n
=
F(—
n, b; b; —z),
ln (1 + z) = z
F(1, 1; 2; —z),
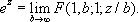
Г. р. имеет смысл, если g не равно нулю или целому отрицательному числу; он сходится при |z| < 1. Если, кроме того, g—a—b >0, то Г. р. сходится и при z = 1. В этом случае справедлива формула Гаусса:
F(a, b; g; 1) = G(g)G(g—a—b)/G(g—a)G(g—b),
где Г (
z) —
гамма-функция
. Аналитическая функция, определяемая для |z| < 1 с помощью Г. р., называется
гипергеометрической функцией
и играет важную роль в теории дифференциальных уравнений.
гипер...
и греч. hidros — пот), чрезмерное
потоотделение
, потливость, у здоровых людей Г. может наблюдаться при высокой температуре окружающей среды как один из механизмов
терморегуляции
, при повышенной физической нагрузке. Общий Г. может наблюдаться при некоторых эндокринных заболеваниях, различных инфекциях и интоксикациях, а также при поражении гипоталамической области головного мозга. Местный Г. (потливость ладоней, стоп, подмышечных впадин и др.,) может зависеть от повышенной возбудимости нервной системы. Г. предрасполагает к простудным заболеваниям, гнойничковой и грибковой инфекциям (проникновение возбудителей через разрыхленный поверхностный слой кожи), потертостям.
Лечение: устранение причины Г.; гигиеническое содержание тела, общеукрепляющее лечение, иногда — физиотерапия, местно-антисептические и адсорбирующие средства.