Страница:
- << Первая
- « Предыдущая
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- Следующая »
- Последняя >>
[329, c. 57], на Франса Ксавера Пфайфера,(7) приводившего фотографические снимки объектов природы и результаты их измерений, на Г.Т.Фехнера,(8) а также на опыты Витмера (Witmer, 1894) и Сегала (Segal, 1906). "Для картин с ясно изображенным горизонтом, у которых расстояние между двумя параллельными линиями, а именно между верхним и нижним краем картины, должно быть разделено третьей параллелью – горизонтом, с давних пор установлено правило, что это деление должно производиться по золотому сечению"
[329, c. 66]. Например, если на картине изображены море и небо (следовательно, и разделяющий их горизонт), то одно должно перевешивать, т.к. видовое различие между ними влечет за собой подчеркивание одной или другой части. Одному отдается предпочтение, но избегая преувеличения. Поиск среднего пути между равенством и преувеличением приводит к определенной пропорции, в результате чего мы обретаем спокойствие, уверенность, впечатление чего-то закрепленного в самом себе. Форматам книг, картинам, входным билетам, бумажникам, сундукам, шоколадным плиткам, пересказывает Тимердинг, часто придается форма, соответствующая золотому сечению (отношение сторон прямоугольника равно соответствующей величине). Опыты с людьми по выбору из десяти прямоугольников разной формы показывали заметное предпочтение золотого сечения.
Впрочем, сам Тимердинг, как рациональный ученый, значительно осторожнее: "Гораздо более правдоподобным является предположение, что золотому сечению первоначально было отдано предпочтение по рассудочным соображениям. Но вследствие того, что это отношение было избрано нормой для бесчисленного множества употребляемых форм и что его приближения, естественно получающиеся путем выбора удобных близких численных соотношений, в общем и целом выдвигаются снова, оно в конце концов так утвердилось в представлении, что даже бессознательный выбор отношения размеров тоже тяготеет к нему" [329, c. 73].
Древние принципы соразмерности действуют как в живописи, так и в архитектуре: от Вавилона (в котором, напомним, роль главной фигуры играл равносторонний треугольник и благодаря ему отношение 1 : ?3 ), Малой Азии, Греции, через искусство рисования и архитектурную готику европейских Средних веков до эпохи Леонардо да Винчи и Дюрера.(9) У египтян и вавилонян соотношение размеров в храме имело священное значение. Витрувий (III, гл.1), которому следовал Лука Пачоли в изложении архитектурных вопросов, выдвигал требование "симметрии" (теперь это слово употребляется в совсем другом смысле). Симметрия происходит от пропорции, которая по-гречески называется "аналогией". Пропорциональность означала при этом "согласованность соответствующих частей постройки между собой и целым". Архитекторам надлежит в совершенстве владеть учением о симметрии. При построении отдельных частей пользуются одним и тем же отношением, обнаруживающимся у целого.
Тимердинг приводит математическую расшифровку: части постройки должны быть членами геометрической прогрессии
с, сx, сx2, сx3, сx4, сx5, …
(13 )
Ее графическое изображение:
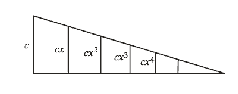
В частном случае, когда прогрессия (13) является возвратной, т.е. когда первый член и, следовательно, каждый другой равен сумме двух последующих,(10) получаем с = сx + сx2, или 1 = x + x 2, что повторяет уравнение для золотого сечения (7).
Сходным образом, отталкиваясь от Цейзинга, Тимердинг интерпретирует и природные явления, в частности закон листорасположения:
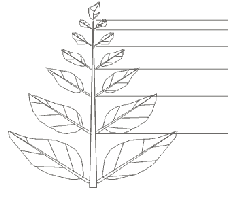
Так, Тимердинг утверждает: "К тому же в природе, по-видимому, действительно выполняется некоторый закон пропорций, не совпадающий, правда, с отношением золотого сечения, но, так сказать, одного с ним направления. Этот закон можно так сформулировать: когда однородные части следуют друг за другом в порядке убывания величины, если нет возмущающих влияний, уменьшение происходит в геометрической прогрессии; так же происходит и увеличение там, где величина частей возрастает" [329, c. 58]. Направление в природных объектах задано ростом, и более старые части, из которых вырастают новые, оказываются либо самыми маленькими, либо, наоборот, самыми большими. Этот закон назвали законом натурального роста. Там, где он соблюдается, может встретиться и отношение золотого сечения, если не точное, то приближенное.
Выше уже упоминалось о связи золотого сечения с числами Фибоначчи. Н.Н.Воробьев уточняет и дополняет сказанное Тимердингом: "Природа дает нам многочисленные примеры расположения однородных предметов, описываемых числами Фибоначчи. В разнообразных спиралевидно расположенных мелких частях растений обычно можно усмотреть два семейства спиралей. В одном из этих семейств спирали завиваются по часовой стрелке, в другом – против. Числа спиралей того и другого типов часто оказываются соседними числами Фибоначчи. Так, взяв сосновую веточку, легко заметить, что хвоины образуют две спирали, идущие справа внизу налево вверх. Вместе с тем они же составляют три спирали, идущие слева снизу направо вверх. На многих шишках семена (т.е. "чешуйки") расположены в трех спиралях, полого навивающихся на стержень шишки. Они же расположены в пяти спиралях, круто навивающихся в противоположном направлении. В крупных шишках удается наблюдать 5 и 8 и даже 8 и 13 спиралей. Хорошо заметны такие спирали и на ананасе: обычно их бывает 8 и 13. У многих сложноцветных (например, у маргаритки или ромашки) заметно спиральное расположение отдельных цветков в соцветиях-корзинках. Число спиралей бывает здесь 13 в одном направлении и 21 в другом и даже соответственно 21 и 34. Особенно много спиралей можно наблюдать в расположении семечек крупного подсолнуха. Их число в каждом из направлений может достигать соответственно 55 и 89" [86, c. 122].
В книге Н.Н.Воробьева обсуждается вопрос и непосредственно о золотом сечении. Приведем две цитаты: "Выдающийся геометр и астроном ХVII века И.Кеплер (известный, впрочем, в свое время больше как астролог) отваживался даже ставить формулировку закономерности золотого сечения на один уровень с таким фундаментальным математическим фактом, как теорема Пифагора" [там же, с. 123]. И на той же странице: "Различными философами древности и средневековья внешняя красота прямоугольников и треугольников золотого сечения, а также других фигур, в которых наблюдается деление в среднем и крайнем отношении, возводилась в эмпирический и даже философский принцип. Золотым сечением и еще некоторыми отношениями пытались не только описывать, но и объяснять явления природы и даже общественной жизни, а с самим числом ? (11) и его подходящими дробями производились разного рода мистические операции. Важную роль в таких рассмотрениях играла фигура, изображенная на рис. 3-5, которая при этом называлась пентаграммой". Далее Н.Н.Воробьев говорит о современном возрождении интереса к золотому сечению, в целом оценивая данный факт как негативный (что, впрочем, не помешало автору уделить значительное внимание этой теме в собственной брошюре). В России вопрос о золотом сечении, помимо Н.Н.Воробьева, затрагивался, например, в книге Е.И.Игнатьева "В царстве смекалки, или Арифметика для всех" [136].
Не следует полагать, что значение закономерности золотого сечения сводится исключительно к миру природы или изобразительных искусств. Так, Р. Якобсон обнаруживает образцы той же формы в литературе. Анализируя стихотворение Гельдерлина, он пишет о "многостороннем противопоставлении трех заключительных строк пяти предшествующим – одном из показателей сложного и преднамеренного формообразования. В последнем "Die Aussicht" Гельдерлина с полной отчетливостью представлено то самое золотое сечение, которое установилось со времен Леонардо. Меньший отрезок (Minor) относится к большему (Major) как больший к целому. Золотое сечение (8 : 5 = 5 : 3) противопоставляет неравные отрезки восьмистишия ‹…›" [402, c. 376]. Таким образом, попутно Якобсон использует и представление гармонической пропорции через числа Фибоначчи: здесь 3, 5, 8, см. ряд (12). Исследованию смысла той же пропорции, ее роли в искусстве, в частности, в музыке, уделял внимание и А.Ф.Лосев, см. [190, c. 356-368].(12) О "стремлении к гармонии имеющихся соотношений целого и его составных частей", о регулирующем правиле золотого сечения, последовательности Фибоначчи начинают говорить и современные политологи, см., напр., [330, c. 55].
На этом ограничим исторический экскурс. По-видимому, он полезен не только из прагматических соображений ("оживление материала"), но так или иначе обозначает позиции, которым придется следовать или, напротив, от которых отталкиваться в процессе дальнейшего изложения. Так, в целом для нас неприемлем, как сказано, ореол "духоведческих", оккультных истолкований, которыми оброс или из которых еще не окончательно вычленился рациональный феномен золотого сечения. Подобные коннотации, если и значимы в настоящем контексте, то лишь настолько, насколько массовым представлениям вообще присуще смешивать здравые начала с "загадочными", непросветленными критическим рассудком. Неудовлетворителен, на наш взгляд, и чисто позитивистский, голо-эмпирический путь, скажем, Цейзинга, Фехнера. Сами по себе опытные измерения не в состоянии подтвердить актуальности золотого сечения в природных явлениях, искусстве, в коллективных предпочтениях, ибо отсутствует действительно строгий критерий для того, чтобы отличить гармоническую пропорцию от других, ей близких. В результате выбор авторами именно золотого деления оставляет впечатление произвольности, недосказанности. Только соединение теории с опытом способно дать то сочетание логической обязательности и фактической подтвержденности, которое отличает науку в собственном смысле.
И в двух первых разделах главы, и в нижеследующих мы стараемся придерживаться именно этой линии. Очень важно, чтобы закономерность золотого сечения (или некие другие, ибо золотым сечением, в чем позже предстоит убедиться, существо вопроса не ограничивается) не оказывалась навязанной какими-то посторонними соображениями, а была необходимым, последовательным результатом содержательной теоретической модели политических систем, отчего в наше распоряжение автоматически попадал бы и ответ на вопрос "почему". (Очевидно, потому, что составные элементы системы обладают сформулированными в теории свойствами.) Теория, конечно, должна проверяться на практике, и в этом мы полностью солидарны с Цейзингом, Фехнером.
Вызывает интерес упомянутый Тимердингом "закон натурального роста". Не берусь судить о его общей формулировке, но в социально-политической сфере он находит определенные выражения. Так, если считать направлением исторического развития, или роста, движение от аграрных обществ к индустриальным, затем к разделению последних на капиталистические и социалистические, то каждая последующая ступень должна быть меньше предыдущей, образуя нечто вроде ступенчатой пирамиды:
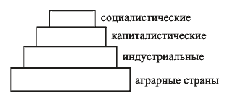
В послевоенном мировом сообществе отношение характеристических объемов четвертой ступени к третьей и, соответственно, третьей ко второй составляли значения, близкие к золотому делению. При этом, правда, остается неясным, существовали ли общие критерии оценки, вернее самооценки, у индустриального мира в целом, с одной стороны, и аграрного, с другой (признак объема промышленной продукции аутентичен лишь для индустриальных государств, но не для аграрных), поэтому трудно сказать что-либо конкретное о числовом соотношении между ними и даже о том, уместны ли вообще в данном случае количественные сравнения. Поэтому на стыке двух первых ступеней названный закон носит лишь описательный, полуметафорический характер.
Однако строение СССР (рис. 3-2, 3-3) в более строгом смысле соответствует названному закону. Именно вокруг РСФСР были объединены национальные окраины, ставшие, таким образом, следующей ступенью социалистического роста или процесса. Впоследствии отношение характеристических объемов "нацреспублики / РСФСР" установилось, как мы помним, вблизи значения, соответствующего золотому сечению. В свою очередь, если общим фундаментом или "корнем" обеих ступеней – и РСФСР, и нацреспублик – считать СССР ("идею СССР"), то и его объем удовлетворял условию (10). Обозначив характеристический объем СССР через с, придем к последовательности типа (13):
с, сx, cx2,
( 14 )
где х? 0,62 – величина, отвечающая золотому сечению, сх– объем РСФСР, сх2 – нацреспублик.
Такие соображения наводят на мысль, что конструктивно-технологические начала в политике, возможно, не столь далеко отстоят от "органических", или естественно-исторических. Природа тоже строит свои "пирамиды".
1 После вступления во францисканский монашеский орден получил имя брата Луки из Борго Сан Сепольеро. Профессор математики в университете и других учебных заведениях Рима, Неаполя, Милана, Флоренции, Болоньи [142, c. 286 ].
2 "Интерес пифагорейцев к симметрии, гармонии, числовым пропорциям привел их к занятиям "золотым делением" (выяснение правильных количественных соотношений между различными частями зданий или скульптурных фигур)", – пишет К.Куманецкий [169, c. 77].
3 В поздней древнегреческой легенде его смерть считалась наказанием за раскрытие тайны богов, "поскольку несказанное и безoбразное всегда должны пребывать сокрытыми". Ямвлих: "О Гиппасе говорят, что он был из числа пифагорейцев; за то, что разгласил и построил впервые сферу из двенадцати пятиугольников, он погиб в море как нечестивец, зато снискал славу первооткрывателя" [347, c. 152].
4 Чтобы подчеркнуть демоническое происхождение звездчатой пентаграммы, ее переворачивали "вверх ногами", в результате чего ее очертания напоминали два рога, два уха и козлиную бороду сатаны (этой разновидностью пользуются и современные сатанисты).
5 Хвост возрожденческой метафизики дотягивается до современности, и новейшие, насквозь коммерциализированные и абсолютно далекие, казалось бы, от высоких соображений модельно-подиумные стандарты диктуют для женской фигуры цифры 90 : 60 : 90, т.е. окружность талии должна составлять 2/3 от окружности бедер и груди. Как мы помним, 2/3 – второе из наилучших приближений к золотому сечению, см. ряд (12).
6 Zeising. Neue Lehre von den Proportionen des menschlichen Korpers. Leipzig, 1854 (Новое учение о пропорциях человеческого тела).
7 Franz Xaver Pfeifer. Der Goldene Schnitt. Augsburg, 1885 (Золотое сечение).
8 G.Th.Fechner. Vorschule der Aesthetik. 12A. 1897 (Введение в эстетику).
9 Основоположник живописи немецкого Возрождения А.Дюрер одновременно был и теоретиком искусства. В "Четырех книгах о пропорциях человека" (1528), составившим итог, или венец, его творчества, указано множество соотношений размеров правильных человеческих тел и лиц, совпадающих с пропорцией золотого сечения.
10 Или предыдущих – в зависимости от порядка расположения членов прогрессии.
11 Такой буквой здесь обозначена величина ? = (1 + ?5 )/2
12 В примечаниях к работе А.Ф.Лосева приведены ссылки на некоторую литературу, например, [201], [202] и о "золотом делении" у И.С.Баха: [439], [440]
3.4. Биполярные партийные системы
Двухпартийные или двухблоковые системы весьма распространены в современных демократических государствах. Республиканцы и демократы в США, консерваторы и лейбористы в Британии, коалиция "ХДС/ХСС – СвДП", с одной стороны, и "СДПГ – зеленые", с другой, в ФРГ, "правые" и "левые" во Франции – лишь некоторые из примеров. Речь идет об отчетливо выраженной дихотомности, основных политических акторов два. Каждый из них участвует в энергичной борьбе за электорат, стремясь привлечь на свою сторону максимальную долю политически активного населения, что удовлетворяет условию "экспансии" рассматриваемой модели.
При этом ни для политической системы в целом, ни для каждого из двух основных политических субъектов в отдельности не представляется возможным окончательное устранение соперника. Обратное означало бы изчезновение главной мишени для критики, конец политической конкуренции, отказ от принятых правил игры. Поэтому в устойчивых либеральных системах один актор не мыслится без другого, условие их "неразрывности" также выполнено.
Те же правила игры диктуют на каждом отдельном этапе разделение на правящую партию(коалицию, блок) и оппозицию. Последняя в демократических государствах, разумеется, не третируется; в одной из старейших демократий, английской, она даже находится под покровительством короны, нося наименование "оппозиции Ее величества". Но при этом, согласно "цивилизованным правилам", от оппозиции ожидается признание за собой статуса проигравшей стороны (пусть временно, до следующих выборов). От нее требуется согласие со статус-кво, как с фактом, соответствующие "сдержанность и смирение", понимание того, что не только в общих, но и в собственных интересах целесообразно придержать до поры реальные претензии на власть. А последняя, строго говоря, есть главная ценность и цель политической партии как таковой. Таким образом выходит, что оппозиция в названных политических системах как бы приносит в жертву свои главные интересы и ценности, не без оснований полагая, что точно так же поступит и противоположная сторона, если после будущих выборов роли поменяются на противоположные. В парламенте меньшинство считает необходимым подчиняться решениям большинства, и эти решения принимаются в качестве общих, исходящих от парламента в целом. Оппозиционное меньшинство, таким образом, демонстрирует готовность принести свои наличные голоса на алтарь действующих демократических правил, впоследствии солидаризируясь с теми законами, которые были приняты – быть может, вопреки конкретному несогласию. Т.е. удовлетворено и третье условие модели.
Обозначим электорат правящей партии или блока через а, оппозиции – через b. За объем целого спримем суммарную численность политически активного населения, отдающего свои голоса за одну из двух политических сил (применительно к таким ситуациям политологи говорят о парадигме "двухпартийного вотума" – см., напр., [68]). Очевидно, что a + b = c. Характеристическими объемами можно также считать размеры фракций в парламенте.
Официально для победы на мажоритарных выборах достаточно 50% плюс один голос, т.е. первое приближение к теоретическим 62 – 38%% начинается с этого значения.(1) Но обычно наибольшая фактическая стабильность отвечает тем странам и тем ситуациям, когда у правящей партии (коалиции) более заметное преимущество, чем единицы голосов или процентов. Если разрыв в количестве голосов или парламентских мест слишком мал, его зачастую оказывается недостаточно, чтобы внушить оппозиции должное "смирение". Малейшие колебания политической конъюнктуры грозят ее бунтом, парламентским и/или правительственным кризисом, угрожают парализовать власть, лишить ее дееспособности. Поэтому требуемые по юридическому закону 50% в стабильных случаях (а именно таковые прежде всего и имеются в виду) практически возрастают.
При этом президентские республики отличаются определенной спецификой. В отличие от парламентских, в которых руководители исполнительной власти назначаются законодательными органами и впоследствии зависят от распределения в них голосов, в президентских республиках (США, Франция, Россия) осуществляются независимые выборы законодательной и глав исполнительной ветвей. Поэтому нередко складывается ситуация, что президент оказывается представителем одной политической силы, а парламентское большинство принадлежит другой. В таких случаях, очевидно, политические пропорции должны определяться для каждой ветви отдельно. На оппозицию здесь не накладывается требование всесторонне жертвовать своими интересами и целями: например, оппозиция подвергается ограничениям и самоограничению в исполнительных функциях государственной власти, тогда как правящей партии приходится проявлять надлежащую "скромность" в законодательной сфере. Подобная "перекрестность" представляет собой более сложную разновидность политического баланса, что не отменяет, однако, рассуждений в духе золотого сечения для каждой из ветвей в отдельности.
Для проверки возьмем страну с наиболее строгой двухпартийной системой, США. Сейчас нас интересует распределение мест в американском конгрессе, при этом предпочтение будет отдано данным конца 50-х – начала 60-х гг. Такое предпочтение не случайно, поскольку на внутренне-политических процессах в США могло сказываться состояние и контемпоральной мировой системы, достигшей зрелости именно к этому сроку, но уже к концу 60-х годов началось ее "разложение". В конце 1960-х гг. и в самих США началась заметная трансформация: экономическая, социальная, культурная, политическая, – что сопровождалось нестабильностью общественных настроений. Мы же, напротив, опираемся на презумпцию стабильности.
Выборы в Конгресс 86-го созыва состоялись 4 ноября 1958 г. В сенате 65 мест принадлежит демократам и 35 республиканцам, т.е. распределение 65% и 35%. В палате представителей из 436 депутатов 283 демократа и 153 республиканца, т.е., аналогично, 65% и 35% [125-60]. Среднее арифметическое по сенату и палате представителей составляет те же 65% и 35, что в целом удовлетворительно соответствует теоретическим 62% и 38%.
Конгресс 87-го созыва, избранный 8 нояб. 1960 г.: в сенате из 100 мест 64 у демократов и 36 у республиканцев, т.е. 64% и 36%; в палате представителей из 437 мест – 259 у демократов и 178 у республиканцев, т.е. 59,3% и 40,7% [125-61]. Средние арифметические, соответственно, – 61,7% и 38,3%, что с точностью до одной десятой процента совпадает со значениями для золотого сечения.
Конгресс 88-го созыва после выборов 6 нояб. 1962 г.: в сенате 68 демократов и 32 республиканца, в палате представителей – 259 демократов и 176 республиканцев [125-63]. Искомые среднеарифметические величины – 63,8% и 36,2%.
Конгресс 89-го созыва (выборы 3 нояб. 1964 г.): сенат – 68 демократов и 32 республиканца, палата представителей – 295 демократов и 140 республиканцев [125-65], т.е. 68% и 32%. Конгресс 90-ого созыва (1966 г.): в сенате 64 места у демократов и 36 у республиканцев (64% и 36), в палате представителей 248 демократов и 187 республиканцев [125-67]– 57% и 43%. Средние на 1966 г.: 60,5% и 39,5%.
Вслед за этим, как и ожидалось, появляются заметные отклонения от равновесных значений. Конгресс 91-го созыва (1968 г.): средние 57% и 43% [125: 1969, вып. 13]. Конгресс 92-го созыва (1970 г.): в сенате 53 демократа, 45 республиканцев и 2 независимых [125-71]. В пересчете только на ведущую пару "демократы – республиканцы": 54% и 46. В палате представителей 255 демократов и 180 республиканцев, т.е. 58,6% и 41,2. Средние – 56,3% и 43,7%. Столь существенное несовпадение данных 1968 и 1970 гг. с цифрами из золотого сечения, по-видимому, служит объективным выражением действительной дестабилизации, перемен в общественных настроениях (как раз на эти годы приходится пик протестов против войны во Вьетнаме, разгар молодежных и антирасистских волнений).
Для полноты картины приведем результаты последующих выборов. В Конгрессе 93-го созыва (1972 г.): в верхней палате 57% демократов и 43% республиканцев, в нижней – 56% и 44 [125-74]. Средние – 56,5% и 44,5%. Конгресс 94-го созыва (1974 г.): в сенате 61% демократов и 39% республиканцев, в палате представителей – 67% и 33 [125-75]. Средние – 64% и 36%. Конгресс 95-го созыва (1976 г.): в сенате 61 демократ, 38 республиканцев, 1 независимый. Соотношение между двумя партиями: 61,5% и 38,5%. В палате представителей – 67 и 33% [125-77]. Средние: 64 и 36%. 1978 г. [125-79]: в сенате 59% демократов и 41% республиканцев, в палате представителей – 63 и 37%. Средние: 61% и 39%.
Конгресс 97-го созыва избран 4 ноября 1980 г. В сенате 47 демократов и 53 республиканца, в палате представителей 243 демократа и 192 республиканца [125-81]. Таким образом, по критерию большинства места в двух палатах распределены взаимно противоположно, что дополнительно – еще более твердо, чем ранее – позволяет констатировать наличие дестабилизации или переходного процесса в настроениях общества в начале президентства Р.Рейгана. Конгресс 98-го созыва (1982 г.): в сенате 46% демократов и 54% республиканцев, в палате представителей – 61,6% демократов и 38,4% республиканцев [125-83], та же картина. 1984 г., Конгресс 99-го созыва: 47% демократов и 53% республиканцев в сенате, 58% демократов и 42% республиканцев в палате представителей [125-85]. Ситуация прежняя. Конгресс 100-го созыва, 1986 г. [125-86]: в сенате 55% демократов, 45% республиканцев; в палате представителей – 59% демократов и 41% республиканцев. Средние – 57 и 43%.
Несколько позже мы научимся более тонким расчетам, однако уже сейчас, по-видимому, оправдан следующий вывод. В период стабильного состояния американского общества распределение голосов между двумя партиями (здесь: опосредованно через места в конгрессе) с удовлетворительной степенью точности отвечает закону золотого сечения, а после вступления США в переходную стадию наблюдаются заметные возмущения. Известны и причины этого положения. В процессе предвыборной борьбы между партиями одна из них занимает психологическую позицию лидера, тогда как другой достается роль догоняющей, или ведомой:
Впрочем, сам Тимердинг, как рациональный ученый, значительно осторожнее: "Гораздо более правдоподобным является предположение, что золотому сечению первоначально было отдано предпочтение по рассудочным соображениям. Но вследствие того, что это отношение было избрано нормой для бесчисленного множества употребляемых форм и что его приближения, естественно получающиеся путем выбора удобных близких численных соотношений, в общем и целом выдвигаются снова, оно в конце концов так утвердилось в представлении, что даже бессознательный выбор отношения размеров тоже тяготеет к нему" [329, c. 73].
Древние принципы соразмерности действуют как в живописи, так и в архитектуре: от Вавилона (в котором, напомним, роль главной фигуры играл равносторонний треугольник и благодаря ему отношение 1 : ?3 ), Малой Азии, Греции, через искусство рисования и архитектурную готику европейских Средних веков до эпохи Леонардо да Винчи и Дюрера.(9) У египтян и вавилонян соотношение размеров в храме имело священное значение. Витрувий (III, гл.1), которому следовал Лука Пачоли в изложении архитектурных вопросов, выдвигал требование "симметрии" (теперь это слово употребляется в совсем другом смысле). Симметрия происходит от пропорции, которая по-гречески называется "аналогией". Пропорциональность означала при этом "согласованность соответствующих частей постройки между собой и целым". Архитекторам надлежит в совершенстве владеть учением о симметрии. При построении отдельных частей пользуются одним и тем же отношением, обнаруживающимся у целого.
Тимердинг приводит математическую расшифровку: части постройки должны быть членами геометрической прогрессии
с, сx, сx2, сx3, сx4, сx5, …
(13 )
Ее графическое изображение:

Рис. 3-7
В частном случае, когда прогрессия (13) является возвратной, т.е. когда первый член и, следовательно, каждый другой равен сумме двух последующих,(10) получаем с = сx + сx2, или 1 = x + x 2, что повторяет уравнение для золотого сечения (7).
Сходным образом, отталкиваясь от Цейзинга, Тимердинг интерпретирует и природные явления, в частности закон листорасположения:

Рис. 3-8
Так, Тимердинг утверждает: "К тому же в природе, по-видимому, действительно выполняется некоторый закон пропорций, не совпадающий, правда, с отношением золотого сечения, но, так сказать, одного с ним направления. Этот закон можно так сформулировать: когда однородные части следуют друг за другом в порядке убывания величины, если нет возмущающих влияний, уменьшение происходит в геометрической прогрессии; так же происходит и увеличение там, где величина частей возрастает" [329, c. 58]. Направление в природных объектах задано ростом, и более старые части, из которых вырастают новые, оказываются либо самыми маленькими, либо, наоборот, самыми большими. Этот закон назвали законом натурального роста. Там, где он соблюдается, может встретиться и отношение золотого сечения, если не точное, то приближенное.
Выше уже упоминалось о связи золотого сечения с числами Фибоначчи. Н.Н.Воробьев уточняет и дополняет сказанное Тимердингом: "Природа дает нам многочисленные примеры расположения однородных предметов, описываемых числами Фибоначчи. В разнообразных спиралевидно расположенных мелких частях растений обычно можно усмотреть два семейства спиралей. В одном из этих семейств спирали завиваются по часовой стрелке, в другом – против. Числа спиралей того и другого типов часто оказываются соседними числами Фибоначчи. Так, взяв сосновую веточку, легко заметить, что хвоины образуют две спирали, идущие справа внизу налево вверх. Вместе с тем они же составляют три спирали, идущие слева снизу направо вверх. На многих шишках семена (т.е. "чешуйки") расположены в трех спиралях, полого навивающихся на стержень шишки. Они же расположены в пяти спиралях, круто навивающихся в противоположном направлении. В крупных шишках удается наблюдать 5 и 8 и даже 8 и 13 спиралей. Хорошо заметны такие спирали и на ананасе: обычно их бывает 8 и 13. У многих сложноцветных (например, у маргаритки или ромашки) заметно спиральное расположение отдельных цветков в соцветиях-корзинках. Число спиралей бывает здесь 13 в одном направлении и 21 в другом и даже соответственно 21 и 34. Особенно много спиралей можно наблюдать в расположении семечек крупного подсолнуха. Их число в каждом из направлений может достигать соответственно 55 и 89" [86, c. 122].
В книге Н.Н.Воробьева обсуждается вопрос и непосредственно о золотом сечении. Приведем две цитаты: "Выдающийся геометр и астроном ХVII века И.Кеплер (известный, впрочем, в свое время больше как астролог) отваживался даже ставить формулировку закономерности золотого сечения на один уровень с таким фундаментальным математическим фактом, как теорема Пифагора" [там же, с. 123]. И на той же странице: "Различными философами древности и средневековья внешняя красота прямоугольников и треугольников золотого сечения, а также других фигур, в которых наблюдается деление в среднем и крайнем отношении, возводилась в эмпирический и даже философский принцип. Золотым сечением и еще некоторыми отношениями пытались не только описывать, но и объяснять явления природы и даже общественной жизни, а с самим числом ? (11) и его подходящими дробями производились разного рода мистические операции. Важную роль в таких рассмотрениях играла фигура, изображенная на рис. 3-5, которая при этом называлась пентаграммой". Далее Н.Н.Воробьев говорит о современном возрождении интереса к золотому сечению, в целом оценивая данный факт как негативный (что, впрочем, не помешало автору уделить значительное внимание этой теме в собственной брошюре). В России вопрос о золотом сечении, помимо Н.Н.Воробьева, затрагивался, например, в книге Е.И.Игнатьева "В царстве смекалки, или Арифметика для всех" [136].
Не следует полагать, что значение закономерности золотого сечения сводится исключительно к миру природы или изобразительных искусств. Так, Р. Якобсон обнаруживает образцы той же формы в литературе. Анализируя стихотворение Гельдерлина, он пишет о "многостороннем противопоставлении трех заключительных строк пяти предшествующим – одном из показателей сложного и преднамеренного формообразования. В последнем "Die Aussicht" Гельдерлина с полной отчетливостью представлено то самое золотое сечение, которое установилось со времен Леонардо. Меньший отрезок (Minor) относится к большему (Major) как больший к целому. Золотое сечение (8 : 5 = 5 : 3) противопоставляет неравные отрезки восьмистишия ‹…›" [402, c. 376]. Таким образом, попутно Якобсон использует и представление гармонической пропорции через числа Фибоначчи: здесь 3, 5, 8, см. ряд (12). Исследованию смысла той же пропорции, ее роли в искусстве, в частности, в музыке, уделял внимание и А.Ф.Лосев, см. [190, c. 356-368].(12) О "стремлении к гармонии имеющихся соотношений целого и его составных частей", о регулирующем правиле золотого сечения, последовательности Фибоначчи начинают говорить и современные политологи, см., напр., [330, c. 55].
На этом ограничим исторический экскурс. По-видимому, он полезен не только из прагматических соображений ("оживление материала"), но так или иначе обозначает позиции, которым придется следовать или, напротив, от которых отталкиваться в процессе дальнейшего изложения. Так, в целом для нас неприемлем, как сказано, ореол "духоведческих", оккультных истолкований, которыми оброс или из которых еще не окончательно вычленился рациональный феномен золотого сечения. Подобные коннотации, если и значимы в настоящем контексте, то лишь настолько, насколько массовым представлениям вообще присуще смешивать здравые начала с "загадочными", непросветленными критическим рассудком. Неудовлетворителен, на наш взгляд, и чисто позитивистский, голо-эмпирический путь, скажем, Цейзинга, Фехнера. Сами по себе опытные измерения не в состоянии подтвердить актуальности золотого сечения в природных явлениях, искусстве, в коллективных предпочтениях, ибо отсутствует действительно строгий критерий для того, чтобы отличить гармоническую пропорцию от других, ей близких. В результате выбор авторами именно золотого деления оставляет впечатление произвольности, недосказанности. Только соединение теории с опытом способно дать то сочетание логической обязательности и фактической подтвержденности, которое отличает науку в собственном смысле.
И в двух первых разделах главы, и в нижеследующих мы стараемся придерживаться именно этой линии. Очень важно, чтобы закономерность золотого сечения (или некие другие, ибо золотым сечением, в чем позже предстоит убедиться, существо вопроса не ограничивается) не оказывалась навязанной какими-то посторонними соображениями, а была необходимым, последовательным результатом содержательной теоретической модели политических систем, отчего в наше распоряжение автоматически попадал бы и ответ на вопрос "почему". (Очевидно, потому, что составные элементы системы обладают сформулированными в теории свойствами.) Теория, конечно, должна проверяться на практике, и в этом мы полностью солидарны с Цейзингом, Фехнером.
Вызывает интерес упомянутый Тимердингом "закон натурального роста". Не берусь судить о его общей формулировке, но в социально-политической сфере он находит определенные выражения. Так, если считать направлением исторического развития, или роста, движение от аграрных обществ к индустриальным, затем к разделению последних на капиталистические и социалистические, то каждая последующая ступень должна быть меньше предыдущей, образуя нечто вроде ступенчатой пирамиды:

Рис. 3-9
В послевоенном мировом сообществе отношение характеристических объемов четвертой ступени к третьей и, соответственно, третьей ко второй составляли значения, близкие к золотому делению. При этом, правда, остается неясным, существовали ли общие критерии оценки, вернее самооценки, у индустриального мира в целом, с одной стороны, и аграрного, с другой (признак объема промышленной продукции аутентичен лишь для индустриальных государств, но не для аграрных), поэтому трудно сказать что-либо конкретное о числовом соотношении между ними и даже о том, уместны ли вообще в данном случае количественные сравнения. Поэтому на стыке двух первых ступеней названный закон носит лишь описательный, полуметафорический характер.
Однако строение СССР (рис. 3-2, 3-3) в более строгом смысле соответствует названному закону. Именно вокруг РСФСР были объединены национальные окраины, ставшие, таким образом, следующей ступенью социалистического роста или процесса. Впоследствии отношение характеристических объемов "нацреспублики / РСФСР" установилось, как мы помним, вблизи значения, соответствующего золотому сечению. В свою очередь, если общим фундаментом или "корнем" обеих ступеней – и РСФСР, и нацреспублик – считать СССР ("идею СССР"), то и его объем удовлетворял условию (10). Обозначив характеристический объем СССР через с, придем к последовательности типа (13):
с, сx, cx2,
( 14 )
где х? 0,62 – величина, отвечающая золотому сечению, сх– объем РСФСР, сх2 – нацреспублик.
Такие соображения наводят на мысль, что конструктивно-технологические начала в политике, возможно, не столь далеко отстоят от "органических", или естественно-исторических. Природа тоже строит свои "пирамиды".
Примечания
1 После вступления во францисканский монашеский орден получил имя брата Луки из Борго Сан Сепольеро. Профессор математики в университете и других учебных заведениях Рима, Неаполя, Милана, Флоренции, Болоньи [142, c. 286 ].
2 "Интерес пифагорейцев к симметрии, гармонии, числовым пропорциям привел их к занятиям "золотым делением" (выяснение правильных количественных соотношений между различными частями зданий или скульптурных фигур)", – пишет К.Куманецкий [169, c. 77].
3 В поздней древнегреческой легенде его смерть считалась наказанием за раскрытие тайны богов, "поскольку несказанное и безoбразное всегда должны пребывать сокрытыми". Ямвлих: "О Гиппасе говорят, что он был из числа пифагорейцев; за то, что разгласил и построил впервые сферу из двенадцати пятиугольников, он погиб в море как нечестивец, зато снискал славу первооткрывателя" [347, c. 152].
4 Чтобы подчеркнуть демоническое происхождение звездчатой пентаграммы, ее переворачивали "вверх ногами", в результате чего ее очертания напоминали два рога, два уха и козлиную бороду сатаны (этой разновидностью пользуются и современные сатанисты).
5 Хвост возрожденческой метафизики дотягивается до современности, и новейшие, насквозь коммерциализированные и абсолютно далекие, казалось бы, от высоких соображений модельно-подиумные стандарты диктуют для женской фигуры цифры 90 : 60 : 90, т.е. окружность талии должна составлять 2/3 от окружности бедер и груди. Как мы помним, 2/3 – второе из наилучших приближений к золотому сечению, см. ряд (12).
6 Zeising. Neue Lehre von den Proportionen des menschlichen Korpers. Leipzig, 1854 (Новое учение о пропорциях человеческого тела).
7 Franz Xaver Pfeifer. Der Goldene Schnitt. Augsburg, 1885 (Золотое сечение).
8 G.Th.Fechner. Vorschule der Aesthetik. 12A. 1897 (Введение в эстетику).
9 Основоположник живописи немецкого Возрождения А.Дюрер одновременно был и теоретиком искусства. В "Четырех книгах о пропорциях человека" (1528), составившим итог, или венец, его творчества, указано множество соотношений размеров правильных человеческих тел и лиц, совпадающих с пропорцией золотого сечения.
10 Или предыдущих – в зависимости от порядка расположения членов прогрессии.
11 Такой буквой здесь обозначена величина ? = (1 + ?5 )/2
12 В примечаниях к работе А.Ф.Лосева приведены ссылки на некоторую литературу, например, [201], [202] и о "золотом делении" у И.С.Баха: [439], [440]
3.4. Биполярные партийные системы
Двухпартийные или двухблоковые системы весьма распространены в современных демократических государствах. Республиканцы и демократы в США, консерваторы и лейбористы в Британии, коалиция "ХДС/ХСС – СвДП", с одной стороны, и "СДПГ – зеленые", с другой, в ФРГ, "правые" и "левые" во Франции – лишь некоторые из примеров. Речь идет об отчетливо выраженной дихотомности, основных политических акторов два. Каждый из них участвует в энергичной борьбе за электорат, стремясь привлечь на свою сторону максимальную долю политически активного населения, что удовлетворяет условию "экспансии" рассматриваемой модели.
При этом ни для политической системы в целом, ни для каждого из двух основных политических субъектов в отдельности не представляется возможным окончательное устранение соперника. Обратное означало бы изчезновение главной мишени для критики, конец политической конкуренции, отказ от принятых правил игры. Поэтому в устойчивых либеральных системах один актор не мыслится без другого, условие их "неразрывности" также выполнено.
Те же правила игры диктуют на каждом отдельном этапе разделение на правящую партию(коалицию, блок) и оппозицию. Последняя в демократических государствах, разумеется, не третируется; в одной из старейших демократий, английской, она даже находится под покровительством короны, нося наименование "оппозиции Ее величества". Но при этом, согласно "цивилизованным правилам", от оппозиции ожидается признание за собой статуса проигравшей стороны (пусть временно, до следующих выборов). От нее требуется согласие со статус-кво, как с фактом, соответствующие "сдержанность и смирение", понимание того, что не только в общих, но и в собственных интересах целесообразно придержать до поры реальные претензии на власть. А последняя, строго говоря, есть главная ценность и цель политической партии как таковой. Таким образом выходит, что оппозиция в названных политических системах как бы приносит в жертву свои главные интересы и ценности, не без оснований полагая, что точно так же поступит и противоположная сторона, если после будущих выборов роли поменяются на противоположные. В парламенте меньшинство считает необходимым подчиняться решениям большинства, и эти решения принимаются в качестве общих, исходящих от парламента в целом. Оппозиционное меньшинство, таким образом, демонстрирует готовность принести свои наличные голоса на алтарь действующих демократических правил, впоследствии солидаризируясь с теми законами, которые были приняты – быть может, вопреки конкретному несогласию. Т.е. удовлетворено и третье условие модели.
Обозначим электорат правящей партии или блока через а, оппозиции – через b. За объем целого спримем суммарную численность политически активного населения, отдающего свои голоса за одну из двух политических сил (применительно к таким ситуациям политологи говорят о парадигме "двухпартийного вотума" – см., напр., [68]). Очевидно, что a + b = c. Характеристическими объемами можно также считать размеры фракций в парламенте.
Официально для победы на мажоритарных выборах достаточно 50% плюс один голос, т.е. первое приближение к теоретическим 62 – 38%% начинается с этого значения.(1) Но обычно наибольшая фактическая стабильность отвечает тем странам и тем ситуациям, когда у правящей партии (коалиции) более заметное преимущество, чем единицы голосов или процентов. Если разрыв в количестве голосов или парламентских мест слишком мал, его зачастую оказывается недостаточно, чтобы внушить оппозиции должное "смирение". Малейшие колебания политической конъюнктуры грозят ее бунтом, парламентским и/или правительственным кризисом, угрожают парализовать власть, лишить ее дееспособности. Поэтому требуемые по юридическому закону 50% в стабильных случаях (а именно таковые прежде всего и имеются в виду) практически возрастают.
При этом президентские республики отличаются определенной спецификой. В отличие от парламентских, в которых руководители исполнительной власти назначаются законодательными органами и впоследствии зависят от распределения в них голосов, в президентских республиках (США, Франция, Россия) осуществляются независимые выборы законодательной и глав исполнительной ветвей. Поэтому нередко складывается ситуация, что президент оказывается представителем одной политической силы, а парламентское большинство принадлежит другой. В таких случаях, очевидно, политические пропорции должны определяться для каждой ветви отдельно. На оппозицию здесь не накладывается требование всесторонне жертвовать своими интересами и целями: например, оппозиция подвергается ограничениям и самоограничению в исполнительных функциях государственной власти, тогда как правящей партии приходится проявлять надлежащую "скромность" в законодательной сфере. Подобная "перекрестность" представляет собой более сложную разновидность политического баланса, что не отменяет, однако, рассуждений в духе золотого сечения для каждой из ветвей в отдельности.
Для проверки возьмем страну с наиболее строгой двухпартийной системой, США. Сейчас нас интересует распределение мест в американском конгрессе, при этом предпочтение будет отдано данным конца 50-х – начала 60-х гг. Такое предпочтение не случайно, поскольку на внутренне-политических процессах в США могло сказываться состояние и контемпоральной мировой системы, достигшей зрелости именно к этому сроку, но уже к концу 60-х годов началось ее "разложение". В конце 1960-х гг. и в самих США началась заметная трансформация: экономическая, социальная, культурная, политическая, – что сопровождалось нестабильностью общественных настроений. Мы же, напротив, опираемся на презумпцию стабильности.
Выборы в Конгресс 86-го созыва состоялись 4 ноября 1958 г. В сенате 65 мест принадлежит демократам и 35 республиканцам, т.е. распределение 65% и 35%. В палате представителей из 436 депутатов 283 демократа и 153 республиканца, т.е., аналогично, 65% и 35% [125-60]. Среднее арифметическое по сенату и палате представителей составляет те же 65% и 35, что в целом удовлетворительно соответствует теоретическим 62% и 38%.
Конгресс 87-го созыва, избранный 8 нояб. 1960 г.: в сенате из 100 мест 64 у демократов и 36 у республиканцев, т.е. 64% и 36%; в палате представителей из 437 мест – 259 у демократов и 178 у республиканцев, т.е. 59,3% и 40,7% [125-61]. Средние арифметические, соответственно, – 61,7% и 38,3%, что с точностью до одной десятой процента совпадает со значениями для золотого сечения.
Конгресс 88-го созыва после выборов 6 нояб. 1962 г.: в сенате 68 демократов и 32 республиканца, в палате представителей – 259 демократов и 176 республиканцев [125-63]. Искомые среднеарифметические величины – 63,8% и 36,2%.
Конгресс 89-го созыва (выборы 3 нояб. 1964 г.): сенат – 68 демократов и 32 республиканца, палата представителей – 295 демократов и 140 республиканцев [125-65], т.е. 68% и 32%. Конгресс 90-ого созыва (1966 г.): в сенате 64 места у демократов и 36 у республиканцев (64% и 36), в палате представителей 248 демократов и 187 республиканцев [125-67]– 57% и 43%. Средние на 1966 г.: 60,5% и 39,5%.
Вслед за этим, как и ожидалось, появляются заметные отклонения от равновесных значений. Конгресс 91-го созыва (1968 г.): средние 57% и 43% [125: 1969, вып. 13]. Конгресс 92-го созыва (1970 г.): в сенате 53 демократа, 45 республиканцев и 2 независимых [125-71]. В пересчете только на ведущую пару "демократы – республиканцы": 54% и 46. В палате представителей 255 демократов и 180 республиканцев, т.е. 58,6% и 41,2. Средние – 56,3% и 43,7%. Столь существенное несовпадение данных 1968 и 1970 гг. с цифрами из золотого сечения, по-видимому, служит объективным выражением действительной дестабилизации, перемен в общественных настроениях (как раз на эти годы приходится пик протестов против войны во Вьетнаме, разгар молодежных и антирасистских волнений).
Для полноты картины приведем результаты последующих выборов. В Конгрессе 93-го созыва (1972 г.): в верхней палате 57% демократов и 43% республиканцев, в нижней – 56% и 44 [125-74]. Средние – 56,5% и 44,5%. Конгресс 94-го созыва (1974 г.): в сенате 61% демократов и 39% республиканцев, в палате представителей – 67% и 33 [125-75]. Средние – 64% и 36%. Конгресс 95-го созыва (1976 г.): в сенате 61 демократ, 38 республиканцев, 1 независимый. Соотношение между двумя партиями: 61,5% и 38,5%. В палате представителей – 67 и 33% [125-77]. Средние: 64 и 36%. 1978 г. [125-79]: в сенате 59% демократов и 41% республиканцев, в палате представителей – 63 и 37%. Средние: 61% и 39%.
Конгресс 97-го созыва избран 4 ноября 1980 г. В сенате 47 демократов и 53 республиканца, в палате представителей 243 демократа и 192 республиканца [125-81]. Таким образом, по критерию большинства места в двух палатах распределены взаимно противоположно, что дополнительно – еще более твердо, чем ранее – позволяет констатировать наличие дестабилизации или переходного процесса в настроениях общества в начале президентства Р.Рейгана. Конгресс 98-го созыва (1982 г.): в сенате 46% демократов и 54% республиканцев, в палате представителей – 61,6% демократов и 38,4% республиканцев [125-83], та же картина. 1984 г., Конгресс 99-го созыва: 47% демократов и 53% республиканцев в сенате, 58% демократов и 42% республиканцев в палате представителей [125-85]. Ситуация прежняя. Конгресс 100-го созыва, 1986 г. [125-86]: в сенате 55% демократов, 45% республиканцев; в палате представителей – 59% демократов и 41% республиканцев. Средние – 57 и 43%.
Несколько позже мы научимся более тонким расчетам, однако уже сейчас, по-видимому, оправдан следующий вывод. В период стабильного состояния американского общества распределение голосов между двумя партиями (здесь: опосредованно через места в конгрессе) с удовлетворительной степенью точности отвечает закону золотого сечения, а после вступления США в переходную стадию наблюдаются заметные возмущения. Известны и причины этого положения. В процессе предвыборной борьбы между партиями одна из них занимает психологическую позицию лидера, тогда как другой достается роль догоняющей, или ведомой:
