Страница:
- << Первая
- « Предыдущая
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- Следующая »
- Последняя >>
Помимо ?2, было найдено немало других чисел с аналогичными свойствами – ?3, ?5 и т.д.,(13) – доказательства строились по уже известному алгоритму. Лишь в Возрождение – в обстановке крушения авторитетов, традиций, в эпоху великих открытий, в контексте принципиально новых математических задач (собственно алгебраических) и методов их решения – был не только чрезвычайно расширен класс таких чисел, но и с ними научились подобающим образом обходиться. Впрочем, название, ставшее термином, сохранило печать былых драм: числа
иррациональные, явный оксюморон (как может число противоречить разуму?).
Как бы там ни было, человек узнал о существовании двух классов чисел: рациональных и иррациональных. В их отношении между собой выступает операция сравнения, но уже не по величине, как раньше (больше-меньше), а по признаку соизмеримости, т.е. наличия или отсутствия общей меры. Всякий раз таким образом сопоставляется пара чисел, пара классов, т.е. данное отношение – бинарно, n = 2. На этом история не закончилась.
Развитие математики и механики выявило особую роль такого часто встречающегося числа как ?, затем открыли другое замечательное число, получившее обозначение e(одна из важнейших постоянных математического анализа).(14) В конце ХVIII в. И.Ламберт и А.Лежандр доказали, что число ? не может быть рациональным, а во второй половине ХIХ в. выяснилось, что ? и eне только иррациональные, но и трансцендентные. Существование класса трансцендентных чисел как таковых впервые установил французский математик Ж.Лиувилль в 1844 г., теорему о трансцендентности числа ? доказал Ф.Линдеман в 1882 г., аналогичную теорему о числе e –Ш.Эрмит в 1873 г.
Вообще в данный период – в канун и вместе с европейскими революциями 1848 г. – в математике происходит много ярких событий, так или иначе имеющих отношение к теме книги, что, возможно, не удивительно: начиналась подлинная революция в математике, предварившая великие потрясения и открытия конца ХIХ – начала ХХ вв. в физике, философии, искусстве, политике и др. Но об этом речь впереди, а в настоящем контексте упомянем немецкого ученого Р.Дедекинда, обосновавшего теорию действительных чисел и предложившего строгий аксиоматический метод введения чисел иррациональных (так называемые дедекиндовы сечения). Однако сейчас нас интересуют числа трансцендентные.
Что они собой представляют? По определению – это те, которые не могут быть корнем никакого многочлена с целыми коэффициентами, т.е. числа неалгебраические, что навряд ли много скажет нематематику. Противопоставление классов алгебраических и неалгебраических (трансцендентных) чисел, тем не менее, исключительно важно, поскольку с алгеброй принято связывать саму нашу логику. Впоследствии такие логики и были формализованы в алгебраическом виде (математическая логика). В таком случае, быть числом неалгебраическим как бы означает "быть нелогичным", что, собственно, и запечатлелось в названии: трансцендентные(снова, и еще более сильный, оксюморон: казалось бы, что "потустороннего" может быть в длине окружности? Но математики знают, о чем говорят).
Пропасть между алгебраическими и трансцендентными числами подчеркивается теорией множеств, ставшей еще одним достижением ХIХ в., особенно второй половины – Б.Больцано, Г.Кантор, Р.Дедекинд. Хотя алгебраических чисел – рациональных и иррациональных – существует бесконечное количество, но их множество, как выражаются, счетно. Это означает, что все такие числа – не на практике, конечно, а в принципе – можно пронумеровать, т.е. их "столько же", сколько чисел в натуральном ряду. Чисел же трансцендентных неизмеримо, качественно "больше". Их множество несчетно и, как говорят в таких случаях, имеет мощность континуума (т.е. трансцендентных чисел "столько же", сколько точек на непрерывной прямой). Возможность что-то пронумеровать – верный признак логичности, о чем же тогда свидетельствует отсутствие подобной возможности?
В прежней среде действительных чисел, но по-новому, была по сути развернута интеллектуальная драма, сходная с той, что некогда произошла при первой исторической встрече с иррациональными числами. К счастью, во второй раз математики оказались более подготовленными в морально-психологическом плане. Посмотрим, что у нас осталось в итоге.
Числа действительные (иначе их называют вещественными) делятся, во-первых, на рациональные и иррациональные, во-вторых, – на алгебраические и трансцендентные. В обоих случаях речь идет о характерной оппозиции: за числами одного сорта признается качество своеобразной "логичности", за числами другого сорта – нет. Сравнение в обоих контрастных противопоставлениях производится попарно, т.е. кратность отношений двойная, n = 2. Если свести вместе обе классификации, построенные над полем действительных чисел, то получится, что последнее состоит из чисел рациональных (целых и дробных), алгебраических иррациональных (наподобие ?2) и трансцендентных. Их разделение фиксирует скачкообразное убывание специфической "логичности" (мы уже знаем, в каком смысле). Изобразим классификацию на рисунке:
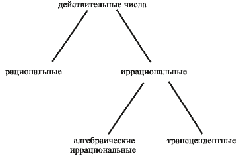
Почему в итоге получилось три непересекающихся класса действительных чисел, т.е. почему М = 3? – Во-первых, в системе задано бинарное отношение сравнения ( n = 2 ); во-вторых, совокупность названных классов мыслится в качестве законченной и целостной. Откуда нам известно последнее? – От самих математиков, ибо они доказали так называемую теорему о полноте, утверждающую, что других классов действительных чисел не существует, сюрпризы с появлением новых не повторятся.
Наверное, стоит извиниться перед читателем за столь длинный и сложный пример, но все же он, надеюсь, короче, чем сама эта история длиной в 2,5 тысячи лет. Данным пассажем можно было бы и пренебречь, но беда в том, что впоследствии (в главе 3) нам еще придется встретиться с иррациональными числами и оттого неплохо бы знать, что за ними стоит. Пока же, коль все равно затрачены время и силы, грех не воспользоваться этим и не сформулировать некоторые полезные выводы, которые пригодятся для понимания и других паттернов.
Во-первых, мы имели случай лишний раз убедиться, что предлагаемая модель – элементарно-математическая по форме, культурологическая по функции – способна работать "поверх" (или "из-под низа") достаточно сложного концептуального материала. Простейшие числа – два и три – справляются с описанием итога длительной работы перворазрядных ученых, причем в данном примере – как раз в области чисел.
Во-вторых, хотелось дать получше почувствовать одну из особенностей нашей модели: она дескриптивна, мы не затронули и тысячной доли содержательного богатства идей упомянутых ученых (как ранее не пытались всерьез выяснить, что представляют собой, скажем, тело-душа-дух или небо-земля-преисподняя). В специальные работы мы практически не вникали, интересуясь лишь "сухим остатком" (для нас это количество элементов). Тем не менее наши выводы совпали с положениями самой математической науки.
В-третьих, небесполезно нагляднее показать не только подспудность схемы n = 2, М = 3, но и драму ее воплощения. Сейчас трудно установить, сколько тысячелетий или десятков тысячелетий потребовалось человеку, чтобы прийти к трехсоставности мироздания, трем лицам, трем временам и т.д., но исторические факты из последнего примера предоставляют шанс догадаться, сколько усилий стоит за подобными, казалось бы тривиальными, вещами. Как после этого мы должны к ним относиться? Достаточно ли мы их ценим?
Наконец, возник повод на новом материале напомнить о принципиальной неотделимости чисел и науки о них от мифологической подоплеки. Флером неизбывной загадочности окутано не только их первоначальное происхождение, но пуповина не была и не будет перерезана никогда. Это касается не только ранних, исторически не вполне достоверных этапов развития: у египетских жрецов, халдейских магов, индийских и китайских мудрецов, у склонных к мистериям пифагорейцев. Впоследствии получили широкую известность и веками тревожили воображение математиков задачи о трисекции угла, удвоении куба, квадратуре круга (и обратно: циркулятуре квадрата). Окончательно с ними разобрались сравнительно недавно, в прошлом веке, и, как выяснилось, проблемы непосредственно связаны с иррациональными и трансцендентными числами. Значение таких задач, как считалось, выходит далеко за границы математики, затрагивая саму тайну жизни и спасения,(15) что можно сравнить разве что с ролью философского камня и гомункулуса у средневековых алхимиков. Многозначительные предания складывались и вокруг не столь отдаленных математических событий. Вероятно, самое яркое из них – о большой, или великой, теореме Ферма, теснейшим образом связанной с соизмеримостью и несоизмеримостью чисел. Вокруг нее периодически поднимается ажиотаж, особенно на переломных исторических отрезках.
О мифологических или легендарных моментах в своей науке современные математики если и говорят, то не без застенчивости и главным образом в кулуарах: дисциплина требует точности и обязательности, а не игривости. Но подобная пуристская поза имеет и изнанку: в отличие от прежних эпох, между числом и мифом, вообще "живою культурой" возведена китайская или берлинская стена. Гуманитарии платят математикам (представителям точных наук) той же монетой, обороняя от них собственную заповедную вотчину, что становится одной из неотъемлемых черт трагедии современного духа, т.е. попросту отсутствия взаимного понимания, ментальной расщепленности.
В заключение экскурса по математике приведем (без обсуждения) еще одну тройку. Наряду с действительными числами, о которых речь только что шла, со школы известны и комплексные. В 1843 г. ирландец У.Гамильтон открыл еще один тип – кватернионы (записывающиеся в виде a + ib + jc + kd,где a, b, c, d– вещественные числа), а Фробениус доказал: все алгебры соответствующего сорта исчерпываются только тремя –алгеброй вещественных чисел, алгеброй комплексных чисел и алгеброй кватернионов [238, 154].
Тринитарные структуры широко распространены и в социальной области. В современных развитых странах принято различать богатый, среднийи бедныйклассы (М = 3); в основу деления положен элементарный критерий уровня доходов: выше или ниже. Подобное сравнение бинарно, n = 2. При этом общество признается единой системой, строение которой рационально.
Раскрывая генезис названного членения, специалисты по ХХ в. обращают внимание, что еще в начале столетия осевой линией социального напряжения был конфликт между богатством и бедностью и что лишь десятилетия последовательных усилий правительств позволили сформировать представительный средний класс, превратившийся в залог общей стабильности. Мало того, и век, и даже полвека назад в массовом сознании доминировала иная, "марксистская" схема членения. Потребовались настойчивая пропагандистская работа и целый ряд реформационных шагов, чтобы внушить народам веру в справедливость чисто денежного подхода, утвердить стандарты общества потребления. Усилия увенчались успехом, и пропасть между богатыми и бедными заполнилась многочисленным средним классом, подставившим плечо системе в целом, разделившим с богатыми заинтересованность в сохранении status quo (поэтому подобное устройство зачастую называют "обществом двух третей"). При этом и бедные – за исключением политических маргиналов – в большинстве признают обязательность общей картины, т.к. проникнуты той же консюмеристской идеологией.
Причины бедности как явления, т.е. причины существования бедного класса, обычно ищут в сфере позитивных фактов: в особенностях института собственности, системы оплаты труда, в несовершенстве социальных программ, дефектах воспитания и образования рекрутов бедности и даже во врожденных психологических чертах, не исключая национальной и расовой принадлежности. На наш взгляд, нет ничего более далекого от существа вопроса. Названные и подобные им обстоятельства в состоянии дать лишь одно объяснение: почему именно эти, а не иные, субъекты (индивиды, группы) оказались среди бедных, тогда как прочие вкушают достаток или богатство. Сам факт наличия бедного класса такими подходами если и затрагивается, то только по касательной: ведь если данному субъекту и удастся преодолеть предпосылки собственной бедности, в ряды бедных непременно попадет другой. Феномен бедности неискореним по совершенно отличной причине.
Его корни, так сказать, в головах, в организующей силе самой идеологии потребления, побуждающей людей делиться по толщине кошелька, согласно ординарному критерию "больше/меньше", n = 2. Если общество признается при этом целостным – а это также удается внушить: "Мы – одна нация", – то социальных классов автоматически три, и значит, один из них неизбежно подпадает под рубрику бедного. Технологический прогресс, повышение ВНП на душу населения без смены самой парадигмы в состоянии повлиять разве что на конкретные признаки бедности: очевидно, что уровень жизни, скажем, американских бедных вполне сравним, если не выше, чем у вполне респектабельных граждан из не столь процветающей страны. Зато последние куда благополучнее в собственном статусе, пользуются уважением и самоуважением, утверждаясь на фоне бедных соотечественников.
Нас, впрочем, не интересуют детали: ни исторический путь западных обществ, ни изыскания социологов. Важен лишь конечный итог: социальная система трехчастна, и теперь мы не удивляемся, почему.
Коль поднят вопрос о социальных структурах, несправедливо обойти вниманием доиндустриальную эпоху. Деление на сословия: дворянство, духовенствои весьма неоднородное третье, – классическое для абсолютистской Европы, особенно для Франции, вплоть до Великой революции. Из трех, господствующими признавались два, они воплощали в себе светскую и духовную ипостаси государства. Хотя отношения между папским престолом и монархами на международной арене, между Церковью и светскими властями в пределах каждой из стран не всегда отличались безоблачностью, их совместная деятельность признавалась необходимым условием для сохранения христианскогохарактера государства и общества. Без покровительства небес, без помазания не мыслились полномочия королей и императоров. Без благодати Церкви, без исповеди и причастия каждого из людей ждала вечная погибель. Но дела земные – в компетенции трона и светских властей, по крайней мере, с тех пор, как везде, за исключением собственно Рима, светские владыки отстояли свои права. Телами распоряжается одна сторона, душами – другая. Первые два сословия и институализировали сии непреложные истины. Социальный фундамент составляла, таким образом, неразрывная пара, n = 2. Поэтому в обществе в целом сословий должно было быть именно три, М = 3.
Еще Платон в "Государстве" полагал идеальным устройством наличие трех сословий: правителей, стражейи так называемое третье сословие, куда включались крестьяне, ремесленники, торговцы и т.д. Разделению социальных функций отвечала специализация трех добродетелей: мудрости, мужества и послушания, – в полном согласии с тем, что человеческая душа состоит из трех частей: разумной, вожделеющей и растительной.(16) Несмотря на то, что абсолютистский социальный канон предметно отличался от платоновского, он ничуть не менее последователен и, следовательно, трехсоставен.
Европейское средневековье придерживалось близкой модели. Вот что пишет известный отечественный медиевист А.Я.Гуревич: "Рассуждая об общественной жизни, средневековые богословы и писатели прибегали к обобщенным абстрактным схемам ‹…› Наиболее распространенной и авторитетной была схема тройственного деления общества в зависимости от функций, которые выполняют члены того или иного разряда – ordo. Согласно этой схеме общество представляет собой иерархическое сочлененное единство, все компоненты которого служат целому. Эти компоненты суть ordo людей, которые молятся (oratores), ordo людей, которые сражаются (bellatores), и ordo людей, которые трудятся (laboratores), или, более конкретно, пашут землю (aratores). Если под первыми разумелось духовенство и монашество, а под вторыми – рыцари, министериалы и прочие воины, то в состав третьего разряда попадали и крестьяне, и ремесленники, и купцы" [111, с. 198].
Сословное членение христианских государств можно усовершенствовать – ведь третье сословие абсолютистской Франции, как, впрочем, и в проекте Платона, в средневековых теориях, получилось пестрым, как Ноев ковчег. И прецедент более детального регламента не преминул родиться. Согласно Уложению 1762 г., в России было введено пять сословий. Два первых их них совпадали с французскими, тогда как другие три: купечество, мещанство, крестьянство, – соответствовали французскому третьему:
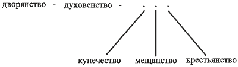
Деление третьего сословия на три части подспудно существовало и раньше. Й.Хейзинга ссылается на незамысловатые миниатюры в календаре-часослове с фигурами усердного хлебопашца, прилежного ремесленника, деятельного торговца [360, с. 63], в России же данное представление было институализировано (следы социальной тройственности наблюдались в Росии и до 1762 г.: согласно петровской табели о рангах, различались три вида государственной службы – военная, статская, придворная, но в подробности едва ли целесообразно вдаваться).
Схема на рис. 1-4 полностью идентична той, что отражает систему личных местоимений (рис. 1-1). Логическое членение при этом тринитарно. Русское сословное уложение повторяло грамматические азы, само став своеобразной "грамматикой" общества вплоть до 1917 г. Россия пришла к абсолютизму позже законодателей европейских социально-политических мод и, учтя концептуальную "недостаточность" французской модели, ее нормативную "грубость", внесла несомненное усовершенствование – причем, в канун Великой французской революции, вообще отменившей сословия. Ирония: "Телега получилась прекрасной, жаль только, другие пересели на паровоз", – представляется неуместной, поскольку мы заняты исключительно числами, а перед ними равны все, не исключая – см. классы богатый, средний и бедный – и нынешних водителей человечества.
Что стоит за предписанием либеральной доктрины о разделении и балансе властей: законодательной, исполнительнойи судебной? У этой идеи, ближайшие истоки которой восходят к Дж.Локку, Ш.Монтескье, к школе естественного права, довольно долгая предыстория.
Непосредственно она родом из эпохи Просвещения, считавшей рассудок мерилом всего, в частности полагавшей, что государственное управление должно быть рациональным. Подход не слишком оригинальный: той же мысли придерживался и Платон, равно как и заключения, что разумное управление способны осуществлять только разумные, образованные люди и потому руководить обществом следует философам. Два тысячелетия спустя настоящее предложение очень понравилось английским и французским философам, которые не только подхватили эстафету, но и многое привнесли от себя. Проект Просвещения предполагал широкое распространение образования, а где знания, разум – там должна быть и власть ("Знание – сила", – утверждал еще Ф.Бэкон). Как философы делятся знаниями с остальными, так и монарх во имя Разума, Справедливости должен поделиться властью с лучшими из подданных.
Первоначально речь шла не об отлучении королей от государственного кормила, а только о разделении полномочий между государем и собранием ученых мудрецов, умеющих придумывать и толковать законы на все случаи жизни. Подобная версия и поныне питает розовые мечты интеллигенции о просвещенном правлении, под сенью которого процветают высокие науки и искусства, а невежество посажено под крепкий замок.
Фактическое разделение власти между монархом и законодательным органом существовало еще до Локка и французских просветителей. Правда, в дореволюционной Франции парламент обладал скорее законосовещательными, чем полноценными законодательными полномочиями – и в этом смысле напоминал Сенат в России, который вдобавок не был выборным, не представлял всех сословий. Но на Британских островах со времен Великой английской революции, начавшейся с выхода из повиновения "Долгого" парламента [35], последний обрел должный вес. Пользуясь словами Ф.Броделя: "Разделение политической власти между парламентом и монархией в 1660 г., в момент Реставрации и в еще большей степени после Декларации прав 1689 г., было по преимуществу началом разделения, имевшего долговременные последствия" [62, с. 617]. Но в новых исторических условиях – в эпоху разума и Просвещения – требовался не отдельный и оттого, возможно, случайный, прецедент, а общее правило. Это правило необходимо сформулировать и прописать, чтобы с ним всегда можно было бы свериться и, следовательно, избежать нарушений. Вклад английских и особенно французских просветителей, собственно, и заключался в возведении разделения властей в рациональный и общеобязательный принцип.
История вопроса полна трогательных подробностей. Философы пытались убедить монархов, как своих, так и чужих, уступить долю власти добровольно. Французские просветители вступают в оживленную переписку с русской Екатериной II, Великой, с прусским Фридрихом II, тоже Великим. Из переписки, естественно, ничего толком не вышло. Как отмечает один из биографов Фридриха II [436, S. 179], последний разделял с Гельвецием, Гольбахом, Руссо и другими властителями дум симпатию к народному просвещению, но при этом не присоединялся к мнению, что просвещенное или способное к просвещению общество должно быть гарантом проведения политических преобразований, что оно должно ограничивать полномочия самодержца, чтобы воспрепятствовать всякому нанесению вреда. "Это был именно тот пункт, в котором Фридрих II вступил в противоречия с французскими идеологами и радикальными немецкими просветителями" [там же]. Таким образом, на деле разум не всегда оказывался всемогущим, что, впрочем, не препятствовало его уверенному царствованию в рамках доктрины. Значит, допустимо судить согласно рациональным критериям и о ней самой.
Идея разделения властей предельно не нова – наряду с приведенными примерами, существуют и более почтенные по возрасту. Еще в первобытных племенах полномочия распределялись между вождем и шаманом (жрецом, колдуном), в средневековой Европе – между Церковью и королями, а в Византии действовало специальное учение о симфониидвух властей: духовной и светской, – в их общем служении Божьему Замыслу. Либерализм, однако, внес качественные коррективы. Свобода совести, отделение Церкви от государства – лозунги, начертанные на его знаменах. Разделению предстояло пройти по телу оставшейся единственно общеобязательной светской, государственной власти. В первом варианте, как сказано, – разбить полномочия между монархом и законодательным органом, парламентом, с таким расчетом, чтобы ограничить произвол, который всегда противен Разуму и Справедливости. С самого начала, таким образом, присутствовала бинарная оппозиция, n = 2.
Пали или отошли в тень монархии, но принцип не только выжил, но и расцвел. Зрелый вид он принял в США, и до сих пор действующую там систему разделения и баланса властных ветвей предъявляют в качестве образца для политических недорослей.
И все-таки почему ветвей три? С одной стороны, государственная власть рассматривается как самостоятельный, целостный феномен, с другой – его можно и нужно делить на счетное количество компонентов. Причем, членение осуществляется согласно "здравой", т.е. бинарной, логике: каждая из ветвей призвана ограничивать любую другую. "Вся эволюция системы "сдержек и противовесов" в США вращается вокруг конфронтации исполнительной и законодательной властей", – конкретизирует обозреватель [339, с. 48]. Ergo: М = 3, см. модель. Для чего же потребовалось столько предварительных слов? – Из осторожности, поскольку априори неясно, насколько корректен в подобных вопросах чисто рациональный подход. Скажем, если власть священна или зиждется исключительно на традициях, любое обсуждение неуместно: ее либо принимают, либо становятся святотатцем. К примеру, рыцарственный православный монарх Николай I воспрещал не только хулу, но и одобрение того, что идет от престола (от одобрения до хулы – один шаг, главное – не рассуждать).
И еще одно. Хотя один из ведущих юристов ФРГ, К.Хессе, и утверждает, что принцип разделения властей – не естественно-правовая догма, а исторически сложившийся принцип [там же], исторические реалии в состоянии бросить свет не более чем на обстоятельства его открытия и принятия, но никак не на рациональную суть. Так, теорема Пифагора была доказана в определенных культурно-исторических условиях, затем два с половиной тысячелетия транслировалась в обществе, признававшем ценность такой трансляции, но отсюда вовсе не вытекает, что ее сущность и смысл являются историческими. Подобные вопросы, впрочем, выходят за пределы компетенции правоведов. Но и обратно: использованный здесь подход навряд ли в состоянии удовлетворить запросы представителей юридической науки. В логико-числовом контексте мы отвлеклись от наиболее репрезентативных философских обоснований целостности системы государственной власти, от учения о правовом государстве, скажем в версии Канта.(17) Сфера права автономна по отношению к этической сфере (как морали, так и нравственности), и как раз в ее строгих рамках совокупность трех ветвей обретает концептуальную полноту, замкнутость, связность. В поставленные же нами цели не входило раскрытие предметного содержания идеи трех властей: мы по-прежнему заняты самыми простыми вещами – числами. К проблеме структуры государственной власти предстоит вернуться в
Как бы там ни было, человек узнал о существовании двух классов чисел: рациональных и иррациональных. В их отношении между собой выступает операция сравнения, но уже не по величине, как раньше (больше-меньше), а по признаку соизмеримости, т.е. наличия или отсутствия общей меры. Всякий раз таким образом сопоставляется пара чисел, пара классов, т.е. данное отношение – бинарно, n = 2. На этом история не закончилась.
Развитие математики и механики выявило особую роль такого часто встречающегося числа как ?, затем открыли другое замечательное число, получившее обозначение e(одна из важнейших постоянных математического анализа).(14) В конце ХVIII в. И.Ламберт и А.Лежандр доказали, что число ? не может быть рациональным, а во второй половине ХIХ в. выяснилось, что ? и eне только иррациональные, но и трансцендентные. Существование класса трансцендентных чисел как таковых впервые установил французский математик Ж.Лиувилль в 1844 г., теорему о трансцендентности числа ? доказал Ф.Линдеман в 1882 г., аналогичную теорему о числе e –Ш.Эрмит в 1873 г.
Вообще в данный период – в канун и вместе с европейскими революциями 1848 г. – в математике происходит много ярких событий, так или иначе имеющих отношение к теме книги, что, возможно, не удивительно: начиналась подлинная революция в математике, предварившая великие потрясения и открытия конца ХIХ – начала ХХ вв. в физике, философии, искусстве, политике и др. Но об этом речь впереди, а в настоящем контексте упомянем немецкого ученого Р.Дедекинда, обосновавшего теорию действительных чисел и предложившего строгий аксиоматический метод введения чисел иррациональных (так называемые дедекиндовы сечения). Однако сейчас нас интересуют числа трансцендентные.
Что они собой представляют? По определению – это те, которые не могут быть корнем никакого многочлена с целыми коэффициентами, т.е. числа неалгебраические, что навряд ли много скажет нематематику. Противопоставление классов алгебраических и неалгебраических (трансцендентных) чисел, тем не менее, исключительно важно, поскольку с алгеброй принято связывать саму нашу логику. Впоследствии такие логики и были формализованы в алгебраическом виде (математическая логика). В таком случае, быть числом неалгебраическим как бы означает "быть нелогичным", что, собственно, и запечатлелось в названии: трансцендентные(снова, и еще более сильный, оксюморон: казалось бы, что "потустороннего" может быть в длине окружности? Но математики знают, о чем говорят).
Пропасть между алгебраическими и трансцендентными числами подчеркивается теорией множеств, ставшей еще одним достижением ХIХ в., особенно второй половины – Б.Больцано, Г.Кантор, Р.Дедекинд. Хотя алгебраических чисел – рациональных и иррациональных – существует бесконечное количество, но их множество, как выражаются, счетно. Это означает, что все такие числа – не на практике, конечно, а в принципе – можно пронумеровать, т.е. их "столько же", сколько чисел в натуральном ряду. Чисел же трансцендентных неизмеримо, качественно "больше". Их множество несчетно и, как говорят в таких случаях, имеет мощность континуума (т.е. трансцендентных чисел "столько же", сколько точек на непрерывной прямой). Возможность что-то пронумеровать – верный признак логичности, о чем же тогда свидетельствует отсутствие подобной возможности?
В прежней среде действительных чисел, но по-новому, была по сути развернута интеллектуальная драма, сходная с той, что некогда произошла при первой исторической встрече с иррациональными числами. К счастью, во второй раз математики оказались более подготовленными в морально-психологическом плане. Посмотрим, что у нас осталось в итоге.
Числа действительные (иначе их называют вещественными) делятся, во-первых, на рациональные и иррациональные, во-вторых, – на алгебраические и трансцендентные. В обоих случаях речь идет о характерной оппозиции: за числами одного сорта признается качество своеобразной "логичности", за числами другого сорта – нет. Сравнение в обоих контрастных противопоставлениях производится попарно, т.е. кратность отношений двойная, n = 2. Если свести вместе обе классификации, построенные над полем действительных чисел, то получится, что последнее состоит из чисел рациональных (целых и дробных), алгебраических иррациональных (наподобие ?2) и трансцендентных. Их разделение фиксирует скачкообразное убывание специфической "логичности" (мы уже знаем, в каком смысле). Изобразим классификацию на рисунке:

Рис. 1-3
Почему в итоге получилось три непересекающихся класса действительных чисел, т.е. почему М = 3? – Во-первых, в системе задано бинарное отношение сравнения ( n = 2 ); во-вторых, совокупность названных классов мыслится в качестве законченной и целостной. Откуда нам известно последнее? – От самих математиков, ибо они доказали так называемую теорему о полноте, утверждающую, что других классов действительных чисел не существует, сюрпризы с появлением новых не повторятся.
Наверное, стоит извиниться перед читателем за столь длинный и сложный пример, но все же он, надеюсь, короче, чем сама эта история длиной в 2,5 тысячи лет. Данным пассажем можно было бы и пренебречь, но беда в том, что впоследствии (в главе 3) нам еще придется встретиться с иррациональными числами и оттого неплохо бы знать, что за ними стоит. Пока же, коль все равно затрачены время и силы, грех не воспользоваться этим и не сформулировать некоторые полезные выводы, которые пригодятся для понимания и других паттернов.
Во-первых, мы имели случай лишний раз убедиться, что предлагаемая модель – элементарно-математическая по форме, культурологическая по функции – способна работать "поверх" (или "из-под низа") достаточно сложного концептуального материала. Простейшие числа – два и три – справляются с описанием итога длительной работы перворазрядных ученых, причем в данном примере – как раз в области чисел.
Во-вторых, хотелось дать получше почувствовать одну из особенностей нашей модели: она дескриптивна, мы не затронули и тысячной доли содержательного богатства идей упомянутых ученых (как ранее не пытались всерьез выяснить, что представляют собой, скажем, тело-душа-дух или небо-земля-преисподняя). В специальные работы мы практически не вникали, интересуясь лишь "сухим остатком" (для нас это количество элементов). Тем не менее наши выводы совпали с положениями самой математической науки.
В-третьих, небесполезно нагляднее показать не только подспудность схемы n = 2, М = 3, но и драму ее воплощения. Сейчас трудно установить, сколько тысячелетий или десятков тысячелетий потребовалось человеку, чтобы прийти к трехсоставности мироздания, трем лицам, трем временам и т.д., но исторические факты из последнего примера предоставляют шанс догадаться, сколько усилий стоит за подобными, казалось бы тривиальными, вещами. Как после этого мы должны к ним относиться? Достаточно ли мы их ценим?
Наконец, возник повод на новом материале напомнить о принципиальной неотделимости чисел и науки о них от мифологической подоплеки. Флером неизбывной загадочности окутано не только их первоначальное происхождение, но пуповина не была и не будет перерезана никогда. Это касается не только ранних, исторически не вполне достоверных этапов развития: у египетских жрецов, халдейских магов, индийских и китайских мудрецов, у склонных к мистериям пифагорейцев. Впоследствии получили широкую известность и веками тревожили воображение математиков задачи о трисекции угла, удвоении куба, квадратуре круга (и обратно: циркулятуре квадрата). Окончательно с ними разобрались сравнительно недавно, в прошлом веке, и, как выяснилось, проблемы непосредственно связаны с иррациональными и трансцендентными числами. Значение таких задач, как считалось, выходит далеко за границы математики, затрагивая саму тайну жизни и спасения,(15) что можно сравнить разве что с ролью философского камня и гомункулуса у средневековых алхимиков. Многозначительные предания складывались и вокруг не столь отдаленных математических событий. Вероятно, самое яркое из них – о большой, или великой, теореме Ферма, теснейшим образом связанной с соизмеримостью и несоизмеримостью чисел. Вокруг нее периодически поднимается ажиотаж, особенно на переломных исторических отрезках.
О мифологических или легендарных моментах в своей науке современные математики если и говорят, то не без застенчивости и главным образом в кулуарах: дисциплина требует точности и обязательности, а не игривости. Но подобная пуристская поза имеет и изнанку: в отличие от прежних эпох, между числом и мифом, вообще "живою культурой" возведена китайская или берлинская стена. Гуманитарии платят математикам (представителям точных наук) той же монетой, обороняя от них собственную заповедную вотчину, что становится одной из неотъемлемых черт трагедии современного духа, т.е. попросту отсутствия взаимного понимания, ментальной расщепленности.
В заключение экскурса по математике приведем (без обсуждения) еще одну тройку. Наряду с действительными числами, о которых речь только что шла, со школы известны и комплексные. В 1843 г. ирландец У.Гамильтон открыл еще один тип – кватернионы (записывающиеся в виде a + ib + jc + kd,где a, b, c, d– вещественные числа), а Фробениус доказал: все алгебры соответствующего сорта исчерпываются только тремя –алгеброй вещественных чисел, алгеброй комплексных чисел и алгеброй кватернионов [238, 154].
Тринитарные структуры широко распространены и в социальной области. В современных развитых странах принято различать богатый, среднийи бедныйклассы (М = 3); в основу деления положен элементарный критерий уровня доходов: выше или ниже. Подобное сравнение бинарно, n = 2. При этом общество признается единой системой, строение которой рационально.
Раскрывая генезис названного членения, специалисты по ХХ в. обращают внимание, что еще в начале столетия осевой линией социального напряжения был конфликт между богатством и бедностью и что лишь десятилетия последовательных усилий правительств позволили сформировать представительный средний класс, превратившийся в залог общей стабильности. Мало того, и век, и даже полвека назад в массовом сознании доминировала иная, "марксистская" схема членения. Потребовались настойчивая пропагандистская работа и целый ряд реформационных шагов, чтобы внушить народам веру в справедливость чисто денежного подхода, утвердить стандарты общества потребления. Усилия увенчались успехом, и пропасть между богатыми и бедными заполнилась многочисленным средним классом, подставившим плечо системе в целом, разделившим с богатыми заинтересованность в сохранении status quo (поэтому подобное устройство зачастую называют "обществом двух третей"). При этом и бедные – за исключением политических маргиналов – в большинстве признают обязательность общей картины, т.к. проникнуты той же консюмеристской идеологией.
Причины бедности как явления, т.е. причины существования бедного класса, обычно ищут в сфере позитивных фактов: в особенностях института собственности, системы оплаты труда, в несовершенстве социальных программ, дефектах воспитания и образования рекрутов бедности и даже во врожденных психологических чертах, не исключая национальной и расовой принадлежности. На наш взгляд, нет ничего более далекого от существа вопроса. Названные и подобные им обстоятельства в состоянии дать лишь одно объяснение: почему именно эти, а не иные, субъекты (индивиды, группы) оказались среди бедных, тогда как прочие вкушают достаток или богатство. Сам факт наличия бедного класса такими подходами если и затрагивается, то только по касательной: ведь если данному субъекту и удастся преодолеть предпосылки собственной бедности, в ряды бедных непременно попадет другой. Феномен бедности неискореним по совершенно отличной причине.
Его корни, так сказать, в головах, в организующей силе самой идеологии потребления, побуждающей людей делиться по толщине кошелька, согласно ординарному критерию "больше/меньше", n = 2. Если общество признается при этом целостным – а это также удается внушить: "Мы – одна нация", – то социальных классов автоматически три, и значит, один из них неизбежно подпадает под рубрику бедного. Технологический прогресс, повышение ВНП на душу населения без смены самой парадигмы в состоянии повлиять разве что на конкретные признаки бедности: очевидно, что уровень жизни, скажем, американских бедных вполне сравним, если не выше, чем у вполне респектабельных граждан из не столь процветающей страны. Зато последние куда благополучнее в собственном статусе, пользуются уважением и самоуважением, утверждаясь на фоне бедных соотечественников.
Нас, впрочем, не интересуют детали: ни исторический путь западных обществ, ни изыскания социологов. Важен лишь конечный итог: социальная система трехчастна, и теперь мы не удивляемся, почему.
Коль поднят вопрос о социальных структурах, несправедливо обойти вниманием доиндустриальную эпоху. Деление на сословия: дворянство, духовенствои весьма неоднородное третье, – классическое для абсолютистской Европы, особенно для Франции, вплоть до Великой революции. Из трех, господствующими признавались два, они воплощали в себе светскую и духовную ипостаси государства. Хотя отношения между папским престолом и монархами на международной арене, между Церковью и светскими властями в пределах каждой из стран не всегда отличались безоблачностью, их совместная деятельность признавалась необходимым условием для сохранения христианскогохарактера государства и общества. Без покровительства небес, без помазания не мыслились полномочия королей и императоров. Без благодати Церкви, без исповеди и причастия каждого из людей ждала вечная погибель. Но дела земные – в компетенции трона и светских властей, по крайней мере, с тех пор, как везде, за исключением собственно Рима, светские владыки отстояли свои права. Телами распоряжается одна сторона, душами – другая. Первые два сословия и институализировали сии непреложные истины. Социальный фундамент составляла, таким образом, неразрывная пара, n = 2. Поэтому в обществе в целом сословий должно было быть именно три, М = 3.
Еще Платон в "Государстве" полагал идеальным устройством наличие трех сословий: правителей, стражейи так называемое третье сословие, куда включались крестьяне, ремесленники, торговцы и т.д. Разделению социальных функций отвечала специализация трех добродетелей: мудрости, мужества и послушания, – в полном согласии с тем, что человеческая душа состоит из трех частей: разумной, вожделеющей и растительной.(16) Несмотря на то, что абсолютистский социальный канон предметно отличался от платоновского, он ничуть не менее последователен и, следовательно, трехсоставен.
Европейское средневековье придерживалось близкой модели. Вот что пишет известный отечественный медиевист А.Я.Гуревич: "Рассуждая об общественной жизни, средневековые богословы и писатели прибегали к обобщенным абстрактным схемам ‹…› Наиболее распространенной и авторитетной была схема тройственного деления общества в зависимости от функций, которые выполняют члены того или иного разряда – ordo. Согласно этой схеме общество представляет собой иерархическое сочлененное единство, все компоненты которого служат целому. Эти компоненты суть ordo людей, которые молятся (oratores), ordo людей, которые сражаются (bellatores), и ordo людей, которые трудятся (laboratores), или, более конкретно, пашут землю (aratores). Если под первыми разумелось духовенство и монашество, а под вторыми – рыцари, министериалы и прочие воины, то в состав третьего разряда попадали и крестьяне, и ремесленники, и купцы" [111, с. 198].
Сословное членение христианских государств можно усовершенствовать – ведь третье сословие абсолютистской Франции, как, впрочем, и в проекте Платона, в средневековых теориях, получилось пестрым, как Ноев ковчег. И прецедент более детального регламента не преминул родиться. Согласно Уложению 1762 г., в России было введено пять сословий. Два первых их них совпадали с французскими, тогда как другие три: купечество, мещанство, крестьянство, – соответствовали французскому третьему:
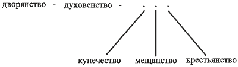
Рис. 1-4
Деление третьего сословия на три части подспудно существовало и раньше. Й.Хейзинга ссылается на незамысловатые миниатюры в календаре-часослове с фигурами усердного хлебопашца, прилежного ремесленника, деятельного торговца [360, с. 63], в России же данное представление было институализировано (следы социальной тройственности наблюдались в Росии и до 1762 г.: согласно петровской табели о рангах, различались три вида государственной службы – военная, статская, придворная, но в подробности едва ли целесообразно вдаваться).
Схема на рис. 1-4 полностью идентична той, что отражает систему личных местоимений (рис. 1-1). Логическое членение при этом тринитарно. Русское сословное уложение повторяло грамматические азы, само став своеобразной "грамматикой" общества вплоть до 1917 г. Россия пришла к абсолютизму позже законодателей европейских социально-политических мод и, учтя концептуальную "недостаточность" французской модели, ее нормативную "грубость", внесла несомненное усовершенствование – причем, в канун Великой французской революции, вообще отменившей сословия. Ирония: "Телега получилась прекрасной, жаль только, другие пересели на паровоз", – представляется неуместной, поскольку мы заняты исключительно числами, а перед ними равны все, не исключая – см. классы богатый, средний и бедный – и нынешних водителей человечества.
Что стоит за предписанием либеральной доктрины о разделении и балансе властей: законодательной, исполнительнойи судебной? У этой идеи, ближайшие истоки которой восходят к Дж.Локку, Ш.Монтескье, к школе естественного права, довольно долгая предыстория.
Непосредственно она родом из эпохи Просвещения, считавшей рассудок мерилом всего, в частности полагавшей, что государственное управление должно быть рациональным. Подход не слишком оригинальный: той же мысли придерживался и Платон, равно как и заключения, что разумное управление способны осуществлять только разумные, образованные люди и потому руководить обществом следует философам. Два тысячелетия спустя настоящее предложение очень понравилось английским и французским философам, которые не только подхватили эстафету, но и многое привнесли от себя. Проект Просвещения предполагал широкое распространение образования, а где знания, разум – там должна быть и власть ("Знание – сила", – утверждал еще Ф.Бэкон). Как философы делятся знаниями с остальными, так и монарх во имя Разума, Справедливости должен поделиться властью с лучшими из подданных.
Первоначально речь шла не об отлучении королей от государственного кормила, а только о разделении полномочий между государем и собранием ученых мудрецов, умеющих придумывать и толковать законы на все случаи жизни. Подобная версия и поныне питает розовые мечты интеллигенции о просвещенном правлении, под сенью которого процветают высокие науки и искусства, а невежество посажено под крепкий замок.
Фактическое разделение власти между монархом и законодательным органом существовало еще до Локка и французских просветителей. Правда, в дореволюционной Франции парламент обладал скорее законосовещательными, чем полноценными законодательными полномочиями – и в этом смысле напоминал Сенат в России, который вдобавок не был выборным, не представлял всех сословий. Но на Британских островах со времен Великой английской революции, начавшейся с выхода из повиновения "Долгого" парламента [35], последний обрел должный вес. Пользуясь словами Ф.Броделя: "Разделение политической власти между парламентом и монархией в 1660 г., в момент Реставрации и в еще большей степени после Декларации прав 1689 г., было по преимуществу началом разделения, имевшего долговременные последствия" [62, с. 617]. Но в новых исторических условиях – в эпоху разума и Просвещения – требовался не отдельный и оттого, возможно, случайный, прецедент, а общее правило. Это правило необходимо сформулировать и прописать, чтобы с ним всегда можно было бы свериться и, следовательно, избежать нарушений. Вклад английских и особенно французских просветителей, собственно, и заключался в возведении разделения властей в рациональный и общеобязательный принцип.
История вопроса полна трогательных подробностей. Философы пытались убедить монархов, как своих, так и чужих, уступить долю власти добровольно. Французские просветители вступают в оживленную переписку с русской Екатериной II, Великой, с прусским Фридрихом II, тоже Великим. Из переписки, естественно, ничего толком не вышло. Как отмечает один из биографов Фридриха II [436, S. 179], последний разделял с Гельвецием, Гольбахом, Руссо и другими властителями дум симпатию к народному просвещению, но при этом не присоединялся к мнению, что просвещенное или способное к просвещению общество должно быть гарантом проведения политических преобразований, что оно должно ограничивать полномочия самодержца, чтобы воспрепятствовать всякому нанесению вреда. "Это был именно тот пункт, в котором Фридрих II вступил в противоречия с французскими идеологами и радикальными немецкими просветителями" [там же]. Таким образом, на деле разум не всегда оказывался всемогущим, что, впрочем, не препятствовало его уверенному царствованию в рамках доктрины. Значит, допустимо судить согласно рациональным критериям и о ней самой.
Идея разделения властей предельно не нова – наряду с приведенными примерами, существуют и более почтенные по возрасту. Еще в первобытных племенах полномочия распределялись между вождем и шаманом (жрецом, колдуном), в средневековой Европе – между Церковью и королями, а в Византии действовало специальное учение о симфониидвух властей: духовной и светской, – в их общем служении Божьему Замыслу. Либерализм, однако, внес качественные коррективы. Свобода совести, отделение Церкви от государства – лозунги, начертанные на его знаменах. Разделению предстояло пройти по телу оставшейся единственно общеобязательной светской, государственной власти. В первом варианте, как сказано, – разбить полномочия между монархом и законодательным органом, парламентом, с таким расчетом, чтобы ограничить произвол, который всегда противен Разуму и Справедливости. С самого начала, таким образом, присутствовала бинарная оппозиция, n = 2.
Пали или отошли в тень монархии, но принцип не только выжил, но и расцвел. Зрелый вид он принял в США, и до сих пор действующую там систему разделения и баланса властных ветвей предъявляют в качестве образца для политических недорослей.
И все-таки почему ветвей три? С одной стороны, государственная власть рассматривается как самостоятельный, целостный феномен, с другой – его можно и нужно делить на счетное количество компонентов. Причем, членение осуществляется согласно "здравой", т.е. бинарной, логике: каждая из ветвей призвана ограничивать любую другую. "Вся эволюция системы "сдержек и противовесов" в США вращается вокруг конфронтации исполнительной и законодательной властей", – конкретизирует обозреватель [339, с. 48]. Ergo: М = 3, см. модель. Для чего же потребовалось столько предварительных слов? – Из осторожности, поскольку априори неясно, насколько корректен в подобных вопросах чисто рациональный подход. Скажем, если власть священна или зиждется исключительно на традициях, любое обсуждение неуместно: ее либо принимают, либо становятся святотатцем. К примеру, рыцарственный православный монарх Николай I воспрещал не только хулу, но и одобрение того, что идет от престола (от одобрения до хулы – один шаг, главное – не рассуждать).
И еще одно. Хотя один из ведущих юристов ФРГ, К.Хессе, и утверждает, что принцип разделения властей – не естественно-правовая догма, а исторически сложившийся принцип [там же], исторические реалии в состоянии бросить свет не более чем на обстоятельства его открытия и принятия, но никак не на рациональную суть. Так, теорема Пифагора была доказана в определенных культурно-исторических условиях, затем два с половиной тысячелетия транслировалась в обществе, признававшем ценность такой трансляции, но отсюда вовсе не вытекает, что ее сущность и смысл являются историческими. Подобные вопросы, впрочем, выходят за пределы компетенции правоведов. Но и обратно: использованный здесь подход навряд ли в состоянии удовлетворить запросы представителей юридической науки. В логико-числовом контексте мы отвлеклись от наиболее репрезентативных философских обоснований целостности системы государственной власти, от учения о правовом государстве, скажем в версии Канта.(17) Сфера права автономна по отношению к этической сфере (как морали, так и нравственности), и как раз в ее строгих рамках совокупность трех ветвей обретает концептуальную полноту, замкнутость, связность. В поставленные же нами цели не входило раскрытие предметного содержания идеи трех властей: мы по-прежнему заняты самыми простыми вещами – числами. К проблеме структуры государственной власти предстоит вернуться в
